Skip to main content
SpringerLink
Log in

Modified Cholesky algorithms: a catalog with new approaches

  • FULL LENGTH PAPER
  • Published:
Mathematical Programming Submit manuscript

Abstract

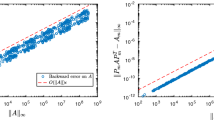
Given an n ×  n symmetric possibly indefinite matrix A, a modified Cholesky algorithm computes a factorization of the positive definite matrix A +  E, where E is a correction matrix. Since the factorization is often used to compute a Newton-like downhill search direction for an optimization problem, the goals are to compute the modification without much additional cost and to keep A +  E well-conditioned and close to A. Gill, Murray and Wright introduced a stable algorithm, with a bound of ||E||2 =  O(n 2). An algorithm of Schnabel and Eskow further guarantees ||E||2 =  O(n). We present variants that also ensure ||E||2 =  O(n). Moré and Sorensen and Cheng and Higham used the block LBL T factorization with blocks of order 1 or 2. Algorithms in this class have a worst-case cost O(n 3) higher than the standard Cholesky factorization. We present a new approach using a sandwiched LTL T-LBL T factorization, with T tridiagonal, that guarantees a modification cost of at most O(n 2).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Aasen J.O. (1971). On the reduction of a symmetric matrix to tridiagonal form. BIT 11(3): 233–242

    Article  MathSciNet  MATH  Google Scholar 

  2. Ashaft C., Grimes R.G. and Lewis J.G. (1998). Accurate symmetric indefinite linear equation solvers. SIAM J. Matrix Anal. Appl. 20(2): 513–561

    Article  Google Scholar 

  3. Bunch J.R. and Kaufman L. (1977). Some stable methods for calculating inertia and solving symmetric linear systems. Math. Comp. 31: 163–179

    Article  MathSciNet  MATH  Google Scholar 

  4. Bunch J.R. and Parlett B.N. (1971). Direct methods for solving symmetric indefinite systems of linear equations. SIAM J. Numer. Anal. 8(4): 639–655

    Article  MathSciNet  Google Scholar 

  5. Cheng, S.H.: Symmetric Indefinite Matrices: Linear System Solvers and Modified Inertia Problems. PhD thesis, University of Manchester (1998)

  6. Cheng S.H. and Higham N.J. (1998). A modified Cholesky algorithm based on a symmetric indefinite factorization. SIAM J. Matrix Anal. Appl. 19(4): 1097–1110

    Article  MathSciNet  MATH  Google Scholar 

  7. Cuppen J.J.M. (1980). A divide and conquer method for the symmetric tridiagonal eigenproblem. Numer. Math. 36(2): 177–195

    Article  MathSciNet  Google Scholar 

  8. Demmel, J.W.: Applied Numerical Linear Algebra. SIAM (1997)

  9. Fang, H.-r.: Matrix Factorization, Triadic Matrices, and Modified Cholesky Factorizations for Optiimization. PhD thesis, University of Maryland (2006)

  10. Fang, H.-r., O’Leary, D.P.: Modified Cholesky algorithms: A catalog with new approaches. Technical Report CS-TR-4807, Computer Science Department, University of Maryland (2006)

  11. Fang H.-r. and O’Leary D.P. (2006). Stable factorizations of symmetric tridiagonal and triadic matrices. SIAM J. Matrix Anal. Appl. 28(2): 576–595

    Article  MathSciNet  MATH  Google Scholar 

  12. Forsgren A., Gill P.E. and Murray W. (1995). Computing modified Newton directions using a partial Cholesky factorization. SIAM J. Sci. Comput. 16(1): 139–150

    Article  MathSciNet  MATH  Google Scholar 

  13. Gill P.E. and Murray W. (1974). Newton-type methods for unconstrained and linearly constrained optimization. Math. Program. 28: 311–350

    Article  MathSciNet  Google Scholar 

  14. Gill P.E., Murray W. and Wright M.H. (1981). Practical Optimization. Academic, New York

    MATH  Google Scholar 

  15. Horn R.A. and Johnson C.R. (1985). Matrix Analysis. Cambridge University Press, Cambridge

    MATH  Google Scholar 

  16. Moré J.J. and Sorensen D.C. (1979). On the use of directions of negative curvature in a modified Newton method. Math. Program. 16: 1–20

    Article  MATH  Google Scholar 

  17. Parlett B.N. and Reid J.K. (1970). On the solution of a system of linear equations whose matrix is symmetric but not definite. BIT 10(3): 386–397

    Google Scholar 

  18. Schnabel R.B. and Eskow E. (1990). A new modified Cholesky factorization. SIAM J. Sci. Stat. Comput. 11: 1136–1158

    Article  MathSciNet  MATH  Google Scholar 

  19. Schnabel R.B. and Eskow E. (1999). A revised modified Cholesky factorization algorithm. SIAM J. Optim. 9(4): 1135–1148

    Article  MathSciNet  MATH  Google Scholar 

  20. Stewart G.W. (1980). The efficient generation of random orthogonal matrices with an application to condition estimation. SIAM J. Numer. Anal. 17: 403–409

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Computer Science and Engineering, University of Minnesota, 200 Union Street, Minneapolis, MN, 55455, USA

    Haw-ren Fang

  2. Department of Computer Science and Institute for Advanced Computer Studies, University of Maryland, A.V. Williams Building, College Park, Maryland, MD, 20742, USA

    Dianne P. O’Leary

Authors
  1. Haw-ren Fang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Dianne P. O’Leary
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dianne P. O’Leary.

Additional information

H.-r. Fang’s work was supported by National Science Foundation Grant CCF 0514213.

D. P. O’Leary’s work was supported by National Science Foundation Grant CCF 0514213 and Department of Energy Grant DEFG0204ER25655.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Fang, Hr., O’Leary, D.P. Modified Cholesky algorithms: a catalog with new approaches. Math. Program. 115, 319–349 (2008). https://doi.org/10.1007/s10107-007-0177-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10107-007-0177-6

Keywords

Search

Navigation