Hydraulic properties of porous sintered glass bead systems

Abstract

In this paper, porous sintered glass bead packings are studied, using X-ray Computed Tomography (XRCT) images at $16\,\upmu \hbox {m}$ voxel resolution, to obtain not only the porosity field, but also other properties like particle sizes, pore throats and the permeability. The influence of the sintering procedure and the original particle size distributions on the microstructure, and thus on the hydraulic properties, is analyzed in detail. The XRCT data are visualized and studied by advanced image filtering and analysis algorithms on to the extracted sub-systems (cubes of different sizes) to determine the correlations between the microstructure and the measured macroscopic hydraulic parameters. Since accurate permeability measurements are not simple, special focus lies on the experimental set up and procedure, for which a new innovative multi-purpose cell based on a modular concept is presented. Furthermore, segmented voxel-based images (defining the microstructure) are used for 3D (three-dimensional) lattice Boltzmann simulations to directly compute some of the properties in the creeping flow regime. A very good agreement between experimental and numerical porosity and permeability could be achieved, in most cases, validating the numerical model and results. Porosity and permeability gradients along the sample height could be related to gravity acting during sintering. Furthermore, porosity increases in the outer zones of the samples due to the different contact geometry between the beads and the confining cylinder wall during sintering (which is replaced by a membrane during permeability testing to close these pores at the surface of the sample). The influence of different filters on the gray scale distributions and the impact of the segmentation procedure on porosity and permeability is systematically studied. The complex relationships and dependencies between numerically determined permeabilities and hydraulic influence parameters are investigated carefully. In accordance to the well-known Kozeny–Carman model, a similar trend for local permeability values in dependence on porosity and particle diameter is obtained. Other than statistical models, which estimate the pore throat distribution on the basis of the particle size distribution, in this study XRCT scans are used to determine the pore throats in sintered granular systems, which are finally linked to the intrinsic permeability through the lattice Boltzmann simulations. From the $\mu$XRCT analysis two distinct peaks in pore throat distributions could be identified, which can be clearly assigned to typical pore throat areas occurring in polydisperse granular systems. Moreover, a linear dependency between average pore throat diameter and porosity as well as between permeability and pore throat diameter is reported. Furthermore, almost identical mean values for porosity and permeability are found from sub-system and full-system REV analysis. For sintered granular systems, the empirical constant in the classical Kozeny–Carman model is determined to be 131, while a value of 180 is expected for perfect mono-disperse sphere packings.

1 Introduction

Numerical and experimental investigations of fluid flow in porous and granular media are of crucial importance in many research areas, such as the recovery of hydrocarbons from oil reservoirs [4, 5], ground water flow [6] or gas diffusion in fuel cells [7]. In spite of extensive scientific research, there are still many open questions namely which and how macroscopic transport factors other than porosity affect the fluid flow in a porous medium with a given microstructure [7,8,9,10,11]. An experimentally and numerically determinable parameter of porous materials is the intrinsic permeability which is highly sensitive to the underlying microstructure. The effective intrinsic permeability depends only on the pore structure of the medium, that is independent of the properties of the fluid. Therefore, a comparison with numerical determined permeability values based on Micro-X-Ray-Computer-Tomographic ($\mu$XRCT) images can increase the understanding of the effects of microstructure on the intrinsic permeability [12,13,14]. The typical workflow of $\mu$XRCT-based permeability investigations comprises

• 1. the $\mu$XRCT-scanning and reconstruction of the porous material;

• 2. the filtering and segmentation of the image data;

• 3. the implementation of image data in numerical simulations;

• 4. validation of numerical calculations with experimental data;

• 5. finding new correlations between microstructure and macroscopic properties by combining the previous steps and insights.

The presented workflow clearly demonstrates that a numerical simulation based on real data sets and the correlation between microscopic and macroscopic properties can be only be as good as the preceding filtering and segmentation procedure [15,16,17,18,19]. Therefore, a special focus lies on this topic. Possible ways are presented how to filter, segment and finally extract essential features of a porous material, which determine the intrinsic permeability.

In this work we investigate, both experimentally and numerically, the intrinsic permeability of artificial produced samples composed of sintered glass beads showing different particle diameters, porosities and degree of polydispersity. In contrast to common rock samples, like e.g. dolomite, sintered glass bead samples are characterized by their chemical stability and inertness, in addition to their relatively simple pore structure. Nevertheless, the pore structure, and thus the intrinsic hydraulic permeability can be influenced by the selection of certain glass beads and special sintering treatments. Another crucial advantage of sintered glass bead samples, in contrast to most rock samples, is the improved gray-scale contrast between the pore space and the solid phase, which considerably simplifies the image segmentation process and thus ensures a better comparability of experimentally and numerically determined permeability values. The filtering and segmentation procedure of sintered glass bead packings is further simplified by single phase composition of the solid matrix. In this respect, sintered glass bead samples can serve as replacement material for soil and rock specimen to provide a benchmark in permeability calculations.

The present paper focuses on the hydraulic properties of porous sintered glass bead systems. The influence of the sintering process on the microstructure, and thus on the permeability of the sintered samples are analyzed in detail by using appropriate XRCT data analysis and visualization methods (AVIZO Fire 8.0.1 and 9.0). In Sect. 2 the well-known Darcy’s law is introduced to define the intrinsic permeability of porous materials in general. Furthermore, the semi-empirical Kozeny–Carman equation, which is often used to determine the intrinsic permeability of granular systems, is presented and discussed in terms of microstructural parameters. In Sect. 3 the Lattice Boltzmann (LB) method and the numerical set-up, which is used to determine the local intrinsic permeabilities of the extracted data sets, is described briefly. For a better understanding of the underlying microstructure, the sintering procedure is described in Sect. 4.1. For validation of numerical data based on discretized $\mu$XRCT/voxel data sets of the produced sintered glass bead samples, the experimental setup and procedure of permeability measurements are described in Sect. 4.2. The developed multi-purpose measuring cell is proposed in Sect. 4.3. Section 5 focuses on the elaborate processing of $\mu$XRCT scans, whereby possible ways are introduced, how to filter, segment and extract essential features, which highly influences the hydraulic properties of porous sintered granular systems. Section 6 starts with presentations and discussion of results obtained from numerical and experimental porosity and permeability measurements. In addition, the results from REV analysis for porosity and permeability and the peripheral porosity development of the samples are depicted and discussed in Sect. 6.1. Moreover, the numerically determined local permeability values are qualitatively and quantitatively compared with the theoretical predictions according to the Kozeny–Carman model. The results for pore throats and their dependency on the porosity and intrinsic permeability is presented and discussed in Sect. 6.2. The study of hydraulic properties of porous sintered granular packings is concluded inSect. 7.

2 Theory

Darcy’s law is the most commonly used empirical relationship for calculation of the pressure drop across a homogeneous, isotropic and non-deformable porous medium [20, 21]. It states that, at the macroscopic level and in the creeping flow regime, the measured pressure drop $\varDelta p/l$ per length applied to a porous medium, and the fluid flux per area $Q_{z}/A$ have a linear relationship given by

$$\begin{aligned} \frac{Q_{z}}{A} = -\frac{k_{z}^{s}}{\mu ^{fR}} \; \overbrace{\left( \frac{\varDelta p}{l} - \rho ^{fR}g\right) }^{=i}, \end{aligned}$$

(1)

where $\mu ^{fR}, A$ and l are dynamic viscosity of the fluid, cross-sectional area and length of the sample [22]. The proportionality constant $k_{z}^{s}$ describes the intrinsic permeability of the porous medium in flow direction z, which strongly depends on the porosity and the microstructure (e.g. particle shape, tortuosity and connectivity of pore channels). The term $\rho ^{fR}\,g$ represents the gravity force-density, driving the fluid flow. The expression given in brackets is often referred to as the hydraulic gradient i.

The semi-empirical approach of Kozeny–Carman is one of the most well-known theories, which relates macroscopic parameters, like the intrinsic permeability, to microstructural parameters, like particle arrangement, shape and orientation or tortuosity (flow path) [20, 23,24,25]. For granular media, the Kozeny–Carman permeability reads

$$\begin{aligned} k_{z}^{s} = \frac{1}{2} \; \frac{\phi ^3}{(1-\phi )^2} \; \left( \frac{1}{\alpha } \right) ^2 \; \left( \frac{1}{S_v} \right) ^2, \end{aligned}$$

(2)

where $S_v$ and $\alpha$ are the volume-based specific surface area and tortuosity of the fluid path. The porosity of the sample is denoted as $\phi$. For monodisperse granular media consisting of particles with diameter $d_p$ the intrinsic permeability is given by

$$\begin{aligned} k_{z}^{s} = \frac{1}{180} \; \frac{\phi ^3}{(1-\phi )^2} \; d_{p}^2. \end{aligned}$$

(3)

Since in most investigated cases the granular medium consists of non-uniform spheres, Carrier [26] have introduced an effective diameter $d_r$ which can be reliably determined on basis of the particle size distribution in accordance with

$$\begin{aligned} d_{r} = \frac{100}{ \sum f_{i} / \bar{d}_{i} }, \end{aligned}$$

(4)

where $f_{i}$ is the fraction of particles between two sieve sizes and $\bar{d}_{i}$ corresponds to the geometrical average particle size between the minimum and maximum sieve size ($d_{min,i}, d_{max,i}$)

$$\begin{aligned} \bar{d}_{i} = \sqrt{d_{min,i} \cdot d_{max,i}}. \end{aligned}$$

(5)

For monodisperse granular media the median diameter $d_{50}$ is commonly used as effective diameter due to the little variation in grain size. The median diameter is the value of the particle diameter at 50% in the cumulative distribution. In the case of a nearly symmetric particle size distribution, the median diameter is often replaced by the arithmetic mean value.

Several approaches have been introduced in recent years to describe the tortuosity (fluid path) in Eq. (2) through porous media [11, 23, 24, 27].

3 The lattice Boltzmann method

For the determination of the numerical intrinsic permeabilities of the extracted differently sized subsets of glass beads the lattice Boltzmann method is used. We follow the procedure to measure permeabilities as described in Narváez et al. [28, 29], Frijters [30] and Frijters and Harting [31]. The LB method itself has proven to be very successful for modeling fluid flow in porous media [32]. It enables a straightforward implementation of complex boundary conditions and is suitable for use in parallel computation due to the high degree of locality of the algorithm. For the LB simulations the Boltzmann equation

$$\begin{aligned} \frac{\partial }{\partial t} f(\mathbf x ,\mathbf c ,t) + \mathbf c \cdot \nabla f(\mathbf x ,\mathbf c ,t) = \varOmega (f(\mathbf x ,\mathbf c ,t)) \end{aligned}$$

(6)

in discretized form is solved to simulate creeping fluid flow through porous media. Equation (6) describes the evolution of a single-particle probability density $f(\mathbf x ,\mathbf c ,t)$, whereby $\mathbf x \in \mathbb {R}^3$ is the position vector, $\mathbf c \in \mathbb {R}^3$ is the velocity vector, t$\in \mathbb {R}$ is the time and $\varOmega (f(\mathbf x ,\mathbf c ,t))$ is the collision operator describing binary collisions between particles. The time discretization is performed by using a time step $\varDelta t$, whereas for the lattice velocities a finite set of vectors $\mathbf c _i$ with $i=1 \ldots 19$ lattice points is applied. The position vector $\mathbf x$ is discretized by using a three-dimensional structured cubic lattice with a lattice constant $\varDelta x$. For the permeability calculations the simulation parameters are chosen in accordance to Narvaez et al. [29], Frijters [30] and Frijters and Harting [31]. As in those publications the well-known D3Q19 lattice for velocities, providing adequate accuracy at moderate computational cost is applied [33]. For the collision matrix $\varOmega$ in Eq. (6) a standard two relaxation time (TRT) model is used, cf. Refs. [29, 34]. Narváez et al. [28, 29] have shown that relaxation times of $\tau =1$ and $\tau _{bulk}=0.84$ provide useful results for permeability calculations.

The porous sample is positioned between two fluid chambers which serve as in- and output to avoid artifacts, cf. Fig. 4a. The on-site boundary condition introduced by Zou and He [35] and later extended to three dimensions and nineteen velocities (D3Q19) by Hecht and Harting [36] is applied to generate a gradient in flow direction (z-direction) by defining the fluid densities at the in- and outlet of the system,

$$\begin{aligned} \rho ^{fR}(z=1)&= 1 +\varDelta \rho ^{fR}, \end{aligned}$$

(7)

$$\begin{aligned} \rho ^{fR}(z=n_{z})&= 1 -\varDelta \rho ^{fR}, \end{aligned}$$

(8)

whereby $n_{z}$ indicates the total number of lattice nodes in flow direction and $\varDelta \rho ^{fR}$ the difference of the fluid density between in- and outlet. To ensure creeping flow with low Reynolds numbers the density difference is chosen in the order of 10$^{-4}$ in lattice units. Furthermore, the computational domain is surrounded by walls in x- and y-directions to prevent flow over boundaries orthogonal to the pressure gradient. The pressure gradient in flow direction z reads then as

$$\begin{aligned} (\nabla p)_{z} = \frac{p(z=n_{z}) - p(z=1)}{n_{z}} = \frac{2 \, \varDelta \rho ^{fR}}{3 \, n_{z}}. \end{aligned}$$

(9)

The intrinsic permeability $k^{s}_{z}$ in flow direction z can be expressed in terms of the lattice Boltzmann relaxation time as

$$\begin{aligned} k^{s}_{z} = \frac{2 \, \tau - 1}{6} \; \frac{3 \, Q_{z} \, n_z}{2 \, \varDelta \rho ^{fR} \, (n_{z} \, n_{y})}, \end{aligned}$$

(10)

whereby $A=n_{z} \,n_{y}$ represents the cross-sectional area of the extracted subset, $n_{z}$ the sample length and $Q_{z}$ the volume flux in z-direction. The system has reached steady state when the mass flux and the permeability are constant over the geometry [29, 30]. For the determination of the permeability of the differently sized samples in flow direction z the permeabilities are averaged over the lattice surfaces in flow direction z.

4 Experiments

4.1 Sintering

In this study various types of glass with different chemical compositions and characteristic particle diameters were used for sintering, see Table 1. The characteristic diameters in Table 1 are obtained from laser granulometry measurements (Mastersizer 2000, Malvern Instruments Ltd.) before the glass beads were sintered. The glass beads were supplied from Muehlmeier GmbH & Co. KG, Germany.

Table 1 Material parameters and characteristic particle diameters of the investigated glass beads in their state before sintering. The sample with the biggest particles had a larger sintering time and larger size (50mm) than the others (30mm), which possibly explains their deviation. The REV sizes from the larger bead samples, as used for LB-simulations, are maybe not representative since there are not enough particles (and thus poor statistics) for a proper comparison with experimental effective permeability results

Depending on the composition, the deformation temperature of the used glass particles varied between 575 and $680~^\circ \hbox {C}$. The used glass beads showed different particle sizes and degree of polydispersity, cf. Table 1. The specific density of the sintered glass beads was at $2.5~\hbox {g/cm}^3$.

It was attempted to generate cylindrical samples and at the same time to ensure the smallest possible deformation of the beads during the sintering process, see also Ref. [39]. The produced cylindrical samples had bulk diameters of 30 and 50 mm, and the lengths of the specimens were 50 mm. Figure 1a shows the experimental sintering set-up for the glass beads.

Fig. 1

Experimental arrangement for sintering (a) and measured temperature curves at five different furnace zones (b)

The sintering of the glass beads were performed in a tubular furnace with heat power of 0.7 kW and a nominal target temperature of $1000~^\circ \hbox {C}$ under atmospheric conditions. The induction furnace was equipped with three programmable temperature controllers (type West 5010) regulating the inner temperature at three different furnace zones. The temperature progression within the furnace was monitored continually at five different places during the sintering process using thermocouples (type K), see Fig. 1a. The measured temperature curves are depicted in Fig. 1b. The glass beads were filled in a quartz glass cylinder (with inner diameters of approximately 30 and 50 mm) and completely enclosed with graphite paper. The melting temperature of the quartz glass cylinder is around $1713~^\circ \hbox {C}$ and thus certainly higher than the deformation temperature of the glass beads (${\approx } 690~^\circ \hbox {C}$). The graphite paper prevented an adhesion or sticking between the beads and the cylinder. The glass beads were manually shaken prior to sintering to reach the closest glass bead packing. The samples were subsequently loaded from the top with different masses ranging between 100 and 300 g corresponding to pressures of 1.39 and $4.16~\hbox {kN/m}^2$ for samples with 30 mm diameter or 0.50 and $1.50~\hbox {kN/m}^2$ for samples with 50 mm diameter, respectively. As can be seen in Fig. 1b the glass beads were heated up with a constant temperature rate of $300~^\circ \hbox {C}$ per hour until the required sintering temperature of $695~^\circ \hbox {C}$ was reached. Holding the beads at this temperature for approximately 2.5 h, the specimen was finally cooled down in an uncontrolled manner by switching off the furnace, cf. temperature curve at position 3 in Fig. 1b. Since the prepared samples were placed centrally in the furnace, only the temperature curve at position 3 is of major relevance. The preprogrammed target temperature of $695~^\circ \hbox {C}$ in the outer zones (position 1 and 5) was not reached due to large heat losses at the top and bottom of the furnace whereas the target temperature at positions 2 and 4 was reached, but delayed by approximately 1–2 h.

Depending on the chemical composition, bead diameter, dead loads of the used masses and sintering duration, the initial heights of the untreated specimens shrank by 1–5 mm. After sintering the samples were cut by a diamond disc to the desired length of 50 mm.

4.2 Permeability measurement set-up

Technical requirements on precise hydraulic measurements are very high [40,41,42]. Therefore, an elaborate setup was built for the stationary permeability measurements, to guarantee proper comparability between numerical and experimental permeabilities, see Fig. 2a.

Fig. 2

Experimental set up for stationary permeability experiments (a) and detailed construction drawing of the multi-task measuring cell in mode for permeability measurements (b)

To minimize the content of air bubbles and to guarantee for reproducible experimental results, use was made of filtered and de-aired water. For this purpose, the water was mechanically filtered in various filter stages until reaching a degassing tank, where the filtered water was de-aired.

The measuring cell including the hose connections were rinsed with carbon dioxide before the cell was flooded with filtered and de-aired water. The carbon dioxide easily dissolves in water. In this way, the content of air bubbles in the cell was minimized and an optimal water saturation of the sample was achieved.

The stationary permeability experiments were performed by controlling the volumetrical flux through the pressure regulator of the degassing tank. During the permeability measurements, the volume flux was stepwise increased by increasing the inertial pressure of the degassing tank through a pressure regulator, cf. Fig. 3a. The pressure regulator ensured that the atmospheric pressure in the degassing tank remained constant. In this manner, different measuring ranges for fluid flux and pressure difference were driven to determine the intrinsic permeability of the produced sintered specimens, see Fig. 3. The measured values for pressure difference and fluid flux were continuously recorded (digital data acquisition, sampling rate 0.5 Hz) during each measurement and subsequently sent to a computer. Depending on the porosity and glass bead diameter of the sintered specimens, different fluid fluxes ranging between 30 and 245 ml/min. were observed. With these volume flows pressure differences up to 35 mbar could be generated. For each measurement the water temperature was measured and found to be in the narrow range of $20~^\circ \hbox {C}<\hbox {T}<22^\circ$.

Fig. 3

Stepwise increase of flow rate $Q_z$ (a) and differential pressure $\varDelta p$ (b) caused by viscous fluid flow through sintered glass beads sample with bead diameters between 0.4 and 0.6 mm in dependence of measuring time t

4.3 Measuring cell

The developed measuring cell has been designed according to a modular concept in order to use it in various applications. Figure 2b shows an illustration of the measuring cell in operating mode for stationary permeability measurements.

It consists of an inner and outer cylinder. The inner cylinder is made of an acrylic glass (PMMA) and produced in various sizes, whereas the outer cylinder is made of aluminium (AlCu4PbMgMn alloy) to stabilize the measuring cell. As can be seen from Fig. 2b, the sintered sample was positioned at the center of the cell and pneumatically fixed by a specially developed specimen holder coated with a 1mm-thick latex membrane. During flow measurements a static air pressure on the latex membrane was applied which fixed the specimen in the current position and prevented a surrounding fluid flow. At the same time, the latex membrane ensured a hermetically sealing off the measuring cell to the outside. The pressure difference, mainly resulting from the viscous friction of the fluid passing through the porous sintered sample, could be taken via the upper and lower pressure port and measured by a high-precision differential pressure transducer (type FDW2JA, ALTHEN, Germany) capturing differential pressures up to 35 mbar (with an accuracy of 0.25%).

5 $\mu$XRCT data processing

$\mu$XRCT data processing is a crucial step towards understanding of fluid flow through complex morphologies like sintered glass beads. It is a important tool for visualization and quantification of parameters, such as porosity, particle sizes or pore throats, determining the hydraulic conductivity of a porous medium [43,44,45]. The correct procedure of the $\mu$XRCT-data including an adequate filtering and thresholding method is essential for a proper comparison between experimental and numerical determined permeabilities [17, 46].

The XRCT device used for imaging of the sintered samples is a ‘nanotom 180’ device provided by the petrophysics laboratory at the Leibniz Institute for Applied Geophysics in Hannover, Germany. The device is equipped with a special water-cooled nanofocus X-ray tube with a maximum 180 kV and 15 W. The minimal focus size is about $0.6~\upmu \hbox {m}$, which results in a detail detectability of $0.2~\upmu \hbox {m}$ [13]. The measurement parameters for the investigated scans are 107 kV and $200~\upmu$A. XRCT images at 900 angles on $360^\circ$ are performed with an integration time of $10 \times 0.1$ s per angle. The initial voxel resolution of the XRCT scans is $16~\upmu \hbox {m}$ and remained constant during the whole $\mu$XRCT data processing.

Fig. 4

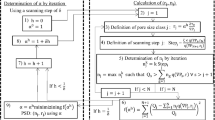
a Computational domain in LB simulations consisting of a porous glass bead sample and the two fluid chambers denoted as in-and output. The fluid is accelerated upwards in the acceleration zone at bottom. b Process flow chart used for extracting influence parameters and quantities determining the hydraulic properties of the sintered glass bead samples from XRCT-data

Figure 4b shows the main image processing steps. Starting from raw data, the image file is filtered in several stages until the desired gray scale distribution is reached. For better visualization of the filter effect, Fig. 5 demonstrates exemplarily the filtering procedure on the basis of slices applied onto the original raw data with the corresponding gray-scale value distribution. For the sake of clarity, during filtering the image is interpreted and processed as a three dimensional volume, and the gray-values of each voxel are numbers of decimals obtained from 16-bit binary representation of the gray level. In the initial state (state A), the gray-scale distribution of the raw data show two peaks which can be clearly attributed to the pore space and the glass beads. Starting from the original raw data a simple logical operator with the so-called “arithmetic” module is applied to remove bright spots from the image file. These bright spots highlighted by a red circle in state A are caused by density fluctuations and chemical impurities of the beads and can be clearly assigned to greater gray-scale values. In the first filtering step, the gray values belonging to these bright spots are lowered artificially by setting a defined maximum threshold for gray-scale values. As highlighted in the example, a maximum threshold of 26,818 is used, cf. Fig. 5b.

Since the gray-scale values belonging to the glass beads and pore space overlap due to their wide distributions, the segmentation procedure becomes difficult. Therefore, in the second step of the filtering procedure the so-called “delineate” filter is applied to enhance the edges of the glass beads and to adjust the contrast between the pore space and the glass beads. Local changes in intensity of gray-scale values constitute a common issue during segmentation. The “delineate” filter, which is based on a phase contrast method, can detect sharp transitions between different phases to finally enhance and contrast the edge of an object to be segmented. As a result, the gray-scale distributions between the glass beads and the pore space are clearly separated from each other (state C), which simplifies the further separation of the glass beads from the pore space.

In the last step, the “median” filter is applied to denoise and smooth the image data. This filter uses morphological operators to set the gray-scale value of a voxel to the median for a defined neighborhood [47]. The gray-scale value distribution from state C is changed only slightly compared to the distribution in state D. Because of the high data quality, which comprises also the high gray-scale contrast between pore space and solid matrix, there is no need to use the so-called “non-local means” filter, which is commonly used to denoise image data especially at the edge of an object to be segmented [17, 48, 49]. The algorithm of this filter compares the neighborhood of a voxel in a given search window with neighbors of the current voxel. A weight is determined from the similarity between the neighbors, with which the values of the voxel value in the search window will influence the new value of the current voxel. The final weight result by applying a Gaussian kernel to the similarity values [48, 49].

Fig. 5

Illustration of the applied multistage filtering process using slice images with $1024 \times 1024$ pixels (sintered sample with $d_p=0.4{-}0.6$ mm): a untreated raw $\mu$XRCT scan data b after removing bright spots, c after applying the “delineate” filter d after applying the “median” filter. The corresponding gray value distributions of the images after each filter step are shown below in the respective panels. The vertical axis is logarithmic and gives the probability of occurrence of the gray values, while the horizontal axis represents the gray value of a voxel

In accordance with the process flow chart shown in Fig. 4b, the filtered gray-scale image data is thresholded to generate a binary map. The threshold is selected manually for each sample in a way that the solid glass beads are assigned to values of unity and the pore space voxels are set to zero. For the determination of porosity and visualization of the pore space the binarized image data is inverted.

5.1 Particle number distribution

For the determination of the particle size distribution, the segmented glass beads are separated using a high-level combination of watershed, distance transform and numerical reconstruction algorithms. After separation, the segmented beads are numerated with the “labeling” module. In this module, each voxel of the same object is assigned to the same value, and each object gets a different value. Based on the labeled system a quantitative analysis is performed to determine the volume-equivalent diameter of each particle object. The equivalent particle diameter $d_p$ is computed by

$$\begin{aligned} d_{p} = \root 3\phantom {a} \of {\frac{6\,V_{p}}{\pi }}, \end{aligned}$$

(11)

where $V_{p}$ is the voxel-based volume of the particle. As a result, Fig. 6 shows (from state A to C) the volume rendered sample in the form of a cuboid with the dimensions $1024 \times 1024 \times 2048$ voxel$^3$ ($16.384 \times 16.384 \times 32.768$ mm$^3$) in the raw, and the segmented and labeled state. In the labeled state different colors are used to distinguish optically between the identified glass particles. It should be stated, that the coloring of the particles occurs randomly. After a certain number of beads the coloring is repeated and the same colors are assigned again to different identified objects. The initial cuboid shown in Fig. 6 contains more than 78,000 particles with diameters ranging mostly between 0.4 and 0.6 mm. The corresponding particle number distributions of the initial cuboid and different sized subsets taken from the initial cuboid are depicted in Fig. 6d. For all investigated subsets a monomodal distribution with maximum around 500 $\upmu \hbox {m}$ occurs, which confirms the representativeness of the investigated subsets, except for the smallest one. The arithmetic mean values and the standard deviations of the particle number distributions shown in Fig. 6d are given in Table 2.

Table 2 Characteristic parameters from particle number distributions gained from $\mu$XRCT (after sintering) for the sample with $d_{p}=0.4{-}0.6\,\hbox {mm}$

Fig. 6

Volume rendering of the 3D initial cuboid with the dimensions $1024 \times 1024 \times 2048$ voxel$^3$, whereby the voxel resolution is $16\,\upmu \hbox {m}$ (sintered sample with $d_p=0.4{-}0.6~\hbox {mm}$). The illustration on top-left shows the initial cuboid before segmentation in the raw state A. State B represent the binarized 3D image after segmentation and state C shows the separated and labeled system used for determination of the particle number distribution. d The resulting particle number distributions of differently sized subsets taken from different positions of the entire scanned region are presented. The initial cuboid contains 78,375 particles, while the other distributions are based on less particles as given in the inset

Fig. 7

a Illustration of main image processing steps for visualization and quantification of pore throat areas in AVIZO 8.0.1. b Resulting pore throat areas $A_{pt}$ in a polydisperse sintered glass bead packing ($d_p=2.0{-}2.5\,\hbox {mm}$) and the principle for determining equivalent pore throat diameter is shown below

5.2 Pore throat determination

A decisive factor, which determines the intrinsic permeability in granular porous systems is the pore throat area. Micro tomographic imaging techniques enable to localize, visualize and quantify such determining areas.

Therefore, Fig. 7a illustrates exemplarily the main image processing steps for determination of pore throats using a 256 voxel-sided cube showing glass bead diameters between 2.0 and 2.5 mm. As denoted in Fig. 7a for the determination of the pore throat areas of the subsets, the pore space was first computed by inverting the segmented glass beads. After inversion the segmented pore space is separated in various pore voids by using the tool of “binseparate”. This module computes the watershed lines of a binary image. In the separation process voxels with at least one common edge are considered as connected and the separation takes place at the narrowest places of the pore space. In the next step, the separated pore space is deducted from the unseparated pore space by using the “arithmetic” function, in order to determine the split planes, which also represent the pore throat areas. After labeling typical pore throat areas formed by three or four particles result, see Fig. 7b. From the computed pore throat areas an equivalent pore throat diameter

$$\begin{aligned} d_{pt} = \sqrt{\frac{4 \, A_{pt}}{\pi }} \end{aligned}$$

(12)

is determined, whereby $A_{pt}$ represents the pore throat area. The pore throat distribution in granular packings was also theoretically investigated by To et al. [50], Jaafar and Likos [3], Reboul et al. [1] and Shire et al. [51], where the pore throat distribution is estimated from the given particle size distribution of the granular packing. To et al. [50] and Reboul et al. [1] considered the flow process of suspensions in porous granular packings and therefore the pore throat areas were described by circular voids, which were smaller than the real constrictions sizes.

In this study, the fluid flow of water in granular sintered packings were investigated, and thus the identified pore throat areas were replaced by circular voids with same area as shown in Fig. 7b. Even when the identified pore throat areas are not close to circular shape, the determination of the pore throat diameter according to Eq. (12) is sufficient to quantify the sizes of the pore throat areas and to investigated their dependency on the permeability or porosity of the investigated differently sized subsets.

Fig. 8

Local distribution of numerically determined porosity (a) and permeability (b) values of subsets with edge lengths of 256 voxels within the initial cuboid with dimensions of $1024 \times 1024 \times 2048$ voxel$^3$ ($16.384 \times 16.384 \times 32.768\,\hbox {mm}^3$) ($d_p=0.4{-}0.6\,\hbox {mm}$)

6 Results and discussion

In this section the results of the determining parameters of the intrinsic permeability, described in previous sections, obtained from $\mu$XRCT analysis and LB simulations are presented successively, discussed and compared with experimental results. Moreover, the dependency of the intrinsic permeability on different parameters and on the localizations and sizes of the investigated subsets are analyzed qualitatively and quantitatively. Please note that the results are only extensively showed for the sintered sample with $d_p=0.4{-}0.6$ mm due to the large amount of data. All other samples were produced in the same way as the sample with $d_p=0.4{-}0.6$ mm and thus show qualitatively the same results.

6.1 Porosity and permeability

Figure 8a, b illustrates the numerical results of porosity and permeability values of extracted subsets with edge lengths of 256 voxel (4.096 mm) in each spatial direction obtained from $\mu$XRCT analysis of the sintered sample with bead diameters ranging between 0.4 and 0.6 mm. In total, $4 \times 4 \times 8 = 128$ cubes with edge lengths of 256 voxel are extracted from the initial cuboid shown in Fig. 6a–c and investigated in terms of porosity and intrinsic permeability. After evaluating the porosity and permeability values of the extracted subsets, the cubes with edge lengths of 256 voxels are arranged in compliance with their spatial coordinates within the initial cuboid depicted in Fig. 6. For both, the porosity and permeability, a clear gradient with sample height can be observed. The permeability and porosity decrease with increasing depth due to the gravitational forces acting on the beads during sintering. The porosities vary only between 0.32 and 0.39, whereas the permeability fluctuations within the initial cuboid are considerably higher ($1.29 \times 10^{-10}{-}2.75 \times 10^{-10}$ m$^2$), see also Fig. 9 (a-b, REV analysis). The porosity fluctuations are around the trend (porosity gradient in flow direction) so that even the relative change of approximately 18% for 256 voxel-sided cubes is overexaggerated. In Fig. 10a, b the intrinsic permeability increases non-linearly with increasing porosity, which confirms the higher relative variation in permeability and that it is compatible with the variation in porosity. In comparison, the effective porosity of the cylindrical specimen is experimentally determined from the bulk and bead densities by

$$\begin{aligned} \phi = 1- \frac{\rho ^s}{\rho ^{sR}} = 37.72\%, \end{aligned}$$

(13)

whereby the $\rho ^s$ and $\rho ^{sR}$ represent the bulk density and the effective true density of the beads, which the sintered sample is composed of. The experimentally determined effective porosity value lies within the porosity range determined from the segmentation of 256 voxel-sided cubes. The differences between experimentally determined porosities and voxel-based local porosities result especially from the spatial porosity gradient across sample height z and that the XRCT data do not capture pore spaces smaller than the resolution limit. Since the phase-contrast between the porous skeleton composed of sintered glass beads and pore space is high, the influence of the segmentation procedure on the voxel-based porosity is assessed to be negligibly small. The permeability values at the top of the initial cuboid are more than twice greater than the permeabilities in the lower regions of the initial cuboid. The higher permeability fluctuations are confirmed in the conventional REV analysis as shown in Fig. 9a, b. The illustrations in Fig. 9a, b show the REV analysis for porosity and permeability of differently sized subsets taken from the initial cuboid. Please note that the REV analysis is constrained to subsets, which were also analyzed in terms of the local permeabilities via LB method and further concerning different parameters, such as pore throat or particle size distributions. Due to the high computation effort of permeability calculations according to the LB method, we have renounced a larger spread of cuboid or cube sizes like in Ref. [52] and considered four different REV sizes. Due to the varying degrees of fluctuations of porosity and permeability, the relative standard deviations related to the arithmetic mean value seem to be a sensible quantity to investigate the effect of the size of REV edges. The percentage values in Fig. 9a, b show the relative standard deviations relative to the arithmetic mean values of the permeabilities being considerably higher than those of the porosities. For example, the standard deviation of porosity for cubes with edge length 256 voxel is only about 5%, while the standard deviation of permeability is significantly higher at 17.77%. This indicates that the permeability in general is more sensitive to the size of the representative volume element than the porosity. Furthermore, the findings from the REV analysis confirm that the mean values for porosity and permeability are (almost) identical to that of the initial cuboid with dimensions of $1024 \times 1024 \times 2048$ voxel$^3$ ($16.384 \times 16.384 \times 32.768$ mm$^3$). A consequence of this result is that, either a few calculations of smaller sided cubes with low costs and computation time requirements can be performed or one cost intensive calculation on the initial cuboid with approximately 78,300 particles can be carried out.

Fig. 9

Results from the conventional representative elementary volume (REV) analysis for porosity (a) and permeability (b). The percentage values reflect the relative standard deviation and the horizontal lines represent the arithmetic mean values of the initial cuboid

Please note that the geometrical tortuosity determined from the centroids of two-dimensional slices of 256 voxel-sided cubes obtained from XRCT scans shows no spatial gradient along the sample height and no correlation is found with the porosity and permeability, cf. Ref. [53].

Figure 10a shows the permeabilities of the subsets as function of their porosities, for three different theoretical estimates, increasing according to Kozeny–Carman.¹ Figure 10b shows the intrinsic permeabilities normalized by the square of the mean particle diameter, confirming the non-linearly increasing trend of the intrinsic permeability with increasing porosity. The colored data points in Fig. 10a represent the predictions according to the Kozeny–Carman model, cf. Eq. (3), whereby the arithmetic (red), harmonic (green) and effective (black) diameter according to Eq. (4) from the particle size distribution are used as representative values to predict the permeabilities of the differently sized subsets. The permeabilities determined from the lattice Boltzmann simulations (open data points) and the predictions according to Kozeny–Carman using the arithmetic mean diameter show a similar increasing trend, whereby the numerically determined permeabilities are higher by a factor of approximately 1.3. The permeability predictions according to Kozeny–Carman using the harmonic or effective diameter according to Eq. (4) (green and black data points) show stronger fluctuations and clearly underestimate the numerically determined permeabilities. Fitting the predicted permeability values depicted in red into numerical results by using the empirical constant $c_1$ as fit parameter, yields a value of 131, see Fig. 10b. This constant contains and reflects the effect of the microstructure (particle shape, tortuosity) as a result of the sintering process on the intrinsic permeability of the glass bead samples.

It is worth noting that the most glass beads show sphericity values around 0.95 after sintering, cf. Ref. [53]. The sphericity values near 1 determined from XRCT scans indicate that the glass beads are almost spherical after the moderate sintering. This confirms also the applicability of the Kozeny–Carman equation, which is predominantly used to predict the intrinsic permeability of sphere packings.

Fig. 10

a Local intrinsic permeabilities of different subsets showing particle diameter between 0.4 and 0.6 mm as a function of porosity. b Normalized permeabilities of differently sized subsets (with maximum edge lengths of right pointing triangle 256 voxel (4.096 mm), diamond 512 voxel (8.192 mm), square 1024 voxel (16.384 mm), triangle 2048 voxel (32.768 mm)) from LB simulations and predicted values according to Kozeny–Carman in dependence of their porosity values. The blue curve represents the best fit, whereby the Kozeny–Carman constant $c_1$ is used as the only fitting parameter. The colors of the squares in the legends describe if the data points are obtained from LB simulations or from Kozeny–Carman predictions with specific diameters. The shape of the data points in the figures refers to the sizes of the investigated subsets. The Hazen diameter is determined according to Eq. (4) (color figure online)

Besides the porosity analysis on differently sized cubes extracted from different regions of the entire scanned region, subvolumes in the form of tubes with varying mean cross-section diameters were segmented to investigate the porosity distribution across the cross-section of the cylindrical sintered samples, cf. Fig. 11 (state b). To guarantee the investigation of meaningful representative volume elements, the pipe thickness is chosen as 3 mm, which is equivalent to 187.5 voxels.

Fig. 11

Cross section view of sintered specimen with glass bead diameter between 0.4 and 0.6 mm: a raw data, b after segmentation of tubes with different mean radii, and c porosity in dependence on the mean radial distance of the pipe cross-section from the center for different specimens featuring different glass bead diameters and degrees of polydispersity

Figure 11c shows the resulting porosity distribution in dependence on the mean pipe cross-section radius of the investigated specimens showing different glass bead diameters and degree of polydispersity. Starting from the center of the investigated samples, the porosities remain relatively constant up to a mean cross-section radii of 11.5 mm and then increase to higher porosities for the largest investigated pipes in the external area of the produced samples. In these outer zones a clear increase of the porosity values for investigated samples can be seen due to the different contact between beads and cylinder wall during the sintering procedure and the gaps remaining between particles and walls. The clear porosity increase on the edges of the sintered samples is a consequence of the sintering procedure caused mainly by the presence of the walls.

Figure 12 summarizes the experimental results from permeability measurements for a sintered sample with bulk diameter of 30 mm showing glass bead diameter between 0.4 and 0.6 mm. The measurements were repeated eight times in order to attain mean reliable results and understand the variation and reproducibility. The almost linear relationship between the filter velocity $Q_{z}/A$, and the pressure drop $\varDelta p/l$, depicted in Fig. 12a, and the nearly constant values of the effective intrinsic permeability $k_{z}^s$ over the test duration t, shown in Fig. 12b, confirm the applicability of Darcy’s law (1) and that the permeability measurements have taken place in the laminar Darcy regime. The measurement of water flow and pressure difference is captured with a sample frequency of 0.5 Hz. For the sake of clarity, only each 150th measuring point is plotted in both figures. The intrinsic permeability of each measurement is determined from the slope of the linear regression lines, cf. Fig. 12a. Measurement uncertainties of the used flow meter and the differential pressure transducer as well as some presence of air bubbles causes the permeability differences between each experiment. Pressure fluctuations and thus permeability differences are additionally enhanced by buckling of the used water hoses. Please note that examined permeabilities for each measurement in Fig. 12 are still in the same order magnitude, which confirms the robustness and reliability of the permeability experiment. For the sintered sample with bead diameters ranging between 0.4 and 0.6 mm, a mean effective permeability of $k_{z}^s= 9.87 \times 10^{-11}\pm \varDelta 1.65 \times 10^{-11}~\hbox {m}^2$ is determined.

Fig. 12

a Filter velocity $Q_{z}/A$ as a function of pressure drop $\varDelta p/l$ normalized by the real fluid viscosity $\mu ^{fR}$. The permeability measurements are repeated 8 times for the sintered glass bead with diameters between 0.4 and 0.6 mm. The almost linear relationship between the filter velocity and the normalized pressure drop confirms the applicability of Darcy’s law and the stability of the experimental setup in a broader range of pressure gradients. b Intrinsic permeability in dependence of test duration t. The intrinsic permeabilities of the different measurements show an almost constant behavior in dependence on the test duration for different volume fluxes. The small fluctuations are caused by uncertainties of the measuring equipment. For the sake of clarity, only each 150th measuring point in both figures is plotted

Fig. 13

Numerically and experimentally determined porosity (a) and permeability (b) for sintered glass bead samples from different particle diameters. The experimentally determined permeability results represent the average value of five to eight independent measurements with the error bar representing the standard deviation of the measurements. The numerical results are obtained from subsets of 1024 voxel-sided cubes. The largest deviation between numerical and experimental permeabilities is observed for the glass bead sample with diameter 3.0 mm. In this case, the representativeness of the investigated subset is not sufficient. For more details on the different samples, see Table 1

The bar diagrams in Fig. 13 show a direct comparison between experimentally and numerically determined porosities and permeabilities of the investigated samples with different glass bead diameters and degrees of polydispersity. The numerical porosity and permeability results, represented by black bars, are obtained from 1024 voxel-sided cubes taken from the center part of the entire scanned regions of the samples and used in LB simulations. The effective permeability results obtained from laboratory experiments, represented by white bars, are averaged values from 5 (or 8) independent permeability measurements, whereby 10 to 15 different measuring ranges for volume fluxes and pressure differences are run during each measurement, cf. Fig. 3. While the porosity values show a good agreement, the permeability results show much larger non-systematic deviations. It should be noticed that small deviations in porosity and particle size can lead to significant deviations in permeabilities due their exponential influence, see Eq. (3). Larger deviations between experimental and numerical permeability results occur for 1.5–2.0 mm and larger particles, since the representativeness of the investigated subsets for numerical permeability calculation decreases with increasing particle diameter. Furthermore, it can be seen from Fig. 13b that the error bars in experimental permeability determinations are small compared to their averaged values, which indicates high reliability, repeatability and robustness of the used experimental permeability setup.

Moreover, the good agreement between voxel-based local and experimental determined global porosity values of the investigated different sintered samples in Fig. 13a proves the correctness of the filtering and segmentation procedure despite the underlying porosity gradient across the sample height. A proper filtering and segmentation procedure is surely essential for subsequent permeability simulations. Incorrect porosity determination during segmentation procedure can lead to substantial errors in permeability calculations, see Eq. (3). In this context sintered glass bead samples as simple replacement material for natural sandstones are suitable to set a benchmark for permeability calculations. Taking into account the porosity and permeability gradients with the sample height, the deviations between experimental and numerical results is insignificant. The maximum deviation factor of 2.4 that is obtained for glass bead diameters of 3.0 mm due to low representativity of the investigated subset is quite reasonable.

From the REV analysis, we have come to the important conclusion that the average value for porosity and permeability of smaller sided cubes is (almost) identical to results obtained from the initial cuboid, cf. Fig. 8. We have found out that the averaged values for permeability are almost equal independent from the size of the investigated subsets.

6.2 Pore throats

In addition to porosity and particle size, the intrinsic permeability in sintered glass samples is also affected by pore throats [11, 54]. The strong influence of pore throats in simple pore systems, consisting of cylinder pores, on the intrinsic permeability can be derived analytically, cf. Ref. [55]. Numerous statistical models for determination of pore throat distribution from particle size distributions of granular packings exist, cf. Refs. [2, 3, 50, 51]. However, the applied models are often inaccurate to determine the constriction size distribution. In addition, the direct link to the intrinsic permeability is missing. Furthermore, the influence of the sintering process remains unconsidered. In such cases, the $\mu$XRCT analysis provide an efficient tool for visualization and quantification of pore throat areas and to investigate their impact on the intrinsic permeability [56]. Therefore, this section presents a simple methodology for the determination of the pore throat areas from $\mu$XRCT data. Moreover, the correlations between the mean pore throat diameter $\langle \hbox {d}_{pt} \rangle$, the porosity $\phi$ and the numerical determined intrinsic permeabilities $k^{s}_{z}$ are investigated in detail.

Fig. 14

a Local spatial distribution of mean pore throat diameter values of subsets with edge lengths of 256 voxels within the initial cuboid sintered sample with particles diameters $d_p=0.4{-}0.6\,\hbox {mm}$. Frequency distribution (red curve) of the equivalent pore throat diameter $d_{pt}$ scaled by the maximum observed at $d_{pt,max} \approx 490~\upmu \hbox {m}$, and the corresponding cumulative curve (green curve) (b) (color figure online)

Fig. 15

Porosity (a) and dimensionless permeability (b) in dependence on the mean pore throat diameter normalized to the mean particle diameter. The data are obtained from the sintered sample with particle diameters $d_p=0.4{-}0.6\,\hbox {mm}$. Both porosity, $\phi$, and normalized intrinsic permeability, $k_{z}^{s}/\langle d_{pt}\rangle ^2$, show a linear dependency on the normalized mean equivalent pore throat diameter $\langle d_{pt} \rangle /\langle d_{p} \rangle$. Note that the linear dependency resulting from the two plots, $k_{z}^{s}/\langle d_{pt}\rangle ^2 = \frac{1}{110} \phi - 2.4\,10^{-3}$, is not in conflict with Eq. (3) since it exactly tangent to the nonlinear Kozeny–Carman relation in the narrow range of porosities around $\phi \approx 0.36$

Figure 14a illustrates the local distribution of mean pore throat diameter from 256 voxel-sided cubes within the cuboid for the sintered sample with bead diameters between 0.4 and 0.6 mm. The normalized pore throat distribution gained from the initial cuboid in Fig. 14b depicted in red shows two distinct peaks which can be clearly assigned to pore throat areas formed by either three or four particles. The larger peak at smaller diameters results from pore throat areas which are formed by three particles whereas the smaller peak at larger diameters is due to four-particle-constellations. The probability of occurrence of pore throats formed by three particles is certainly higher compared to pore throat areas resulting from four-particle-constellations. Downscaling to smaller volume elements (up to 256 voxel-sided cubes) showed qualitatively the same pore throat distributions. In accordance with local distributions for porosity and permeability, the equivalent mean pore throat diameter also shows a spatial gradient along the sample height z, see Fig. 14a, decreasing from top to bottom about 14% due to compaction in deeper layers.

The correlation of the permeability, the porosity and the mean pore throat diameter for the sintered sample with bead diameters of 0.4–0.6 mm is plotted in Fig. 15, displaying the porosities $\phi$ (a) and the normalized intrinsic permeabilities $k_{z}^s/\langle d_{p}\rangle ^2$ (b) of differently sized subsets taken from the initial cuboid in dependence on their normalized mean pore throat diameters $\langle d_{pt} \rangle /\langle d_{p} \rangle$. For both, the porosity and the normalized permeability a clear linear dependency on the normalized mean pore throat diameter $\langle d_{pt} \rangle /\langle d_{p} \rangle$ can be seen, with correlation coefficients of the fits of 0.9378 and 0.9675, respectively. The higher mean pore throat diameters correlating with the higher porosity and the higher permeability values are located at the top of the investigated cuboid and decrease towards deeper layers.

7 Conclusion

In summary, we have demonstrated that the hydraulic properties of sintered glass beads are highly affected by the pore throats, in addition to the porosities and particle sizes. In this respect, the non-destructive X-ray Computed Tomography is an efficient tool, which enables the visualization and quantification of internal (microstructural) parameters including the (voxel-based) morphometry of the porous sample. The way $\mu$XRCT data are processed is crucial. In this study, different ways have been introduced in order to identify the essential control parameters for the hydraulic properties of the sintered glass bead systems. The presented framework can in future be used to evaluate also the hydraulic characteristics of other kinds of porous media.

The main findings of this study can be summarized as:

• The intrinsic permeability in sintered granular packings depends not only on the porosity, but also correlates with the equivalent pore throat mean diameter.

• The pore throat distributions in polydisperse packings show two distinct peaks arising from typical three- or four-particle constellations.

• In the given narrow porosity and permeability range, a linear dependency of the permeability with the equivalent pore throat diameter is observed.

• The quantitative comparison between experimental and numerical permeability values requires a proper filtering and segmentation procedure and an appropriate domain size, and then can lead to good agreement, even there are a few unexplained outliers, possibly due to channeling (higher permeability) or due to particularly dense samples (lower porosity).

For the examined sintered glass bead samples a clear spatial gradient of microscopic porosity, permeability and mean pore throat diameter along the sample height could be detected as a result of gravitational compaction during sintering.

Local REV analysis has revealed that the averaged values for porosity and intrinsic permeability of smaller sided cubes are (almost) identical to results of larger subsets obtained from the cuboid. A consequence of this result is that, we can either perform many cost effective and time-saving computations on small subsets, which are less representative, or compute one cost and time intensive large subset. For the calculations of effective quantities new strategies can be developed on the basis of results gained from the REV analysis.

From the REV data, the porosity development across the radial direction was analyzed. A slight increase of porosity at peripheral outer zones could be identified due to the contacts of the beads with the cylinder wall during sintering. Rotational sintering under pressure-controlled gas atmosphere may eventually lead to more homogeneous samples avoiding spatial gradients of porosity and permeability. From the experimental point of view, the presence of air bubbles in the measuring cell poses a big challenge, which can highly affect the measurement of pressure differences, and thus of the intrinsic permeability. Taking into account these difficulties, a comparison between numerical and experimental determined intrinsic permeability values gives us the possibility to better understand the system. Eventually, we have achieved qualitatively and quantitatively a good agreement between experiment, microstructural analysis and numerical simulations.

We have demonstrated through 3D LB simulations that a proper filtering and segmentation procedure during $\mu$XRCT analysis is essential for porosity determinations and to obtain accurate permeability results. We have found that an almost linear correlation between both intrinsic permeability and porosity with the pore throat equivalent diameter can be observed if systematic errors during filtering and segmentation are avoided. Our numerical and experimental permeabilities are in general agreement with permeability predictions according Kozeny–Carman, although the validity of the Kozeny–Carman equation is limited to monodisperse and non-sintered granular packings. In contrast to the factor $c_{1}=180$ for idealized sphere packings, a value of $c_{1}=131$ for the empirical constant, which takes into account microstructural effects resulting from the sintering treatment of the polydisperse glass bead packing, could be determined by fitting the predicted permeability values to numerical results from LB simulations.

In this study XRCT structural and permeability analysis have been performed for several polydisperse sintered glass bead samples with different primary particle average diameters. The observed micro-macro relations scale with the average diameters of the rather large particles. Further work is needed to extend the study towards systems with smaller particles, higher polydispersity or systems with longer sintering duration time and thus lower porosity. It has to be seen if the presented approach for the processing of the XRCT data and the resulting main findings, for instance the linear dependency of the intrinsic permeability with the pore throats, can be also found in those systems, and in natural porous materials like sandstone.