1 Introduction

If torque conversion with high gear ratio, compact installation space and 90-degree axis-crossing angle is needed, often worm gears are used. Due to their high power density and sliding speeds within the tooth contact, frictional heat and thermal stresses are higher compared to helical, bevel and hypoid gears, and thus the thermal load capacity of worm gears is lower [24]. Therefore, the prediction of the heat balance and component temperatures of gearboxes containing one or more worm gear stages is very important, especially during the design phase.

The simulation program WTplus [16] has been developed to investigate the efficiency and heat balance of gearbox systems. The efficiency is based on the power loss calculation of gears, bearings, seals and other rotating elements. The subsequent calculation of the heat balance of the gearbox is based on the so-called “Thermal Network Method” (TNM) [11, 15], which is a mathematical method for determining the heat transfer between single components, as well as the heat dissipation to the environment. A suitable abstraction of the gearbox system by nodal points forms the basis for an efficient and accurate calculation of local component temperatures. The current version of WTplus can analyze gearbox systems containing cylindrical and bevel gears.

In this study, an automatic simulation method for analyzing the efficiency and heat balance of various design of worm gears is developed and integrated in WTplus. First, suitable methods and calculations regarding the efficiency and heat balance calculation of worm gears are shown. Its integration into the simulation program WTplus is described afterwards. Finally, simulated efficiency and heat balance results of various worm gearboxes are compared to measurements from research and industry.

2 State of the art

Niemann [23] and Weber [40] mathematically modelled the tooth contact of worm gears. Wilkesmann [41] performed elastohydrodynamic lubrication (EHL) calculations for different worm tooth geometries. Predki [29] carried out parameter studies and developed relative key figures, which form the basis of DIN 3996:2019-09 [9]. Bouché [3] formulated a physics-based model for the calculation of the coefficient of friction under mixed friction for worm gears. Magyar [20] investigated the dynamics of worm gears and derived a tribological calculation model for the calculation of the coefficient of friction, which is the basis for a new standardizable approach for the calculation of worm gear efficiency [25].

Monz [22] and Mautner et al. [21] investigated the load capacity and efficiency of worm gears lubricated by consistent grease. They used a specific TNM for heat balance calculations, which correspond closely to the measurements. Further approaches to using TNMs for heat balance and temperature calculations with regard to gearboxes can be found in [26] for worm gears, [14] for hypoid gears, [4, 11, 19] for spur gears, [6, 42] for planetary gears and [38] for helical gears.

Although there are several approaches for the efficiency and heat balance calculation of worm gears, none of them uses an automatic approach to building the TNM. They either abstract their investigated gearbox as an isothermal system for which no temperature distribution can be calculated, or they build the TNM statically and specifically for an experimentally considered worm gearbox.

This is where the method shown in this paper excels: It describes a method for an automatic efficiency and heat balance calculation for various designs of worm gears.

3 Efficiency calculation

The calculation of the efficiency of a system requires the knowledge of either the power input \(P_{\mathrm{A}}\) and power loss \(P_{\mathrm{V}}\), or the power input \(P_{\mathrm{A}}\) and power output \(P_{\mathrm{a}}\):

$$\eta =\frac{P_{\mathrm{A}}-P_{\mathrm{V}}}{P_{\mathrm{A}}}=\frac{P_{\mathrm{a}}}{P_{\mathrm{a}}+P_{\mathrm{V}}}=\frac{P_{\mathrm{a}}}{P_{\mathrm{A}}}$$
(1)

With regard to gearboxes, the overall power loss \(P_{\mathrm{V}}\) can be described as the sum of partial power losses of the gearbox components as shown in Eq. (2). They are usually caused significantly by the gears (\(\mathrm{Z}\)) and bearings (\(\mathrm{L}\)), and by contacting seals (\(\mathrm{D}\)). Depending on the gearbox, other losses (\(\mathrm{X}\)) from auxiliary units, for example, may also occur. Gear losses and bearing losses can be subdivided into no-load (\(\mathrm{0}\)) and load-dependent (\(\mathrm{P}\)) losses [13].

$$P_{\mathrm{V}}=\underset{\text{Gear losses}}{\underbrace{P_{\mathrm{VZ0}}+P_{\mathrm{VZP}}}}+\underset{\text{Bearing losses}}{\underbrace{P_{\mathrm{VL0}}+P_{\mathrm{VLP}}}}+\underset{\text{Sealing losses}}{\underbrace{P_{\mathrm{VD}}}}+\underset{\text{Other losses}}{\underbrace{P_{\mathrm{VX}}}}$$
(2)

Fig. 1 shows a Sankey diagram outlining the correlation of power input, power output and power losses, which are ultimately converted to heat.

Fig. 1
figure 1

General gearbox power flow in form of a Sankey diagram based on Eq. (2)

Full size image

3.1 Gear losses

Gear losses generally cause a significant proportion of the overall power loss. Friction within the contact of two tooth flanks relates to the applied load of the tooth system and results in load-dependent gear losses (\(P_{\mathrm{VZP}}\)). Churning losses, squeezing losses, impulse losses and ventilation losses are related to the oil flow in the gearbox [18]. They are referred to as no-load gear losses (\(P_{\mathrm{VZ0}}\)) as they are almost independent from the applied load.

In terms of an efficiency calculation, values for every single one of the named forms of power loss are needed in as much detail as possible. Thus, a lot of research focuses on the formulation of calculation models to quantify load-dependent and no-load losses. The following two subsections present common and recent calculation models for predicting load-dependent and no-load gear losses of worm gears.

3.1.1 Load-dependent gear losses

The load-dependent gear losses \(P_{\mathrm{VZP}}\) correlate to the friction between meshing tooth flanks. According to DIN 3996:2019-09 [9], it can be described asFootnote 1:

$$P_{\mathrm{VZP}}=\underset{\approx 0.1}{\underbrace{\frac{2\cdot \pi }{60}}}\cdot \frac{T_{2}\cdot n_{1}}{u}\cdot \left(\frac{1}{\eta _{\mathrm{z}}}-1\right)$$
(3)

Since worm gears show different gear losses, depending on the direction of the power flow, the calculation of the meshing efficiency \(\eta_{\mathrm{z}}\) must be considered separately. When the worm shaft is driving, according to DIN 3996:2019-09 [9], Eq. (4) is used:

$$\eta _{\mathrm{z}}=\frac{\tan \left(\gamma _{\mathrm{m}}\right)}{\tan \left(\gamma _{\mathrm{m}}+\arctan \left(\mu _{\mathrm{mz}}\right)\right)}$$
(4)

When the worm wheel is driving, the efficiency is generally lower. Furthermore, a self-locking effect can occur in this operation mode if the meshing efficiency \(\eta _{\mathrm{z}}\) is less than 0.5. According to DIN 3996:2019-09 [9], Eq. (5) is applied:

$${\eta _{\mathrm{z}}}'=\frac{\tan \left(\gamma _{\mathrm{m}}-\arctan \left(\mu _{\mathrm{mz}}\right)\right)}{\tan \left(\gamma _{\mathrm{m}}\right)}$$
(5)

With regard to Eq. (3)–(5), beside geometrical and operational data as gear ratio \(u\), worm wheel torque \(T_{2}\), worm shaft drive speed \(n_{1}\) and pitch angle of the worm \(\gamma _{\mathrm{m}}\), the calculation of the load-dependent gear losses comes down to the mean coefficient of friction \(\mu _{\mathrm{mz}}\).

The mean coefficient of friction \(\mu _{\mathrm{mz}}\) represents the complex friction characteristic of meshing tooth flanks by one single mean value. In terms of worm gears, there are currently two different approaches and calculation models available. DIN 3996:2012-09 [8] describes a simpler, empirical model, while Oehler et al. [27] present a more detailed, semi-analytical one. The latter was standardized in DIN 3996:2019-09 [9], replacing the simpler approach in DIN 3996:2012-09 [8] very recently.

The empirical model in line with DIN 3996:2012-09 [8] depends on a base coefficient of friction \(\mu _{\mathrm{0T}}\) multiplied by the size factor \(Y_{\mathrm{S}}\), geometry factor \(Y_{\mathrm{G}}\), material factor \(Y_{\mathrm{W}}\) and roughness factor \(Y_{\mathrm{R}}\). Based on a reference gearbox, these factors take the deviation of the actual gearbox into account:

$$\mu _{\mathrm{mz}}=\mu _{\mathrm{0T}}\cdot \underset{f\left(a\right)}{\underbrace{Y_{\mathrm{S}}}}\cdot \underset{f\left(h^{*}\right)}{\underbrace{Y_{\mathrm{G}}}}\cdot \underset{f\left(\text{material}\right)}{\underbrace{Y_{\mathrm{W}}}}\cdot \underset{f\left(\mathrm{Ra}\right)}{\underbrace{Y_{\mathrm{R}}}}$$
(6)

The base coefficient of friction \(\mu _{\mathrm{0T}}\) is another empirical value that depends on the sliding velocity \(v_{\mathrm{gm}}\), the oil type and the material of the worm wheel:

$$\mu _{\mathrm{0T}}=f(v_{\mathrm{gm}},\text{oiltype},\text{material})$$
(7)

The semi-analytical model by Oehler et al. [9, 27] considers notable more calculation parameters, and is overall a more precise model from a physical perspective. The mean coefficient of friction \(\mu _{\mathrm{mz}}\) is based on the concept of load sharing dividing into a boundary coefficient of friction \(\mu _{\mathrm{Gr}}\) and fluid coefficient of friction \(\mu _{\mathrm{Fl}}\).

$$\mu _{\mathrm{mz}}=\psi \cdot \mu _{\mathrm{Gr}}+\left(1-\psi \right)\cdot \mu _{\mathrm{Fl}}$$
(8)

The solid load portion \(\psi\) depends on the relative lubricant film thickness \(\lambda\), which can be calculated by dividing the minimal mean lubrication gap thickness \(h_{\mathrm{min ,m}}\) according to DIN 3996:2019-09 [9] and the quadratic mean roughness \(\mathrm{Rq_{1,2}}\) of the contacting meshing partner.

$$\psi =f\left(\lambda \right)\quad\text{with}\quad\lambda =f\left(h_{\mathrm{min ,m}},\mathrm{Rq}_{1,2}\right)$$
(9)

The boundary coefficient of friction \(\mu _{\mathrm{Gr}}\) relates to solid asperity contacts of the gear flanks. Oehler et al. [27] investigated the behavior of boundary friction experimentally and derived oil type-specific, simplified formulae, which describe the boundary coefficient of friction \(\mu _{\mathrm{Gr}}\) as function of the mean flank pressure \(\sigma _{\mathrm{Hm}}\) according to DIN 3996:2019-09 [9]:

$$\mu _{\mathrm{Gr}}=f\left(\sigma _{\mathrm{Hm}}\right)$$
(10)

The fluid coefficient of friction \(\mu _{\mathrm{Fl}}\) relates to shearing of the fluid. The influence parameters are the shear stress of the fluid \(\tau _{\mathrm{Fl}}\), the mean flank pressure \(\sigma _{\mathrm{Hm}}\) as well as the solid load portion \(\psi\). To calculate the fluid shear stress, Oehler et al. [25] use a limiting shear stress flow model of Bair and Winer model according to [1].

$$\mu _{\mathrm{Fl}}=f\left(\tau _{\mathrm{Fl}}\left(\tau _{\lim },\eta _{\mathrm{m}},v_{\mathrm{gm}},h_{\mathrm{min ,m}}\right),\sigma _{\mathrm{Hm}},\psi \right)$$
(11)

3.1.2 No-load gear losses

Currently, no specific, validated calculation model is available for the no-load gear losses \(P_{\mathrm{VZ0}}\) of worm gears. Even though DIN 3996:2012-09 [8] offers an equation for calculating the overall no-load loss of gearboxes with worm gears, it does not differentiate between the different power loss portions, as there are the gears, bearings and seals. Therefore, from a more gear component-specific perspective, this does not meet the requirements of a detailed analysis of the efficiency and heat balance of gearboxes with worm gears. This is in accordance with DIN 3996:2019-09 [9], where this approach was removed.

Calculating the no-load bearing losses, as well as the seal losses, and subtracting them from calculated overall no-load loss according to DIN 3996:2012-09 [8] does, theoretically, lead to the no-load gear loss of worm gears, but in practice, this is not useful. Also, calculations show that depending on the operating point, this may result in a negative no-load gear loss due to high calculated no-load bearing losses, which does not make sense.

Oehler et al. [27] used a calculation model for churning losses of spur gears and transferred it to worm gears as shown in Eqs. (12)–(13). They used the model developed by Changenet et al. [5], which can, theoretically, be applied to other type of gears:

$$P_{\mathrm{VZ0}}=\left(\frac{1}{2}\cdot \rho _{\mathrm{oil}}\cdot \left(\frac{\pi \cdot n_{i}}{30}\right)^{2}\cdot A\cdot \left(\frac{d_{\mathrm{m}}}{2}\right)^{3}\cdot C_{\mathrm{m}}\right)\cdot \omega _{i}$$
(12)
$$ C_{\mathrm{m}} =\left(\frac{2\cdot h_{\mathrm{ID}}}{d_{\mathrm{m}}}\right)^{0.45}\cdot \left(\frac{V_{0}}{d_{\mathrm{m}}}\right)^{0,1} \cdot \left(\underset{Fr}{\underbrace{\frac{{\omega _{i}}^{2}\cdot d_{\mathrm{m}}}{2\cdot g}}}\right)^{-0.6}\cdot \left(\underset{Re}{\underbrace{\frac{\omega _{i}\cdot {d_{\mathrm{m}}}^{2}}{4\cdot \nu }}}\right)^{-0.21} $$
(13)

Oehler et al. [27] points out that using this model may lead to uncertainties and minor miscalculations. For lack of a better solution, this may currently be the most precise calculation model for no-load gear losses of worm gears.

3.2 Bearing losses

Relative movement between the inner and outer bearing ring as well as the cage and rolling elements causes power losses within bearings. Schleich [33] divides bearing losses into four main causes: rolling friction, sliding friction, inner friction of the lubricant and ventilation losses, which can be determined by several existing calculation models.

For example, the bearing manufacturers SKF [36] (cf. Eq. (14)). and Schaeffler/INA/FAG [32] (cf. Eq. (15)). provide simple empirical calculation models specifically for their bearing designs. Both models are based on the addition of no-load and load-dependent bearing losses.

$$P_{\mathrm{VL,SKF}}=\left(\underset{T_{\mathrm{VLP}}}{\underbrace{T_{\mathrm{rr}}+T_{\mathrm{sl}}}}+\underset{T_{\mathrm{VL0}}}{\underbrace{T_{\mathrm{seal}}+T_{\mathrm{drag}}}}\right)\cdot 2\cdot \pi \cdot n$$
(14)
$$P_{\mathrm{VL,INA}}=\left(T_{\mathrm{VL0}}+T_{\mathrm{VLP}}\right)\cdot 2\cdot \pi \cdot n$$
(15)

More comprehensive approaches that take into account the stiffness and local friction calculation can be found in the method of Wang [39], implemented in the simulation program LAGER2 [17], and the local friction model developed by Schleich [33], which is based on the addition of the torque losses of the individual rolling elements. Since the calculation is local in nature, many input parameters are needed.

A powerful and complex commercial program is Bearinx by Schaeffler [31].

3.3 Seal losses

Seal losses can be calculated according to ISO/TR 14179-2:2001-08 [13], in which losses are dependent on the shaft diameter \(d_{\mathrm{sh}}\) as well as the shaft rotation speed \(n\):

$$P_{\mathrm{VD}}=7.69\cdot 10^{-6}\cdot {d_{\mathrm{sh}}}^{2}\cdot n$$
(16)

Eq. (16) only covers radial shaft seals, which means that mechanical seals cannot be calculated, for instance. According to ISO/TR 14179-2:2001-08 [13], non-contacting seals result in almost no power loss.

4 Temperature calculation

Since temperature influences oil viscosity, which greatly affects the power loss of a gearbox, a temperature calculation model is required for an automatic and precise efficiency calculation. Since a gearbox shows local differences in temperature, it is reasonable to not only calculate a mean temperature for the whole gearbox but also specific local temperatures of the single components. This local heat balance analysis not only provides an opportunity to predict the thermal load capacity, but also to detect hot spots inside a gearbox. Using a TNM makes it possible to determine component temperatures in gearbox systems.

When the TNM is used, a system is divided into isothermal parts represented by nodal points. Depending on the structure of the system, those nodal points are linked where needed, considering a thermal resistance between them. Finally, a network comparable to an electrical circuit builds up what makes the transfer of the well-known mathematical laws of Ohm possible:

$$U=R_{\mathrm{ohm}}\cdot I\quad\rightarrow\quad \Updelta T=R_{\mathrm{th}}\cdot \dot{Q}$$
(17)

Rearranging Eq. (17) and replacing the thermal resistance \(R_{\mathrm{th}}\) with the thermal conductance \(L\) forms the base equation for the thermal calculation:

$$\dot{Q}=\Updelta T\cdot L\quad\text{with}\quad R_{\mathrm{th}}=\frac{1}{L}$$
(18)

Eq. (18) applies to every linked pair of nodes, meaning that whenever a difference in temperature \(\Updelta T\) exists between those nodes, the rate of heat flow \(\dot{Q}\) depends on the thermal conductance \(L\).

Similarly to electrical circuits, another principle of thermal networks is heat and power balance for every node. This means that the sum of all heat flow \(\dot{Q}\) and power \(P\) flowing towards a node \(i\) must run off again for a stationary state:

$$\sum \dot{Q}_{\mathrm{in},i}+P_{i}=\sum \dot{Q}_{\mathrm{out},i}$$
(19)

Rearranging and using Eq. (19) with Eq. (18) and putting it into the context of a thermal network with \(n\) nodes, an expression for the temperature calculation of each node can be formulated:

$$P_{i}-\sum _{j,j\neq i}^{n}\left(T_{i}-T_{j}\right)\cdot L_{i,j}=0$$
(20)

When expressed as a matrix, Eq. (20) contains \(n-1\) linearly independent equations and a single boundary condition, making it suitable for numerical solution. This formulation of an efficient, suitable thermal network is needed when it comes to an automatic and precise calculation of the efficiency and heat balance of gearboxes.

5 Implementation in simulation program

The efficiency and temperature calculation described in Sects. 3 and 4 appropriate to gearboxes with worm gears is customized and implemented in the simulation program WTplus [16], which is currently applicable to gearbox systems containing cylindrical and bevel gears. WTplus uses routines for the calculation of the efficiency and heat balance as shown in Fig. 2. Initially, a routine reads the input data followed by the macro geometry and parameter calculation according to [7, 8]. Where necessary, data is automatically complemented. WTplus then calculates the efficiency (blue) and heat balance (red) iteratively. If the calculation results in enough exactitude, an output file containing all relevant data is generated. The efficiency and temperature calculation, as well as the required extensions for gearboxes with worm gears, are described in the following Sects. 5.1 and 5.2.

Fig. 2
figure 2

Flowchart of efficiency and heat balance simulation

Full size image

5.1 Efficiency calculation

The simulation program calculates all torques and speeds, including a power flow analysis, according to Stangl [37]. Initially, these torques and speeds are not affected by any losses (lossless) but are only dependent on the kinematics of the gearing system.

Next, with the torques and speeds known, forces caused by the tooth system of worm gears can be calculated according to DIN 3996:2019-09 [9]. Subsequently, the tooth system forces are put into shaft-bearing context and thus the simulation program determines the reactive bearing forces. Then, oil data as viscosity and density is calculated to determine the tribological factors (cf. Sect. 3.1.1). Considering these values, the specific power loss portions of gears, bearings and seals are computed (cf. Sect. 3.1, 3.2 and 3.3). Lastly, the simulation program calculates all torques and speeds again, but this time it takes into consideration power losses that reduce the torques (lossy). Since these reduced torques change the tooth system forces, this leads to different bearing forces and thus changed power losses. Therefore, an iterative solution must be considered, comparing the output torques of two subsequent iterations. If the deviation between those results is below a given limit, efficiency is considered solved and the temperature calculation begins.

5.2 Local temperature calculation

The simulation program is not only able to solve the oil temperature, but can also solve local temperatures of single components fully automatically, based on the TNM explained in Sect. 4.

It is notable that the thermal network is built up fully automatically, abstracting the gearbox by suitable nodalization, linking those nodes and calculating necessary thermal conductances. The following explains the process of the abstraction for worm gears and shows solutions for the calculation of thermal conductances.

5.2.1 Nodalization

The gearbox with its gears, shafts, bearings, housing and oil is considered a system, which is nodalized. The housing is considered an isothermal body, and thus abstracted by a single node. It is linked to the environment, oil and bearings. The environment acts as a boundary condition in the form of a heat sink with a specified temperature. The oil sump is assumed to be isothermal and thus is abstracted by a single node, like the housing. Hence, the effect of temperature differences due to oil flow is neglected. Funck [10] investigated the heat balance of gearboxes and derived formulae to describe the thermal behavior of the gearbox housing and oil sump.

Schleich [33] investigated the thermal behaviour of bearings using a thermal network. Due to uncertainties and several assumptions, he concludes that dividing bearings into their components represented by a thermal network is challenging. Therefore, bearings are simplified and a single node assuming a mean temperature of the bearing is used.

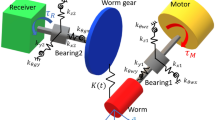
Regarding shafts, Geiger [11] shows the need to divide long narrow bodies suitably into several isothermal sections in order to minimize calculation errors and preserve compact network size. In terms of axial distance, the width of an isothermal section is set accordingly as less than or equal to its shaft diameter. Furthermore, the simulation program generates a new isothermal section wherever a component (bearing or gear) or a diameter change of the shaft is located (cf. Fig. 3).

Fig. 3
figure 3

Distribution of nodes for a worm shaft (schematically)

Full size image

Regarding the gears, it is reasonable to subdivide them into the gear body, teeth and tooth flanks. Two-piece worm wheels, as are often used, can be considered by abstracting the wheel hub and sprocket by discrete nodes. Overall, the refinement of the gears allows a more detailed resolution of the temperature.

Since the tooth system of a worm gear is extended in an axial direction, it is divided into sections similarly to the shafts. The determining parameters are the contact length \(\overline{AE}\) and axial pitch \(p_{\mathrm{x}}\) according to DIN 3975-1:2017-09 [7]. It is assumed, that the section determined by the contact length \(\overline{AE}\) lies in the middle of the tooth system representing the area of tooth contact. It can be calculated by an empirical model according to [35]. Since the tooth system of worm gears is usually longer than the contact, the remaining area is divided equally into a section of a maximal length of the axial pitch \(p_{\mathrm{x}}\) as shown in Fig. 3. This subdivision allows a more refined resolution of the heat distribution within the tooth system compared to the use of a single node.

5.2.2 Calculation of thermal conductance

Besides building the structure of the thermal network by a suitable abstraction of the components and reasonable linking, the determination of the thermal conductances \(L\) between nodes is essential (cf. Eq. (18)). Driven by a difference in temperature \(\Updelta T\), the heat transfer between linked nodes is based on the physical mechanisms conduction, convection and radiation. Depending on the mechanism and the boundary conditions, a heat transfer coefficient \(\alpha\) is established. Multiplied by the interacting surface \(A\), the thermal conductance \(L\) can be calculated:

$$L=\alpha \cdot A$$
(21)

In order to describe the conditions between nodes (e.g. shaft ↔ shaft, shaft ↔ bearing, shaft ↔ gear body, etc.), simple analogue models such as heat transfer through a plain wall or heat transfer through a cylinder are used in line with Greiner [12] wherever possible. If not applicable, substitute models are taken.

In the following, the distribution of the load-dependent gear loss to the contacting meshing partners and the calculation of thermal conductance between tooth flank ↔ oil and tooth flank ↔ tooth body are explained in more detail.

Distribution of load-dependent gear loss between gears

Apparent power loss is fully converged to heat. Thus, the load-dependent gear loss is modelled as a heat source located between the tooth flanks of the contacting meshing partners. According to the model based on [2, 30], the heat is distributed proportionally to the tangential velocities \(v_{\mathrm{t1,2}}\) and material parameters \(b_{1,2}\) of the contact partners:

$$\frac{\dot{Q}_{1}}{\dot{Q}_{2}}=\sqrt{\frac{v_{\mathrm{t1}}\cdot b_{1}}{v_{\mathrm{t2}}\cdot b_{2}}}\quad\text{where}\quad\dot{Q}_{1}+\dot{Q}_{2}=P_{\mathrm{VZP}}$$
(22)
$$\text{with}\quad b_{1,2}=\sqrt{\lambda _{1,2}\cdot \rho _{1,2}\cdot c_{1,2}}$$
(23)

Due to the high sliding speeds and thus high tangential velocities in worm gears, a typical heat distribution is about \(\dot{Q}_{1}/\dot{Q}_{2}\approx 0.8/0.2\) whereas for spur gears the heat distribution is about up to \(\dot{Q}_{1}/\dot{Q}_{2}\approx 0.6/0.4\).

Since the contact line of the meshing gears is diametrically changing as it travels from the tooth root to the tooth tip, and thus the sliding velocity is changing, 100 different meshing positions are calculated as per Eq. (22), and subsequently averaged. This allows the specific changing sliding velocity to be considered.

Thermal conductance tooth flank ↔ oil

When the gearbox is dip-lubricated, a model is needed to calculate thermal conductance between the tooth flank and oil. Since the worm shaft and worm wheel have fundamentally different geometries, distinct models are used depending on the gear in question.

With regard to the worm shaft, a Nusselt correlation of a rotating cylinder according to Changenet et al. [4] is used in order to determine the heat transfer coefficient \(\alpha \colon\)

$$\alpha =\frac{Nu\cdot \lambda }{l}$$
(24)
$$\text{with}\quad Nu=0.133\cdot Re^{2/3}\cdot Pr^{1/3}$$
(25)
$$\text{with}\quad Re=\frac{l\cdot d_{m}}{\nu }$$
(26)
$$\text{with}\quad Pr=\frac{\nu \cdot \rho \cdot c}{\lambda }$$
(27)

The interacting surface \(A\) is assumed by a simplified surface of the worm shaft consisting of the teeth tip surface (a), teeth flank surface (b) and teeth root surface (c) as shown in Fig. 4. Since the rotation of a simplified cylinder surface will cause less turbulence in the oil than the actual geometry of the worm shaft, an underestimation of the heat transfer coefficient is expected.

Fig. 4
figure 4

Simplified surface of the worm shaft (d) consisting of teeth tip surface (a), teeth flank surface (b) and teeth root surface (c)

Full size image

According to Changenet at al. [4], the thermal conductance between the worm wheel tooth flank and the oil is approached by Blok’s centrifugal flying-off theory:

$$L=\frac{2\cdot \pi \cdot \sqrt{b}}{F\cdot l\cdot 2\cdot z\cdot h_{\mathrm{ID}}\cdot \lambda \cdot \omega \cdot \sqrt{\tau }}$$
(28)
$$\text{with}\quad F=\left\{\begin{array}{cc} 1.14, & \psi <0.68\\ \left(1.55-0.6\cdot \psi \right), & 0.68<\psi <1.5 \end{array}\right.$$
(29)
$$\text{with}\quad\psi =\left(d_{\mathrm{w}}\cdot b\cdot \frac{\left(\omega \cdot \tau \right)^{2}}{2\cdot h\cdot \nu }\right)^{1/4}$$
(30)

Thermal conductance tooth flank ↔ tooth

The thermal conductance between the tooth flank and the tooth body can be described using the analogue model of heat transfer through a plain wall. The interacting surface is represented by the effective tooth surface \(A_{\mathrm{eff}}\). It is calculated by the active tooth surface \(A_{\mathrm{act}}\) multiplied by a factor depending on the gear ratio.

Depending on the gear in question, the active tooth surface is the assumed cumulated tooth contact surface during meshing of either the worm shaft or wheel (cf. Fig. 5).

Fig. 5
figure 5

Assumed active tooth surface of the worm shaft (a) and the worm wheel (b)

Full size image

Since the worm shaft and the worm wheel have a different number of teeth, a single tooth passes the contact more or less frequently, depending on the gear under consideration. Using the worm shaft as a reference, the teeth of the worm wheel pass the contact less frequently. This means that the time for heat dissipation is greater, which can equally be seen as the transferred heat being distributed over a larger surface. Seitzinger [34] investigates the heating of spur gears and develops a simple empirical model that considers this particular issue, using a single factor depending on the gear ratio \(u\). In the simulation program, Eq. (31) is used:

$$A_{2,\mathrm{eff}}=\frac{A_{2,\mathrm{act}}}{1+0.11\cdot \left(u-1\right)^{2}}$$
(31)

A more detailed explanation of the build of a worm gear’s thermal network is found in [28].

6 Results

The efficiency and heat balance model developed was validated by numerous measurements of different worm gearboxes with different centre distances \(a\) from 40 to 200 mm and gear ratios \(u\) from 5 to 63.

Heat balance calculations were performed using the TNM, taking into account the nodalization and determination of thermal conductances according to Sect. 5.2.

With regard to efficiency, both the empirical and semi-analytic model described in Sect. 3.1.1 are compared with measurements. Fig. 6 shows that the simulation and measurement results are very close to each other. Eighty-two percent of the simulation results lie within a deviation of less than ten percent, which is illustrated by the dashed line.

Fig. 6
figure 6

Comparison of experimental and simulated efficiency data of different worm gearboxes and operating points

Full size image

Fig. 7 displays simulated and measured component temperatures of five different gearboxes. Some environmental influences including ambient temperature, temperature and speed of cooling airflow as well as gearbox foundation are estimated due to lack of detailed input data. Nevertheless, calculation results correspond closely to the measurements.

Fig. 7
figure 7

Comparison of measured and simulated component temperatures of different worm gearboxes

Full size image

7 Summary

In this study, a simulation method was developed to determine the efficiency and heat balance of gearboxes with worm gears, and integrated into the simulation program WTplus. First, the general context of power loss and heat balance calculation of gearboxes was shown. Then, calculation models for the component-specific determination of power losses in worm gearbox were shown as well as the use of an automatically building thermal network for heat balance calculation. The application of the thermal network to a worm gearbox was presented afterwards, including the nodalization and calculation of important thermal conductances. Simulation results of the efficiency calculation and heat balance calculation showed very good correlation with measurements.