Abstract
Collective adaptive systems exhibit a particular notion of interaction where environmental conditions largely influence interactions. Previously, we proposed a calculus, named AbC, to model and reason about CAS. The calculus proved to be effective by naturally modelling essential CAS features. However, the question on the tradeoff between its expressiveness and its efficiency, when implemented to program CAS applications, is to be answered. In this article, we propose an efficient and distributed coordination infrastructure for AbC. We prove its correctness, and we evaluate its performance. The main novelty of our approach is that AbC components are infrastructure agnostic. Thus the code of a component does not specify how messages are routed in the infrastructure but rather what properties a target component must satisfy. We also developed a Go API, named \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\), and an Eclipse plugin to program in a high-level syntax which can be automatically used to generate matching Go code. We showcase our development through a non-trivial case study.
Similar content being viewed by others
1 Introduction
Collective adaptive systems (CAS) [20] consist of a large number of components that interact anonymously, based on their properties and on contextual data, and combine their behaviours to achieve global goals. The boundaries of CAS are fluid, and components may enter or leave the system at any time. Components may also adapt to their environmental conditions.
Most of the current communication models cannot naturally model highly adaptive and loosely coupled systems with fluid boundaries like CAS. They actually suffer from limitations due to: lack of knowledge representation, e.g. \(\pi \)-calculus [28] or rigid communication interfaces, e.g. CBS [31]. To mitigate the shortcomings of the current communication paradigms when dealing with CAS, we have proposed a kernel calculus, named AbC [3, 9], to program CAS interactions. The idea is to permit the construction of formally verifiable CAS systems by relying on a minimal set of interaction primitives. Such primitives provide a language-based approach to programming and thus can be used to implement different features and mechanisms. Clearly, this is more desirable when compared to self-organising algorithms [12, 15] that are developed for specific features.
AbC ’s primitives are attribute-based [1, 4] and abstract from the underlying coordination infrastructure (i.e. they are infrastructure agnostic). They rely on anonymous multicast communication where components interact based on mutual interests. Message transmission is non-blocking, while reception is not. Each component has a set of attributes to represent its run-time status. Communication actions (both send and receive) are decorated with predicates over attributes that partners have to satisfy to make the interaction possible. The interaction predicates are also parametrised with local attribute values, and when values change, the interaction groups do implicitly change, introducing opportunistic interactions.
Basing the interaction on run-time attribute values is indeed a nice idea, but it needs to be supported by a middleware that provides efficient ways for distributing messages, checking attribute values, and updating them. A typical approach is to rely on a centralised broker that keeps track of all components, intercepts every message and forwards it to registered components. It is then the responsibility of each component to decide whether to receive or discard the message. This is the approach used in the Java-based implementation [2] of AbC. Clearly, any centralised solution may not scale with CAS dynamics and thus becomes a bottleneck for performance. A distributed approach is definitely preferable for large systems. However, distributed coordination infrastructures for managing the interaction are still scarce and/or inefficient [34]. Also the correctness of their overall behaviour is often not obvious.
One solution is to rely on existing protocols for total-order broadcast to handle message exchange. However, these protocols are mostly centralised [18] or rely on consensus [34]. Centralised solutions have scalability and efficiency issues, while consensus-based ones are not only inefficient but also impossible in asynchronous systems where components might fail [21]. Consensus algorithms also assume that components know each other and can agree on a specific ordering. However, this contradicts the main design principles of the AbC calculus where anonymity and openendedness are crucial factors. Since AbC components are agnostic to the infrastructure, they cannot participate in establishing a total ordering. Thus, we need an infrastructure that guarantees total ordering seamlessly.
In this article, we present a theoretical foundation of a distributed coordination infrastructure for message exchange and prove its correctness with respect to the original semantics of AbC [9]. We also provide an actual implementation of this infrastructure and evaluate its performance by means of stochastic simulation. The infrastructure is implemented in Google Go because we believe that Go is more appropriate to deal with CAS due to its clean concurrency model. In essence, we provide an attribute-based API for Go, named \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\), with the goal of using the AbC primitives to program the interaction of CAS applications directly in Go. The actual implementation of \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) fully relies on the formal semantics of AbC and is parametric with respect to the infrastructure that mediates interactions. We provide a one-to-one correspondence between the AbC primitives and the programming constructs of \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\). We also provide an Eclipse plugin for \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) to permit programming in a high-level syntax which can be analysed via formal methods by relying on the operational semantics of AbC. This article is an extended and a more refined version of the works presented in [6, 7]. Here we enhance the presentation, fix imprecisions, and provide the proof details of the correctness of the proposed infrastructure.
The rest of this article is structured as follows: In Sect. 2, we briefly review the AbC calculus. In Sect. 3, we give a full formal account of a distributed coordination infrastructure for AbC and its correctness. In Sect. 4, we present the \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) API and show how to program a distributed graph colouring algorithm in \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) and we briefly comment on the Eclipse plugin. In Sect. 5, we provide a detailed performance evaluation. Finally, in Sects. 6 and 7 we conclude the article and survey-related works.
2 The AbC calculus
In this section, we briefly introduce the AbC calculus by means of a running example. We give an intuition of how to model a distributed variant of the well-known Graph Colouring Problem [24] using AbC constructs. We render the problem as a typical CAS scenario where a collective of agents, executing the same code, collaborate to achieve a system-level goal without any centralised control. The presentation is intended to be intuitive, and full details of the syntax and the semantics of AbC can be found in [3, 9]. The example will be presented thoroughly in Sect. 4.3.
The problem consists of assigning a colour (an integer) to each vertex in a graph while avoiding that two neighbours get the same colour. The algorithm consists of a sequence of rounds for colour selection. At the end of each round, at least one vertex is assigned a colour. A vertex, with identity id, uses messages of the form (“try", c, r) to inform its neighbours that at round r it wants to select colour c and messages of the form (“done", c, r) to communicate that it has chosen colour c at the end of round r. At the beginning of a round, each vertex selects a colour and sends a try-message to all of its neighbours \({\mathsf {N}}\). A vertex also collects try-messages from its neighbours. The selected colour is assigned to a vertex only if it has the greatest id among those that have selected the same colour in that round. After the assignment, a done-message (associated with the current round) is sent to neighbours.
AbCSyntax. A component, \(\varGamma \!:_{I}\!{P}\), is a process P associated with an attribute environment\(\varGamma \), and an interfaceI. An attribute environment is a partial map from attribute \(a \in \mathscr {A}\) to values \(v \in \mathscr {V}\) where \(\mathscr {A}\cap \mathscr {V}=\emptyset \). A value could be a number, a name (string), a tuple, etc., An interface\(I\subseteq \mathscr {A}\) consists of a set of attributes that are exposed by a component to control the interactions with other components. We will refer to the attributes in I as public attributes, and to those in \(dom(\varGamma )-I\) as private attributes. During interaction, a component exposes the environment \(\varGamma \downarrow I\) which represents the portion of the \(\varGamma \) that can be perceived by the context. It can be obtained from the local \(\varGamma \) by limiting its domain to the attributes in the interface I as defined below:
is a partial map from attribute \(a \in \mathscr {A}\) to values \(v \in \mathscr {V}\) where \(\mathscr {A}\cap \mathscr {V}=\emptyset \). A value could be a number, a name (string), a tuple, etc., An interface\(I\subseteq \mathscr {A}\) consists of a set of attributes that are exposed by a component to control the interactions with other components. We will refer to the attributes in I as public attributes, and to those in \(dom(\varGamma )-I\) as private attributes. During interaction, a component exposes the environment \(\varGamma \downarrow I\) which represents the portion of the \(\varGamma \) that can be perceived by the context. It can be obtained from the local \(\varGamma \) by limiting its domain to the attributes in the interface I as defined below:
Components are composed with parallel operator \(C_1\Vert C_2\).
Example (step 1/7): Each vertex is modelled in AbC as a component of the form \(C_i=\varGamma _{i}\!:_{\{\mathsf {id},{\mathsf {N}}\}}\!{P_C}\). Public attributes \(\mathsf {id}\) and \({\mathsf {N}}\) are used to represent the vertex id and the set of neighboursN, respectively. The overall system is defined as the parallel composition of existing components (i.e. \(C_1\Vert C_2\Vert ,\dots ,\Vert C_n\)).
The attribute environment of a vertex \(\varGamma _{i}\) relies on the following attributes to control the behaviour of a vertex: The attribute “\(\mathsf {round}\)" stores the current round, while “\(\mathsf {used}\)" is a set registering the colours used by neighbours. The attribute “\(\mathsf {counter}\)" counts the number of messages collected by a component, while “\(\mathsf {send}\)" is used to enable/disable forwarding of messages to neighbours. Attribute “\(\mathsf {assigned}\)" indicates if a vertex is assigned a colour while “\(\mathsf {colour}\)" is a colour proposal. These attributes initially have the following values:
\(\mathsf {round}=0\), \(\mathsf {used}=\emptyset \), \(\mathsf {send}=\mathsf{tt}\), and \({\mathsf {assigned}=\mathsf{ff}}\).
Note that no global knowledge is required and new values for these attributes can only be learnt by means of message exchange among vertices. Also the fact that a vertex knows its neighbours is example-dependent. Thanks to predicates, fully anonymous interactions can be modelled in AbC. \(\square \)
The behaviour of an AbC process can be generated by the following grammar:
The process \(\mathsf{0}\) denotes the inactive process; \(\alpha .U\) denotes a process that executes action \(\alpha \) and (possibly) the attribute updates in U and continues as P. Note that the attribute updates \([{{a}}:={{E}}]U\) are applied instantaneously with the action preceding them. The attribute environment is thus updated by setting the value of attribute a to the evaluation of the expression E. The term \(\langle {\varPi }\rangle P \) is an awareness process, it blocks the execution of process P until the predicate \(\varPi \) evaluates to true; the processes \(P_1 + P_2\), \(P_1|P_2\), and K are standard for nondeterminism, parallel composition, and process definition, respectively. The parallel operator “|" does not allow communication between \(P_1\) and \(P_2\) they can only interleave, while the parallel operator \(``\Vert " \) at the component level allows communication between components. The expression \(\texttt {this}{.}{\mathsf {b}}\) denotes the value of attribute \({\mathsf {b}}\) in the current component.
Example (step 2/7): Process \(P_{C}\) specifying the behaviour of a vertex is now defined as the parallel composition of these four processes: \(P_{C}\triangleq F\ |\ T\ |\ D\ |\ A\).
Process F forwards try-messages to neighbours, T handles try-messages, D handles done-messages, and A is used for assigning a final colour. \(\square \)
The AbC communication actions ranged by \(\alpha \) can be either \(({{\tilde{E}}})@{\varPi }\) or \( {\varPi }({{\tilde{x}}})\). The construct \(({{\tilde{E}}})@{\varPi }\) denotes an output action, it evaluates the sequence of expressions \({\tilde{E}}\) under the local attribute environment and then sends the result to the components whose attributes satisfy the predicate \(\varPi \). Furthermore, \({\varPi }({{\tilde{x}}})\) denotes an input action, it binds to sequence \({\tilde{x}}\) the corresponding received values from components whose communicated attributes or values satisfy \(\varPi \).
Example (step 3/7): We further specify process F and a part of process T.
In process F, when the value of attribute \(\mathsf {send}\) becomes true, a new colour is selected, \(\mathsf {send}\) is turned off, and a message containing this colour and the current round is sent to all the vertices having \(\texttt {this}{.}\mathsf {id}\) as neighbour. The new colour is the smallest colour that has not yet been selected by neighbours, that is \(\min \{ i \not \in \texttt {this}{.}\mathsf {used}\}\). Remember that attribute \(\mathsf {used}\) is local and initially is empty and thus all colours are available for a vertex initially. Furthermore, a vertex may only update the value of \(\mathsf {used}\) at run-time when it receives messages informing that a specific colour is selected. The guard \(\lnot {\mathsf {assigned}}\) is used to make sure that vertices with assigned colours do not take part in the colour selection anymore.
Process T receives messages of the form (“try", c, r). If \(r=\texttt {this}{.}\mathsf {round}\), then the received message was originated by a vertex performing the same round of the algorithm. The condition \(\texttt {this}{.}\mathsf {id}>\mathsf {id}\) means that the sender has an id smaller than the id of the receiver. In this case, the message is ignored (there is no conflict), simply the counter of collected messages (\(\texttt {this}{.}\mathsf {counter}\)) is incremented. Other cases, not reported here, e.g. \(\texttt {this}{.}\mathsf {id}<\mathsf {id}\), the received colour is recorded to check the presence of conflicts. Note that since the \(\mathsf {id}\) of the sender is an interface attribute (i.e. \(\mathsf {id}\in I\)), it is automatically added to the message being communicated and this is the reason why the receiver can predicate on the identity of the sender. \(\square \)
AbCSemantics. The main semantics rules of AbC are reported in Table 1. Rule Comp states that a component evolves with (send \({\varGamma \triangleright \overline{\varPi }({\tilde{v}})}\) or receive \({\varGamma \triangleright \varPi ({\tilde{v}})}\), denoted by \(\lambda \)) if its internal behaviour, denoted by the relation \(\mapsto \), allows it. Rule fComp states that a component can discard a message \({\varGamma \triangleright \varPi ({\tilde{v}})}\) if its internal behaviour does not allow the reception of this message by generating the discarding label \({\widetilde{\varGamma \triangleright \varPi ({\tilde{v}})}}\). Rule ComL states that if \(C_1\) evolves to \(C'_1\) by sending a message \({\varGamma \triangleright \overline{\varPi }({\tilde{v}})}\), then this message should be delivered to \(C_2\) which evolves to \(C'_2\) as a result. Rule ComR is the symmetric rule of ComL. Note that \(C_2\) can be also a parallel composition of different components. Thus, rule Sync states that multiple components can be delivered the same message in a single transition.
The semantics of the parallel composition operator, in rules ComL, ComR, and Sync in Table 1, abstracts from the underlying coordination infrastructure that mediates the interactions between components and thus the semantics assumes atomic message exchange. This implies that no component can evolve before the sent message is delivered to all components executing in parallel. Individual components are in charge of using or discarding incoming messages. Message transmission is non-blocking, but reception is not. For instance, a component can still send a message even if there is no receiver (i.e. all the target components discard the message); a receive operation can, instead, only take place through synchronisation with an available message. However, if we want to use the attribute-based paradigm to program the interactions of distributed applications, atomicity and synchrony are neither efficient nor applicable.
The focus of this article is on providing an efficient distributed coordination infrastructure that behaves in agreement with the parallel composition operator of AbC. Thus in Table 1, we only formalise the external behaviour of a component, i.e. its ability to send and receive. We show in the example below how interactions are derived based on internal behaviour.
Example (step 4/7): Consider the vertices \( C_1, C_2,\) and \(C_3 \) where \(\varGamma _2({\mathsf {N}})=\{{3}\}\), \(\varGamma _3({\mathsf {N}})=\{{1,4}\}\), and \(\varGamma _3(\mathsf {id})=3\). Now \(C_1\) sent a try message:

We have that \(C_2\) discards this message because it is not a neighbour \(\varGamma _2\downarrow I\not \models (1\in {\mathsf {N}})\), i.e. \(1\not \in \varGamma _2({\mathsf {N}})\) because \(\varGamma _2({\mathsf {N}})=\{3\}\). Furthermore \(C_3\) accepts the message because \(1\in \varGamma _3({\mathsf {N}})\). The system evolves with rule ComL as follows:
\(\square \)
3 A distributed coordination infrastructure
In this section, we consider a tree-based coordination infrastructure that we have also implemented in Google Go. This infrastructure is introduced to behave in agreement with the parallel composition operator of AbC while allowing components to execute asynchronously. Our approach consists of labelling each message with an id that is uniquely identified at the infrastructure level. Components execute asynchronously, while the semantics of the parallel composition operator is preserved by relying on the unique identities of exchanged messages. In essence, if a component wants to send a message, it sends a request to the infrastructure for a fresh id. The infrastructure replies back with a fresh id, and then the component sends a data (the actual) message with the received id. A component receives a data message only when the difference between the incoming data message id and the id of the last received data message equals 1. Otherwise, the data message is added to the component waiting queue until the condition is satisfied.
In this article, we give a full formal account of the tree infrastructure and also investigate its correctness with respect to the semantics of the parallel composition operator of AbC. Further details regarding other alternatives can be found in [7]. For the sake of completeness, we will briefly describe these infrastructures. The reason of our focus on the tree infrastructure is because that the tree is more efficient and theoretically more challenging.
3.1 Cluster-based infrastructure
An example of a cluster infrastructure is reported in Fig. 1a. It is composed of a set of server nodes \(\mathcal {S}\), sharing a counter ctr for sequencing messages and one input FIFO queue \(\mathcal {I}\) to store messages sent by any component C. Cluster nodes can have exclusive locks on both the cluster’s counter and the queue. Components register directly to the cluster (i.e. their addresses are registered in \(\mathcal {D}\)) and send messages to be added to the input FIFO queue. When a server node retrieves a request from the cluster queue, it replies to the requester with the value of the cluster counter. By doing so, the cluster counter is incremented. If a server retrieves a data message, it forwards the message to all components in the cluster except for the sender.
3.2 Ring-based infrastructure
An example of a ring infrastructure is reported in Fig. 1c. It is composed of a set of server nodes \(\mathcal {S}\), organised in a logical ring and sharing a counter ctr for sequencing messages coming from components. Each node manages a group of components (i.e. unlike cluster nodes, each ring node has a dedicated registration queue \(\mathcal {D}\)) and can have exclusive locks to the ring counter. When a request message arrives to a node from one of its components, the node acquires a lock on the ring counter, copies it current value, releases it after incrementing it by 1, and finally sends a reply, carrying a fresh id, to the requester. Data messages are directly added to the node’s waiting queue and will be only forwarded to the node’s components and to the neighbour node when all previous messages (i.e. with a smaller id) are received.
3.3 A tree-based infrastructure
An example of a tree infrastructure is reported in Fig 1c. It is composed of a set of servers \(\mathcal {S}\), organised in a logical tree. A component C can be connected to one server (its parent) in the tree and can interact with others in any part of the tree by only dealing with its parent. When a component wants to send a message, it asks for a fresh id from its parent. If the parent is the root of the tree, it replies with a fresh id; otherwise, it forwards the message to its own parent in the tree. Only the root of the tree can sequence messages. As the case with the ring, each tree node has a registration queue \(\mathcal {D}\) and is responsible for only a group of components.
We would like to mention that our results in this article do not consider reliability of the communication infrastructures. We only focus on the efficiency and the correctness of coordination, and we leave the reliability issue open for future work. We strongly believe that standard approaches that consider replication of server nodes can be used to guarantee the overall reliability of the considered infrastructures. However, an interesting direction would be to consider infrastructures that adapt to failure and reconfigure themselves to maintain their reliability, see [8, 11].
In the following, we provide a full formal account of the tree infrastructure.
3.4 Preliminary notations and definitions
We report the required set of notations and definitions we use to formalise the semantics of the tree infrastructure. Furthermore we define a general definition of an infrastructure component. The idea is to keep the infrastructure component totally decoupled from the type of the infrastructure it is connected to. This way the behaviour of a component will be totally independent from the one of the infrastructure.
We use the following definition of a Configuration to provide a compact semantics. For clarity, we postfix the configuration of a component, an infrastructure, and a server with the letters a, n, and s, respectively.
Definition 1
(Configuration) A configuration C, is a set of the form \(C=\langle c_1,\ \dots ,\ c_n\rangle \). The symbol ‘...’ is formally regarded as a meta-variable ranging over unmentioned elements of the configuration. The explicit ‘...’ is obligatory, and ensures that unmentioned elements of a configuration are never excluded, but they do not play any role in the current context. Different occurrences of ‘...’ in the same context stand for the same set of unmentioned elements. This definition is borrowed from Peter Mosses’ style of defining labels in modular structure operational semantics [29].
We use the reduction relation  to define the semantics of a configuration where \({\textsc {Cfig}}\) denotes the set of configurations, \({\textsc {Lab}}\) denotes the set of reduction labels which can be a message m, a silent transition \(\tau \), or an empty label, and
to define the semantics of a configuration where \({\textsc {Cfig}}\) denotes the set of configurations, \({\textsc {Lab}}\) denotes the set of reduction labels which can be a message m, a silent transition \(\tau \), or an empty label, and  denotes the transitive closure of
denotes the transitive closure of  . Moreover, we will use the following notations:
. Moreover, we will use the following notations:
-
We have two kinds of messages, an AbC message ‘msg’ (i.e. \({\varGamma \triangleright \varPi ({\tilde{v}})}\)) and an infrastructure message ‘m’; the latter can be of three different templates: (i) request {‘Q’, route, dest}, (ii) reply {‘R’, id, route, dest}, and (iii) data {‘D’, id, src, dest, msg}. The route field in a request or a reply message is a linked list containing the addresses of the nodes that the message traversed.
-
The notation \(\overset{?}{=}\) denotes a template matching.
-
The notation T[f] denotes the value of the element f in T.
-
The notation \(m\,{:}{:}\,\mathcal {W}\) denotes a queue with message m on top of it.
We also use these operations: L.get() returns the element at the front of a list/queue, while  returns the list/queue resulting from adding m to the back of L, and \(L\backslash x\) removes x from L and returns the rest.
returns the list/queue resulting from adding m to the back of L, and \(L\backslash x\) removes x from L and returns the rest.
3.5 Infrastructure component
We formally define a general infrastructure component and its external behaviour. In the following sections, we proceed by formally defining the tree infrastructure and its behaviour.
Definition 2
(Infrastructure component) An infrastructure component, a, is defined by the configuration: \(a=\langle addr, nid,\)\(mid, on, \mathcal {W}, \mathcal {X}, G\rangle \) where addr refers to its address, nid (initially 0) refers to the id of the next data message to be received, mid (initially − 1) refers to the id of the most recent reply, on (initially 0) indicates whether a request message can be sent. \(\mathcal {W}\) is a priority waiting queue where the top of \(\mathcal {W}\) is the data message with the least id, and \(\mathcal {X}\) refers to the address of the parent server. Furthermore, G ranges over \(\varGamma \!:_{I}\!{P}\) and \([\varGamma \!:_{I}\!{P}]\) where \([\varGamma \!:_{I}\!{P}]\) indicates an AbC component in an intermediate state.
The intermediate state, in Definition 2, is important to allow co-located processes (running in the same component) to interleave their behaviours without compromising the semantics, i.e. \([\varGamma \!:_{I}\!{P_1|P_2}]\) where \(P_1\) is waiting an id to send and \(P_2\) is willing to receive. Here \(P_2\) can only receive a message if it was able to do so before the intermediate state as we will explain later.
The semantics of an infrastructure component is reported in Table 2. Rule Out states that if the AbC component \(\varGamma \!:_{I}\!{P}\) encapsulated inside an infrastructure component is able to send a message \({\varGamma \!:_{I}\!{P}\xrightarrow {\varGamma '\triangleright \overline{\varPi }({\tilde{v}})}\varGamma ''\!:_{I}\!{P'}}\), the flag on is set to 1 and \(\varGamma \!:_{I}\!{P}\) goes into an intermediate state \([\varGamma \!:_{I}\!{P}]\). Rule Med states that an intermediate state component can only receive a message \({\varGamma \triangleright \varPi ({\tilde{v}})}\) if it was able to receive it before the intermediate state. Rule Req states that a component sends a request, to the parent server, only if \(on==1\). In this case, it adds its address to the route of the message and resets on to 0. Rule RcvR states that a component receives a reply if the destination field of the reply matches its address; after that mid gets the value of the id received in the reply. Rule Snd states that a component \(\varGamma \!:_{I}\!{P}\) can send a message \({\varGamma '\triangleright \overline{\varPi }({\tilde{v}})}\) and evolves to \(\varGamma ''\!:_{I}\!{P'}\) only if \(nid==mid\); this implies that a fresh id is received (\(mid\ne -1\)) and all messages with \(m[id]<mid\) have been already received. By doing so, an infrastructure data message, with msg field equal to \({\varGamma \triangleright \varPi ({\tilde{v}})}\), is sent, nid is incremented, and mid is reset. Rule RcvD states that a component receives a data message from the infrastructure if \(m[id]\ge nid\); this is important to avoid duplicate messages. The message is then added to the priority queue, \(\mathcal {W}\). Finally, rule Hnd states that when the id of the message on top of \(\mathcal {W}\) matches nid, component G is allowed to receive that message; as a result, nid is incremented by 1 and thus m is removed.
Example (step 5/7): As the semantics suggests, an infrastructure component is an encapsulation of an AbC component and thus these details are hidden from the programmer. In other words, the programmer can create an infrastructure component (Definition 2 ) for our example in Sect. 2 by only specifying the address \(\mathcal {X}\) of the parent server, substituting a vertex component \(\varGamma _{i}\!:_{\{\mathsf {id},{\mathsf {N}}\}}\!{P_C}\) in place of G and set other parts to their initial values as follows:
Note that in a real application a DHCP server automatically assigns a unique address addr to a component when executed. We will discuss these implementation details in Sect. 4.
3.6 A formal definition of the tree infrastructure
In this section, we formally define the structure of the tree and its semantics. Furthermore we provide a proof of correctness of its behaviour with respect to the semantics of the parallel composition operator of AbC.
Definition 3
(Tree server) A tree server s is a configuration: \(s=\langle addr,\ ctr,\ nid,\ \mathcal {D},\ \mathcal {M},\ \mathcal {I},\ \mathcal {W},\ \mathcal {X}\rangle \) where ctr is a counter to generate fresh ids, \(\mathcal {D}\) is a set containing the addresses of the server’s children which include connected components and servers, \(\mathcal {M}\) is a multicast set (initially \(\mathcal {M}=\mathcal {D}\)), and \(\mathcal {I}\) is a FIFO input queue. The rest are defined as before.
Definition 4
(Tree infrastructure) A tree infrastructure \(\mathcal {N}\) is defined by the configuration: \(\mathcal {N}=\langle \mathcal {S},\mathcal {A}\rangle \) where \(\mathcal {S}\) denotes the set of servers and \(\mathcal {A}\) denotes the set of connected components such that:
-
\(\forall s_1, s_2\in \mathcal {S}\), we say that \(s_1\) is a direct child of \(s_2\), written \(s_1\prec s_2\), if and only if \(s_1[\mathcal {X}]=s_2[addr]\); \(\prec ^{+}\) denotes the transitive closure of \(\prec \).
-
\(\forall s\in \mathcal {S},\ \text {we have that}\ s\not \prec ^{+} s\).
-
The root: \(\exists s\in \mathcal {S}\) such that for any \(s'\in (\mathcal {S}\backslash \{s\}), s'\prec ^{+}s\) and we have that:
-
\(s'[nid]\le s[ctr]\).
-
For any message \(m\in s'[\mathcal {W}]\) we have that \(m[id]\le s[ctr]\).
-
-
A root is unique: if \(s,s'\in \mathcal {S}\) and \(s[\mathcal {X}]=s'[\mathcal {X}]=\bot \) then we have that \(s=s'\).
-
\(\forall s\in \mathcal {S}\) and for each message \(m\in s[\mathcal {W}]\), we have that \(m[id]\ge s[nid]\).
The semantics rules of a tree infrastructure are reported in Table 3. The rules (\({\textsc {s}}\leftrightarrow {\textsc {s}}\)) and (\({\textsc {s}}\leftrightarrow {\textsc {a}}\)) state that a tree evolves when a message m is exchanged either between two of its servers (\(s_1\) and \(s_2\)) or between a server and a component, respectively. Furthermore, the rules (s) and (a) state that a tree evolves when one of its servers or one of its connected components evolves independently.
The semantics rules of a tree server are defined by the rules in Table 4. Rule In states that a server receives a message m and adds it to the back of its input queue ( ) if the destination field of m matches its own address addr. Rule Reply states that if a root server gets a request from the front of its input queue \(m\,{:}{:}\,\mathcal {I}'\), it sends a reply to the requester by getting its address from the route of the message \(x=route.get()\). The id of the reply is assigned the value of the root’s counter ctr. By doing so, the counter is incremented. On the other hand, a non-root server adds its address to the message’s route and forwards it to its parent as stated by rule qFwd. Rule rFwd instead is used for forwarding reply messages. Rule wIn states that if a server gets a data message from its input queue \(\mathcal {I}\) and it is the root or its parent is the source of the message (i.e. \(\mathcal {X}== addr'\vee \mathcal {X}==\bot \)), the server evolves silently and the message is added to its waiting queue. If the condition (\(\mathcal {X}== addr'\vee \mathcal {X}==\bot \)) does not hold, the message is also forwarded to the parent as stated by rule wNxt. Furthermore, rule dFwd states that when the id of the message on top of \(\mathcal {W}\) matches nid (i.e. \(m[id]==nid\)), the server starts forwarding m to its children one by one except for the sender. Note that this rule can be applied many times as long as the multicast set \(\mathcal {M}\) contains more than one element, i.e. \(|\mathcal {M}|>1\). Once \(\mathcal {M}\) has only one element, rule eFwd is applied to forward the message to the last address in \(\mathcal {M}\). As a result, nid is incremented, m is removed from \(\mathcal {W}\), and the multicast set \(\mathcal {M}\) is reset to its initial value. Note that rule nFwd handles the case when \(\mathcal {M}\) has only the address of the sender. Thus the message is discarded as the sender cannot receive its own message.
) if the destination field of m matches its own address addr. Rule Reply states that if a root server gets a request from the front of its input queue \(m\,{:}{:}\,\mathcal {I}'\), it sends a reply to the requester by getting its address from the route of the message \(x=route.get()\). The id of the reply is assigned the value of the root’s counter ctr. By doing so, the counter is incremented. On the other hand, a non-root server adds its address to the message’s route and forwards it to its parent as stated by rule qFwd. Rule rFwd instead is used for forwarding reply messages. Rule wIn states that if a server gets a data message from its input queue \(\mathcal {I}\) and it is the root or its parent is the source of the message (i.e. \(\mathcal {X}== addr'\vee \mathcal {X}==\bot \)), the server evolves silently and the message is added to its waiting queue. If the condition (\(\mathcal {X}== addr'\vee \mathcal {X}==\bot \)) does not hold, the message is also forwarded to the parent as stated by rule wNxt. Furthermore, rule dFwd states that when the id of the message on top of \(\mathcal {W}\) matches nid (i.e. \(m[id]==nid\)), the server starts forwarding m to its children one by one except for the sender. Note that this rule can be applied many times as long as the multicast set \(\mathcal {M}\) contains more than one element, i.e. \(|\mathcal {M}|>1\). Once \(\mathcal {M}\) has only one element, rule eFwd is applied to forward the message to the last address in \(\mathcal {M}\). As a result, nid is incremented, m is removed from \(\mathcal {W}\), and the multicast set \(\mathcal {M}\) is reset to its initial value. Note that rule nFwd handles the case when \(\mathcal {M}\) has only the address of the sender. Thus the message is discarded as the sender cannot receive its own message.
Correctness. Since there is a single sequencer in the tree, i.e. the root, two messages can never have the same id. We only need the following results to ensure that the tree behaves in agreement with the AbC parallel composition operator. In essence, Proposition 2 ensures that if any component in the tree sends a request for a fresh id, it will get it. Proposition 4 ensures that any two components in the tree with different nid will converge to the same one. However, to prove Proposition 4, we need to prove Lemma 1 and Proposition 3 which guarantee the same results among tree’ servers. This implies that messages are delivered to all components. Proposition 5 instead ensures that no message stays in the waiting queue indefinitely.
Proposition 1
For each pair of nodes \(s_1,s_2\in \mathcal {N}[\mathcal {S}]\), if \(s_1\) sends a request to \(s_2\), then eventually \(s_2\) will send a reply to \(s_1\).
Proof
The proof proceeds by induction on the level of \(s_2\) in the tree, \(L(s_2)\).
-
Base case: \(L(s_2)=0\), this implies that node \(s_2\) is the root of the tree (i.e. \(s_1[\mathcal {X}]=s_2[addr]\)). By Table 4, rule qFwd, when \(s_1\) gets a request from its input queue, it adds its address to the route of the message and forwards it to its next node, in this case and by Table 4, rule In, \(s_2\) adds the request to its input queue. The overall infrastructure evolves by applying rule \(s\leftrightarrow s\), Table 3. The tree \(\mathcal {N}\) evolves by multiple applications of the rules in Table 3 until \(s_2\) gets the request from its input queue. It labels it with a fresh id and sends a reply back to the requester by applying rule Reply and \(s_1\) receives the reply by applying rule In, Table 4. So we have that
 we have that \(s_2\) will eventually send a reply back to \(s_1\).
we have that \(s_2\) will eventually send a reply back to \(s_1\). -
Inductive hypothesis: \(L(s_2)\le k\), if \(s_1\) sends a request to \(s_2\), then \(s_2\) will eventually reply to \(s_1\).
-
Inductive step: Now it is sufficient to prove the claim for \(s_2\), where \(L(s_2)=k+1\). By Table 4, rule qFwd, when \(s_1\) gets a request from its input queue, it adds its address to the route of the message and forwards it to \(s_2\). We have that according to Table 3
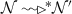 and \(s_2\) can also forward the request to its next node, say \(s'\) where \(L(s')=k\), by Table 4, rule qFwd. By the induction hypothesis, we have that \(s'\) will eventually send a reply to \(s_2\) since the claim holds for level k. When the reply arrives to \(s_2\), it will send it to \(s_1\) by applying rule rFwd as required.
and \(s_2\) can also forward the request to its next node, say \(s'\) where \(L(s')=k\), by Table 4, rule qFwd. By the induction hypothesis, we have that \(s'\) will eventually send a reply to \(s_2\) since the claim holds for level k. When the reply arrives to \(s_2\), it will send it to \(s_1\) by applying rule rFwd as required.
\(\square \)
Proposition 2
For any component, with address addr and a parent \(\mathcal {X}\), connected to a tree infrastructure \(\mathcal {N}\), we have that if

then  and
and

Proof
A component \(a_1\) can send a request by applying rule Req, Table 2 and its node, say \(s_1\), can receive it by applying rule In, Table 4 and adds it to its input queue. The tree evolves with rule \(s\leftrightarrow a\), Table 3. By relying on Proposition 1 and  , \(s_1\) will send a reply back to \(a_1\) by applying either rule Reply or rFwd, Table 4. On the other hand, \(a_1\) will receive the reply by applying rule RcvR and the tree evolves with rule \(s\leftrightarrow a\), Table 3 as required. \(\square \)
, \(s_1\) will send a reply back to \(a_1\) by applying either rule Reply or rFwd, Table 4. On the other hand, \(a_1\) will receive the reply by applying rule RcvR and the tree evolves with rule \(s\leftrightarrow a\), Table 3 as required. \(\square \)
To prove Proposition 3, we need first to prove the following lemma. This lemma ensures that adjacent nodes will eventually converge to the same nid. In other words, a node must forward the removed data message from its queue to all immediate neighbours (i.e. tree nodes in its \(\mathcal {D}\)) before incrementing its nid.
Lemma 1
For every two tree nodes \(s_1\) and \(s_2\) and a tree-based infrastructure \(\mathcal {N}\) such that \(s_1,s_2\in \mathcal {N}[\mathcal {S}]\), we have that:
-
If \(s_1\prec s_2\wedge \ s_1[nid]<s_2[nid]\) then
 and \( s_1[nid]=s_2[nid]\).
and \( s_1[nid]=s_2[nid]\). -
If \(s_2\prec s_1\wedge \ s_1[nid]<s_2[nid]\) then
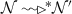 and \( s_1[nid]=s_2[nid]\).
and \( s_1[nid]=s_2[nid]\).
Proof
The proof proceed by induction on the difference between \(s_2[nid]\) and \(s_1[nid]\). We only prove the first statement as the second one is analogous.
-
Base case, \(s_2[nid]-s_1[nid]=1\): From Table 4, rule eFwd, nid is only incremented after message m, where \(m[id]=s_2[nid]-1\), is forwarded to the last child in \(\mathcal {D}\). It can also be incremented when the message is discarded by rule nFwd to avoid sending the message back to the sender. But \(s_1\prec s_2\), so we know that \(s_1\) already received m and added m to its input queue by rule In. Thus
 and finally m moves from the input queue to the waiting queue i.e. \(s_1[\mathcal {W}]=m\,{:}{:}\,q\) by either rule wIn or rule wNxt. Note that this is a priority queue that sorts its messages according to their identities. Since \(s_2[nid]-s_1[nid]=1\), we have that \(s_2[nid]-1=s_1[nid]=m[id]\). This means that m is ordered with respect to \(s_1\). By multiple applications of rule dFwd and followed by one application of rule eFwd and/or nFwd, Table 4 to forward m to children, we have that \(s_1[nid]=s_1[nid]+1=s_2[nid]\) as required.
and finally m moves from the input queue to the waiting queue i.e. \(s_1[\mathcal {W}]=m\,{:}{:}\,q\) by either rule wIn or rule wNxt. Note that this is a priority queue that sorts its messages according to their identities. Since \(s_2[nid]-s_1[nid]=1\), we have that \(s_2[nid]-1=s_1[nid]=m[id]\). This means that m is ordered with respect to \(s_1\). By multiple applications of rule dFwd and followed by one application of rule eFwd and/or nFwd, Table 4 to forward m to children, we have that \(s_1[nid]=s_1[nid]+1=s_2[nid]\) as required. -
Inductive hypothesis: \(s_2[nid]-s_1[nid]\le k\) given that \(s_1\prec s_2\), then
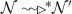 and \(s_1[nid]=s_2[nid]\).
and \(s_1[nid]=s_2[nid]\). -
Inductive step: Now it is sufficient to prove the claim for \(s_1\) and \(s_2\) such that \(s_2[nid]-s_1[nid]=k+1\).
From Table 4, rules eFwd and nFwd, we know that message m, where \(m[id]=s_2[nid]-1\), has been already forwarded to children in \(\mathcal {D}\) and/or to next node by rule wNxt and \(s_1\) already received m and added m to its input queue. We have that
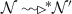 and finally m moves from the input queue to the waiting queue by either rule wIn or rule wNxt. Since \(s_2[nid]-s_1[nid]=k+1\) then \(m[id]-s_1[nid]=k\). This means that k-messages from \(s_2\) already exist in the queue of \(s_1\) and need to be processed first and then after m can be processed. By the induction hypothesis,
and finally m moves from the input queue to the waiting queue by either rule wIn or rule wNxt. Since \(s_2[nid]-s_1[nid]=k+1\) then \(m[id]-s_1[nid]=k\). This means that k-messages from \(s_2\) already exist in the queue of \(s_1\) and need to be processed first and then after m can be processed. By the induction hypothesis,  and \( s_1[nid]=s_2[nid]\) where \(s_2[nid]-s_1[nid]\le k\). So we have that \(s_1[nid]=s_1[nid]+k\), but \(m[id]-s_1[nid]=k\). This implies that \(m[id]=s_1[nid]\), i.e. message m is ordered with respect to \(s_1\). Now again by Table 4, multiple applications of rule dFwd followed by one application of rule eFwd and/or nFwd,
and \( s_1[nid]=s_2[nid]\) where \(s_2[nid]-s_1[nid]\le k\). So we have that \(s_1[nid]=s_1[nid]+k\), but \(m[id]-s_1[nid]=k\). This implies that \(m[id]=s_1[nid]\), i.e. message m is ordered with respect to \(s_1\). Now again by Table 4, multiple applications of rule dFwd followed by one application of rule eFwd and/or nFwd,  and \(s_2[nid]=s_1[nid]\) as required. \(\square \)
and \(s_2[nid]=s_1[nid]\) as required. \(\square \)
Proposition 3
Let \(s_1\) and \(s_2\) be two tree nodes and \(\mathcal {N}\) be a tree-based infrastructure, \(\forall s_1,s_2\in \mathcal {N}[\mathcal {S}]\wedge \ s_1[nid]<s_2[nid]\), we have that  and \( s_1[nid]=s_2[nid]\).
and \( s_1[nid]=s_2[nid]\).
Proof
The proof proceeds by case analysis on \(s\prec ^{+}s'\). Since the topology of the infrastructure is tree based, we have three cases.
-
Case 1, \(s_1\prec ^{+}s_2\): This case can be proved by induction on the distance, \(d(s_1,s_2)\), between \(s_1\) and \(s_2\) in the tree. Function \(d(s_1,s_2)\) is defined inductively as follows:
$$\begin{aligned} d(s_1,s_2) = {\left\{ \begin{array}{ll} 0, &{} \text {for } s_1\prec s_2\ \text {or}\ s_2\prec s_1\\ 1+d(t',s_2), &{} \text {for } s_1\prec ^{+}s_2\ \text {where}\ s_1\prec t'\\ 1+d(s_1,t'), &{} \text {for } s_2\prec ^{+}s_1\ \text {where}\ s_2\prec t' \end{array}\right. } \end{aligned}$$-
Base case, \(d(s_1,s_2)=0\): directly from Lemma 1.
-
Inductive hypothesis:
Suppose that \(\forall s_1{,}s_2\in \mathcal {N}[\mathcal {S}]{:}d(s_1{,}s_2){\le } k\) where \(k{>}0\) and given \(s_1[nid]{<}s_2[nid]\), we have that
 .
. -
Inductive step: Now it is sufficient to prove the claim for \(s_1\) and \(s_2\) where \(d(s_1,s_2)=k+1\).
From Lemma 1, for \(s_2\) at distance \(k+1\) from \(s_1\) and \(s_3\) at distance k from \(s_1\), i.e. \(s_1\prec ^{+} s_3\prec s_2\), we have that
 and \(s_3[nid]=s_2[nid]\). But \(d(s_1,s_3)=k\), so by the induction hypothesis we have that
and \(s_3[nid]=s_2[nid]\). But \(d(s_1,s_3)=k\), so by the induction hypothesis we have that 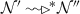 and \(s_1[nid]=s_3[nid]=s_2[nid]\) as required.
and \(s_1[nid]=s_3[nid]=s_2[nid]\) as required.
-
-
Case 2, \(s_2\prec ^{+}s_1\): is analogous to the previous case.
-
Case 3, \(\exists s_3:s_1\prec ^{+}s_3\wedge \ s_2\prec ^{+}s_3\): we have several cases, but here we only consider one case and the others follow in a similar way. If \(s_1[nid]>s_3[nid]<s_2[nid]\), we first take \(s_3\) and \(s_2\) and by Case 2, we have that
 and \( s_3[nid]=s_2[nid]>s_1[nid]\). Now for \(s_1\) and \(s_3\) and by Case 1, we have that
and \( s_3[nid]=s_2[nid]>s_1[nid]\). Now for \(s_1\) and \(s_3\) and by Case 1, we have that 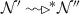 and \( s_1[nid]=s_2[nid]\) as required. \(\square \)
and \( s_1[nid]=s_2[nid]\) as required. \(\square \)
Proposition 4
Given any two components \(a_1\) and \(a_2\) in a tree infrastructure \(\mathcal {N}\) such that \(a_1[nid]<a_2[nid]\), we have that  and \(a_1[nid]=a_2[nid]\).
and \(a_1[nid]=a_2[nid]\).
Proof
The proof follows directly by Proposition 3 and the semantics rules in Tables 2 and 3.\(\square \)
Proposition 5
Given a tree infrastructure \(\mathcal {N}=\langle {\mathcal {S},\mathcal {A}}\rangle \), for any \(c\in \mathcal {S}\cup \mathcal {A}\) where \(c[\mathcal {W}]=m::\mathcal {W}'\), we have that  and
and  where
where  returns a priority queue composed by the sub-queues \(\mathcal {W}'\) and \(\mathcal {W}''\).
returns a priority queue composed by the sub-queues \(\mathcal {W}'\) and \(\mathcal {W}''\).
Proof
The proof follows from Propositions 2, 3 and 4, and by induction on the difference between c[nid] and m[id].\(\square \)
Proposition 5 states that a message m on top of the waiting queue \(\mathcal {W}\) of a component cannot stay forever as the infrastructure \(\mathcal {N}\) evolves. The component processes m and removes it from \(\mathcal {W}\) during the infrastructure evolution. While doing so, other messages (represented by a sub-queue \(\mathcal {W}''\)) may arrive to the end of \(\mathcal {W}\).
4 A go attribute-based interaction API
\(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\)Footnote 1 is a distributed programming API for supporting attribute-based interaction directly in Google Go. Go is a new programming language, developed by Google to handle the complexities of networked systems and massive computation clusters, and to make working in these environments more productive. It supports concurrency and inter-process communication through a compact set of powerful primitives and lightweight processes, called goroutines.
As opposed to Java, Go provides an intuitive and lightweight concurrency model with a well-understood semantics. It extends the CSP model [23] with mobility by allowing channel-passing, like in \(\pi \)-calculus [28]. However, channel-passing in Go is possible only locally between goroutines. Go also supports buffered channels with a finite size. When the buffer size is 0, goroutines block execution and can only communicate by means of synchronisation. Otherwise, channels behave like mailboxes in Erlang which is, however, actor-based [5], and for interaction, it relies on identities rather than on channels. Note that such concurrency features of Go can be mimicked with the core.async concurrency library of Clojure. However, the main difference is that concurrency in Go is an actual ingredient of the language rather than an integrated library. Also note that Clojure way of dealing with concurrency is similar to the one of Java and thus without the core.async library, concurrent programming in Clojure is not an ideal choice. On the other hand, Clojure is less verbose and has a clean typing system when compared to Go. Thus using Clojure with the core.async library provides an elegant and clean environment to write concurrent programs. Another candidate would be using the Akka concurrency library in Scala. Akka handles concurrency based on the Actor model as the case of Erlang. However, being integrated in a rich and functional language like Scala, it unlocks the reuse of Scala internal DSL features and easily supports interoperability of Java and other JVM-based languages.
All of these alternatives have their pros and cons, and it would be interesting as a future work to find out what class of applications each one of them handles the best. However, since this is out of the scope of this article, we only focus on the Go language. We believe that the generality, efficiency and the clean concurrency model of Go make it an appropriate language for programming CAS. Thus, we integrated attribute-based interaction in Go via the distributed\(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) API to move the mobility of Go concurrency to the next level.
In what follows, we present the actual implementation of the distributed coordination infrastructures in Google Go and present the syntax of the \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) API.
4.1 A Go implementation of infrastructures
In this section, we consider a Go implementation of three distributed coordination infrastructures for managing message exchange of the \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) API. These infrastructures model faithfully the parallel composition operator of the AbC calculus.
The projection of a \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) system with respect to a specific component is reported in Fig. 2. It mainly consists of three parts: (i) component, (ii) agent, and (iii) infrastructure. The agent provides a standard interface between a \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) component and the underlying coordination infrastructure and mediates message exchange between them. Actually, the agent hides the details of the infrastructure from a component. An agent can be seen as a piece of software that handles the interaction between a component and the infrastructure server connected to it. A component registers to a server in the infrastructure by creating a dedicated agent through a registration address to handle their interactions.
In what follows, we provide a brief description of the implementation and of the dynamics of our distributed coordination infrastructures.
The Component. As reported in Fig. 2, a \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) component consists of a behavioural part represented by its running processes and an interface (its agent) to deal with the infrastructure’s server connected to it. The interface consists of three entities: the Input handler, the Msg dispatcher, and the Msg ID handler.
The Input handler is used to collect all incoming messages from the infrastructure’s server and to forward reply messages to the Msg ID handler.
The Msg dispatcher stores a message in the waiting queue of the component until all messages with smaller id have been sent/delivered. Once this condition is satisfied, the Msg dispatcher forwards the message to a process; if the process accepts, the message is considered as delivered; otherwise, the Msg dispatcher tries with another process. The procedure continues until either the message is accepted by some process or all processes have rejected it. In both cases, the message is considered as delivered and the new id is notified to the Msg ID handler which updates the id of the next message to receive. It is important to note that any change to the attributes during the decision of accepting or rejecting the message can be only committed if the message is accepted; otherwise, it will be rolled-back.
The Msg ID handler deals with requests of processes wanting to send a message, and provides them with fresh ids. The handler forwards the request to the infrastructure’s server. While the process is waiting to send its message, dispatched messages are added to the waiting queue of the component. Once a reply message with a fresh id is received, the Msg ID handler forwards it to the process only when all messages with smaller id have been processed. The process can now manipulate the attributes environment and send a new message to the Msg ID handler which will forward it to the infrastructure’s agent. All attribute updates are committed, and the msg dispatcher is notified about the new id.
The Coordination Infrastructures. These infrastructures are responsible for forwarding messages to components and also for issuing fresh message ids. Each kind of infrastructure consists of a set of server nodes that are logically connected in a specific way and collaborate to deliver sent messages to all connected components except for the sender. The implementation details of each infrastructure are reported below:
-
The Cluster Infrastructure It consists of a registration node and a set of servers sharing a counter node and an input queue. A \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) component needs to register itself to the cluster. The component contacts the registration node which will forward its network address to all cluster’ servers. The component forwards its messages to the input queue of the cluster. A cluster server gets a message from the input queue which acts as a synchronisation point. If the message is a request for a fresh id, the server asks for a fresh id from the counter node and sends a reply back to the requester; otherwise, the message is forwarded to all components connected to the cluster except for the sender. This kind of infrastructure is a straightforward generalisation of a centralised implementation where only a single server is responsible for forwarding and sequencing messages.
-
The Ring Infrastructure It consists of a registration node and a set of servers sharing a counter node. Upon registration, a component is only registered to one server (a parent) in the ring. This server will be the only interface for the component to interact with the infrastructure. The fact that components are assigned to specific servers allows us to reuse the same TCP connection. This would avoid unnecessary delays caused by re-establishing the connection every time a message is exchanged. A component forwards its messages to the input queue of its parent server. A ring server gets a message from its input queue: if it is a request message, the server asks for a fresh id from the counter node and sends a reply back to the requester; otherwise, the message is forwarded to all components directly connected to this server except for the sender. The message is also forwarded to its neighbour in the ring. When a server receives a message from its neighbour, it will accept the message only when its id is greater than the id of the last message processed at this server; otherwise, the message is discarded.
-
The Tree Infrastructure. The tree infrastructure consists of a registration node and a set of servers organised in a logical tree. The registration node handles the construction of the infrastructure and the registration of components. When a component registers to the infrastructure through its agent, the registration node associates the agent to a specific server by assigning it communication ports to manage interaction with the selected server. The root of the tree is the only server that is responsible for generating sequence numbers. Each server is responsible for a group of agents and has its own input queue. The agent forwards its component messages to the input queue of its parent server. The server gets a message from its input queue: if it is a request message and the server is the root of the tree, the server assigns it a fresh id and sends a reply back to the requester; otherwise, the server forwards the message to its parent until the message reaches the root. Every time a request message traverses a server, it records its address in a linked list to help trace back the reply to the original requester with a minimal number of messages. If the server receives a reply message, it will forward it to the address on top of the message’s linked list storing the path. As a consequence, this address is removed from the linked list. Finally, when a data message is received, it is forwarded to all connected agents and servers except for the sender.
In what follows, we briefly introduce the programming constructs of the \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) API and show how they relate to the AbC primitives.
4.2 The programming interface
The main programming constructs of the \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) API are reported in Fig. 3.
A component is the main building block of a \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) system; each component contains a set of processes, defining its behaviour, and a set of attributes, defining its run-time status and contextual data. A \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) system consists of a collection of \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) components. Components execute in parallel and exchange messages only through message passing. In Fig. 3, Part 1, we show how to define a \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) component, connect it to an infrastructure, and manipulate its attribute values. The method \(\mathsf { NewComponent(Agent,}\mathsf {Environment)}\) takes an agent which is created based on the registration address of an infrastructure \(\mathsf {Addr}\). It also takes an attribute environment \(\mathsf {Environment}\) and creates a \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) component. Components are parametric with respect to the infrastructure that mediates their interactions and the programmer needs only to know the registration address of components in the infrastructure. Currently, three types of infrastructures are supported, namely Tree, Cluster, and Ring. The attribute environment of a component is defined as a map from attribute identifiers to their values. The attributes of a component can be retrieved and set via the methods \(\mathsf { Comp(attribute)}\) and \(\mathsf { Set(attribute, value)}\), respectively.
Example (step 6/7): In our example, we create a vertex as follows:

In Fig. 3, Part 2, the method \(\mathsf {Run}\) is used to assign a behaviour to a \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) component and also to start its execution. This method takes a process as an argument and executes it within the scope of the current component. The code inside the \(\mathsf {Run}\) method represents the actual behaviour of a component.
Example (step 7/7): In our example processes, \(\mathsf {processF}\), \(\mathsf {processT}\), \(\mathsf {processD}\) and \(\mathsf {processA}\) are created inside the vertex and they start executing as follows:

Processes \(\mathsf {processF}\), \(\mathsf {processT}\), \(\mathsf {processD}\), and \(\mathsf {processA}\) code will be detailed in Sect. 4.3.
The generic behaviour of a \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) process is implemented via a Go function as reported in Fig. 3, Part 3. This function takes a reference to a \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) process and executes its commands. Note that beside \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) commands, which will be explained later, the usual loop and branching statements of Go can also be used. Furthermore, in Fig. 3, Part 4, we define the available \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) commands. The main communication actions, send and receive, are implemented via \(\mathsf { Send(Tuple, Predicate)}\) and \(\mathsf {Receive}\)\(\mathsf {(accept func(attr *Attributes, msg Tuple) bool)}\)
methods. The send method communicates a tuple of values, \(\mathsf { Tuple}\), to components whose attributes satisfy the predicate \(\mathsf { Predicate}\). The receive method accepts a message and passes it to a Boolean function that checks if it satisfies the receiving predicate of a component. We also provide two other versions of the send action: a side-effect send \(\mathsf { SendUpd}\) and a guarded side-effect send \(\mathsf { GSendUpd}\). The former has immediate attribute updates once executed, and the latter can also be guarded by a predicate \(\mathsf { Guard}\) that blocks the execution until the guard is satisfied.
\(\mathsf {Spawn}\) dynamically creates a new process \(\mathsf { Process}\) and executes them in parallel with the main process at run-time, while \(\mathsf {Call(Process)}\) implements a process call. The awareness operator, implemented via the method \(\mathsf {WaitUntilTrue}\mathsf {(Predicate)}\), blocks the execution of a process until predicate \(\mathsf {Predicate}\) is satisfied. The method \(\mathsf {Select(cases}\)\(\mathsf {...Case)}\) is a non-deterministic selection of guarded processes. This method takes a finite number of arguments of type \(\mathsf { Case}\), each of which is composed of an action guarded by a predicate and a continuation process as shown in the syntax of a case. When the guarding predicate of one branch is satisfied, the method enables it and terminates other branches. Finally, Part 5 shows some of the supported predicates, i.e. \(\mathsf { Equals, And,}\)\(\mathsf { Belong}\), and \(\mathsf { Not}\) correspond to \(=,\ \wedge ,\ \in \) and \(\lnot \), respectively. Other standard predicates are also available. We use Receiver(a) in the sender predicate to evaluate the predicate based on the value of attribute a in the receiver side. For instance, Belong(goat.Comp("id") , goat.Receiver("N")) is equivalent to \(\texttt {this}{.}\mathsf {id}\in {\mathsf {N}}\).
4.3 Case study: a distributed graph colouring
In this section, we show how to use the programming constructs of the \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) API to program a distributed variant of the graph colouring algorithm [24] presented in the running example. We render the problem as a typical CAS scenario where a collective of agents, executing the same code, collaborate to achieve a system-level goal without any centralised control. To avoid verbosity, we omit all auxiliary functions, but we comment on their behaviour.
Process \({\mathsf {F}}\), reported below, proposes a colour. If a vertex is not assigned a colour and the value of attribute \(\mathsf {send\_try}\) is true, the process sends a try message to its neighbours identifying them by the predicate \(\mathsf {Belong(goat.Comp("id"),}\)\(\mathsf {goat.Receiver("N"))}\). The try message contains a \(\mathsf {try}\) label, the proposed colour, the current round, and the id of this vertex. The proposed colour is the smallest colour that has not yet been selected by neighbours (not in \(\mathsf {used}\)). The function \(\mathsf { Evaluate(minColorNot, goat.Comp("used"))}\) is used to propose a colour. As side effects, the attribute \(\mathsf {colour}\) is assigned the new colour and the attribute \(\mathsf { send\_try}\) is set to false.

Process \({\mathsf {T}}\) deals with try-messages \(\mathsf {(``{try}", y, z, tid)}\) as mentioned before. If the current round equals the round attached in the message \({\mathsf {z}}\), then the received message has been originated by another component performing the same round of the algorithm and we have two cases (Lines 12-19). The first case is executed when the id of the vertex is greater than the id of the message \(\mathsf {tid}\), i.e. the sender has an id smaller than the id of the receiver. In this case, the message is ignored (there is no conflict), simply the counter of received messages is incremented. In the second case, the received colour is recorded to check the presence of conflicts. The value of \({\mathsf {y}}\) is added to constraints, and the counter is incremented by 1. If \({\mathsf {z}}\) is greater than the current round, as in (Lines 21-32), then the received message has been originated by a component executing a successive round and two possible alternatives are considered (\(\mathsf {thisId > tid}\) or \(\mathsf {thisId < tid}\)). In both cases, round is set to \({\mathsf {z}}\), \(\mathsf {send\_try}\) and \(\mathsf {counter}\) are updated accordingly, and \(\mathsf {constraints}\) is set to the value of \({\mathsf {y}}\) if \(\mathsf {thisId < tid}\).

Process \({\mathsf {D}}\), below, is used to receive done-messages of the form \(\mathsf {(``{done}", y, z, tid)}\) where \({\mathsf {y}}\) is the assigned colour, \({\mathsf {z}}\) is the attached round, and \(\mathsf {tid}\) is the sender id. These are sent by components that have reached a final decision about their colour. We have two cases: either the attribute \(\mathsf {round}\) is \(\mathsf {< z}\) or \(\mathsf {\ge z}\). In both cases, the used colour is registered in \(\mathsf {used}\) and the counter \(\mathsf {done}\) is incremented. However, in the second case, private attributes are updated to indicate the startup of a new round (\({\mathsf {z}}\)).

Process A, reported below, is used to assign a final colour to a vertex. It can only be executed when messages from neighbours (which are not assigned colours) have been received and no conflict has been found (i.e. the colour is neither in \(\mathsf {used}\) nor in \(\mathsf {constraints}\)). When the above conditions are satisfied, message \(\mathsf {(``{done}",}\)
\( \mathsf {colour, round + 1, id)}\) is sent to neighbours, the attribute \(\mathsf {Assigned}\) is set to true, and the process terminates.

4.4 The eclipse plugin for \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\)
In this section, we would like to briefly comment on the Eclipse pluginFootnote 2 we have developed for \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\). The main goal of the \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) plugin is to permit programming in a high-level syntax (i.e. the syntax of the original calculus AbC).
This syntax can be then analysed via formal methods by relying on the operational semantics of the AbC calculus. Once the code has been analysed, the \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) plugin will generate formally verifiable Go code because of the correspondence results we prove in this article. In this article, we focus on the implementation part and we will consider verification tools for future works.
Figure 4 shows the project explorer of a \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) plugin project. The source folder src consists of two main files: the infrastructure file with .ginf extension and the system file with .goat extension. The infrastructure file is used to create an infrastructure which can be of three types: cluster, ring, and tree. We also support local concurrency. The system file contains the actual \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) specifications and a reference to the infrastructure that mediates the interaction between \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) components. Once these files are saved, the \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) plugin automatically generates Go code in the src-gen folder. We plan to integrate, in the near future, formal tools and rely on static analysis to inspect \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) specifications before code generation.
Below, we show how Process \({\mathsf {F}}\) in Sect. 4.3 would be written using the Eclipse plugin. Clearly, the syntax is clean and less verbose which helps the modellers to focus on the problem they are trying to solve rather than worrying about complicated syntactic constructions.

Other examples can be found in the WebPage of \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\). There, we also show how to program a complex and sophisticated variant of the well-known problem of Stable Allocation in Content Delivery Network (CDN) [27] using the \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) plugin. We show that although our solution is more open and less restrictive, the complexity of our solution is still comparable to the original one adopted by Akamai’s CDN, one of the largest distributed systems available.
5 Performance evaluation
We compare the above-mentioned infrastructures by modelling them in terms of a Continuous Time Markov Process [32]. Note that we use Markov Processes to model and evaluate our infrastructures because it is very hard, or even impossible, to perform statistical analyses of a real distributed system when the number of participants is large, like in the scenarios considered in this section. We do not have enough computation resources to set up large infrastructures and conduct the comparison. If we rely on small infrastructures, we would get subjective results. It is clear that the tree would perform better in large settings, while the cluster performs better in small ones. Thus, all results in this section are based on stochastic simulation which anyway provides a quality approximation of the actual performance of the \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) implementation.
The state of a process represents possible infrastructure configurations, while the transitions (that are selected probabilistically) are associated with events on messages. We have three types of events: a new message sent by a component; a message transmitted from a node to another in the infrastructure; a message locally handled by a node (i.e. removed from an input/waiting queue). Each event is associated with a rate that is the parameter of the exponentially distributed random variable governing the event duration. We developed a simulatorFootnote 3 for performance evaluation.
To perform the simulation, we need to fix three parameters: the component sending rate\(\lambda _s\); the infrastructure transmission rate\(\lambda _t\); and the handling rate\(\lambda _h\). In all experiments, we fix the following values: \(\lambda _s=1.0\), \(\lambda _t=15.0\), and \(\lambda _h=1000.0\) and rely on kinetic Monte Carlo simulation [33]. The infrastructure configurations are defined as follows:
-
C[x, y], indicates a cluster with x nodes and y components;
-
R[x, y] indicates a ring with x nodes each of which manages y components;
-
T[x, y, z] indicates a tree with x levels. Each node (but the leafs) has \(y+z\) children: y nodes and z components. A leaf node has z components.
We consider two scenarios: (1) Data Providers (DP): In this scenario, only a fraction of components send data messages that they, for example, acquire via sensors in the environment where they operate. An example could be a Traffic Control System where data providers are devices located in the city and data receivers are the vehicles travelling in the area; (2) communication intensive (CI): This scenario is used to estimate the performance when all components send messages continuously at a fixed rate so that we can evaluate situations of overloaded infrastructures. The former scenario is more realistic for CAS.
We consider two measures: the average delivery time and the average message time gap. The first measure indicates the time needed for a message to reach all components, while the latter indicates the interval between two different messages received by a single component. Data provider scenario (DP)
We consider configurations with 31 server nodes 155, 310, or 620 components and assume that only \(10\%\) of the components is sending data. The average delivery time is reported in Fig. 5, while the average message time gap (with confidence intervals) is reported in Fig. 6. The tree structure offers the best performance, while the cluster one is the worst. When the cluster reaches an equilibrium (at time \(\sim 2000\)), \(\sim 90\) time units are needed to deliver a message to 155 components, while the ring and the tree need only \(\sim 25\) and \(\sim 10\) time units, respectively. The reason is that in the cluster all server nodes share the same input queue, while in the tree and the ring each server node has its own queue. We can also observe that the performance of the ring in this scenario is close to the one of the tree. Moreover, in the cluster, the performance degrades when the number of components increases. This does not happen for the tree and the ring. Finally, we can observe that messages are delivered more frequently in the ring (\(\sim 1.9\) time units) and the tree (\(\sim 1.1\) time units) than in the cluster (\(\sim 5.5\) time units) as reported in Fig. 6.
Communication intensive scenario (CI) We consider infrastructures composed by 155 components that continuously send messages to all the others. Simulations are based on the following configurations:
-
Cluster-based: C[10, 155], C[20, 155] and C[31, 155];
-
Ring-based: R[5, 31] and R[31, 5];
-
Tree-based: T[5, 2, 5] and T[3, 5, 5].
Figure 7 shows the average delivery time for a cluster of 155 connected components and 10, 20 or 31 server nodes.Clearly, when the cluster reaches an equilibrium (\(\sim 2000\)), \(\sim 800\) time units are needed to deliver a message to all components. We also observe that the number of server nodes in the cluster has a minimal impact on this measure because they all share the same input queue. The Average Message Time Gap of the cluster, in Fig. 8, indicates that in the long run a component receives a message every 6/5.5 time units even if the number of servers is increased from 10 to 31.
Better performance can be obtained for the ring infrastructure. In the first two plots of Fig. 9, we report the average delivery time for the configurations R[5, 31] and R[31, 5]. The last plot compares the average message time gap of the two configurations. In the first one, a message is delivered to all the components in 350 time units, while in the second one 250 time units are needed. This indicates that increasing the number of nodes in the ring enhances performance. This is because in the ring all nodes cooperate to deliver a given message. Also the time gap decreases, i.e. a message is received every 2.6 and 1.8 time units.
Figure 10 shows how the average delivery time changes during the simulation for T[5, 2, 5] and T[3, 5, 5]. The two configurations have exactly the same number of nodes (31) with a different arrangement. The two configurations work almost in the same way: a message is delivered to all the components in about 120 time units. Clearly, the tree is 5-time faster than the cluster and 2-time faster than the ring. Moreover, in the tree-based approach, a message is delivered to components every \(\sim 1.1\) time units as reported in Fig. 11. This means that messages are constantly delivered after an initial delay.
The summarised results of the infrastructures with 31 nodes when measuring the average delivery time for 155 and 310 connected components are reported in Fig. 12. These results show that tree infrastructures offer the best performance; cluster-based ones do not work well, while ring-based ones are in between the two. Differences become clearer when increasing the number of components from 155 to 310 (right side of Fig. 12).
6 Related work
In this section, we relate our work to existing ones in terms of: collective formation, adaptation and distributed coordination through total-order broadcast.
Several frameworks have been proposed to target the problem of collective (or ensemble) formation. These approaches usually differ in the way they represent collectives and in their generality. The SCEL language [19], proposed in the ASCENS project [35], is a kernel language that has been designed to support the programming of autonomic computing systems. This language relies on the notions of autonomic components representing the collective members, and autonomic component ensembles representing collectives. Each component is equipped with an interface, consisting of a collection of attributes, describing its features. Attributes are used by components to dynamically organise themselves into ensembles and as a way to select partners for interaction. SCEL has inspired the development of the core calculus AbC to study the impact of attribute-based communication. Compared with SCEL, the knowledge representation in AbC is abstract and is not designed for detailed reasoning during the model evolution. This reflects the different objectives of SCEL and AbC. While SCEL focuses on programming issues, AbC concentrates on a minimal set of primitives to study attribute-based communication.
DEECo [14] and Helena [25] adopt an architecture-based approach to specify ensembles. In general, they impose logical conditions on the membership of ensembles that components have to satisfy. As opposed to \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\), the ensemble is a first class entity in these languages, while in \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) ensemble are logical entities implied by the run-time status of components and the interaction predicates.
JULIA [13] is also architecture based and achieves adaptation by defining systems that can adapt their configurations with respect to contextual conditions. System components manipulate their internal structure by adding, removing, or modifying connectors. However, in this approach interaction is still based on explicit connectors. In \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) predefined connections simply do not exist, and we do not assume a specific architecture or containment relations between components.
Furthermore, Context Oriented Programming [22] provides linguistic primitives is to define context-dependent behavioural variations. These variations are expressed as partial definitions of modules that can be overridden at run-time to adapt to contextual information. They can be grouped via layers to be activated or deactivated together dynamically. These layers can be also composed according to some scoping constructs. Our approach is different in that components adapt their behaviour by considering the run-time changes of the values of their attributes which might be triggered by either contextual conditions or by local interaction.
Other approaches that target similar problems revolve around team formation [30]. However, these approaches are usually developed for a specific purpose and thus have limited reusability. A more general and reusable framework, named RMASBench [26], was proposed for multi-agent coordination. Its main focus is on benchmarking of distributed constraints optimisation algorithms used within this framework to resolve team formation of agents.
Regarding total-order broadcast protocols, we would like to mention (1) the fixed sequencer approach [18], (2) the moving sequencer approach [16], and (3) the privilege-based approach [17]. The first approach is centralised and relies on a single sequencer of messages. We can consider the cluster infrastructure as a natural generalisation of this approach where instead of a single server, many servers collaborate to deliver messages. The second approach is similar to the ring infrastructure with the only exception that the role of the sequencer is transferred between the ring servers. This is achieved by circulating a specific token between ring servers. However, the liveness of this approach depends on the token and fairness is hard to achieve if one server has a larger number of senders than the other servers. The third approach relies on consensus between components to establish a total order. As mentioned before, consensus-based approaches are not suitable for open systems and they cannot deal with component failures.
7 Concluding remarks and future works
We proposed a distributed coordination infrastructure for the AbC calculus, and we proved its correctness. We developed a corresponding programming API, named \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\), to exploit the main interaction primitives of the AbC calculus directly in Go. The actual implementation of the API fully relies on the formal semantics of AbC and is parametric with respect to the coordination infrastructure that manages the interaction between components. We used the \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) API to program a distributed variant of the graph colouring problem and commented about the simplicity of its use. We evaluated the performance of the proposed infrastructure with respect to others. The results showed that our infrastructure exhibits a good performance. We also developed an Eclipse plugin for \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) to permit programming in a high-level syntax which is less verbose and helps programmers to focus on the problem they want to solve rather than worrying about complicated syntactic constructions.
We consider the tools that we have developed so far as a starting point for integrating formal tools that analyse the \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) plugin code and ensure that it satisfies specific properties before code generation. We also plan to enhance the implementation of our infrastructures by considering fairness and reliability issues. We also want to consider the challenging problem of verifying collective properties of \(\mathcal {G}{} \textit{o}\mathcal {A}{} \textit{t}\) code. As a step in this direction, we developed the \(\mathsf {ReCiPe}\) framework [10] (a symbolic representation of AbC specifications) and we extended LTL to be able to specify collective properties.
References
Abd Alrahman, Y., De Nicola, R., Loreti, M.: On the power of attribute-based communication. In: Formal Techniques for Distributed Objects, Components, and Systems—36th IFIP International Conference, FORTE. Springer, pp. 1–18 (2016)
Abd Alrahman, Y., De Nicola, R., Loreti, M.: Programming of CAS systems by relying on attribute-based communication. In: Leveraging Applications of Formal Methods, Verification and Validation: Foundational Techniques—7th International Symposium, ISoLA ’16, Proceedings, Part I. Springer, pp. 539–553 (2016)
Abd Alrahman, Y., De Nicola, R., Loreti, M.: Programming the Interactions of Collective Adaptive Systems by Relying on Attribute-based Communication. ArXiv e-prints (2017)
Abd Alrahman, Y., De Nicola, R., Loreti, M., Tiezzi, F., Vigo, R.: A calculus for attribute-based communication. In: Proceedings of the 30th Annual ACM Symposium on Applied Computing, SAC ’15. ACM, pp. 1840–1845 (2015)
Agha, G.: Actors: A Model of Concurrent Computation in Distributed Systems. MIT Press, Cambridge (1986)
Alrahman, Y.A., De Nicola, R., Garbi, G.: GoAt: Attribute-based interaction in Google go. In: Leveraging Applications of Formal Methods, Verification and Validation. Distributed Systems—8th International Symposium, ISoLA 2018, pp. 288–303 (2018)
Alrahman, Y.A., De Nicola, R., Garbi, G., Loreti, M.: A distributed coordination infrastructure for attribute-based interaction. In: Formal Techniques for Distributed Objects, Components, and Systems—38th IFIP WG 6.1 International Conference, FORTE 2018, Proceedings, pp. 1–20 (2018)
Alrahman, Y.A., Mezzina, C.A., Vieira, H.T.: Testing for coordination fidelity. In: Boreale, M., Corradini, F., Loreti, M., Pugliese, R. (eds.) Models, Languages, and Tools for Concurrent and Distributed Programming, pp. 152–169. Springer, Berlin (2019)
Alrahman, Y.A., Nicola, R.D., Loreti, M.: A calculus for collective-adaptive systems and its behavioural theory. Inf. Comput. 268, 104457 (2019)
Alrahman, Y.A., Perelli, G., Piterman, N.: A computational framework for adaptive systems and its verification. CoRR (2019). arXiv:1906.10793
Alrahman, Y.A., Vieira, H.T.: A coordination protocol language for power grid operation control. J. Log. Algebraic Methods Program. 109, 100487 (2019)
Bonabeau, E.: From classical models of morphogenesis to agent-based models of pattern formation. Artif. Life 3(3), 191–211 (1997)
Bruneton, E., Coupaye, T., Leclercq, M., Quéma, V., Stefani, J.-B.: The fractal component model and its support in Java. Softw. Pract. Exp. 36(11–12), 1257–1284 (2006)
Bures, T., Plasil, F., Kit, M., Tuma, P., Hoch, N.: Software abstractions for component interaction in the internet of things. IEEE Comput. 49(12), 50–59 (2016)
Camazine, S., Deneubourg, J., Franks, N.R., Sneyd, J., Theraulaz, G.: Self-organization in Biological Systems. Princeton studies in complexity. Princeton University Press, Princeton (2003)
Chang, J.-M., Maxemchuk, N.F.: Reliable broadcast protocols. ACM Trans. Comput. Syst. 2, 251–273 (1984)
Cristian, F.: Asynchronous atomic broadcast. IBM Tech. Discl. Bull. 33(9), 115–116 (1991)
Cristian, F., Mishra, S.: The pinwheel asynchronous atomic broadcast protocols. In: Second International Symposium on Autonomous Decentralized Systems, 1995. Proceedings. ISADS 95, pp. 215–221. IEEE (1995)
De Nicola, R., Latella, D., Lluch-Lafuente, A., Loreti, M., Margheri, A., Massink, M., Morichetta, A., Pugliese, R., Tiezzi, F., Vandin, A.: The SCEL language: design, implementation, verification. In: Wirsing, M., Hölzl, M., Koch, N., Mayer, P. (eds.) Software Engineering for Collective Autonomic Systems-The ASCENS Approach, pp. 3–71. Springer, Berlin (2015)
Ferscha, A.: Collective adaptive systems. In: Adjunct Proceedings of the 2015 ACM International Joint Conference on Pervasive and Ubiquitous Computing and Proceedings of the 2015 ACM International Symposium on Wearable Computers, UbiComp/ISWC’15 Adjunct, pp. 893–895, New York, NY, USA. ACM (2015)
Fischer, M.J., Lynch, N.A., Paterson, M.S.: Impossibility of distributed consensus with one faulty process. J. ACM 32(2), 374–382 (1985)
Hirschfeld, R., Costanza, P., Nierstrasz, O.: Context-oriented programming. J. Object Technol. 7(3), 125–151 (2008)
Hoare, C.A.R.: Communicating sequential processes. Commun. ACM 21(8), 666–677 (1978)
Jensen, T.R., Toft, B.: Graph Coloring Problems, vol. 39. Wiley, New York (1995)
Klarl, A., Cichella, L., Hennicker, R.: From Helena ensemble specifications to executable code. In: Formal Aspects of Component Software—11th International Symposium, FACS 2014, pp. 183–190 (2014)
Kleiner, A., Farinelli, A., Ramchurn, S.D., Shi, B., Maffioletti, F., Reffato, R.: Rmasbench: benchmarking dynamic multi-agent coordination in urban search and rescue. In: International Conference on Autonomous Agents and Multi-Agent Systems, AAMAS ’13, Saint Paul, MN, USA, May 6–10, 2013, pp. 1195–1196 (2013)
Maggs, B.M., Sitaraman, R.K.: Algorithmic nuggets in content delivery. SIGCOMM Comput. Commun. Rev. 45(3), 52–66 (2015)
Milner, R., Parrow, J., Walker, D.: A calculus of mobile processes, II. Inf. Comput. 100(1), 41–77 (1992)
Mosses, P.D.: Modular structural operational semantics. J. Log. Algebraic Program. 60–61, 195–228 (2004)
Parker, J., Nunes, E., Godoy, J., Gini, M.L.: Exploiting spatial locality and heterogeneity of agents for search and rescue teamwork. J. Field Robot. 33(7), 877–900 (2016)
Prasad, K.: A calculus of broadcasting systems. In: TAPSOFT’91, pp. 338–358. Springer (1991)
Robertson, J.B.: Continuous-time Markov chains (W. J. anderson). SIAM Rev. 36(2), 316–317 (1994)
Schulze, T.P.: Efficient kinetic monte carlo simulation. J. Comput. Phys. 227(4), 2455–2462 (2008)
Vukolić, M.: The quest for scalable blockchain fabric: proof-of-work vs. bft replication. In: Camenisch, J., Kesdoğan, D. (eds.) Open Problems in Network Security, pp. 112–125. Springer, Cham (2016)
Wirsing, M., Hölzl, M.M., Koch, N., Mayer, P. (eds.): Software Engineering for Collective Autonomic Systems—The ASCENS Approach. Lecture Notes in Computer Science, vol. 8998. Springer, Berlin (2015)
Acknowledgements
Open access funding provided by University of Gothenburg.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We want to thank Rocco De Nicola and Michele Loreti for early discussions about the conference version of this article. Yehia Abd Alrahman is funded by the ERC consolidator grant D-SynMA under the European Union’s Horizon 2020 research and innovation programme (Grant No 772459).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Abd Alrahman, Y., Garbi, G. A distributed API for coordinating AbC programs. Int J Softw Tools Technol Transfer 22, 477–496 (2020). https://doi.org/10.1007/s10009-020-00553-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10009-020-00553-4






 we have that
we have that 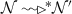 and
and  and
and 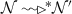 and
and  and finally m moves from the input queue to the waiting queue i.e.
and finally m moves from the input queue to the waiting queue i.e.  and
and  and finally m moves from the input queue to the waiting queue by either rule
and finally m moves from the input queue to the waiting queue by either rule  and
and  and
and  .
. and
and  and
and  and
and  and
and 









