Portfolio optimisation with strictly positive transaction costs and impulse control

Abstract.

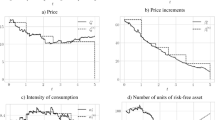
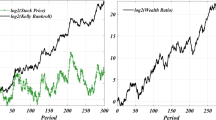
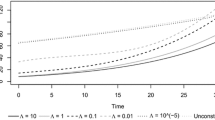
One crucial assumption in modern portfolio theory of continuous-time models is the no transaction cost assumption. This assumption normally leads to trading strategies with infinite variation. However, following such a strategy in the presence of transaction costs will lead to immediate ruin. We present an impulse control approach where the investor can change his portfolio only finitely often in finite time intervals. Further, we consider transaction costs including a fixed and a proportional cost component. For the solution of the resulting control problems we present a formal optimal stopping approach and an approach using quasi-variational inequalities. As an application we derive a nontrivial asymptotically optimal solution for the problem of exponential utility maximisation.