A Black–Scholes inequality: applications and generalisations

Abstract

The space of call price curves has a natural noncommutative semigroup structure with an involution. A basic example is the Black–Scholes call price surface, from which an interesting inequality for Black–Scholes implied volatility is derived. The binary operation is compatible with the convex order, and therefore a one-parameter sub-semigroup gives rise to an arbitrage-free market model. It is shown that each such one-parameter semigroup corresponds to a unique log-concave probability density, providing a family of tractable call price surface parametrisations in the spirit of the Gatheral–Jacquier SVI surface. An explicit example is given to illustrate the idea. The key observation is an isomorphism linking an initial call price curve to the lift zonoid of the terminal price of the underlying asset.

1 Introduction

We define the Black–Scholes call price function $C_{\mathrm{BS}}: [0,\infty) \times[0,\infty) \to[0,1]$ by the formula

$$\begin{aligned} C_{\mathrm{BS}}(\kappa,y) &= \int_{-\infty}^{\infty} \big(\varphi (z+y) - \kappa\ \varphi(z)\big)^{+} d z \\ & = \left\{ \textstyle\begin{array}{ll} {\Phi}(-\frac{\log\kappa}{y} + \frac{y}{2}) - \kappa{\Phi} (-\frac{\log\kappa}{y} - \frac{y}{2}) &\qquad \mbox{ if } y > 0, \kappa> 0,\\ (1-\kappa)^{+} & \qquad \mbox{ if } y =0, \\ 1 & \qquad \mbox{ if } \kappa=0, \end{array}\displaystyle \right. \end{aligned}$$

where $\varphi(z) = \frac{1}{\sqrt{2\pi}} e^{-z^{2}/2}$ is the density and $\Phi(x) = \int_{-\infty}^{x} \varphi(z) d z$ is the distribution function of a standard normal random variable. Recall the financial context of this definition: a market with a risk-free zero-coupon bond of unit face value, maturity $T$ and initial price $B_{0,T}$; a stock with initial price $S_{0}$ that pays no dividend; and a European call option written on the stock with maturity $T$ and strike price $K$. In the Black–Scholes model, the initial price $C_{0,T,K}$ of the call option is given by the formula

$$ C_{0,T,K} = S_{0} \ C_{\mathrm{BS}}\bigg( \frac{K B_{0,T} }{S_{0} } , \sigma\sqrt{T} \bigg), $$

where $\sigma$ is the volatility of the stock price. In particular, the first argument of $C_{\mathrm{BS}}$ plays the role of the moneyness $\kappa=K B_{0,T}/S_{0}$ and the second argument plays the role of the total standard deviation $y = \sigma\sqrt{T}$ of the terminal log stock price.

The starting point of this note is the following observation.

Theorem 1.1

For$\kappa_{1}, \kappa_{2} > 0$and$y_{1}, y_{2} > 0$, we have

$$ C_{\mathrm{BS}}(\kappa_{1} \kappa_{2}, y_{1} + y_{2} ) \le C_{\mathrm{BS}}(\kappa_{1}, y_{1} ) + \kappa_{1} C_{\mathrm{BS}}(\kappa_{2}, y_{2} ), $$

with equality if and only if

$$ -\frac{ \log\kappa_{1}}{y_{1}} - \frac{y_{1}}{2} = -\frac{ \log \kappa_{2}}{y_{2}} + \frac{y_{2}}{2}. $$

While it is fairly straightforward to prove Theorem 1.1 directly, the proof is omitted as it is a special case of Theorem 3.8 below. Indeed, the purpose of this paper is to try to understand the fundamental principle that gives rise to such an inequality. As a hint of things to come, it is worth pointing out that the expression $y_{1}+y_{2}$ appearing on the left-hand side of the inequality corresponds to the sum of the standard deviations—not the sum of the variances. From this observation, it may not be surprising to see that a key idea underpinning Theorem 1.1 is that of adding comonotonic—not independent—normal random variables. These vague comments will be made precise in Theorem 2.16 below.

Before proceeding, we re-express Theorem 1.1 in terms of the Black–Scholes implied total standard deviation function, defined for $\kappa> 0$ to be the inverse function

$$ Y_{\mathrm{BS}}(\kappa, \cdot): [ (1-\kappa)^{+}, 1 ] \to[0,\infty] $$

such that

$$ y = Y_{\mathrm{BS}}(\kappa, c)\quad \Longleftrightarrow \quad C_{\mathrm{BS}}(\kappa,y) = c. $$

In particular, the quantity $Y_{\mathrm{BS}}(\kappa,c)$ denotes the implied total standard deviation of an option of moneyness $\kappa$ whose normalised price is $c$. We find it notationally convenient to set $Y_{\mathrm{BS}}(\kappa,c) = \infty$ for $c \ge1$. With this notation, we have the following interesting reformulation which requires no proof:

Corollary 1.2

For all$\kappa_{1}, \kappa_{2} > 0$and$(1-\kappa _{i})^{+} < c_{i} < 1$for$i=1,2$, we have

$$ Y_{\mathrm{BS}}(\kappa_{1}, c_{1}) + Y_{\mathrm{BS}}(\kappa_{2}, c_{2}) \le Y_{\mathrm{BS}}( \kappa_{1} \kappa_{2}, c_{1} + \kappa_{1} c_{2} ) , $$

with equality if and only if

$$ -\frac{ \log\kappa_{1}}{y_{1}} - \frac{y_{1}}{2} = -\frac{ \log \kappa_{2}}{y_{2}} + \frac{y_{2}}{2}, $$

where$y_{i} = Y_{\mathrm{BS}}(\kappa_{i}, c_{i})$for$i=1,2$.

To add some context, we recall the following related bounds on the functions $C_{\mathrm{BS}}$ and $Y_{\mathrm{BS}}$; see [31, Theorem 3.1].

Theorem 1.3

For all$\kappa> 0$, $y > 0$and$0 < p < 1$, we have

$$ C_{\mathrm{BS}}(\kappa,y) \ge\Phi\big( \Phi^{-1}(p) + y\big) - p\kappa, $$

with equality if and only if

$$ p = \Phi\bigg(-\frac{\log\kappa}{y} - \frac{y}{2} \bigg). $$

Equivalently, for all$\kappa> 0$, $(1-\kappa)^{+} < c < 1$and$0 < p < 1$, we have

$$ Y_{\mathrm{BS}}(\kappa,c) \le\Phi^{-1}(c + p\kappa) - \Phi^{-1}(p), $$

where$\Phi^{-1}(u) = + \infty$for$u \ge1$.

In [31], Theorem 1.3 was used to derive upper bounds on the implied total standard deviation function $Y_{\mathrm{BS}}$ by selecting various values of $p$ to insert into the inequality.

The function $\Phi( \Phi^{-1}(\cdot) + y )$ has appeared elsewhere in various contexts. For instance, it is the value function for a problem of maximising the probability of hitting a target considered by Kulldorff [27, Theorem 6]. (Also see the book of Karatzas [23, Sect. 2.6].) In insurance mathematics, the function is often called the Wang transform and was proposed in [32, Definition 2] as a method of distorting a probability distribution in order to introduce a risk premium. In a somewhat unrelated context, Kulik and Tymoshkevych [26, Proof of Theorem 2: Statement I] observed, while proving a certain log-Sobolev inequality, that the family of functions $\Phi( \Phi^{-1}(\cdot) + y)$ indexed by $y \ge0$ forms a semigroup under function composition. We shall see that this semigroup property is the essential idea of our proof of Theorem 1.1 and its subsequent generalisations.

The rest of this paper is arranged as follows. In Sect. 2, we introduce a space of call price curves and explore some of its properties. In particular, we shall see that it has a natural noncommutative semigroup structure with an involution. The binary operation has a natural financial interpretation as the maximum price of an option to swap one share of the first asset for a fixed number of shares of a second asset. In Sect. 3, we introduce a space of call price surfaces and provide in Theorem 3.2 equivalent characterisations in terms of either a single supermartingale or two martingales. Furthermore, it is shown that the binary operation is compatible with the decreasing convex order, and therefore a one-parameter sub-semigroup of the semigroup of call price curves can be associated with an arbitrage-free market model. A main result of this article is Theorem 3.11: each such one-parameter sub-semigroup corresponds to a unique (up to translation and scaling) log-concave probability density, generalising the Black–Scholes call price surface and providing a family of reasonably tractable call surface parametrisations in the spirit of the SVI surface. In Sect. 4, further properties of these call price surfaces are explored, including the asymptotics of their implied volatility. In addition, an explicit example is given to illustrate the idea, and is calibrated to real-world call price data. In Sect. 5, the proof of Theorem 3.11 is given. The key observation is that the Legendre transform is an isomorphism converting the binary operation on call price curves to function composition. The isomorphism has the additional interpretation as the lift zonoid of a related random variable.

2 The algebraic properties of call prices

2.1 The space of call price curves

For motivation, consider a market with two (non-dividend-paying) assets whose prices at time $t$ are $A_{t}$ and $B_{t}$. We assume that both prices are always nonnegative and that the initial prices $A_{0}$ and $B_{0}$ are strictly positive. We further assume that there exists a martingale deflator $Y =(Y_{t})_{t \ge0}$, that is, a positive adapted process such that the processes $YA$ and $YB$ are both martingales. The assumption of the existence of a martingale deflator ensures that there is no arbitrage in the market. (Conversely, one can show that no-arbitrage in a discrete-time model implies the existence of a martingale deflator, even if the time horizon is infinite and if the market does not admit a numéraire portfolio; see [30, Theorem 2.10].)

Now introduce an option to swap one share of asset $A$ with $K$ shares of asset $B$ at a fixed time $T > 0$, so the payout is $(A_{T} - K B_{T})^{+}$. If the asset $B$ is a risk-free zero-coupon bond of maturity $T$ and unit face value, then the option is a standard call option. It will prove useful in our discussion to let asset $B$ be arbitrary, but we still refer to this option as a call option.

There is no arbitrage in the augmented market if the time-$t$ price of this call option is

$$ C_{t,T, K} = \frac{1}{Y_{t}}\mathbb{E} [ Y_{T}( A_{T} - K B_{T})^{+} | \mathcal{F} _{t}]. $$

In particular, setting

$$ \alpha= \frac{Y_{T} A_{T}}{Y_{0} A_{0}}\qquad \mbox{and} \qquad \beta = \frac{Y_{T} B_{T}}{Y_{0} B_{0}}, $$

the initial price of this option, normalised by the initial price of asset $A$, can be written as

$$ \frac{C_{0,T,K}}{A_{0}} = \mathbb{E} [ (\alpha- \kappa\beta)^{+} ], $$

where the moneyness is given by $\kappa= \frac{K B_{0}}{A_{0}}$.

The above discussion motivates the following definition.

Definition 2.1

A function $C:[0,\infty) \to[0, 1]$ is a call price curve if there exist nonnegative random variables $\alpha$ and $\beta$ defined on some probability space such that $\mathbb{E} [\alpha] = 1 = \mathbb{E} [\beta]$, and

$$ C(\kappa) = \mathbb{E} [ (\alpha- \kappa\beta)^{+} ]\qquad \mbox{for all } \kappa\ge0, $$

in which case the ordered pair $(\alpha, \beta)$ of random variables is called a basic representation of $C$. The set of all call price curves is denoted $\mathcal {C}$.

From a practical perspective, the normalised call price $C(\kappa)$ is directly observed, while the law of the pair $(\alpha, \beta)$ is not. Therefore, a theme of this paper is to try to express notions in terms of the call price curve. Here is a first result of this type.

Theorem 2.2

Given a function$C:[0,\infty) \to[0,1]$, the following are equivalent:

1) $C \in\mathcal {C}$.

2) There exists a nonnegative random variable$S$with$\mathbb{E} [S] \le1$such that

$$ C(\kappa) = 1 - \mathbb{E} [ S \wedge\kappa] \qquad \textit{for all } \kappa\ge0. $$

3) $C$is convex and such that$C(\kappa) \ge(1-\kappa)^{+}$for all$\kappa\ge0$.

Furthermore, in 2), we have

$$ \mathbb{P} [S > 0 ] = - C'(0) \quad \textit{and}\quad \mathbb{E} [S ] = 1 - C(\infty), $$

and more generally that

$$ \mathbb{P} [S > \kappa] = - C'(\kappa) \qquad \textit{for all } \kappa\ge0, $$

where$C'$denotes the right derivative of$C$.

Proof

The implications 1) ⇒ 3) and 2) ⇒ 3) are straightforward, so their proofs are omitted. Furthermore, the claim that the distribution of $S$ can be recovered from $C$ is essentially the Breeden and Litzenberger [3, Eq. (1)] formula.

3) ⇒ 2): By convexity, the right derivative $C'$ is defined everywhere and is nondecreasing and right-continuous. Furthermore, since $(1-\kappa)^{+} \le C(\kappa) \le1$ for all $\kappa$, we have $-1 \le C'(\kappa) \le0$ for all $\kappa$. Let $S$ be a random variable such that $\mathbb{P} [S > \kappa] = - C'(\kappa)$. Note that

$$\begin{aligned} \mathbb{E} [ S \wedge\kappa] = \int_{0}^{\kappa}\mathbb{P} [S > u] du = 1 - C(\kappa) \end{aligned}$$

by Fubini’s theorem and the absolute continuity of the convex function $C$.

It remains to show that either 2) ⇒ 1) or 3) ⇒ 1). That is, we must construct a basic representation $(\alpha, \beta)$ from either the random variable $S$ or the function $C$. We give a construction showing 2) ⇒ 1) in the proof of Theorem 2.15, and a rather different construction showing 3) ⇒ 1) in the proof of Theorem 3.2. To avoid repetition, we omit a construction here. □

By definition, a call price curve $C$ is determined by two random variables $\alpha$ and $\beta$. However, the distribution of the pair $(\alpha, \beta)$ cannot be inferred solely from $C$. In contrast, Theorem 2.2 above says that a call price curve $C$ is also determined by a single random variable $S$, and furthermore, the law of $S$ is unique and can be recovered from $C$. This observation motivates the following definition.

Definition 2.3

Given a call price curve $C \in\mathcal {C}$, suppose that $S$ is a nonnegative random variable such that $C(\kappa) = 1 - \mathbb{E} [ S \wedge\kappa]$ for all $\kappa\ge0$. Then $S$ is called a primal representation of $C$.

Remark 2.4

As hinted by the name primal, we shall shortly introduce a dual representation.

Figure 1 plots the graph of a typical element $C \in\mathcal {C}$.

Fig. 1

The graph of a typical function $C \in\mathcal {C}$. The random variable $S^{\star}$ is introduced in Definition 2.11

Remark 2.5

An example of an element of $\mathcal {C}$ is the Black–Scholes call price function $C_{\mathrm{BS}}( \cdot, y )$ for any $y \ge0$. A primal representation is

$$ S^{(y)} = \frac{\varphi(Z+y)}{\varphi(Z)} = e^{-y Z - y^{2}/2}, $$

where $Z \sim{\mathcal{N}}(0,1)$ has the standard normal distribution.

Remark 2.6

We note that there are alternative financial interpretations of call price curves $C \in\mathcal {C}$ in the case $C(\infty) > 0$. One popularised by Cox and Hobson [12] is to model the primal representation as the terminal price $S$ of an asset experiencing a bubble in the sense that the price process discounted by the price of the risk-free $T$-zero-coupon bond is a strict local martingale under a fixed $T$-forward measure. For this interpretation, the option payout must be modified: rather than the payout of a standard (naked) call option, the quantity $C(\kappa)$ in this interpretation models the normalised price of a fully collateralised (covered) call with payout

$$ (S - \kappa)^{+} + 1 - S = 1 - S\wedge \kappa. $$

One could argue that there are two related shortcomings of this interpretation. Firstly, this type of bubble phenomenon can only arise in continuous-time models since in discrete time (even over an infinite horizon), a nonnegative local martingale with an integrable initial condition is necessarily a true martingale. Secondly, in the case $\mathbb{E} [S] < 1$ where the underlying stock is not priced by expectation, it is not clear from a modelling perspective why the market should then assign the price $C(\kappa) = \mathbb{E} [ (S - \kappa)^{+} + 1 - S]$ to the call option. Both shortcomings highlight the subtlety of continuous-time arbitrage theory, in particular, the sensitive dependence on the choice of numéraire on the definition of arbitrage (and related arbitrage-like conditions). See the paper of Herdegen and Schweizer [17] for a discussion of these issues in the context of a semimartingale market model where prices may vanish.

2.2 The involution

There is a natural involution on the space of call prices:

Definition 2.7

Given a call price curve $C \in\mathcal {C}$ with basic representation $(\alpha, \beta)$, the function $C^{\star}$ is the call price curve with basic representation $(\beta, \alpha)$.

This leads to a straightforward financial interpretation of the involution. As described above, we may think of $C(\kappa)$ as the initial price, normalised by $A_{0}$, of the option to swap one share of asset $A$ for $K$ shares of asset $B$, where $K B_{0} = \kappa A_{0}$. Then $C^{\star}(\kappa)$ is the initial price, normalised by $B_{0}$, of the option to swap one share of asset $B$ for $K^{\star}$ shares of asset $A$, where $K^{\star}A_{0} = \kappa B_{0}$.

We now record a fact about this involution ^⋆, expressed directly in terms of call prices. The proof is a straightforward verification and hence omitted.

Theorem 2.8

Fix$C \in\mathcal {C}$. Then$C^{\star}(0) = 1$and

$$ C^{\star}(\kappa) = 1 - \kappa+ \kappa C(1/\kappa) \qquad \textit{for all } \kappa> 0. $$

Remark 2.9

As an example, notice that for the Black–Scholes call function, we have

$$ C_{\mathrm{BS}}( \cdot, y)^{\star}= C_{\mathrm{BS}}( \cdot, y) \qquad \mbox{for all } y \ge0 $$

by the classical put–call symmetry formula.

Remark 2.10

The function $C^{\star}$ is related to the well-known perspective function of the convex function $C$ defined by $(\eta, \kappa) \mapsto\eta C( \kappa/\eta)$; see for instance the book of Boyd and Vanderberghe [6, Sect. 3.2.6].

As hinted above, we can define another random variable in terms of this involution:

Definition 2.11

Given a call price curve $C \in \mathcal {C}$, a nonnegative random variable $S^{\star}$ is a dual representation of $C$ if $S^{\star}$ is a primal representation of the call price curve $C^{\star}$.

That this dual random variable should be called a representation of a call price is due to the following observation. Again the proof is straightforward and hence omitted.

Theorem 2.12

Given a call price$C \in\mathcal {C}$with dual representation$S^{\star}$, we have

$$ C(\kappa) = \mathbb{E} [ (1 - S^{\star}\kappa)^{+} ] = 1 - \mathbb {E} [ 1 \wedge(S^{\star}\kappa)] \qquad \textit{for all } \kappa\ge0. $$

In particular, we have$\mathbb{P} [S^{\star}> 0] = 1- C(\infty)\ \textit{and}\ \mathbb{E} [S^{\star}] = - C'(0)$. Finally, for all$\kappa\ge0$, we have

$$\begin{aligned} C(\kappa) &= \mathbb{P} [S^{\star}< 1/\kappa] - \kappa \mathbb{P} [S > \kappa] \\ & = \mathbb{P} [S^{\star}\le1/\kappa] - \kappa \mathbb{P} [S \ge \kappa]. \end{aligned}$$

Remark 2.13

The papers of De Marco et al. [13, Appendix A.1] and Jacquier and Keller-Ressel [21, Theorem 3.7] have a related financial interpretation of the relationship between the primal and dual representations in terms of a continuous-time market possibly experiencing a bubble à la Cox and Hobson.

2.3 The binary operation

We have introduced one algebraic operation, the involution ^⋆, on the set of call price curves. We now come to the second algebraic operation which will help to contextualise the Black–Scholes inequality of Theorem 1.1. To motivate it, consider a market with three assets with time-$t$ prices $A_{1,t}, A_{2,t}$ and $B_{t}$. We know the initial cost of an option to swap one share of asset $A_{1}$ with $H_{1}$ shares of asset $B$, as well as the initial cost of an option to swap one share of asset $B$ with $H_{2}$ shares of asset $A_{2}$, for various values of $H_{1}$ and $H_{2}$, where all the options mature at a fixed date $T>0$. Our goal is to find an upper bound on the cost of an option to swap one share of asset $A_{1}$ for $K$ shares of asset $A_{2}$, for the same maturity date $T$.

Definition 2.14

For call price curves $C_{1}, C_{2} \in\mathcal {C}$, define a binary operation • on $\mathcal {C}$ by

$$ C_{1} \bullet C_{2} (\kappa) = \sup_{\alpha_{1}, \beta, \alpha_{2} } \mathbb{E} [ (\alpha_{1} - \kappa\alpha_{2})^{+} ], $$

where the supremum is taken over nonnegative random variables $\alpha_{1}, \beta, \alpha_{2}$ defined on the same probability space such that $(\alpha_{1}, \beta)$ is a basic representation of $C_{1}$ and $(\beta, \alpha_{2})$ is a basic representation of $C_{2}$.

At this stage, it is not immediately clear that given two call price curves $C_{1}$ and $C_{2}$, one can find a triple $(\alpha_{1}, \beta, \alpha_{2})$ satisfying the definition of the binary operation •, and in principle, we should complete the definition with the usual convention that $\sup\emptyset = - \infty$. Fortunately, this caveat is not necessary, as can be deduced from the following result.

Theorem 2.15

For call price curves$C_{1}, C_{2} \in\mathcal {C}$, we have

$$ C_{1} \bullet C_{2} (\kappa) = \sup_{S_{1}, S_{2}^{\star}} \big( 1 - \mathbb{E} [ S_{1} \wedge(S_{2}^{\star}\kappa)] \big), $$

where the supremum is taken over random variables$S_{1}$and$S_{2}^{\star}$defined on the same space, where$S_{1}$is a primal representation of$C_{1}$and$S_{2}^{\star}$is a dual representation of $C_{2}$.

Proof

First, let $S_{1}$ be a primal representation of $C_{1}$ and $S_{2}^{\star}$ a dual representation of $C_{2}$, defined on the same probability space. We shall exhibit random variables $(\alpha_{1}, \beta, \alpha _{2})$ such that $(\alpha_{1}, \beta)$ is a basic representation of $C_{1}$ and $(\beta, \alpha_{2})$ is a basic representation of $C_{2}$.

For the construction, we introduce Bernoulli random variables $\gamma_{1}, \gamma_{2}, \delta_{1}, \delta_{2}$, independent of $(S_{1}, S_{2}^{\star})$ and each other, with

$$ \mathbb{P} [\gamma_{1}=1] = \mathbb{E} [S_{1}], \qquad \mathbb{P} [\gamma_{2} = 1] = \mathbb{E} [S_{2}^{\star}], \qquad \mathbb{P} [\delta_{1} = 1] = \mathbb{P} [\delta_{2} = 1] = \frac{1}{2}. $$

If $\mathbb{P} [S_{1}= 0] < 1$, then set

$$ a_{1} = \frac{S_{1}}{\mathbb{E} [S_{1}]} \qquad \mbox{and} \qquad b_{1} = \frac{\gamma_{1}}{\mathbb{E} [S_{1}]}, $$

and if $S_{1}=0$ almost surely, set $a_{1}= 2 \delta_{1}$ and $b_{1}=2(1-\delta_{1})$. Similarly, if $\mathbb{P} [S_{2}^{\star}= 0] < 1$, then set

$$ a_{2} = \frac{S_{2}^{\star}}{\mathbb{E} [S_{2}^{\star}]} \qquad \mbox{and} \qquad b_{2} = \frac{\gamma_{2}}{\mathbb{E} [S_{2}^{\star}]}, $$

and if $S_{2}^{\star}=0$ almost surely, set $a_{2}= 2 \delta_{2}$ and $b_{2}=2(1-\delta_{2})$. Finally, set

$$ \alpha_{1} = a_{1} b_{2},\qquad \beta= b_{1} b_{2},\qquad \alpha _{2} = a_{2} b_{1}. $$

It is easy to check that the triplet $(\alpha_{1}, \beta, \alpha _{2})$ is the desired representation. This shows

$$ C_{1} \bullet C_{2} (\kappa) \ge \sup_{S_{1}, S_{2}^{\star}} \big( 1 - \mathbb{E} [ S_{1} \wedge(S_{2}^{\star}\kappa)] \big). $$

For the converse inequality, given a basic representation $(\alpha _{1}, \beta)$ of $C_{1}$ and a basic representation $(\beta, \alpha_{2})$ of $C_{2}$ defined on the same probability space $(\Omega, \mathcal{F} , \mathbb{P} )$, we let

and define an absolutely continuous measure $\mathbb{P} ^{\beta}$ by $\frac{d \mathbb{P} ^{\beta}}{d \mathbb{P} } = \beta$. It is easy to check that $S_{1}$ is a primal representation of $C_{1}$ and $S_{2}^{\star}$ is a dual representation of $C_{2}$ under $\mathbb {P} ^{\beta}$ and

 □

Given the laws of two random variables $X_{1}$ and $X_{2}$ and a convex function $g$, it is well known that the quantity $\mathbb{E} [ g(X_{1} + X_{2}) ]$ is maximised when $X_{1}$ and $X_{2}$ are comonotonic. See for instance the paper of Kaas et al. [22, Theorem 6] for a proof. By rewriting the expression

$$ 1 - S_{1} \wedge(S_{2}^{\star}\kappa) = (S_{1} - \kappa S_{2}^{\star})^{+} + 1 - S_{1}, $$

we see that the supremum defining the binary operation • is achieved when $S_{1}$ and $S^{\star}_{2}$ are countermonotonic. We recover this fact in the following result, which also continues our theme of expressing notions directly in terms of the call prices. In this case, the binary operation • can be expressed via a minimisation problem:

Theorem 2.16

Let$S_{1}$be a primal representation of$C_{1} \in\mathcal {C}$and$S_{2}^{\star}$a dual representation of$C_{2} \in\mathcal {C}$, where$S_{1}$and$S_{2}^{\star}$are defined on the same probability space. Then

$$ 1 - \mathbb{E} [ S_{1} \wedge(\kappa S_{2}^{\star})] \le C_{1}(\eta) + \eta\ C_{2}(\kappa/\eta) $$

for all$\kappa\ge0$and$\eta\ge0$, with the convention$0 \, C_{2}(\kappa/0) = 0$. There is equality if the following hold true:

1) $S_{1}$and$S_{2}^{\star}$are countermonotonic, and

2) $\mathbb{P} [S_{1} < \eta] \le \mathbb{P} [S_{2}^{\star}\ge\eta /\kappa]$and$\mathbb{P} [S_{1} \le\eta] \ge\mathbb{P} [S_{2}^{\star}> \eta /\kappa]$.

In particular, we have

$$ C_{1} \bullet C_{2}(\kappa) = \inf_{\eta\ge0} \big(C_{1}(\eta) + \eta C_{2}(\kappa/\eta)\big) \qquad \textit{for all } \kappa\ge0. $$

Proof

Recall that for real $a,b$, we have

$$ (a+b)^{+} \le a^{+} + b^{+}, $$

with equality if $ab \ge0$. Hence, fixing $\kappa\ge0$, we have

$$\begin{aligned} 1 - \mathbb{E}[S_{1} \wedge(S_{2}^{\star}\kappa)] & = \mathbb{E}[ (S_{1} - \kappa S_{2}^{\star})^{+}] + 1 - \mathbb{E} [S_{1}] \\ &\le \mathbb{E}[ (S_{1} - \eta)^{+}] + 1 - \mathbb{E}[S_{1}] + \mathbb{E}[ (\eta- \kappa S_{2}^{\star})^{+} ] \\ &= C_{1}(\eta) + \eta C_{2}(\kappa/\eta) \end{aligned}$$

(2.1)

for all $\eta\ge0$.

Now pick $\eta\ge0$ such that

$$\begin{aligned} \mathbb{P} [S_{1} < \eta] &\le \mathbb{P} [S_{2}^{\star}\ge\eta /\kappa] , \\ \mathbb{P} [S_{1} \le\eta] &\ge\mathbb{P} [S_{2}^{\star}> \eta /\kappa]. \end{aligned}$$

Also assume that $S_{1}$ and $S_{2}^{\star}$ are countermonotonic so that

$$\begin{aligned} \{S_{1} < \eta\} &\subseteq\{ S_{2}^{\star}\ge\eta/\kappa\} , \\ \{ S_{1} \le\eta\} &\supseteq\{ S_{2}^{\star}> \eta/\kappa\}. \end{aligned}$$

Notice that in this case, we have

$$ (S_{1} - \eta)( \eta- \kappa S^{\star}_{2}) \ge0 \qquad \mbox{ almost surely} $$

and hence there is equality in (2.1) above. □

Remark 2.17

This result is related to the upper bound on basket options found by Hobson et al. [20, Theorem 3.1].

Remark 2.18

Given the conclusion of Theorem 2.16, we caution that the operation • is not the well-known inf-convolution $\square$; however, we shall see in Sect. 5.2 below that • is related to the inf-convolution $\square$ via an exponential map.

In light of the formula for the binary operation • appearing in Theorem 2.16, the Black–Scholes inequality of Theorem 1.1 amounts to the claim that for $y_{1}, y_{2} \ge0$, we have

$$ C_{\mathrm{BS}}( \cdot, y_{1} ) \bullet C_{\mathrm{BS}}( \cdot, y_{2} ) = C_{\mathrm{BS}}( \cdot, y_{1}+y_{2} ). $$

This is a special case of Theorem 3.8, stated and proved below.

We now come to the key observation of this paper. To state it, we distinguish two particular elements $E, Z \in\mathcal {C}$ defined by

$$ E(\kappa) = (1-\kappa)^{+} \quad \mbox{ and } \quad Z(\kappa) = 1 \qquad \mbox{for all } \kappa\ge0. $$

Note that the random variables representing $E$ and $Z$ are constant, with $S = 1= S^{\star}$ representing $E$ and $S=0=S^{\star}$ representing $Z$. The following result shows that $\mathcal {C}$ is a noncommutative semigroup with respect to • with involution ^⋆, where $E$ is the identity element and $Z$ is the absorbing element. The proof is straightforward, and hence omitted.

Theorem 2.19

For every$C, C_{1}, C_{2}, C_{3} \in\mathcal {C}$, we have

1) $C_{1} \bullet C_{2} \in\mathcal {C}$.

2) $C_{1} \bullet (C_{2} \bullet C_{3}) = (C_{1} \bullet C_{2} ) \bullet C_{3}$.

3) $(C_{1} \bullet C_{2})^{\star}= C_{2}^{\star}\bullet C_{1}^{\star}$.

4) $E \bullet C = C \bullet E = C$.

5) $Z \bullet C = C \bullet Z = Z$.

We conclude this section by introducing two useful subsets of the set of call price curves.

Definition 2.20

Let

$$ \mathcal {C}_{+} = \{ C \in\mathcal {C}: C'(0) = - 1 \} $$

and

$$ \mathcal {C}_{1} = \{ C \in\mathcal {C}: C(\infty) = 0 \}. $$

That is, fix a call price curve $C \in\mathcal {C}$ with primal representation $S$ and dual representation $S^{\star}$. The call price curve $C$ is in $\mathcal {C}_{+}$ if and only if $\mathbb{P} [S > 0 ] = \mathbb{E} [S^{\star}] = 1$, while $C$ is in $\mathcal {C}_{1}$ if and only if $\mathbb{P} [S^{\star}> 0 ] = \mathbb{E} [S] = 1$.

Remark 2.21

As an example, notice that for the Black–Scholes call function, we have

$$ C_{\mathrm{BS}}( \cdot, y) \in C_{1} \cap C_{+} \qquad \mbox{for all } y \ge0. $$

The subsets $\mathcal {C}_{+}$ and $\mathcal {C}_{1}$ are closed with respect to the binary operation.

Proposition 2.22

Given$C_{1}, C_{2} \in\mathcal {C}$, we have:

1) $C_{1} \bullet C_{2} \in\mathcal {C}_{1}$if and only if both$C_{1} \in\mathcal {C}_{1}$and$C_{2} \in\mathcal {C}_{1}$.

2) $C_{1} \bullet C_{2} \in\mathcal {C}_{+}$if and only if both$C_{1} \in\mathcal {C}_{+}$and$C_{2} \in\mathcal {C}_{+}$.

Proof

By Theorem 2.16, we have

$$ C_{1} \bullet C_{2}(\kappa) = 1 - \mathbb{E} [ S_{1} \wedge(\kappa S_{2}^{\star})] \qquad \mbox{for all } \kappa\ge0, $$

where $S_{1}$ is a primal representation of $C_{1}$, $S_{2}^{\star}$ is a dual representation of $C_{2}$ and $S_{1}$ and $S_{2}^{\star}$ are countermonotonic. For implication 1), note that

$$ \mathbb{E} [ S_{1} \wedge(\kappa S_{2}^{\star})] \longrightarrow 1 \qquad \mbox{as } \kappa\to\infty $$

if and only if

$$ \mathbb{E} [S_{1}] = 1 \quad \mbox{and}\quad \mathbb{P} [S_{2}^{\star}> 0] = 1. $$

For implication 2), apply Theorem 2.19, 3) and the fact that $(\mathcal {C}_{+})^{\star}= \mathcal {C}_{1}$. □

3 One-parameter semigroups, peacocks and lyrebirds

3.1 The space of call price surfaces

With the motivation at the beginning of Sect. 2, we consider the family of prices of options when the maturity date is allowed to vary. We now introduce the following definition.

Definition 3.1

A call price surface is a function $C:[0,\infty) \times[0,\infty) \to[0,1]$ such that there exists a pair of nonnegative martingales $(\alpha_{t}, \beta_{t})_{t \ge0}$ such that $\alpha_{0} = 1 = \beta_{0}$ and

$$ C(\kappa, t) = \mathbb{E} [ (\alpha_{t} - \kappa\beta_{t})^{+} ] \qquad \mbox{for all } \kappa\ge0, t \ge0. $$

Our goal is to understand the structure of the space of call price surfaces, and relate this structure to the binary operation • introduced in the last section.

Theorem 3.2

Given a function$C:[0,\infty)\times[0,\infty) \to[0,1]$, the following are equivalent:

1) $C$is a call price surface.

2) There exists a nonnegative supermartingale$S$such that$S_{0}=1$and

$$ C(\kappa, t) = 1 - \mathbb{E} [ S_{t} \wedge\kappa] \qquad \textit{for all } (\kappa, t). $$

3) There exists a nonnegative supermartingale$S^{\star}$such that$S^{\star}_{0}=1$and

$$ C(\kappa, t) = 1 - \mathbb{E} [ 1 \wedge(\kappa S^{\star}_{t})] \qquad \textit{for all } (\kappa, t). $$

4) For all$\varepsilon> 0$, there exist bounded nonnegative martingales$\alpha$and$\beta$such that$\alpha_{0}=1 =\beta_{0}$and

$$ C(\kappa, t) = \mathbb{E} [ (\alpha_{t} - \kappa\beta_{t})^{+}] \qquad \textit{for all } (\kappa, t) $$

and such that$\alpha_{t} + \varepsilon\beta_{t} = 1 + \varepsilon$for all$t \ge0$.

5) $C(\kappa, \cdot)$is nondecreasing with$C(\kappa, 0) = (1-\kappa)^{+}$for all$\kappa\ge0$, and$C(\cdot, t)$is convex for all$t \ge0$.

Proof

The implications $n$) ⇒ 5) for $1 \le n \le4$ are easy to check by the conditional version of Jensen’s inequality.

The implications 5) ⇒ 2) and 5) ⇒ 3) are proved as follows. By Theorems 2.2 and 2.12, there exist families of random variables $(S_{t})_{t\ge0}$ and $(S^{\star}_{t})_{t \ge0}$ such that

$$ C(\kappa, t) = 1 - \mathbb{E} [ S_{t} \wedge\kappa] = 1 - \mathbb {E} [ 1 \wedge(\kappa S_{t}^{\star}) ] $$

for all $\kappa\ge0$ and $t \ge0$. The assumption that $C(\kappa, \cdot)$ is nondecreasing implies that both families of random variables (or more precisely, both families of laws) are nondecreasing in the decreasing-convex order. The implications then follow from Kellerer’s theorem [24, Theorem 3].

Implication 4) ⇒ 1) is obvious. So it remains to show the implication 5) ⇒ 4). Fix $\varepsilon> 0$ and let

$$ \tilde{C}(\kappa, t) = \left\{ \textstyle\begin{array}{ll} C( \frac{\varepsilon\kappa}{1+\varepsilon-\kappa}, t ) (1 - \frac{\kappa}{1+\varepsilon} ) & \qquad \mbox{if } 0 \le \kappa< 1+ \varepsilon, \\ 0 & \qquad \mbox{if } \kappa\ge 1+ \varepsilon. \end{array}\displaystyle \right. $$

It is straightforward to verify that $\tilde{C}$ satisfies 5). Hence there exists a nonnegative supermartingale $\alpha$ such that

$$ \tilde{C}(\kappa, t) = 1 - \mathbb{E} [ \alpha_{t} \wedge\kappa] \qquad \mbox{for all } (\kappa,t). $$

But since $\tilde{C}(\kappa, t) = 0$ for all $\kappa\ge1+ \varepsilon$, we can conclude that for all $t$, we have both $\mathbb{E} [ \alpha_{t}] = 1$ and $\alpha_{t} \le1+ \varepsilon$ a.s. In particular, $\alpha$ is a true martingale so that

$$ \tilde{C}(\kappa, t) = \mathbb{E} [ ( \alpha_{t} - \kappa)^{+} ], $$

or equivalently

$$ C(\kappa, t) = \mathbb{E} [ ( \alpha_{t} - \kappa\beta_{t})^{+} ], $$

where $\beta= \frac{1}{\varepsilon}(1+ \varepsilon- \alpha)$ as claimed. □

Remark 3.3

The implication 5) ⇒ 2) is well known, especially in the case where $C(\infty, t) = 0$ for all $t \ge0$ where the supermartingale $S$ is a martingale. See for instance the paper of Carr and Madan [8, Sect. 3]. However, the implication 5) ⇒ 4) seems new.

3.2 One-parameter semigroups

Returning to the topics of Sect. 2, we note that the operation • interacts well with the natural partial ordering on the space of call price curves.

Proposition 3.4

For any$C_{1}, C_{2} \in\mathcal {C}$, we have

$$ \max\{ C_{1}(\kappa), C_{2}(\kappa) \} \le C_{1} \bullet C_{2}(\kappa) \qquad \textit{for all } \kappa\ge0. $$

Proof

Let $S_{1}$ be a primal representation of $C_{1}$ and $S_{2}^{\star}$ a dual representation of $C_{2}$. Suppose $S_{1}$ and $S_{2}^{\star}$ are independent. Then by Theorem 2.15, we have

$$\begin{aligned} C_{1} \bullet C_{2}(\kappa) & \ge1 - \mathbb{E} [ S_{1} \wedge (\kappa S_{2}^{\star})] \\ & \ge1 - \mathbb{E} \left[ \mathbb{E} [S_{1}] \wedge(\kappa S_{2}^{\star})\right] \\ & \ge1 - \mathbb{E} [ 1 \wedge(\kappa S_{2}^{\star})] \\ & = C_{2}(\kappa), \end{aligned}$$

by first conditioning on $S_{2}^{\star}$ and applying the conditional Jensen inequality, and then using the bound $\mathbb{E} [S_{1}] \le1$. The other implication is proved similarly. □

Combining Theorem 3.2 and Proposition 3.4 brings us to the main observation of this paper: If $(C(\cdot, t) )_{t \ge0}$ is a one-parameter sub-semigroup of $\mathcal {C}$, then $C(\cdot, \cdot)$ is a call price surface. Fortunately, we shall see that all such sub-semigroups can be explicitly characterised and are reasonably tractable.

With the motivation of finding a tractable family of call price surfaces, we now study a family of one-parameter sub-semigroups of $\mathcal {C}$. We use the notation $y$, rather than $t$, to denote the parameter since we think of $y$ not literally as the maturity date of the option, but rather as an increasing function of that date. For instance, in the Black–Scholes framework, we have $y=\sigma\sqrt{t}$ corresponding to total standard deviation.

We make use of the following notation. For a probability density function $f$, let

$$ C_{f}(\kappa,y) = \int_{-\infty}^{\infty} \big( f(z+y)- \kappa f(z)\big)^{+} dz = 1 - \int_{-\infty}^{\infty} f(z+y) \wedge \big( \kappa f(z) \big) dz $$

for $y \in\mathbb{R}$ and $\kappa\ge0$. Note that

$$ C_{\mathrm{BS}}(\cdot, y) = C_{\varphi}(\cdot, y) $$

for $y \ge0$, where $\varphi$ is the standard normal density.

It will be useful to distinguish a special class of densities.

Definition 3.5

A probability density function $f: \mathbb{R} \to [0,\infty)$ is log-concave if $\log f: \mathbb{R} \to[-\infty, \infty)$ is concave.

We use repeatedly a useful characterisation of log-concave densities due to Bobkov [4, Proposition A.1].

Proposition 3.6

(Bobkov)

Let$f$be a probability density supported on the interval$[L,R]$and strictly positive on the interval$(L,R)$. Let$F(x) = \int_{L}^{x} f(z) dz$be the corresponding cumulative distribution function and$F^{-1}: [0,1] \to[L,R]$its quantile function. The following are equivalent:

1) $f$is log-concave.

2) $f( \cdot+ y )/f(\cdot)$is nonincreasing on$(L,R)$for each$y \ge0$.

3) $f \circ F^{-1}(\cdot)$is concave on$(0,1)$.

Remark 3.7

In Bobkov’s formulation of Proposition 3.6 above, condition 2) was replaced with $2^{\prime}$) $F( F^{-1}(\cdot) + y)$ is concave on $(0,1)$ for all $y \ge0$. Note that conditions 2) and $2^{\prime}$) are equivalent. To see why, note that the derivative of $g= F( F^{-1}(\cdot) + y)$ is $g' = f( F^{-1}(\cdot)+y)/f( F^{-1}(\cdot))$. Since the function $F^{-1}$ is strictly increasing, the claim amounts to the statement that $g$ is concave if and only $g'$ is nonincreasing.

Let $f$ be a log-concave density supported on the closed interval $[L,R]$, where $-\infty\le L < R \le+ \infty$. It is well known that a convex function $g:\mathbb{R} \to\mathbb{R} \cup\{ + \infty\}$ is continuous on the interior of the interval $\{ g < \infty\}$; see for instance the book of Borwein and Vanderwerff [5, Theorem 2.1.2]. Consequently, the log-concave function $f$ is continuous on the open interval $(L,R)$. However, if either $L > -\infty$ or $R < \infty$, it might be that $f$ has a discontinuity at the boundary of the support; consider for example the log-concave density which is continuous at $L=0$ but discontinuous at $R=1$. But given a log-concave density $f$ supported on $[L,R]$, we can find another log-concave function $\tilde{f}$ with the same support such that $\tilde{f} = f$ on the open interval $(L,R)$ and such that $\tilde{f}$ is right-continuous at $L$ and left-continuous at $R$ by setting $\tilde{f}(L) = \lim_{x \downarrow L} f(x)$ and $\tilde{f}(R) = \lim_{x \uparrow R} f(x)$. Therefore, without loss of generality, we make the convention that if$f$is a log-concave density, then$f$is continuous on its support$[L,R]$.

We now present a family of one-parameter sub-semigroups of $\mathcal {C}$.

Theorem 3.8

Let$f$be a log-concave probability density function. Then

$$ C_{f}(\cdot, y_{1} ) \bullet C_{f}( \cdot, y_{2} ) = C_{f}(\cdot, y_{1}+y_{2} ) \qquad \textit{for all } y_{1}, y_{2} \ge0. $$

Note that Theorems 2.16 and 3.8 together say that for all $\kappa_{1}, \kappa_{2} > 0$ and $y_{1}, y_{2} > 0$, we have

$$ C_{f}(\kappa_{1} \kappa_{2}, y_{1} + y_{2}) \le C_{f}(\kappa_{1}, y_{1}) + \kappa_{1} C_{f}(\kappa_{2}, y_{2}), $$

proving Theorem 1.1.

While Theorem 3.8 is not especially difficult to prove, we offer two proofs with each highlighting a different perspective on the operation •. The first is below and the second is in Sect. 5.1.

Proof of Theorem 3.8

Letting $Z$ be a random variable with density $f$, note that $f(Z+y)/f(Z)$ is a primal representation of $C_{f}( \cdot, y)$. Note also that by log-concavity of $f$, the function $z \mapsto f(z+y)/f(z)$ is nonincreasing when $y \ge0$. Similarly, $f(Z-y)/f(Z)$ is a dual representation of $C_{f}( \cdot, y)$ and $z \mapsto f(z-y)/f(z)$ is nondecreasing. In particular, the random variables $f(Z+y_{1})/f(Z)$ and $f(Z-y_{2})/f(Z)$ are countermonotonic, and hence by Theorem 2.16, we have

$$ C_{f}(\cdot, y_{1}) \bullet C_{f}( \cdot, y_{2})(\kappa) = 1 - \int_{-\infty}^{\infty} f(z+y_{1}) \wedge\big(\kappa f(z-y_{2})\big) dz. $$

The conclusion follows from changing variables in the integral on the right-hand side. □

The upshot of Proposition 3.4 and Theorem 3.8 is that given a log-concave density $f$, the function $C_{f}(\kappa, \cdot)$ is nondecreasing for each $\kappa\ge0$. Hence, given an increasing function $\Upsilon$, we can conclude from Theorem 3.2 that we can define a call price surface by

$$ (\kappa,t) \mapsto C_{f}\big(\kappa, \Upsilon(t) \big). $$

The above formula is reasonably tractable and could be seen to be in the same spirit as the SVI parametrisation of the implied volatility surface given by Gatheral and Jacquier [15]. Note that we can recover the Black–Scholes model by setting the density to $f = \varphi$, the standard normal density, and the increasing function to $\Upsilon(t) = \sigma\sqrt{t}$, where $\sigma$ is the volatility of the stock. We provide another worked example in Sect. 4.2.

At this point, we explain the name of this section. We recall the definitions of terms popularised by Hirsch et al. [19, Definition 1.3] and Ewald and Yor [14, Definition 2.1], among others.

Definition 3.9

A lyrebird is a family $X = (X_{t})_{t \ge0}$ of integrable random variables such that there exists a submartingale $Y = (Y_{t})_{t \ge0}$ defined on some (possibly different) probability space such that the random variables $X_{t}$ and $Y_{t}$ have the same distribution for all $t \ge0$. A peacock$X$ is a family of random variables such that both $X$ and $-X$ are lyrebirds, i.e., there exists a martingale with the same marginal laws as $X$.

The term peacock is derived from the French acronym PCOC, processus croissant pour l’ordre convexe, and lyrebird is the name of an Australian bird with peacock-like tail feathers.

Combining Proposition 3.4 and Theorem 3.8 yields the following tractable family of lyrebirds and peacocks.

Theorem 3.10

Let$f$be a log-concave density, let$Z$be a random variable having density$f$, and let$\Upsilon:[0,\infty) \to[0,\infty)$be increasing. Set

$$ S_{t} = \frac{f(Z+\Upsilon(t))}{f(Z)} \qquad \textit{for } t \ge0. $$

The family of random variables$-S=(-S_{t})_{t \ge0}$is a lyrebird. If the support of$f$is of the form$(-\infty, R]$, then$S$is a peacock.

Note that the semigroup $( C_{f}(\cdot, y) )_{y \ge0}$ does not correspond to a unique log-concave density. Indeed, fix a log-concave density $f$ and set

$$ f^{(\lambda,\mu)}(z) = |\lambda| f(\lambda z + \mu) $$

for $\lambda, \mu\in\mathbb{R}$, $\lambda\ne0$. Note that

$$ C_{f^{(\lambda,\mu)}}( \kappa, y) = C_{f}( \kappa, \lambda y ) \qquad \mbox{for all } \kappa\ge0, y \in\mathbb{R} . $$

However, we shall see below that the semigroup does identify the density $f$ up to arbitrary scaling and centring parameters.

Also, note that by varying the scale parameter $\lambda$, we can interpolate between two possibilities. On the one hand, we have for all $\kappa\ge0$ and $y \in\mathbb{R}$ that

$$ C_{f^{(\lambda,\mu)}}(\kappa, y) \longrightarrow (1- \kappa)^{+} \qquad \mbox{as } \lambda \to0 $$

and, on the other hand, when $y \ne0$, that

$$ C_{f^{(\lambda,\mu)}}(\kappa, y) \longrightarrow 1 \qquad \mbox{as } |\lambda| \to\infty $$

by the dominated convergence theorem.

Recall that the call price curve $E(\kappa) = (1-\kappa)^{+}$ is the identity element for the binary operation •. Hence the family $C_{\mathrm{triv}}$ defined by $C_{\mathrm{triv}}(\cdot, y) = E$ for all $y \ge0$ is another example of a sub-semigroup of $\mathcal {C}$.

Similarly, the call price curve $Z(\kappa) = 1$ is the absorbing element for •. Hence the family $C_{\mathrm{null}}$ defined by $C_{\mathrm{null}}(\cdot, 0) = E$ and $C_{\mathrm{null}}(\cdot, y) = Z$ for all $y > 0$ is yet another example of a sub-semigroup of $\mathcal {C}$.

The following theorem says that the above examples exhaust the possibilities.

Theorem 3.11

Suppose that

$$ C(\kappa,0) = (1-\kappa)^{+} \qquad \textit{for all } \kappa\ge0 $$

and

$$ C(\cdot, y_{1}) \bullet C(\cdot, y_{2}) = C(\cdot, y_{1}+ y_{2}) \qquad \textit{for all } y_{1}, y_{2} \ge0. $$

Then exactly one of the following holds true:

1) $C(\kappa, y) = (1-\kappa)^{+}$for all$\kappa\ge0, y > 0$.

2) $C(\kappa,y) = 1$for all$\kappa\ge0, y > 0$.

3) $C=C_{f}$for a log-concave density$f$.

In case 3), the density$f$is uniquely defined by the semigroup, up to centring and scaling.

The proof appears in Sect. 5.1.

Remark 3.12

One could certainly consider other binary operations on the space $\mathcal {C}$ which are also compatible with the partial order. For instance, we could let

$$\begin{aligned} C_{1} \clubsuit C_{2}(\kappa) = 1 - \mathbb{E} [S_{1} \wedge(\kappa S_{2}^{\star}) ] , \end{aligned}$$

where the primal representation $S_{1}$ of $C_{1}$ is independent of the dual representation $S_{2}^{\star}$ of $C_{2}$. Note that this binary operation $\clubsuit$ is commutative, and indeed we have

$$\begin{aligned} C_{1} \clubsuit C_{2}(\kappa) = 1 - \mathbb{E} [ (S_{1} S_{2}) \wedge \kappa], \end{aligned}$$

where $S_{2}$ is a primal representation of $C_{2}$, again independent of $S_{1}$. In fact, the binary operation $\clubsuit$ can be expressed (somewhat awkwardly) in terms of the call price curves $C_{1}$ and $C_{2}$ as

As described above, one could construct call price surfaces by studying one-parameter semigroups for this binary operation $\clubsuit$. Indeed, such semigroups are easy to describe since their primal representations are essentially exponential Lévy processes. Unfortunately, the call prices given by an exponential Lévy process are not easy to write down in general. However, we have seen that the one-parameter semigroups of call prices for the binary operation • are extremely simple to write down. It is the simplicity of these formulae that is the claim to practicality of the results presented here.

4 Calibrating the surface

4.1 An exploration of $C_{f}$

We have argued that if $f$ is a log-concave density and $\Upsilon$ an increasing function, then the family $\{ C_{f}(\kappa, \Upsilon(t)): \kappa\ge0, t \ge0 \}$ is a call price surface as defined in Sect. 3.1, where the notation $C_{f}$ is defined in Sect. 3.2. The motivation of this section is to bring this observation from theory to practice. In particular, to calibrate the functions $f$ and $\Upsilon$ to market data, it is useful to have at hand some properties, including asymptotic properties, of the function $C_{f}$.

In what follows, we assume that the density $f$ has its support of the form $[L, R]$ for some constants $-\infty\le L < R \le+ \infty$. Recall that we assume$f$ is continuous on $[L,R]$. Now let $Z$ be a random variable with density $f$. For each $y\in\mathbb{R}$, define a nonnegative random variable by

$$ S^{(y)} = \frac{f(Z+y)}{f(Z)}. $$

Note that $S^{(y)}$ is well defined since $L < Z < R$ almost surely, and hence $f(Z) > 0$ almost surely. In this notation, we have for all $y \in\mathbb{R}$ that

$$ C_{f}(\kappa,y) = 1 - \mathbb{E} [ S^{(y)} \wedge\kappa ] $$

so that by Theorem 2.2, we have $C_{f}( \cdot, y) \in\mathcal {C}$ and $S^{(y)}$ is a primal representation of $C_{f}(\cdot, y)$.

Note that $S^{(y)} = 0$ almost surely for $|y| \ge R-L$, while for $|y| < R-L$, we have

$$ \mathbb{P} [ S^{(y)} > 0 ] = \mathbb{P} [L + y^{-} < Z < R - y^{+}] $$

and

$$ \mathbb{E} [ S^{(y)} ] = \mathbb{P} [ L + y^{+} < Z < R - y^{-}]. $$

In particular, for $y > 0$, we have

$$\begin{aligned} C_{f}( \cdot, y) &\in\mathcal {C}_{+} \qquad \mbox{if } R = + \infty, \\ C_{f}( \cdot, y) &\in\mathcal {C}_{1} \qquad \mbox{if } L = - \infty, \end{aligned}$$

where the sets $\mathcal {C}_{+}$ and $\mathcal {C}_{1}$ are defined in Sect. 2.3.

By changing variables, we find that a dual representation of $C_{f}(\cdot, y)$ is given by

$$ S^{(y)\star} = \frac{f(Z-y)}{f(Z)} = S^{(-y)} $$

and therefore

$$ C_{f}(\cdot,y)^{\star}= C_{f}(\cdot,-y). $$

It is interesting to observe that the call price surface $C_{f}$ satisfies the put–call symmetry formula $C_{f}(\cdot ,y)^{\star}= C_{f}(\cdot,y)$ if the density $f$ is an even function. Put–call symmetry has found applications for instance in the semi-static hedging of certain barrier-type contingent claims; see the paper of Carr and Lee [7, Theorem 5.10].

Due to the implication 1) ⇒ 2) in Proposition 3.6, the map $z \mapsto\frac{f(z +y)}{f(z)}$ is nonincreasing for $y \ge0$. Let

$$ d_{f}( \kappa,y) = \sup\left\{ z > L: \frac{f(z+y)}{f(z)} \ge \kappa\right\} \qquad \mbox{for } \kappa\ge0, y \ge0, $$

with the convention that $\sup\emptyset= L$. Note that $\frac{f(z+y)}{f(z)} \ge\kappa$ if and only if $d_{f}(y, \kappa) \ge z$. With this notation, we have

$$ C_{f}(\kappa, y) = F\big( d_{f}( \kappa, y) + y\big) - \kappa F\big( d_{f} (\kappa, y)\big) \qquad \mbox{for all } \kappa\ge 0, y \ge 0, $$

where $F(x) = \int_{L}^{x} f(z) dz$ is the cumulative distribution function corresponding to $f$.

Remark 4.1

The standard normal density $\varphi$ is log-concave and we have the computation

$$ d_{\varphi}(\kappa,y) = - \frac{ \log\kappa}{y} - \frac{y}{2}, $$

yielding the usual Black–Scholes formula.

Theorem 4.2 below might seem like a curiosity, but in fact is a useful alternative formula for computing $C_{f}$ numerically, given the density $f$. In particular, the following formula does not require the evaluation of the function $d_{f}$ defined above. This is a generalisation of Theorem 3.1 of [31]. The proof is essentially the same, but included here for completeness. We use the notation

$$ \hat{C}_{f}(p,y) = F\big( F^{-1}(p) + y\big). $$

Theorem 4.2

For$\kappa, y \ge0$, we have

$$ C_{f}(\kappa, y ) = \sup_{0 \le p \le1} \big(\hat{C}_{f}(p, y) - p \kappa\big). $$

Proof

Fix $\kappa, p, y$ and let $z=F^{-1}(p)$. Note that

$$\begin{aligned} F(z+y) - \kappa F(z) &= \int_{-\infty}^{z} \big(f(u+y)-\kappa f(u)\big) du \\ &\le\int_{-\infty}^{z} \big(f(u+y)-\kappa f(u)\big)^{+} du \\ &\le \int_{-\infty}^{\infty} \big(f(u+y)-\kappa f(u)\big)^{+} du \\ & = C_{f}(\kappa, y). \end{aligned}$$

Given $\kappa$, there is equality when $z= d_{f}(\kappa,y)$. □

The next result gives an asymptotic expression for call prices at short maturities and close to the money. In what follows, we use the notation

$$ H_{f}(x) = f(L) + \int_{L }^{R } \big(f'(z) - f(z) x\big)^{+} dz = f(R)- \int_{L }^{R } f'(z) \wedge\big( f(z) x \big) dz, $$

where $f'$ is the right derivative of $f$. Recall that $f'$ always exists on the interval $(L,R)$.

Theorem 4.3

As$\varepsilon\downarrow0$, we have that

$$ \frac{1}{\varepsilon} C_{f}(e^{\varepsilon x}, \varepsilon) \longrightarrow H_{f}(x). $$

Proof

Let $a$ be a maximum of $f$ so that $f(z+\varepsilon) \ge f(z)$ for $z \le a-\varepsilon$ and $f(z+\varepsilon) \le f(z)$ for $z \ge R-\varepsilon$. We only consider the case $L < a < R$, as the cases $a=L$ and $a = R$ are similar.

Fix $x$ and $a-L < \varepsilon< R-a$ and write

$$ \frac{1}{\varepsilon}C_{f}(e^{\varepsilon x}, \varepsilon) = I_{1} + I_{2} + I_{3}, $$

where

$$\begin{aligned} I_{1} &= \frac{1}{\varepsilon}\int_{a}^{R-\varepsilon} \big(f(z+ \varepsilon) - e^{\varepsilon x} f(z) \big)^{+} dz, \\ I_{2} &= \frac{1}{\varepsilon}\int_{a-\varepsilon}^{a} \big(f(z+ \varepsilon) - e^{\varepsilon x} f(z) \big)^{+} dz, \\ I_{3} &= \frac{1}{\varepsilon}\int_{L-\varepsilon}^{a-\varepsilon} \big(f(z+\varepsilon) - e^{\varepsilon x} f(z) \big)^{+} dz. \end{aligned}$$

Note that for $a \le z \le R - \varepsilon$, we have

$$ \frac{1}{\varepsilon}\big(f(z+\varepsilon) - e^{\varepsilon x} f(z) \big)^{+} \le x^{-} f(z) $$

so that

$$ I_{1} \longrightarrow \int_{a}^{R} \big(f'(z) - x f(z)\big)^{+} dz $$

by the dominated convergence theorem. For the second term, note that by the continuity of $f$ at the point $a$, we have

$$ \sup_{a-\varepsilon\le z \le a} |f(z+\varepsilon) - e^{\varepsilon x} f(z) | \longrightarrow 0 $$

as $\varepsilon\downarrow0$. In particular, we have $I_{2} \to0$. Finally, for the third term, apply the put–call parity formula to get

$$\begin{aligned} I_{3} &= \frac{1}{\varepsilon} \int_{L-\varepsilon}^{a- \varepsilon} \big(f(z+\varepsilon) - e^{\varepsilon x} f(z) \big) dz + \frac{1}{\varepsilon} \int_{L-\varepsilon}^{a-\varepsilon} \big(e^{\varepsilon x} f(z) - f(z+\varepsilon)\big)^{+} dz \\ &\longrightarrow f(a) - x F(a) + \int_{L}^{a} \big( x f(z) - f'(z)\big)^{+} dz, \end{aligned}$$

again by the dominated convergence theorem. The conclusion follows from another application of put–call parity and recombining the integrals. □

There are two interesting consequences of Theorem 4.3. The first is that the density $f$ can be recovered from short-time asymptotics. We use the notation

$$ \hat{H}_{f}(p) = f \circ F^{-1}(p) $$

for $0 \le p \le1$. The proof follows the same pattern as that of Theorem 4.2, so it is omitted.

Theorem 4.4

For all$0 \le p \le1$, we have

$$\begin{aligned} \hat{H}_{f}(p) = \inf_{x \in\mathbb{R} } \big( H_{f}(x) + xp \big). \end{aligned}$$

Remark 4.5

Given the function $\hat{H}_{f}$, we can recover $f$, up to centring, as follows. Fix $0 < p_{0} < 1$ and set $F(0) = p_{0}$. Then we have

$$ F^{-1}(p) = \int_{p_{0}}^{p} \frac{dq}{\hat{H}_{f}(q)}. $$

We note in passing that the call price function $C_{f}$ satisfies a nonlinear partial differential equation featuring the function $\hat{H}_{f}$ when $f$ is suitably well behaved as specified in the following proposition.

Proposition 4.6

Let$f$be a strictly log-concave density supported on all of ℝ. Suppose that$f$is$C^{1}$and such that

$$ \lim_{z \downarrow- \infty} \frac{f'(z)}{f(z)} = + \infty\qquad \textit{and}\qquad \lim_{z \uparrow+ \infty} \frac{f'(z)}{f(z)} = - \infty. $$

Then

$$\begin{aligned} \frac{\partial C_{f}}{\partial y} = \kappa \hat{H} \left( - \frac{\partial C_{f}}{\partial\kappa} \right) = \hat{H} \left( C_{f} - \kappa\frac{\partial C_{f}}{\partial\kappa} \right) \end{aligned}$$

for$( \kappa, y) \in(0,\infty) \times(0, \infty)$.

Proof

By log-concavity, we have for all $z \in\mathbb{R}$ and $y > 0$ that

$$ \frac{f'(z+y)}{f(z+y)} \le\frac{1}{y} \log\frac{f(z+y)}{f(z)} \le \frac{f'(z)}{f(z)} $$

and hence

$$ \lim_{z \downarrow-\infty} \frac{f(z+y)}{f(z)} = +\infty\qquad \mbox{ and} \qquad \lim_{z \uparrow+\infty} \frac{f(z+y)}{f(z)} = 0. $$

Also, by the strict log-concavity of $f$, the map $z \mapsto\frac{f(z+y)}{f(z)}$ is strictly decreasing. This shows that $d_{f}(\kappa, y)$ is finite for all $\kappa > 0$ and that

$$ f\big(d_{f}(\kappa, y) +y \big)= \kappa f\big( d_{f}(\kappa, y)\big). $$

By the differentiability of $f$ and the implicit function theorem, the function $d_{f}$ is differentiable for $(\kappa, y) \in(0, \infty) \times(0, \infty)$.

One checks that

$$\begin{aligned} \frac{\partial C_{f}}{\partial y} &= f\big( d_{f}(\kappa, y) + y \big), \\ \frac{\partial C_{f}}{\partial\kappa} &= - F\big( d_{f}(\kappa ,y)\big). \end{aligned}$$

The conclusion follows. □

We now comment on a second interesting consequence of Theorem 4.3. Note that for $\varepsilon\downarrow0$, the limit for the Black–Scholes call function is

$$ \frac{1}{\varepsilon} C_{\mathrm{BS}}(e^{\varepsilon x}, \varepsilon) \longrightarrow H_{\varphi}(x) = \varphi(x) - x \Phi(-x). $$

The function $H_{\varphi}$ has an interesting financial interpretation. Recall that in the Bachelier model, assuming zero interest rates, the initial price of a call option of maturity $T$ and strike $K$ is given by

$$ C_{0,T, K} = \sigma\sqrt{T} H_{\varphi} \left( \frac{ K - S_{0}}{\sigma\sqrt{T}} \right), $$

where $S_{0}$ is the initial price of the stock and $\sigma$ is its arithmetic volatility. Hence $H_{\varphi}$ can be interpreted as a normalised call price function in the Bachelier model.

Following the motivation of this section, we are interested not only in the call price surface itself, but also in the corresponding implied volatility surface. Recall that the function $Y_{\mathrm{BS}}$ is defined by

$$ y = Y_{\mathrm{BS}}(\kappa, c) \quad \Longleftrightarrow\quad C_{\mathrm{BS}}(\kappa,y) = c. $$

We use the notation

$$ Y_{f}(\kappa, y) = Y_{\mathrm{BS}}\big( \kappa, C_{f}(\kappa, y) \big). $$

Recall that if the normalised price of a call of moneyness $\kappa$ and maturity $t$ is given by $C_{f}(\kappa, \Upsilon(t) )$, then the option’s implied volatility is given by $\frac{1}{\sqrt{t}} Y_{f}(\kappa, \Upsilon(t))$.

Remark 4.7

A word of warning: We have noted that the function $C_{\mathrm{BS}}$ is the restriction of the function $C_{\varphi}$ to $[0,\infty) \times[0,\infty)$. However, it is not the case that the function $Y_{\mathrm{BS}}$ is a restriction of the function $Y_{\varphi}$. Indeed, the second argument of $Y_{\mathrm{BS}}$ is a number $c$ in $[0,1]$, while the second argument of $Y_{\varphi}$ is a number $y$ in $[0,\infty)$.

With this setup, we now present a result that gives the asymptotics of the implied volatility surface in the short-maturity, close-to-the-money limit.

Theorem 4.8

We have as $\epsilon\downarrow0$ that

$$ \frac{1}{\varepsilon} Y_{f}(1, \varepsilon) \longrightarrow \sqrt {2\pi} \max_{z} f(z), $$

and more generally that

$$ \frac{1}{\varepsilon} Y_{f}(e^{\varepsilon x}, \varepsilon) \to \Lambda_{\mathrm{Ba}}\big(x, H_{f}(x)\big), $$

where $\Lambda_{\mathrm{Ba}}(x, c )$ is defined by

$$ \Lambda_{\mathrm{Ba}}(x, c ) = \lambda\quad \Longleftrightarrow \quad \lambda H_{\varphi}(x/\lambda) = c. $$

Proof

Fix $x \in\mathbb{R}$ and $\delta> 0$. Let $\lambda= \Lambda _{\mathrm {Ba}}(x, H_{f}(x) + \delta)$. By Theorem 4.3, there exists $\varepsilon_{0} > 0$ such that

$$ \frac{1}{\varepsilon} C_{f}(e^{\varepsilon x}, \varepsilon) \le H_{f}(x) + \frac{1}{2}\delta, $$

while

$$ \frac{1}{\varepsilon} C_{\varphi}(e^{\varepsilon x}, \lambda \varepsilon) \ge \lambda H_{\varphi}(x/\lambda) - \frac{1}{2} \delta $$

for all $0 < \varepsilon< \varepsilon_{0}$. Hence $C_{f}(e^{\varepsilon x}, \varepsilon) \le C_{\mathrm{BS}}(e^{\varepsilon x}, \lambda\varepsilon)$ and therefore

$$ \limsup_{\varepsilon\downarrow0} \frac{1}{\varepsilon} Y_{f}(e^{\varepsilon x}, \varepsilon) \le \liminf_{\delta\downarrow0} \Lambda_{\mathrm{Ba}}\big(x, H_{f}(x) + \delta \big). $$

A lower bound is established similarly. The conclusion follows from the continuity of $\Lambda_{\mathrm{Ba}}$. □

For the final theorem of this section, we fix the maturity date and now compute extreme strike asymptotics of the implied volatility. In what follows, we say that an eventually positive function $g$varies regularly at infinity with exponent$\alpha$ if

$$ \frac{g(\lambda x)}{g(x)} \longrightarrow \lambda^{\alpha}\qquad \mbox{as } x \to \infty \mbox{ for all } \lambda> 0. $$

Regular variation at zero is defined analogously.

Theorem 4.9

Suppose that$f$is a log-concave density such that$-\log\circ f \circ\log$varies regularly at infinity with exponent$a > 0$and varies regularly at zero with exponent$- b < 0$. Then for$y >0$, we have

$$\begin{aligned} \limsup_{\kappa\uparrow\infty} \frac{ Y_{f}(\kappa,y)}{\sqrt {\log\kappa}} &= \sqrt{ 2 \tanh \frac{by}{4} }, \\ \limsup_{\kappa\downarrow0} \frac{ Y_{f}(\kappa,y)}{\sqrt{-\log \kappa}} &= \sqrt{ 2 \tanh \frac{ay}{4} }. \end{aligned}$$

Proof

The key observation is that $f^{\theta}$ is Lebesgue-integrable if and only if $\theta> 0$. Indeed, since $f$ is integrable and log-concave, there exist constants $A, B$ with $B>0$ such that $f(z) \le e^{A - B|z|}$, and hence $f^{\theta}$ is bounded from above by an integrable function for $\theta> 0$ and bounded from below by a non-integrable function for $\theta\le0$.

Fix $y > 0$. The moment-generating function of $\log S^{(y)}$ is calculated as

$$\begin{aligned} M(p) = \mathbb{E} [ (S^{(y)})^{p} ] = I_{1} + I_{2} \end{aligned}$$

where

$$ I_{1} = \int_{-\infty}^{0} f(z+y)^{p} f(z)^{1-p} dz,\qquad I_{2} = \int_{0}^{\infty} f(z+y)^{p} f(z)^{1-p} dz. $$

By assumption,

$$ \frac{ \log f(z+y) }{\log f(z)} \longrightarrow e^{-by} \qquad \mbox{as } z \to- \infty, $$

or equivalently $f(z+y) = f(z)^{e^{-by} + \delta(z)}$, where $\delta(z) \to0$ as $z \to-\infty$, yielding the expression

$$ f(z+y)^{p} f(z)^{1-p} = f(z)^{ 1 - p(1 - e^{-by} - \delta(z) )}. $$

The exponent of $f$ on the right-hand side is eventually positive, implying $I_{1}$ is finite, if

$$ p < \frac{1}{1- e^{-by}}, $$

and the exponent is eventually negative, implying $I_{1}$ is infinite, if

$$ p > \frac{1}{1- e^{-by}}. $$

On the other hand, $f(z+y) = f(z)^{e^{ay} + \varepsilon(z)}$, where $\varepsilon(z) \to0$ as $z \to\infty$. Writing

$$ f(z+y)^{p} f(z)^{1-p} = f(z)^{ 1 + p(e^{ay} -1 + \varepsilon(z)) }, $$

we see that for any $p \ge0$, the exponent of $f$ on the right-hand side is eventually positive, implying $I_{2}$ is finite.

Therefore, we have shown that

$$ p^{*} = \sup\{ p \ge1: M(p) < \infty\} = \frac{1}{1- e^{-by}}. $$

By Lee’s moment formula [28, Theorem 3.2], we have

$$ \limsup_{\kappa\uparrow\infty} \frac{ Y_{f}(\kappa,y)}{\sqrt {\log\kappa}} = \sqrt{2} \big(\sqrt{p^{*}} - \sqrt{p^{*}-1}\big) $$

from which the first conclusion follows. The calculation of the left-hand wing is similar. □

4.2 A parametric example

In this section, we consider a parametrised family of log-concave densities in which several interesting calculations can be performed explicitly. We then try to fit this family to real call price data as a proof of concept.

Consider the family of densities of the form

$$ f (x) = \frac{1}{Z } \left\{ \textstyle\begin{array}{ll} e^{r(c+a)x - r e^{ax} } & \qquad \mbox{if } x \ge0, \\ e^{r(c-b)x - r e^{-bx} } & \qquad \mbox{if } x < 0, \end{array}\displaystyle \right. $$

for strictly positive parameters $a,b,r$ and real $c$, with normalising constant

$$ Z = \frac{1}{a}r^{-r(1 + c/a)} \bar{\Gamma}\big(r; r(1 + c/a)\big) + \frac{1}{b }r^{-r(1 - c/b)}\bar{\Gamma}\big(r; r(1 - c/b)\big) , $$

where $\bar{\Gamma}(x, \theta) = \int_{x}^{\infty} z^{\theta-1} e^{-z}dz$ is the complementary incomplete gamma function. It is straightforward to check that $f$ is a log-concave probability density.

Letting $a=b=r^{-1/2}$ and $c=0$ and then sending $r \to\infty$ recovers the Black–Scholes model $f \to\varphi$. Roughly speaking, $a$ controls the left wing, $b$ the right wing, $c$ the at-the-money skew and $r$ the at-the-money convexity. Although there are four parameters, recall from Sect. 3.2 that we have

$$ C_{f_{(\lambda a, \lambda b, \lambda c,r)}}(\kappa, y ) = C_{f_{(a,b,c,r)}}(\kappa, \lambda y ) $$

for $\kappa\ge0$, $y \ge0$ and $\lambda> 0$. Hence there is no loss of generality if we impose for instance that $abr = 1$, leaving us with only three free parameters.

The distribution function is given explicitly by

$$ F(x) = \left\{ \textstyle\begin{array}{ll} 1 - \frac{1}{Za} r^{-r(1 + c/a)}\bar{\Gamma}(re^{ax}; r(1 + c/a)) &\qquad \mbox{if } x \ge0, \\ \frac{1}{Zb }r^{-r(1 - c/b)}\bar{\Gamma}(re^{-bx}; r(1 - c/b)) & \qquad \mbox{if } x < 0 . \end{array}\displaystyle \right. $$

The function $d_{f}$ can be calculated explicitly when the absolute log-moneyness $|\log\kappa|$ is sufficiently large; we get

$$ d_{f}(\kappa, y) = \left\{ \textstyle\begin{array}{ll} \frac{1}{a} \log \frac{ (c+a)y - \frac{1}{r}\log \kappa}{ e^{ay} -1 } & \qquad \mbox{for } \kappa\le e^{r(c+a)y - r(e^{ay} -1 )} ,\\ -\frac{1}{b} \log\frac{ - (c-b)y + \frac{1}{r}\log\kappa}{ 1 -e^{-by} } & \qquad \mbox{for } \kappa\ge e^{ r(c-b)y + r(e^{by} -1 )}. \end{array}\displaystyle \right. $$

Otherwise $d_{f}(\kappa, y)$ is the unique root $-y < d < 0$ of the equation

$$ (c+a) y + (a+b) d = e^{a d + ay} - e^{-b d} + \frac{1}{r} \log\kappa, $$

which can be calculated numerically for instance by the bisection method.

The call price curve can be calculated by the formula

$$ C_{f}(\kappa, y) = F\big( d_{f}(\kappa, y) + y \big) - \kappa F\big(d_{f}(\kappa, y) \big). $$

Note that this formula is rather explicit when the absolute log-moneyness is sufficiently large, and furthermore, it is numerically tractable in all cases.

This choice of $f$ has the advantage that call prices can be calculated very quickly. Also, for other vanilla options, numerical integration is very efficient since the density function $f$ is smooth and decays quickly at infinity. Alternatively, rejection sampling is available, since the density is bounded for instance by a Gaussian density.

When it comes to calibrating the model, we must find parameters $a,b,c,r$ and an increasing function $\Upsilon$ such that

$$ C_{f_{(a,b,c,r)}}\big(\kappa, \Upsilon(t) \big) \approx C^{\mathrm {obs}}(\kappa, t) \qquad \mbox{for all } ( \kappa, t) \in\mathcal {S}, $$

where $C^{\mathrm{obs}}(\kappa, t)$ is the observed normalised price of a call option of moneyness $\kappa$ and maturity $t$ and $\mathcal {S}$ is the set of pairs $(\kappa, t)$ for which there is available market data. Equivalently, we fit the parameters $a,b,c,r$ and the function $\Upsilon$ to try to approximate the observed implied volatility surface.

For this exercise, E-mini S&P MidCap 400 call options call and put option price data were downloaded from the CME Group FTP site [11], for maturities $t_{1}=0.2$, $t_{2}= 0.4$, $t_{3}=0.7$ years for all available strikes. Letting

$$ \mathcal {S}_{i} = \{ \kappa: (\kappa, t_{i}) \in\mathcal {S} \} $$

be the set of available strikes for maturity $t_{i}$, we have $|\mathcal {S}_{1}| = 251, |\mathcal {S}_{2}| = 248$ and $|\mathcal {S}_{3}| = 232$ observations. There are six parameters to find, namely $a, c,r$ and $\Upsilon(t_{1}) = y_{1}$, $\Upsilon(t_{2}) = y_{2}, \Upsilon(t_{3}) = y_{3}$, to fit $251+248+232=731$ observations.

To speed up the calibration, we can use the asymptotic implied total standard deviation calculations of Sect. 4.1. In particular, we can apply Theorem 4.9 by noting that

$$ -\log\circ f \circ\log(x) = \log Z + \left\{ \textstyle\begin{array}{ll} r x^{a} - r(a+c) \log x & \qquad \mbox{if } x \ge1, \\ r x^{-b} + r(b-c) \log x & \qquad \mbox{if } x < 1. \end{array}\displaystyle \right. $$

However, we can do better and replace each lim sup with a proper limit by applying standard asymptotic properties of the complementary incomplete gamma function and the tail-wing formula of Benaim–Friz [2] and Gulisashvili [16] to find

$$\begin{aligned} \frac{Y_{f}(\kappa, y) }{\sqrt{\log\kappa}} &\longrightarrow \sqrt{2 \tanh\frac{ b y}{4} } \qquad \mbox{as } \kappa\to\infty, \\ \frac{Y_{f}(\kappa, y) }{\sqrt{-\log\kappa}} &\longrightarrow \sqrt{2 \tanh\frac{ a y}{4} }\qquad \mbox{as } \kappa\to0. \end{aligned}$$

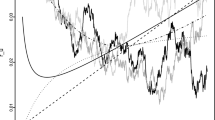
Figure 2 shows a calibration of this family of call prices to real market data. It is important to stress that there is no a priori reason why this data should resemble the call surfaces generated by this family of models. Nevertheless, although the fit is not perfect, it does seem to indicate that this modelling approach is worth pursuing further.

Fig. 2

Implied volatility vs. log-moneyness for market data versus fitted density (red) with $a=3.63$, $b =0.0545$, $c = -0.0665$, $r= 6.89$ and $y_{1} = 0.234$, $y_{2} = 0.356$, $y_{3} = 0.439$

4.3 A nonparametric calibration

In this section, we take a somewhat different approach. Rather than assuming that the log-concave density $f$ is a fixed parametric family, we use the results of Sect. 4.1 to estimate $f$ nonparametrically. In particular, we assume that

$$ C^{\mathrm{obs}}(\kappa, t_{1}) \approx C_{f }\big(\kappa, \Upsilon (t_{1}) \big) \qquad \mbox{for all } \kappa\in\mathcal {S}_{1}, $$

where now the function $f$ is unknown. Since the fit of the parametric model was reasonably good, we set $\Upsilon(t_{1})$ to be the same value $y_{1}$ found in Sect. 4.2.

Recall that Theorem 4.3 says that

$$ C_{f}(e^{\varepsilon x}, \varepsilon) = \varepsilon H_{f}(x) + o(\varepsilon). $$

It is straightforward to check that if $f$ satisfies a mild regularity condition as in the hypothesis of Proposition 4.6, then we have the slightly improved asymptotic formula

$$ C_{f}(e^{\varepsilon x}, \varepsilon)e^{-\varepsilon x/2} = \varepsilon H_{f}(x) + o(\varepsilon^{2}). $$

Hence we assume that

$$ C_{f }(\kappa, y_{1} ) \kappa^{-1/2} \approx y_{1} H_{f}\bigg(\frac {\log\kappa}{y_{1}}\bigg), $$

since $y_{1}$ is small. Theorem 4.4 tells us that

$$ f \circ F^{-1}(p) \approx\frac{1}{y_{1}} \inf_{\kappa\in\mathcal{S}_{1}} \big( C^{\mathrm{obs}}(\kappa, t_{1}) \kappa^{-1/2} + p \log\kappa\big). $$

An estimate of the density $f$ can now be computed numerically.

Figure 3 compares $\log f$ when estimated nonparametrically with the calibrated parametric example from the last section. Considering the fact that the nonparametric density is estimated from the earliest maturity date while the parametric density is calibrated using all three maturity dates, the agreement is uncanny.

Fig. 3

$\log f$ estimated nonparametrically (blue), versus the parametric fit (red). Both are centred so that their maxima are at the origin

Given that the calibrated parametric density seems to recover market data reasonably well, and that the nonparametric density agrees with the parametric one reasonably well, it is natural to compare the market implied volatility to that predicted by the nonparametric model. Recall that the model call surface is determined by the density $f$ and the increasing function $\Upsilon$. We have estimated $f$ from the short-maturity call prices and the assumption that $\Upsilon(t_{1}) = y_{1}$, where $y_{1}$ was found from the parametric calibration. However, we still need to estimate the function $\Upsilon(t_{i})$ for $i=2, 3$. For lack of a better idea, we let $\Upsilon(t_{i}) = y_{i}$ for $i=2,3$ as well.

Figure 4 compares the market implied volatility (the same as in Fig. 2) with the implied volatility computed from the nonparametric model. Since the estimated density $f$ is not given by an explicit formula, the formula in Theorem 4.2 was used to compute the call prices. Again, given that the density $f$ is estimated using only the call price curve for $t_{1}$, it is interesting that the model-implied volatility for maturities $t_{2}$ and $t_{3}$ should match the market data at all.

Fig. 4

Implied volatility vs. log-moneyness from market data (blue), versus the nonparametrically estimated density (red)

5 An isomorphism and lift zonoids

5.1 The isomorphism

In this section, to help understand the binary operation • on the space $\mathcal {C}$, we show that there is a nice isomorphism of $\mathcal {C}$ to another function space which converts the somewhat complicated operation • into simple function composition ∘.

We introduce a transformation $\hat{ \ }$ on the space $\mathcal {C}$ which will be particularly useful. For $C \in\mathcal {C}$, we define a new function $\hat{C}$ on $[0,1]$ by the formula

$$ \hat{C}(p) = \inf_{\kappa\ge0} \big( C(\kappa) + p\kappa\big) \qquad \mbox{for } 0 \le p \le1. $$

We quickly note that the notation $\hat{ \ }$ introduced here is in fact consistent with the prior occurrence of this notation in Sect. 4.1. Indeed, the connection between the transformation $\hat{ \ }: \mathcal {C} \to\hat{ \mathcal {C}}$ defined here and the conclusion of Theorem 4.4 is explored in Sect. 5.2 below.

Given a call price curve $C \in\mathcal {C}$, we can immediately read off some properties of the new function $\hat{C}$. The proof is routine and hence omitted.

Proposition 5.1

Fix$C \in\mathcal {C}$with primal representation$S$and dual representation$S^{\star}$.

1) $\hat{C}$is nondecreasing and concave.

2) $\hat{C}$is continuous and

$$ \hat{C}(0) = C(\infty) = 1- \mathbb{E} [S] = \mathbb{P} [S^{\star}= 0 ]. $$

3) For$0 \le p \le1$and$\kappa\ge0$such that

$$ \mathbb{P} [S > \kappa ] \le p \le\mathbb{P} [S \ge\kappa], $$

we have$\hat{C}(p) = C(\kappa) + p\kappa$.

4) $\min\{ p \ge0: \hat{C}(p) = 1 \} = - C'(0) = \mathbb{P} [S > 0] = \mathbb{E} [S^{\star}]$.

5) $\hat{C}(p) \ge p$for all$0 \le p \le1$.

Figure 5 plots the graph of a typical element $\hat{C} \in \hat{\mathcal {C}}$.

Fig. 5

A typical element of $\hat{\mathcal {C}}$

The next result identifies the image $\hat{\mathcal {C}}$ of the map $\, \hat{ }\,\,$, and further shows that $\,\hat{ }\,: \mathcal {C} \to\hat{\mathcal {C}}$ is a bijection.

Theorem 5.2

Suppose$g:[0,1] \to[0,1]$is continuous and concave with$g(1)=1$. Let

$$ C(\kappa) = \max_{0 \le p \le1} \big( g(p) - p \kappa\big) \qquad \textit{for all } \kappa\ge0. $$

Then$C \in\mathcal {C}$and$g = \hat{C}$.

The above theorem is a minor variant of the Fenchel biconjugation theorem of convex analysis. See the book of Borwein and Vanderwerff [5, Theorem 2.4.4].

The following theorem explains our interest in the bijection $\,\hat{ }\,$: it converts the binary operation • to function composition ∘. A version of this result can be found in the book of Borwein and Vanderwerff [5, Exercise 2.4.31].

Theorem 5.3

For$C_{1}, C_{2} \in\mathcal {C}$, we have

$$ \widehat{C_{1} \bullet C_{2}} = \hat{C_{1}} \circ\hat{C_{2}}. $$

Proof

By the continuity at $\kappa=0$ of a function $C \in \mathcal {C}$, we have the equivalent expression

$$ \hat{C}(p) = \inf_{\kappa> 0} \big( C(\kappa) + p\kappa\big) \qquad \mbox{for } 0 \le p \le1. $$

Hence for any $0 \le p \le1$, we have

$$\begin{aligned} \widehat{C_{1} \bullet C_{2}}(p) & = \inf_{\kappa> 0} \big( C_{1} \bullet C_{2} (\kappa) + p\kappa\big) \\ & = \inf_{\kappa> 0} \Big( \inf_{\eta> 0} \big( C_{1}(\eta) + \eta C_{2} (\kappa/\eta) \big) + p\kappa\Big) \\ & = \inf_{\eta> 0} \Big( C_{1}(\eta) + \eta\inf_{\kappa> 0} \big( C_{2} (\kappa) + p\kappa\big) \Big) \\ & = \hat{C_{1}} \circ\hat{C_{2}}(p). \end{aligned}$$

 □

In light of Theorem 5.3, Theorem 2.19 says that the set $\hat{\mathcal {C}}$ of conjugate functions is a semigroup with respect to function composition ∘, with identity element $\hat{E}(p) = p$ and absorbing element $\hat{Z}(p) = 1$. The involution on $\hat{\mathcal {C}}$ induced by ^⋆ is identified in Theorem 5.6 below.

In preparation for reproving Theorem 3.8 and proving Theorem 3.11, we identify the image of the set $C_{f}$ of functions under the isomorphism $\,\hat{ }\,$. As the notation introduced in Sect. 4.1 suggests, we have

$$ \widehat{C_{f}(\cdot, y)}(p) = F\big( F^{-1}(p) + y\big) $$

by Theorems 4.2 and 5.2. For notational ease, we continue to use the notation

$$ \hat{C}_{f}(p,y) = \widehat{C_{f} (\cdot, y)}(p). $$

Another proof of Theorem 3.8

The family of functions $( \hat{C}_{f}(\cdot, y) )_{y \ge0}$ forms a semigroup with respect to function composition. The result follows from applying Theorems 5.2 and 5.3. □

We now come to the proof of Theorem 3.11.

Proof of Theorem 3.11

If a function $C:[0,\infty)\times[0,\infty) \to[0,1]$ satisfies the hypotheses of the theorem, then the conjugate function $\hat{C}:[0,1]\times[0,\infty) \to[0,1]$ is such that

$$ \hat{C}(p,0) = p \qquad \mbox{for all } 0\le p \le1 $$

and satisfies the translation equation

$$ \hat{C}\big( \hat{C}(p,y_{1}), y_{2}\big) = \hat{C}(p, y_{1}+y_{2}) \qquad \mbox{for all } 0 \le p \le1 \mbox{ and } y_{1}, y_{2} \ge0. $$

The conclusion of the theorem is that there are only three types of solutions to the above functional equation such that $\hat{C}( \cdot, y) \in\hat{ \mathcal {C}}$ for all $y > 0$:

1) $\hat{C}(p,y) = p$ for all $0\le p \le1$ and $y > 0$.

2) $\hat{C}(p, y) = 1$ for all $0\le p \le1$ and $y > 0$.

3) $\hat{C}(p, y) = F( F^{-1}(p) + y )$ for all $0\le p \le1$ and $y > 0$, where we define $F(z) = \int_{-\infty}^{z} f(x) dx$ and $f$ is a log-concave probability density.

Once we have ruled out cases 1) and 2), we can appeal to the result of Cherny and Filipović [10, Theorem 2.1], which says that concave solutions of the translation equation on $[0,1]$ are of the form $G^{-1}( G(\cdot) + y )$, where

$$ G(p) = \int_{p_{0}}^{p} \frac{ dq}{ \hat{H}(q) } $$

for a positive concave function $\hat{H}$ and fixed $0 < p_{0} <1$. Note that for $0 < p < 1$, the integral is well defined and finite as $\hat{H}$ is positive and continuous by concavity. Let $L = G(0)$ and $R= G(1)$, define a function $F:[L,R] \to[0,1]$ as the inverse function $F = G^{-1}$ and extend $F$ to all of ℝ by $F(x) = 0$ for $x \le L$ and $F(x) = 1$ for $x \ge R$. Note that we can compute the derivative as

$$ F'(x) = \frac{1}{G' \circ G^{-1}(x)} = \hat{H}\big( F(x) \big) \qquad \mbox{for all } x \in\mathbb{R} . $$

Setting $f= F'$, we have $\hat{H} = f \circ F^{-1}$. Since $\hat{H}$ is concave, Bobkov’s result in Proposition 3.6 implies that $f$ is log-concave. □

Remark 5.4

An earlier study of the translation equation without the concavity assumption can be found in the book of Aczél [1, Chap. 6.1].

5.2 Infinitesimal generators and the inf-convolution

In this section, we briefly and informally discuss the connection between the binary operation • defined in Sect. 2.3 and the well-known inf-convolution $\square$.

Let $f$ be a log-concave density with distribution function $F$ and set

$$ \hat{C}(p, y) = F\big( F^{-1}(p) + y\big) \qquad \mbox{for all } 0 \le p \le1, y \ge0. $$

The content of Theorem 3.11 is that aside from the trivial and null semigroups, the only sub-semigroups of $\hat{\mathcal {C}}$ with respect to composition are of the above form. The infinitesimal generator is given by

$$ \frac{\partial}{\partial y} \hat{C}(p, y) \bigg|_{y=0} = \hat{H}(p) \qquad \mbox{for all } 0 \le p \le1, $$

where $\hat{H} = f \circ F^{-1}$ and we have taken the version of $f$ which is continuous on its support $[L,R]$. Note that this equation also holds for the trivial sub-semigroup $(\hat{C}_{\mathrm {triv}}(\cdot, y))_{y \ge0}$ with the function $\hat{H} = 0$, where $\hat{C}_{\mathrm{triv}}(p, y) = p$ for all $0 \le p \le1$ and $y \ge0$.

The key property of the function $\hat{H}$ is that it is nonnegative and concave. Let

$$ \hat{ \mathcal {H}} = \{ h:[0,1] \to[0,\infty): \mbox{$h$ is concave} \}. $$

Note that for every element of $\hat{\mathcal{H}}$, aside from $\hat{H}=0$, one can assign a unique (up to centring) log-concave density $f$ by the discussion of Sect. 4.1.

The space $\hat{\mathcal {H}}$ is closed under addition. Furthermore, we have for every non-null one-parameter sub-semigroup $(\hat{C}(\cdot, y))_{y \ge0}$ of $\hat{ \mathcal {C}}$ that

$$ \hat{C}(p, \varepsilon) \approx p + \varepsilon\hat{H}(p) \qquad \mbox{for small } \varepsilon> 0 $$

for some $\hat{H} \in\hat{\mathcal{H}}$. Let $(\hat{C}_{1}(\cdot,y))_{y \ge0}$ and $(\hat{C}_{2}(\cdot, y))_{y \ge0}$ be two such sub-semigroups. Note that

$$\begin{aligned} \hat{C}_{1}\big(\hat{C}_{2}(p, \varepsilon), \varepsilon\big) & \approx p + \varepsilon\big(\hat{H}_{1}(p) + \hat{H}_{2}(p) \big), \end{aligned}$$

implying that function composition near the identity element of $\hat {\mathcal {C}}$ amounts to addition in the space of generators $\hat{ \mathcal {H}}$.

Similarly, let

$$ \mathcal {H} = \{ H: \mathbb{R} \to[0,\infty): \mbox{$H$ is convex with $0 \le H(x) - (-x)^{+} \le\hbox{const.}$\}}. $$

For $H \in\mathcal {H}$, let

$$ \hat{H}(p) = \inf_{x \in\mathbb{R} } \big(H(x) + xp \big) \qquad \mbox{for } 0 \le p \le1. $$

One can check that $\hat{ \ }$ is a bijection between the sets ℋ and $\hat{\mathcal {H}}$ by a version of the Fenchel biconjugation theorem. In particular, the space ℋ can be identified with the generators of one-parameter semigroups in ${\mathcal {C}}$.

Recall that the inf-convolution of two functions $f_{1}, f_{2}: \mathbb {R} \to\mathbb{R}$ is defined by

$$ (f_{1} \square f_{2})(x) = \inf_{y \in\mathbb{R} } \big( f_{1}(x-y) + f_{2}(y) \big) \qquad \mbox{for } x \in\mathbb{R} . $$

The basic property of the inf-convolution (see for example [5, Exercise 2.3.15]) is that it becomes addition under conjugation, i.e.,

$$\begin{aligned} \widehat{f_{1} \square f_{2}}(p) &= \inf_{x \in\mathbb{R} } \inf_{y \in\mathbb{R} } \big( f_{1}(x-y) + f_{2}(y) + xp \big) \\ & = \inf_{z \in\mathbb{R} } \big( f_{1}(z) + zp \big) + \inf_{y \in \mathbb{R} } \big( f_{2}(y) + yp \big) \\ & = \hat{f}_{1}(p) + \hat{f}_{2}(p), \end{aligned}$$

in analogy with Theorem 5.3. Since there is an exponential map lifting function addition + to function composition ∘ in $\hat{\mathcal {C}}$, we can apply the isomorphism $\hat{ \ }$ to conclude that there is an exponential map lifting inf-convolution $\square$ to the binary operation • in $\mathcal {C}$. Indeed, let $(C(\cdot, y))_{y \ge0}$ be a one-parameter sub-semigroup of $\mathcal {C}$ with generator $H$ so that

$$ C(e^{\varepsilon x}, \varepsilon) \approx\varepsilon H(x) \qquad \mbox{for small } \varepsilon> 0. $$

Letting $(C_{1}(\cdot, y))_{y \ge0}$ and $(C_{2}(\cdot, y))_{y \ge 0}$ be two such sub-semigroups, we have

$$ C_{1}( \cdot, \varepsilon) \bullet C_{2}( \cdot, \varepsilon )(e^{\varepsilon x}) \approx \varepsilon \inf_{y} \big( H_{1}(y) + e^{\varepsilon y}H_{2}(x-y)\big) \approx\varepsilon H_{1} \square H_{2}(x) $$

5.3 Lift zonoids

Finally, to see why one might want to compute the Legendre transform of a call price with respect to the strike parameter, we recall that the zonoid of an integrable random $d$-vector $X$ is the set

$$ Z_{X} = \{ \mathbb{E} [X g(X) ] : g:\mathbb{R} ^{d} \to[0,1] \mbox{ is measurable}\} \subseteq\mathbb{R} ^{d}, $$

and the lift zonoid of $X$ is the zonoid of the $(1+d)$-vector $(1,X)$, hence given by

$$\begin{aligned} \hat{Z}_{X} &= \big\{ \big( \mathbb{E} [g(X)], \mathbb{E} [ X g(X) ] \big): g:\mathbb{R} ^{d} \to[0,1] \mbox{ is measurable} \big\} \subseteq \mathbb{R} ^{1+d}. \end{aligned}$$

The notion of lift zonoid was introduced in the paper of Koshevoy and Mosler [25, Definition 3.1].

In the case $d=1$, the lift zonoid $\hat{Z}_{X}$ is a convex set contained in the rectangle $[0,1] \times[-m_{-}, m_{+} ]$, where $m_{\pm} = \mathbb{E} [ X^{\pm}]$. The precise shape of this set is intimately related to call and put prices as seen in the following theorem.

Theorem 5.5

Let$X$be an integrable random variable. Its lift zonoid$\hat{Z}_{X}$is given by

$$ \left\{ (p, q): \sup_{x \in\mathbb{R} }\big( px - \mathbb{E} [ (x-X)^{+} ] \big) \le q \le\inf_{x \in\mathbb{R} } \big( px + \mathbb{E} [ (X-x)^{+} ] \big), \ \ 0 \le p \le1 \right\}. $$

Note that if we let

$$ \Theta(x) = \mathbb{P} [X \ge x], $$

then we have

$$ \mathbb{E} [ (X-x)^{+} ] = \int_{x}^{\infty} \Theta(\xi) d\xi $$

by Fubini’s theorem. Also, if we define the inverse function $\Theta^{-1}$ for $0 < p < 1$ by

$$ \Theta^{-1}(p) = \inf\{ x: \Theta(x) \ge p \}, $$

then by a result of Koshevoy and Mosler [25, Lemma 3.1], we have

$$ \hat{Z}_{X}= \left\{ (p, q): \int_{1-p}^{1} \Theta^{-1}(\phi) d\phi \le q \le \int_{0}^{p} \Theta^{-1}(\phi) d\phi, \ \ 0 \le p \le1 \right\}, $$

from which Theorem 5.5 can be proved by Young’s inequality. However, since the result can be viewed as an application of the Neyman–Pearson lemma, we include a short proof for completeness.

Proof of Theorem 5.5

First, fix a point $(p,q) \in\hat{Z}_{X}$. This means that there is a measurable function $g$ valued in $[0,1]$ such that $p = \mathbb{E}[g(X)]$ and $q= \mathbb{E}[X g(X)]$. Since the almost sure inequality

$$ X g(X) \le x g(X) + (X-x)^{+} $$

holds for all $x$, we have

$$ q \le \inf_{x} \big( xp + \mathbb{E}[ (X-x)^{+}] \big). $$

Similarly, we have the inequality

$$ X g(X) \ge x g(X) - (x-X)^{+} $$

and hence

$$ q \ge \sup_{x} \big( xp - \mathbb{E}[ (x-X)^{+}] \big). $$

We now show that if $0\le p \le1$ and

$$ \sup_{x}\big( xp + \mathbb{E}[(x-X)^{+}] \big) \le q \le \inf_{x} \big( xp + \mathbb{E}[ (X-x)^{+}] \big), $$

then $(p,q) \in\hat{Z}_{X}$. Since the lift zonoid $\hat{Z}_{X}$ is clearly convex, it is sufficient to show that $q$ can attain the upper and lower bounds for fixed $p$. Fix $p \in[0,1]$. There exists an $x$ such that

$$ \mathbb{P}[X > x] \le p \le\mathbb{P}[X \ge x]. $$

For this choice of $x$, there exists a $\theta\in[0,1]$ such that

$$ p = \theta\mathbb{P}[X > x] + (1-\theta) \mathbb{P}[X \ge x]. $$

Note that then $p = \mathbb{E}[g(X)]$, where

Since for this choice of $g$, we have the almost sure equality

$$ X g(X) = x g(x) + (X-x)^{+}, $$

computing expectations on both sides shows that the upper bound is attained, i.e.,

$$ q = \mathbb{E}[X g(X)] = xp + \mathbb{E}[ (X-x)^{+}]. $$

That the lower bound is also attained follows from a similar calculation. □

We remark that the explicit connection between lift zonoids and the price of call options has been noted before, for instance in the paper of Molchanov and Schmutz [29, proof of Theorem 2.1]. In the setting of the present paper, given $C \in\mathcal {C}$ represented by $S$, the lift zonoid of $S$ is given by the set

$$ \hat{Z}_{S} = \{ (p,q) : 1 - \hat{C}(1-p) \le q \le\mathbb{E} [S] -1 + \hat{C}(p), 0 \le p \le1 \}. $$

We recall that a random vector $X_{1}$ is dominated by $X_{2}$ in the lift zonoid order if $\hat{Z}_{X_{1}} \subseteq\hat{Z}_{X_{2}}$. Koshevoy and Mosler [25, Theorem 5.2] noticed that in the case $d=1$, the lift zonoid order is exactly the convex order.

We conclude this section by exploiting Theorem 5.5 to obtain an interesting identity. A similar formula can be found in the paper of Hiriart-Urruty and Martínez-Legaz [18, Theorem 2].

Theorem 5.6

Given$C \in\mathcal {C}$, let

$$ \hat{C}^{-1}(q) = \inf\{ p \ge0: \hat{C}(p) \ge q \} \qquad \textit{for all } 0 \le q \le1. $$

Then

$$ \widehat{ C^{\star}} (p ) = 1 - \hat{C}^{-1}(1-p) \qquad \textit{for all } 0 \le p \le1. $$

Proof

Let $S$ be a primal representation and $S^{\star}$ a dual representation of $C$. Note that for all $0 \le p\le1$, we have

$$ \hat{C}(p) - \hat{C}(0) = \sup\{ \mathbb{E} [ S g(S)] : g:\mathbb{R} \to[0,1] \mbox{ with } \mathbb{E} [g(S) ] = p \}, $$

and hence for any $0 \le q \le1$, we have

where we have used the observation that the optimal $g$ in the final maximisation problem assigns zero weight to the event $\{ S^{\star}= 0 \}$. □

5.4 An extension

Let $F$ be the distribution function of a log-concave density $f$ which is supported on all of ℝ, so that $L=-\infty$ and $R = + \infty$ in the notation of Sect. 3.2. Let

$$ \hat{C}_{f}(p,y) = F\big( F^{-1}(p) + y \big) \qquad \mbox{for all } 0 \le p \le1, y \in\mathbb{R} . $$

By Theorem 4.2, we have

$$ \hat{C}_{f}(p,y) = \widehat{C_{f}(\cdot, y)}(p) \qquad \mbox{for all } 0 \le p \le1, y \ge0. $$

It is interesting to note that the family of functions $\hat{C}_{f}(\cdot,y)$ indexed by $y \in\mathbb{R}$ is a group under function composition, not just a semigroup. Indeed, we have

$$ \hat{C}_{f}(\cdot,-y) = \hat{C}_{f}(\cdot,y)^{-1} \qquad \mbox{for all } y \in\mathbb{R} . $$

Note that $\hat{C}_{f}(\cdot,y)$ is increasing for all $y$, is concave if $y \ge0$, but is convex if $y < 0$. In particular, when $y<0$, the function $\hat{C}_{f}(\cdot,y)$ is not the concave conjugate of a call function in $\mathcal {C}$. Unfortunately, the probabilistic or financial interpretation of the inverse is not readily apparent.

For comparison, note that for $y \ge0$, we have by Theorem 5.6 that

$$ \widehat{C_{f}(\cdot, -y)}(p) = \widehat{C_{f}(\cdot, y)^{\star}}(p) = 1 - F\big( F^{-1}(1-p) -y \big) \qquad \mbox{for all } 0 \le p \le1. $$