Nonlinear active control of thermally induced pyro-coupled vibrations in porous-agglomerated CNT core sandwich plate with magneto-piezo-elastic facings

Abstract

In this article, the damped nonlinear transient response of a smart sandwich plate (SSP) comprising of agglomerated CNT-reinforced porous nanocomposite core with multifunctional magneto-piezo-elastic (MPE) facesheets, subjected to the thermal environment, is numerically investigated. The synergistic influence of agglomeration, porosity and pyro-coupling on vibration control is studied for the first time under the finite element framework. The attenuation of the vibrations is caused by active constrained layer damping (ACLD) treatment. The kinematics of the plate is based on the layer-wise shear deformation theory and von-Karman’s nonlinearity. The viscoelastic properties of the ACLD patch and CNT agglomeration of the core are mathematically modelled using Golla–Hughes–McTavish and Eshelby–Mori–Tanaka methods, respectively. A comprehensive examination of the inter-related effects of different agglomeration states, porosity distributions and thermal loading profiles has been performed. The new insights on controlling pyro-coupled induced vibrations of smart sandwich plates by supplying control voltage directly to the MPE facesheets without ACLD treatment have been discussed thoroughly. The numerical analysis confirms the significant effects of pyro-coupling associated with active vibration control response of SSP.

1 Introduction

In the modern era, composite structures are being extensively used for various engineering applications ranging from civil to aerospace, owing to their flexibility and tailorability. The probability that these structures are exposed to hazardous environmental conditions is significantly high, drastically influencing the material properties [1] and the structural responses [2]. To this end, numerous researchers have explored the hygrothermal (HT) effects on the various structural responses of hybrid and natural composites. Based on the finite strip method, the effect of the HT environment on the frequency and stability performance of composite plates was studied by Amoushahi and Goodarzian [3]. Tang and Dai [4] analytically assessed the nonlinear vibrations of composite plates with CNTs exposed to HT conditions. The effect of porosity associated with the HT environment on the coupled bending response of piezoelectric sandwich shells was investigated by Sobhy and Radwan [5]. Similarly, Wang et al. [6] investigated the buckling behaviour of HT-loaded bi-directional porous structures. Li et al. simulated the influence of HT environment on their dynamic behaviour for rotating structures like wind blades, helicopter rotors, etc. [7]. Zenkour and El-Shahrany [8] studied the HT effect on the vibration of magnetostrictive laminates. Panda et al. [9] experimentally investigated the effect of HT loads associated with delamination on the frequency response of composite plates. Natarajan et al. [10] probed the cut-out effects on the HT-loaded composite plate's frequency using the spatial discretisation method. Gupta et al. [11] investigated the static and dynamic response of composite plates using the non-uniform rational B-splines technique.

Engineering structures are always prone to undesired vibrations threatening their operating and service life. Eliminating or reducing the vibrations is crucial for the structures' optimum performance [12,13,14,15,16,17]. Several researchers have worked on different methodologies to suppress/attenuate the vibrations. Among them, the active vibration control (AVC) strategy is effective for low-frequency mitigation [18]. AVC predominantly use active constrained layer damping (ACLD) treatment wherein piezoelectric (PE) and viscoelastic (VE) patches are attached to the host structures, and a control voltage proportional to the displacement of the plate is fed to these layers. Song et al. [19] exploited the benefits of higher-order shear deformation theory (HSDT) and assessed the suppression capability of AVC on the functionally graded (FG) carbon nanotube (CNT) reinforced plates. Selim et al. [20] proposed a mathematical model using HSDT and investigated the AVC response of FG plates integrated with PE layers. The influence of uniform and non-uniform electric fields on the AVC response of the FG-PE plate was investigated by Li et al. [21]. Considering a thin Aluminium plate, the influence of AVC on damped response was experimentally demonstrated by Lu et al. [22]. The AVC effect on the structural response of the PE plate with all sides clamped was probed by Li et al. [23] using a disturbance rejection controller. Ly et al. [24] employed the zig-zag theory and examined the damped response of CNT plates subjected to AVC treatment. Zhao et al. [25] experimentally investigated the influence of using an MRE core on the semi-AVC response of a sandwich plate. Jiang et al. [26] explored the benefits of ACLD and attempted to reduce the vibrations of the rotating hub plate. Balasubramanian et al. [27] experimentally demonstrated the AVC of an electro-mechanically coupled sandwich plate.

Smart materials such as PE are extremely used in many vibration control applications [28,29,30]. Very recently, a new category of smart material which responds to both electric and magnetic fields, known as magneto-piezo-elastic (MPE) composites, is gaining much attention from researchers due to its enhanced coupling features [31]. Apart from their conventional structural applications [13, 32,33,34,35,36,37,38,39], their usage in AVC is well-established in the open literature. Kattimani and Ray, for the first time, demonstrated the controlled response of MPE structures [40, 41] subjected to the ACLD treatment. Further, Vinyas [42, 43] demonstrated the damping response of skewed MPE plates with different control parameters. Mahesh [44, 45] investigated the influence of CNT agglomeration on the AVC of ACLD-treated MPE sandwich plates and shells. The effect of PE and piezomagnetic (PM) interphases on the attenuated vibration response of MPE plates was mathematically examined by Vinyas [46]. Similarly, considering the fibrous MPE composites, the effect of ACLD on the controlled structural behaviour of the smart plate was studied by Mahesh and Kattimani [47].

More importantly, when operated in the thermal environment, the MPE materials display an extra coupling between magnetic-thermal, electric-thermal, and elastic-thermal fields. This leads to the 'pyro-coupling' effect, which significantly alters the structural response of MPE composites. The pyro-coupling generates an additional load on the structure, enhancing the electric and magnetic potentials generated by MPE composites. Vinyas and Kattimani [48, 49] designed a new form of MPE structure known as stepped-FG (SFG). They investigated the bending response of MPE composites when exposed to different thermal loading conditions. They observed that the multifunctional capabilities of SFG structures were better than the conventional layered MPE structures. Considering pyro-coupling effects, the static performance of multiphase MPE beams was assessed by Vinyas and Kattimani [50]. On the same grounds, the nonlinear-bending and vibration behaviour of CNT-reinforced MPE shells [51, 52] and plates [53] were investigated by Mahesh. By considering the synergistic influence of thermal and blast loads, the transient response of MPE structures was studied by Mahesh et al. [54, 55] through a finite element (FE) framework. The effect of auxetic cores on the degree of MPE composite’s pyro-coupling was analysed by Mahesh [56]. Mahesh and team recently demonstrated the advantages of predictive tools such as artificial neural networks (ANN) in comparing the structural behaviour of MPE composites with and without pyro-coupling [57, 58].

To the author’s best knowledge, no work has been reported on evaluating the thermally induced nonlinear damped response of smart sandwich plates with agglomerated CNT porous core with MPE facesheets. Hence, as a first endeavour, the author has attempted to address this problem by developing a multiscale mathematical model within the framework of finite element methods. Also, the synergistic influence of agglomeration, porosity, and pyro-coupling on the active control response of sandwich plates has been dealt with for the first time in the literature. Various temperature profiles, agglomeration states, porosity patterns and volume fractions have been considered for assessment. The governing equations are obtained through Hamilton's principle in conjunction with layer-wise shear deformation theory (LSDT) and von-Karman's nonlinearity.

2 Problem description

In this research, three forms of temperature profiles are assumed to be acting on the smart sandwich plate (SSP) embedded with an ACLD patch. The details are encapsulated as follows [57]:

Linear temperature rise (LTR: HT-LB):

$$\begin{gathered} T(z) = \left( {T_{ts} - T_{bs} } \right)\left\{ {\frac{z}{h} + \frac{1}{2}} \right\} + T_{bs} \hfill \\ T_{ts} = \, 400\;{\text{K}}\;{\text{and}}\;T_{bs} = \, 300\;{\text{K}} \hfill \\ \end{gathered}$$

(1a)

Linear temperature rise (LTR: LT-HB):

$$\begin{gathered} T(z) = \left( {T_{bs} - T_{ts} } \right)\left\{ {\frac{z}{h} + \frac{1}{2}} \right\} + T_{ts} \hfill \\ T_{bs} = \, 400\;{\text{K}}\;{\text{and}}\;T_{ts} = \, 300\;{\text{K}} \hfill \\ \end{gathered}$$

(1b)

Uniform temperature rise (UTR)

$$T(z) = \Delta T = { 3}00\;{\text{K}}$$

(1c)

T_ts and T_bs are the temperatures at the top and bottom surfaces.

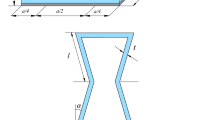
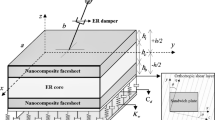
The core of the SSP is made of nanocomposite with agglomerated CNTs and pores. The facesheets of SSP are of MPE material with a 50% volume fraction each of the Barium Titanate (piezoelectric) and Cobalt Ferrite (piezomagnetic) phases. Further, the MPE material in this study belongs to 2–2 laminate composite category and can be fabricated using chemical vapour deposition, atomic layer deposition (ALD), sputtering, or laser ablation [59, 60]. The dimensions of the SSP considered, such as side length (a), width (b), overall thickness (h), core thickness (h_c) and facesheet thickness (h_fs), are represented in Fig. 1a. The ACLD patch embedded on the top of SSP comprises 1–3 PZC and viscoelastic layers whose thickness are denoted by h_p and h_v, respectively. The coordinates of the bottom (h₁) and top (h₂) layers of the bottom MPE facesheet, bottom (h₃) and top (h₄) layers of the top MPE facesheet, the bottom (h₅) and top (h₆) layers of 1–3 PZC layer are also shown in Fig. 1a. Table 1 shows the material properties of MPE facesheets, 1–3 PZC layer, while Table 2 depicts the properties of the polymer matrix and CNTs used in this work.

Fig. 1

Geometric representation of a SSP b RVE of agglomerated CNT porous core

Table 1 Material properties of MEE material and the piezoelectric patch of ACLD [41]

Table 2 Material properties of polymer material and CNT [62]

3 Materials and methods

Figure 1b shows the representative volume element (RVE) of the ACNT core. Further, using Eshelby-Mori–Tanaka (EMT) equations, it can be shown that [59]

$$V^{r} = V_{{{\text{incl}}}}^{r} + V_{m}^{r}$$

(2)

where, ${V}^{r}$ is the volume of CNTs existing inside the RVE, ${V}_{m}^{r}$ is the volume of the matrix, and ${V}_{\text{incl}}^{r}$ denotes the volume fraction of CNTs inside the agglomeration.

The agglomeration parameters μ and η are expressed as,

$$\mu = \frac{{V_{{{\text{incl}}}} }}{V};\eta = \frac{{V_{{{\text{incl}}}}^{r} }}{{V^{r} }};f_{r} = \frac{{V_{{}}^{r} }}{V}$$

(3)

Meanwhile, the shear and bulk modulus of the regions inside and outside (represented by subscripts 'in' and 'out', respectively) of the agglomeration can be represented as

$$\begin{aligned} K_{{{\text{in}}}} & = K_{m} + \frac{{\left( {\delta_{r} - 3K_{m} \alpha_{r} } \right)f_{r} \eta }}{{3\left( {\mu - f_{r} \eta \left( {1 - \alpha_{r} } \right)} \right)}} \\ K_{{{\text{out}}}}& = K_{m} + \frac{{\left( {\delta_{r} - 3K_{m} \alpha_{r} } \right)f_{r} \left( {1 - \eta } \right)}}{{3\left[ {1 - \mu - f\left( {1 - \eta } \right) + \left( {1 - \eta } \right)f_{r} \alpha_{r} } \right]}} \\ G_{{{\text{in}}}} &= G_{m} + \frac{{\left( {\eta_{r} - 3G_{m} \beta_{r} } \right)f_{r} \eta }}{{2\left( {\mu - f_{r} \eta \left( {1 - \beta_{r} } \right)} \right)}} \\ G_{{{\text{out}}}} &= G_{m} + \frac{{\left( {\eta_{r} - 2G_{m} \beta_{r} } \right)f_{r} \left( {1 - \eta } \right)}}{{2\left[ {1 - \mu - f_{r} \left( {1 - \eta } \right) + f_{r} \left( {1 - \eta } \right)\beta_{r} } \right]}} \\ \end{aligned}$$

(4)

here, the sub-script 'm' denotes the matrix, and

$$\begin{aligned} \alpha_{r} = \; & \frac{{k_{r} - l_{r} + 3\left( {K_{m} + G_{m} } \right)}}{{3\left( {K_{m} + k_{r} } \right)}} \\ \beta_{r} = \; & \frac{1}{5}\left\{ {\frac{{4G_{m} + 2k_{r} + l_{r} }}{{3\left( {G_{m} + k_{r} } \right)}} + \frac{{4G_{m} }}{{G_{m} + p_{r} }} + \frac{{2\left[ {G_{m} \left( {3K_{m} + G_{m} } \right) + G_{m} \left( {3K_{m} + 7G_{m} } \right)} \right]}}{{G_{m} \left( {3K_{m} + G_{m} } \right) + m_{r} \left( {3K_{m} + 7G_{m} } \right)}}} \right\} \\ \delta_{r} = \; & \frac{1}{3}\left[ {\eta_{r} + 2l_{r} + \frac{{\left( {2k_{r} + l_{r} } \right)\left( {3K_{m} + G_{m} - l_{r} } \right)}}{{G_{m} + k_{r} }}} \right] \\ \eta_{r} = \; & \frac{1}{5}\left[ {\frac{2}{3}\left( {\eta_{r} - l_{r} } \right) + \frac{{8G_{m} p_{r} }}{{G_{m} + p_{r} }} + \frac{{8m_{r} G_{m} \left( {3K_{m} + 4G_{m} } \right)}}{{3K_{m} \left( {G_{m} + p_{r} } \right) + G_{m} \left( {7m_{r} + G_{m} } \right)}} + \frac{{2\left( {k_{r} - l_{r} } \right)\left( {2G_{m} + l_{r} } \right)}}{{3(G_{m} + k_{r} )}}} \right] \\ \end{aligned}$$

(5)

In the next step, the composite's effective bulk (K) and shear moduli (G) are obtained using Eqs. (4) and (5):

$K = K_{\text{out}} \left[ {1 + \frac{{\mu \left( {\frac{{K_{in} }}{{K_{\text{out}} }} - 1} \right)}}{{1 + \alpha \left( {1 - \mu } \right)\left( {\frac{{K_{in} }}{{K_{\text{out}} }} - 1} \right)}}} \right]$; $G = G_{\text{out}} \left[ {1 + \frac{{\mu \left( {\frac{{G_{in} }}{{G_{\text{out}} }} - 1} \right)}}{{1 + \beta \left( {1 - \mu } \right)\left( {\frac{{G_{in} }}{{G_{\text{out}} }} - 1} \right)}}} \right]$.

here,

$$\nu_{\text{out}} = \frac{{\left( {3K_{{{\text{out}}}} - 2G_{{{\text{out}}}} } \right)}}{{2\left( {3K_{{{\text{out}}}} + 2G_{{{\text{out}}}} } \right)}};\quad \alpha = \frac{{1 + \nu_{{{\text{out}}}} }}{{3\left( {1 - \nu_{{{\text{out}}}} } \right)}};\quad \beta = \frac{{2\left( {4 - 5\nu_{\text{out}} } \right)}}{{15\left( {1 - \nu_{\text{out}} } \right)}}$$

(6)

With further simplification, it can be shown that

$$E = \frac{9KG}{{3K + G}};\nu = \frac{3K - 2G}{{6K + 2G}}$$

(7)

where ‘E’ and ‘ν’ is the agglomerated nanocomposite’s effective elastic modulus and Poisson’s ratio.

Using Voigt’s rule, the effective mass density ($\rho$) can be calculated as:

$$\rho = f_{r} \rho_{r} + f_{m} \rho_{m}$$

(8)

where, the sub-scripts ‘r’ and ‘m’ are associated with CNTs and matrix, respectively. Further, ‘f’ and ‘ρ’ denote volume fractions and densities of the corresponding phases. Meanwhile, for an ACNT core, the coefficient of thermal expansion (COTE) can be written as [61, 62]

$$\alpha = \frac{{\left[ {E + 4\nu \left( {1 + \nu } \right)K} \right]\alpha_{11} + 4\left( {1 + \nu } \right)K\alpha_{22} }}{{E + 4\left( {1 + \nu } \right)^{2} K}}$$

(9)

in which,

$$\begin{gathered} \alpha_{11} = \frac{{f_{r} E_{11}^{CNT} \alpha_{{_{11} }}^{CNT} + f_{m} E_{m} \alpha_{m} }}{{f_{r} E_{11}^{CNT} + f_{m} E_{m} }} \hfill \\ \alpha_{22} = \left( {1 + \nu_{CNT} } \right)f_{r} \alpha_{{_{22} }}^{CNT} + \left( {1 + \nu_{m} } \right)f_{r} \alpha_{m} - \nu \alpha_{11} \hfill \\ \end{gathered}$$

(10)

The Young’s modulus (E^c) and density (ρ^c) of the various forms (UD, FG-S and FG-NS) of ACNT-P cores can be explicitly represented as [63],

$$\begin{gathered} {\text{FG-S}}:E^{c} = \left( {1 - \lambda_{o} \cos \left( {\pi z/h_{c} } \right)} \right)E;\rho^{c} = \left( {1 - \left( {1 - \sqrt {1 - \lambda_{o} } } \right)\cos \left( {\pi z/h_{c} } \right)} \right)\rho \hfill \\ {\text{FG-NS}}:E^{c} = \left( {1 - \lambda_{o} \cos \left( {{\raise0.7ex\hbox{${\pi z}$} \!\mathord{\left/ {\vphantom {{\pi z} {2h_{c} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${2h_{c} }$}} + {\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi 4}}\right.\kern-0pt} \!\lower0.7ex\hbox{$4$}}} \right)} \right)E;\rho^{c} = \left( {1 - \left( {1 - \sqrt {1 - \lambda_{o} } } \right)\cos \left( {{\raise0.7ex\hbox{${\pi z}$} \!\mathord{\left/ {\vphantom {{\pi z} {2h_{c} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${2h_{c} }$}} + {\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi 4}}\right.\kern-0pt} \!\lower0.7ex\hbox{$4$}}} \right)} \right)\rho \hfill \\ {\text{UD}}:E^{c} = \left( {\frac{2}{\pi }\sqrt {1 - \lambda_{o} } - \frac{2}{\pi } + 1} \right)^{2} E;\rho^{c} = \left( {\frac{2}{\pi }\sqrt {1 - \lambda_{o} } - \frac{2}{\pi } + 1} \right)^{2} \rho \hfill \\ \end{gathered}$$

(11)

here, λ_ο is the porosity volume, and E is Young’s modulus of agglomerated CNT. Further, the Poisson’s ratio of the core (ν^c) can be written as [63],

$$\nu^{c} = 0.221\left( {1 - \frac{{\rho^{c} }}{\rho }} \right) + \nu \left( {0.342\left( {1 - \frac{{\rho^{c} }}{\rho }} \right)^{2} - 1.21\left( {1 - \frac{{\rho^{c} }}{\rho }} \right) + 1} \right)$$

(12)

Further, this study assumes that the COTE of ACNT-P core varies similarly to E^c.

The constitutive relation of the MPE facesheets can be expressed as follows [49]:

$$\begin{gathered} \left\{ \sigma \right\} = \left[ Q \right]\left\{ \varepsilon \right\} - \left[ e \right]\left\{ E \right\} - \left[ q \right]\left\{ H \right\} - \left[ Q \right]\left[ \alpha \right]\Delta T \hfill \\ \left\{ D \right\} = \left[ e \right]^{T} \left\{ \varepsilon \right\} + \left[ \eta \right]\left\{ E \right\} + \left[ m \right]\left\{ H \right\} + \left[ p \right]\Delta T \hfill \\ \left\{ B \right\} = \left[ q \right]^{T} \left\{ \varepsilon \right\} + \left[ m \right]\left\{ E \right\} + \left[ \mu \right]\left\{ H \right\} + \left[ \tau \right]\Delta T \hfill \\ \end{gathered}$$

(13)

Also, the constitutive relations of bending $\left\{{\sigma }_{b}^{p}\right\}$ and shear stress $\left\{{\sigma }_{s}^{p}\right\}$ vectors of the ACLD’s 1–3 PZC are expressed as [41]:

$$\begin{gathered} \left\{ {\sigma_{b}^{p} } \right\} = \left[ {Q_{b}^{p} } \right]\left\{ {\varepsilon_{b}^{p} } \right\} - \left[ {Q_{bs}^{p} } \right]\left\{ {\varepsilon_{s}^{p} } \right\} - \left\{ {\overline{e}_{b}^{p} } \right\}E_{z} \hfill \\ \left\{ {\sigma_{s}^{p} } \right\} = \left[ {Q_{bs}^{p} } \right]^{T} \left\{ {\varepsilon_{b}^{p} } \right\} + \left[ {Q_{s}^{p} } \right]\left\{ {\varepsilon_{s}^{p} } \right\} - \left\{ {\overline{e}_{b}^{p} } \right\}E_{z} \hfill \\ D_{z}^{p} = \left\{ {\overline{e}_{b}^{p} } \right\}^{T} \left\{ {\varepsilon_{b}^{p} } \right\} + \left\{ {\overline{e}_{s}^{p} } \right\}^{T} \left\{ {\varepsilon_{s}^{p} } \right\} + \overline{ \in }_{33}^{p} E_{z}^{p} \hfill \\ \end{gathered}$$

(14)

Exploiting the Golla-Hughes-McTavish (GHM) method, the shear stress of the ACLD patch’s viscoelastic layer is represented as [41]:

$$\left( {\sigma_{{\text{s}}} } \right)_{{\text{v}}} = \int\limits_{0}^{t} {G\left( {t - \tau } \right)} \frac{{\partial \left( {\varepsilon_{{\text{s}}}^{{\text{k}}} } \right)}}{\partial \tau }\partial \tau$$

(15)

4 Formulation

In order to assess laminated composite structures, various computational theories have been proposed by numerous researchers. Among them, 3D elasticity theory (3D-ET), equivalent single-layer (ESL) theories, zig-zag theories and layerwise theories are considered to be prominent. However, 3D-ET demands high computational efforts, ESL fails to accurately simulate thick structures or structures with distinct layer properties and zig-zag models cannot directly obtain the transverse stresses from the constitutive models. To this end, layerwise theories prove to be handy as it considers each layer individually for assessment. As a result, the accuracy of simulation is on par with 3D elasticity solutions and C0 continuity is satisfied [64]. These advantages exhibited by the layerwise theories motivated the authors to adopt the LSDT for the current study. The displacement components u, v and w of the SSP are assumed to vary in the x-, y- and z- directions, respectively, based on LSDT, whose mathematical expressions can be written using the mid-plane displacement components u0, v0 and w0 as [41],

$$\begin{gathered} u = u_{0} + \left( {z - \left\langle {z - \frac{h}{2}} \right\rangle } \right)\theta_{x} + \left( {\left\langle {z - \frac{h}{2}} \right\rangle - \left\langle {z - h_{{\text{N + 2}}} } \right\rangle } \right)\kappa_{x} + \left\langle {z - h_{{\text{N + 2}}} } \right\rangle \gamma_{x} \hfill \\ v = v_{0} + \left( {z - \left\langle {z - \frac{h}{2}} \right\rangle } \right)\theta_{y} + \left( {\left\langle {z - \frac{h}{2}} \right\rangle - \left\langle {z - h_{{\text{N + 2}}} } \right\rangle } \right)\kappa_{y} + \left\langle {z - h_{{\text{N + 2}}} } \right\rangle \gamma_{y} \hfill \\ \end{gathered}$$

(16a)

To achieve the parabolic distribution of transverse shear stress across the thickness of each layer and to utilize the vertical actuation by the active constraining layer of the ACLD treatment, the transverse displacement has been assumed for the overall plate as follows

$$w = w_{0} + z\theta_{z} + z^{2} \kappa_{z}$$

(16b)

where, the rotational degrees of freedom about the normal to mid-plane of the SSP, ACLD's viscoelastic and 1–3 PZC are θ_x, κ_x and γ_x, respectively. Similarly, the corresponding rotations about the x-axis are shown as θ_y, κ_y and γ_y.

The nonlinear strains of the actively controlled SSP are written as:

$$\begin{gathered} \left\{ {\varepsilon_{{\text{b}}}^{{}} } \right\} = \left\{ {\varepsilon_{{{\text{bt}}}} } \right\} + \left[ {Z_{1} } \right]\left\{ {\varepsilon_{{{\text{rb}}}} } \right\} + \left\{ {\varepsilon_{{{\text{bt\_NL}}}} } \right\} \hfill \\ \left\{ {\varepsilon_{{\text{b}}}^{{\text{P}}} } \right\} = \left\{ {\varepsilon_{{{\text{bt}}}} } \right\} + \left[ {Z_{2} } \right]\left\{ {\varepsilon_{{{\text{rb}}}} } \right\} + \left\{ {\varepsilon_{{{\text{bt\_NL}}}} } \right\} \hfill \\ \left\{ {\varepsilon_{{\text{s}}}^{{}} } \right\} = \left\{ {\varepsilon_{{{\text{ts}}}} } \right\} + \left[ {Z_{3} } \right]\left\{ {\varepsilon_{{{\text{rs}}}} } \right\} \hfill \\ \left\{ {\varepsilon_{{\text{s}}}^{{{\text{Vis}}}} } \right\} = \left\{ {\varepsilon_{{{\text{ts}}}} } \right\} + \left[ {Z_{4} } \right]\left\{ {\varepsilon_{{{\text{rs}}}} } \right\} \hfill \\ \left\{ {\varepsilon_{{\text{s}}}^{{\text{P}}} } \right\} = \left\{ {\varepsilon_{{{\text{ts}}}} } \right\} + \left[ {Z_{5} } \right]\left\{ {\varepsilon_{{{\text{rs}}}} } \right\} \hfill \\ \end{gathered}$$

(17)

The effective potential (ϕ and ψ) of the two MPE facesheets is the summation of potentials of each facesheet layer as shown in Eq. (18). The variation of the potentials across the top (superscript ‘t’; ϕ^t and ψ^t) and bottom (superscript ‘b’; ϕ^b and ψ.^b) MPE facesheets are written as [41]

$$\begin{gathered} \phi = \phi^{t} + \phi^{b} ;\phi^{t} = \left( {\frac{{z - h_{3} }}{h}} \right)\overline{\phi } ; \, \phi^{b} = \left( {\frac{{h_{2} - z}}{h}} \right)\overline{\phi } ; \hfill \\ \psi = \psi^{t} + \psi^{b} ;\psi^{t} = \left( {\frac{{z - h_{3} }}{h}} \right)\overline{\psi } ; \, \psi^{b} = \left( {\frac{{h_{2} - z}}{h}} \right)\overline{\psi } ; \hfill \\ \end{gathered}$$

(18)

Here, $\overline{\phi }$ and $\overline{\psi }$ denote the electric and magnetic potential on the top surface of the upper MPE facesheet, respectively.

Further, since the plate thickness is small, the polarisation along the length and breadth of SSP is minimal; hence, the associated electric and magnetic field components can be neglected. Therefore, through Maxwell’s equation, the electric and magnetic fields acting across the facesheets of the SSP can be expressed as [41]

$$E_{z} = - \frac{\partial \phi }{{\partial z}} = - \left( {\frac{{\partial \phi^{t} }}{\partial z} + \frac{{\partial \phi^{b} }}{\partial z}} \right);H_{z} = - \frac{\partial \psi }{{\partial z}} = - \left( {\frac{{\partial \psi^{t} }}{\partial z} + \frac{{\partial \psi^{b} }}{\partial z}} \right)$$

(19)

The FE model of the SSP is discretised using an 8-noded isoparametric element. Meanwhile, the nodal displacement degrees of freedom (d.o.f) are expressed as follows:

$$\left\{ {s_{ti} } \right\} = \left[ {\begin{array}{*{20}c} {u_{0i} } & {v_{0i} } & {w_{0i} } \\ \end{array} } \right]^{T} ;\left\{ {s_{ri} } \right\} = \left[ {\begin{array}{*{20}c} {\theta_{xi} } & {\theta_{yi} } & {\theta_{zi} } & {\kappa_{zi} } & {\kappa_{xi} } & {\kappa_{yi} } & {\gamma_{xi} } & \gamma \\ \end{array}_{yi} } \right]^{T} \, (i = 1,2 \cdots 8)$$

(20)

For each element, the generalised d.o.f can be expressed using the shape functions as follows:

$$\left\{ {s_{t} } \right\} = \left[ {N_{t} } \right]\left\{ {s_{t}^{e} } \right\};\quad \left\{ {s_{r} } \right\} = \left[ {N_{r} } \right]\left\{ {s_{r}^{e} } \right\};\quad \phi = \left[ {N_{\phi } } \right]\left\{ {\phi^{e} } \right\};\psi = \left[ {N_{\psi } } \right]\left\{ {\psi^{e} } \right\}$$

(21)

To overcome the hurdle of shear locking and effectively calculate the stiffness matrices associated with the transverse shear deformation, a selective integration rule is adopted in this work [41].

Further, the fields shown in Eq. (19) can be re-written using FE parameters as,

$$E_{z}^{{}} = - \frac{1}{h}\left[ {N_{\phi } } \right]\left\{ {\phi^{{\text{e}}} } \right\};\quad H_{z} = - \frac{1}{h}\left[ {N_{\psi } } \right]\left\{ {\psi^{{\text{e}}} } \right\}$$

(22)

Replacing the strain components of Eq. (17) in terms of FE entities, it can be shown that

$$\begin{gathered} \left\{ {\varepsilon_{{\text{b}}}^{{\text{h}}} } \right\} = \left[ {SD_{{{\text{tb}}}} } \right]\left\{ {s_{{\text{t}}}^{{\text{e}}} } \right\} + \left[ {Z_{1} } \right]\left[ {SD_{{{\text{rb}}}} } \right]\left\{ {s_{{\text{r}}}^{{\text{e}}} } \right\} + \frac{1}{2}\left[ {SD_{1} } \right]\left[ {SD_{2} } \right]\left\{ {s_{{\text{t}}}^{{\text{e}}} } \right\}; \hfill \\ \left\{ {\varepsilon_{{\text{b}}}^{{\text{p}}} } \right\} = \left[ {SD_{{{\text{tb}}}} } \right]\left\{ {s_{{\text{t}}}^{{\text{e}}} } \right\} + \left[ {Z_{2} } \right]\left[ {SD_{{{\text{rb}}}} } \right]\left\{ {s_{{\text{r}}}^{{\text{e}}} } \right\} + \frac{1}{2}\left[ {SD_{1} } \right]\left[ {SD_{2} } \right]\left\{ {s_{{\text{t}}}^{{\text{e}}} } \right\}; \hfill \\ \left\{ {\varepsilon_{{\text{s}}}^{{\text{h}}} } \right\} = \left[ {SD_{{{\text{ts}}}} } \right]\left\{ {s_{{\text{t}}}^{{\text{e}}} } \right\} + \left[ {Z_{3} } \right]\left[ {SD_{{{\text{rs}}}} } \right]\left\{ {s_{{\text{r}}}^{{\text{e}}} } \right\}; \hfill \\ \left\{ {\varepsilon_{{\text{s}}}^{{\text{v}}} } \right\} = \left[ {SD_{{{\text{ts}}}} } \right]\left\{ {s_{{\text{t}}}^{{\text{e}}} } \right\} + \left[ {Z_{4} } \right]\left[ {SD_{{{\text{rs}}}} } \right]\left\{ {s_{{\text{r}}}^{{\text{e}}} } \right\} \hfill \\ \left\{ {\varepsilon_{{\text{s}}}^{{\text{p}}} } \right\} = \left[ {SD_{{{\text{ts}}}} } \right]\left\{ {s_{{\text{t}}}^{{\text{e}}} } \right\} + \left[ {Z_{5} } \right]\left[ {SD_{{{\text{rs}}}} } \right]\left\{ {s_{{\text{r}}}^{{\text{e}}} } \right\} \hfill \\ \end{gathered}$$

(23)

The exploded form of different strain component matrices ([Z1] to [Z5]) and the shape function derivative matrices are highlighted in the Appendix.

For an SSP integrated with an ACLD patch, the equations of motion can be derived by invoking the principle of virtual work as [41]

$$\begin{aligned} &\sum\limits_{N = 1}^{3} {\left( {\int\limits_{{\Omega^{h} }} {\delta \left\{ {\varepsilon_{b}^{h} } \right\}^{T} \left\{ {\sigma_{b}^{h} } \right\}d\Omega^{h} + } \int\limits_{{\Omega^{h} }} {\delta \left\{ {\varepsilon_{s}^{h} } \right\}^{T} \left\{ {\sigma_{s}^{h} } \right\}d\Omega^{h} } } \right)}+\int\limits_{{\Omega^{V} }} {\delta \left\{ {\varepsilon_{s}^{v} } \right\}^{T} \left\{ {\sigma_{s}^{v} } \right\}d\Omega^{v} } + \int\limits_{{\Omega^{P} }} {\delta \left\{ {\varepsilon_{b}^{p} } \right\}^{T} \left\{ {\sigma_{b}^{p} } \right\}d\Omega^{p} } \\ & \qquad + \quad\int\limits_{{\Omega^{p} }} {\delta \left\{ {\varepsilon_{s}^{p} } \right\}^{T} \left\{ {\sigma_{s}^{p} } \right\}d\Omega^{p} - } \int\limits_{{\Omega^{p} }} {\delta E_{z} D_{z} d\Omega^{p} } + \int\limits_{A} {Q^{\phi } } \delta \phi dA + \int\limits_{A} {Q^{\psi } } \delta \psi dA \\ &\qquad - \sum\limits_{N = 1}^{3} {\left( {\int\limits_{{\Omega^{h} }} {\delta E_{z} } D_{z} (z)d\Omega^{h} } \right)}- \sum\limits_{N = 1}^{3} {\left( {\int\limits_{{\Omega^{h} }} {\delta H_{z} } B_{z} (z)d\Omega^{h} } \right)} - \int\limits_{A} \delta \left\{ {s_{t} } \right\}^{T} \left\{ f \right\}dA \\ &\qquad + \sum\limits_{N = 1}^{3} {\left( {\frac{1}{2}\int\limits_{{\Omega^{h} }} {\delta \left\{ {s_{t} } \right\}^{T} \rho_{h} (z)\left\{ {\ddot{s}_{t} } \right\}d\Omega^{h} } } \right)} + \frac{1}{2}\int\limits_{{\Omega^{v} }} {\delta \left\{ {s_{t} } \right\}^{T} \rho_{v} (z)\left\{ {\ddot{s}_{t} } \right\}d\Omega^{v} + } \frac{1}{2}\int\limits_{{\Omega^{p} }} {\delta \left\{ {s_{t} } \right\}^{T} \rho_{p} (z)\left\{ {\ddot{s}_{{\varvec{t}}} } \right\}d\Omega^{p} = 0} \end{aligned}$$

(24)

Replacing the terms of Eq. (24) with the constitutive, strain–displacement and Maxwell’s equations, it can be simplified as follows:

$$\begin{aligned} & \left[ {M^{e} } \right]\left\{ {\ddot{s}_{t}^{e} } \right\} + \left[ {k_{T15}^{e} } \right]\left\{ {s_{t}^{e} } \right\} + \left[ {k_{T16}^{e} } \right]\left\{ {s_{r}^{e} } \right\} \hfill \\ & \quad + \left[ {k_{31}^{e} } \right]\int\limits_{0}^{t} {G\left( {t - \tau } \right)} \frac{{\partial \left\{ {s_{t}^{e} } \right\}}}{\partial \tau }d\tau + \left[ {k_{32}^{e} } \right]\int\limits_{0}^{t} {G\left( {t - \tau } \right)} \frac{{\partial \left\{ {s_{r}^{e} } \right\}}}{\partial \tau }d\tau \hfill \\ & \quad + \left[ {k_{T3}^{e} } \right]\left\{ {\phi^{e} } \right\} + \left[ {k_{T4}^{e} } \right]\left\{ {\psi^{e} } \right\} = \left\{ {F_{th}^{e} } \right\} - \left\{ {F_{{_{tp1} }}^{e} } \right\}V - \left\{ {F_{{_{tpn1} }}^{e} } \right\}V \hfill \left[ {k_{{{\text{T17}}}}^{{\text{e}}} } \right]\left\{ {s_{{\text{t}}}^{{\text{e}}} } \right\} + \left[ {k_{{{\text{T18}}}}^{{\text{e}}} } \right]\left\{ {s_{{\text{r}}}^{{\text{e}}} } \right\} + \left[ {k_{{{32}}}^{{\text{e}}} } \right]\int\limits_{0}^{t} \hfill \\ & \quad {G\left( {t - \tau } \right)} \frac{{\partial \left\{ {s_{{\text{t}}}^{{\text{e}}} } \right\}}}{\partial \tau }{\text{d}}\tau+\left[ {k_{{{30}}}^{{\text{e}}} } \right]\int\limits_{0}^{t} {G\left( {t - \tau } \right)} \frac{{\partial \left\{ {s_{{\text{r}}}^{{\text{e}}} } \right\}}}{\partial \tau }{\text{d}}\tau + \left[ {k_{{3}}^{{\text{e}}} } \right]\left\{ {\phi^{{\text{e}}} } \right\} + \left[ {k_{{4}}^{{\text{e}}} } \right]\left\{ {\psi^{{\text{e}}} } \right\} = - \left( {\left\{ {F_{{{\text{rp1}}}}^{{\text{e}}} } \right\} + \left\{ {F_{{{\text{rp2}}}}^{{\text{e}}} } \right\}} \right)V \hfill \\ \end{aligned}$$

(25)

$$\left[ {k_{{{33}}}^{{\text{e}}} } \right]\left\{ {s_{{\text{t}}}^{{\text{e}}} } \right\} + \left[ {k_{{_{{{34}}} }}^{{\text{e}}} } \right]^{{\text{T}}} \left\{ {s_{{\text{r}}}^{{\text{e}}} } \right\} - \left[ {k_{{_{{{35}}} }}^{{\text{e}}} } \right]\left\{ {\phi^{{\text{e}}} } \right\} - \left[ {k_{{_{{{36}}} }}^{{\text{e}}} } \right]\left\{ {\psi^{{\text{e}}} } \right\} = \left\{ {F_{th\_\phi } } \right\}$$

$$\left[ {k_{37}^{e} } \right]\left\{ {s_{t}^{e} } \right\} + \left[ {k_{{_{38} }}^{e} } \right]\left\{ {s_{r}^{e} } \right\} - \left[ {k_{{_{39} }}^{e} } \right]^{T} \left\{ {\phi^{e} } \right\} - \left[ {k_{{_{40} }}^{e} } \right]\left\{ {\psi^{e} } \right\} = \left\{ {F_{th\_\psi } } \right\}$$

$\left\{{F}_{th}^{e}\right\}$, $\left\{{F}_{th\_\phi }^{e}\right\}$ and $\left\{{F}_{th\_\psi }^{e}\right\}$ are the thermal, pyro-electric and pyro-magnetic load vectors. Also, $\left\{{F}_{rp1}^{e}\right\}$, $\left\{{F}_{rp2}^{e}\right\}$, $\left\{{F}_{tpn1}^{e}\right\}$ and $\left\{{F}_{tp1}^{e}\right\}$ are the rotational and translational component vectors.

After employing the Laplace transform, Eq. (25) can be simplified as,

$$\begin{aligned} s^{2} &\left[ M \right]\left\{ {\tilde{X}_{t} } \right\} + L\left( {\left[ {k_{C12} } \right]\left\{ {X_{t} } \right\} + \left[ {k_{C13} } \right]\left\{ {X_{r} } \right\}} \right) + \left[ {k_{tsv} } \right]s\tilde{G}\left( s \right)\left\{ {\tilde{X}_{t} } \right\} + \left[ {k_{trsv} } \right]s\tilde{G}\left( s \right)\left\{ {\tilde{X}_{r} } \right\} \\ & \quad = \left\{ {\tilde{F}_{th\_eq} } \right\} - \left\{ {F_{tp} } \right\}\tilde{V} - L\left\{ {F_{tpn} } \right\}\tilde{V} \\ & \quad L\left( {\left[ {k_{C17} } \right]\left\{ {X_{t} } \right\} + \left[ {k_{C18} } \right]\left\{ {X_{r} } \right\}} \right) + \left[ {k_{trsv} } \right]^{T} s\tilde{G}\left( s \right)\left\{ {\tilde{X}_{t} } \right\} + \left[ {k_{rrsv} } \right]s\tilde{G}\left( s \right)\left\{ {\tilde{X}_{r} } \right\} = - \left\{ {F_{rp} } \right\}\tilde{V} \end{aligned}$$

(26)

The terms $\left\{\widetilde{{X}_{t}}\right\}, \left\{\widetilde{{X}_{\mathrm{r}}}\right\}$ and $\left\{{\widetilde{F}}_{th\_eq}\right\}$ are the Laplace transform of {X_t}_, {X_t} and {F_{th_eq}}. The single mini oscillator term for ACLD’s viscoelastic layer can be expressed through the material modulus ($\mathrm{s}\widetilde{\mathrm{G}}\left(\mathrm{s}\right)$) in the Laplace domain and final relaxation value (${\mathrm{G}}^{\infty }$) using the GHM approach as follows:

$$s\tilde{G}\left( s \right) = G^{\infty } \left[ {1 + \alpha \frac{{s^{2} + 2\hat{\xi }\hat{\omega }s}}{{s^{2} + 2\hat{\xi }\hat{\omega }s + \hat{\omega }^{2} }}} \right]$$

(27)

The auxiliary dissipation coordinates are introduced through the terms Z and Zr, and its Laplace transform is obtained to express

$$\begin{gathered} s\tilde{G}\left( s \right)\left\{ {\tilde{X}_{t} } \right\} = G^{\infty } \left[ {\left( {1 + \alpha } \right)} \right]\left\{ {\tilde{X}_{t} } \right\} - \alpha \tilde{Z}\left( s \right) \hfill \\ s\tilde{G}\left( s \right)\left\{ {\tilde{X}_{r} } \right\} = G^{\infty } \left[ {\left( {1 + \alpha } \right)} \right]\left\{ {\tilde{X}_{r} } \right\} - \alpha \tilde{Z}_{r} \left( s \right) \hfill \\ \tilde{Z}\left( s \right) = \frac{{\hat{\omega }^{2} }}{{s^{2} + 2\hat{\xi }\hat{\omega }s + \hat{\omega }^{2} }}\left\{ {X_{t} } \right\} \hfill \\ \tilde{Z}_{r} \left( s \right) = \frac{{\hat{\omega }^{2} }}{{s^{2} + 2\hat{\xi }\hat{\omega }s + \hat{\omega }^{2} }}\left\{ {X_{r} } \right\} \hfill \\ \end{gathered}$$

(28)

Using inverse Laplace transformations and a closed-loop model, the final equations of motion of SSP are written as follows [41]:

$$\left[ {M^{*} } \right]\left\{ {\ddot{X}_{t} } \right\} + \left[ {C_{d}^{*} } \right]\left\{ {\dot{X}_{t} } \right\}\left[ {K^{*} } \right]\left\{ {X_{t} } \right\} = \left\{ {F^{*} } \right\}$$

(29)

$\left[{M}^{*}\right]$, $\left[{C}_{\mathrm{d}}^{*}\right]$, and $\left[{K}^{*}\right]$ are the equivalent mass, damping and stiffness matrices.

5 Results and discussion

The damped response of SSP subjected to the different thermal environments is evaluated in this section. In-line with the outcome of the convergence study shown in Table 3, a converged mesh size of 10 × 10 is adopted in the subsequent analysis. For the subsequent numerical evaluation following values are considered: a = b = 1.0 m; a/h = 50; h_v = 50.8 μm; h_p = 250 μm; K_d = 600; UTR with ΔT = 300; λ_ο = 0.8; UD of CNTs; f_r = 2%

Table 3 Convergence of natural frequency of MEE plate with mesh size

The SSP is enforced with the simply supported constraints, which can be expressed as,

$$\begin{gathered} v_{0}^{{}} = w_{0}^{{}} = \theta_{y}^{{}} = \kappa_{y}^{{}} = \gamma_{y}^{{}} = \theta_{z}^{{}} = \kappa_{z}^{{}} = 0\quad {\text{at}}\;x = 0\;{\text{ and}}\;x = a \hfill \\ u_{0} = w_{0} = \theta_{x} = \kappa_{x} = \gamma_{x} = \theta_{z} = \kappa_{z} = 0\quad {\text{at}}\;y = 0\;{\text{ and}}\;y = b \hfill \\ \end{gathered}$$

(30)

To verify the proposed model, comparison studies are performed with the previously published literature by Chen et al. [38], Craveiro and Loja [66]. Table 4 shows that the proposed FE model effectively incorporates the coupling fields and accurately predicts the natural frequencies of the layered MPE plate. Extending the assessment, the results are compared with Craveiro and Loja [66] for a case study of the frequency response of agglomerated CNT plates. From Table 5, it is affirmed that the agglomeration of CNTs is properly included in the formulation, and hence it is reliable.

Table 4 Comparison of the natural frequencies of MEE plates (h = 0.3 m; a = b = 1 m)

Table 5 Verification of fundamental natural frequencies of completely agglomerated plates

To begin with, the influence of SSP's core materials, namely pure polymer, porous and CNT-reinforced nanocomposite core (CNT-NCC), on its AVC response when subjected to UTR is investigated. The pure polymer variant is the one without ant pores or CNTs. Similarly, a porous core encompasses pores but not CNTs, whereas CNT-NCC comprises only CNTs. Figure 2 suggests that the AVC response follows the porous > pure polymer > CNT-NCC trend, with the highest deflection amplitude, noticed for an SSP with the porous core. The variation of this trend is directly relatable to the material's stiffness. An SSP experiences the highest stiffness when its core is reinforced with CNTs. Meanwhile, including pores in the polymeric core drastically reduce the stiffness, and hence a greater deflection is witnessed. A greater degree of pyro-coupling is noticed for an SSP with a porous polymer core due to enhanced pyro-loads generated due to superior pyro-electric and pyro-magnetic field interactions in the MPE facesheets.

Fig. 2

Influence of core on the controlled response of multiphase sandwich plate subjected to uniform thermal environment

Figure 3a–c elucidate the AVC response of porous core-SSP with different porosity patterns (Eq. (11)) subjected to different temperature profiles. It can be seen from these figures that the influence of porosity patterns varies according to the temperature profile the SSP is subjected to. However, the predominant deflection amplitude is witnessed when SSP is exposed to the HT-LB temperature profile. The degree of pyro-coupling is also significant for the same temperature loading (HT-LB) as opposed to the other two (UTR and LT-HB). An extreme AVC response of the SSP is seen for UD porosity when exposed to UTR and LT-HB temperatures. Analogously, a higher deflection is noticed for the HT-LB profile for FG-S porosity. This trend might result from the elasto-thermo field interactions, significantly affecting the coupled structural response.

Fig. 3

Influence of porosity pattern and thermal profiles on the controlled response of multiphase sandwich plate with porous core (λ_ο = 0.8)

This section considers an SSP with UD porous core exposed to UTR and LTR (HT-LB) profiles, and their AVC response is recorded in Fig. 4a and b by varying the porosity volume. Since the stiffness of the plate drastically diminishes with higher porosity volume, the AVC response of SSP shows a greater amplitude with increasing porosity volume. Meanwhile, the effect of porosity volume and associated pyro-coupling is marginally higher for the LTR (HT-LB) profile in contrast to the UTR profile. In addition, the degree of pyro-coupling associated with the porosity volume is found to increase gradually with the higher values of porosity volume. This is because, at higher porosity volume, the overall stiffness of the plate is predominantly lower. Hence, the deflection amplitude shoots up with the same magnitude of external loading.

Fig. 4

Influence of porosity volume and thermal profiles on the controlled response of multiphase sandwich plate with porous core

Considering an SSP with CNT-NCC, the influence of complete and partial agglomeration states on its AVC response is studied. To this end, the agglomeration parameters µ and η are varied, and the deflection amplitude is recorded in Figs. 5 and 6, respectively. It can be seen from these figures that better controlling of the SSP's AVC response can be achieved when the CNT-NCC is tuned to have higher and lower values of µ and η, respectively. In contrast to the partial agglomeration, a higher deflection amplitude and degree of pyro-coupling are seen for SSP with completely agglomerated CNT-NCC. This can be owed to the variation in the structure's stiffness. Also, as seen in the previous analysis, a significant pyro-coupling effect is noticed for the LTR profile.

Fig. 5

Influence of the parameter µ on the controlled response of multiphase sandwich plate with complete agglomerated CNT nanocomposite core

Fig. 6

Influence of the parameter η on the controlled response of multiphase sandwich plate with partial agglomerated CNT nanocomposite core

The AVC response of SSP with porous-agglomerated CNT-NCC is studied in this section. The UTR profile is assumed for this assessment. Also, a comparison is made between the deflection amplitude of SSP with CNT-NCC but without pores to better understand the collective impact of porosity and agglomeration. Figure 7a–c show the SSP's AVC response with the partially agglomerated core. It can be witnessed from these figures that a better attenuation can be achieved when an SSP has a core with FG-S porosity and a minimum value of η. In addition, the influence of η associated with the porosity is found to be maximum for the UD porosity distribution. However, for the AVC response of SSP with a completely agglomerated CNT-NCC core, a predominant effect of porosity is associated with the lower values of µ, as seen from Fig. 8a–c. The previous conclusions concerning the variation trend of porosity distribution patterns also hold well here. The integrated effect of different porosity patterns and agglomeration states on the degree of pyro-coupling of SSP exposed to different temperature loads are illustrated in Tables 6, 7 and 8. It can be realised from the data presented in these tables that the pyro-coupling effect is significantly enhanced in the SSP with the inclusion of pores in the ACNT core.

Fig. 7

Synergistic influence of the porosity pattern and agglomeration on the controlled response of multiphase sandwich plate with partially agglomerated CNT nanocomposite core

Fig. 8

Synergistic influence of the porosity pattern and agglomeration on the controlled response of multiphase sandwich plate with complete agglomerated CNT nanocomposite core

Table 6 Percentage contribution of the pyro-coupling on the maximum deflection amplitude of the sandwich plate with agglomerated CNTs and porous core with MEE facesheets subjected to the uniform temperature gradient (ΔT = 100, λ_ο = 0.8)

Table 7 Percentage contribution of the pyro-coupling on the maximum deflection amplitude of the sandwich plate with agglomerated CNTs and porous core with MEE facesheets subjected to the linear temperature gradient (HT-LB, λ_ο = 0.8)

Table 8 Percentage contribution of the pyro-coupling on the maximum deflection amplitude of the sandwich plate with agglomerated CNTs and porous core with MEE facesheets subjected to the linear temperature gradient (LT-HB, λ_ο = 0.8)

Next, the assessment is done on similar grounds but considering porosity volume as the variant. To this end, the SSP with UD porous core is chosen. From Fig. 9a–d, it can be seen that a higher volume fraction has a profound effect associated with agglomeration. In other words, a higher volume fraction of pores results in poor dispersion of the CNTs and enhances the agglomeration effect. Therefore, the discrepancies between the amplitudes of the deflection curve are more for higher porosity volume.

Fig. 9

Synergistic influence of the porosity volume and agglomeration on the controlled response of multiphase sandwich plate with agglomerated CNT nanocomposite core

The effect of pyro-coupling and MEE coupling associated with the different combinations of porosity volume, distribution patterns and agglomerated states of SSP subjected to LTP (HT-LB) is shown in Fig. 10a–c. The discrepancies between the deflection amplitude of SSP resulting from the complete coupling between magnetic-electric-elastic fields and elastic fields alone are used to evaluate the influence of MEE coupling. It can be seen from these figures that the pyro-coupling effect significantly enhances with higher porosity volume, irrespective of the porosity pattern. This is due to the reduction in the stiffness of the plate parallel to the magnification of effective/equivalent loads. Meanwhile, the pyro-coupling is found be significant for FG-S distribution, as the deflections are more compared to UD and FG-NS patterns. Analogously, the MEE coupling is superior for lower porosity volume fraction and FG-NS pattern owing to the enhanced stiffness developed by these configurations.

Fig. 10

Effect of the pyro-coupling and MEE coupling on the controlled deflection of the multiphase sandwich plate with agglomerated CNT nanocomposite/porous core of different volume fraction

The SSP comprises multifunctional magneto-piezo-elastic facesheets that are reactive to external voltages. This section investigates the controlled response of SSP, where the control voltage is fed directly to the facesheets instead of the piezo patch of the ACLD layer. The SSP with agglomerated CNT-NCC with porosity is considered for evaluation. From Fig. 11, it is witnessed that the technique of directly controlling SSP is less efficient than the control achieved through the ACLD treatment. However, the efficiency of the direct control strategy becomes on par with that of the ACLD treatment when the porosity volume and agglomeration effect are reduced, as shown in Fig. 12.

Fig. 11

Comparison of the controlled deflection of the multiphase sandwich plate with agglomerated CNT nanocomposite/porous core using ACLD and direct control techniques

Fig. 12

Effect of agglomeration and porosity volume of the percentage difference between the controlled deflection amplitudes of SSP achieved using ACLD and direct control techniques

The influences of core material and agglomeration states on the stability of the SSP treated with ACLD are shown in Figs. 13, 14 and 15, respectively. It can be inferred from these figures that ACLD treatment helps attenuate the vibrations effectively. In other words, the velocity of the SSP drastically reduces with time. Since the velocity of the SSP is directly proportional to the control voltage, it can be justified that the efforts required to control the vibration get minimal as time improves with the application of ACLD. In addition, it is also seen that the pyro-coupling effects make the attenuation cumbersome and demand more control voltage. In contrast to the partial agglomeration state, a higher control voltage is needed to reduce the vibrations of SSP with a complete agglomeration state. Among all the temperature profiles considered, LTP (HT-LB) creates more instability in the SSP, as seen from Figs. 14 and 15. Further, the degree of stability of SSP against the pyro-coupling effects is more for partial agglomerated core and LTP (LT-HB) temperature effects.

Fig. 13

Effect of core material on the velocity–displacement plots of SSP achieved using ACLD (UTR)

Fig. 14

Effect of temperature profile on the velocity–displacement plots of SSP with partial agglomerated CNT-porous core

Fig. 15

Effect of temperature profile on the velocity–displacement plots of SSP with complete agglomerated CNT-porous core

6 Conclusions

This work presents the damped response of the smart sandwich plates with agglomerated/porous cores subjected to thermal loads using a finite element framework. The vibration attenuation is accomplished through the active damping procedure. A special emphasis has been placed on investigating the influence of pyro-coupling associated with different temperature profiles on the damped response of SSP. The numerical evaluation reveals new outcomes relevant to the smart structure and system design. Porosity in the core of SSP results in higher vibration amplitude as opposed to pure polymer and CNT-reinforced nanocomposite cores. Among the three different temperature profiles considered, the linear temperature with the highest temperature at the top facesheets and the lowest temperature at the bottom facesheets shows a predominant effect on the vibration amplitude and pyro-coupling effects. Better structural stability is displayed by the FG-S and FG-NS types of porosities when the SSP is operated under uniform temperature and linear temperature profiles, respectively. Meanwhile, the superior pyro-coupling is exhibited by the FG-S type of porosity when operated with a linear temperature profile. Increasing the porosity volume results in tedious vibration controllability and enhanced pyro-coupling.

Further, as the porosity volume reduces, the agglomeration effect diminishes and enhances the damping characteristics of SSP. The pyro-coupling effect enhances the vibration amplitude by 19.7% and 9.82% for SSP with NCC of complete and partial agglomeration states with 80% porosity volume. In comparison, these percentages reduce to 7.68% and 3.8% for 20% porosity volume. The state of partial agglomeration shows better attenuation and lesser pyro-coupling effect than the complete agglomeration state. The proposed methodology and structural analysis can be further extended considering the complete coupling of the thermal field with MPE fields, which is neglected in this work.

Appendices

Appendix A

The matrices relating the strains and displacement are written as follows:

$$\left[ {SD_{tb} } \right] = \left[ {\begin{array}{*{20}l} {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-0pt} {\partial x}}} &\quad 0 &\quad 0 \\ 0 &\quad {{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-0pt} {\partial y}}} &\quad 0 \\ 0 &\quad 0 &\quad 0 \\ {{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-0pt} {\partial y}}} &\quad {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-0pt} {\partial x}}} &\quad 0 \\ \end{array} } \right];\left[ {SD_{ts} } \right] = \left[ {\begin{array}{*{20}l} 0 &\quad 0 &\quad {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-0pt} {\partial x}}} \\ 0 &\quad 0 &\quad {{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-0pt} {\partial y}}} \\ \end{array} } \right]$$

$$\left[ {SD_{rb} } \right] = \left[ {\begin{array}{*{20}l} {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-0pt} {\partial x}}} &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad {{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-0pt} {\partial y}}} &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ {{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-0pt} {\partial y}}} &\quad {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-0pt} {\partial x}}} &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 1 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 1 &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-0pt} {\partial x}}} &\quad 0 & \quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad {{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-0pt} {\partial y}}} &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad {{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-0pt} {\partial y}}} &\quad {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-0pt} {\partial x}}} &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-0pt} {\partial x}}} &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad {{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-0pt} {\partial y}}} \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad {{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-0pt} {\partial y}}} &\quad {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-0pt} {\partial x}}} \\ \end{array} } \right],$$

$$\left[ {SD_{{rs}} } \right] = \left[ {\begin{array}{*{20}l} 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ 0 \hfill & 0 \hfill & {\partial /\partial x} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {\partial /\partial y} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {\partial /\partial x} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {\partial /\partial y} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right].$$

The expanded form of matrices [Z1]–[Z5] are as follows:

$$\begin{gathered} \left[ {Z_{1} } \right] = \left[ {\begin{array}{*{20}l} z &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad z &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 1 &\quad {2z} &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad z &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ \end{array} } \right] \hfill \\ \left[ {Z_{2} } \right] = \left[ {\begin{array}{*{20}l} {{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}} &\quad 0 & \quad 0 &\quad 0 &\quad 0 &\quad {h_{{\text{v}}} } &\quad 0 &\quad 0 &\quad {\left( {z - h_{{\text{v}}} - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}} \right)} & \quad 0 &\quad 0 \\ 0 &\quad {{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}} &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad {h_{{\text{v}}} } &\quad 0 &\quad 0 &\quad {\left( {z - h_{{\text{v}}} - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}} \right)} & \quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 1 &\quad {2z} &\quad 0 &\quad 0 & \quad 0 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad {{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}} &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad {h_{{\text{v}}} } &\quad 0 &\quad 0 &\quad {\left( {z - h_{{\text{v}}} - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}} \right)} \\ \end{array} } \right] \hfill \\ \left[ {Z_{3} } \right] = \left[ {\begin{array}{*{20}c} 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad z &\quad 0 &\quad {z^{2} } & \quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad z & \quad 0 &\quad {z^{2} } \\ \end{array} } \right];\;\left[ {Z_{4} } \right] = \left[ {\begin{array}{*{20}c} 0 &\quad 0 &\quad 1 &\quad 0 &\quad 0 &\quad 0 &\quad z &\quad 0 &\quad {z^{2} } &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 1 &\quad 0 &\quad 0 &\quad 0 &\quad z & \quad 0 &\quad {z^{2} } \\ \end{array} } \right] \hfill \\ \left[ {Z_{5} } \right] = \left[ {\begin{array}{*{20}l} 0 &\quad 0 &\quad 0 &\quad 0 &\quad 1 &\quad 0 &\quad z &\quad 0 &\quad {z^{2} } &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 1 &\quad 0 &\quad z &\quad 0 &\quad z \\ \end{array} } \right] \hfill \\ \end{gathered}$$

(A1)

Appendix-B

The various FE entities of Eq. (29) can be shown as follows:

$$\left[ {k_{NL1}^{e} } \right] = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{2} } \right]^{T} \left[ {SD_{1} } \right]^{T} \left[ {D_{1} } \right]\left[ {SD_{tb} } \right]} } \, {\text{d}}x{\text{d}}y;\left[ {k_{NL2}^{e} } \right] = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{2} } \right]^{T} \left[ {SD_{1} } \right]^{T} \left[ {D_{2} } \right]\left[ {SD_{rb} } \right]} } \, {\text{d}}x{\text{d}}y;$$

$$\left[ {k_{NL2}^{e} } \right] = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{2} } \right]^{T} \left[ {SD_{1} } \right]^{T} \left[ {D_{2} } \right]\left[ {SD_{rb} } \right]} } \, {\text{d}}x{\text{d}}y;$$

$$\left[ {k_{NL3}^{e} } \right] = \frac{1}{4}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{2} } \right]^{T} \left[ {SD_{1} } \right]^{T} \left[ {D_{1} } \right]\left[ {SD_{1} } \right]} } \left[ {SD_{2} } \right] \, {\text{d}}x{\text{d}}y;$$

$$\left[ {k_{NL4}^{e} } \right] = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{2} } \right]^{T} \left[ {SD_{1} } \right]^{T} \left[ {D_{3} } \right]} } \, \left[ {N_{\phi } } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{NL5}^{e} } \right] = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{2} } \right]^{T} \left[ {SD_{1} } \right]^{T} \left[ {D_{4} } \right]} } \, \left[ {N_{\psi } } \right]{\text{d}}x{\text{d}}y;\left[ {k_{NL6}^{e} } \right] = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{rb} } \right]^{T} \left[ {D_{5} } \right]} } \, \left[ {SD_{1} } \right]\left[ {SD_{2} } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{NL6}^{e} } \right] = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{rb} } \right]^{T} \left[ {D_{5} } \right]} } \, \left[ {SD_{1} } \right]\left[ {SD_{2} } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{NL7}^{e} } \right] = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{tb} } \right]^{T} \left[ {D_{1} } \right]} } \, \left[ {SD_{1} } \right]\left[ {SD_{2} } \right]{\text{d}}x{\text{d}}y;\left[ {k_{NL8}^{e} } \right] = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{2} } \right]^{T} \left[ {SD_{1} } \right]^{T} \left[ {D_{13} } \right]} } \, \left[ {SD_{tb} } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{NL9}^{e} } \right] = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{2} } \right]^{T} \left[ {SD_{1} } \right]^{T} \left[ {D_{14} } \right]} } \, \left[ {SD_{rb} } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{NL10}^{e} } \right] = \frac{1}{4}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{2} } \right]^{T} \left[ {SD_{1} } \right]^{T} \left[ {D_{13} } \right]} } \, \left[ {SD_{1} } \right]\left[ {SD_{2} } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{NL11}^{e} } \right] = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{2} } \right]^{T} \left[ {SD_{1} } \right]^{T} \left[ {D_{14} } \right]} } \, \left[ {SD_{ts} } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{NL12}^{e} } \right] = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{2} } \right]^{T} \left[ {SD_{1} } \right]^{T} \left[ {D_{15} } \right]} } \, \left[ {SD_{rs} } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{NL13}^{e} } \right] = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{rb} } \right]^{T} \left[ {D_{17} } \right]} } \, \left[ {SD_{1} } \right]\left[ {SD_{2} } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{NL14}^{e} } \right] = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{tb} } \right]^{T} \left[ {D_{13} } \right]} } \, \left[ {SD_{1} } \right]\left[ {SD_{2} } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{NL15}^{e} } \right] = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{rs} } \right]^{T} \left[ {D_{24} } \right]} } \, \left[ {SD_{1} } \right]\left[ {SD_{2} } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{NL16}^{e} } \right] = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{ts} } \right]^{T} \left[ {D_{24} } \right]} } \, \left[ {SD_{1} } \right]\left[ {SD_{2} } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{1}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{rb} } \right]^{T} \left[ {D_{5} } \right]} } \, \left[ {SD_{tb} } \right]{\text{d}}x{\text{d}}y;\left[ {k_{2}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{rb} } \right]^{T} \left[ {D_{6} } \right]} } \, \left[ {SD_{rb} } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{3}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{rb} } \right]^{T} \left[ {D_{7} } \right]} } \, \left[ {N_{\phi } } \right]{\text{d}}x{\text{d}}y;\left[ {k_{4}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{rb} } \right]^{T} \left[ {D_{8} } \right]} } \, \left[ {N_{\psi } } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{5}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{tb} } \right]^{T} \left[ {D_{1} } \right]} } \, \left[ {SD_{tb} } \right]{\text{d}}x{\text{d}}y;\left[ {k_{6}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{tb} } \right]^{T} \left[ {D_{2} } \right]} } \, \left[ {SD_{rb} } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{7}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{tb} } \right]^{T} \left[ {D_{3} } \right]} } \, \left[ {N_{\phi } } \right]{\text{d}}x{\text{d}}y;\left[ {k_{8}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{tb} } \right]^{T} \left[ {D_{4} } \right]} } \, \left[ {N_{\psi } } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{9}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{rs} } \right]^{T} \left[ {D_{9} } \right]} } \, \left[ {SD_{ts} } \right]{\text{d}}x{\text{d}}y;\left[ {k_{10}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{rs} } \right]^{T} \left[ {D_{10} } \right]} } \, \left[ {SD_{rs} } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{11}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{ts} } \right]^{T} \left[ {D_{11} } \right]} } \, \left[ {SD_{ts} } \right]{\text{d}}x{\text{d}}y;\left[ {k_{12}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{ts} } \right]^{T} \left[ {D_{12} } \right]} } \, \left[ {SD_{rs} } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{13}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{rb} } \right]^{T} \left[ {D_{17} } \right]} } \, \left[ {SD_{tb} } \right]{\text{d}}x{\text{d}}y;\left[ {k_{14}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{rb} } \right]^{T} \left[ {D_{18} } \right]} } \, \left[ {SD_{rb} } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{15}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{rb} } \right]^{T} \left[ {D_{17s} } \right]} } \, \left[ {SD_{ts} } \right]{\text{d}}x{\text{d}}y;\left[ {k_{16}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{rb} } \right]^{T} \left[ {D_{19} } \right]} } \, \left[ {SD_{rs} } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{17}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{tb} } \right]^{T} \left[ {D_{13} } \right]} } \, \left[ {SD_{tb} } \right]{\text{d}}x{\text{d}}y;\left[ {k_{18}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{tb} } \right]^{T} \left[ {D_{14} } \right]} } \, \left[ {SD_{rb} } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{19}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{tb} } \right]^{T} \left[ {D_{21} } \right]} } \, \left[ {SD_{ts} } \right]{\text{d}}x{\text{d}}y;\left[ {k_{20}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{tb} } \right]^{T} \left[ {D_{22} } \right]} } \, \left[ {SD_{rs} } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{21}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{rs} } \right]^{T} \left[ {D_{24} } \right]} } \, \left[ {SD_{tb} } \right]{\text{d}}x{\text{d}}y;\left[ {k_{22}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{rs} } \right]^{T} \left[ {D_{25} } \right]} } \, \left[ {SD_{rb} } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{23}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{rs} } \right]^{T} \left[ {D_{25} } \right]} } \, \left[ {SD_{ts} } \right]{\text{d}}x{\text{d}}y;\left[ {k_{24}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{rs} } \right]^{T} \left[ {D_{26} } \right]} } \, \left[ {SD_{rs} } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{25}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{ts} } \right]^{T} \left[ {D_{24} } \right]} } \, \left[ {SD_{tb} } \right]{\text{d}}x{\text{d}}y;\left[ {k_{26}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{ts} } \right]^{T} \left[ {D_{28} } \right]} } \, \left[ {SD_{rb} } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{27}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{ts} } \right]^{T} \left[ {D_{29} } \right]} } \, \left[ {SD_{ts} } \right]{\text{d}}x{\text{d}}y;\left[ {k_{28}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{ts} } \right]^{T} \left[ {D_{30} } \right]} } \, \left[ {SD_{rs} } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{29}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{rs} } \right]^{T} \left[ {D_{31} } \right]} } \, \left[ {SD_{ts} } \right]{\text{d}}x{\text{d}}y;\left[ {k_{30}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{rs} } \right]^{T} \left[ {D_{32} } \right]} } \, \left[ {SD_{rs} } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{31}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{ts} } \right]^{T} \left[ {D_{33} } \right]} } \, \left[ {SD_{ts} } \right]{\text{d}}x{\text{d}}y;\left[ {k_{32}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{ts} } \right]^{T} \left[ {D_{34} } \right]} } \, \left[ {SD_{rs} } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{33}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {N_{\phi } } \right]^{T} \left[ {D_{35} } \right]} } \, \left[ {SD_{tb} } \right]{\text{d}}x{\text{d}}y;\left[ {k_{34}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {N_{\phi } } \right]^{T} \left[ {D_{36} } \right]} } \, \left[ {SD_{rb} } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{35}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {N_{\phi } } \right]^{T} \left[ {D_{37} } \right]} } \, \left[ {N_{\phi } } \right]{\text{d}}x{\text{d}}y;\left[ {k_{36}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {N_{\phi } } \right]^{T} \left[ {D_{38} } \right]} } \, \left[ {N_{\psi } } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{37}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {N_{\psi } } \right]^{T} \left[ {D_{39} } \right]} } \, \left[ {SD_{tb} } \right]{\text{d}}x{\text{d}}y;\left[ {k_{38}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {N_{\psi } } \right]^{T} \left[ {D_{40} } \right]} } \, \left[ {SD_{rb} } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {k_{39}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {N_{\psi } } \right]^{T} \left[ {D_{41} } \right]} } \, \left[ {N_{\phi } } \right]{\text{d}}x{\text{d}}y;\left[ {k_{40}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {N_{\psi } } \right]^{T} \left[ {D_{42} } \right]} } \, \left[ {N_{\psi } } \right]{\text{d}}x{\text{d}}y;$$

$$\left[ {F_{tpN1}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{1} } \right]^{T} \left[ {SD_{2} } \right]\left[ {D_{16} } \right]} } \, {\text{d}}x{\text{d}}y;\left[ {F_{tp1}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{tb} } \right]^{T} \left[ {D_{23} } \right]} } \, {\text{d}}x{\text{d}}y;$$

$$\left[ {F_{tp2}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{ts} } \right]^{T} \left[ {D_{27} } \right]} } \, {\text{d}}x{\text{d}}y;\left[ {F_{rp1}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{rb} } \right]^{T} \left[ {D_{20} } \right]} } \, {\text{d}}x{\text{d}}y;$$

$$\left[ {F_{rp2}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {SD_{rs} } \right]^{T} \left[ {D_{27} } \right]} } \, {\text{d}}x{\text{d}}y;$$

$$\left[ {k_{T1}^{e} } \right] = \left[ {k_{NL1} } \right] + \left[ {k_{NL3} } \right] + \left[ {k_{5} } \right] + \left[ {k_{NL17} } \right] + \left[ {k_{11} } \right];\left[ {k_{T2}^{e} } \right] = \left[ {k_{NL2} } \right] + \left[ {k_{6} } \right] + \left[ {k_{12} } \right];$$

$$\left[ {k_{T3}^{e} } \right] = \left[ {k_{NL14} } \right] + \left[ {k_{7} } \right];\left[ {k_{T4}^{e} } \right] = \left[ {k_{NL15} } \right] + \left[ {k_{8} } \right];\left[ {k_{T5}^{e} } \right] = \left[ {k_{NL6} } \right] + \left[ {k_{1} } \right] + \left[ {k_{9} } \right];$$

$$\left[ {k_{T6}^{e} } \right] = \left[ {k_{2} } \right] + \left[ {k_{10} } \right];\left[ {k_{T7}^{e} } \right] = \left[ {k_{NL8} } \right] + \left[ {k_{NL10} } \right] + \left[ {k_{17} } \right] + \left[ {k_{NL11} } \right] + \left[ {k_{19} } \right] + \left[ {k_{NL14} } \right];$$

$$\left[ {k_{T8}^{e} } \right] = \left[ {k_{NL19} } \right] + \left[ {k_{NL12} } \right] + \left[ {k_{18} } \right] + \left[ {k_{20} } \right];\left[ {k_{T9}^{e} } \right] = \left[ {k_{NL13} } \right] + \left[ {k_{13} } \right] + \left[ {k_{15} } \right];\left[ {k_{T10}^{e} } \right] = \left[ {k_{14} } \right] + \left[ {k_{16} } \right];$$

$$\left[ {k_{T11}^{e} } \right] = \left[ {k_{NL15} } \right] + \left[ {k_{21} } \right] + \left[ {k_{23} } \right];\left[ {k_{T12}^{e} } \right] = \left[ {k_{22} } \right] + \left[ {k_{24} } \right];$$

$$\left[ {k_{T13}^{e} } \right] = \left[ {k_{NL16} } \right] + \left[ {k_{25} } \right] + \left[ {k_{27} } \right];\left[ {k_{T14}^{e} } \right] = \left[ {k_{26} } \right] + \left[ {k_{28} } \right] + \left[ {k_{32} } \right];\left[ {k_{T15}^{e} } \right] = \left[ {k_{T1} } \right] + \left[ {k_{T7} } \right] + \left[ {k_{T13} } \right];$$

$$\left[ {k_{T16}^{e} } \right] = \left[ {k_{T2} } \right] + \left[ {k_{T8} } \right] + \left[ {k_{T14} } \right];\left[ {k_{T17}^{e} } \right] = \left[ {k_{T5} } \right] + \left[ {k_{T9} } \right] + \left[ {k_{T11} } \right] + \left[ {k_{T29} } \right];$$

$$\left[ {k_{T17}^{e} } \right] = \left[ {k_{T5} } \right] + \left[ {k_{T9} } \right] + \left[ {k_{T11} } \right] + \left[ {k_{T29} } \right];\left[ {k_{T18}^{e} } \right] = \left[ {k_{T6} } \right] + \left[ {k_{T10} } \right] + \left[ {k_{T12} } \right] + \left[ {k_{30} } \right];$$

$$\begin{aligned} \left\{ {F_{{}}^{*} } \right\} = & \left( {\left\{ {F_{th} } \right\} + \left\{ {F_{th\_\phi } } \right\} + \left\{ {F_{th} \_\psi } \right\}} \right) - \left( {\left\{ {F_{tp1} } \right\} + \left\{ {F_{tp2} } \right\} + \left\{ {F_{tpN1} } \right\}} \right)V \hfill \\ & \quad +\left[ {k_{C18} } \right]\left[ {k_{C13} } \right]\left( {\left\{ {F_{rp1} } \right\} + \left\{ {F_{rp2} } \right\}} \right)V \hfill \\ \end{aligned}$$

(B1)

The following section shows the exploded form of rigidity matrices of Eq. (B1):

$$\left[ {D_{1} } \right] = \sum\limits_{N = 1}^{3} {\int\limits_{{h_{N} }}^{{h_{N + 1} }} {\left[ {\overline{Q}_{b}^{h} } \right]} \, {\text{d}}z;} \left[ {D_{2} } \right] = \sum\limits_{N = 1}^{3} {\int\limits_{{h_{N} }}^{{h_{N + 1} }} {\left[ {\overline{Q}_{b}^{h} } \right]} \left[ {Z_{1} } \right] \, } {\text{d}}z;\left[ {D_{3} } \right] = \sum\limits_{N = 1}^{3} {\int\limits_{{h_{N} }}^{{h_{N + 1} }} {\left\{ {\overline{e}_{b}^{h} } \right\}\frac{1}{h}} \, } {\text{d}}z;$$

$$\left[ {D_{4} } \right] = \sum\limits_{N = 1}^{3} {\int\limits_{{h_{N} }}^{{h_{N + 1} }} {\left\{ {\overline{q}_{b}^{h} } \right\}\frac{1}{h}} \, } {\text{d}}z;\left[ {D_{5} } \right] = \sum\limits_{N = 1}^{3} {\int\limits_{{h_{N} }}^{{h_{N + 1} }} {\left[ {Z_{1} } \right]^{T} \left[ {\overline{Q}_{b}^{h} } \right]} \, {\text{d}}z;} \left[ {D_{6} } \right] = \sum\limits_{N = 1}^{3} {\int\limits_{{h_{N} }}^{{h_{N + 1} }} {\left[ {Z_{1} } \right]^{T} \left[ {\overline{Q}_{b}^{h} } \right]} \left[ {Z_{1} } \right] \, {\text{d}}z;}$$

$$\left[ {D_{7} } \right] = \sum\limits_{N = 1}^{3} {\int\limits_{{h_{N} }}^{{h_{N + 1} }} {\left[ {z_{1} } \right]^{T} \left\{ {\overline{e}_{b}^{h} } \right\}\frac{1}{h}} \, {\text{d}}z;} \left[ {D_{8} } \right] = \sum\limits_{N = 1}^{3} {\int\limits_{{h_{N} }}^{{h_{N + 1} }} {\left[ {Z_{1} } \right]^{T} \left\{ {\overline{q}_{b}^{h} } \right\}} \frac{1}{h}{\text{d}}z;} \left[ {D_{9} } \right] = \sum\limits_{N = 1}^{3} {\int\limits_{{h_{N} }}^{{h_{N + 1} }} {\left[ {Z_{3} } \right]^{T} \left[ {\overline{Q}_{s}^{h} } \right]} \, {\text{d}}z;}$$

$$\left[ {D_{10} } \right] = \sum\limits_{N = 1}^{3} {\int\limits_{{h_{N} }}^{{h_{N + 1} }} {\left[ {Z_{3} } \right]^{T} \left[ {\overline{Q}_{s}^{h} } \right]} \left[ {Z_{3} } \right] \, {\text{d}}z;} \left[ {D_{11} } \right] = \sum\limits_{N = 1}^{3} {\int\limits_{{h_{N} }}^{{h_{N + 1} }} {\left[ {\overline{Q}_{s}^{h} } \right]} \, {\text{d}}z;}$$

$$\left[ {D_{12} } \right] = \sum\limits_{N = 1}^{3} {\int\limits_{{h_{N} }}^{{h_{N + 1} }} {\left[ {\overline{Q}_{s}^{h} } \right]} \left[ {Z_{3} } \right]{\text{d}}z;} \left[ {D_{13} } \right] = \int\limits_{{h_{N + 1} }}^{{h_{N + 2} }} {\left[ {\overline{Q}_{b}^{p} } \right]} \, {\text{d}}z;\left[ {D_{14} } \right] = \int\limits_{{h_{N + 1} }}^{{h_{N + 2} }} {\left[ {\overline{Q}_{b}^{p} } \right]} \left[ {Z_{2} } \right] \, {\text{d}}z;$$

$$\left[ {D_{14} } \right] = \int\limits_{{h_{N + 1} }}^{{h_{N + 2} }} {\left[ {\overline{Q}_{bs}^{p} } \right]} \, {\text{d}}z;\left[ {D_{15} } \right] = \int\limits_{{h_{N + 1} }}^{{h_{N + 2} }} {\left[ {\overline{Q}_{bs}^{p} } \right]} \left[ {Z_{5} } \right] \, {\text{d}}z;\left[ {D_{16} } \right] = \int\limits_{{h_{N + 1} }}^{{h_{N + 2} }} {\left\{ {e_{b}^{p} } \right\}\frac{1}{{h_{p} }}} \, {\text{d}}z;$$

$$\left[ {D_{17} } \right] = \int\limits_{{h_{N + 1} }}^{{h_{N + 2} }} {\left[ {Z_{2} } \right]^{T} \, \left[ {\overline{Q}_{b}^{p} } \right]} \, {\text{d}}z;\left[ {D_{17s} } \right] = \int\limits_{{h_{N + 1} }}^{{h_{N + 2} }} {\left[ {Z_{2} } \right]^{T} \, \left[ {\overline{Q}_{bs}^{p} } \right]} \, {\text{d}}z;\left[ {D_{18} } \right] = \int\limits_{{h_{N + 1} }}^{{h_{N + 2} }} {\left[ {Z_{2} } \right]^{T} \, \left[ {\overline{Q}_{b}^{p} } \right]} \left[ {Z_{2} } \right] \, {\text{d}}z;$$

$$\left[ {D_{19} } \right] = \int\limits_{{h_{N + 1} }}^{{h_{N + 2} }} {\left[ {Z_{2} } \right]^{T} \, \left[ {\overline{Q}_{bs}^{p} } \right]} \left[ {Z_{5} } \right] \, {\text{d}}z;\left[ {D_{20} } \right] = \int\limits_{{h_{N + 1} }}^{{h_{N + 2} }} {\left[ {Z_{2} } \right]^{T} \left\{ {e_{b}^{p} } \right\}\frac{1}{{h_{p} }}} \, {\text{d}}z;\left[ {D_{21} } \right] = \int\limits_{{h_{N + 1} }}^{{h_{N + 2} }} { \, \left[ {\overline{Q}_{bs}^{p} } \right]} \, {\text{d}}z;$$

$$\left[ {D_{22} } \right] = \int\limits_{{h_{N + 1} }}^{{h_{N + 2} }} { \, \left[ {\overline{Q}_{bs}^{p} } \right]} \left[ {Z_{5} } \right] \, {\text{d}}z;\left[ {D_{23} } \right] = \left[ {D_{16} } \right];\left[ {D_{24} } \right] = \int\limits_{{h_{N + 1} }}^{{h_{N + 2} }} { \, \left[ {Z_{5} } \right]^{T} \left[ {\overline{Q}_{bs}^{p} } \right]^{T} } {\text{d}}z;$$

$$\left[ {D_{25} } \right] = \int\limits_{{h_{N + 1} }}^{{h_{N + 2} }} { \, \left[ {Z_{5} } \right]^{T} \left[ {\overline{Q}_{bs}^{p} } \right]^{T} } \left[ {Z_{2} } \right]{\text{d}}z;\left[ {D_{25\_s} } \right] = \int\limits_{{h_{N + 1} }}^{{h_{N + 2} }} { \, \left[ {Z_{5} } \right]^{T} \left[ {\overline{Q}_{s}^{p} } \right]} \, {\text{d}}z;$$

$$\left[ {D_{26} } \right] = \int\limits_{{h_{N + 1} }}^{{h_{N + 2} }} { \, \left[ {Z_{5} } \right]^{T} \left[ {\overline{Q}_{s}^{p} } \right]^{T} } \left[ {Z_{5} } \right]{\text{d}}z;\left[ {D_{27} } \right] = \int\limits_{{h_{N + 1} }}^{{h_{N + 2} }} {\left[ {z_{5} } \right]^{T} \left\{ {e_{s}^{p} } \right\}\frac{1}{{h_{p} }}} \, {\text{d}}z;$$

$$\left[ {D_{28} } \right] = \int\limits_{{h_{N + 1} }}^{{h_{N + 2} }} { \, \left[ {\overline{Q}_{bs}^{p} } \right]^{T} } \left[ {Z_{2} } \right]{\text{d}}z;\left[ {D_{29} } \right] = \int\limits_{{h_{N + 1} }}^{{h_{N + 2} }} { \, \left[ {\overline{Q}_{s}^{p} } \right]} \, {\text{d}}z;\left[ {D_{30} } \right] = \int\limits_{{h_{N + 1} }}^{{h_{N + 2} }} { \, \left[ {\overline{Q}_{s}^{p} } \right]} \left[ {Z_{5} } \right]{\text{d}}z;$$

$$\left[ {D_{31} } \right] = \int\limits_{{h_{N + 2} }}^{{h_{N + 3} }} { \, \left[ {Z_{4} } \right]^{T} \left[ {\overline{Q}_{s}^{v} } \right] \, } {\text{d}}z;\left[ {D_{32} } \right] = \int\limits_{{h_{N + 2} }}^{{h_{N + 3} }} { \, \left[ {Z_{4} } \right]^{T} \left[ {\overline{Q}_{s}^{v} } \right]\left[ {Z_{4} } \right] \, } {\text{d}}z;\left[ {D_{33} } \right] = \int\limits_{{h_{N + 2} }}^{{h_{N + 3} }} { \, \left[ {\overline{Q}_{s}^{v} } \right] \, } {\text{d}}z;$$

$$\left[ {D_{34} } \right] = \int\limits_{{h_{N + 2} }}^{{h_{N + 3} }} { \, \left[ {\overline{Q}_{s}^{v} } \right]\left[ {Z_{4} } \right] \, } {\text{d}}z;\left[ {D_{35} } \right] = \left[ {D_{3} } \right]^{T} ;\left[ {D_{36} } \right] = \sum\limits_{N = 1}^{3} {\int\limits_{{h_{N} }}^{{h_{N + 1} }} {\left\{ {e_{b}^{h} } \right\}\frac{1}{h}\left[ {Z_{1} } \right]} \, {\text{d}}z;}$$

$$\left[ {D_{37} } \right] = \sum\limits_{N = 1}^{3} {} \int\limits_{{h_{N} }}^{{h_{N + 1} }} {\frac{{\overline{ \in }_{33}^{h} }}{h}} \, {\text{d}}z;\left[ {D_{38} } \right] = \sum\limits_{N = 1}^{3} {\int\limits_{{h_{N} }}^{{h_{N + 1} }} {\frac{{\overline{d}_{33}^{h} }}{h}} \, {\text{d}}z;} \left[ {D_{39} } \right] = \left[ {D_{4} } \right]^{T} ;$$

$$\left[ {D_{40} } \right] = \sum\limits_{N = 1}^{3} {\int\limits_{{h_{N} }}^{{h_{N + 1} }} {\left\{ {q_{b}^{h} } \right\}\frac{1}{h}\left[ {Z_{1} } \right]} \, {\text{d}}z;} \;\left[ {D_{41} } \right] = \left[ {D_{38} } \right];\;\left[ {D_{42} } \right] = \sum\limits_{N = 1}^{3} {\int\limits_{{h_{N} }}^{{h_{N + 1} }} {\frac{{\overline{\mu }_{33}^{h} }}{h} \, } {\text{d}}z;}$$

(B2)