Rainfall-derived growing season characteristics for agricultural impact assessments in South Africa

Abstract

Precipitation variability imposes significant pressure in areas where agricultural practice is dominated by smallholder farmers who are dependent on subsistence farming. Advances in the understanding of this variability, in both time and space, have an important role to play in increasing the resilience of agricultural systems. The need is particularly pressing in regions of the world such as the African continent, which is already affected by multiple stresses including poverty and economic and political instability. In this paper, we explore the use of generalised linear models (GLMs) for this purpose, via a case study from north-east South Africa. A GLM is used to link the local rainfall variability to large-scale climate drivers identified from previous subcontinental-scale analyses, and the ability of the resulting model to simulate precipitation features that are relevant in agricultural applications is evaluated. We focus in particular on a set of growing season indices, proposed for the investigation of intraseasonal characteristics relevant for maize production in the region. Seven indices were computed from spatially averaged daily rainfall series from nine stations in the study area. As a first attempt to use GLMs for this type of application, the results are encouraging and suggest that the models are able to reproduce a range of agriculture-relevant indices. However, further research into spatial correlation structure is recommended to improve the multisite generation of the rainfall-derived characteristics.

Appendices

Appendix

1.1 Inter-site dependence for rainfall occurrence

In this Appendix, we provide some implementation details for the latent Gaussian scheme used to represent inter-site dependence in rainfall occurrence via Eq. 3. As described there, the latent correlation for a pair of sites can be estimated so as to match the proportion of days for which both sites experience rain. Specifically, suppose there are n days for which observations are available at both sites $s_{1}$ and $s_{2}$; let $Y_{s_{1}t}$ and $Y_{s_{1}t}$ be indicator variables taking the value 1 if the corresponding sites experience rain on day t and 0 otherwise. The observed proportion of days for which both sites experience rain is thus $n^{-1} \sum _{t} Y_{s_{1}t}Y_{s_{2}t}$, where the sum is over days for which both sites have data. The expected proportion is $n^{-1} \sum _{t} P\left (Z_{s_{1}} > \lambda _{s_{1}t},Z_{s_{1}} > \lambda _{s_{2}t}\right )$, similarly (recall that the thresholds $\lambda _{s_{1}t}$ and $\lambda _{s_{2}t}$ depend on the probabilities derived from the occurrence model). Thus, we choose the correlation $\rho _{s_{1}s_{2}}$ to solve the equation

$$ \sum\limits_{t} P\left(Z_{s_{1}} > \lambda_{s_{1}t},Z_{s_{2}} > \lambda_{s_{2}t}\right) = \sum\limits_{t} Y_{s_{1}t}Y_{s_{2}t} \ . $$

(4)

For a given value of $\rho _{s_{1}s_{2}}$, the probability on the left-hand side of Eq. 4 can be calculated using algorithms such as that of Donnelly (1973). A numerical search is then carried out to solve the equation for $\rho _{s_{1}s_{2}}$. This is significantly more accurate and faster than the simulation-based procedure of Wilks (1998) and Brissette et al. (2007).

A potential problem here is that the matrix obtained by solving Eq. 4 for each pair of sites is not guaranteed to be positive definite and is therefore not necessarily a valid correlation matrix (in other words, the latent correlations estimated in this way are not guaranteed to be mutually consistent). This can cause simulation algorithms to fail. The difficulty can be overcome by fitting a valid spatial (distance-dependent) correlation function to the estimated latent correlations, for example, by minimising a weighted sum of squared differences between the modelled and estimated correlations where the weights are proportional to the sample sizes for each site pair.

Another potential problem is that a solution to Eq. 4 is not guaranteed. This is because as $\rho _{s_{1}s_{2}}$ varies from its minimum value of $-$1 to its maximum value of $+1$, $P(Y_{s_{1}t} = Y_{s_{2}t} = 1)$ can be shown to vary correspondingly from $\max \left (p_{s_{1}t}+p_{s_{2}t}-1,0\right )$ to $\min \left (p_{s_{1}t}, p_{s_{2}t}\right )$. Here, $p_{s_{1}t}$ and $p_{s_{2}t}$ are the rainfall occurrence probabilities derived from model 1. Thus, the left-hand side of Eq. 4 is constrained to lie in the range

$$\sum\limits_{t} \left[\max\left(p_{s_{1}t}+p_{s_{2}t}-1,0\right), \min\left(p_{s_{1}t}, p_{s_{2}t}\right) \right]\ .$$

However, the right-hand side is not so constrained and—either due to sampling variation or to slight misspecification of the modelled occurrence probabilities—can occasionally produce values outside this range. If this occurs for a pair of sites, the corresponding latent correlation can be estimated as −1 or +1 as appropriate.

Having estimated the inter-site latent correlation matrix, simulation of a dependent vector of rainfall occurrence indicators is straightforward: for each day of simulation, calculate the marginal probabilities as predicted by the occurrence model, simulate a vector $\mathbf {Z}$ from a multivariate normal distribution with the specified correlation structure and then threshold the simulated Zs according to Eq. 3.

Imputation of missing values in historical records is more difficult, however. It requires the ability to simulate from the conditional distribution of $\mathbf {Z}$ given the observed elements of $\mathbf {Y}_{t}$; then, the missing observations can be generated by thresholding the elements of $\mathbf {Z}$ as before. The problem is in simulating from the conditional distribution of $\mathbf {Z}$. A naïve algorithm is as follows:

• 1. Sample a value of $\mathbf {Z}$ from its unconditional distribution.

• 2. If all of the observed elements of $\mathbf {Y}_{t}$ are consistent with the corresponding elements of $\mathbf {Z}$, continue; otherwise, reject the sampled $\mathbf {Z}$ and return to step 1.

This is essentially the algorithm proposed by Wilks (2009). The problem here is that if observations are available at many sites, a large number of attempts will be required to obtain a value of $\mathbf {Z}$ that is consistent with all of the available observations. This makes the algorithm very slow, and a more refined approach is needed.

We proceed in two stages. Specifically, denote by $\tilde {\mathbf {Y}}_{t}$ the vector of non-missing components of $\mathbf {Y}_{t}$ (i.e. components for which observations are available) and by $\tilde {\mathbf {Z}}$ the corresponding elements of $\mathbf {Z}$. Then, the first step is to sample from the joint distribution of $\tilde {\mathbf {Z}}$ conditional on $\tilde {\mathbf {Y}}_{t}$; the second step is to sample the remaining elements of $\mathbf {Z}$ from their distribution given $\tilde {\mathbf {Z}}$ (which is straightforward since the joint distribution is multivariate normal) and to threshold these remaining sampled elements to impute the missing values of $\mathbf {Y}_{t}$. Efficient sampling from the distribution of $\tilde {\mathbf {Z}} |\tilde {\mathbf {Y}}_{t}$ itself is non-trivial: the algorithm implemented here is a Gibbs sampler (Gelman et al. 2004, Section 11.3) in which the elements of $\tilde {\mathbf {Z}}$ are initialised independently by sampling from normal distributions truncated at the corresponding thresholds $\{\lambda _{st}\}$, and then, each element of $\tilde {\mathbf {Z}}$ is visited in turn and updated by sampling from its conditional distribution given the current configuration of the remaining elements and of $\tilde {\mathbf {Y}}$. Specifically, according to the model considered here, the unconditional distribution of $\tilde {\mathbf {Z}}$ is multivariate normal with mean $\mathbf {0}$ and covariance matrix $\mathbf {\Sigma }$, say. Let $\tilde {Z}_{i}$ denote the ith element of $\tilde {\mathbf {Z}}$ and let $\tilde {Z}_{(-i)}$ denote the vector of the remaining elements. Moreover, let $\sigma ^{(ii)}$ denote the ith diagonal element of $\mathbf {\Sigma }^{-1}$ and let $\mathbf {\Sigma }^{-1}_{(i,-i)}$ denote the ith row of $\mathbf {\Sigma }^{-1}$ with the ith element removed. Then, using standard results for conditioning in the multivariate normal distribution (Krzanowski 1988), Section 7.2, as well as the formula for the inverse of a partitioned matrix (Horn and Johnson 1985), p. 18, it may be shown that the distribution of $\tilde {Z}_{i}$ given $\tilde {\mathbf {Z}}_{(-i)}$ is normal with mean $-\mathbf {\Sigma }^{-1}_{(i,-i)}\tilde {\mathbf {Z}}_{(-i)} / \sigma ^{(ii)}$ and variance $1 / \sigma ^{(ii)}$. To update the value of $\tilde {Z}_{i}$ therefore requires sampling from this normal distribution, truncated as appropriate for consistency with the corresponding observation $\tilde {Y}_{i}$, say.

In the present context, a single iteration of the Gibbs sampler consists of a sequence of updates in which every element of $\tilde {\mathbf {Z}}$ is visited once. If the procedure is repeated for a large number of iterations, the resulting $\tilde {\mathbf {Z}}$ will be sampled approximately from the required distribution. There is a trade-off between accuracy and speed: more iterations improve the approximation in the sampling, but at the expense of increased simulation time. For the purposes of imputing binary wet/dry indicators however, excessive accuracy is probably unnecessary and speed of execution is a priority. Some experimentation suggests that for practical purposes, just 10 Gibbs iterations are sufficient here; this provides a fast and accurate imputation procedure.

Logistic regression model for rainfall occurrence

The baseline occurrence model includes terms representing regional variation, seasonality and autocorrelation. Even though the study area is not particularly large, the topographic complexity requires the inclusion of Legendre polynomials up to degree 4. The topographic variation was computed over a 30 × 30-km² area. A west–east slope (over 30 × 30 km²) term also proved to be significant, possibly due to the moisture flow coming primarily from the South Indian Ocean. The temporal autocorrelation structure has been included using the persistence indicator and the previous rainfall occurrence at lags of 1 and 2 days transformed using a distance-based weighted average across all sites, with weights decreasing with distance from the current site.

In addition to main effects, the model includes significant two- and three-way interactions. These interactions suggest that the contribution of the altitude and the autocorrelation structure varies across the area of study.

Out of the four climate drivers identified from the subcontinental scale analysis as drivers of southern African rainfall variability (see Table 1), only two proved to be statistically significant at local scale in the occurrence model: relative humidity (RHUM) and southern hemisphere temperature (SHT). The effect of the SHT index is a linear function of longitude and stronger in the far west of the area, where the overall effect of an increasing SHT can be linked to a decrease in rainfall probabilities. A similar pattern was found in all of southern Africa (Ambrosino et al. 2011). The modelled effect of the RHUM index varies across the region and seasons. The strongest effect is during the rainy season and in the far north-eastern corner of the region. In general, an overall increase in the index is associated with an increase in the probabilities of rainfall in the summer months (wet season). A similar pattern is found in winter (dry season). However, because it is the dry season, the effect on the precipitation occurrences is almost negligible. The results are comparable to those obtained by Ambrosino et al. (2011).

To check for unexplained systematic structure in the final model, mean Pearson residuals were computed for each month of the year, each year of record and each site. No clear structure was visible in the monthly residual means apart from a sequence of negative values during the dry season (May–October), where the model seemed to overestimate the probability of precipitation. However, the performance of the model during the dry season is relatively unimportant for agricultural applications. There was some suggestion of a multidecadal oscillation in the annual means, but this could not be explained by any of the other climate drivers identified in Ambrosino et al. (2011).

The Pearson residual means for each site are shown in Fig. 8a. Thick lines correspond to residual means that are significantly different from zero at the 5 % level. By definition, if the model spatial structure is correct, this should occur at around 5 % of the sites. That is not the case here, although no clear structure is recognisable. For example, in the north of the domain, the cluster of sites from site 37 to 48 all have residuals that differ significantly from zero but in different directions. In the south-east, the residual mean for site 15 is significantly different from zero and positive but surrounded by negative residual means at sites 13, 16 and 17. Such inconsistencies were also experienced in a similar case study for a smaller and flatter area in southern England by Yang et al. (2005). Inconsistencies of this type between neighbouring stations must be due either to very local-scale climatological variations or to differences in observer practice. Since the model already contains a very flexible representation of smooth spatial variation, it is not considered worthwhile to try and improve the fit further.

Fig. 8

Occurrence (a) and amounts (b) model mean Pearson residuals by site on a topographic map of the region. The black dots represent the station locations, circles the mean residuals and solid lines for positive and dashed for negative residuals. The thick lines indicate mean residuals that are significantly different from zero at the 5 % level. Circle sizes are indicative only

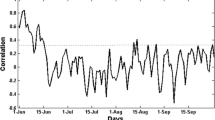
For simulation purposes, a latent Gaussian correlation model has been used as described above. Figure 9a shows the estimated latent inter-site correlations as a function of inter-site distance, together with the fitted correlation model (which is a Matérn function).

Fig. 9

Spatial correlation structure for the occurrence (a) and amounts (b) model fitted to pairs of inter-site correlations according to their inter-site distances

1.1 Gamma distribution model for rainfall amounts

Gamma distributions are fitted to the same dataset on wet days only, in a model of the form given by Eq. 2. Once again, a large number of terms are needed to represent the complex geography of the area: four degrees of Legendre polynomials, a west–east slope over 30 × 30 km² consistently with the Indian Ocean being the primary source of moisture for the region), and, as for the occurrence model, the mapped altitude and the standard deviation of the altitude over 30 × 30 km².

The autocorrelation structure is expressed using the logarithm of one and two previous days rainfall amounts, once again transformed using a distance-based weighted average across all sites. The covariate at site s and day t can be expressed as

$$\ln\left(1 + \sum\limits_{r} w_{r,s} \log\left(1+Y_{[t-k]}^{(r)}\right)\right) $$

where the weights ${w_{r,s}}$, associated with site r when predicting for site s, sum to 1 and are proportional to exp$[-ad_{r,s}]$ (Chandler 2002).

Similarly, a 2-day persistence indicator and Fourier terms representing the annual cycle and its first and second harmonic are included. In addition, the model contains a smooth month adjustment for August due to high Pearson residual means previously found under a sine and cosine wave model only. The adjustment allows to smoothly model a departure from the overall seasonal cycle avoiding unnatural discontinuities, reaching the maximum value of 1 in the middle of the month and smoothly decaying to 0 at the ends (Chandler and Wheater 2002).

Geographical interactions include latitude and longitude with altitude terms and, similarly to the occurrence model, west–east slope.

With respect to the subcontinental study (Ambrosino et al. 2011), time-varying climate indices such as relative humidity, El Niño, SHT and South-West Indian Ocean Index, and their interactions, retained their significance in explaining part of the variability in daily rainfall amounts for the study area.

After finalising the model, Pearson residual means were inspected to check for unexplained structure. They showed no obvious seasonal structure nor was there any inter-annual structure, in contrast with the multidecadal oscillation found in the occurrence model. Once again, however, spatial inconsistencies are visible when the Pearson residual means are plotted by site in Fig. 8b—despite the inclusion of 22 terms (including interactions) in the model to represent the systematic regional variation. However, the spatial inconsistencies are less dramatic than for the occurrence model. As before, the complexity of the geography cannot be resolved further without risking overfitting the model; therefore, the results have been considered as good as can realistically be achieved.

To represent inter-site dependence in rainfall amounts, a spatial correlation model was fitted to the Anscombe residuals. Figure 9b shows the Anscombe residual correlations and the fitted model, which here is of powered exponential form.