Experimental validation of compact damping models of perforated MEMS devices

Abstract

Measured damping coefficients of six different perforated micromechanical test structures are compared with damping coefficients given by published compact models. The motion of the perforated plates is almost translational, the surface shape is rectangular, and the perforation is uniform validating the assumptions made for compact models. In the structures, the perforation ratio varies from 24 to 59%. The study of the structure shows that the compressibility and inertia do not contribute to the damping at the frequencies used (130–220 kHz). The damping coefficients given by all four compact models underestimate the measured damping coefficient by approximately 20%. The reasons for this underestimation are discussed by studying the various flow components in the models.

Appendix

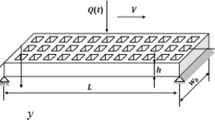
This Appendix contains equations for four compact models M1,…, M4. The dimensions and symbols in Fig. 1 are used: the length and width of the perforated plate are L and W. The side lengths of the square holes and the square perforation cells are s ₀ and s _X  = s ₀ + s ₁, respectively. Figure 6 shows the structure of a perforation cell and the internal lumped flow resistances used in models M3,…, M6.

1.1 Model M1 equations

The equations for a narrow hole plate (L ≫ W) are given in (Bao et al. 2003). Note, in the following equations a = W/2 and b = L/2. The equivalent radii for the circular cell and hole are given in Eqs. 8 and 9. The damping coefficient c is

$$ c = 2aL\frac{{8\mu h_{\text{C}} }}{{\beta^{2} r_{0}^{2} }}\left( {1 + \frac{{3r_{0}^{4} K(\beta )}}{{16h_{\text{C}} h^{3} }}} \right)\left[ {1 - \frac{l}{a}\tanh \left( {\frac{a}{l}} \right)} \right] $$

where

$$ \begin{gathered} K\left( \beta \right) = 4\beta^{2} - \beta^{4} - 4\ln \beta - 3 \hfill \\ l = \sqrt {\frac{{2h^{3} H_{\text{eff}} \eta \left( \beta \right)}}{{3\beta^{2} r_{0}^{2} }}} \hfill \\ \eta \left( \beta \right) = 1 + \frac{{3r_{0}^{4} K\left( \beta \right)}}{{16h_{\text{C}} h^{3} }} \hfill \\ \beta = \frac{{r_{0} }}{{r_{C} }} \hfill \\ H_{\text{eff}} = h_{\text{C}} + \frac{{3\pi r_{0} }}{8} \hfill \\ \end{gathered} $$

1.2 Model M2 equations

The equations for an arbitrary shaped rectangular plate are also included in (Bao et al. 2003). Also, in the following equations a = W/2 and b = L/2. The equivalent radii for the circular cell and hole are given in Eqs. 8 and 9. The damping coefficient c is

$$ c = - \gamma \frac{{\mu \left( {2a} \right)^{3} \left( {2b} \right)}}{{h^{3} }} $$

where

$$ \begin{aligned} \gamma = 3\alpha^{2} & - 6\alpha^{3} \frac{{\sinh^{2} \left( {1/\alpha } \right)}}{{\sinh \left( {2/\alpha } \right)}} - \\ & \frac{{24\alpha^{3} \kappa }}{{\pi^{2} }}\sum\limits_{n = 1,3,5, \ldots }^{\infty } {\frac{{\tanh \frac{{\sqrt {1 + \left( {n\pi \alpha /2} \right)^{2} } }}{\alpha \kappa }}}{{n^{2} \left[ {1 + \left( {n\pi \alpha /2} \right)^{2} } \right]^{{\frac{3}{2}}} }}} \\ \end{aligned} $$

$$ \kappa = \frac{a}{b},\quad \alpha = \frac{l}{a} $$

Above, l is the same as used in M1 equations.

1.3 Model M3 equations

A model for a circular perforation cell is derived in (Veijola 2006a), and the damping coefficient of a rectangular perforated plate is given in the paper. Note, in the following equations a = W and b = L. The equivalent radii for the circular cell and hole are given in Eqs. 8 and 9. The damping coefficient c is

$$ c = \sum\limits_{m = 1,3,5, \ldots }^{\infty } {\sum\limits_{n = 1,3,5, \ldots }^{\infty } {\frac{1}{{G_{m,n} \left( {a_{\text{eff}} ,b_{\text{eff}} } \right) + 1/R_{m,n} }}} } $$

(11)

Where the effective surface dimensions are

$$ \begin{gathered} a_{\text{eff}} = a + 1.3\left( {1 + 3.3K_{\text{ch}} } \right)h \hfill \\ b_{\text{eff}} = b + 1.3\left( {1 + 3.3K_{\text{ch}} } \right)h \hfill \\ \end{gathered} $$

and

$$ \begin{gathered} G_{m,n} \left( {a,b} \right) = \left( {\frac{{m^{2} }}{{a^{2} }} + \frac{{n^{2} }}{{b^{2} }}} \right)\frac{{m^{2} n^{2} \pi^{6} h^{3} Q_{\text{ch}} }}{{ 7 6 8\mu {\text{ab}}}} \hfill \\ R_{m,n} = \frac{{64MNR_{\text{P}} }}{{m^{ 2} n^{2} \pi^{4} }} \hfill \\ \end{gathered} $$

The flow resistance of a single perforation cell is

$$ \begin{gathered} R_{\text{P}} = R_{\text{S}} + R_{\text{IS}} + R_{\text{IB}} + \frac{{r_{X}^{ 4} }}{{r_{ 0}^{ 4} }}\left( {R_{\text{IC}} + R_{\text{C}} + R_{\text{E}} } \right) \hfill \\ R_{\text{S}} = \frac{{12\pi \mu r_{X}^{ 4} }}{{Q_{\text{ch}} h^{3} }}\left( {\frac{1}{2}\ln \frac{{r_{X} }}{{r_{0} }} - \frac{3}{8} + \frac{{r_{0}^{2} }}{{2r_{X}^{ 2} }} - \frac{{r_{0}^{4} }}{{8r_{X}^{ 4} }}} \right) \hfill \\ R_{\text{IS}} = \frac{{6\pi \mu \left( {r_{X}^{ 2} - r_{0}^{2} } \right)^{2} }}{{r_{0} h^{2} }}\Updelta_{\text{S}} \hfill \\ R_{\text{IB}} = 8\pi \mu r_{0} \Updelta_{\text{B}} \hfill \\ R_{\text{IC}} = 8\pi \mu r_{0} \Updelta_{\text{C}} \hfill \\ R_{\text{C}} + R_{\text{E}} = 8\pi \mu \left( {\frac{{h_{\text{C}} }}{{Q_{\text{tb}} }} + \Updelta_{\text{E}} r_{0} } \right) \hfill \\ \end{gathered} $$

where the elongations are

$$ \begin{gathered} \Updelta_{\text{S}} = \frac{{0.56 - 0.32\frac{{r_{0} }}{{r_{X} }} + 0.86\frac{{r_{0}^{2} }}{{r_{X}^{2} }}}}{{1 + 2.5K_{\text{ch}} }} \hfill \\ \Updelta_{\text{B}} = 1.33\left( {1 - 0.812\frac{{r_{0}^{2} }}{{r_{X}^{2} }}} \right)\frac{{1 + 0.732K_{\text{tb}} }}{{1 + K_{\text{ch}} }}f_{\text{B}} \left( {\frac{{r_{0} }}{h},\frac{{h_{\text{C}} }}{h}} \right) \hfill \\ \end{gathered} $$

$$ \begin{aligned} \Updelta_{\text{C}} = \left( {1 + 6K_{\text{tb}} } \right)\left( {0.66 - 0.41\frac{{r_{0} }}{{r_{X} }} - 0.25\frac{{r_{0}^{2} }}{{r_{X}^{2} }}} \right) \\ \Updelta_{\text{E}} = & \frac{{0.944 \times 3\pi \left( {1 + 0.216K_{\text{tb}} } \right)}}{16} \times \\ & \left( {1 + 0.2\frac{{r_{0}^{2} }}{{r_{X}^{2} }} - 0.754\frac{{r_{0}^{4} }}{{r_{X}^{4} }}} \right)f_{\text{E}} \left( {\frac{{r_{0} }}{h}} \right) \\ \end{aligned} $$

where the functions are

$$ \begin{gathered} f_{\text{B}} \left( {x,y} \right) = 1 + \frac{{x^{4} y^{3} }}{{7.11\left( {43y^{3} + 1} \right)}} \hfill \\ f_{\text{E}} \left( x \right) = 1 + \frac{{x^{3.5} }}{{178\left( {1 + 17.5K_{\text{ch}} } \right)}} \hfill \\ \end{gathered} $$

The flow rate coefficients and Knudsen numbers for the air gap and the holes are

$$ \begin{gathered} Q_{\text{ch}} = 1 + 6K_{\text{ch}} ,\quad K_{\text{ch}} = \frac{\lambda }{h} \hfill \\ Q_{\text{tb}} = 1 + 4K_{\text{tb}} ,\quad K_{\text{tb}} = \frac{\lambda }{{r_{0} }} \hfill \\ \end{gathered} $$

1.4 Model M4 equations

A model for a rectangular perforation cell has been given in (Veijola 2006b). Note, in the following equations a = W and b = L. The damping coefficient c is given by Eq. 11, where R _P for a rectangular hole is

$$ \begin{gathered} R_{\text{P}} = R_{\text{S}} + R_{\text{IS}} + R_{\text{IB}} + \frac{{s_{X}^{ 4} }}{{s_{ 0}^{ 4} }}\left( {R_{\text{IC}} + R_{\text{C}} + R_{\text{E}} } \right) \hfill \\ R_{\text{S}} = \frac{{12\pi \mu r_{\text{X}}^{ 4} }}{{Q_{\text{ch}} h^{3} }}\left( {\frac{1}{2}\ln \frac{{r_{\text{X}} }}{{r_{{0{\text{E}}}} }} - \frac{3}{8} + \frac{{r_{{0{\text{E}}}}^{2} }}{{2r_{\text{X}}^{ 2} }} - \frac{{r_{{0{\text{E}}}}^{4} }}{{8r_{\text{X}}^{ 4} }}} \right) \hfill \\ R_{\text{IS}} = \frac{{3\mu \left( {s_{\text{X}}^{ 2} - s_{0}^{2} } \right)^{2} }}{{s_{0} h^{2} }}\Updelta_{\text{S}} \hfill \\ R_{\text{IB}} = 0 \hfill \\ R_{\text{IC}} = 28.454\mu s_{0} \Updelta_{\text{C}} \hfill \\ R_{\text{C}} + R_{\text{E}} = 28.454\mu \left( {\frac{{h_{\text{C}} }}{{Q_{\text{sq}} }} + \Updelta_{\text{E}} s_{0} } \right) \hfill \\ \end{gathered} $$

where the elongations are

$$ \begin{gathered} \Updelta_{\text{S}} = 0.122\left( {1 + 6.5\xi - 3.8\xi^{2} } \right) \hfill \\ \Updelta_{\text{C}} = 0.302 \hfill \\ \Updelta_{\text{E}} = 0.242\left( {1 + 4K_{\text{sq}} } \right)\left( {1 - \xi^{4} } \right)\left( {1 + 0.019\left( {\frac{{s_{0} }}{h}} \right)^{2.83} } \right) \hfill \\ \end{gathered} $$

where

$$ \xi = \frac{{s_{0} }}{{s_{X} }} $$

The equation for Δ_E includes a misprint in (Veijola 2006b). The corrected equation is shown above. The flow rate coefficients and Knudsen numbers for the square hole are

$$ Q_{\text{sq}} = 1 + 7.567K_{\text{sq}} ,\quad K_{\text{sq}} = \frac{\lambda }{{s_{0} }} $$

The effective radius is

$$ r_{{0{\text{E}}}} = \frac{{0.58076s_{0} }}{{1 + 0.02108\xi^{2} + 0.008\xi^{4} }} $$