A P-spline ANOVA type model in space-time disease mapping

Abstract

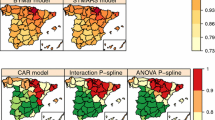
One of the main objectives in disease mapping is the identification of temporal trends and the production of a series of smoothed maps from which spatial patterns of mortality risks can be monitored over time. When studying rare diseases, conditional autoregressive models have been commonly used for smoothing risks. In this work, a P-spline ANOVA type model is used instead. The model is anisotropic and explicitly considers different smooth terms for space, time, and space-time interaction avoiding, in addition, model identifiability problems. The mean squared error of the log-risk predictor is derived accounting for the variability associated to the estimation of the smoothing parameters. The procedure is illustrated analyzing Spanish prostate cancer mortality data in the period 1975–2008.

Appendix

In this section, detailed expressions for ${{\partial{\bf G}}\over {\partial\lambda_j}}$ and ${{\partial{\bf V}^{-1}}\over {\partial\lambda_j}}$ are provided.

$${\frac{\partial{\mathbf G}}{\partial\lambda_j}}= {\frac{\partial{\mathbf F}^{-1}}{\partial\lambda_j}}= -{\mathbf F}^{-1}{\frac{\partial{\mathbf F}}{\partial\lambda_j}}{\mathbf F}^{-1},\\ {\frac{\partial{\mathbf V}^{-1}}{\partial\lambda_j}} = -{\mathbf V}^{-1}{\frac{\partial{\mathbf V}}{\partial\lambda_j}}{\mathbf V}^{-1}={\mathbf V}^{-1}{\mathbf Z}{\mathbf F}^{-1}{\frac{\partial{\mathbf F}}{\partial\lambda_j}}{\mathbf F}^{-1}{\mathbf Z}'{\mathbf V}^{-1}.$$

In this model there are six variance components corresponding to the smoothing parameters of the ANOVA type model

$$ {{\varvec{\uplambda}}}=(\lambda_1,\lambda_2,\lambda_t,\tau_1,\tau_2,\tau_t)', $$

and then

$$ \frac{\partial{\bf F}}{\partial\lambda_j}=\hbox{diag} \left(\frac{\partial{\bf F}_{1}}{\partial\lambda_j}, \frac{\partial{\bf F}_{2}}{\partial\lambda_j},\frac{\partial{\bf F}_{3}}{\partial\lambda_j},\frac{\partial{\bf F}_{4}} {\partial\lambda_j}, \frac{\partial{\bf F}_{5}} {\partial\lambda_j},\frac{\partial{\bf F}_{6}} {\partial\lambda_j},\frac{\partial{\bf F}_{7}} {\partial\lambda_j}, \frac{\partial{\bf F}_{8}} {\partial\lambda_j},\frac{\partial{\bf F}_{9}} {\partial\lambda_j},\frac{\partial{\bf F}_{10}} {\partial\lambda_j},\frac{\partial{\bf F}_{11}} {\partial\lambda_j} \right), $$

with λ _j denoting the jth component of λ.

$$ \begin{aligned} & {{\partial{\bf F}_{1}}\over {\partial\lambda_1}} = {\bf 0}, \quad {{\partial{\bf F}_{1}}\over {\partial\lambda_2}} = \widetilde{{\bf{\Upsigma}}}_2\otimes{\bf I}_{2}, \quad {{\partial{\bf F}_{1}}\over {\partial\lambda_t}} = {{\partial{\bf F}_{1}}\over {\partial\tau_i}} = {\bf 0}, \\ & {{\partial{\bf F}_{2}}\over {\partial\lambda_1}} = {\bf I}_{2}\otimes\widetilde{{\bf{\Upsigma}}}_1, \quad {{\partial{\bf F}_{2}}\over {\partial\lambda_2}} = {{\partial{\bf F}_{2}}\over {\partial\lambda_t}} = {{\partial{\bf F}_{2}}\over {\partial\tau_i}} = {\bf 0}, \\ & {{\partial{\bf F}_{3}}\over {\partial\lambda_1}} ={\bf I}_{c_2-2}\otimes\widetilde{{\bf{\Upsigma}}}_1, \quad {{\partial{\bf F}_{3}}\over {\partial\lambda_2}} =\widetilde{{\bf{\Upsigma}}}_2\otimes{\bf I}_{c_1-2}, \quad {{\partial{\bf F}_{3}}\over {\partial\lambda_t}} = {{\partial{\bf F}_{3}}\over {\partial\tau_i}} = {\bf 0}, \\ & {{\partial{\bf F}_{4}}\over {\partial\lambda_1}} = {{\partial{\bf F}_{4}}\over {\partial\lambda_2}} = {\bf 0},\quad {{\partial{\bf F}_{4}}\over {\partial\lambda_t}} = \widetilde{{\bf{\Upsigma}}}_3, \quad {{\partial{\bf F}_{4}}\over {\partial\tau_i}} = {\bf 0}, \\ & {{\partial{\bf F}_{5}}\over {\partial\lambda_i}} = {{\partial{\bf F}_{5}}\over {\partial\tau_1}} = {\bf 0},\quad {{\partial{\bf F}_{5}}\over {\partial\tau_2}} = \widetilde{{\bf{\Upsigma}}}_2\otimes{\bf I}_{2},\quad {{\partial{\bf F}_{5}}\over {\partial\tau_t}} = {\bf 0}, \\ & {{\partial{\bf F}_{6}}\over {\partial\lambda_1}} = {{\partial{\bf F}_{6}}\over {\partial\lambda_2}} = {{\partial{\bf F}_{6}}\over {\partial\lambda_t}} = {\bf 0},\quad {{\partial{\bf F}_{6}}\over {\partial\tau_1}} = {\bf I}_{2}\otimes\widetilde{{\bf{\Upsigma}}}_1,\quad {{\partial{\bf F}_{6}}\over {\partial\tau_2}} = {{\partial{\bf F}_{6}}\over {\partial\tau_t}} = {\bf 0}, \\ & {{\partial{\bf F}_{7}}\over {\partial\lambda_i}} = {\bf 0}, \quad {{\partial{\bf F}_{7}}\over {\partial\tau_1}} = {\bf I}_{c_2-2}\otimes\widetilde{{\bf{\Upsigma}}}_1,\quad {{\partial{\bf F}_{7}}\over {\partial\tau_2}} = \widetilde{{\bf{\Upsigma}}}_2\otimes{\bf I}_{c_1-2}\quad {{\partial{\bf F}_{7}}\over {\partial\tau_t}} = {\bf 0}, \\ & {{\partial{\bf F}_{8}}\over {\partial\lambda_i}} = {{\partial{\bf F}_{8}}\over {\partial\tau_1}} = {{\partial{\bf F}_{8}}\over {\partial\tau_2}} = {\bf 0}, \quad {{\partial{\bf F}_{8}}\over {\partial\tau_t}} = {\bf I}_{3}\otimes\widetilde{{\bf{\Upsigma}}}_t \\ & {{\partial{\bf F}_{9}}\over {\partial\lambda_i}} = {{\partial{\bf F}_{9}}\over {\partial\tau_1}} = {\bf 0}, \quad {{\partial{\bf F}_{9}}\over {\partial\tau_2}} = \widetilde{{\bf{\Upsigma}}}_2\otimes{\bf I}_{2}\otimes{\bf I}_{{c_t}-2}, \quad {{\partial{\bf F}_{9}}\over {\partial\tau_t}} = {\bf I}_{c_2-2}\otimes{\bf I}_{2}\otimes\widetilde{{\bf{\Upsigma}}}_t, \\ & {{\partial{\bf F}_{10}}\over {\partial\lambda_i}} = {\bf 0}, \quad {{\partial{\bf F}_{10}}\over {\partial\tau_1}} = {\bf I}_{2}\otimes\widetilde{{\bf{\Upsigma}}}_1\otimes{\bf I}_{{c_t}-2},\quad {{\partial{\bf F}_{10}}\over {\partial\tau_2}} = {\bf 0},\quad {{\partial{\bf F}_{10}}\over {\partial\tau_t}} = {\bf I}_{2}\otimes{\bf I}_{c_1-2}\otimes\widetilde{{\bf{\Upsigma}}}_t. \\ & {{\partial{\bf F}_{11}}\over {\partial\lambda_i}} = {\bf 0},\quad {{\partial{\bf F}_{11}}\over {\partial\tau_1}} = {\bf I}_{c_2-2}\otimes\widetilde{{\bf{\Upsigma}}}_1\otimes{\bf I}_{{c_t}-2},\quad {{\partial{\bf F}_{11}}\over {\partial\tau_2}} = \widetilde{{\bf{\Upsigma}}}_2\otimes{\bf I}_{c_1-2}\otimes{\bf I}_{{c_t}-2}, \\ & {{\partial{\bf F}_{11}}\over {\partial\tau_t}} = {\bf I}_{c_2-2}\otimes{\bf I}_{c_1-2}\otimes\widetilde{{\bf{\Upsigma}}}_{t}. \end{aligned} $$