Skip to main content
SpringerLink
Log in

Homogenization of random heterogeneous media with inclusions of arbitrary shape modeled by XFEM

  • Original Paper
  • Published:
Computational Mechanics Aims and scope Submit manuscript

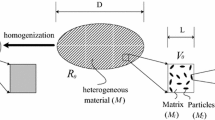
Abstract

The paper deals with the homogenization of random heterogeneous media with arbitrarily shaped inclusions simulated with the extended finite element method (XFEM) coupled with Monte Carlo simulation (MCS). The implementation of XFEM is particularly suitable for this type of problems since there is no need to generate a new finite element mesh at each MCS. The inclusions are randomly distributed and oriented within the medium while their shape is implicitly modeled by the iso-zero of an analytically defined random level set function, which also serves as the enrichment function in the framework of XFEM. Homogenization is performed based on Hill’s energy condition and MCS. The homogenization involves the generation of a large number of random realizations of the microstructure geometry based on a given volume fraction of the inclusions and other parameters (shape, spatial distribution and orientation). The influence of the inclusion shape on the effective properties of the random media is highlighted. It is shown that the statistical characteristics of the effective properties can be significantly affected by the shape of the inclusions especially in the case of large volume fraction and stiffness ratio.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23

Similar content being viewed by others

References

  1. Babuška I, Banerjee U (2012) Stable generalized finite element method (SGFEM). Comput Methods Appl Mech Eng 201–204:91–111

    Article  Google Scholar 

  2. Baxter S, Hossain MI, Graham L (2001) Micromechanics based random material property fields for particulate reinforced composites. Int J Solids Struct 38(50):9209–9220

    Article  MATH  Google Scholar 

  3. Belytschko T, Moës N, Usui S, Parimi C (2001) Arbitrary discontinuities in finite elements. Int J Numer Methods Eng 50(4):993–1013

    Article  MATH  Google Scholar 

  4. Belytschko T, Gracie R, Ventura G (2009) A review of extended/generalized finite element methods for material modeling. Modell Simul Mater Sci Eng 17(4):1–24

    Article  MathSciNet  Google Scholar 

  5. Bordas S, Nguyen PV, Dunant C, Guidoum A, Nguyen-Dang H (2007) An extended finite element library. Int J Numer Methods Eng 71(6):703–732

    Article  MATH  Google Scholar 

  6. Charalambakis N (2010) Homogenization techniques and micromechanics. A survey and perspectives. Appl Mech Rev 63(3)

  7. Clément A, Soize C, Yvonnet J (2013) Uncertainty quantification in computational stochastic multiscale analysis of nonlinear elastic materials. Comput Methods Appl Mech Eng 254:61–82

    Article  Google Scholar 

  8. Farsad M, Vernerey FJ, Park HS (2010) An extended finite element/level set method to study surface effects on the mechanical behavior and properties of nanomaterials. Int J Numer Methods Eng 84(12):1466–1489

    Article  MathSciNet  MATH  Google Scholar 

  9. Fries TP (2008) A corrected XFEM approximation without problems in blending elements. Int J Numer Methods Eng 75(5):503–532

    Article  MathSciNet  MATH  Google Scholar 

  10. Geers M, Kouznetsova V, Brekelmans W (2010) Multi-scale computational homogenization: trends and challenges. J Comput Appl Math 234(7):2175–2182

    Article  MATH  Google Scholar 

  11. Greene MS, Xu H, Tang S, Chen W, Liu WK (2013) A generalized uncertainty propagation criterion from benchmark studies of microstructured material systems. Comput Methods Appl Mech Eng 254:271–291

    Article  MathSciNet  Google Scholar 

  12. Hashin Z (1983) Analysis of composite materials: a survey. J Appl Mech 50(2):481–505

    Article  MATH  Google Scholar 

  13. Hill R (1963) Elastic properties of reinforced solids: some theoretical principles. J Mech Phys Solids 11(5):357–372

    Article  MATH  Google Scholar 

  14. Hiriyur B, Waisman H, Deodatis G (2011) Uncertainty quantification in homogenization of heterogeneous microstructures modeled by XFEM. Int J Numer Methods Eng 88(3):257–278

    Article  MathSciNet  MATH  Google Scholar 

  15. Huyse L, Maes MA (2001) Random field modeling of elastic properties using homogenization. J Eng Mech 127(1):27–36

    Article  Google Scholar 

  16. Kamiński M, Kleiber M (2000) Perturbation based stochastic finite element method for homogenization of two-phase elastic composites. Comput Struct 78(6):811–826

    Article  Google Scholar 

  17. Krongauz Y, Belytschko T (1998) EFG approximation with discontinuous derivatives. Int J Numer Meth Eng 41(7):1215–1233

    Article  MathSciNet  MATH  Google Scholar 

  18. Lang C, Doostan A, Maute K (2013) Extended stochastic FEM for diffusion problems with uncertain material interfaces. Comput Mech 51:1031–1049

    Article  MathSciNet  MATH  Google Scholar 

  19. Legay A, Wang H, Belytschko T (2005) Strong and weak arbitrary discontinuities in spectral finite elements. Int J Numer Methods Eng 64(8):991–1008

    Article  MathSciNet  MATH  Google Scholar 

  20. Ma J, Temizer I, Wriggers P (2011) Random homogenization analysis in linear elasticity based on analytical bounds and estimates. Int J Solids Struct 48(2):280–291

    Article  MATH  Google Scholar 

  21. Melenk JM, Babuška I (1996) The partition of unity finite element method: basic theory and applications. Comput Methods Appl Mech Eng 139(1):289–314

    Article  MATH  Google Scholar 

  22. Miehe C, Koch A (2002) Computational micro-to-macro transitions of discretized microstructures undergoing small strains. Arch Appl Mech 72(4–5):300–317

    Article  MATH  Google Scholar 

  23. Moës N, Dolbow J, Belytschko T (1999) A finite element method for crack growth without remeshing. Int J Numer Meth Eng 46:131–150

    Article  MATH  Google Scholar 

  24. Moës N, Cloirec M, Cartraud P, Remacle JF (2003) A computational approach to handle complex microstructure geometries. Comput Methods Appl Mech Eng 192(28):3163–3177

    Article  MATH  Google Scholar 

  25. Ostoja-Starzewski M, Wang X (1999) Stochastic finite elements as a bridge between random material microstructure and global response. Comput Methods Appl Mech Eng 168(1):35–49

  26. Sethian JA (1999) Level set methods and fast marching methods, evolving interfaces in computational geometry, fluid mechanics, computer vision, and materials science. Cambridge university press, Cambridge

    MATH  Google Scholar 

  27. Sonon B, Francois B, Massart T (2012) A unified level set based methodology for fast generation of complex microstructural multi-phase RVEs. Comput Methods Appl Mech Eng 223–224:103–122

    Article  Google Scholar 

  28. Stefanou G, Nouy A, Clément A (2009) Identification of random shapes from images through polynomial chaos expansion of random level set functions. Int J Numer Methods Eng 79(2):127–155

    Article  MATH  Google Scholar 

  29. Sukumar N, Chopp DL, Moës N, Belytschko T (2001) Modeling holes and inclusions by level sets in the extended finite-element method. Comput Methods Appl Mech Eng 190(46):6183–6200

    Article  MATH  Google Scholar 

  30. Talebi H, Zi G, Silani M, Samaniego E, Rabczuk T (2012) A simple circular cell method for multilevel finite element analysis. J Appl Math. doi:10.1155/2012/526846

  31. Talebi H, Silani M, Bordas SP, Kerfriden P, Rabczuk T (2014) A computational library for multiscale modeling of material failure. Comput Mech 53(5):1047–1071

    Article  MathSciNet  MATH  Google Scholar 

  32. Torquato S (2002) Random heterogeneous materials: microstructure and macroscopic properties. Springer, New York

    Book  Google Scholar 

  33. Tran A, Yvonnet J, He QC, Toulemonde C, Sanahuja J (2011) A multiple level set approach to prevent numerical artefacts in complex microstructures with nearby inclusions within XFEM. Int J Numer Methods Eng 85(11):1436–1459

    Article  MATH  Google Scholar 

  34. Xu XF, Graham-Brady L (2005) A stochastic computational method for evaluation of global and local behavior of random elastic media. Comput Methods Appl Mech Eng 194(42):4362–4385

    Article  MATH  Google Scholar 

  35. Yoon YC, Song JH (2014a) Extended particle difference method for weak and strong discontinuity problems: part I, derivation of the extended particle derivative approximation for the representation of weak and strong discontinuities. Comput Mech 53(6):1087–1103

    Article  MathSciNet  MATH  Google Scholar 

  36. Yoon YC, Song JH (2014b) Extended particle difference method for weak and strong discontinuity problems: part II, formulations and applications for various interfacial singularity problems. Comput Mech 53(6):1105–1128

    Article  MathSciNet  MATH  Google Scholar 

  37. Yuan Z, Fish J (2008) Toward realization of computational homogenization in practice. Int J Numer Methods Eng 73(3):361–380

    Article  MathSciNet  MATH  Google Scholar 

  38. Yvonnet J, Quang HL, He QC (2008) An XFEM/level set approach to modelling surface/interface effects and to computing the size-dependent effective properties of nanocomposites. Comput Mech 42(1):119–131

    Article  MathSciNet  MATH  Google Scholar 

  39. Zhao X, Bordas SP, Qu J (2013a) A hybrid smoothed extended finite element/level set method for modeling equilibrium shapes of nano-inhomogeneities. Comput Mech 52(6):1417–1428

    Article  MathSciNet  MATH  Google Scholar 

  40. Zhao X, Duddu R, Bordas SP, Qu J (2013b) Effects of elastic strain energy and interfacial stress on the equilibrium morphology of misfit particles in heterogeneous solids. J Mech Phys Solids 61(6):1433–1445

    Article  MathSciNet  Google Scholar 

  41. Zohdi TI, Wriggers P (2008) An introduction to computational micromechanics, 2nd edn., Lecture notes in applied and computational mechanics, vol 20, Springer, Heidelberg

Download references

Acknowledgments

This work is implemented within the framework of the research project “MICROLINK: Linking micromechanics-based properties with the stochastic finite element method: a challenge for multiscale modeling of heterogeneous materials and structures” - Action “Supporting Postdoctoral Researchers” of the Operational Program “Education and Lifelong Learning” (Action’s Beneficiary: General Secretariat for Research and Technology), and is co-financed by the European Social Fund (ESF) and the Greek State. The provided financial support is gratefully acknowledged. M. Papadrakakis acknowledges the support from the European Research Council Advanced Grant “MASTER–Mastering the computational challenges in numerical modeling and optimum design of CNT reinforced composites” (ERC-2011-ADG 20110209). Special thanks are also due to Professor Haim Waisman for providing the computer code of the XFEM model for inclusions of elliptical shape.

Author information

Authors and Affiliations

  1. School of Civil Engineering, Institute of Structural Analysis & Antiseismic Research, National Technical University of Athens, 9 Iroon Polytechneiou, Zografou Campus, 15780, Athens, Greece

    Dimitris Savvas, George Stefanou & Manolis Papadrakakis

  2. Department of Civil Engineering, Institute of Structural Analysis & Dynamics of Structures, Aristotle University of Thessaloniki, 54124, Thessaloniki, Greece

    George Stefanou

  3. Department of Civil Engineering & Engineering Mechanics, Columbia University, New York, NY, 10027, USA

    George Stefanou & George Deodatis

Authors
  1. Dimitris Savvas
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. George Stefanou
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Manolis Papadrakakis
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. George Deodatis
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to George Stefanou.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Savvas, D., Stefanou, G., Papadrakakis, M. et al. Homogenization of random heterogeneous media with inclusions of arbitrary shape modeled by XFEM. Comput Mech 54, 1221–1235 (2014). https://doi.org/10.1007/s00466-014-1053-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00466-014-1053-x

Keywords

Search

Navigation