Abstract
Given a sample of an abstract manifold immersed in some Euclidean space, we describe a way to recover the singular homology of the original manifold. It consists in estimating its tangent bundle—seen as subset of another Euclidean space—from a measure theoretical point of view, and in applying measure-based filtrations for persistent homology. The construction we propose is consistent and stable, and does not require the dimension of the manifold.




































Similar content being viewed by others
References
Aamari, E.: Vitesses de Convergence en Inférence Géométrique. PhD thesis, Université Paris-Saclay (2017)
Aamari, E., Kim, J., Chazal, F., Michel, B., Rinaldo, A., Wasserman, L.: Estimating the reach of a manifold. Electron. J. Stat. 13(1), 1359–1399 (2019)
Aamari, E., Levrard, C.: Nonasymptotic rates for manifold, tangent space and curvature estimation. Ann. Stat. 47(1), 177–204 (2019)
Alexander, S.B., Bishop, R.L.: Gauss equation and injectivity radii for subspaces in spaces of curvature bounded above. Geometriae Dedicata 117, 65–84 (2006)
Anai, H., Chazal, F., Glisse, M., Ike, Y., Inakoshi, H., Tinarrage, R., Umeda, Y.: DTM-based filtrations. In: Topological Data Analysis (Abel Symposium, Geiranger 2018). Abel Symp., vol. 15, pp. 33–66. Springer, Cham (2020)
Arias-Castro, E., Lerman, G., Zhang, T.: Spectral clustering based on local PCA. J. Mach. Learn. Res. 18(1), # 9 (2017)
Attali, D., Edelsbrunner, H., Mileyko, Yu.: Weak witnesses for Delaunay triangulations of submanifolds. In: 2007 ACM Symposium on Solid and Physical Modeling (Beijing 2007), pp. 143–150. ACM, New York (2007)
Attali, D., Lieutier, A., Salinas, D.: Vietoris-Rips complexes also provide topologically correct reconstructions of sampled shapes. Comput. Geom. 46(4), 448–465 (2013)
Boissonnat, J.D., Chazal, F., Yvinec, M.: Geometric and Topological Inference. Cambridge Texts in Applied Mathematics, vol. 57. Cambridge University Press, Cambridge (2018)
Boissonnat, J.D., Ghosh, A.: Manifold reconstruction using tangential Delaunay complexes. Discrete Comput. Geom. 51(1), 221–267 (2014)
Boissonnat, J.D., Lieutier, A., Wintraecken, M.: The reach, metric distortion, geodesic convexity and the variation of tangent spaces. J. Appl. Comput. Topol. 3(1–2), 29–58 (2019)
Botnan, M., Crawley-Boevey, W.: Decomposition of persistence modules. Proc. Am. Math. Soc. 148(11), 4581–4596 (2020)
Bubenik, P., Carlsson, G., Kim, P.T., Luo, Z.M.: Statistical topology via Morse theory persistence and nonparametric estimation. In: Algebraic Methods in Statistics and Probability II (Champaign 2009). Contemp. Math., vol. 516, pp. 75–92. American Mathematical Society, Providence (2010)
Buchet, M., Chazal, F., Oudot, S.Y., Sheehy, D.R.: Efficient and robust persistent homology for measures. Comput. Geom. 58, 70–96 (2016)
Buet, B., Leonardi, G.P., Masnou, S.: A varifold approach to surface approximation. Arch. Ration. Mech. Anal. 226(2), 639–694 (2017)
Buet, B., Leonardi, G.P., Masnou, S.: Weak and approximate curvatures of a measure: a varifold perspective. Nonlinear Analysis 222, # 112983 (2022)
do Carmo, M.: Riemannian Geometry. Mathematics: Theory & Applications. Birkhäuser, Boston (1992)
Charon, N., Trouvé, A.: The varifold representation of nonoriented shapes for diffeomorphic registration. SIAM J. Imaging Sci. 6(4), 2547–2580 (2013)
Chazal, F., Cohen-Steiner, D., Lieutier, A.: A sampling theory for compact sets in Euclidean space. Discrete Comput. Geom. 41(3), 461–479 (2009)
Chazal, F., Cohen-Steiner, D., Mérigot, Q.: Geometric inference for probability measures. Found. Comput. Math. 11(6), 733–751 (2011)
Chazal, F., Lieutier, A.: Stability and computation of topological invariants of solids in \(\mathbb{R} ^n\). Discrete Comput. Geom. 37(4), 601–617 (2007)
Chazal, F., Lieutier, A.: Smooth manifold reconstruction from noisy and non-uniform approximation with guarantees. Comput. Geom. 40(2), 156–170 (2008)
Chazal, F., Oudot, S.Y.: Towards persistence-based reconstruction in Euclidean spaces. In: 24th Annual Symposium on Computational Geometry (College Park 2008), pp. 232–241. ACM, New York (2008)
Chazal, F., de Silva, V., Glisse, M., Oudot, S.: The Structure and Stability of Persistence Modules. SpringerBriefs in Mathematics. Springer, Cham (2016)
Cheng, S.-W., Chiu, M.-K.: Tangent estimation from point samples. Discrete Comput. Geom. 56(3), 505–557 (2016)
Díaz Martínez, D.H., Mémoli, F., Mio, W.: The shape of data and probability measures. Appl. Comput. Harmonic Anal. 48(1), 149–181 (2018)
Edelsbrunner, H.: The union of balls and its dual shape. In: 9th Annual Symposium on Computational Geometry (San Diego 1993), pp. 218–231. ACM, New York (1993)
Edelsbrunner, H., Harer, J.: Computational Topology: An Introduction. American Mathematical Society, Providence (2010)
Edelsbrunner, H., Mücke, E.P.: Three-dimensional alpha shapes. ACM Trans. Graph. 13(1), 43–72 (1994)
Fasy, B.T., Komendarczyk, R., Majhi, S., Wenk, C.: On the reconstruction of geodesic subspaces of \({\mathbb{R} }^n\). Internat. J. Comput. Geom. Appl. 32(1–2), 91–117 (2022)
Fasy, B.T., Lecci, F., Rinaldo, A., Wasserman, L., Balakrishnan, S., Singh, A.: Confidence sets for persistence diagrams. Ann. Stat. 42(6), 2301–2339 (2014)
Federer, H.: Curvature measures. Trans. Am. Math. Soc. 93(3), 418–491 (1959)
Gong, D., Zhao, X., Medioni, G.: Robust multiple manifolds structure learning (2012). arXiv:1206.4624
Gray, A.: Tubes. Progress in Mathematics, vol. 221. Birkhäuser, Basel (2004)
Guibas, L., Morozov, D., Mérigot, Q.: Witnessed k-distance. Discrete Comput. Geom. 49(1), 22–45 (2013)
Hatcher, A.: Algebraic Topology. Cambridge University Press, Cambridge (2002)
Herbert, R.J.: Multiple points of immersed manifolds. Mem. Am. Math. Soc. 34, # 250 (1981)
Kalisnik, S., Lesnik, D.: Finding the homology of manifolds using ellipsoids (2020). arXiv:2006.09194
Kim, J., Rinaldo, A., Wasserman, L.: Minimax rates for estimating the dimension of a manifold (2016). J. Comput. Geom. 10(1), 42–95 (2019)
Kim, J., Shin, J., Chazal, F., Rinaldo, A., Wasserman, L.: Homotopy reconstruction via the Cech complex and the Vietoris–Rips complex (2019). arXiv:1903.06955
Koltchinskii, V.I.: Empirical geometry of multivariate data: a deconvolution approach. Ann. Stat. 28(2), 591–629 (2000)
Little, A.V., Lee, J., Jung, Y.-M., Maggioni, M.: Estimation of intrinsic dimensionality of samples from noisy low-dimensional manifolds in high dimensions with multiscale SVD. In: 15th IEEE/SP Workshop on Statistical Signal Processing (Cardiff 2009), pp. 85–88. IEEE (2009)
Lytchak, A.: Almost convex subsets. Geometriae Dedicata 115, 201–218 (2005)
Mémoli, F., Smith, Z., Wan, Z.: The Wasserstein transform. In: 36th International Conference on Machine Learning (Long Beach 2019). Proceedings of Machine Learning Research, vol. 97, pp. 4496–4504 (2019)
Mordohai, P., Medioni, G.: Dimensionality estimation, manifold learning and function approximation using tensor voting. J. Mach. Learn. Res. 11, 411–450 (2010)
Morgan, F.: Geometric Measure Theory: A Beginner’s Guide. Academic Press, New York (2016)
Niyogi, P., Smale, S., Weinberger, S.: Finding the homology of submanifolds with high confidence from random samples. Discrete Comput. Geom. 39(1–3), 419–441 (2008)
Phillips, J., Wang, B., Zheng, Y.: Geometric inference on kernel density estimates. In: 31st International Symposium on Computational Geometry (Eindhoven 2015). Leibniz Int. Proc. Inform., vol. 34, pp. 857–871. Leibniz-Zent. Inform., Wadern (2015)
de Silva, V., Carlsson, G.E.: Topological estimation using witness complexes. In: Symposium on Point-Based Graphics (Zürich 2004), pp. 157–166. Eurographics Association (2004)
Singer, A., Wu, H.-T.: Vector diffusion maps and the connection Laplacian. Commun. Pure Appl. Math. 65(8), 1067–1144 (2012)
Tinarrage, R.: Computing Stiefel–Whitney classes of line bundles. J. Appl. Comput. Topol. 6(1), 65–125 (2022)
Turner, K., Mileyko, Yu., Mukherjee, S., Harer, J.: Fréchet means for distributions of persistence diagrams. Discrete Comput. Geom. 52(1), 44–70 (2014)
Wang, Y., Jiang, Y., Wu, Y., Zhou, Z.-H.: Spectral clustering on multiple manifolds. IEEE Trans. Neural Netw. 22(7), 1149–1161 (2011)
Acknowledgements
I would like to thank Frédéric Chazal, Marc Glisse, and Théo Lacombe for fruitful discussions and corrections. I also thank the anonymous reviewers for their precious corrections and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Editor in Charge: Kenneth Clarkson
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Appendices
A Notations
We adopt the following notations:
-
\(n, d > 0\) are integers.
-
If \(x, y \in {\mathbb {R}}\), \(\min {(x,y)}\) is the minimum of x and y.
-
I is the interval \([0, +\infty )\) or [0, T] for \(T \ge 0\).
-
\(E = {\mathbb {R}}^n\) is the Euclidean space, \( \textrm{M}(E) \) the vector space of \(n \times n\) matrices, \( \mathscr {G}_{d}(E) \) the Grassmannian of d-planes in E.
-
A is a subset of E, \( \textrm{med}\left( A \right) \) denotes its medial axis, \({\text {reach}}(A)\) its reach. For every \(x\in E\), \( {\text {dist}}(x, A) \) is the distance from x to A.
-
For \(x,y \in E\), \(x\,\bot \,y\) denotes the orthogonality of x and y.
-
If \(x,y\in E\), \(x \otimes y = x {}^ty \in \textrm{M}(E) \) is the outer product, and \( {x}^{\otimes 2} = x \otimes x\).
-
\(\Vert \,{\cdot }\,\Vert \) is the Euclidean norm on E and \(\langle \,{\cdot }\,, \,{\cdot }\,\rangle \) the corresponding inner product, \( \left\| \,{\cdot }\,\right\| _\textrm{F} \) the Frobenius norm on \( \textrm{M}(E) \), \(\Vert \,{\cdot }\,\Vert _\gamma \) the \(\gamma \)-norm on \(E \times \textrm{M}(E) \) (defined in Sect. 4.1).
-
\( \textrm{W}_{p} \) is the p-Wasserstein distance between measures on E, \( \textrm{W}_{p,\gamma } \) is the \((p,\gamma )\)-Wasserstein distance between measures on \(E \times \textrm{M}(E) \) (defined in Sect. 4.1).
-
\( \mathscr {H} ^d\) is the d-dimensional Hausdorff measure on E or on a subspace \(T \subset E\) (not renormalized).
-
If \(\mu \) is a measure of positive finite mass, \(|\mu |\) denotes its mass, \(\overline{\mu }={\mu }/{|\mu |}\) is the associated probability measure,
 denotes the associated lifted measure (introduced in Sect. 4.1).
denotes the associated lifted measure (introduced in Sect. 4.1). -
\(1_A\) is the indicator function of a measurable set A.
-
If T is a subspace of E, \(p_T\) denotes the orthogonal projection matrix on T.
-
\( \mathscr {B} (x,r) \) and \( \overline{ \mathscr {B} }\left( x,r\right) \) denote the open and closed balls of E, \( \partial \mathscr {B}\left( x,r\right) \) the sphere. \( V_{d} \) and \( S_{d-1} \) denote \( \mathscr {H} ^d( \mathscr {B} (0,1) )\) and \( \mathscr {H} ^{d-1}( \partial \mathscr {B}\left( 0,1\right) )\) (note that \( S_{d-1} = d V_{d} \)).
-
\( \mathscr {M}_0 \) is a Riemannian manifold, and \( \mathscr {B} _{ \mathscr {M}_0 }(x,r) \) and \( \overline{ \mathscr {B} }_{ \mathscr {M}_0 }(x,r) \) denote the open and closed geodesics balls. For \(x_0, y_0 \in \mathscr {M}_0 \), \( d_{ \mathscr {M}_0 }(x_0, y_0) \) denotes the geodesic distance.
-
If T is a subspace of E, \( \mathscr {B} _{T}(x,r) \) and \( \overline{ \mathscr {B} }_{T}(x,r) \) denote the open and closed balls of T for the Euclidean distance.
-
If f is a map with values in \({\mathbb {R}}\) and \(t \in {\mathbb {R}}\), \(f^t\) denotes the sublevel set \(f^t = f^{-1}((-\infty , t])\).
B Table of Constants
In the following table, each constant is preceded by the result where it appeared first. If a constant is defined from the others, it is indicated here. The indices are arbitrary and only reflect the order of apparition of each result.
Index | Result | Constant |
|---|---|---|
1 | Corollary 2.9 | a, \(c_{1} = 8{\text {diam}}{({\text {supp}}(\mu ))} + 5\), \(c_{1}' = 2a^{-{1}/{d}}\) |
2 | Hypothesis 2 | \(\rho \) |
3 | Hypothesis 3 | \(L_0\), \(f_{\min }\), \(f_{\max }\) |
4 | Hypothesis 4 | \(c_{4}\), \(r_{4}\) |
5 | Lemma 3.5 | \(c_{5}:t \mapsto \bigl ({1 - \sqrt{1 - 2t}}\bigr )/ t\) |
6 | Lemma 3.10 | \( J_{\min }=({23}/{24})^d\), \( J_{\max }= ({5}/{4})^d\) |
7 | Lemma 3.12 | \(c_{7} = 4 L_0 J_{\max }+d\rho f_{\max } /2\) |
8 | Proposition 3.14 | \(c_{8} = c_{7} + f_{\max } J_{\max }d 2^{d} \rho \) |
9 | \(c_{9} = f_{\min } J_{\min } V_{d} \) | |
10 | \(c_{10} = d 2^{d} f_{\max } J_{\max } V_{d} \) | |
11 | \(c_{11}= ({ f_{\max } J_{\max }}/({ f_{\min } J_{\min }}))\bigl ({\rho }/{\sqrt{4 - \sqrt{13}}}\bigr )^d d 2^{2d} \sqrt{3}\) | |
12 | Section 3.3 | \(\varDelta \), \(\varDelta _0\), \(\varTheta \) |
13 | Proposition 3.20 | \(r_{13} = \min {\bigl ({\sin \varTheta }/({8\rho }),{(\sin \varTheta )^2}/{4}, {\varDelta _0\sin \varTheta }/{4},\varDelta \bigr )}\) |
\(c_{13} =({2}/{\sin \theta })^\alpha V_{\alpha } f_{\max } \mathscr {H} ^{d'}_{ \mathscr {M}_0 }( \mathscr {N}_0 )\) | ||
14 | Proposition 4.3 | \(c_{14} = 6 \rho + ( 4c_{7} + f_{\max } 2^d d \rho + c_{8})/( f_{\min } J_{\min })\), |
15 | Lemma 4.7 | \(c_{\textrm{15}} = 2(1+4\cdot 5^{d-1}/{3^d})({c_{10}}/{c_{9}})\) |
16 | Lemma 4.8 | \(c_{\textrm{16}} = (2 + {2^{5/2}5^{d-{1/2}}}/{3^d})({c_{11}}/{c_{9}})\) |
17 | Lemma 4.9 | \(c_{17} ={2^{d-1}}/c_{9}+ 2({12 \cdot 5^{d-1}c_{10}+1})/({3^d c_{9}})\) |
\(+\,2^{d+3}({(3/{2})^{d-1}c_{10}+1})/{c_{9}}\) | ||
18 | Lemma 4.10 | \(c_{18} ={2^{d-2}}/{c_{9}} + ({4 \cdot 3^{1/2}5^{d-{1/2}} c_{11}+4^{d-{1/2}}})/({3^d c_{9}})\) |
\(+\,2\cdot 4^d({2 c_{11} (3/2)^{d-1/2}+1})/({3^d c_{9}})\) | ||
19 | Proposition 4.13 | \(c_{19} = 4(1 + c_{20})\), \(c_{19}'=4c_{18}\) |
20 | Lemma 4.15 | \(c_{20} = 3 +c_{15} +c_{16} + c_{17}\) |
21 | Theorem 4.16 | \(c_{21} = 2 +c_{19}'/2= 2(1 + c_{18})\) |
22 | Corollary 4.19 | \(c_{22} = c_{21}(c_{4})^{1/p} + c_{19} + c_{14}\) |
23 | Section 5.2 |
|
24 | Corollary 5.5 |
|
C Supplementary Material for Sect. 2
Proof of Lemma 2.4
The proof is based on the following observations. We can use the triangle inequality, then the Pythagorean Theorem with \(\langle v, y-x\rangle = 0\) and Lemma 2.3 (i) to get
For any \(r \le {1}/{\rho }\), consider the equation
By squaring this equality, we get \(({\rho }/{2})^2t^4 - (1+\rho r)t^2+(r^2-t^2)=0\). By considering the polynomial \(T\mapsto ({\rho }/{2})^2 T^2 - (1+\rho r)T +r^2-t^2\), whose discriminant is \(1 + 2\rho r + (\rho t)^2>0\), we see that the solutions of (49) are
Following the same ideas, one obtains
Moreover, the equation
admits the following roots:
We now prove the five points successively.
(i) Observe that \(\dot{\phi }(t) = 2\langle \dot{\gamma }(t), \gamma (t) - x\rangle \), and that
By Cauchy–Schwarz inequality, \(\langle \ddot{\gamma }(t), \gamma (t) - x\rangle \ge -\Vert \ddot{\gamma }(t)\Vert \cdot \Vert \gamma (t) - x\Vert \). Note that \(\langle \dot{\gamma }(t), \dot{\gamma }(t)\rangle = 1\) since \(\gamma \) is parametrized by arc-length, and that \(\Vert \ddot{\gamma }(t)\Vert \le \rho \) by (1). Hence we get
Consider (49) with \(r ={1}/{\rho }\). We see that \(\Vert \gamma (t) - x\Vert \le {1}/{\rho }\) when t is lower than
In this case, \(\ddot{\phi }(t) \ge 0\) according to (51). Since \(\dot{\phi }(0) = 0\), we deduce that \(\phi \) is increasing on \([0,T_1]\).
(ii) As we have seen with (50), we have \(\Vert \gamma (t)-x\Vert > r\) when \(t \in (T_2, T_2')\). In order to give an upper bound on \(T_2\), we use the inequality \(\sqrt{b} - \sqrt{a} = (b-a)/\bigl ({\sqrt{a}+\sqrt{b}}\bigr ) \le (b-a)/{\sqrt{b}}\), where \(a<b\), to get
and we conclude that \(T_2 \le {\sqrt{2}}\sqrt{r^2 - l^2}/{\sqrt{1-\rho r}} \). Since \(r \le {1}/({2\rho })\), we obtain \(T_2 \le 2 \sqrt{r^2 - l^2}\).
(iii) When \(l = 0\), algebraic manipulations show that \(T_2 =(1-\sqrt{1-2\rho r})/\rho \) and \(T_2' =(1+\sqrt{1-2\rho r})/\rho \).
(iv) Consider the map \(\phi :t \mapsto \Vert \gamma (t) - x\Vert ^2\). By definition of b, for \(t \in (0,b)\), we have \(\Vert \gamma (t) - x\Vert \le r\). Hence (51) gives \(\ddot{\phi }(t) \ge 2(1-\rho r)\). It follows that \(\dot{\phi }(t) \ge 2(1-\rho r)t\), and that
Note that \(r^2 = \phi (b)\). Besides, \(s^2 = \phi (a)\) or \(s^2 < \phi (a)\), depending on whether \(s \ge l\) or \(s < l\). In both cases, we have \(r^2 - s^2 \ge \phi (b)-\phi (a)\), and we deduce that
Writing \(r^2-s^2 = (r+s)(r-s)\) and \(b^2-a^2 =(b+a)(b-a)\) leads to
Now, let us give a lower bound on b. According to (49), b is lower bounded by
Using the inequality \(\sqrt{b} - \sqrt{a} =(b-a)/\bigl ({\sqrt{b}+\sqrt{a}}\bigr ) \ge (b-a)/{2\sqrt{b}}\), where \(a<b\), we get
and \(b \ge (1+\rho r)^{-{1}/{2}}\sqrt{r^2 - s^2}\). Inserting \(b+a \ge b \ge (1+\rho r)^{-{1}/{2}}\sqrt{r^2 - s^2}\) in (52) yields
Under the hypothesis \(r \le {1}/({2\rho })\), we get \(b-a \le \sqrt{6}\sqrt{r^2-s^2}\).
(v) When \(l=0\), we have \(b(v)+a(v)\ge r+s\). Hence (52) yields \(b(v)-a(v)\le (r-s)/({1-\rho r})\). Using \(r \le 1/(2\rho )\), we obtain \(b(v)-a(v)\le 2(r-s)\). \(\square \)
Proof of Corollary 2.9
We shall first study an intermediate quantity. Let \(\mu \) be a probability measure on \(E={\mathbb {R}}^n\), \(m\in (0,1)\), and \( {\text {d}}_{\mu ,m} \) the corresponding DTM. Consider the quantity \(c(\mu , m)\) is defined as
Suppose that \(\mu \) satisfies the following for \(r <({m}/{a})^{1/d}\): for all \(x \in {\text {supp}}(\mu )\), \(\mu ( \mathscr {B} (x,r) ) \ge a r^d\). Let us show that \(c(\mu , m) \le C m^{1/d}\) with \(C = a^{-{1/d}}\). By definition,
Using the assumption \(\mu ( \mathscr {B} (x,r) ) \ge a r^d\) for all \(x \in {\text {supp}}(\mu )\), we get \(\delta _{\mu , t}(x) \le ({t}/{a})^{1/d}\), and a simple computation yields
which yields the result.
We can now prove the corollary. Let \(\pi \) be an optimal transport plan for \(w=W _2(\mu ,\nu )\). Denote \(\alpha = w^{1/2}\) and \(D = {\text {diam}}{({\text {supp}}(\mu ))}\). Define \(\pi '\) to be \(\pi \) restricted to the set \(\{x,y \in E \mid \Vert x-y\Vert <\alpha \}\). We denote its marginals \(\mu '\) and \(\nu '\). By the Markov inequality, \(1-|\pi '| \le {w^2}/{\alpha ^2} = w\), where we recall that \(|\pi '|\) denotes the total mass of \(\pi '\). Consider the probability measures \(\overline{\mu '}=\mu '/{|\mu '|}\) and \(\overline{\nu '}=\nu '/{|\nu '|}\). Let us show that we have
The first inequality is an application of Lemma 4.6:
To obtain the second inequality, we write
Hence the Jensen inequality leads to \(W _2(\overline{\mu '},\overline{\nu '})\le {w}/{|\pi '|^{1/2}}\). Since \(1-|\pi '| \le w\), we have \({w}/{|\pi '|^{1/2}} \le {w}/({1-w})\), and the assumption \(w \le {1}/{4}\) yields \({w}/({1-w}) \le \alpha \). This proves the second point. Finally, we obtain the third inequality by applying the triangle inequality:
Next, let us deduce that
The first inequality follows from the stability of the DTM (see (3)):
and we conclude with \(W _2(\mu ,\overline{\mu '})= 2D \alpha \). In order to prove the second inequality, we also use (3):
Since \(\pi '\) has support included in \(\{x,y \in E \mid \Vert x-y\Vert <\alpha \}\), we use the fact that the DTM is 1-Lipschitz to obtain
and we deduce
We can now conclude with Theorem 2.8. In our context, it reads
where we used (53) and (54) in the last line. Since \(m \le 1\), we can simplify this expression into
We conclude the proof by using the inequality \(c(\mu ,m) \le a^{-{1/d}} m^{1/d}\) shown at the beginning of the proof. \(\square \)
About this article
Cite this article
Tinarrage, R. Recovering the Homology of Immersed Manifolds. Discrete Comput Geom 69, 659–744 (2023). https://doi.org/10.1007/s00454-022-00409-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00454-022-00409-5



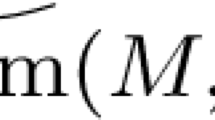
 denotes the associated lifted measure (introduced in Sect.
denotes the associated lifted measure (introduced in Sect.  ,
,  ,
, 
 ,
, 