Introduction

Unacceptably sluggish or oscillatory controllers are generally classified as either “fair” or “poor” while controllers with minor performance deviations are classified as “acceptable” or “excellent”. Desbourough and Miller [1] state that 32% of 26,000 controllers investigated in industry is classified as “poor” or “fair”. Only one third of the controllers were classified as acceptable performers and two thirds had significant improvement opportunity. Figure 1 shows an example of an experimental run for specific growth rate control in vaccine production on lab-scale. The strong oscillations show the poor performance and indicate the relevance of automatic tuning in this field of application.

Fig. 1
figure 1

Illustration of a process showing poor performance. Fed-batch cultivation with specific growth rate control for an experimental run of vaccine production on lab-scale [5]

Full size image

In biopharmaceutical production micro-organisms are cultivated in batch or fed-batch systems. Most vaccines, such as whooping cough, are produced in batch cultivation. Production of pertussis toxin (which is one of the important antigens in the vaccine against infection with whooping cough) is strongly growth-associated [2, 3]. Deviations in specific growth rate will therefore lead to deviations in antigen levels and vaccine quality. To obtain a high quality-vaccine and to ensure batch-to-batch consistency, it is important to control the specific growth rate at a constant level. Soons et al. [4] developed a specific growth rate controller by combining a reference model and a cultivation model. The result is a control law, which is adaptive for changes in volume and biomass. It was shown that the choice of the reference model is a main factor determining the performance of the specific growth rate controller.

Apart from the reference model, biological behavior is essential for the controller performance and as we know biological behavior is not perfectly known. Despite good performance in [4], the method does not correct for residual errors due to model-process mismatches [5]. Changes in the system, inaccurate knowledge about kinetics, varying properties of micro–organisms and response times of sensor systems are reasons for model-process mismatches. Online automatic tuning has the capability to deal with the mismatches and to improve controller performance by adjusting the controller parameters [6].

The aim of this paper is to investigate schemes for automating and to speed up the tuning procedures. To this end, the specific growth rate controller for fed-batch cultivation developed in [4] is extended with an automatic tuning method that is driven by the persistence of the residual errors. A direct method (in which the adjustment rule makes directly updates of the controller parameters) is preferred over an indirect method (in which process parameters are estimated to update controller parameters) as in this way a degree of imperfection of the model for model-based control can be handled. Moreover, probing should be avoided, because it may affect the critical variables in biopharmaceutical production.

Although a priori closed loop stability is hard to guarantee for a fed-batch system in which the biomass increases exponentially, stability of the control loops under application of the designed control law is evaluated.

This paper is organized as follows. First a brief description of the process and control system is given. Next, controller evaluation criteria are defined. Then, a short literature review and a textbook method for online automatic tuning using the MIT rule are presented. Due to unsatisfactory results of this method three algorithms are derived and evaluated by simulations in Sect. "Online automatic tuning methods". Also, stability of the closed loop is considered. Finally, the two best methods are tested in laboratory experiments for B. pertussis in Sect. “Experimental Results”.

Process description

Process model

A process model for vaccine production of B. pertussis is used to evaluate the controllers with automatic tuning. The production is performed in fed-batch cultivation, in which the specific growth rate is controlled to achieve a higher level of batch-to-batch consistency. Growth of B. pertussis is limited by two substrates [7] and is modeled by the following dual substrate model assuming Monod kinetics and oxygen excess [4, 8–10] during fed-batch cultivation (Eqs. 1–13). The changes of dissolved oxygen in time are equal to the oxygen transfer rate minus the oxygen uptake rate minus the dilution due to the substrate feed rate.

$$ \mu(C_{\rm G},C_{\rm L})= \mu_{\max}f_{\rm G}(C_{\rm G})+\mu_{\rm enh}f_{\rm G}(C_{\rm G})f_{\rm L}(C_{\rm L}) $$
(1)
$$ f_{\rm G} (C_{\rm G}) = \frac{{C_{\rm G}}}{{K_{\rm G} + C_{\rm G}}}\quad\hbox{and}\quad f_{\rm L} (C_{\rm L})=\frac{C_{\rm L}}{K_{\rm L}+C_{\rm L}} $$
(2)
$$ \frac{{\rm d}V}{{\rm d}t}=F_{G+L}^{\rm in} $$
(3)
$$ \frac{{{\rm d}C_{X}}}{{{\rm d}t}} = {\left({\mu - \frac{{F^{{\rm in}}_{{G + L}}}}{V}} \right)}C_{X} = {\left({\mu_{{\max}} f_{\rm G} (C_{\rm G}) + \mu_{{\rm enh}} f_{\rm G} (C_{\rm G})f_{\rm L} (C_{\rm L}) - \frac{{F^{{\rm in}}_{{G + L}}}}{V}} \right)}C_{X} $$
(4)
$$ \frac{{{\rm d}C_{\rm G}}}{{{\rm d}t}} = \frac{{F^{{\rm in}}_{{G + L}}}}{V}{\left({C^{{\rm in}}_{\rm G} - C_{\rm G}} \right)} - {\left({\frac{{\mu_{{\max}} f_{\rm G} (C_{\rm G})}}{{Y_{{\rm G1}}}} - \frac{{\mu_{{\rm enh}} f_{\rm G} (C_{\rm G})f_{\rm L} (C_{\rm L})}}{{Y_{{\rm G2}}}} + m_{\rm G}} \right)}C_{X} $$
(5)
$$ \frac{{{\rm d}C_{\rm L}}}{{{\rm d}t}} = \frac{{F^{{\rm in}}_{{G + L}}}}{V}{\left({C^{{\rm in}}_{\rm L} - C_{\rm L}} \right)} - {\left({\frac{{\mu_{{\rm enh}} f_{\rm G} (C_{\rm G})f_{\rm L} (C_{\rm L})}}{{Y_{{L2}}}} + m_{\rm L}} \right)}C_{X} $$
(6)
$$ \frac{{{\rm dDO}}}{{{\rm d}t}} = {\rm OTR} - {\rm OUR} - \frac{{F^{{\rm in}}_{{G + L}}}}{V} \cdot {\rm DO} $$
(7)

The oxygen uptake rate (OUR) is the sum of oxygen used for growth (μ/Y O) and oxygen used for maintenance (m O):

$$ {\rm OUR} = {\left({\frac{\mu}{{Y_{o}}} + m_{o}} \right)}C_{x} $$
(8)

The bioreactor is aerated using headspace aeration only. The liquid phase oxygen concentration (O h2 ) in equilibrium with the gas phase in the headspace following Henry’s law [9], the dissolved oxygen (DO), and the oxygen transfer coefficient k L a determine the oxygen transfer rate (OTR):

$$ {\rm OTR} = k_{l} a \cdot (O^{h}_{2} - {\rm DO}) $$
(9)

The dynamics of oxygen is much faster than the dynamics of the other relevant processes (e.g. biomass, substrates) [11] and the contribution of the dilution term is small (third term Eq. 7) compared to the rate of change of dissolved oxygen. As a consequence, Eq. 7 is considered in steady-state and OUR is calculated every minute during the experiment using Eq. 10:

$$ {\rm OUR} \approx {\rm OTR} $$
(10)

O h2 is assumed equal to O in2 because of the high aeration rate:

$$ O^{h}_{2} \approx O^{{\rm in}}_{2} $$
(11)

The DO sensor has a response time around 20 s, and is modeled as a first order system:

$$ \frac{{{\rm dDO}_{{\rm sensor}}}}{{{\rm d}t}} = - \frac{1}{{\tau_{{\rm sensor}}}} \cdot {\rm DO}_{{\rm sensor}} + \frac{1}{{\tau_{{\rm sensor}}}} \cdot {\rm DO} $$
(12)

Dissolved oxygen is controlled by changing the incoming oxygen fraction (O in2 ) in an oxygen/air/nitrogen mixture. The controller is based on an already installed PI controller:

$$ O^{{\rm in}}_{2} = K_{C} \cdot ({\rm DO}_{{\rm set}} - {\rm DO}_{{\rm sensor}}) + {\int_0^t {\frac{{K_{C}}}{{\tau_{I}}} \cdot ({\rm DO}_{{\rm set}} - {\rm DO}_{{\rm sensor}})}}{\rm d}t + C_{\rm N} $$
(13)

Specific growth rate control system

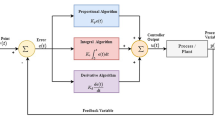
Figure 2 gives an overview of the proposed control system for fed-batch cultivation. It is the same as the scheme presented by Soons et al. [4], except that it is extended with an automatic tuning method. The control purpose is to regulate the specific growth rate (μ) to a desired value by adding a feed with limiting substrates. The grey block defines the specific growth rate controller, which will be briefly reviewed below.

Fig. 2
figure 2

The control system for adaptive specific growth rate control with automatic tuning

Full size image

The definition of the specific growth rate controller given in [4] started from a second order reference model:

$$ \frac{{{\rm d}\hat{\mu}}}{{{\rm d}t}} = \frac{{\mu_{{\rm set}} - \hat{\mu}}}{{\gamma_{1}}} + {\int\limits_0^t {\frac{{\mu_{{\rm set}} - \hat{\mu}}}{{\gamma_{2}}}{\rm d}t}} $$
(14)

where the tuning parameters γ1 and γ2 determine the convergence speed of the controller and therefore controller performance. The reference model is stable if γ1 and γ2 are strictly positive numbers. Combination with the process model yields an adaptive “PI” controller:

$$ F^{{\rm in}}_{{G + L}} = \frac{{ac + bd}}{{aC^{{\rm in}}_{\rm G} + bC^{{\rm in}}_{\rm L}}} \hat{C}_{X} V + K_{P} \cdot (\mu_{{\rm set}} - \hat{\mu})\; + {\int\limits_0^t {K_{I} \cdot (\mu_{{\rm set}} - \hat{\mu}){\rm d}t}} $$
(15a)

where the controller gains K P and K I are adjusted online to the changing volume:

$$ K_{P} = \frac{V}{{\gamma_{1} (aC^{{\rm in}}_{\rm G} + bC^{{\rm in}}_{\rm L})}}\quad \hbox{and}\quad K_{I} = \frac{V}{{\gamma_{2} (aC^{{\rm in}}_{\rm G} + bC^{{\rm in}}_{\rm L})}} $$
(15b)

a, b, c, and d are constants depending on the micro-organism (in this work Bordetella pertussis [4]).

Biomass and specific growth rate measurements are often not available online. Therefore, an Extended Kalman Filter (EKF) estimates specific growth rate \((\hat{\mu})\) and biomass \((\hat{C}_{X})\) using the measured oxygen uptake rate every minute [4, 12]. This software sensor showed fast convergence and fitted well to the data (see Appendix 1 for an application on continuous cultivation). Therefore, for controller design the estimations of the EKF are taken as replacement of actual measurements \((\mu = \hat{\mu}\;\hbox{and}\;C_{X} = \hat{C}_{X}).\)

Central point of this work is the extension of the specific growth rate controller (Eq. 15) with three methods for automatic tuning, which adapt the controller parameters γ1 and γ2 on the basis of the error in specific growth rate (see Fig. 2). So the approach does not require probing which can disturb the critical variables in biopharmaceutical production.

Controller evaluation

Evaluation methods

The model (Eqs. 1–13) is used to evaluate controller performance in simulations in Sect. "Online automatic tuning methods". To obtain realistic tests of the robustness of the controller and performance of the automatic tuning several disturbances have been introduced in the simulation as in [4]: time-varying or drifting kinetics, initialization errors on the controller tuning parameters, and noise. We assumed a drift plus a sinus with different frequencies on the model parameters, whereas in the controller, the model parameters p were set constant:

$$ p^{d} = p + a_{1} t + a_{2} \sin (a_{3} \pi t + a_{4} \pi) + a_{5} \sin (a_{6} \pi t + a_{7} \pi) $$
(16)

where p d are the disturbed parameters for μmax, μenh, Y G1, Y G2, Y L , C in G , C in L , K G , and K L . The parameters and initial values are given in Table 1, the disturbances on the parameters in Table 2.

Table 1 Model parameters and initial conditions for simulations with the dual substrate model of B. pertussis
Full size table
Table 2 Disturbances on the model parameters for B. pertussis
Full size table

In practice, dissolved oxygen measurements contain observation noise. In the simulations noise is introduced by adding white noise with an intensity proportional to OUR (0.1 initially to 3% at end). This intensity was chosen to mimic the observed fact that DO is more noisy toward the end:

$$ {\rm DO}^{m}_{{\rm sensor}} (t_{k}) = {\rm DO}_{{\rm sensor}} (t_{k}) + v(t_{k}) $$
(17)

In addition to [4], controller tuning parameters γ1 and γ2 are initialized far below the required values, which results in underdamped behavior. When the specific growth rate controller without automatic tuning method is applied with these settings, oscillations were present for almost 30 h (Fig. 3), underlining the need for additional adaptation. Experimental data showed similar profiles (Fig. 1). Additional simulations are performed with different values for the tuning parameters.

Fig. 3
figure 3

Illustration of a simulation with specific growth rate control for poorly tuned and fixed γ1 and γ2

Full size image

Evaluation criteria

To evaluate the significance of the automatic tuning system, two criteria are used. The criteria reflect the performance of the specific growth rate controller. In addition the simulation and experimental results are evaluated by comparing graphs.

Babuška et al. [13] used the following measures to detect a potential loss of performance. The first measure is the mean absolute error over the past N points of a moving window at time point k:

$$ E(k) = \frac{1}{N} \cdot {\sum\limits_{k - N}^k {{\left| {\varepsilon (k)} \right|}}} $$
(18)

The second is the oscillation measure and is defined by

$$ O(k) = \frac{1}{N} \cdot {\left({{\sum\limits_{k - N}^k {{\left| {\varepsilon (k)} \right|}}} - {\sum\limits_{k - N}^k {\varepsilon (k)}}} \right)} $$
(19)

where the error ɛ is the set point minus the estimated specific growth rate \((\mu_{{\rm set}} - \hat{\mu }).\)

Literature

Literature review

Åström and Wittenmark [14] give examples of model-based adaptive control to adapt control parameters to changing process behavior. The adaptation of the controllers for a bioreactor as designed in [15–19] is also derived from a process model. This solution is limited by the accuracy of the models. Many adaptive controllers require measurement of the state variables such as biomass and substrates [20–24], which are often not available. Other approaches require identification of the system by introducing systematic disturbances [13, 25]. Such “probing” should be avoided in cultivation systems for biopharmaceutical production as it may affect critical variables. Dagci et al. [6] used sliding mode control to adapt controller parameters. The authors show good control performance during continuous cultivation, but in fed-batch cultivation for vaccine production control performance was not satisfactory.

Classical automatic tuning approaches using PID control also require undesirable disturbances of the process [26]. Adaptation by a model predictive control approach proposed in [27] needs an open-loop model with the disadvantage that accuracy is not guaranteed. Another drawback of some of the reported solutions is the complex implementation in practice.

Industrial applications of adaptive control are often rule-based instead of model-based [28]. However, for control of complex and difficult industrial processes model-based control approaches have been proven the most effective among the different types of adaptive controllers [13].

Automatic tuning based on the mit rule

The task of the automatic tuning method is to pursue the best trade-off between tracking behavior, disturbance rejection, and stability. The automatic tuning method, therefore, should have the following abilities. At one hand, if control parameters γ1 and γ2 are initialized too small (Eq. 14), the automatic tuning method must increase the value of γ1 and γ2 to avoid underdamped behavior. On the other hand, the automatic tuning method should reduce the values of γ1 and γ2 if the error converges too slowly to zero. The automatic tuning method has to be derived so that a stable system is obtained in the sense that the error remains bounded.

In model-reference adaptive control according to the textbook of Åström and Wittenmark [14], the MIT rule is used to obtain adaptation. The error between the reference model and process output \((e = \mu_{{\rm ref}} - \hat{\mu})\) is the driver for the adaptation. Following the MIT rule the parameters γ are adjusted such that a squared error is minimized:

$$ \frac{{\rm d}\gamma}{{\rm d}t}=-\beta \cdot e \cdot \frac{\partial e}{\partial \gamma} $$
(20)

The vector \(\frac{{\partial e}}{{\partial \gamma}}\) is the sensitivity of the error with respect to the controller parameter vector γ (error sensitivity). The coefficient β determines the adaptation rate and must be chosen so that the controller parameters change slower than the specific growth rate and dissolved oxygen, but fast enough to obtain adaptation.

Online automatic tuning methods

Adaptation based on the MIT rule is driven by the error e which arises from set-point changes and disturbances. Systematic set-point changes must be avoided in cultivation systems for biopharmaceutical production as it may affect critical variables. As a consequence, in this work, adaptation is only driven by errors caused by disturbances. The model error e equals the set-point error ɛ and the reference model has become redundant.

The MIT rule requires knowledge of the error sensitivity, which is difficult to derive. Therefore, in literature approximations for the error sensitivity have been made [14]. Simulations with the outcome of several approximations gave poor results in the cultivation for vaccine production. Therefore alternative adaptation schemes are applied in the next section. Several (weighted) combinations of ɛ, ɛ2, and \(\int\varepsilon\) are investigated to approximate the sensitivity derivative:

$$ \frac{{\partial \varepsilon}}{{\partial \gamma}} = c_{1} \cdot 1 + c_{2} \cdot \varepsilon + c_{3} \cdot {\int\limits_0^t \varepsilon} $$
(21)

Method 1: Adaptation based on the error

The most simple mechanism is assuming the sensitivity derivative to be one [29, 30] (c 1 = −1, c 2 = c 3 = 0).

$$ \frac{{{\rm d}\gamma}}{{{\rm d}t}} = \beta \cdot \varepsilon $$
(22)

which appears to work well for adaptation of estimated process parameters. A test of Eq. 22 revealed that it is not a good mechanism for adaptation of controller parameters, because negative and positive errors will result in opposite adjustments of γ and do not cancel oscillations.

Method 2: Adaptation based on the (intergral) error

In the second automatic tuning method the error sensitivity \(\frac{{\partial \varepsilon}}{{\partial \gamma }}\) in Eq. 20 is replaced by a combination of the error and the integral error (c 1 = 0, c 2 = −1, c 3 = −1).

$$ \begin{aligned} \frac{{{\rm d}\gamma_{1}}}{{{\rm d}t}} &= \varepsilon \cdot {\left({\beta_{2} \varepsilon + \beta_{3} {\int\limits_0^t \varepsilon}{\rm d}t} \right)} \\ \frac{{{\rm d}\gamma_{2}}}{{{\rm d}t}} &= \varepsilon \cdot {\left({\beta_{2} \varepsilon + \beta_{3} {\int\limits_0^t \varepsilon}{\rm d}t} \right)} \\ \end{aligned} $$
(23)

where β2 and β3 are a combination of β and c 2 and c 3 (β2 = βc 2 and β3 = βc 3). The automatic tuning method (Eq. 23) adapts control parameters γ1 and γ2 proportional to ɛ2 and \(\varepsilon {\int \varepsilon}.\) So, γ1 and γ2 are predominately adapted when the quadratic error is large and/or when the error persists. The choice of the adaptation rate β2 and β3 is based on simulations. Too large values make adaptation faster than the change of the other variables in the system and make the adaptation mechanism react on instant errors instead of persistent errors, thereby avoiding the “basic” controller (Eq. 15) to counteract on these errors. Too small values of β give slow adaptation, which results in the requirement for multiple tuning runs to upgrade performance. The choice of the adaptation rates for γ1 and γ2 is a choice for the designer of the controller, but simulations showed that distinction between the adaptation rates of γ1 and γ2 was not necessary.

This online automatic tuning method is applied to simulations of fed-batch cultivations in which γ1 and γ2 were initialized too small. By initiating the automatic tuning method at the start of the fed-batch, control performance was significantly upgraded within 5 h of cultivation (Fig. 4 shows a typical simulation). The mean absolute error and oscillation measure decreased fast after the start of the fed–batch resulting in upgraded controller performance (Fig. 4c, d). Compared to a simulation without adaptation of the controller tuning parameters, oscillations were attenuated five times faster (compare Figs. 3, 4).

Fig. 4
figure 4

Simulation results of specific growth rate control with automatic tuning based on the error and the integral error (method 2, Eq. 23). β2 = 225, β3 = 550. Fed-batch start at t = 22 h. a Specific growth rate (μ). b Controller tuning parameters. c Mean absolute error. d Oscillation measure

Full size image

Method 3: Adaptation based on the (squared) error

The third automatic tuning scheme consists of a combination of the error and the squared error, normalized by \(\mu_{\rm set} \cdot (c_{1} = - \frac{1}{{\mu_{{\rm set}}}},c_{2} = - \frac{1}{{\mu_{{\rm set}}^{2}}}, c_{3}= 0).\)

$$ \begin{aligned}\frac{{{\rm d}\gamma_{1}}}{{{\rm d}t}} &= \beta_{1} \cdot \frac{\varepsilon}{{\mu_{{\rm set}}}} + \beta_{2} \cdot \frac{{\varepsilon^{2}}}{{\mu_{{\rm set}}^{2}}} \\ \frac{{{\rm d}\gamma_{2}}}{{{\rm d}t}} &= \beta_{1} \cdot \frac{\varepsilon}{{\mu_{{\rm set}}}} + \beta_{2} \cdot \frac{{\varepsilon^{2}}}{{\mu_{{\rm set}}^{2}}} \\ \end{aligned} $$
(24)

where β1 and β2 are a combination of β and c 1 and c 2 (β1 = βc 1 and β2 = βc 2). Analogous to method 2 no distinction is made in β i -values for the adaptation rates for γ1 and γ2. The automatic tuning method (Eq. 24) adapts control parameters γ1 and γ2 proportional to the error ɛ and proportional to the quadratic error ɛ2, which is large if the error is large.

The fed-batch phase of the simulation in Fig. 5 started at 22 h. At the same time the specific growth rate controller was switched on with initial values of γ1 and γ2, which were chosen too low as in Fig. 3. The graph shows that these values resulted in underdamped responses (Fig. 5a), but the adjustment of γ1 and γ2 (Fig. 5b) was so strong that within 5 h the deviations were minimal and oscillations were cancelled (Fig. 5d). Figure 5c shows that controller performance was significantly upgraded with respect to the mean absolute error. Note that the mean absolute error and the oscillation measure were delayed 1.5 h to calculate their measures. Disturbances due to time-varying parameters and noise do not influence controller performance.

Fig. 5
figure 5

Simulation results of specific growth rate control with automatic tuning based on the error and the squared error (method 3, Eq. 24), β1 = 0.25, β2 = 0.5. Fed-batch start at t = 22 h. a Specific growth rate (μ). b Controller tuning parameters. c Mean absolute error d Oscillation measure

Full size image

In other applications, the desired behavior can be acquired quickly by using this automatic tuning method.

Although the MIT rule was the starting point for derivation of the online automatic tuning method, concepts applying directly the MIT rule did not give satisfactory results. The alternatives presented in the last two sections were capable to upgrading performance.

Comparison method 2 and 3 for different β and γ

Adaptation using the integral error as well as adaptation using squared error give similar results for γ1 and γ2 (Figs. 4, 5). Both adaptation mechanisms require 5 h to upgrade controller performance and to cancel underdamped behavior. Controller tuning parameters γ1 and γ2 converge to similar values, but adaptation using the integral error is smoother.

Figure 6 shows simulations with different initialized values of the controller parameters γ. Figure 6a, b illustrates once again the adaptation of γ1 and γ2 initialized with too small values. Simulations initialized close to the end-values of the previous run (Fig. 6a, b) showed that the adaptation mechanisms leave the tuning parameters almost unchanged (Fig. 6c, d). Similar adaptation results are found for simulations initialized with large initial parameters (Fig. 6e, f). Large tuning parameters slow down the controller actions, but only marginally decrease controller performance. As a result, the driving force (or error) for adaptation is small and so is the adaptation of controller parameters.

Fig. 6
figure 6

Tuning parameters γ1 and γ2 for different initializations of γ. Fed-batch start at t = 22 h. a, c, e Method 2 (integral errors, Eq. 23, β2 = 225, β3 = 550). b, d, f Method 3 (squared errors Eq. 24, β1 = 0.25, β2 = 0.5). a, b γ1 and γ2 initialized too small. c, d γ1 and γ2 initialized close to the end-values of the previous run. e, f γ1 and γ2 initialized too large

Full size image

Figure 7 shows additional simulations with different values of the adaptation rate β. Figure 7c, d illustrates once again the effect of the chosen adaptation rate β on μ and γ as a reference. Small values for the adaptation rate β give slow adaptation of controller parameters γ (Fig. 7a, b). The oscillations are attenuated two to three times slower compared with the chosen β and about two times faster relative to fixed γ (β = 0, compare with Fig. 3). If β is chosen larger, adaptation becomes faster and larger values for γ are obtained (Fig. 7e). Large tuning parameters slow down the controller actions and may give small offsets. The adaptation rate β in Fig. 7f is chosen too large and gives interference with other dynamics (dissolved oxygen and specific growth rate). So, if the adaptation rate β is not chosen too fast, both methods show robust adaptation.

Fig. 7
figure 7

The effect of different β values on adaptation of tuning parameters γ1 and γ2 ({\it right axis}) and on μ ({\it left axis}). Fed-batch start at t = 22 h. c, d β initialized with the chosen values. c β2 = 225, β3 = 550. d β1 = 0.25, β2 = 0.5. a, c, e Method 2 (integral errors, Eq. 23). b, d, f Method 3 (squared errors Eq. 24). a, b β initialized ten times smaller. e, f β initialized ten times larger

Full size image

Stability

In previous sections the automatic tuning mechanisms were evaluated by simulations. Although performance is good the effect of changing the tuning parameters on stability is yet unknown. Bastin and Dochain [31] state that stability of fed-batch cultivations is not an issue because the exponentially increasing biomass and volume make the system inherent unstable and result in positive poles. However, because the positive poles can be cancelled in the controller loops it makes sense to examine stability properties of the control loops.

Dagci et al. [6] “solve” the stability issue by examining the stability of the control loop; others [4, 5, 16] refer to the stability of the reference model. In this work, stability is examined by considering the poles of the closed loop. The full system is given by Eqs. 3, 4, 7–9, 12, and the derivative of Eq. 1 including the controller Eqs. 13 and 15. The following time-varying state space model represents the linearized form of this system along the trajectory of fed-batch cultivation (see Appendix 2 for the equations and the linearization of the system):

$$ \begin{aligned} & \frac{{{\rm d}x}}{{{\rm d}t}}= A(t)x + B(t)u \\ & y = C(t)x \\ & u = F(t)x \\ \end{aligned} $$
(25)

with x the state variables, y the output variables, u the input variables, A the system matrix, B the input matrix, C the output matrix, and F the state feedback matrix.

The closed loop is stable if the poles of the matrix (A + BF) are in the left half plane. The poles are calculated numerically for each time instant and each set of tuning parameters γ1 and γ2 during the simulation experiments. Figure 8 gives an illustration of the effect of γ1 and γ2 on closed loop stability and on controller performance for a range (250 data points between 1.65 × 10−5 to 1.03 for γ1 and 6.5 × 10−6 to 0.41 for γ2), where the ratio γ1/γ2 is fixed at one point of the trajectory (t = 26.7 h). Similar results are obtained at other points along the trajectory. All real parts of the poles in Fig. 8a–e are negative. Figure 8f and g show positive poles that are dominated by the exponentially increasing biomass and volume according to the associated eigenvectors.

Fig. 8
figure 8

Example of real and imaginary poles of the closed loop system for a range of γ1 and γ2 calculated by offline simulation of the process at one time point along the trajectory. The arrows indicate the direction in which the poles move with increasing controller tuning parameters γ1 and γ2

Full size image

Small values of γ increase the stability margin for most poles. Large values, on the other hand, result in a smooth control of the specific growth rate. Evaluation of the transfer functions μ (s)/μset (s) and DO(s)/DOset (s) showed that the positive poles are cancelled in these transfer functions and only negative poles are relevant for these functions.

Experimental results

Controlled fed-batch cultivations with the dual substrate consuming bacterium B. pertussis (causative agent of whooping cough disease) were performed in a 7-l laboratory bioreactor with a chemically defined medium containing glutamate and L-lactate as the main carbon sources [7]. Bioreactor conditions, analysis, and software were applied as reported in [4]. The fed-batch, the μ controller, and the automatic tuning started automatically when the limiting substrates were almost depleted and μ dropped to the set-point.

Control performance of the automatic tuning method and the specific growth rate controller were evaluated for the best methods of the simulations: method 2: based on the (integral) error (Eq. 23) and method 3: based on the (squared) error (Eq. 24).

Method 2: Adaptation based on the (integral) error

The automatic tuning method based on the (integral) error (Eq. 23) was implemented and tested by initializing control parameters γ1 and γ2 with values, which turned out to be too small in practice. In simulations it turned out that the adaptation parameter γ is slightly increasing as the experiment proceeds toward the end. This makes the γ correction mechanism more sensitive to errors than necessary. Therefore, in order to safeguard the experiment, it was decided to use in the experiment Eq. 26 instead of Eq. 23, which leads to down-tuning of the adaptation toward the end of the cultivation.

$$ \begin{aligned} \frac{{{\rm d}\gamma_{1}}}{{{\rm d}t}} &= \varepsilon \cdot {\left({\beta_{2} \frac{\varepsilon}{{\gamma_{1}}} + \beta_{3} {\int\limits_0^t {\frac{\varepsilon}{{\gamma_{2}}}{\rm d}t}}} \right)} \\ \frac{{{\rm d}\gamma_{2}}}{{{\rm d}t}} &= \varepsilon \cdot {\left({\beta_{2} \frac{\varepsilon}{{\gamma_{1}}} + \beta_{3} {\int\limits_0^t {\frac{\varepsilon}{{\gamma_{2}}}{\rm d}t}}} \right)} \\ \end{aligned} $$
(26)

Evaluation after the experiment showed that the difference with the original γ adaptation is small, so that, on retrospect, the precaution was unnecessary.

The laboratory experiment showed that by initiating the automatic tuning method at the start of the fed-batch at about 20 hours control performance was upgraded (Fig. 9). The mean absolute error and oscillation measure decrease with time. The adaptation of γ1 and γ2 continues during the whole fed-batch cultivation, but the changes in the first period are the strongest and at the end the values are close to the steady state.

Fig. 9
figure 9

Results for laboratory experiments with automatic tuning based on (integral) errors (method 2, Eq. 26). Fed-batch start at t = 19.7 h, β2 = 20, β3 = 20. a Oxygen uptake rate (OUR). b Specific growth rate (μ). c Biomass. d Substrate feed rate. e Controller tuning parameters. f Mean absolute error. g Oscillation measure

Full size image

A standard deviation of 0.005 h−1 on μ is obtained during the fed-batch phase and indicates that the long-term performance is good. The controller maintained μ close to μset in the presence of various uncertainties including disturbances on dissolved oxygen consumption, uncertain parameters, and initialization errors.

An exponentially increasing feed rate (Fig. 9d) was added into the bioreactor to cope with the exponentially increasing biomass (Fig. 9c). At t = 33.5 h agitation speed was increased with 100 rpm to meet the increasing the oxygen demand during the fed-batch phase. The resulting peak in the dissolved oxygen concentration caused a disturbance in the estimated specific growth rate at t = 33.5 h and in the mean absolute error and oscillation error. The controller parameters were hardly adapted and the specific growth rate was properly controlled until the end of the cultivation.

At t = 40 h the mean absolute error and the oscillation measure became approximately constant. As an option a performance monitor can be added to the system, which can be used to evaluate the performance criteria and as a manager to (de)activate the automatic tuning method. The first function of the performance monitor is to qualify controller performance using the criteria given in Eqs. 18 and 19. Next, based on the qualification, the performance monitor decides to retune the process using an automatic tuning method or to continue with the current settings. If control performance is upgraded and the performance measures are constant, tuning is finished and the specific growth rate controller can continue with the obtained settings. In the experiment at t = 40 h in Fig. 9, the performance monitor would decide to continue the cultivation with the current settings for γ1 and γ2 and to deactivate the automatic tuning method. Subsequently, the following cultivations can be performed with the obtained settings.

Method 3: Adaptation based on the (squared) error

Figure 10 shows a part of a long-term experiment direct after initialization of the automatic tuning controller. The oscillations that occur due to an incorrect choice of γ1 and γ2 vanish within three hours. The offset at the end of this period disappears in some hours. The tuning method is doing its task well.

Fig. 10
figure 10

Detail of results for laboratory experiments with adaptation based on the (squared) error (method 3, Eq. 24, β1 = 0.25, β2 = 0.5). Fed-batch start at t = 21.7 h. a Specific growth rate (μ). b Controller tuning parameters

Full size image

The adaptation of γ1 and γ2 continues and has not come to steady state after 3 h. The oscillations that were observed in the simulations for this tuning method in the courses of γ1 and γ2 are hardly present in the experiment (compare Fig. 10 with Fig. 6)

Comparing the simulation (Fig. 6) with the experimental results (Fig. 10), it can be observed that the tuning parameters γ1 and γ2 giving the best performance during laboratory experiments are a factor five to six larger than the tuning parameters giving the best performance during simulations. Mismatches between experimental-simulation are common for biological processes. The experiments show that the automatic tuning method compensates for these mismatches by adapting the controller settings such that the desired behavior is acquired.

Calculation of the poles of the closed loop for the laboratory experiments shows that the tuning parameters are adapted into the proper direction within the stability area. These results confirm the closed loop stability, which was already calculated for the simulated process.

Conclusions

The challenge was to upgrade performance of poorly acting controllers. Online automatic tuning has this capability. Three automatic tuning methods were applied to upgrade control performance for specific growth rate control during fed-batch cultivation. The best two methods were qualified by laboratory experiments for B. pertussis. In the first method, the adaptation rate is proportional to the product of the error and the integral error. The second uses an adaptation rate proportional to the error and the squared error. The methods do not require online identification, thus avoiding the need for process perturbation and complex implementation. The qualifications of the controller and automatic tuning method are:

  • Control performance is evaluated online on the basis of the current mean absolute error and oscillation measure. A performance monitor can be used to activate or deactivate the automatic tuning device.

  • If control performance is poor, application of automatic tuning yields good performance within 5 h by adapting the controller parameters such that the mean absolute error and oscillation measure decrease at least tenfold. The automatic tuning methods are robust against disturbances among others noise, parameter uncertainties, and initialization errors.

  • We expect that a cultivation controlled at the desired specific growth rate will result in smaller variations in end quality (vaccine titer) and thus yield a better product (vaccine).

  • The closed loop with automatic tuning is stable at any point along the trajectory of fed-batch cultivation.

  • Adaptation of control parameters is straightforward, fast and accurate. This feature, furthermore, is neither specific to fed-batch cultivation nor for specific growth rate control and hence can also be applied to other systems.

The applied automatic tuning methods improve controller performance and reduce the tuning effort by automatically adjusting the tuning parameters in one or more tuning runs.