Skip to main content
SpringerLink
Log in

On the fractional homogenization of one-dimensional elastic metamaterials with viscoelastic foundation

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

This work investigates the application of space–time fractional-order operators to the simulation of linear elastic waves propagating in 1D periodic structures resting on a viscoelastic foundation. More specifically, this study focuses on the possible application of fractional-order mathematics as the foundation to develop efficient reduced-order models capable of capturing the wave dynamics in periodic, viscoelastic one-dimensional metamaterials. By leveraging a space–time fractional formulation of the wave equation, we develop a homogenized model capable of capturing either material or geometric inhomogeneity and viscoelastic behavior. First, we derive the dispersion relation for a 1D infinite periodic bar resting on a longitudinal viscoelastic foundation using integer order formulation, which serves as a reference point in this work. Then, we obtain the dispersion relationships associated with two different fractional formulations. The first formulation relies on the use of time-fractional derivatives and focuses on capturing the dissipation induced by the viscoelastic foundation. The second formulation relies on the use of space–time fractional derivatives in order to lead to a homogenized one-dimensional model of the periodic bar. In order to achieve real-valued fractional orders, a matching approach between the dispersion relations of the fractional- and integer-order differential equations is used. Numerical simulations show that the space–time fractional wave equation serves as an effective homogenized model that well represents the wave propagation in a 1D periodic bar on a viscoelastic foundation. The results also illustrate that the use of space-fractional derivatives allows modeling the dynamics within (low order) frequency band gaps, a result typically not achievable with classical homogenization techniques.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Notes

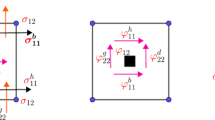
  1. Recall that for a 1D viscoelastic element the stress and strain (also strain rate) are related as: \(\sigma (x) = E \epsilon (x) + E^\prime {\dot{\epsilon }}(x) \equiv E {\mathrm {d}u}/{\mathrm {d}x} + E^\prime {\mathrm {d} {\dot{u}}}/{\mathrm {d}x}\) [13]

Abbreviations

\(\rho _i\) :

Mass density for material i

\({\hat{\rho }}_i\) :

Effective mass density for material i in time-fractional wave equation

\({\hat{\rho }}\) :

Effective mass density in space–time fractional wave equation

\(E_i\) :

Young’s modulus for material i

\({\hat{E}}\) :

Effective Young’s modulus in space–time fractional wave equation

\(L_i\) :

Length of material i within the unit cell

\(\Delta _{\mathrm{L}}\) :

Length of the unit cell

A :

Cross-sectional area

k :

Elastic stiffness parameter of the viscoelastic foundation

c :

Damping parameter of the viscoelastic foundation

\({\overline{k}}\) :

Effective elastic stiffness parameter of the viscoelastic foundation

\({\overline{c}}\) :

Effective damping parameter of the viscoelastic foundation

\(\mu \) :

Wavenumber in integer-order Bloch wave solution

\({\tilde{\mu }}\) :

Wavenumber in time-fractional Bloch wave solution

:

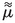Wavenumber in space–time fractional Bloch wave solution

f :

Frequency

\(\omega \) :

Angular frequency

\(\Re (\cdot )\) :

Real component

\(\Im (\cdot )\) :

Imaginary component

\(u_i\) :

Integer-order Bloch wave solution for material i

\({\tilde{u}}_i\) :

Time-fractional Bloch wave solution for material i

:

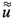Space–time fractional Bloch wave solution

\(U_i\) :

Periodic function defined in integer-order Bloch wave solution for material i

\({\tilde{U}}_i\) :

Periodic function defined in time-fractional Bloch wave solution for material i

:

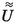Amplitude in space–time fractional Bloch wave solution

\(\lambda _i\) :

Exponent defined in integer-order Bloch wave solution for material i

\({\tilde{\lambda }}_i\) :

Exponent defined in time-fractional Bloch wave solution for material i

\(\beta _i\) :

Time-fractional order for material i in time-fractional wave equation

\(\alpha \) :

Space-fractional order in space–time fractional wave equation

\(\beta \) :

Time-fractional order in space–time fractional wave equation

References

  1. Craster, R.V., Guenneau, S.: Acoustic Metamaterials: Negative Refraction, Imaging, Lensing and Cloaking, vol. 166. Springer, Berlin (2012)

    Google Scholar 

  2. Hussein, M.I., Leamy, M.J., Ruzzene, M.: Dynamics of phononic materials and structures: historical origins, recent progress, and future outlook. Appl. Mech. Rev. 66, 38 (2014)

    Article  Google Scholar 

  3. Trainiti, G., Ruzzene, M.: Non-reciprocal elastic wave propagation in spatiotemporal periodic structures. New J. Phys. 18, 083047 (2016)

    Article  Google Scholar 

  4. Zhu, H., Patnaik, S., Walsh, T.F., Jared, B.H., Semperlotti, F.: Nonlocal elastic metasurfaces: enabling broadband wave control via intentional nonlocality. Proc. Natl. Acad. Sci. 117, 26099–26108 (2020)

    Article  Google Scholar 

  5. Nair, S., Jokar, M., Semperlotti, F.: Nonlocal acoustic black hole metastructures: achieving broadband and low frequency passive vibration attenuation. Mech. Syst. Signal Process. 169, 108716 (2022)

    Article  Google Scholar 

  6. Ao, X., Chan, C.T.: Far-field image magnification for acoustic waves using anisotropic acoustic metamaterials. Phys. Rev. E 77, 025601 (2008)

    Article  Google Scholar 

  7. Zhang, S., Xia, C., Fang, N.: Broadband acoustic cloak for ultrasound waves. Phys. Rev. Lett. 106, 024301 (2011)

    Article  Google Scholar 

  8. Zhu, H., Semperlotti, F.: Metamaterial based embedded acoustic filters for structural applications. AIP Adv. 3, 092121 (2013)

    Article  Google Scholar 

  9. Zhu, H., Semperlotti, F.: Phononic thin plates with embedded acoustic black holes. Phys. Rev. B 91, 104304 (2015)

    Article  Google Scholar 

  10. Miniaci, M., et al.: Design and fabrication of bioinspired hierarchical dissipative elastic metamaterials. Phys. Rev. Appl. 10, 024012 (2018)

    Article  Google Scholar 

  11. Bhattiprolu, U., Bajaj, A.K., Davies, P.: Periodic response predictions of beams on nonlinear and viscoelastic unilateral foundations using incremental harmonic balance method. Int. J. Solids Struct. 99, 28–39 (2016)

    Article  Google Scholar 

  12. Erturk, A., Inman, D.J.: Piezoelectric Energy Harvesting. Wiley, Hoboken (2011)

    Book  Google Scholar 

  13. Kerr, A.D.: Elastic and viscoelastic foundation models. J. Appl. Mech. 31, 491–498 (1964)

    Article  MATH  Google Scholar 

  14. Yadav, O.P., Vyas, N.S.: Stick-slips and jerks in an SDOF system with dry friction and clearance. Int. J. Non-Linear Mech. 137, 103790 (2021)

    Article  Google Scholar 

  15. Khan, M., Li, B., Tan, K.: Impact load wave transmission in elastic metamaterials. Int. J. Impact Eng. 118, 50–59 (2018)

    Article  Google Scholar 

  16. Yadav, O.P., Balaga, S.R., Vyas, N.S.: Forced vibrations of a spring-dashpot mechanism with dry friction and backlash. Int. J. Non-Linear Mech. 124, 103500 (2020)

    Article  Google Scholar 

  17. Kargarnovin, M., Younesian, D., Thompson, D., Jones, C.: Response of beams on nonlinear viscoelastic foundations to harmonic moving loads. Comput. Struct. 83, 1865–1877 (2005)

    Article  Google Scholar 

  18. Failla, G., Zingales, M.: Advanced materials modelling via fractional calculus: challenges and perspectives. Proc. R. Soc. A 378, 20200050 (2020)

    Google Scholar 

  19. Navarro, E.A., Gimeno, B., Cruz, J.L.: Modelling of periodic structures using the finite difference time domain method combined with the Floquet theorem. Electron. Lett. 29, 446–447 (1993)

    Article  Google Scholar 

  20. Sigalas, M.M., Garcıa, N.: Theoretical study of three dimensional elastic band gaps with the finite-difference time-domain method. J. Appl. Phys. 87, 3122–3125 (2000)

    Article  Google Scholar 

  21. Shi, S., Chen, C., Prather, D.W.: Plane-wave expansion method for calculating band structure of photonic crystal slabs with perfectly matched layers. J. Opt. Soc. Am. A 21, 1769–1775 (2004)

    Article  Google Scholar 

  22. Nemat-Nasser, S.: General variational methods for waves in elastic composites. J. Elast. 2, 73–90 (1972)

    Article  Google Scholar 

  23. Patnaik, S., Jokar, M., Semperlotti, F.: Variable-order approach to nonlocal elasticity: theoretical formulation, order identification via deep learning, and applications. Comput. Mech. 69, 267–298 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  24. Patnaik, S., Jokar, M., Ding, W., Semperlotti, F.: On the role of the microstructure in the deformation of porous solids (2022). arXiv preprint arXiv:2202.06750

  25. Mei, J., Liu, Z., Wen, W., Sheng, P.: Effective dynamic mass density of composites. Phys. Rev. B 76, 134205 (2007)

    Article  Google Scholar 

  26. Manevitch, L.I., Andrianov, I.V., Oshmyan, V.G.: Mechanics of Periodically Heterogeneous Structures. Springer, Berlin (2013)

    MATH  Google Scholar 

  27. Craster, R.V., Kaplunov, J., Pichugin, A.V.: High-frequency homogenization for periodic media. Proc. R. Soc. A Math. Phys. Eng. Sci. 466, 2341–2362 (2010)

    MathSciNet  MATH  Google Scholar 

  28. Hollkamp, J.P., Sen, M., Semperlotti, F.: Analysis of dispersion and propagation properties in a periodic rod using a space-fractional wave equation. J. Sound Vib. 441, 204–220 (2019)

    Article  Google Scholar 

  29. Andrianov, I.V., Bolshakov, V.I., Danishevskyy, V.V., Weichert, D.: Higher order asymptotic homogenization and wave propagation in periodic composite materials. Proc. R. Soc. A Math. Phys. Eng. Sci. 464, 1181–1201 (2008)

    MathSciNet  MATH  Google Scholar 

  30. Chatterjee, A.: Asymptotic solution for solitary waves in a chain of elastic spheres. Phys. Rev. E 59, 5912 (1999)

    Article  Google Scholar 

  31. Ramírez-Torres, A., et al.: Three scales asymptotic homogenization and its application to layered hierarchical hard tissues. Int. J. Solids Struct. 130, 190–198 (2018)

    Article  Google Scholar 

  32. Goda, I., Ganghoffer, J.-F.: 3d plastic collapse and brittle fracture surface models of trabecular bone from asymptotic homogenization method. Int. J. Eng. Sci. 87, 58–82 (2015)

    Article  MATH  Google Scholar 

  33. Huang, Y., Yan, D., Yang, Z., Liu, G.: 2d and 3d homogenization and fracture analysis of concrete based on in-situ x-ray computed tomography images and monte carlo simulations. Eng. Fract. Mech. 163, 37–54 (2016)

    Article  Google Scholar 

  34. Ramírez-Torres, A., et al.: An asymptotic homogenization approach to the microstructural evolution of heterogeneous media. Int. J. Non-Linear Mech. 106, 245–257 (2018)

    Article  Google Scholar 

  35. Fish, J., Yang, Z., Yuan, Z.: A second-order reduced asymptotic homogenization approach for nonlinear periodic heterogeneous materials. Int. J. Numer. Methods Eng. 119, 469–489 (2019)

    Article  MathSciNet  Google Scholar 

  36. Saeb, S., Steinmann, P., Javili, A.: Aspects of computational homogenization at finite deformations: a unifying review from Reuss’ to Voigt’s bound. Appl. Mech. Rev. 68, 33 (2016)

    Article  Google Scholar 

  37. Kouznetsova, V., Geers, M.G., Brekelmans, W.: Multi-scale second-order computational homogenization of multi-phase materials: a nested finite element solution strategy. Comput. Methods Appl. Mech. Eng. 193, 5525–5550 (2004)

    Article  MATH  Google Scholar 

  38. Yvonnet, J.: Computational Homogenization of Heterogeneous Materials with Finite Elements. Springer, Berlin (2019)

    Book  MATH  Google Scholar 

  39. Moulinec, H., Suquet, P.: A numerical method for computing the overall response of nonlinear composites with complex microstructure. Comput. Methods Appl. Mech. Eng. 157, 69–94 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  40. Schneider, M., Ospald, F., Kabel, M.: Computational homogenization of elasticity on a staggered grid. Int. J. Numer. Methods Eng. 105, 693–720 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  41. Le, B., Yvonnet, J., He, Q.-C.: Computational homogenization of nonlinear elastic materials using neural networks. Int. J. Numer. Methods Eng. 104, 1061–1084 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  42. Lu, X., et al.: A data-driven computational homogenization method based on neural networks for the nonlinear anisotropic electrical response of graphene/polymer nanocomposites. Comput. Mech. 64, 307–321 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  43. Hollkamp, J.P., Sen, M., Semperlotti, F.: Model-order reduction of lumped parameter systems via fractional calculus. J. Sound Vib. 419, 526–543 (2018)

    Article  Google Scholar 

  44. Hollkamp, J.P., Semperlotti, F.: Application of fractional order operators to the simulation of ducts with acoustic black hole terminations. J. Sound Vib. 465, 115035 (2020)

    Article  Google Scholar 

  45. Patnaik, S., Semperlotti, F.: A generalized fractional-order elastodynamic theory for non-local attenuating media. Proc. R. Soc. A 476, 20200200 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  46. Patnaik, S., Hollkamp, J.P., Sidhardh, S., Semperlotti, F.: Fractional order models for the homogenization and wave propagation analysis in periodic elastic beams. Meccanica 57, 1–17 (2021)

    MathSciNet  Google Scholar 

  47. Szajek, K., Sumelka, W., Bekus, K., Blaszczyk, T.: Designing of dynamic spectrum shifting in terms of non-local space-fractional mechanics. Energies 14, 506 (2021)

    Article  Google Scholar 

  48. Lazopoulos, K.: Non-local continuum mechanics and fractional calculus. Mech. Res. Commun. 33, 753–757 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  49. Carpinteri, A., Cornetti, P., Sapora, A.: A fractional calculus approach to nonlocal elasticity. Eur. Phys. J. Spec. Top. 193, 193–204 (2011)

    Article  MATH  Google Scholar 

  50. Ding, W., Patnaik, S., Semperlotti, F.: Multiscale nonlocal elasticity: a distributed order fractional formulation (2021). arXiv preprint arXiv:2201.01219

  51. Szajek, K., Sumelka, W.: Discrete mass-spring structure identification in nonlocal continuum space-fractional model. Eur. Phys. J. Plus 134, 1–19 (2019)

    Article  Google Scholar 

  52. Alvarez-Ramirez, J., Fernandez-Anaya, G., Valdes-Parada, F.J., Ochoa-Tapia, J.A.: A high-order extension for the Cattaneo’s diffusion equation. Physica A Stat. Mech. Appl. 368, 345–354 (2006)

    Article  MathSciNet  Google Scholar 

  53. Tarasov, V.E.: Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media. Springer, Berlin (2011)

    Google Scholar 

  54. Magin, R.L.: Fractional calculus models of complex dynamics in biological tissues. Comput. Math. Appl. 59, 1586–1593 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  55. Szabo, T.L.: Causal theories and data for acoustic attenuation obeying a frequency power law. J. Acoust. Soc. Am. 97, 14–24 (1995)

    Article  Google Scholar 

  56. Chen, W., Holm, S.: Fractional Laplacian time–space models for linear and nonlinear lossy media exhibiting arbitrary frequency power-law dependency. J. Acoust. Soc. Am. 115, 1424–1430 (2004)

    Article  Google Scholar 

  57. Holm, S., Näsholm, S.P.: A causal and fractional all-frequency wave equation for lossy media. J. Acoust. Soc. Am. 130, 2195–2202 (2011)

    Article  Google Scholar 

  58. Chatterjee, A.: Statistical origins of fractional derivatives in viscoelasticity. J. Sound Vib. 284, 1239–1245 (2005)

    Article  Google Scholar 

  59. Mainardi, F.: Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models. World Scientific, Singapore (2010)

    Book  MATH  Google Scholar 

  60. Patnaik, S., Semperlotti, F.: Modeling contacts and hysteretic behavior in discrete systems via variable-order fractional operators. J. Comput. Nonlinear Dyn. 15, 10 (2020)

    Google Scholar 

  61. Patnaik, S., Semperlotti, F.: Variable-order fracture mechanics and its application to dynamic fracture. NPJ Comput. Mater. 7, 1–8 (2021)

    Article  Google Scholar 

  62. Meng, R., Yin, D., Drapaca, C.S.: Variable-order fractional description of compression deformation of amorphous glassy polymers. Comput. Mech. 64, 163–171 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  63. Orosco, J., Coimbra, C.F.M.: Variable-order modeling of nonlocal emergence in many-body systems: application to radiative dispersion. Phys. Rev. E 98, 032208 (2018)

    Article  Google Scholar 

  64. Akhavan-Safaei, A., Samiee, M., Zayernouri, M.: Data-driven fractional subgrid-scale modeling for scalar turbulence: a nonlocal les approach. J. Comput. Phys. 446, 110571 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  65. Suzuki, J.L., Tuttle, T.G., Roccabianca, S., Zayernouri, M.: A data-driven memory-dependent modeling framework for anomalous rheology: application to urinary bladder tissue. Fractal Fract. 5, 223 (2021)

    Article  Google Scholar 

  66. Manconi, E., Sorokin, S.: On the effect of damping on dispersion curves in plates. Int. J. Solids Struct. 50, 1966–1973 (2013)

    Article  Google Scholar 

  67. Wang, Y.-F., Wang, Y.-S., Laude, V.: Wave propagation in two-dimensional viscoelastic metamaterials. Phys. Rev. B 92, 104110 (2015)

    Article  Google Scholar 

  68. Frazier, M.J., Hussein, M.I.: Generalized Bloch’s theorem for viscous metamaterials: dispersion and effective properties based on frequencies and wavenumbers that are simultaneously complex. C. R. Phys. 17, 565–577 (2016)

    Article  Google Scholar 

  69. Aladwani, A., Nouh, M.: Mechanics of metadamping in flexural dissipative metamaterials: analysis and design in frequency and time domains. Int. J. Mech. Sci. 173, 105459 (2020)

    Article  Google Scholar 

  70. Aladwani, A., Nouh, M.: Strategic damping placement in viscoelastic bandgap structures: dissecting the metadamping phenomenon in multiresonator metamaterials. J. Appl. Mech. 88, 021003 (2021)

    Article  Google Scholar 

  71. Brillouin, L.: Wave Propagation in Periodic Structures: Electric Filters and Crystal Lattices. Courier Corporation, Chelmsford (2003)

    MATH  Google Scholar 

  72. Yu, D., Wen, J., Shen, H., Xiao, Y., Wen, X.: Propagation of flexural wave in periodic beam on elastic foundations. Phys. Lett. A 376, 626–630 (2012)

    Article  Google Scholar 

  73. Wang, K., Zhou, J., Xu, D., Ouyang, H.: Lower band gaps of longitudinal wave in a one-dimensional periodic rod by exploiting geometrical nonlinearity. Mech. Syst. Signal Process. 124, 664–678 (2019)

    Article  Google Scholar 

  74. Bagley, R.L., Torvik, P.: A theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol. 27, 201–210 (1983)

    Article  MATH  Google Scholar 

  75. Torvik, P., Bagley, R.: On the appearance of the fractional derivative in the behavior of real materials. J. Appl. Mech. Trans. ASME 51, 294–298 (1984)

    Article  MATH  Google Scholar 

  76. Narahari Achar, B., Hanneken, J.: Microscopic formulation of fractional calculus theory of viscoelasticity based on lattice dynamics. Physica Scr. 2009, 014011–014018 (2009)

    Article  Google Scholar 

  77. Mashayekhi, S., Miles, P., Hussaini, M.Y., Oates, W.S.: Fractional viscoelasticity in fractal and non-fractal media: theory, experimental validation, and uncertainty analysis. J. Mech. Phys. Solids 111, 134–156 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  78. Mashayekhi, S., Hussaini, M.Y., Oates, W.: A physical interpretation of fractional viscoelasticity based on the fractal structure of media: theory and experimental validation. J. Mech. Phys. Solids 128, 137–150 (2019)

    Article  MathSciNet  Google Scholar 

  79. Mainardi, F.: The time fractional diffusion-wave equation. Radiophys. Quantum Electron. 38, 13–24 (1995)

    Article  MathSciNet  Google Scholar 

  80. Alotta, G., Di Paola, M., Failla, G., Pinnola, F.P.: On the dynamics of non-local fractional viscoelastic beams under stochastic agencies. Compos. Part B Eng. 137, 102–110 (2018)

    Article  Google Scholar 

  81. Diethelm, K.: The Analysis of Fractional Differential Equations. Springer, New York (2004)

    Google Scholar 

  82. Garrappa, R., Kaslik, E., Popolizio, M.: Evaluation of fractional integrals and derivatives of elementary functions: overview and tutorial. Mathematics 7, 407 (2019)

    Article  Google Scholar 

  83. Patnaik, S., Sidhardh, S., Semperlotti, F.: Towards a unified approach to nonlocal elasticity via fractional-order mechanics. Int. J. Mech. Sci. 189, 105992 (2021)

    Article  MATH  Google Scholar 

  84. Gómez-Aguilar, J., et al.: Modeling of a mass-spring-damper system by fractional derivatives with and without a singular kernel. Entropy 17, 6289–6303 (2015)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors gratefully acknowledge the financial support of the National Science Foundation (NSF) under grants MOMS #1761423, and the Defense Advanced Research Project Agency (DARPA) under grant #D19AP00052. J.P.H. acknowledges the financial support of the National Defense Science and Engineering Graduate Fellowship (NDSEG). S.P. acknowledges the financial support of the School of Mechanical Engineering, Purdue University, through the Hugh W. and Edna M. Donnan Fellowship. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation. The content and information presented in this manuscript do not necessarily reflect the position or the policy of the government. The material is approved for public release; distribution is unlimited.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Ray W. Herrick Laboratories, 177 S. Russell St., West Lafayette, IN, 47907, USA

    Wei Ding, John P. Hollkamp, Sansit Patnaik & Fabio Semperlotti

Authors
  1. Wei Ding
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. John P. Hollkamp
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sansit Patnaik
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Fabio Semperlotti
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Wei Ding or Fabio Semperlotti.

Ethics declarations

Conflict of interest

The authors declare no competing interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

Below is the link to the electronic supplementary material.

Supplementary file 1 (pdf 3174 KB)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ding, W., Hollkamp, J.P., Patnaik, S. et al. On the fractional homogenization of one-dimensional elastic metamaterials with viscoelastic foundation. Arch Appl Mech 93, 261–286 (2023). https://doi.org/10.1007/s00419-022-02170-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-022-02170-w

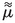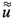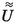Keywords

Search

Navigation