Skip to main content
SpringerLink
Log in

Computational first-order homogenization in chemo-mechanics

  • Special
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

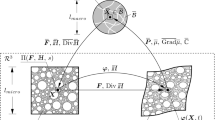
In the present contribution, we consider species diffusion coupled to finite deformations in strongly heterogeneous microstructures. A semi-dual energy formulation parameterized in terms of the chemical potential is obtained by Legendre transformation of the free energy. Doing so avoids the presence of higher gradients of the deformation field. The constitutive response at the macroscopic level is obtained using variationally consistent homogenization (Larson et al. in Int J Numer Method Eng 81(13):1659–1686, 2010. doi:10.1002/nme.2747). This approach allows to treat transient microscale problems on a representative volume element which has a finite size, i.e., the scales are not clearly separated. Full details of the implementation are provided. A series of numerical examples compares the homogenization results to single-scale formulations which fully resolve all microstructural features.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Notes

  1. It is assumed that no solid mass is produced, that is the identity \(\rho _0 \, \hbox {d}V= \rho _t \, \hbox {d}v\) relates the solid mass densities at the reference and current configuration via \(\rho _0 = J \rho _t\).

  2. Quantities labeled by \({}^{\text {M}}{\{\bullet \}}\) belong to the macroscale.

  3. Note that a physically motivated choice of the free energy function takes the form \(\psi ^{\text {chem}}(c) = A c\ln c + B c\). Nonetheless, the polynomial approach is computationally less expensive and is used in the following. This can be compared to the phenomenological approach of using a fourth-order polynomial to approximate the configurational free energy of a Cahn–Hilliard system rather than a logarithmic function, see the discussion in [28].

  4. The concentration is evaluated in a nested loop at every quadrature point using a nonlinear Newton–Raphson solver. The update procedure is given by \(c \leftarrow c - [\psi ,{}_{cc}]^{-1}[\psi ,{}_c-\mu ]\).

References

  1. Larsson, F., Runesson, K., Su, F.: Variationally consistent computational homogenization of transient heat flow. Int. J. Numer. Method. Eng. 81(13), 1659–1686 (2010). doi:10.1002/nme.2747

    MathSciNet  MATH  Google Scholar 

  2. Aifantis, E.C.: On the problem of diffusion in solids. Acta Mech. 37(3), 265–296 (1980). doi:10.1007/BF01202949

    Article  MathSciNet  MATH  Google Scholar 

  3. Kojic, M., Milosevic, M., Kojic, N., Isailovic, V., Petrovic, D., Filipovic, N., Ferrari, M., Ziemys, A.: Transport phenomena: computational models for convective and diffusive transport in capillaries and tissue. In: De, S., Hwang, W., Kuhl, E. (eds.) Multiscale Modeling in Biomechanics and Mechanobiology, pp. 131–156. Springer, London (2015). doi:10.1007/978-1-4471-6599-6_7

    Google Scholar 

  4. Ubachs, R., Schreurs, P., Geers, M.: A nonlocal diffuse interface model for microstructure evolution of tin–lead solder. J. Mech. Phys. Solids 52(8), 1763–1792 (2004). doi:10.1016/j.jmps.2004.02.002

    Article  MATH  Google Scholar 

  5. Salvadori, A., Bosco, E., Grazioli, D.: A computational homogenization approach for li-ion battery cells: part 1 - formulation. J. Mech. Phys. Solids 65, 114–137 (2014). doi:10.1016/j.jmps.2013.08.010

    Article  MathSciNet  MATH  Google Scholar 

  6. Chan, C.K., Peng, H., Liu, G., McIlwrath, K., Zhang, X.F., Huggins, R.A., Cui, Y.: High-performance lithium battery anodes using silicon nanowires. Nat. Nanotechnol. 3(1), 31–35 (2008)

    Article  Google Scholar 

  7. Di Leo, C.V., Anand, L.: Hydrogen in metals: a coupled theory for species diffusion and large elastic-plastic deformations. Int. J. Plast. 43, 42–69 (2013). doi:10.1016/j.ijplas.2012.11.005

    Article  Google Scholar 

  8. Di Leo, C.V., Rejovitzky, E., Anand, L.: A Cahn–Hilliard-type phase-field theory for species diffusion coupled with large elastic deformations: application to phase-separating li-ion electrode materials. J. Mech. Phys. Solids 70, 1–29 (2014). doi:10.1016/j.jmps.2014.05.001

    Article  MathSciNet  MATH  Google Scholar 

  9. Zhao, Y., Stein, P., Xu, B.-X.: Isogeometric analysis of mechanically coupled Cahn-Hilliard phase segregation in hyperelastic electrodes of li-ion batteries. Comput. Methods Appl. Mech. Eng. 297, 325–347 (2015). doi:10.1016/j.cma.2015.09.008

    Article  MathSciNet  Google Scholar 

  10. Miehe, C., Dal, H., Schänzel, L.-M., Raina, A.: A phase-field model for chemo-mechanical induced fracture in lithium-ion battery electrode particles. Int. J. Numer. Method. Eng. 106, 683–711 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  11. Smit, R., Brekelmans, W., Meijer, H.: Prediction of the mechanical behavior of nonlinear heterogeneous systems by multi-level finite element modeling. Comput. Methods Appl. Mech. Eng. 155(1), 181–192 (1998). doi:10.1016/S0045-7825(97)00139-4

  12. Kouznetsova, V., Brekelmans, W.A.M., Baaijens, F.P.T.: An approach to micro–macro modeling of heterogeneous materials. Comput. Mech. 27(1), 37–48 (2001). doi:10.1007/s004660000212

    Article  MATH  Google Scholar 

  13. Miehe, C., Koch, A.: Computational micro-to-macro transitions of discretized microstructures undergoing small strains. Arch. Appl. Mech. 72(4), 300–317 (2002). doi:10.1007/s00419-002-0212-2

    Article  MATH  Google Scholar 

  14. Miehe, C.: Computational micro-to-macro transitions for discretized micro-structures of heterogeneous materials at finite strains based on the minimization of averaged incremental energy. Comput. Methods Appl. Mech. Eng. 192(5–6), 559–591 (2003). doi:10.1016/S0045-7825(02)00564-9

    Article  MathSciNet  MATH  Google Scholar 

  15. Saeb, S., Steinmann, P., Javili, A.: Aspects of computational homogenization at finite deformations: a unifying review from reuss’ to voigt’s bound. Appl. Mech. Rev. 68(5), 050801 (2016)

    Article  Google Scholar 

  16. Özdemir, I., Brekelmans, W.A.M., Geers, M.G.D.: Computational homogenization for heat conduction in heterogeneous solids. Int. J. Numer. Method. Eng. 73(2), 185–204 (2008). doi:10.1002/nme.2068

    Article  MathSciNet  MATH  Google Scholar 

  17. Özdemir, I., Brekelmans, W., Geers, M.: Computational homogenization for the thermo-mechanical analysis of heterogeneous solids. Comput. Methods Appl. Mech. Eng. 198(3–4), 602–613 (2008). doi:10.1016/j.cma.2008.09.008

    Article  MathSciNet  MATH  Google Scholar 

  18. Temizer, I., Wriggers, P.: Homogenization in finite thermoelasticity. J. Mech. Phys. Solids 59(2), 344–372 (2011). doi:10.1016/j.jmps.2010.10.004

    Article  MathSciNet  MATH  Google Scholar 

  19. Su, F., Larsson, F., Runesson, K.: Computational homogenization of coupled consolidation problems in micro-heterogeneous porous media. Int. J. Numer. Method. Eng. 88(11), 1198–1218 (2011). doi:10.1002/nme.3221

    Article  MathSciNet  MATH  Google Scholar 

  20. Sýkora, J., Krejčí, T., Kruis, J., Šejnoha, M.: Computational homogenization of non-stationary transport processes in masonry structures. J. Comput. Appl. Math. 236 (18) (2012) 4745 – 4755, FEMTEC 2011: 3rd International Conference on Computational Methods in Engineering and Science, May 9–13, 2011. doi:10.1016/j.cam.2012.02.031

  21. Pham, K., Kouznetsova, V., Geers, M.: Transient computational homogenization for heterogeneous materials under dynamic excitation. J. Mech. Phys. Solids 61(11), 2125–2146 (2013). doi:10.1016/j.jmps.2013.07.005

    Article  MathSciNet  MATH  Google Scholar 

  22. Runesson, K., Ekh, M., Larsson, F.: Computational homogenization of mesoscale gradient viscoplasticity, Comput. Methods Appl. Mech. Eng. (2017)—Accepted for publication. doi:10.1016/j.cma.2016.11.032

  23. Kaessmair, S., Steinmann, P.: Comparative computational analysis of the Cahn–Hilliard equation with emphasis on C1-continuous methods. J. Comput. Phys. 322, 783–803 (2016). doi:10.1016/j.jcp.2016.07.005

    Article  MathSciNet  MATH  Google Scholar 

  24. Saad, Y., Schultz, M.H.: GMRES: a generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 7(3), 856–869 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  25. Miehe, C.: Numerical computation of algorithmic (consistent) tangent moduli in large-strain computational inelasticity. Comput. Methods Appl. Mech. Eng. 134(3), 223–240, (1996). doi:10.1016/0045-7825(96)01019-5. http://www.sciencedirect.com/science/article/pii/0045782596010195

  26. Kouznetsova, V., Geers, M., Brekelmans, W.: Multi-scale second-order computational homogenization of multi-phase materials: a nested finite element solution strategy. Comput. Methods Appl. Mech. Eng. 193(48–51), 5525–5550 (2004). doi:10.1016/j.cma.2003.12.073

    Article  MATH  Google Scholar 

  27. Temizer, I., Wriggers, P.: On the computation of the macroscopic tangent for multiscale volumetric homogenization problems. Comput. Methods Appl. Mech. Eng. 198(3–4), 495–510 (2008). doi:10.1016/j.cma.2008.08.018

    Article  MathSciNet  MATH  Google Scholar 

  28. Gómez, H., Calo, V.M., Bazilevs, Y., Hughes, T.J.: Isogeometric analysis of the Cahn–Hilliard phase-field model. Comput. Methods Appl. Mech. Eng. 197(49–50), 4333–4352 (2008). doi:10.1016/j.cma.2008.05.003

  29. Miehe, C., Mauthe, S., Ulmer, H.: Formulation and numerical exploitation of mixed variational principles for coupled problems of Cahn–Hilliard-type and standard diffusion in elastic solids. Int. J. Numer. Method. Eng. 99(10), 737–762 (2014). doi:10.1002/nme.4700

    Article  MathSciNet  MATH  Google Scholar 

  30. Lu, S., Pister, K.S.: Decomposition of deformation and representation of the free energy function for isotropic thermoelastic solids. Int. J. Solids Struct. 11(7–8), 927–934 (1975)

    Article  MATH  Google Scholar 

Download references

Acknowledgements

The authors gratefully acknowledge the support by the German Research Foundation (DFG) under Grant STE 544/48.

Author information

Authors and Affiliations

  1. Chair of Applied Mechanics, Friedrich–Alexander Universität Erlangen–Nürnberg, Paul-Gordan-Str. 3, 91052, Erlangen, Germany

    Stefan Kaessmair & Paul Steinmann

Authors
  1. Stefan Kaessmair
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Paul Steinmann
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Paul Steinmann.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kaessmair, S., Steinmann, P. Computational first-order homogenization in chemo-mechanics. Arch Appl Mech 88, 271–286 (2018). https://doi.org/10.1007/s00419-017-1287-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-017-1287-0

Keywords

Search

Navigation