Emulsion rheology for steady and oscillatory shear flows at moderate and high viscosity ratio

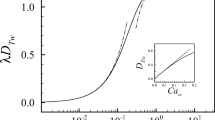
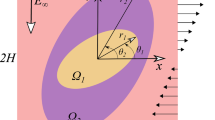
Abstract

A numerical simulation scheme based on a three-dimensional boundary integral method is used for the purpose of estimating the macroscopic flow from the microscale drop deformation for emulsions of high viscosity ratio under steady, oscillatory shear, and extensional flows. The effects of drop deformation and shear rate are examined for moderate and high viscosity ratio. The accuracy and convergence of the numerical simulations is illustrated by comparing drop deformation and rheology with experimental observations and an asymptotic theory based on a second-order small deformation theory also developed in this work. We also examine an emulsion undergoing a pure extensional flow and an extensional viscosity of the emulsion is computed by the theory and the numerical simulations. In addition, we also explore regimes of linear and nonlinear viscoelasticity when the emulsion is subjected to oscillatory shear for different viscosity ratio. Emulsion Fourier modes are examined for two different viscosity ratio. For a more concentrate emulsion with an unit viscosity ratio, a static shear elastic modulus is computed as a function of drop volume fraction and compared with experimental data. The numerical simulation results are validated against theory and experimental observation of drops in shear and extensional flows. A very good agreement is observed for moderate and high viscosity ratio. The regime of emulsions with relatively high viscosity ratios has not been much explored in the current theoretical and experimental literature. The boundary integral numerical simulations developed in this work has the ability to predict what we expect on the behavior of emulsion with moderate and high viscosity ratio.

Appendix

Periodic green’s function

The kernel functions ${\boldsymbol {\mathcal {G}}}^{P}$ and ${\boldsymbol {\mathcal {T}}}^{P}$ are the periodic stokeslet and stresslet in a periodic lattice defined as an Ewald-summation on the reciprocal lattice of image points (Beenakker 1986).

$$ {\boldsymbol{\mathcal{G}}}^{P}({\textit{\textbf{x}}},\eta)=-\textbf{M}_{o}(\eta)+\sum\limits_{r}{\boldsymbol{\mathcal{G}}}_{1}(\textbf{r})+\frac{8\pi}{\ell^{3}}\sum\limits_{k\not=0} {\boldsymbol{\mathcal{G}}}_{2}(\textbf{k},\eta) $$

(68)

$$ {\boldsymbol{\mathcal{T}}}^{P}({\textit{\textbf{x}}},\eta)=-\sum\limits_{r}{\textbf{H}_{1}(\textbf{r},\eta)+\frac{8\pi}{\ell^{3}}\sum\limits_{k\not= 0}{\textbf{H}_{2}(\textbf{k},\eta)}}. $$

(69)

These tensors include terms with respect to the lattice sums in real space r, $({\boldsymbol {\mathcal {G}}}_{1},\textbf {H}_{1})$ and the reciprocal space k $({\boldsymbol {\mathcal {G}}}_{2},\textbf {H}_{2})$. Here

$$ {\boldsymbol{\mathcal{G}}}_{1}(\textbf{r})=\alpha(r)\frac{\textbf{I}}{r}+\beta(r)\frac{\textbf{rr}}{r^{3}} $$

(70)

$$ \textbf{H}_{1}(\textbf{r})=\gamma(r)\frac{{\mathbf{rrr}}}{r^{5}}+8\eta^{3}\frac{r^{3}}{\pi^{1/2}}\exp(-\eta^{2}r^{2})\left( \nabla{\textbf{G}}_{o}(\textbf{r})+\frac{3}{r^{5}}\textbf{rrr}\right) $$

(71)

$$ {\boldsymbol{\mathcal{G}}}_{2}(\textbf{k})=\left( \frac{\textbf{I}}{k^{2}}-\frac{\mathbf{kk}}{k^{4}}\right)F(k,\eta)\exp(-k^{2}/4\eta^{2})\cos(\textbf{k}\cdot\textbf{x}) $$

(72)

$$\begin{array}{@{}rcl@{}} \textbf{H}_{2}(\textbf{k})&=&2 F(k,\eta)\frac{\textbf{kkk}}{k^{4}}-\left( \nabla{\mathbf{H}}_{o}(\textbf{k})+\frac{\textbf{kkk}}{k^{4}}\right)\\ &&\exp(-k^{2}/4\eta^{2})\sin(\textbf{k}\cdot\textbf{x}) \end{array} $$

(73)

where

$$\textbf{G}_{o}(r)=\frac{\textbf{I}}{r}+\frac{\textbf{rr}}{r^{3}};\quad\textbf{H}_{o}(k)=\frac{\mathbf{I}}{k^{2}}+\frac{\textbf{kk}}{k^{4}};\quad \textbf{M}_{o}=\frac{8\eta}{\pi^{1/2}}\textbf{I}. $$

Here, α(r), β(r), γ(r) are mobility functions defined in Beenakker (1986). It is straightforward to show that the above boundary integral formulation is consistent with the expression of the threedimensional boundary integral given by Rallison and Acrivos (1978) for a viscous drop under a general shear in the free space. For this cases, the kernel functions ${\boldsymbol {\mathcal {G}}}^{P}$ and ${\boldsymbol {\mathcal {T}}}^{P}$ reduce to the Greenś functions of the free space, being

$${\boldsymbol{\mathcal{G}}}^{P}=\frac{\textbf{I}}{r}+\frac{\textbf{xx}}{r^{3}}, \,\,\text{and}\qquad {\textit{\textbf{T}}T}^{P}=\frac{\textbf{xxx}}{r^{3}}. $$