Using regional scaling for temperature forecasts with the Stochastic Seasonal to Interannual Prediction System (StocSIPS)

Abstract

Over time scales between 10 days and 10–20 years—the macroweather regime—atmospheric fields, including the temperature, respect statistical scale symmetries, such as power-law correlations, that imply the existence of a huge memory in the system that can be exploited for long-term forecasts. The Stochastic Seasonal to Interannual Prediction System (StocSIPS) is a stochastic model that exploits these symmetries to perform long-term forecasts. It models the temperature as the high-frequency limit of the (fractional) energy balance equation, which governs radiative equilibrium processes when the relevant equilibrium relaxation processes are power law, rather than exponential. They are obtained when the order of the relaxation equation is fractional rather than integer and they are solved as past value problems rather than initial value problems. StocSIPS was first developed for monthly and seasonal forecast of globally averaged temperature. In this paper, we extend it to the prediction of the spatially resolved temperature field by treating each grid point as an independent time series. Compared to traditional global circulation models (GCMs), StocSIPS has the advantage of forcing predictions to converge to the real-world climate. It extracts the internal variability (weather noise) directly from past data and does not suffer from model drift. Here we apply StocSIPS to obtain monthly and seasonal predictions of the surface temperature and show some preliminary comparison with multi-model ensemble (MME) GCM results. For 1 month lead time, our simple stochastic model shows similar—but somewhat higher—values of the skill scores than the much more complex deterministic models.

Appendices

Appendix 1: Basic theory for fGn processes

1.1 Continuous-in-time fGn

In DRAL, the stochastic natural variability component of the globally averaged temperature was represented as an fGn process. The main properties of fGn relevant for the present paper are summarized in the following.

An fGn process at resolution $\tau$ (the scale at which the series is averaged) has the following integral representation:

$$T_{\tau } \left( t \right) = \frac{1}{\tau }\frac{{c_{H} \sigma_{T} }}{{\Gamma \left( {H + {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}} \right)}}\left[ {\int\limits_{ - \infty }^{t} {\left( {t - t^{\prime}} \right)^{{H + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \gamma \left( {t^{\prime}} \right)dt^{\prime}} - \int\limits_{ - \infty }^{t - \tau } {\left( {t - \tau - t^{\prime}} \right)^{{H + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \gamma \left( {t^{\prime}} \right)dt^{\prime}} } \right],$$

(15)

where $\gamma \left(t\right)$ is a unit Gaussian $\delta$-correlated white noise process with $\langle \gamma \left(t\right)\rangle =0$ and $\langle \gamma \left(t\right)\gamma \left(t^{\prime}\right)\rangle =\delta \left(t-t^{\prime}\right)$ [$\delta \left(x\right)$ is the Dirac function], $\Gamma \left(x\right)$ is the Euler gamma function, ${\sigma }_{T}$ is the ensemble standard deviation (for $\tau =1$) and

$$c_{H}^{2} = \frac{\pi }{{2\cos \left( {\pi H} \right)\Gamma \left( { - 2 - 2H} \right)}}.$$

(16)

This is the canonical value for the constant ${c}_{H}$ that was chosen to make the expression for the statistics particularly simple. In particular, the variance is $\langle {{T}_{\tau }\left(t\right)}^{2}\rangle ={{\sigma }_{T}}^{2}{\tau }^{2H}$ for all $t$, where $\langle \bullet \rangle$ denotes ensemble (infinite realizations) averaging. The parameter $H$, with $-1<H<0$, is the fluctuation exponent of the corresponding fractional Gaussian noise process, the Hurst exponent, ${H}^{^{\prime}}=H+1$. Fluctuation exponents are used due to their wider generality; they are well defined even for strongly intermittent non-Gaussian multifractal processes and they can be any real value. For a discussion, see page 643 in Lovejoy et al. (2015).

Equation (15) can be interpreted as the smoothing of the fractional integral of a white noise process or as the power-law weighted average of past innovations, $\gamma \left(t\right)$. This power-law weighting accounts for the memory effects in the temperature series. The closer the fluctuation exponent is to zero, the larger is the influence of past values on the current temperature. This is evidenced by the behaviour of the autocorrelation function:

$$R_{H} \left( {\Delta t} \right) = \frac{{\left\langle {T_{\tau } \left( t \right)T_{\tau } \left( {t + \Delta t} \right)} \right\rangle }}{{\left\langle {T_{\tau } \left( t \right)^{2} } \right\rangle }} = \frac{1}{2}\left( {\left| {\frac{\Delta t}{\tau } + 1} \right|^{2H + 2} + \left| {\frac{\Delta t}{\tau } - 1} \right|^{2H + 2} - 2\left| {\frac{\Delta t}{\tau }} \right|^{2H + 2} } \right),$$

(17)

for $\left|\Delta t\right|\ge \tau$. In particular, for $\Delta t\gg \tau$ we obtain:

$$R_{H} \left( {\Delta t} \right) \approx \left( {H + 1} \right)\left( {2H + 1} \right)\left( {\frac{\Delta t}{\tau }} \right)^{2H} ,$$

(18)

which has a power–law behaviour with the same exponent as the average squared fluctuation and due to the Wiener–Khinchin theorem, it implies the spectrum exponent $\beta =1+2H$. For more details on fGn processes see Mandelbrot and Van Ness (1968), Gripenberg and Norros (1996) and Biagini et al. (2008).

1.2 Discrete-in-time fGn

A detailed explanation of the theory for modeling and predicting using the discrete version of fGn processes was presented in DRAL; the main results are summarized next. The analogue of Eq. (15) in the discrete case for a finite series, ${\left\{{T}_{t}\right\}}_{t=1,\dots ,N}$, with length $N$ and zero mean is:

$$T_{t} = \sum\limits_{j = 1}^{t} {m_{tj} \gamma_{t + 1 - j} } = m_{t1} \gamma_{t} + \cdots + m_{tt} \gamma_{1} ,$$

(19)

for $t=1,\dots ,N$, where ${\left\{{\gamma }_{t}\right\}}_{t=1,\dots ,N}$ is a discrete white noise process and the coefficients ${m}_{ij}$ are the elements of the lower triangular matrix ${\mathbf{M}}_{H,{\sigma }_{T}}^{N}$ given by the Cholesky decomposition of the autocovariance matrix, ${\mathbf{C}}_{H,{\sigma }_{T}}^{N}={{\sigma }_{T}}^{2}{\left[{R}_{H}\left(i-j\right)\right]}_{i,j=1,\dots ,N}$:

$${\mathbf{C}}_{{H,\sigma_{T} }}^{N} = {\mathbf{M}}_{{H,\sigma_{T} }}^{N} \left( {{\mathbf{M}}_{{H,\sigma_{T} }}^{N} } \right)^{T} ,$$

(20)

with ${m}_{ij}=0$ for $j>i$ (we assume $\tau =1$ is the smallest scale in our system). The superscript $T$ denotes transpose operation.

In vector form, Eq. (19) can be written as:

$${\mathbf{T}}_{N} = {\mathbf{M}}_{{H,\sigma_{T} }}^{N} {{\varvec{\upgamma}}}_{N}$$

(21)

Equations (19–21) can be used to create synthetic samples of fGn with a given length $N$, autocorrelation function given by Eq. (17) and set of parameters ${\sigma }_{T}>0$ and $-1<H<0$ (the mean of the series is always assumed equal to zero). Conversely, given an actual temperature series with vector ${\mathbf{T}}_{N}={\left[{T}_{1},\dots ,{T}_{N}\right]}^{T}$, we can estimate the parameters ${\sigma }_{T}$ and $H$ using the maximum likelihood method (details are given in Appendix 1 of DRAL) and we can verify that it could be well approximated by an fGn model by inverting Eq. (21) and obtaining the residual vector of innovations:

$${{\varvec{\upgamma}}}_{N} = \left( {{\mathbf{M}}_{{H,\sigma_{T} }}^{N} } \right)^{ - 1} {\mathbf{T}}_{N} .$$

(22)

If the model provides a good description of the data, the residual vector ${{\varvec{\upgamma}}}_{N}={\left[{\gamma }_{1},\dots ,{\gamma }_{N}\right]}^{T}$ is a white noise, i.e. the elements should be $\text{NID}\left(\text{0,1}\right)$ with autocorrelation function $\langle {\gamma }_{i}{\gamma }_{j}\rangle ={\delta }_{ij}$ (${\delta }_{ij}$ is the Kronecker delta and $\text{NID}\left(\text{0,1}\right)$ stands for Normally and Independently Distributed with mean $0$ and variance 1). It is worth mentioning that a white noise process is a particular case of fGn with $H=-1/2$.

1.3 fRn correlation function for $0<{\varvec{H}}<1$

The fractional Relaxation noise (fRn) process was introduced in Lovejoy (2019) generalizing both fGn, fBm and Ornstein–Uhlenbeck processes. For short time scales (compared to some characteristic relaxation time, ${\tau }_{r}$) and for exponents $-1/2<H<0$, the fRn is close to an fGn process. For fluctuation exponents in the range $0<H<1$ the high-frequency approximation to fRn is no longer an fGn process. In this case, to leading order, the correlation function is:

$$\begin{array}{*{20}c} {R_{{{\text{fRn}}}} \left( {\Delta t} \right) = 1 - A_{H} \left( {\frac{\Delta t}{{\tau_{r} }}} \right)^{2H} + O\left( {\frac{\Delta t}{{\tau_{r} }}} \right)^{3H + 1/2} ;} & {\begin{array}{*{20}c} {\Delta t < \tau_{r} ;} & {0 < H < 1} \\ \end{array} } \\ \end{array}$$

(23)

where ${\tau }_{r}$ is the relaxation time and ${A}_{H}$ is an $H$-dependent numerical factor [see (Lovejoy 2019)]. The same correlation function was obtained by Delignières (2015) as an approximation to short segments of discrete-in-time fractional Brownian motion (fBm) process that is the integral of an fGn process (but with $H$ increased by 1). This shows that although fBm is nonstationary, short segments approximate (the stationary) fRn process. When $0<H<1$, fBm is a high-frequency approximation to an fRn process.

1.4 Prediction

In DRAL it was shown that, if ${\left\{{T}_{t}\right\}}_{t<0}$ is an fGn process, the optimal k-steps predictor for ${T}_{k}$ ($k>0$), based on a finite number, $m$ (memory), of past values, is given by:

$$\hat{T}_{k} = \sum\limits_{j = - m}^{0} {\phi_{j} \left( k \right)T_{j} } = \phi_{ - m} \left( k \right)T_{ - m} + \cdots + \phi_{0} \left( k \right)T_{0} ,$$

(24)

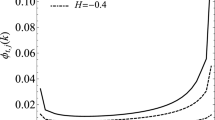
where the vector of predictor coefficients, ${\varvec{\upphi}}\left(k\right)={\left[{\phi }_{-m}\left(k\right),\dots ,{\phi }_{0}\left(k\right)\right]}^{T}$, satisfies the Yule–Walker equations:

$${\mathbf{R}}_{H} {{\varvec\upphi}}\left( k \right) = {\mathbf{r}}_{H} \left( k \right),$$

(25)

with the vector ${\mathbf{r}}_{H}\left(k\right)={\left[{R}_{H}\left(k-i\right) \right]}_{i=-m,\dots ,0}^{T}={\left[{R}_{H}\left(m+k\right),\dots ,{R}_{H}\left(k\right) \right]}^{T}$ and ${\mathbf{R}}_{H}={\left[{R}_{H}\left(i-j\right)\right]}_{i,j=-t,\dots ,0}$ being the autocorrelation matrix (see Eq. 17). In those regions with consecutive values positively correlated (blue regions in Fig. 4a with $-1/2<H<0$ or the increments in the yellow region with$1/2<H<1$), the elements ${R}_{H}\left(\Delta t\right)$ are obtained from Eq. (17). In the places with consecutive increments negatively correlated, where $0<H<1/2$ (red in Fig. 4a), instead of forecasting the fGn increments, we forecast directly the fRn process and we get the elements ${R}_{H}\left(\Delta t\right)$ from Eq. (23). To use this autocorrelation for fRn, we estimate the constant ${A}_{H}$ in Eq. (23) for each location by fitting the empirical autocorrelation function.

The root mean square error ($\text{RMSE}$) for the predictor at a future time $k$, using a memory of $m$ values, is defined as:

$${\text{RMSE}}\left( {k,m} \right) = \sqrt {\left\langle {\left[ {T_{k} - \hat{T}_{k} \left( m \right)} \right]^{2} } \right\rangle } .$$

(26)

Following the results presented in DRAL and using that, for positive $H$ the fRn is the integral of the corresponding fGn process, we obtain the following analytical expression for the $\text{RMSE}$ of the predictor of the natural variability component:

$${\text{RMSE}}_{{{\text{nat}}}}^{{{\text{theory}}}} \left( k \right) = {\text{RMSE}}\left( {k,m,\sigma_{T} ,H} \right) = \left\{ {\begin{array}{*{20}l} {\sigma_{T} \sqrt {1 - {\mathbf{r}}_{H} \left( k \right)^{T} \left( {{\mathbf{R}}_{H} } \right)^{ - 1} {\mathbf{r}}_{H} \left( k \right)} {;}} \hfill & {{\text{for}}\; - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} < H < 0} \hfill \\ {\sigma_{T} k^{H} \sqrt {1 - {\mathbf{r}}_{H - 1} \left( 1 \right)^{T} \left( {{\mathbf{R}}_{H - 1} } \right)^{ - 1} {\mathbf{r}}_{H - 1} \left( 1 \right)} {;}} \hfill & {{\text{for}}\;0 < H < 1} \hfill \\ \end{array} } \right..$$

(27)

For a given forecast horizon, $k$, the $\text{RMSE}$ only depends on the parameters ${\sigma }_{T}$ and $H$, and the memory used, $m$. In Fig. 3 of DRAL it was shown that only a few past datapoints are needed as memory to obtain an error approaching—with more than 95% agreement—the asymptotical value corresponding to $m=\infty$, for all possible values of $H$.

The theoretical mean square skill score ($\text{MSSS}$), is defined as:

$${\text{MSSS}}\left( k \right) = 1 - \frac{{\left\langle {\left[ {T\left( k \right) - \hat{T}\left( k \right)} \right]^{2} } \right\rangle }}{{\left\langle {T\left( k \right)^{2} } \right\rangle }}$$

(28)

(the reference forecast is the mean of the series, assumed equal to zero here).

From the definition of the $\text{RMSE}$, Eq. (26), we obtain the theoretical value for fGn:

$${\text{MSSS}}_{{{\text{nat}}}}^{{{\text{theory}}}} \left( k \right) = {\text{MSSS}}\left( {k,m,H} \right){ = 1} - \frac{{{\text{RMSE}}\left( {k,m,\sigma_{T} ,H} \right)^{2} }}{{\sigma_{T}^{2} }}$$

(29)

or, replacing Eq. (27) for $-1/2<H<0$:

$${\text{MSSS}}\left( {k,m,H} \right) = {\mathbf{r}}_{H} \left( k \right)^{T} \left( {{\mathbf{R}}_{H} } \right)^{ - 1} {\mathbf{r}}_{H} \left( k \right) = {{\varvec\upphi}}\left( k \right) \cdot {\mathbf{r}}_{H} \left( k \right).$$

(30)

In Fig. 19 we show graphs of the theoretical $\text{MSSS}$ as a function of $H$ for different values of $k$. A memory $m=50$ was used for computing the $\text{MSSS}$. As expected, the skill decreases as the forecast horizon increases. For $H=-0.5$, the fGn process is a white noise process and $\text{MSSS}=0$. The skill increases with $H$ and (with infinite past data) the process becomes perfectly predictable when $H\to 0$.

Fig. 19

Graphs of the theoretical $\text{MSSS}$ (Eq. 46) as a function of $H$ for different values of $k$. A memory $m=50$ was used for computing the $\text{MSSS}$

Appendix 2: Verification metrics

2.1 Definitions

The verification metrics used in this paper were defined following the recommendations in the Standardized verification system for long-range forecasts (SVS-LRF) for the practical details of producing and exchanging appropriate verification scores (WMO 2010a, b). Let ${x}_{i}\left(t\right)$ and ${f}_{i}\left(t\right)$, ($t=1,\dots ,N$) denote time series of observations and forecasts, respectively, for a grid point i over the period of verification (POV) with $N$ time steps. Then, their averages for the POV, ${\stackrel{-}{x}}_{i}$ and ${\stackrel{-}{f}}_{i}$ and their sample variances ${{s}_{{x}_{i}}}^{2}$ and ${{s}_{{f}_{i}}}^{2}$ are given by:

$$\begin{aligned} & \overline{x}_{i} = \frac{1}{N}\sum\limits_{t = 1}^{N} {x_{i} \left( t \right)} {,}\quad \overline{f}_{i} = \frac{1}{N}\sum\limits_{t = 1}^{N} {f_{i} \left( t \right)} \\ & s_{xi}^{2} = \frac{1}{N}\sum\limits_{t = 1}^{N} {\left[ {x_{i} \left( t \right) - \overline{x}_{i} } \right]^{2} } {,}\quad s_{fi}^{2} = \frac{1}{N}\sum\limits_{t = 1}^{N} {\left[ {f_{i} \left( t \right) - \overline{f}_{i} } \right]^{2} } . \\ \end{aligned}$$

(31)

The mean square error ($\text{MSE}$) of the forecast for grid point i is:

$${\text{MSE}}_{i} = \frac{1}{N}\sum\limits_{t = 1}^{N} {\left[ {f_{i} \left( t \right) - x_{i} \left( t \right)} \right]^{ \, 2} }$$

(32)

and the root mean square error ($\text{RMSE}$) is:

$${\text{RMSE}}_{i} = \sqrt {{\text{MSE}}_{i} } .$$

(33)

For leave-one-out cross-validated data in the POV (WMO 2010a), the $\text{MSE}$ of climatology forecasts is:

$${\text{MSE}}_{{{\text{C}}i}} = \left( {\frac{N}{N - 1}} \right)^{ \, 2} s_{xi}^{ \, 2} .$$

(34)

The mean square skill score ($\text{MSSS}$) for grid point i, taking as reference the climatology forecast, is defined as:

$${\text{MSSS}}_{i} = 1 - \frac{{{\text{MSE}}_{i} }}{{{\text{MSE}}_{{{\text{C}}i}} }}.$$

(35)

The temporal correlation coefficient ($\text{TCC}$) is:

$${\text{TCC}}_{i} = \frac{{\frac{1}{N}\sum\nolimits_{t = 1}^{N} {\left[ {x_{i} \left( t \right) - \overline{x}_{i} } \right]\left[ {f_{i} \left( t \right) - \overline{f}_{i} } \right]} }}{{s_{xi} s_{fi} }}.$$

(36)

Both the ${\text{MSE}}_{i}$ and the ${\text{TCC}}_{i}$ are computed using temporal averages for a given location i, conversely, the anomaly pattern correlation coefficient ($\text{ACC}$) (Jolliffe and Stephenson 2011) is defined using spatial averages for a given time t:

$${\text{ACC}}\left( t \right) = \frac{{\sum\nolimits_{i = 1}^{n} {\cos \theta_{i} \left[ {x^{\prime}_{i} \left( t \right) - \left\langle {x^{\prime}\left( t \right)} \right\rangle } \right]\left[ {f^{\prime}_{i} \left( t \right) - \left\langle {f^{\prime}\left( t \right)} \right\rangle } \right]} }}{{\sqrt {\sum\nolimits_{i = 1}^{n} {\cos \theta_{i} \left[ {x^{\prime}_{i} \left( t \right) - \left\langle {x^{\prime}\left( t \right)} \right\rangle } \right]^{ \, 2} } } \sqrt {\sum\nolimits_{i = 1}^{n} {\cos \theta_{i} \left[ {f^{\prime}_{i} \left( t \right) - \left\langle {f^{\prime}\left( t \right)} \right\rangle } \right]^{ \, 2} } } }},$$

(37)

where $n$ is the number of grid points, ${\theta }_{i}$ is the latitude at location i, ${x}_{i}^{^{\prime}}\left(t\right)$ and ${f}_{i}^{^{\prime}}\left(t\right)$ are observation and forecast anomalies for the POV, respectively, and the spatial averages $x^{\prime}\left( t \right)$ and $f^{\prime}\left( t \right)$ are given by:

$$\left\langle {x^{\prime}\left( t \right)} \right\rangle = \frac{{\sum\nolimits_{i = 1}^{n} {\cos \theta_{i} x^{\prime}_{i} \left( t \right)} }}{{\sum\nolimits_{i = 1}^{n} {\cos \theta_{i} } }}{,}\quad \left\langle {f^{\prime}\left( t \right)} \right\rangle = \frac{{\sum\nolimits_{i = 1}^{n} {\cos \theta_{i} f^{\prime}_{i} \left( t \right)} }}{{\sum\nolimits_{i = 1}^{n} {\cos \theta_{i} } }}.$$

(38)

2.2 Averaged scores

To take the average of nonlinear scores, they should be transformed so the corresponding variables are Gaussian. The spatial average $\text{RMSE}$ (considering the area factor) is:

$$\left\langle {{\text{RMSE}}} \right\rangle = \sqrt {\frac{{\sum\nolimits_{i = 1}^{n} {{\text{MSE}}_{i} \cos \theta_{i} } }}{{\sum\nolimits_{i = 1}^{n} {\cos \theta_{i} } }}} .$$

(39)

Similarly, the average $\text{MSSS}$ is:

$$\left\langle {{\text{MSSS}}} \right\rangle = 1 - \frac{{\sum\nolimits_{i = 1}^{n} {{\text{MSE}}_{i} \cos \theta_{i} } }}{{\sum\nolimits_{i = 1}^{n} {{\text{MSE}}_{{{\text{C}}i}} \cos \theta_{i} } }}.$$

(40)

For the correlation coefficients, the Fisher Z-transform must be taken first. This is defined as:

$$Z\left( r \right) = \frac{1}{2}\ln \left( {\frac{1 + r}{{1 - r}}} \right) = \tanh^{ - 1} r$$

(41)

The spatial average $\text{TCC}$ is the defined as:

$$\left\langle {{\text{TCC}}} \right\rangle = Z^{ \, - 1} \left[ {\sqrt {\frac{{\sum\nolimits_{i = 1}^{n} {Z\left( {{\text{TCC}}_{i} } \right)\cos \theta_{i} } }}{{\sum\nolimits_{i = 1}^{n} {\cos \theta_{i} } }}} } \right]$$

(42)

and the temporal average $\text{ACC}$ is

$$\left\langle {{\text{ACC}}} \right\rangle = Z^{ \, - 1} \left\{ {\frac{1}{N}\sum\limits_{t = 1}^{N} {Z\left[ {{\text{ACC}}\left( t \right)} \right]} } \right\}.$$

(43)

2.3 Orthogonality principle and MSSS decomposition

The $\text{MSSS}$ (Eq. 35), can be expanded for leave-one-out cross-validated forecasts (Murphy 1988). Using Eqs. (31), (32), (34) and (36) in (35), we obtain:

$${\text{MSSS}}_{i} = {{\left\{ {2\frac{{s_{fi} }}{{s_{xi} }}{\text{TCC}}_{i} - \left( {\frac{{s_{fi} }}{{s_{xi} }}} \right)^{2} - \left( {\frac{{\left[ {\overline{f}_{i} - \overline{x}_{i} } \right]}}{{s_{xi} }}} \right)^{2} + \frac{2N - 1}{{\left( {N - 1} \right)^{2} }}} \right\}} \mathord{\left/ {\vphantom {{\left\{ {2\frac{{s_{fi} }}{{s_{xi} }}{\text{TCC}}_{i} - \left( {\frac{{s_{fi} }}{{s_{xi} }}} \right)^{2} - \left( {\frac{{\left[ {\overline{f}_{i} - \overline{x}_{i} } \right]}}{{s_{xi} }}} \right)^{2} + \frac{2N - 1}{{\left( {N - 1} \right)^{2} }}} \right\}} {\left\{ {1 + \frac{2N - 1}{{\left( {N - 1} \right)^{2} }}} \right\}}}} \right. \kern-\nulldelimiterspace} {\left\{ {1 + \frac{2N - 1}{{\left( {N - 1} \right)^{2} }}} \right\}}}.$$

(44)

This equation gives a relation between the $\text{MSSS}$ and the $\text{TCC}$. For forecasts with the same variance as that of observations and no overall bias, the $\text{MSSS}$ is only positive ($\text{MSE}$ lower than for climatology) if the $\text{TCC}$ is larger than approximately 0.5.

A more simplified relation can be obtained in our case for the prediction of the detrended anomalies (natural variability). As we mentioned in Appendix 1.4, the predictor (Eq. 24) is built in such a way that the coefficients satisfy the Yule Walker equations, which are derived from the orthogonality principle (Wold 1938; Brockwell and Davis 1991; Hipel and McLeod 1994; Palma 2007; Box et al. 2008). This principle states that the error of the optimal predictor, ${e}_{i}\left(t\right)={x}_{i}\left(t\right)-{f}_{i}\left(t\right)$ (in a mean square error sense) is orthogonal to any possible estimator:

$$\left\langle {e_{i} \left( t \right)f_{i} \left( t \right)} \right\rangle = 0.$$

(45)

From this ensemble average condition, we get the analytical expressions for the coefficients as a function of the fluctuation exponent, $H$, for the fGn process. If the model realistically describes the actual temperature anomalies, then the condition Eq. (45) can be approximated by the temporal average in the POV:

$$\frac{1}{N}\sum\limits_{t = i}^{N} {\left[ {e_{i} \left( t \right)f_{i} \left( t \right)} \right]} = 0.$$

(46)

or

$$\frac{1}{N}\sum\limits_{t = i}^{N} {\left[ {x_{i} \left( t \right) - f_{i} \left( t \right)} \right]} f_{i} \left( t \right) = 0.$$

(47)

from which:

$$\frac{1}{N}\sum\limits_{t = i}^{N} {\left[ {x_{i} \left( t \right)f_{i} \left( t \right)} \right]} = \frac{1}{N}\sum\limits_{t = i}^{N} {f_{i} \left( t \right)^{2} } .$$

(48)

For ${\stackrel{-}{x}}_{i}={\stackrel{-}{f}}_{i}=0$, dividing by the product ${s}_{{x}_{i}}{s}_{{f}_{i}}$ and using Eqs. (31) and (36), we can rewrite Eq. (48) as:

$${\text{TCC}}_{i} = \frac{{s_{fi} }}{{s_{xi} }}.$$

(49)

Using this ratio in Eq. (44) we finally obtain:

$${\text{MSSS}}_{i} = \frac{{{\text{TCC}}_{i}^{2} + \frac{2N - 1}{{\left( {N - 1} \right)^{2} }}}}{{1 + \frac{2N - 1}{{\left( {N - 1} \right)^{2} }}}}.$$

(50)

A more detailed analysis gives the same expression with the weaker condition of overall unbiased estimates ${\stackrel{-}{x}}_{i}-{\stackrel{-}{f}}_{i}=0$ (not necessarily each of them must be zero).

In our case, for the forecast of the detrended anomalies (natural variability) at monthly resolution in the POV 1951–2019 ($N=828$ months), the N-dependent term in Eq. (50) is negligible:

$$\frac{2N - 1}{{\left( {N - 1} \right)^{2} }} \approx 0.0024,$$

(51)

so, with good approximation we obtain:

$${\text{MSSS}}_{i} \approx {\text{TCC}}_{i}^{2} .$$

(52)

The orthogonality principle, Eq. (47) (or equivalently, Eq. (49) or Eq. (52)), is the condition that maximizes the $\text{MSSS}$. In our case, where the autoregressive coefficients in our predictor are analytical functions of only one parameter ($H$), if Eq. (52) is verified then our predictor is optimal in a mean square error sense and our model is suitable for describing the natural temperature variability.