Linking the northern hemisphere sea-ice reduction trend and the quasi-decadal arctic sea-ice oscillation

Abstract

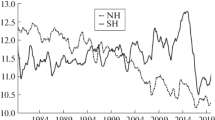
The nature of the reduction trend and quasi-decadal oscillation in Northern Hemisphere sea-ice extent is investigated. The trend and oscillation that seem to be two separate phenomena have been found in data. This study examines a hypothesis that the Arctic sea-ice reduction trend in the last three decades amplified the quasi-decadal Arctic sea-ice oscillation (ASIO) due to a positive ice/ocean-albedo feedback, based on data analysis and a conceptual model proposed by Ikeda et al. The theoretical, conceptual model predicts that the quasi-decadal oscillation is amplified by the thinning sea-ice, leading to the ASIO, which is driven by the strong positive feedback between the atmosphere and ice-ocean systems. Such oscillation is predicted to be out-of-phase between the Arctic Basin and the Nordic Seas with a phase difference of 3π/4, with the Nordic Seas leading the Arctic. The wavelet analysis of the sea ice data reveals that the quasi-decadal ASIO occurred actively since the 1970s following the trend starting in the 1960s (i.e., as sea-ice became thinner and thinner), as the atmosphere experienced quasi-decadal oscillations during the last century. The wavelet analysis also confirms the prediction of such out-of-phase feature between these two basins, which varied from 0.62π in 1960 to 0.25π in 1995. Furthermore, a coupled ice-ocean general circulation model (GCM) was used to simulate two scenarios, one without the greenhouse gas warming and the other having realistic atmospheric forcing along with the warming that leads to sea-ice reduction trend. The quasi-decadal ASIO is excited in the latter case compared to the no-warming case. The wavelet analyses of the simulated ice volume were also conducted to derive decadal ASIO and similar phase relationship between the Arctic Ocean and the Nordic Seas. An independent data source was used to confirm such decadal oscillation in the upper layer (or freshwater) thickness, which is consistent with the model simulation. A modified feedback loop for the sea-ice trend and ASIO was proposed based on the previous one by Mysak and Venegas and the ice/albedo and cloud/albedo feedabcks, which are responsible for the sea ice reduction trend.

Appendices

Appendix 1 wavelet analysis

Introduction

The most commonly used method to analyze a geophysical time series is the Fourier transform (FT). To increase the applicability of Fourier analysis, various methods have been developed to adapt the usual Fourier methods to allow analysis of the frequency content of a signal locally. While some success has been achieved, these adaptations to the Fourier methods are not completely satisfactory. One of the most famous modified FT is the windowed Fourier transform. The windowed Fourier transform (WFT) was first introduced by Gabor (1946) in order to study a non-stationary time series signal. This method studies a time series signal by localizing signals in both frequency and time domains simultaneously. However, the amount of localization in each dimension (or the width of time-frequency window) remains fixed, and it does not adapt to the frequency content of the signal. For a fixed window width, more cycles are included in the window in the high frequency region of the signal, and fewer cycles are included in the low-frequency region of the signal. Since a precise definition of high frequency oscillations requires a narrow time window while a thorough description of low-frequency oscillations requires a wide time window, the WFT method has limited application for simultaneously detecting high-frequency signals embedded within low-frequency phenomena.

It is ideal to search for a method such as the WFT, which can localize the signal simultaneously in both frequency and time, but with an adaptive window width. The hope is that the width of the time-frequency window automatically narrows when focusing on high frequency oscillations and widens on the low-frequency background. The wavelet transform (WT) relates the window width with the frequency of the signal exactly as we hoped. The WT decomposes a time series into time-frequency space so that one is able to determine both the dominant modes of variability and how those modes vary in time. In WT, a given time series is divided into components with different scale, which allows the investigation of each component with a resolution matched to its scale. The one-dimemsional continuous wavelet transform was first introduced by Morlet (1982), and Grossman and Morlet (1984). Combes et al. (1990), Farge (1992), and Mayer (1993) have given detailed description of wavelets and their application in geophysics. The WT has now been widely used for numerous studies in geophysical time series signal. Weng and Lau (1994) studied the organization of convection over the tropical Western Pacific. Gu and Philander (1995) and Wang and Wang (1996) investigated the temporal structure of the El Nino-Southern Oscillation. Meyers et al. (1993) used the WT to study dispersion of Yunai waves. An excellent review of the WT can be found in Torrence and Compo (1998).

The wavelet transform

The continuous wavelet transform was developed as an alternative approach to the WFT to overcome the fixed window width problem. The term wavelet means a small wave. Denoted by ψ(t), the WT is basically the convolution between signal and a set of wavelets formed by dilations [e.g., ψ(t) →ψ(at) for a>0] and translation [e.g., ψ(t) →ψ(t+b) for any real b] of ψ(t). To be a wavelet, the function of ψ(t) must have finite energy, that is, ψ(t) needs to be square integrable on space L² (R) and a zero mean. The function ψ(t) is called the “mother wavelet,” while the dilated and translated function from the “mother wavelet” are called “daughter wavelet” or simply “wavelet.” To be a mother wavelet both formally and in practice ψ(t) must have the following properties:

• (i) It must be a function centered at zero and in the limit as |t|→∞, ψ(t)→0 rapidly. This condition means that the CWT (continuous WT) defined in (Eq. 5) below is only affected by the signal in a local region about t=b, therefore produces the local nature of wavelet analysis.

• (ii) The zero mean property of ψ(t). This is known as the admissibility condition. Note that this is a very important condition because it implies the invertability condition of the WT. Since the original signal can be obtained from the wavelet coefficients using

  $$ {\text{x}}({\text{t}}) = 1/{\text{C}}\iint {{\text{CWT}}_\psi (a,b)\psi _{a,b} (t)\,{\text{d}}a\,{\text{d}}b} $$

  (3)

  where $C = 1/\int {\psi ^* (\omega )/\omega \,{\text{d}}\omega }$ with ψ^* (ω) the FT of ψ. For (Eq. 3) to be meaningful, C has to be finite, which is equivalent to ψ^* (0)=0. Therefore the admissibility condition can be rewritten as ψ^* (0)=0.

The daughter wavelets have the same shape as that of the mother wavelet. Their amplitudes must rapidly decay away from the center of the wave in both time and frequency domains. Mathematically, a daughter wavelet on the scale a and at the position b is expressed as

$$ \psi _{a,b} (t) = a^{ - 1/2} \psi ((t - b)/a),\;{\text{for}}\;a,b\;{\text{real}}\;{\text{and}}\;a > 0 $$

(4)

The continuous WT of a signal x(t) is basically the convolution of x(t) with a set of daughter wavelets ψ_a,b(t) defined in (Eq. 4). That is

$$ {\text{CWT}}_\psi = (a,b) = \left\langle {x,\psi _{a,b} } \right\rangle = a^{ - 1/2} \int {\psi ((t - b)/a)x(t)\,{\text{d}}t.} $$

(5)

Equation (4) expands a one dimensional time series into the two dimensional parameter space (a, B) and yields a local measure of the relative amplitude over the entire dataset.

For most real valued geophysical time series, it is suitable to choose a continuous WT with complex-valued wavelets. A complex-valued wavelet provides important information of (i) the signal via the L² modulus, which gives the energy density, (ii) the phase, which detects singularities and measures instantaneous frequencies, and (iii) the real part of the wavelet coefficients, which depicts both the intensity and phase of the signal variation, at particular scales and locations in the wavelet domain (the time –frequency domain). A commonly used complex-valued wavelet is the Morlet wavelet, having the form

$$ \psi (t) = \pi ^{ - 1/4} \,{\text{exp}}\,(i\omega _0 \eta )\,{\text{exp}}\,( - \eta ^2 /2), $$

(6)

where ω₀ is the non-dimensional frequency, which can be chosen as 6 to satisfy the admissibility condition. Some other examples of mother wavelets can be found in Farge (1992) and Coulibaly (1992).

Once the mother wavelet is chosen, it is necessary to choose a set of scales to compute the wavelet coefficients using (Eq. 5). The CWT is calculated for all values of a. However, depending on the signal, a complete transform is usually not necessary. For practical purposes, the signals are band-limited, and therefore, computation of the CWT for a limited interval of scales is usually adequate. For convenience, the scales are usually written as powers of two. For each given scale, the wavelet is placed at the beginning of the signal. Then the wavelet function at this scale is multiplied by the signal and integrated over all the time as shown in (Eq. 5). If the signal has a spectral component corresponding to the current value of the scale a, the product of the wavelet with the signal at the location, where this spectral component exists, gives a relatively large value, therefore gives a large modulus value. If the spectral component that corresponds to the current value of a is not present in the signal, the modulus value at this location will be small. This is why we can use the WT to find the frequency information of the signal.

Phase information

To compare the phase difference between regions 5+6 (the Nordic Seas) and 2+7 (the Arctic Basin), the phase information for the period of 10 years was extracted from the wavelet transform of the data. Denote the real part and the imaginary part of the wavelet transform by R(W(b)) and I(W(b)), respectively, the phase information for each region for the period of 10 years is then, tan⁻¹ [ I(W(b))/ R(W(b))]. Note that the tangent inverse command atan2 in Matlab gives phases in [-π, π], therefore π is added to atan2 to insure the range of the phase falling in [0, 2 π]. After retrieving the phase information for the Nordic Seas and the Arctic Basin, the phase difference between the two regions was obtained by subtracting the phase of region 2+7 from the phase of region 5+6. The phase difference is then plotted against time, as shown in Fig. 6 (bottom).