Abstract
The subject of this work is random coefficient regression models with only one observation per observational unit (individual). An analytical solution in form of optimality conditions is proposed for optimal designs for the prediction of individual random effect for a group of selected individuals. The behavior of optimal designs is illustrated by the example of linear regression models.
Similar content being viewed by others
1 Introduction
The subject of this work is random coefficient regression (RCR) models in which only one observation per observational unit (individual) is possible. These models are popular e.g. in psychology (see Freund and Holling (2008)) and pharmacokinetics (see Patan and Bogacka (2007)). The main purpose of the present paper is to obtain an analytical solution for the designs that are optimal for the prediction of random effects. Optimal designs for prediction in RCR models have been discussed e.g. in Gladitz and Pilz (1982), Fedorov and Hackl (1997), Prus and Schwabe (2016) and Prus (2023). In Gladitz and Pilz (1982) and Prus and Schwabe (2016) the number of observations per individual is required to be not smaller than the number of unknown model parameters, which excludes the case of only one observation. Also the same design for all individuals has been assumed in the both papers. Fedorov and Hackl (1997) investigated models with specific regression functions. The models considered in the present work may be seen as a particular case (with one individual per group) of the multiple-group models discussed in Prus (2023). However, the solution developed in that paper is based on the assumption of sufficient number of observations per individual, i.e. not smaller than the number of parameters. Models with only one observation per individual were discussed e.g. in Patan and Bogacka (2007) and Graßhoff et al. (2012). Patan and Bogacka (2007) investigated non-linear mixed-effects models. Graßhoff et al. (2012) proposed a solution for optimal designs in form of an optimality condition for RCR models. In these papers optimal design were determined for estimation of fixed effects. However, not much has been done for prediction of random effects.
In the present work we determine optimal designs for prediction of random effects for a group of selected individuals in RCR models with one observation per individual. The obtained design criterion (linear criterion) results in a multiple-design problem, for which the standard approach for design optimization proposed in Kiefer (1974) cannot be applied. We make use of the optimality conditions for multiple-design problems proposed in Prus (2022). The obtained analytical results are illustrated by examples of linear regression models with particular covariance matrices.
The paper has the following structure: In the second section the model is specified and the mean squared error (MSE) matrix for the best linear unbiased prediction (BLUP) of the random effects is determined. In Sect. 3 the linear design criterion for the prediction and the resulting optimality conditions are formulated. The analytical results are illustrated by examples in Sect. 4. The paper is concluded by a short discussion in Sect. 5.
2 Model specification
In this work we the consider RCR models with only one observation per observational unit (individual) of the following form:
where \(Y_i\) is an observation at the i-th individual, n is the number of individuals, \(\textbf{f} =(f_1, \dots ,f_p)^\top \) is a vector of known regression functions, experimental settings \(x_i\) come from an experimental region \(\mathcal {X}\). The observational errors \(\varepsilon _{i}\) are assumed to have zero mean and common variance \(\sigma ^2>0\). The individual parameters \(\varvec{\beta }_i=( \beta _{i1}, \dots , \beta _{ip})^\top \) have unknown expected value (population mean) \(\textrm{E}\,(\varvec{\beta }_i)={\varvec{\beta }}\) and known covariance matrix \(\textrm{Cov}\,(\varvec{\beta }_i)=\sigma ^2\textbf{D}\). All individual parameters \(\varvec{\beta }_{i}\) and all observational errors \(\varepsilon _{i}\) are assumed to be uncorrelated.
According to Graßhoff et al. (2012) the covariance matrix of the best linear unbiased estimator (BLUE) \(\hat{\varvec{\beta }}\) for the population parameter (fixed effects) \(\varvec{\beta }\) is given by
where
In this work we focus on random effects, in particular on the individual deviations from the mean: \(\textbf{b}_i=\varvec{\beta }_i-\varvec{\beta }\) (see e.g. Prus and Schwabe (2013)). Namely, we consider the situation in which our main interest is in some selected individuals. We determine optimal experimental settings for prediction of the individual effects for the k selected individuals: \({\varvec{\Psi }}=\frac{1}{k}\sum _{i=1}^k\textbf{b}_i\), for \(k\in [p,n-p]\). We assume \(n\ge 2p\), otherwise \([p,n-p]=\emptyset \). Note that the order of the individuals does not matter in this case. Therefore, we can consider k first individuals without loss of generality.
Further we search for experimental settings that minimize the MSE matrix of the BLUP \(\hat{{\varvec{\Psi }}}\) for the individual deviations \({\varvec{\Psi }}\).
Lemma 1
The MSE matrix of the BLUP \(\hat{{\varvec{\Psi }}}\) is given by
where \(\textbf{M}_{k}=\sum _{i=1}^k\textbf{M}(x_i)\).
The proof of Lemma 1 is deferred to Appendix A.
3 Experimental design
We consider the following two groups of individuals: the k selected individuals build the first group (Group 1), and the second group (Group 2) consists of the \(n-k\) remaining individuals. We also allow for group-specific restrictions with respect to experimental settings, i.e. the experimental regions for the two groups of individuals may differ from each other. In practice it can be useful in case of some particular restrictions in two centers/clinics/etc. Further \(\mathcal {X}_{\ell }\) denotes the experimental region for group \(\ell \), \(\ell =1,2\), and \(\mathcal {X}_1\cup \mathcal {X}_2=\mathcal {X}\). The particular case \(\mathcal {X}_1=\mathcal {X}_2=\mathcal {X}\) will be later considered more detailed. We add the group index to experimental settings for clear notation and we define an exact design in group \(\ell \) as
where \(x_{\ell j}\in \mathcal {X}_\ell \) are the support point of \(\xi _{\ell ,e}\), \(m_{\ell j}>0\) is the number of observations at \(x_{\ell j}\) with \(\sum _{j=1}^{N_1}{m_{1j}}=k\) and \(\sum _{j=1}^{N_2}{m_{2j}}=n-k\) and \(N_{\ell }=|\{x_{\ell 1},\dots , x_{\ell N_\ell }\}|\). Note that \(m_{\ell j}\) can be larger than one in case if observations for more than one individual are taken at point \(x_{\ell j}\). Note also that the set \(\{x_{1 1},\dots , x_{1 N_1}\}\) coincides with \(\{x_1, \dots x_k\}\) in model (1) (and \(\{x_{2 1},\dots , x_{2 N_2}\}\) coincides with \(\{x_{k+1}, \dots x_n\}\)).
For analytical purposes we also introduce approximate designs:
where \(w_{\ell j}> 0\) denotes the weight of observations at \(x_{\ell j}\), \(\sum _{j=1}^{\tilde{N_\ell }}{w_{\ell j}}=1\), \(\ell =1,2\), and \(\tilde{N_{\ell }}=|\{x_{\ell 1},\dots , x_{\ell \tilde{N_\ell }}\}|\). Note that \(\tilde{N_{\ell }}=N_{\ell }\) for exact designs. Further we use the notation \(\xi =(\xi _1, \xi _2)\) for the pair of group designs.
We also define the information (or moment) matrices for the first and second design as
and
respectively.
For exact designs we obtain \(w_{1j}=m_{1j}/k\), \(w_{2j}=m_{2j}/(n-k)\), \(\textbf{M}_{k}=k\textbf{M}_{1,\xi }\) and
In this work we focus on the linear criterion for the prediction of individual deviations for the selected individuals, which is defined for exact designs as
where \(\mathcal {L}\) denotes the transformation matrix.
Neglecting the constants that have no influence on designs, we obtain for approximate designs the following results.
Theorem 1
The linear criterion for the prediction of individual effects \({\varvec{\Psi }}\) is given by
where \(\tilde{\textbf{L}}=\textbf{D}\textbf{L}\textbf{D}\) and \(\textbf{L}=\mathcal {L}^\top \mathcal {L}\).
The proof of this result is deferred to Appendix B.
Note that we assume matrices \(\textbf{M}_{1,\xi }\) and \(\textbf{M}_{2,\xi }\) and consequently \(\textbf{M}_{k}\) non-singular, which requires \(k\in [p,n-p]\). Otherwise linear criterion (7) cannot be written in form (8).
As we can see by formula (8), the linear criterion depends on two designs simultaneously. In this case the general equivalence theorem (see Kiefer (1974)) cannot be directly applied. Instead we use the extended version for multiple-design problems proposed in Prus (2022). To make use of the equivalence theorems presented in that work, we have to verify convexity of the criterion.
Lemma 2
The linear criterion for the prediction of individual effects \({\varvec{\Psi }}\) is convex with respect to \((\textbf{M}_{1,\xi },\textbf{M}_{2,\xi })\).
For the proof of Lemma 2 see Appendix C.
As the linear criterion for the prediction of the individual deviations is differentiable and convex with respect to both moment matrices, optimality conditions can be formulated.
Theorem 2
Approximate designs \(\xi ^*=(\xi _1^*,\xi _2^*)\) are L-optimal for the prediction of the individual effects \({\varvec{\Psi }}\) iff
for all \(x \in \mathcal {X}_1\), and
for all \(x \in \mathcal {X}_2\).
For support points of \(\xi _1^*\) and \(\xi _2^*\) equalities hold in (9) and (10), respectively.
The proof is deferred to Appendix D.
Note that optimal designs depend on the dispersion matrix of random effects \(\textbf{D}\), the total number of individuals n and the number of selected individuals k.
Note also that in case where the design region is the same for all individuals \(\mathcal {X}_1=\mathcal {X}_2=\mathcal {X}\), optimal designs may be also the same for both groups, i.e. \(\textbf{M}_{1,\xi ^*}=\textbf{M}_{2,\xi ^*}\). In this situation design criterion (8) simplifies to
which is linear in design, i.e. singular designs (that result in a singular moment matrix) or all permissible designs may be optimal. The optimality conditions simplify to the following inequality:
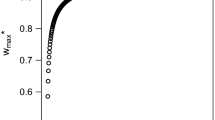
Behavior of such designs will be illustrated by Example 4.1.
4 Examples
We consider the linear regression model
which is the particular case of model (1) with \(\textbf{f}(x)=(1,x)^\top \), and we assume the diagonal structure of the covariance matrix of random effects: \(\textbf{D}=\textrm{diag}(d_1,d_2)\).
Further we distinguish between the two different cases: the same design region for all individuals (Example 4.1) and different design regions for different groups (Example 4.2). We focus on the A-optimality criterion, i.e. \(\textbf{L}=\mathbb {I}_p\), where \(\mathbb {I}_p\) denotes the \(p\times p\) identity matrix.
4.1 Example 1
In this example we consider the situation where there are no particular restrictions for the designs for the selected individuals (that are of our main interest) or for all other individuals, i.e. the design region is the same for both groups: \(\mathcal {X}_1=\mathcal {X}_2=\mathcal {X}\). In particular, we consider symmetric design regions: \(\mathcal {X}=[-a,a]\), for \(a>0\). Further we focus on the designs that are the same for both groups: \(\xi _1=\xi _2\) with all observations at the endpoints:
where w is the weight of observations at point a. The total number of individuals n and the number of selected individuals k have no influence on designs in the present case and do not need to be specified. If optimal designs of form (14) exist, they assign \(w=0\) or \(w=1\) (and make the moment matrix singular) or all values of w are equally good.
For the present model we obtain
and
The simplified linear criterion (11) is given by
which is independent of the designs, i.e. all designs (all \(w\in (0,1)\)) are optimal or there is no optimal designs of form (14) at all. The optimality condition (12) is given by
which is satisfied only in case
Hence, under condition (15) all design are equally good. Otherwise, there is no solution with \(\xi _1=\xi _2\), where \(\xi _1\) is of form (14).
4.2 Example 2
In this example we assume different design regions \(\mathcal {X}_1\) and \(\mathcal {X}_2\). In particular, we concentrate on symmetric design regions of different lengths: \(\mathcal {X}=[-1,1]\) and \(\mathcal {X}=[-a,a]\), for \(a>0\). We consider the endpoints-designs
and
where \(w_1\) and \(w_2\) are the weights of observations at points 1 and a for the first and the second group, respectively. We simplified the notations \(w_{12}\) and \(w_{22}\) to \(w_1\) and \(w_2\), as there are only two support points for each design. Further we consider two different cases for the covariance matrix of random effects: random intercept and random slope.
Case 1 \(d_1=d\) and \(d_2=0\)
In the case of random intercept we have
and
Linear criterion (8) for this model will not be presented here because of its complexity. We use software Maple2020 for further computations. For the following points the first derivative of the criterion function is zero:
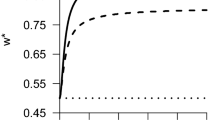
All designs with property (18) turn out to be optimal, i.e. they satisfy optimality conditions (9) and (10) for all possible values of a. Note that the designs are independent of the variance parameter d.
Case 2 \(d_1=0\) and \(d_2=d\)
For the random slope we obtain
and
Using the same approach as for the random intercept case, it can be verified that all designs with
are optimal for all \(a>0\).
Note that in both cases: random intercept and random slope, the obtained designs are optimal for all values of the total number of individuals n and the number of selected individuals \(k\in [p,n-p]\). Note also that \(a=1\) would lead to \(w_1=w_2\), which is in accordance with Example 4.1.
5 Discussion
We considered RCR models in which only one observation per individual is possible. We focused on individual random effects for a group of selected individuals, in particular on the mean random effect in the group. The solution for optimal designs is proposed in form of optimality conditions. The number of selected individuals k is assumed to be between the number of parameters p and \(n-p\), where n is the total number of individuals, which is possible only for models with \(n\ge 2p\). If the main interest is in a very small, i.e. \(k<p\), or a very large number of selected individuals, another approach is, however, needed. Optimal designs are determined for the BLUP of the random effects, which depends on the variance parameters (covariance matrices). The variance parameters are assumed to be known, which is in general not the case in practice. In a practical situation, where the covariance matrices have to be estimated, we deal with estimated BLUP (EBLUP). The obtained optimal designs in general depend on the variance parameters and are, therefore, locally optimal. The problem of local optimality may be solved for particular models by considering robust design criteria, for example minimax-criterion. For specific covariance structure, optimal designs may be independent of variance parameters, which has been illustrated by the example of the linear regression models with random intercept and random slope. All observational errors were assumed to have the same variance. Heteroscedastic errors, especially depending on the experimental settings (as considered by Graßhoff et al. (2012)), are analytically more challenging. However, an extension may be considered in a future research. Moreover optimal designs have been obtained for individual effects (individual deviations from the population parameter) via their arithmetic mean. Design optimization for the prediction of the individual deviations or individual parameters themselves turned out to be more challenging. It may also be a subject of future investigations, especially for particular models.
References
Bernstein DS (2018) Scalar, vector, and matrix mathematics. Princeton University Press, Princeton
Fedorov V, Hackl P (1997) Model-oriented design of experiments. Springer, New York
Freund PA, Holling H (2008) Creativity in the classroom: a multilevel analysis investigating the impact of creativity and reasoning ability on GPA. Creat Res J 20:309–318
Gladitz J, Pilz J (1982) Construction of optimal designs in random coefficient regression models. Math Oper Stat Ser Stat 13:371–385
Graßhoff U, Doebler A, Holling H, Schwabe R (2012) Optimal design for linear regression models in the presence of heteroscedasticity caused by random coefficients. J Stat Plann Infer 142:1108–1113
Henderson CR (1975) Best linear unbiased estimation and prediction under a selection model. Biometrics 31:423–477
Kiefer J (1974) General equivalence theory for optimum designs (approximate theory). Ann Stat 2:849–879
Patan M, Bogacka B (2007) Efficient sampling windows for parameter estimation in mixed effects models. In: López-Fidalgo J, Rodríguez-Díaz JM, Torsney B (eds) mODa 8—advances in model-oriented design and analysis. Physica, Heidelberg, pp 147–155
Prus M (2022) Equivalence theorems for multiple-design problems with application in mixed models. J Stat Plann Infer 217:153–164
Prus M (2023) Optimal designs for prediction of random effects in two groups linear mixed models. https://www.researchgate.net/publication/353660007_Optimal_designs_for_prediction_of_random_effects_in_multiple-group_linear_mixed_models
Prus M, Schwabe R (2013) Optimal designs for the prediction of individual effects in random coefficient regression. In: Uciński D, Atkinson AC, Patan M (eds) mODa 10—advances in model-oriented design and analysis. Springer, Cham, pp 211–218
Prus M, Schwabe R (2016) Optimal designs for the prediction of individual parameters in hierarchical models. J R Stat Soc B 78:175–191
Acknowledgements
This research was partially supported by Grant SCHW 531/16 of the German Research Foundation (DFG). A part of the research has been performed as the author was visiting Laboratoire d’Informatique, Signaux et Systèmes de Sophia Antipolis in Nice in framework of the postdoc program (PKZ 91672803) of German Academic Exchange Service (DAAD). The author thanks two anonymous referees for helpful comments which improved the presentation of the results.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
A Proof of Lemma 1
Model (1) can be rewritten in vector form as follows
with \(\textbf{X}=(\textbf{f}(x_1), \dots \textbf{f}(x_n))^\top \), \(\textbf{Z}=\text {block-diag}(\textbf{f}(x_1)^\top , \dots \textbf{f}(x_n)^\top )\) and \(\text {block-diag}\left( \textbf{A}_1, \dots , \textbf{A}_n \right) \) is the block-diagonal matrix with blocks \(\textbf{A}_1, \dots , \textbf{A}_n\). This model is the classical linear mixed model considered e.g. in Henderson (1975).
Then the MSE matrix for the BLUP \(\hat{\textbf{b}}\) for random effects \(\textbf{b}=(\textbf{b}_1^\top , \dots , \textbf{b}_n^\top )^\top \) can be computed as follows:
where \(\textbf{G}=\text{ Cov }\,(\textbf{b})\), \(\textbf{R}=\text{ Cov }\,(\varvec{\varepsilon })\) and \(\textbf{W}=\textbf{Z}^\top \textbf{R}^{-1}\textbf{Z} +\textbf{G}^{-1}\). For \(\textbf{R}=\sigma ^2\mathbb {I}_n\) and \(\textbf{G}=\sigma ^2\mathbb {I}_n\otimes \textbf{D}\) we obtain
and
which result in
Then from \({\varvec{\Psi }}=\frac{1}{k}\left( \left( \textbf{1}_k^\top , \textbf{0}_{n-k}^\top \right) \otimes \mathbb {I}_p\right) b\) and consequently
follows Eq. (6).
B Proof of Theorem 1
To determine the linear criterion for approximate designs, we use the basic formula (7) and we replace matrices \(\textbf{M}_{k}\) and \(\textbf{M}\) by \(k\textbf{M}_{1,\xi }\) and \(k\textbf{M}_{1,\xi }+(n-k)\textbf{M}_{2,\xi }\), respectively. Then we suppress the first term (\(\frac{1}{k}\text {tr}(\textbf{D})\)), which is independent of designs, and the multiplicator \(\sigma ^2/k^2\), and we obtain
which can be easily simplified to (8) using the properties of the trace and the standard formula for the inverse of sum of two non-singular matrices.
C Proof of Lemma 2
The function \(h(\textbf{N})=\textbf{N}^{-1}\) is non-increasing in Loewner ordering and matrix-convex for any positive definite matrix \(\textbf{N}\). Then
is matrix-convex and
is matrix-concave in \((\textbf{M}_{1,\xi }, \textbf{M}_{2,\xi })\), respectively (see e. g. Bernstein (2018), ch. 10). Consequently,
is convex with respect to \((\textbf{M}_{1,\xi }, \textbf{M}_{2,\xi })\) for any positive semi-definite matrix \(\varvec{\tilde{{L}}}\).
D Proof of Theorem 2
According to Theorem 2 in Prus (2022), designs \(\xi ^*=(\xi _1^*,\xi _2^*)\) minimize a convex criterion \(\Phi \) if and only if the directional derivative of \(\Phi \) at \((\textbf{M}_{1,\xi ^*},\textbf{M}_{2,\xi ^*})\) in the direction of \((\textbf{g}(x)\textbf{g}(x)^\top ,\textbf{M}_{2,\xi ^*})\) is non-negative for all \(x \in \mathcal {X}_1\), and the directional derivative of \(\Phi \) at \((\textbf{M}_{1,\xi ^*},\textbf{M}_{2,\xi ^*})\) in the direction of \((\textbf{M}_{2,\xi ^*},\textbf{g}(x)\textbf{g}(x)^\top )\) is non-negative for all \(x \in \mathcal {X}_2\). For support points of \(\xi _1^*\) and \(\xi _2^*\) the related directional derivatives are equal to zero. By computing the directional derivatives for linear criterion (8), i. e. \(\Phi =\Phi _L(\xi )\), and setting them non-negative, we obtain inequalities (9) and (10).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Prus, M. Optimal designs for prediction in random coefficient regression with one observation per individual. Stat Papers 64, 1057–1068 (2023). https://doi.org/10.1007/s00362-023-01440-1
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00362-023-01440-1