Deforming static fluid interfaces with magnetic fields: application to the Rayleigh–Taylor instability

Abstract

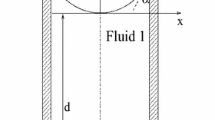
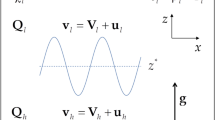
Shaping arbitrary fluid interfaces opens interesting perspectives for fluid-based processes and experiments. We demonstrate an experimental method to create non-planar static interfaces of almost arbitrary shape between two fluids, one of which is made highly magnetically permeable by the addition of a magnetic compound. By relying on spatially modulated magnetic fields, a non-homogeneous magnetic force is added to Earth's gravitational force, and a non-planar static interface can be stabilized. Precision experimental measurements are possible because we have developed a general method that allows us to predict numerically the shape of the interface, thereby facilitating the optimal experimental design before actually implementing it. As a first example, we apply this method to the Rayleigh–Taylor instability between two immiscible fluids. The results we obtain demonstrate the feasibility of the experimental method and the accuracy of the numerical predictions.

Appendix: Proof of uniqueness for the energy minimization problem

Theorem

We claim that (1) if a functional has a Lagrangian whose Hessian is positive definite, then it has a single absolute minimum and (2) provided that the equivalent gravity always points to the same half-plane, the energy of the equilibrium interface admits a unique minimum.

Proof 1

Note that this mathematical result is well known and can be found, for instance, in Ekeland and Temam (1976).

Suppose F a functional whose Lagrangian f is defined by

$$ F(\eta)=\int \hbox{d}y f(\eta,\eta^{\prime}), $$

where η′ = dη/dy, and suppose we want to minimize F.

Let f be a regular function with a second derivative whose Hessian, defined by

$$ D=\left(\begin{array}{cc} \frac{\partial^{2} f}{\partial \eta^{2}} & \frac{\partial^{2} f}{\partial \eta \partial \eta^{\prime}} \\ \frac{\partial^{2} f}{\partial \eta \partial \eta^{\prime}} & \frac{\partial^{2} f}{\partial \eta^{\prime 2}} \\ \end{array} \right), $$

is positive definite, e.g., for any non-zero vector ν

$$ \sum_{jj^{\prime}}D_{jj^{\prime}}\nu_{j}\nu^{\ast}_{j^{\prime}}>0. $$

That f has a positive definite Hessian is equivalent to f being strictly convex (see Ekeland and Temam 1976). Suppose now that we find a minimum of functional F for η = η _m , then we claim that this minimum is unique. Specifically, we can introduce the function G defined on the interval [0,1] by: $G(\lambda)=F(\eta_{m}+\lambda\Updelta)$ with $\Updelta=\eta-\eta_{m}$. Note that G(0) = F(η _m ) and G(1) = F(η). And let us define

$$ \begin{aligned} p(\lambda)&=\left.\frac{\partial^{2} f}{\partial \eta^{2}}\right|_{(\eta_{m}+\lambda\Updelta, \eta_{m}^{\prime}+\lambda\Updelta^{\prime})}\Updelta^{2}\\ &\quad + \left. 2 \frac{\partial^{2} f}{\partial \eta \partial \eta^{\prime}}\right|_{(\eta_{m}+\lambda\Updelta, \eta_{m}^{\prime}+\lambda\Updelta^{\prime})}\Updelta\Updelta^{\prime}\\ &\quad + \left.\frac{\partial^{2} f}{\partial \eta^{\prime 2}}\right|_{(\eta_{m}+\lambda\Updelta, \eta_{m}^{\prime}+\lambda\Updelta')}\Updelta^{\prime 2}>0, \end{aligned} $$

(7)

where $\Updelta^{\prime}= \hbox{d}\Updelta/\hbox{d}y$ and $\eta^{\prime}_{m}=\hbox{d} \eta_{m}/ \hbox{d}y$.

The inequality above follows from the fact that D is positive definite (this can be found by letting $\nu=(\begin{array}{c} \Updelta \\ \Updelta^{\prime}\\ \end{array})$).

Now let us first see whether we can find η so that F(η) < F(η _m ).

We can write that

$$ \begin{aligned} F(\eta)&=G(1)=G(0)+\int\limits_0^1 \hbox{d}\lambda \, \left. \frac{\hbox{d}F}{\hbox{d}\lambda}\right|_{\lambda}\\ &= F(\eta_{m})+ \int\limits_0^1 \hbox{d}\lambda\left(\left.\frac{\hbox{d}F}{\hbox{d}\lambda}\right|_{\lambda=0}+ \int\limits_0^{\lambda}\hbox{d}\lambda^{\prime} \, \left.\frac{\hbox{d}^{2}F}{\hbox{d}\lambda^{\prime 2}} \right|_{\lambda^{\prime}}\right) \end{aligned} $$

(8)

This follows from the definition of the integral, first applied to $G(\lambda)=F(\eta_{m}+\lambda\Updelta)$ and then to its derivative dG/dλ. Implementing this, we find that

$$ \begin{aligned} F(\eta)&=F(\eta_{m})+\int \hbox{d}y\left(\left.\frac{\partial f}{\partial \eta}\right|_{(\eta_{m}, \eta^{\prime}_{m})}\Updelta + \left.\frac{\partial f}{\partial \eta^{\prime}}\right|_{(\eta_{m}, \eta^{\prime}_{m})}\Updelta^{\prime}\right) \\ & \quad + \int \hbox{d}y \int\limits_0^1 \hbox{d}\lambda \int\limits_0^{\lambda} \hbox{d}\lambda^{\prime}p(\lambda^{\prime}) \end{aligned} $$

(9)

By assumption η _m is an extremum. Thus, the second term (first integral) on the right-hand side is zero (note that the domain of definition of f is not bounded). Now, the last term, as an integral of a strictly non-negative quantity, is strictly non-negative. It follows that there is no η such that F(η) < F(η _m ).

Let us now examine whether we can find η ≠ η _m such that F(η) = F(η _m ). Suppose that such an η exists. Since f is, by assumption, a regular and strictly convex function, the integral of f on a bounded domain (such as F) is strictly convex too. By using the strict convexity of F on the interval [η _m , η], we can write that for all $t\in ]0,1[$,

$$ F(t\eta + (1-t)\eta_{m})<tF(\eta)+(1-t)F(\eta_{m}). $$

Taking $t=\frac{1}{2}$ (for example), we find that

$$ F\left(\frac{\eta + \eta_{m}}{2}\right)<\frac{1}{2}(F(\eta)+F(\eta_{m}))=F(\eta_{m}), $$

which means that for η _m , the value of F is larger than for $\frac{\eta + \eta_{m}}{2},$ which is not possible according to the previous result. Thus, there is no η ≠ η _m such that F(η) = F(η _m ).

Consequently, we can claim that η _m is the single absolute minimum of F. $\square$

Proof 2

For our particular case, the Lagrangian of our energy functional E is given by:

$$ \begin{aligned} f&=Bol^{2} \,\left[\frac{1}{2}(\bar{\rho_{2}}-\bar{\rho_{1}})(\bar{ \eta}^{2}-\bar{\eta}_{ref}^{2}) + \frac{1}{2} \, \alpha (\chi_{1}-\chi_{2})\int\limits_{\bar{\eta}_{ref}}^{\bar{\eta}}\bar{H^{2}}(\bar{y},\bar{z})d\bar{z}\right] \\ & \quad +[1+(l \bar{\eta}^{\prime})^{2}]^{1/2}-1. \end{aligned} $$

(10)

Calculating the determinant of its Hessian leads to:

$$ \begin{aligned} det(D)&=\frac{l^{4}Bo}{(1+(l\bar{\eta}^{\prime})^{2})^{3/2}}\\ &\quad \times \left(-(\bar{\rho_{1}}-\bar{\rho_{2}})+\bar{H}\left.\frac{\partial \bar{H}} {\partial \bar{\eta}}\right|_{(\bar{y}, \bar{\eta})}(\chi_{1}-\chi_{2})\alpha\right). \end{aligned} $$

(11)

Since we have constrained the equivalent gravity always to point to the same half-plane, we have

$$ \bar{H}\left.\frac{\partial \bar{H}}{\partial \bar{\eta}}\right|_{(\bar{y}, \bar{\eta})}(\chi_{1}-\chi_{2})\alpha>\bar{\rho_{1}}-\bar{\rho_{2}}, $$

which means that D in our case is positive definite. Thus, the solution to our energy minimization problem is unique under the chosen set of assumptions.$\square$