Multi-harmonic detection in wavelength modulation spectroscopy systems

Abstract

Two multi-harmonic detection methods for wavelength modulation spectroscopy (WMS) systems are presented and compared. The two possibilities discussed in this paper are: simultaneous curve fitting of multiple harmonic spectra, and reconstruction of the transmission from harmonic coefficients. The optimum number of harmonics is four and 25 harmonics, respectively. Compared with standard single-harmonic curve fitting, the methods give about a factor of 3 better performance than standard second-harmonic curve fitting. Concluding, multi-harmonic detection is better than single-harmonic detection and should be used if the system bandwidth is high enough to allow for proper detection of the higher harmonics.

Appendices

Appendix A: Wavelength modulation spectroscopy

Let ν denote the wavenumber or frequency of the central laser emission (without the sinusoidal modulation) which implements the slow (discrete) laser emission frequency sweep. The sweep is discrete, because ultimately the spectra are sampled at distinct frequency points and also ν has to be constant during at least one sinusoidal modulation period, so that the harmonic coefficients can be properly determined by the lock-in amplifier. The instantaneous laser emission frequency ν _L (t) is given by

(5)

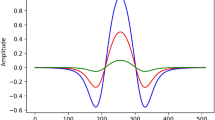
with ν _a the frequency modulation amplitude and f _m the modulation or repetition frequency (typically in the kHz range). The n-th harmonic output of the lock-in amplifier of the normalized light power variation T(ν _L (t)) after passing through the sample with transmission T(ν) is called the harmonic coefficient H _n =H _n (ν;ν _a ) (Fig. 1). Mathematically, the Fourier series decomposition

(6)

is computed (by solving for H _n (ν;ν _a )). Note that the definition of harmonic spectra only requires knowledge of the normalized detector signal during one modulation period. The same is true for a practical realization of a digital lock-in. But for optimum noise performance all periods between two sampling points of ν should be averaged before Fourier decomposition is carried out. Also note that the Fourier decomposition is done in phase with the frequency modulation. The proper detection phase setting in a real lock-in amplifier is thus to compensate for the phase shift of the laser driver and the intrinsic phase shift between laser current and emission frequency [13]. Ideal harmonic spectra have no out-of-phase component. Out-of-phase components encountered in experimental systems may occur despite proper adjustment of the detection phase if there is additional laser amplitude modulation with an AM-FM phase shift. These out-of-phase components, however, contain no or only very little information about the gas spectrum, so only the in-phase component undergoes further signal processing.

Due to the inherent linearity of the signal processing, there is also an ideally linear relationship between the transmission spectrum and the corresponding harmonic spectra. It is linear in the sense that scaling and summation in the transmission also results in scaling and summation of the corresponding harmonic spectra. As a consequence, the relationship can be modeled as a convolution, and general closed-form expressions for the convolution kernel as well as for its Fourier transform can be derived [16]. The linearity of the relationship essentially means that, for unsaturated absorption lines, the individual lines simply add in both the transmission and the harmonic spectra. The concentration or peak absorbance scales the harmonic spectrum, whereas for orders n greater than zero additionally the large offset is removed. This is due to linearity of the relationship and the fact that the harmonic spectrum of a flat transmission is zero for higher orders. This offset removal property of WMS is usually considered as one of its advantages, because detection of a small signal on a large offset is not needed. Furthermore, it can be shown that the n-th harmonic spectrum has the polynomial components of n-th degree in the transmission removed, i.e., the second harmonic spectrum is insensitive to linear slopes and the third harmonic insensitive to linear and quadratic components in the transmission, and so on. However, when the computation of the harmonic spectra is done by digital signal processing, one could also devise filtering methods to direct transmission spectra which have the same or possibly even better properties.

If the width of a line in the transmission changes, generally a complex change of the shape of the harmonic spectra is observed. Both the width and amplitude of the harmonic spectrum change. The overall shape of the harmonic spectrum generally depends on the modulation index, the ratio of line width and frequency modulation amplitude. The width of the harmonic spectrum is also generally much larger than the width of the absorption line, since the “broadening” is dominated by the frequency modulation amplitude, which is usually a factor of 2 to 3 larger than the absorption line half-width (see also Fig. 2). A more detailed and accurate description of the generation of harmonic spectra, which is not further relevant in this paper, can be found in Refs. [4, 16] or [17].

An interesting analogy between the Taylor series and harmonic spectra becomes evident from the reconstruction method in Sect. 2. In the case where all derivatives of the transmission T(ν) at a certain point ν ₀ are known, then T(ν) can be reconstructed in a certain range around ν ₀. This is a consequence of the Taylor theorem:

(7)

If we insert the asymptotic expression for harmonic spectra [17]

(8)

with ϵ ₀=1 and ϵ _n =2, for n≠0, we obtain

(9)

However, this would only be valid for low values of ν _A where the signal-to-noise ratio is non-optimum. On the other hand the formula derived for the multi-harmonic detection scheme Eq. (1) has no such limitation, but has a very similar structure. For the convenience of the reader, Eq. (1) is stated again:

(10)

The functions in Eq. (9) are 1, x, 2x ², 4x ³, 8x ⁴,… , whereas in the exact case the Chebyshev polynomials are given by 1, x, 2x ²−1, 4x ³−3x, 8x ⁴−8x ²+1,… with x=(ν−ν ₀)/ν _A as a shorthand notation. By comparison we see that the approximate formula Eq. (9) only contains the leading coefficients of the Chebyshev polynomials in the exact formula Eq. (1).

Appendix B: Theoretical noise performance

The (theoretical) overall white noise performance of any tunable diode laser absorption spectroscopy (TDLAS) method only depends on the system model, the total spectral frequency coverage during one scan (“which wavelengths/frequencies”), and the relative distribution of time the laser spends on different frequency regions during one scan (“how long?”). The system model is independent of the specific detection method; it essentially describes the behavior of the black-box containing the optical system with laser and detector. This system has just an electrical input (laser control) and electrical output (detector current or preamplifier output). From Table 1 it can be seen that the covered wavelength range is approximately the same for direct spectroscopy and WMS. Hence, only the distribution of time (as a fraction of total time per scan) that the laser dwells on the individual frequencies of one spectral scan can influence noise performance. The specific variation in time of the frequency is not important, as long as the distribution of the dwelling time is the same. If “important” regions of the transmission (i.e., those which are more sensitive to changes in parameters we are interested in) are measured over longer time fractions than other frequency regions, we can expect a better quality of extraction of wanted parameters from the measurement. Vice versa, if less important regions of the transmission are sampled over relatively long fractions of time, the extraction will be of lower quality. For example, this may be illustrated in a very simplified model, where we scan over a single absorption line and are only interested in the peak absorbance. If in this case the measurement of the baseline consumes far more time than measurement of the absorption line peak, the performance will be non-optimum. The reason is that the peak absorbance is the difference between both values, and we should measure them with the same accuracy, i.e., spend the same amount of time on both measurements. So even if it is fixed which wavelengths are to be sampled, the length of time that they are sampled also affects performance [12].

WMS with spectral frequency scanning and direct spectroscopy both realize an (approximately) uniform coverage of the wavelength during one scan. For WMS at a single point the absence of scanning gives a non-uniform frequency (sinusoidal) coverage over time. However, the deviation to uniform (linear) variation is not great, and numerical simulations have shown that the overall effect on noise performance is only on the order of 10 % (at least for the spectral model used in this paper).