Controlled EIT and signal storage in metamaterial with tripod structure

Abstract

In the present paper we have discussed in detail electromagnetically induced transparency and signal storing in the case of one signal pulse propagating in a classical electric medium resembles this of four-level atoms in the tripod configuration. Our theoretical results confirm recently observed dependence of transparency windows position on coupling parameters. In the process of storing, the pulse energy is confined inside the metamaterial as electric charge oscillations, and after required time it is possible to switch the control fields on again and to release the trapped signal. By manipulating the driving fields, one can thus control the parameters of the released signal and even to divide it on demand into arbitrary parts.

1 Introduction

A striking and important example of the phenomenon which completely alters the conditions for propagation of the electromagnetic waves through a medium is the electromagnetically induced transparency (EIT) [1, 2]. It consists in making the medium transparent for a pulse resonant with some atomic transition by switching on a strong field resonant with two unpopulated levels. Generic EIT scheme consists of a gas comprised of three-level atoms in so-called $\Lambda$ configuration that are driven by a strong control field and a weak probe one on separate transition. If the frequencies of probe and control fields are in two-photon resonance, the atoms are driven into a dark-state that is decoupled from the light fields. This mechanism creates the transparency window in the absorption spectrum of the probe field irradiating the medium, and the steep normal dispersion at the center of the dip of the absorption and results in significant reduction of the group velocity of the signal and enhancement of nonlinear interaction. By admitting the control fields to adiabatically change in time, it has become possible to dynamically change the properties of the medium while the probe pulse travels inside it; in particular one can not only slow down the pulse group velocity but even stop the pulse by switching the control field off. By switching it again, one can release the stored pulse, preserving the phase relations. A tripod-type four-level configuration, the classical analog of which will be considered in this paper, consists of three ground levels coupled with one upper level. Even at a first glance, one can see that this configuration, due to an additional unpopulated long-living lower state coupled by control or second signal beam with upper state, is richer than generic $\Lambda$ scheme and gives an opportunity to study different new aspect of pulse propagation. We will focus on the situation of one signal coupling populated ground level with the upper level and two strong control fields coupled with two low-lying empty levels. This medium exhibits in general two transparency windows of different widths and different slopes of normal dispersion curve [3], what means that the group velocity in the two windows can be different. Extensive studies of possibilities of slowing, stopping, performing manipulations on stored signal in order to obtain the desired properties of the released pulse or pulses in a tripod-type atomic medium were done by one Raczyński et al. [4] and confirmed experimentally by Yang et al. [5]. Nowadays a lot of attention has been paid to classical analog of EIT metamaterials [6, 7], where one expects to perform similar experiments taking advantage of operating at room temperatures. Moreover, in metamaterials consisting of coupled split-ring resonators, no quantum mechanical atomic states are required to observe EIT which may lead to slow-light applications in a wide range of frequency, from microwave up to the terahertz [8] and infrared [9] regime. Recently the storage of a signal in metamaterial has been demonstrated [10]. The investigations of classical analogs of EIT media has been motivated by recognition of wide bandwidth, low loss propagation of signal through initially thick media, opening many prospects on novel optical components such as tunable delay elements, highly sensitive sensors and nonlinear devices. Our paper is a contribution to this area. Some aspects of the atom-field interaction can be described by classical theory so we attempt to present the classical systems that mimic tripod configuration and explore the signal storage in such media. Tripod scheme allows one to perform manipulations on the signal pulse stopped in the medium, and after some time to release it in one or more parts, preserving information of the incident field, including its amplitude, phase and polarization stage. A classical scheme that mimics tripod has been investigated recently by Bai et al. [11] in the context of double EIT and plasmon-induced transparency [12], but all these papers considered two weak propagating fields coupling populated low-lying levels in the medium dressed by one control beam. Studies of EIT in metamaterials of plasmonic tripod system has also been performed by Xu et al. [13], who considered the off-resonant situation of all three fields. We investigate the EIT in classical tripod medium built of three RLC circuits coupled by two capacitances with electric resistors and alternating voltage source, or alternatively by several metal strips. Our model could be practically realized using planar complementary metamaterials in which generic EIT was successfully demonstrated by Liu et al. [9]. The electric susceptibility of such a system allows one for opening two transparency windows for an incident external field, with their width depending on system geometry and coupling capacitances. Recently Harden et al. [14] considered EIT in media of Y-configuration which is similar to tripod one, but here we investigate not only EIT but also slowing and storing of the signal which, to our knowledge, has never been done in tripod metamaterial.

Our paper is organized as follows. In the first section, the classical model of atomic tripod system is discussed and the means of control over the medium dispersion are explained. Then, the application of finite difference time domain (FDTD) method to the simulation of pulse propagation through EIT metamaterial is described. Finally, the simulation results are presented, including verification of the medium model and simulation of signal stopping and its release as a single part or in a series of pulses.

2 Classical analogues of an atomic tripod system

2.1 The model

Fig. 1

a Model of a three-level tripod configuration with a single probe field $\varOmega _p$ and two control fields $\varOmega _{c1}$, $\varOmega _{c2}$ b Electric circuit model of the system

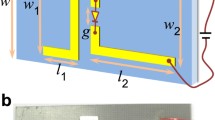
The electric analog of the atomic system in tripod configuration with a single probe and two strong control fields (Fig. 1a) is presented in Fig. 1b [14]. The currents in the circuit model are described by the system of equations

$$\begin{aligned} V_{\text {ext}}=\, & L_3 \frac{\partial i_3}{\partial t} + R_3 i_3 + \frac{1}{C_3}\int i_3 {\text {d}}t \nonumber \\&\quad + \frac{1}{C_{13}}\int (i_3-i_1) {\text {d}}t + \frac{1}{C_{23}}\int (i_3-i_2) {\text {d}}t, \nonumber \\ 0= \,& {} L_1 \frac{\partial i_1}{\partial t} + R_1 i_1 + \frac{1}{C_1}\int i_1 {\text {d}}t - \frac{1}{C_{13}}\int (i_3-i_1) {\text {d}}t, \nonumber \\ 0=\, & {} L_2 \frac{\partial i_2}{\partial t} + R_2 i_2 + \frac{1}{C_2}\int i_2 {\text {d}}t - \frac{1}{C_{12}}\int (i_3-i_2) {\text {d}}t. \end{aligned}$$

(1)

In terms of an electric charge q, where ${\dot{q}}=i$ the above set of equations takes the form

$$\begin{aligned} V_{\text {ext}}=\, & {} L \ddot{q_3} + R_3 \dot{q_3} + \left(\frac{1}{C_3}+\frac{1}{C_{13}}+\frac{1}{C_{23}}\right)q_3 \\&\quad - \frac{1}{C_{13}}q_1 - \frac{1}{C_{23}}q_2, \nonumber \\ 0=\, & {} L \ddot{q_1} + R_1 \dot{q_1} + \left(\frac{1}{C_1}+\frac{1}{C_{13}}\right)q_1 - \frac{1}{C_{13}}q_3, \nonumber \\ 0=\, & {} L \ddot{q_2} + R_2 \dot{q_2} + \left(\frac{1}{C_2}+\frac{1}{C_{23}}\right)q_2 - \frac{1}{C_{23}}q_3. \end{aligned}$$

(2)

where, without loss of generality, $L_1=L_2=L_3=L$ was assumed. Finally, we arrive at the equations for three coupled, harmonic electric oscillators

$$\begin{aligned}&\ddot{q_3} + \gamma _3 \dot{q_3} + \omega _3^2 q_3 - \varOmega _{1}^2 q_1 - \varOmega _{2}^2 q_2 = \frac{V_{\text {ext}}}{L}, \nonumber \\&\ddot{q_1} + \gamma _1 \dot{q_1} + \omega _1^2 q_1 - \varOmega _{1}^2 q_3 = 0, \nonumber \\&\ddot{q_2} + \gamma _2 \dot{q_2} + \omega _2^2 q_2 - \varOmega _{2}^2 q_3 = 0, \end{aligned}$$

(3)

where

$$\begin{aligned} \omega _1^2= & {} \left(\frac{1}{LC_1}+\frac{1}{LC_{13}}\right) \qquad \gamma _1 = \frac{R_1}{L}, \nonumber \\ \omega _2^2= & {} \left(\frac{1}{LC_2}+\frac{1}{LC_{23}}\right) \qquad \gamma _2 = \frac{R_2}{L}, \nonumber \\ \omega _3^2= & {} \left(\frac{1}{LC_3}+\frac{1}{LC_{13}}+\frac{1}{LC_{23}}\right) \qquad \gamma _3 = \frac{R_3}{L}, \nonumber \\ \varOmega _{1}^2= & {} \frac{1}{LC_{13}} \qquad \varOmega _{2}^2 = \frac{1}{LC_{23}}. \end{aligned}$$

(4)

The presented circuit and obtained system of equations is analogous to the one described in [11], with the exception that in our case, only one lower level is populated, so a single probe field $E_{\text {ext}}$ generating potential $V_{\text {ext}}$ is assumed. The result is a straightforward extension of the models for a lambda EIT system [15, 16]. The control over the system is provided by variable capacitors (varactors) $C_{13}$ and $C_{23}$. The circuit model is an approximation of the EIT metamaterial structure [13] which allows for a simple analysis of the system.

The potential $V_{\text {ext}}=V_0 \exp (-i\omega t)$ generated by external field $E_{\text {ext}}=E_0\exp (-i\omega t)$ causes the charge oscillations in the form $q_i=q_{0i}\exp (-i\omega t)$ for $i=1,2,3$. Substituting these expressions into Eq. 3, we are able to solve for the steady-state solution in the form

$$\begin{aligned} q_{03}(\omega ) = \frac{1/L}{\omega _3^2 - \omega ^2 - i\gamma _3\omega - \frac{\varOmega _1^4}{\omega _1^2 - \omega ^2 - i\gamma _1\omega } - \frac{\varOmega _2^4}{\omega _2^2 - \omega ^2 - i\gamma _2\omega }}V_0 \end{aligned}$$

(5)

The equation links the charge $q_{03}$ with the potential $V_0$ and is expressed in units of capacitance; $q_{03}(\omega ) = C_{\text {eff}}(\omega )V_0$ where $C_{\text {eff}}$ is an effective capacitance of the circuit. Suppose that the circuit is a model of a metallic structure of the length d reacting to the external electric field $E_{\text {ext}}$. Then, the potential is $V_0 = E_0d$ and the induced charge generates a dipole moment $P=q_{03}d$. Thus we can write

$$\begin{aligned} q_{03}d=\, & {} C_{\text {eff}}(\omega )E_0d^2 \\ P(\omega )=\, & {} d^2 C_{\text {eff}}(\omega )E_0 \end{aligned}$$

so the susceptibility, which in general is a complex function, is given by

$$\begin{aligned} \chi (\omega ) = \frac{d^2/\epsilon _0 L}{\omega _3^2 - \omega ^2 - i\gamma _3\omega - \frac{\varOmega _1^4}{\omega _1^2 - \omega ^2 - i\gamma _1\omega } - \frac{\varOmega _2^4}{\omega _2^2 - \omega ^2 - i\gamma _2\omega }}. \end{aligned}$$

(6)

Fig. 2

The real part of $\chi (\omega )$ for the medium parameters $L=100$, $R_1=R_2=0.1$, $R_3=1$, $C_1=C_3=1$, $C_2=1.5$, $C_{13}=C_{23}=2$

In the case of low detuning, very close to the resonance, when $\omega _1 \approx \omega _2 \approx \omega _3 \approx \omega$, we have

$$\begin{aligned} \omega _i^2 - \omega ^2 \approx 2\omega (\omega _i - \omega ) \end{aligned}$$

(7)

for $i=1,2,3$. This approximation holds true for the frequencies inside the transparency window. Introducing new quantities

$$\begin{aligned} \varOmega _{c1}^2= & {} \frac{\varOmega _1^4}{4 \omega ^2} \approx \frac{\varOmega _1^4}{4 \omega _1^2} = \frac{C_1}{4LC_{13}(C_1+C_{13})} \nonumber \\ \varOmega _{c2}^2= & {} \frac{\varOmega _2^4}{4 \omega ^2} \approx \frac{\varOmega _2^4}{4 \omega _2^2} = \frac{C_2}{4LC_{23}(C_2+C_{23})} \nonumber \\ \gamma _{ab}= & {} \frac{\gamma _3}{2}, \qquad \gamma _{bc} = \frac{\gamma _1}{2}, \qquad \gamma _{bd} = \frac{\gamma _2}{2}, \end{aligned}$$

(8)

it is possible to obtain the dispersion relation for the atomic tripod system

$$\begin{aligned} \chi (\omega ) = \frac{-A}{\omega - \omega _3 + i \gamma _{ab} - \frac{\varOmega _{c1}^2}{\omega - \omega _1 + i\gamma _{bc}} - \frac{\varOmega _{c2}^2}{\omega - \omega _2 + i\gamma _{bd}}} \end{aligned}$$

(9)

where A is a positive constant. Note, that setting $\varOmega _{c2}=0$ in Eq. 9, one gets the dispersion relation for a three-level lambda system. For a while we would like to concentrate on susceptibilities given by Eqs. 6 and 9, describing the classical electric analog of EIT system and the quantum system, respectively. It can be seen from Fig. 2 there is a close correspondence between both susceptibility values for the most important frequency region inside the transparency window and normal dispersion. The approximation used above (Eq. 7) causes a small discrepancy between susceptibility for semiclassical and classical model of the medium, which is noticeable outside the transparency windows, in the regions of anomalous dispersion and high absorption.

2.2 Steering of dispersion in classical tripod medium

Fig. 3

Real and imaginary part of $\chi (\omega )$ for the parameters $L=100$, $R_1=R_2=0.01$, $R_3=2$, $C_2=C_3=1$, $C_1=1.3$, with both coupling strengths equal ($C_{13}=C_{23}=10$), different ($C_{23}=3C_{13}$) or one of them disabled ($C_{13} \rightarrow \infty$ or $C_{23} \rightarrow \infty$)

The most interesting property of a EIT system is the possibility of an active control over the transparency windows. On Fig. 3, one can see the real and imaginary part of the susceptibility, featuring two transparency windows. When one of the control fields is disabled, a generic $\Lambda$ system with single window is obtained while for nondegenerated tripod system it is possible to get two transparency windows, the widths of which depend on the control fields strengths. From Eq. 8, one can see that in the electrical circuit model of tripod medium, the Rabi frequencies of the control fields $\varOmega _{c1}$ and $\varOmega _{c2}$ are functions which depend on capacitances and inductance. To close one of the window, one has to take $\varOmega _{c1}=0$ which corresponds to $C_{13} \rightarrow \infty$, and a finite value of $C_{23}$. As the capacitance $C_{13}$ increases, the coupling $\varOmega _{c1}$ becomes weaker, eventually vanishing in the limit of $C_{13} \rightarrow \infty$ meanwhile the transparency window becomes narrower and also its position is shifted to the lower frequency due to the effect of $C_{13}$ on $\omega _1$. However, in the case of weak coupling and narrow window, $C_{13}\gg C_1$ and $C_{13}\gg C_2$, so that the frequency shift of the window is negligible. It is worth mentioning that the effect of down-shifting the position of transparency window due to increasing coupling capacitance was recently observed by Feng et al. [17], but presented above considerations allow one to explain their observations. In the electrical circuit model, the vanishing of the control fields $\varOmega _{c1}$ and $\varOmega _{c2}$ can be realized by removing or bypassing the capacitors $C_{13}$ and $C_{23}$. Another degree of control is realized by modification of the frequencies $\omega _1$, $\omega _2$, $\omega _3$. In particular, the temperature dependence of the carrier concentration in semiconductors can be used to alter the plasma frequency and shift the transparency window [18]. In the presented circuit model, such a control corresponds to the change of the capacitances $C_1$, $C_2$, $C_3$.

3 Numerical simulation of EIT metamaterial

The finite difference time domain method has been used to simulate the pulse propagation through EIT metamaterial. A one-dimensional system has been assumed. The pulse consists of Gaussian envelope on a plane waves and travels along ${{\hat{x}}}$ axis. At every point of space, single electric field vector component $E_y$ and magnetic field component $H_z$ is defined. The usual field update formulas derived from Maxwell’s equations [19] are complemented by the material response calculated with the auxiliary differential equations (ADE) method. The basis of the calculation is the time domain formulas presented in Eq. 3. Assuming a unit scaling where $\epsilon _0=\mu _0=c=1$, one can write the Maxwell’s equations in the form

$$\begin{aligned} -\frac{\partial }{\partial x} E=\, & {} \sigma _m H +\frac{\partial }{\partial t}\left( H + M\right) , \nonumber \\ -\frac{\partial }{\partial x} H=\, & {} \sigma _e E + \frac{\partial }{\partial t}\left( E + P\right) . \end{aligned}$$

(10)

where P and M are the polarization and magnetization vector components and $\sigma$ are the conductivities. By introducing the notation

$$\begin{aligned} E(x\Delta x, n\Delta t) = E_x^n \end{aligned}$$

(11)

where $\Delta x$ and $\Delta t$ are finite spatial and time steps, one obtains the update equations

$$\begin{aligned} H_{x+\frac{1}{2}}^{n+\frac{1}{2}}=\,& {} \frac{2 - \sigma _m \Delta t}{2 + \sigma _m \Delta t} H_{x+\frac{1}{2}}^{n-\frac{1}{2}} \nonumber \\&- \frac{2\Delta t}{2 + \sigma _m \Delta t}\left[ \frac{E_{x+1}^n - E_x^n}{\Delta x} + \frac{M_{x+\frac{1}{2}}^{n+\frac{1}{2}}-M_{x+\frac{1}{2}}^{n-\frac{1}{2}}}{\Delta t}\right] , \nonumber \\ E_x^{n+1}=\, & {} \frac{2 - \sigma _e \Delta t}{2 + \sigma _e \Delta t} E_x^{n} \nonumber \\& - \frac{2\Delta t}{2 + \sigma _e \Delta t}\left[ \frac{H_{x+\frac{1}{2}}^{n+\frac{1}{2}} - H_{x-\frac{1}{2}}^{n+\frac{1}{2}}}{\Delta x} + \frac{P_{x}^{n+1}-P_{x}^{n}}{\Delta t} \right] . \end{aligned}$$

(12)

The medium is assumed to be magnetically inactive, i.e., $M=0$. The oscillating charges described by Eq. 3 give rise to three polarization values $P_1$, $P_2$, $P_3$. Only the third one is connected with the external field, so that $P=P_3=q_3d$, where d is a constant length of the metamaterial structure. As with the electric and magnetic field, the polarizations are calculated using the first order differences, similar as it was done in our previous work [7]. To ensure a satisfactory stability of the dispersion calculation scheme, for a spatial step $\Delta x=1$, the time step was set to $\Delta t=0.5$. The frequency of the propagating pulse is such that its period $T \approx 50 \Delta t$, making numerical dispersion negligible [19]. The particular units of time and space are left as a free parameter, and they are connected by relation $c=\Delta t/\Delta x$.

Moreover, it was should be kept in mind that trapping and retrieving of electromagnetic waves of GHz regime has been performed in the metamaterial constructed of electric circuits structures with inductance of $L=180$ nH and capacitances of order of pF [10]. Since all the medium parameters in Eq. 4 have units of frequency which is affected by scaling of $\Delta t$, our medium can be described by arbitrary, convenient numerical values of R, L, C. Therefore, the presented results are general and no reference to single, specific system is made.

4 Simulation results

Dynamic modulation of the EIT properties enables to slow, stop or even store the electromagnetical signal in the medium and after performing controlled manipulations to retrieve it. As it was described in previous sections, tripod medium offers richer possibilities to store and retrieve the signal than the generic lambda system. In order to illustrate it we perform the dynamic switching between EIT on and off regime, which enables one to store the signal in the EIT metamaterial and subsequently release it in two parts. The medium control is provided by modification of capacitances $C_{13}$ and $C_{23}$ which correspond with changing the Rabi frequencies $\varOmega _{c1}$ and $\varOmega _{c2}$ respectively. The parameters were set in such a way that in the initial state, when both control fields are active there are no detunings so that $\omega _1=\omega _2=\omega _3=\omega _0$, where $\omega _0$ is the central frequency of the pulse.

The control field strengths are shown on Fig. 4a. They are equal at the storage stage but the field 1 precedes the field 2 by some time at the release stage. At $t=60$, both control fields decrease, vanishing completely at $t=70$. In terms of the circuit model, this corresponds to the situation where coupling capacitances increase significantly, transforming the system into three separate circuits.

The storage process is illustrated on Fig. 4b. One can see the entering pulse at the left hand side which is then stored inside the medium. After the storage stage, when the pulse energy is confined inside the metamaterial as electric charge oscillations denoted by currents $i_1$ and $i_2$ the signal is released in two portions, i.e., on 4a, at $t=110$, first control signal is turned on again, releasing the first part of the pulse, similarly as in the simple $\Lambda$ system. The stored energy starts to be radiated when the transparency window begins to open. Finally, the second part is released at $t=150$ by increasing $\varOmega _{c2}$. The latter releasing occurs in the presence of both control fields, which gives rise to a difference of the two parts of the signal, as concerns their heights and initial velocities, which is clearly seen in Fig. 4b. The first part has been released with a zero initial velocity while the second part has a nonzero velocity from the very beginning because two control fields are on. To obtain a full symmetry one should switch the first control field off before switching the second one on. Then one would obtain two identical released pulses shifted in time, as in two independent simple $\Lambda$ systems.

One can see that a significant fraction of the pulse is restored, but some leaked signal continues to propagate through the medium when the control fields are off (see Fig. 4b). The point is that due to dynamical changes of $C_{13}$ and $C_{23}$ at the time when both control fields $\varOmega _{c1}$ and $\varOmega _{c2}$ are switched off, the significant shifts of frequencies $\omega _1$, $\omega _2$ and $\omega _3$ appeared (see Eq. 3) causing a distortion of the window. As a consequence, at some point during the storage process, when the coupling field strength is weak, the central frequency of the pulse is outside of the narrow window and, as a result, some part of the signal is not absorbed. The shift of frequencies $\omega _1$, $\omega _2$ and $\omega _3$ can be minimized when the coupling capacitances $C_{13}$ and $C_{23}$ are much bigger than $C_1$, $C_2$ and $C_3$.

Finally, Fig. 4c depicts the normalized measure of the energy stored in the system. In a classical way, we can calculate the energy

$$\begin{aligned} E_1= & {} \frac{1}{2}L\omega _1^2q_1^2 + \frac{1}{2}L \dot{q_1}^2, \nonumber \\ E_2= & {} \frac{1}{2}L\omega _2^2q_2^2 + \frac{1}{2}L \dot{q_2}^2, \nonumber \\ E_3= & {} \frac{1}{2}L\omega _3^2q_3^2 + \frac{1}{2}L \dot{q_3}^2 + q_3V_{\text {ext}} + E^2, \end{aligned}$$

(13)

stored in the medium polarizations. In terms of RLC circuit, these two factors correspond to the energy stored in capacitor and induction coil, respectively. Moreover, the part $E_3$ contains also the energy of field-polarization interaction $q_3V_{\text {ext}}$ and the vacuum field energy $\epsilon _0 E^2$, where $\epsilon _0=1$.

One can see that the energy reaches the maximum value when the pulse enters the system (Fig. 4c, 1). Then, when the window is closed, it is stored in the form of polarizations $P_1$ and $P_2$ (2). The points (3) and (4) mark the moments when one of the control fields is turned on and one part of the pulse is released. Interestingly, when the second control field is switched of, the energy oscillates between $P_1$ and $P_2$ for some time. However, the total energy is conserved. As expected, the total energy decreases exponentially. Some transient effects are visible at the points when the window is opening or closing, indicating that the measure given by Eq. 13 is sufficient only for a steady state.

Fig. 4

Simulation results for $L=100$, $C_1=C_2=1$, $C_3=2$, $R_1=R_2=0.01$, $R_3=1$. a Control field strengths as a function of time; b Time and space dependence of the field strength, showing the storage process; c Dispersion relation of the medium when constant values of $\omega _1$, $\omega _2$, $\omega _3$ are preserved. d Normalized energy contained in polarizations $P_1$, $P_2$, $P_3$ and external field

4.1 Train of pulses

It is possible to release the stored signal in a form of multiple subsequent pulses by increasing the coupling strengths in multiple steps at the releasing. The simulation results for such a case is presented on Fig. 5. To better understand the dynamics of the storage process, field snapshots have been taken at the characteristic moments. On the first panel of Fig. 5b, one can see the initial, propagating pulse which consists of the electric field E and the two polarizations $P_1$, $P_2$ coupled by $\varOmega _{c1}$ and $\varOmega _{c2}$. When the control fields are disabled (Fig. 5a, 1), the pulse is stored inside the medium in the form of localized oscillations of $P_1$ and $P_2$. When the first control field is turned on, the polarization $P_1$ becomes coupled to the external field $E_{\text {ext}}$. As a consequence, a propagating pulse is formed (third panel). Then, when the amplitude of the second control field is increased, another pulse is generated by using the energy stored in polarization $P_2$. At the same time, the first pulse also becomes coupled to $P_2$, forming a new, localized perturbation of $P_1$ and $P_2$. As a result, further changes of one of the control fields generate two pulses (fifth panel). This is easily visible on Fig. 5a, where the last four changes of the control fields generate pair of pulses each. The positions of these pulses correspond to the points where the initial released pulse was located when the first and second control fields were switched on (Fig. 5a, 3, 4).

Fig. 5

Simulation results for storage and release of the signal in many parts, forming a train of pulses. a Time and space dependence of the pulse amplitude along with the control field strengths, illustrating the storage of the pulse and its release in multiple stages. b Field snapshots at the specific times, showing both the propagating and stored part of the signal

5 Conclusions

We have considered the details of EIT and the dynamics of pulse propagation in a classical analogs of tripod system such as electric circuit. Some quantitative predictions concerning the characteristics of a pulses stored in such media have been presented and discussed both analytically and numerically in terms of the energy and polarization of the system. Considered above classical model of the tripod structure allows one for steering the propagation through different combinations of coupling capacitors. Our theoretical and numerical results confirm and explain recently observed effect of the dependence of transparency window position on coupling capacitances [10]. Due to rich dynamics and controllability, the tripod medium allows for a flexible and effective processing of the stored signal and its release on demand in one or more parts with prefect control of their intensity. The performed FDTD simulations confirm the close analogy between atomic tripod system and its classical, metamaterial counterpart and provide an insight into the dynamics of the signal processing. Moreover, slow-light techniques realized in semiclassical media and solid state metamaterials hold great promise for applications in telecom and quantum information processing.