Dielectric, modulus and impedance analysis of lead-free ceramics Ba_0.8La_0.133Ti_1−x Sn _x O₃ (x=0.15 and 0.2)

Abstract

Titanate barium (BaTiO₃)-type oxide ceramics Ba_0.8La_0.133Ti_1−x Sn _x O₃ (BLTS) (here x=0.15 and 0.2) have been synthesized by the standard solid-state reaction method. Preliminary room temperature X-ray study confirms the formation of single-phase compounds in a rhombohedral crystal system. The electrical properties of BLTS were studied using the ac impedance spectroscopy technique over a wide range of temperature (120–320 K) in the frequency range of 40 Hz to 10 MHz. The presence of a single arc in the complex modulus spectrum at different temperatures confirms the single-phase character of the BLTS compounds.

1 Introduction

The most important ferroelectric ceramics crystallize in the ABO₃ structured perovskite. The flexible structure of perovskite shows diverse physical properties which are interesting for functional applications [1–4]. It has already been established that a wide range of complex compounds, obtained by single- or multi-element doping at the A and/or B sites of the perovskite structure, are potentially suitable for applications such as transducers, sensors, electro-optic modulators, memory components and many other active and passive devices [5–8]. The researchers paid more attention to improve the dielectric properties of pure BaTiO₃ via partial substitution of either Ba-ions (A-site doping) or Ti-ions (B-site doping), which may result in high permittivity, high piezoelectric and ferroelectric properties; the absence of lead increases their application as non-polluting materials [9]. So far, many new materials with excellent properties have been developed, such as Ba_1−x Sr _x TiO₃ [10], BaTi_1−x Sn _x O₃ [11–13] and (BaSr)(SnTi)O₃ [14, 15] ceramics. Research is now on the way in producing such lead-free ceramics with relaxing behavior at room temperature which are of great interest for a wide range of applications [16–22]. In view that the important properties exhibited by the materials and also their conductivity and impedance spectroscopy studies have not yet been reported in the literature, an attempt has been made to study the structural, electrical properties of Ba_0.8La_0.133Ti_1−x Sn _x O₃ ceramics. The permittivity (ε ^∗), impedance (Z ^∗), electrical modulus (M ^∗), and conductivity (σ ^∗) spectroscopy techniques have been studied over the wide range of temperature (120–320 K) and frequency (40 Hz to 10 MHz).

2 Experimental details

2.1 Ceramic route synthesis of phases Ba_0.8La_0.133Ti_1−x Sn _x O₃

The polycrystalline compounds of Ba_0.8La_0.133Ti_1−x Sn _x O₃ (where x=0.15 and 0.2) were prepared by the standard solid-state reaction method using high purity (more than 99.9 %) starting compounds such as BaCO₃, La₂O₃, TiO₂ and SnO₂. All the samples were preheated before weighing. The initial mixtures of ingredients were thoroughly grounded and calcined at 1173 K for 24 hours in a muffle furnace. The resultant powders were taken out, re-ground thoroughly and pressed into pellets. The pellets were sintered at 1673 K for 3 hours each with intermediate re-grinding and pelletization.

2.2 Material characterization

The determination of lattice parameters of the unit cell structure and identification of phase were carried out at room temperature by powder X-ray diffraction (XRD) technique recorded by Siemens D-5000 diffractometer (Cu K _α radiation). These XRD patterns were calculated by the Rietveld method to obtain the structure model with the least deviation. Surface morphology of the sintered samples was examined by scanning electron microscope (SEM, Philips XL30 with an energy dispersive X-ray spectrometer). Afterwards, a pellet of about 4 mm in diameter and 1 mm in thickness was used for the electrical measurements. Dielectric response from 120 up to 320 K was measured using Agilent 4294 A impedance analyzer at frequencies from 40 Hz to 10 MHz.

3 Results and discussion

3.1 SEM observations

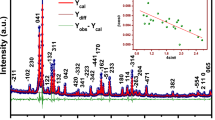
The morphology and the grain size of samples were examined by SEM. The inset of Fig. 1 shows a typical SEM image of the composition specimen of x=0.15. The image shows homogenous grains distributed over the entire volume of the sample and a good crystallization. The average grain size decreases from 298.79 nm for x=0.15 to 291.2 nm for x=0.2, depending on the Sn⁴⁺ content.

Fig. 1

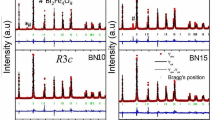
Observed (solid circles) and calculated (solid line) XRD patterns of Ba_0.8La_0.133Ti_0.85Sn_0.15O₃ samples obtained at room temperature. The difference between these spectra is plotted at the room temperature. Bragg reflections are indicated by ticks. The inset represents the SEM micrograph of the sample

3.2 Structural properties

The powder X-ray diffraction patterns of the polycrystalline ceramic samples Ba_0.8La_0.133Ti_1−x Sn _x O₃ collected at room temperature are shown in Fig. 1. The figure presents the measured, calculated (refined) X-ray diffraction pattern and positions of Bragg reflections for the sample Ba_0.8La_0.133Ti_0.85Sn_0.15O₃ as an example of this series. As can be seen from the figure, all the reflection peaks of the X-ray profile are indexed and lattice parameters are determined using a least-squares method with the help of a standard program (Wintplor [23]). On the basis of the best agreement between calculated (cal) and observed (obs) results, a suitable unit cell of the compound in the rhombohedra system with space group R$\bar{3}c$ was selected. Using the refined crystallographic data, the unit cell parameters and other fitting parameters of all the samples were computed and are reported in Table 1. For two samples, the distortion ratio (c/a) is high as compared with the parent BaTiO₃ (2.444). Such a significant increase exists due to the substitution of either Ba-ions by La or Ti-ions by Sn in perovskite BaTiO₃, since these substituted ions have large variation in ionic radii, i.e., (La³⁺ (1.22 Ǻ) and Sn⁴⁺ (0.69 Ǻ)), with parent BaTiO₃ (Ba²⁺ (1.216 Ǻ) and Ti⁴⁺ (0.605 Ǻ)) [24].

Table 1 Applied conditions and results of refinement by Rietveld method

3.3 Impedance spectroscopy

The complex impedance spectroscopy (CIS) technique [25] was used to analyze the electrical response (i.e., transport properties) of a polycrystalline sample in a wide range of frequency at different temperatures. The CIS gives the direct correlation between the response of a real system and an idealized model circuit composed of discrete electrical components. Figure 2 shows temperature-dependent spectra (Nyquist plot) of BLTS samples. The impedance spectrum is distinguished by semicircles. A single semicircle indicates that only one primary mechanism exists for the electrical conduction within the samples at 120 K<T<320 K. The depressed semicircles have their centers on a line below the real axis, which indicates departure from the ideal Debye behavior [25]. The absence of second semicircle in the complex impedance plots suggests the dominance of bulk contributions in the BLTS compounds [26]. With increasing the temperature, intercept point on the real axis shifts toward the origin indicating the decrease in the resistive property of the material. The experimental impedance spectra were simulated by the impedance of equivalent circuit composed of bulk resistance R _p and constant phase CPE elements connected in parallel (see Fig. 3). The CPE, defined by two values, CPE-T and CPE-P, is expressed by the following equation:

$$ Z = \frac{1}{ [ T ( j\omega )^{P} ]} $$

(1)

where T (CPE-T) is expressed in units of capacitance component and ω is angular frequency (ω=2πf). The CPE is identical to a capacitance component when the exponent P (CPE-P) equals 1, to a resistance component when P=0, and to a Warburg element when p=0.5. When the CPE is placed in parallel to a resistance, a Cole element (depressed semicircle) is produced. The expressions of real (Z′) and imaginary (Z″) components of impedance related to the equivalent circuit are:

(2)

(3)

Fig. 2

Experimental and simulated semicircles plot at different temperatures for the samples Ba_0.8La_0.133Ti_0.85Sn_0.15O₃ and Ba_0.8La_0.133Ti_0.80Sn_0.2O₃

Fig. 3

The appropriate equivalent electrical circuits of the samples BLTS0.15 and BLTS0.2

The parameters of each fitting are summarized in Table 2 and were determined using a non-linear least-squares fitting. Here, it is noted that the values of R _p , resistances of each of the BLTS composition, exhibit decreasing trend with the increase in temperature. It indicates that the conductivity increases with increase in temperature supporting the typical negative temperature coefficient of resistance behavior (i.e., NTCR) of the materials usually shown by semiconductors. As the values of p vary in the range 0.9–1 confirming the weakness interaction between localized sites, the conductivity σ _p is obtained from R _p by means of the relation

$$ \sigma_{p} = \frac{e}{SR_{p}} $$

(4)

Table 2 The estimated values of the equivalent circuits’ parameters

Here e is the thickness and S the effective area of the investigated material. The electrical conductivity dependence on temperature is shown in Fig. 4 in the form of Ln (σ _dc) versus (1/T) plot. Following the Arrhenius law, the obtained activation energies are E _p =0.1 eV in region I (T>238 K) and 0.018 eV in region II (T<238 K) for x=0.15, and E _p =0.1 eV in region I (T>232 K) and 0.017 eV in region II (T<232 K) for x=0.2.

Fig. 4

Arrhenius plot of σ _p versus 1/T for the samples Ba_0.8La_0.133Ti_0.85Sn_0.15O₃ and Ba_0.8La_0.133Ti_0.8Sn_0.2O₃

3.4 Electrical conductivity analysis

The study of frequency-dependent conductivity is a well-established method for characterizing the hopping dynamics of the charge carrier/ions. Variation of conductivity σ of the sample Ba_0.8La_0.133Ti_0.85Sn_0.15O₃ as a function of frequency at several temperatures (120–320 K) is depicted in Fig. 5. The conductivity plots show significant frequency dispersion at lower frequencies that shifts to higher frequency with increase in temperature, quite similar to the vast majority of solids. Extrapolating these conductivity curves at lower frequencies gives the DC conductivity. At the high-frequency end, the curves approach each other, once again indicating the possibility of the presence of space charges [27]. A basic fact about the conductivity is that σ increases with frequency (any hopping model has this feature). The observed frequency-independent σ _dc is explained by the relaxation jump model [28]. According to this model, at low frequencies and/or higher temperatures, conduction occurs through hopping of charged particles from one localized state to another resulting in long-range translational motion of charge carriers contributing to σ _dc. Conductivities in a variety of perovskite oxides have long been found to obey a power law proposed by Jonscher [28]:

$$ \sigma = \sigma_{\mathrm{dc}} + \sigma_{\mathrm{ac}} ( \omega ) = \sigma_{\mathrm{dc}} + A\omega^{s} $$

(5)

where σ(ω), σ _dc and σ _ac(ω) have the usual meaning, A is a constant and s is the power exponent that can take values less than 1 [29]. The transport mechanism is explained by the thermally activated hopping process between two sites separated by an energy barrier. Equation (5) was used to fit the conductivity data. In the fitting procedure, the A and s values have been varied simultaneously to get the best fits. However, similar observations have been made by Cramer [30] and Papathanassiou [31, 32]. Figure 6 shows the variation of σ as a function of frequency at the temperature T=120 K for Ba_0.8La_0.133Ti_1−x Sn _x O₃ (x=0.15 and 0.2) compounds. These curves reveal an increase of the conductivity when increasing the Sn doping concentration. In Table 3 we have presented the values of σ _dc, A and s of BLTS0.15 and BLTS0.2 determined at the temperature T=120 K. From the table we can conclude that σ _dc and s increase while A decreases when increasing the Sn doping concentration. DC conductivity data are plotted in Arrhenius format as ln (σ _dc) vs. 1/T for all the samples (see Fig. 7), and show Arrhenius-type behavior described by $\sigma_{\mathrm{dc}} = \sigma_{0}\exp( - \frac{E_{\mathrm{dc}}}{k_{B}T} )$, where σ ₀ is the pre-exponential factor corresponding to 1/T=0, E _dc is the activation energy for charge transfer, k _B the Boltzmann constant and T the absolute temperature [33]. The activation energy values, for samples with different Sn concentrations calculated from the plot of ln (σ _dc) vs. 1/T are listed in Table 3. These values match nicely with the values from Eq. (4). The obtained values suggest that the conduction is created by thermally activated mechanism.

Fig. 5

Frequency dependence of the conductivity (σ) of Ba_0.8La_0.133Ti_0.85Sn_0.15O₃ at different temperatures. Solid lines are the fitting to the experimental data using universal Jonscher’s power law

Fig. 6

Frequency dependency of conductivity of BLTS0.15 and BLTS0.2 at T=120 K

Fig. 7

Plot of dc conductivity vs. 1/T. The open symbols are experimental data points and the solid lines are the least-squares straight-line fit

Table 3 Values of the dc conductivity (σ _dc), the constant (A), the slope (s) and the activation energies E _dc for Ba_0.8La_0.133Ti_1−x Sn _x O₃ (x=0.15 and 0.2) compounds determined at the temperature T=120 K

3.5 Complex permittivity representation

The study of the dielectric properties is another important source of valuable information about conduction processes since it can be used to understand the origin of the dielectric losses, the electrical and dipolar relaxation time [34]. It is observed that the complex permittivity data of our samples obey the Cole–Cole equation [35]:

$$ \varepsilon^{{*}} = \varepsilon' + i\varepsilon'' = \varepsilon_{\infty} + \frac{\varepsilon_{s} - \varepsilon_{\infty}}{ 1 + (i\omega \tau )^{1 - \alpha}} - i\frac{\sigma_{\mathrm{dc}}}{\varepsilon_{0}\omega} $$

(6)

Here, ε _s and ε _∞ are the dielectric constants on low and high frequency sides of the relaxation, ω is the angular frequency τ is the mean relaxation time instead of the single relaxation time of pure Debye process while the Cole–Cole parameter α indicates the width of the relaxation time distribution and provides a measure of the polydispersive nature. The last term at the right-hand-side is due to the high conducting behavior contributing only to the imaginary part [36], which is due to the displacement of charge carriers, rather than the effect of polarization mechanism.

Consequently, the complex permittivity may be decomposed into real and imaginary parts, i.e.

(7)

and

(8)

Figure 8 shows the frequency dependence of the imaginary part (ε″) of dielectric constant at different temperatures for the samples BLTS0.15 and BLTS0.2. Analysis of experimental data was carried out on the basis of Eq. (8). No loss peak are observed in the ε″ spectra. The high values of ε″ and especially at high temperatures and the large drop of ε″ when the frequency increases seem to indicate the influence of conductivity and space charge polarization mask the ferroelectric relaxation. Thus, the observed dielectric dispersion at low frequency may be due to the polarization mechanism associated with the thermally activated conduction of mobile ions and/or other defects. Similar behavior has been reported by Kamal et al. [37] on the sample of Ba(Al_1/2Nb_1/2)O₃.

Fig. 8

Variation of the imaginary part of dielectric constant vs. frequency for of (Ba_0.8La_0.133Ti_1−x Sn _x O₃) ceramic where x=0.15 and 0.2 at various temperatures

3.6 Electric modulus studies

The impedance data can be analyzed in a much better way by replotting the data in the complex modulus (M ^∗) formalism, which is based on the polarization analysis. The electric modulus (M ^∗) is defined as M ^∗=M′+jM″=1/ε ^∗=jωC ₀ Z ^∗, where $M'\ (\mathrm{real\ part}) = \omega C_{0}Z''$ and $M''\ (\mathrm{imaginary\ part}) = \omega C_{0} Z'$ ($\omega = \mathrm{angular}\ \mathrm{frequency} \mathrm{i.e.}, 2\pi f$), (C ₀=geometrical capacitance=ε ₀ S/e), (ε ₀=permittivity of free space). The temperature dependence of the complex modulus spectrum (M″ vs. M′) of BLTS0.15 compounds is shown in Fig. 9. From this figure, we can notice that the samples modulus spectrum has a typical semicircle pattern with its center lying below the real axis (unlike the ideal Debye type response). This is evident from the shape of the deformed arcs with their centers positioned below the x-axis [38]. The presence of a single semicircular arc confirms the single phase formation of the compounds.

Fig. 9

Variation of M″ versus M′ of Ba_0.8La_0.133Ti_0.85Sn_0.15O₃ at selected temperatures

Scaling behavior of the samples was studied by replotting normalized parameters (i.e. $M''/M''_{\max}$) versus (f/f _max); f _max is frequency corresponding to $M''_{\max}$ at different temperatures (Fig. 10). The modulus scaling behavior gives an insight into the dielectric processes occurring inside the material. The low frequency side of the peak in $M''/M''_{\max}$ versus f/f _max curve represents the range of frequencies in which the charge carriers can move over a long distance (i.e. charge carriers can perform successful hopping from one site to the neighboring site). The high frequency side of $M''/M''_{\max}$ versus f/f _max curve represents the range of frequencies in which the charge carriers are spatially confined to their potential wells, and thus could make localized motions inside the well. The region where the peak occurs is an indication of the transition from long-range to short-range. The perfect overlapping of all the curves at different temperatures suggests that all possible relaxation mechanisms occurring at different frequencies exhibit the same thermal energy and the dynamical processes are temperature-independent [39]. The modulus plot can be characterized by full width at half height or in terms of a non exponential decay function [40, 41] $\varphi(t) = \exp\{ - ( \frac{t}{\tau} )^{\beta} \}$, where τ is a characteristic time and β is a non-exponential parameter representative of a distribution of relaxation time. The value of β is positioned in the range 0<β<1, which represents the departure from the linear exponential (β=1). The β value can be determined by knowing the full width-at-half-maximum (FWHM) of the $M''/M''_{\max}$ spectrum (β=1.14/FWHM). In our case, the values of β estimated for BLTS0.15 and BLTS0.2 are 0.2 and 0.19 respectively. This indicates that the relaxation process for all the tested samples is of non-Debye-type relaxation phenomena in good agreement with the observations from complex permittivity spectrum.

Fig. 10

Modulus master curve of Ba_0.8La_0.133Ti_0.85Sn_0.15O₃ material

A comparison of the impedance with the electric modulus data allows the determination of the bulk response in terms of localized or non-localized conduction [42]. In Fig. 11, the normalized parameters $M''/M''_{\max}$ and $Z''/Z''_{\max}$ for the composition x=0.15 and 0.2 as a function of frequency at 120 K are shown. The overlapping of peak positions of the $M''/M''_{\max}$ and $Z''/Z''_{\max}$ curves is an evidence of delocalized or long-range relaxation [42]. However, for the present system the $M''/M''_{\max}$ and $Z''/Z''_{\max}$ peaks do not overlap but are very close, suggesting the components from both long-range localized relaxations.

Fig. 11

Frequency (angular) dependence of normalized peaks, $M''/M''_{\max}$ and $Z''/Z''_{\max}$, for BLTS0.15 and BLTS0.2 at 120 K

4 Conclusion

A new composition of BLTS (Ba_0.8La_0.133Ti_1−x Sn _x O₃) was prepared in a single phase by a solid-state reaction technique. The investigations of (Ba_0.8La_0.133Ti_1−x Sn _x O₃) by Rietveld analysis indicate that these samples crystallize in rhombohedral structure with $R\bar{3}c$ like a space group. Impedance spectroscopy is used to study the dielectric relaxation (conduction) for the synthesized samples. Interpretation of impedance data in the light of their ideal equivalent circuits confirmed that the vacancy diffusion in the microstructure for Ba_0.8La_0.133Ti_1−x Sn _x O₃ (x=0.15 and 0.2) ceramics is a thermally activated process. The frequency-dependent conductivity plots show two regions of conduction process, i.e., a low frequency region due to DC conduction and a high-frequency region due to localized hopping and/or reorientational motion. Modulus analysis confirmed the single-phase behavior of materials in a good agreement with the information received from XRD study. The activation energies calculated both from impedance and electric modulus spectra are comparable.