Interchanging Space and Time in Nonlinear Optics Modeling and Dispersion Management Models

Abstract

Interchanging the role of space and time is widely used in nonlinear optics for modeling the evolution of light pulses in glass fibers. A phenomenological model for the mathematical description of light pulses in glass fibers with a periodic structure in this set-up is the so-called dispersion management equation. It is the purpose of this paper to answer the question whether the dispersion management equation or other modulation equations are more than phenomenological models in this situation. Using Floquet theory we prove that in case of comparable wave lengths of the light and of the fiber periodicity the NLS equation and NLS like modulation equations with constant coefficients can be derived and justified through error estimates under the assumption that rather strong stability and non-resonance conditions hold. This is the first NLS approximation result documented for time-periodic dispersive systems. We explain that the failure of these conditions allows us to prove that these modulation equations in general make wrong predictions. The reasons for this failure and the behavior of the system for a fiber periodicity much larger than the wave length of light shows that interchanging the role of space and time for glass fibers with a periodic structure leads to unwanted phenomena.

1 Introduction

Dispersion management is used in various applications such as in mode-locked fiber lasers or in optical fiber communication, cf. Ganapathy (2008). These systems are described by Maxwell’s equations with a weakly nonlinear material law for the polarization of the medium. In such systems dispersion occurs, i.e., the scattering of energy, which is an unwanted phenomenon w.r.t. the purpose of these devices. An active dispersion management is used in order to minimize the possible dispersion of the light pulses. One aims to stabilize the pulses by a periodic arrangement of two materials with opposite dispersion coefficients, cf. Kurtzke (1993). See Turitsyn et al. (2003) for a nice review article.

For the subsequent considerations we use time-periodic systems instead of spatially periodic systems due to the modeling used in nonlinear optics. There, the role of the spatial variable $x_\mathrm{phys}$ and of the temporal variable $t_\mathrm{phys}$ is interchanged, and $x_\mathrm{phys}$ is taken as evolutionary variable, see Fig. 1. In order to have the usual mathematical notation we use t for the evolutionary variable which corresponds in the physical model to the spatial variable $x_\mathrm{phys}$.

Fig. 1

In geometric or nonlinear optics, cf. Rauch (2012) and Agrawal (2013), the space variable $x_\mathrm{phys}$ is very often taken as the evolutionary variable. The initial condition is given by the time evolution at the lower end of the fiber. Since the system is periodic in space we have chosen (1) to be periodic w.r.t. our evolutionary variable $t = x_\mathrm{phys}$

As a toy model for discussing these questions we consider in this introduction the following time-periodic dispersive system

$$\begin{aligned} \partial _t^2 u = \alpha _1 \partial _x^2 u + \alpha _2 \partial _x^2 \partial _t^2 u - \alpha _3 u + \alpha _4 u^3 , \end{aligned}$$

(1)

with $x,t,u(x,t) \in {{\mathbb {R}}}$, and where the $\alpha _j = \alpha _j(t)$ for $j =1,2,3,4$ are real-valued 2L-time-periodic (step) functions which are defined by

$$\begin{aligned} \alpha _j(t) = \left\{ \begin{array}{cl} \alpha _{j;1}, &{}\quad \text {for } t \in [0,L),\\ \alpha _{j;2}, &{}\quad \text {for } t \in [L,2 L), \end{array} \right. \end{aligned}$$

(2)

with $\alpha _{j;1},\alpha _{j;2}\in {{\mathbb {R}}}$ and $L> 0$. (1) is not derived from Maxwell’s equations, but we strongly believe that the subsequent results hold similarly for models which come directly from Maxwell’s equations. For notational simplicity we have chosen both intervals to be of the same length L. In the following many 2L-time periodic step functions will occur. They are defined as in (2). The two coefficients of such a step function a are denoted by $a_{;n} \in {\mathbb {R}}$ for $n = 1,2$.

Remark 1.1

a) Except of the term $+ \alpha _2 \partial _x^2 \partial _t^2 u$ Eq. (1) is the cubic Klein–Gordon equation which is a phenomenological model often used in nonlinear optics.

b) The term $+ \alpha _2 \partial _x^2 \partial _t^2 u$ is added to change the convex curves of eigenvalues for $\alpha _2=0$ into curves with a local concave behavior which is necessary for dispersion management.

c) The step functions w.r.t. time are used in the introductory Sects. 1 and 2 and in the discussion Sect. 7.2 in order to simplify our explanations. In the subsequent approximation and non-approximation theorem we use smooth functions w.r.t. time. This is justified by the fact that all phenomena which we would like to address already appear in smooth systems.

Light pulses are modulated electromagnetic waves consisting of an underlying carrier wave modulated by a pulse-like envelope. The carrier wave and the envelope live on different temporal and spatial scales. For an approximate description of this multiple scaling problem effective equations¹ for the dynamics of the envelope can be derived by perturbation analysis. We are interested in the question: which of these modulation equations make correct predictions about the dynamics of the original system in the above set-up? We do so by proving error estimates for these identified formal approximations.

In the homogenous situation, i.e., in case $\alpha _j= \alpha _{j;1} = \alpha _{j;2}$, by inserting the ansatz

$$\begin{aligned} u(x,t) \approx \varepsilon \psi _{\varepsilon }(x,t) = \varepsilon A(X,T) E(x,t) + c.c. + {\mathcal {O}}(\varepsilon ^3), \end{aligned}$$

(3)

with the envelope $A(X,T) \in {{\mathbb {C}}}$, the carrier wave $E(x,t) = e^{i (k_0 x + \omega _0 t)}$ with $k_0, \omega _0 \in {{\mathbb {R}}}$, the small perturbation parameter $0 < \varepsilon ^2 \ll 1$, the slow time variable $T=\varepsilon ^2 t$, and the slow spatial variable $X=\varepsilon (x+c t)$ with $c \in {{\mathbb {R}}}$, into (1) and by equating the coefficients in front of $\varepsilon E$, $\varepsilon ^2 E$, and $\varepsilon ^3 E$ to zero yields that the temporal wave number $\omega _0$ and the spatial wave number $k_0$ have to satisfy the linear dispersion relation

$$\begin{aligned} \omega _{0}^2 = \alpha _{1} k_0^2 - \alpha _{2} k_0^2 \omega _{0}^2 + \alpha _{3}, \end{aligned}$$

that the group velocity c is given by

$$\begin{aligned} c = \frac{\mathrm{d}\omega _{0}}{\mathrm{d}k}|_{k=k_0} = \frac{\alpha _{1} k_0 - \alpha _{2} \omega _{0}^2 k_0}{(1+\alpha _2 k_0^2)\omega _{0}}, \end{aligned}$$

and that A satisfies in lowest order the NLS equation

$$\begin{aligned} i \nu _{0} \partial _T A = \nu _{1} \partial _X^2 A + 3 \nu _{2} A | A|^2, \end{aligned}$$

(4)

with coefficients

$$\begin{aligned} \nu _{0} = 2 \omega _{0} + 2 \alpha _{2} k_0^2 \omega _{0}, \quad \nu _{1} = \left( \alpha _{1}- c^2 + \alpha _{2} \omega _{0}^2\right) , \quad \text {and} \quad \nu _{2} = \alpha _{4}. \end{aligned}$$

Since (1) contains no quadratic terms, the proof of the following approximation theorem is straightforward and can be found for instance in Kirrmann et al. (1992).

Theorem 1.2

Fix $T_0 > 0$ and let $A \in C([0,T_0], H^{6}({{\mathbb {R}}},{{\mathbb {C}}}))$ be a solution of (4). Then there exist $\varepsilon _0 >0$, $C>0$ such that for all $\varepsilon \in (0,\varepsilon _0)$ there are solutions $u \in C([0,T_0/\varepsilon ^2], H^{1}({{\mathbb {R}}},{{\mathbb {R}}}))$ of (1) with

$$\begin{aligned} \sup _{t \in [0,T_0/\varepsilon ^2]} \sup _{x \in {{\mathbb {R}}}} |u(x,t) - \varepsilon \psi _{\varepsilon }(x,t) | \le C \varepsilon ^{3/2}, \end{aligned}$$

where $\varepsilon \psi _{\varepsilon }$ has been introduced in (3).

It is the purpose of this paper to answer the question which modulation equation takes over the role of the NLS equation from the homogeneous to the time-periodic case, in particular we would like to investigate whether the so-called dispersion management equation

$$\begin{aligned} i \partial _T A = {\widetilde{\varepsilon }}^{-1}\nu _{2}\left( \frac{T}{ {\widetilde{\varepsilon }}}\right) \partial _X^2 A + \nu _{nl} A | A|^2, \end{aligned}$$

(5)

with $\nu _{nl} \in {{\mathbb {R}}}$, $\nu _2$ a $2 \pi$-periodic real-valued function, which is widely used for understanding dispersion management phenomena, is more than a phenomenological model in this situation. Its properties have been analyzed in a number of papers, cf. Bronski and Kutz (1997), Zharnitsky et al. (2001), Kunze et al. (2005), Erdoğan et al. (2011), Hundertmark et al. (2015) and Green and Hundertmark (2016), in particular, when the mean value of $\nu _2$ vanishes. The present paper will shed some new light on the validity of the dispersion management equation in the chosen set-up.

Our results are as follows. Using Floquet theory we prove that, in case of comparable wave lengths of the light and of the fiber periodicity, NLS and NLS like modulation equations, with constant time-independent coefficients, can be derived and justified through error estimates under the assumption that rather strong stability and nonlinear non-resonance conditions hold. In detail, in Sect. 3 we use linear Floquet theory to transfer (1) into a system with autonomous linear part. In Sect. 4 we make two preliminary considerations about linear instabilities occurring in time-periodic systems and about nonlinear resonances. In Sect. 5 we justify the NLS equation (4) and the modulation equation, which appears for vanishing mean dispersion, by proving error estimates for the associated approximations under the assumption that various linear stability and nonlinear non-resonance conditions hold. This is the first NLS approximation result documented for time-periodic dispersive systems. In Sect. 6 we prove that in case of a failure of the linear stability conditions the modulation equations make wrong predictions. In all these sections we consider the situation $L = {\mathcal {O}}(1)$. The paper is closed with a longer discussion. In Sect. 7.1 we discuss possible generalizations of the presented theory. In Sect. 7.2 we explain that for the fiber periodicity $L \gg {\mathcal {O}}(1)$ which has to be chosen for a possible derivation of the dispersion management equation a cascade of modulated wave packets occur which cannot be described by a single dispersion management equation. Thus, it turns out that in the chosen set-up the dispersion management equation is at most a phenomenological model. It cannot be derived and justified for the modeling of Nonlinear Optics used in this paper.

Before we start, in Sect. 2 we give a number of heuristic arguments for the occurrence of various modulation equations and their validity. These arguments will make a connection to the dispersion management equation. However, our heuristics will turn out to be rather misleading as the subsequent mathematics will show.

Notation

The Fourier transform of a function u is denoted by ${\widehat{u}}$. Similarly, to an operator M the associated operator in Fourier space is denoted by ${\widehat{M}}$. $L^2_s$ is the subset of $L^2$ for which the norm

$$\begin{aligned} \Vert {\widehat{u}} \Vert _{L^2_s} = \left( \int _{{\mathbb {R}}} | {\widehat{u}}(k) |^2 (1+k^2)^s \mathrm{d}k \right) ^{\frac{1}{2}} \end{aligned}$$

is finite. The Sobolev space $H^s$ is equipped with the norm $\Vert u \Vert _{H^s} = \Vert {\widehat{u}}(k) \Vert _{L^2_s}$. This norm coincides with the usual Sobolev norm for $s \in {\mathbb {N}}_0$.

Possibly different constants are denoted with the same symbol C if they can be chosen independently of the small perturbation parameter $0 < \varepsilon \ll 1$.

2 Some Heuristics

In this section we explain why variants of the dispersion management equation can be expected to occur as effective modulation equations in the time-periodic case. Already in this section it will be clear that for periods $2 L = {\mathcal {O}}(1)$ no dispersion management equation can occur as modulation equation and that autonomous modulation equations, such as the NLS equation, will appear in a natural way.

2.1 The Time-Oscillatory Modulation Equation

One way to come from (1), with step functions $\alpha _j = \alpha _j(t)$, to a time-oscillatory modulation equation is as follows. For each of the two intervals we make the usual multiple scaling NLS ansatz as before, namely

$$\begin{aligned} u(x,t) \approx \varepsilon \psi _{\varepsilon }(x,t) = \varepsilon A(X,T) E(x,t) + c.c. + {\mathcal {O}}(\varepsilon ^3), \end{aligned}$$

(6)

but now with step functions $c(t), \omega _0(t) \in {{\mathbb {R}}}$ defining the carrier wave $E(x,t) = e^{i (k_0 x + \omega _0(t) t)}$, and the slow spatial variable $X=\varepsilon (x+c(t) t)$. Inserting the ansatz $\varepsilon \psi _{\varepsilon }$ into (1) gives now the conditions

$$\begin{aligned} \omega _{0;n}^2= & {} \alpha _{1;n} k_0^2 - \alpha _{2;n} k_0^2 \omega _{0;n}^2 + \alpha _{3;n}, \end{aligned}$$

(7)

$$\begin{aligned} c_{;n}= & {} \frac{\mathrm{d}\omega _{0;n}}{\mathrm{d}k}|_{k=k_0} = \frac{\alpha _{1;n} k_0 - \alpha _{2;n} \omega _{0;n}^2 k_0}{(1+\alpha _{2;n} k_0^2)\omega _{0;n}}, \end{aligned}$$

(8)

and that A satisfies in lowest order the non-autonomous NLS equation

$$\begin{aligned} i \nu _{0} \partial _T A = \nu _{1} \partial _X^2 A + 3 \nu _{2} A | A|^2, \end{aligned}$$

(9)

with 2L-periodic coefficient functions $\nu _j(t) = \nu _j (T/\varepsilon ^2 )$, where

$$\begin{aligned} \nu _{0;n} = 2 \omega _{0;n} + 2 \alpha _{2;n} k_0^2 \omega _{0;n}, \quad \nu _{1;n} = (\alpha _{1;n}- c_{;n}^2 + \alpha _{2;n} \omega _{0;n}^2), \quad \text {and} \quad \nu _{2;n} = \alpha _{4;n}. \end{aligned}$$

For every $t \in [nL,(n+1)L)$, with $n \in {{\mathbb {N}}}$, the modulation equation (9) is an NLS equation with constant coefficients. In Antonelli et al. (2013) local and global well-posedness results and the possibility of finite time blow-up in Sobolev spaces has been established. At the jump points $t = nL$, with $n \in {{\mathbb {N}}}$, there is continuity in time such that (9) is a well-defined dynamical system. However, as we will see in Sect. 7 we not only have to approximate the original system in the interior of the intervals $(nL,(n+1)L)$, but also have to control the handover of the solutions at the jump points.

The question occurs whether (9) with its highly oscillating coefficient functions makes correct predictions about the dynamics of (1). In order to answer this question positively one has to prove an approximation result in the sense of Theorem 1.2. However, already on a formal level a number of questions occur which we will discuss now.

2.2 The Averaged Modulation Equation

A description by the limit equation (9) is not satisfactory since the coefficient functions $\nu _j$ of (9) are highly oscillating and depend singularly on the small perturbation parameter $0 < \varepsilon \ll 1$.

In order to obtain a limit equation which is independent of $0 < \varepsilon \ll 1$ we write (4) as

$$\begin{aligned} i \partial _T A = \mu _0 \partial _X^2 A + \mu _1 A |A|^2, \end{aligned}$$

(10)

with the 2L-periodic coefficient functions $\mu _j = \mu _j(T/\varepsilon ^2)= \mu _j(t)$, where $\mu _{0;n} = \nu _{1;n}/\nu _{0;n}$ and $\mu _{1;n} = \nu _{2;n}/\nu _{0;n}$. Because of the highly oscillating coefficient functions $\mu _j$ it can be expected that the effective dynamics of (4) can be described by the averaged equation

$$\begin{aligned} i \partial _T A_{av} = \langle \mu _0 \rangle \partial _X^2 A_{av} + \langle \mu _1 \rangle A_{av} |A_{av}|^2, \end{aligned}$$

(11)

where $\langle \mu _j\rangle = \frac{1}{2} (\mu _{j;1}+\mu _{j;2})$. In Antonelli et al. (2013) the scaling limit of fast dispersion management has been considered and the convergence of the solutions of (10) towards the solutions of (11) has been established for time-independent $\mu _1$. Again the question occurs whether for (11) an approximation result in the sense of Theorem 1.2 can be proven.

2.3 The Vanishing Mean Dispersion Case

The case of a vanishing averaged dispersion coefficient $\langle \mu _0 \rangle$ is of particular interest since it is the physically desired situation. For the description of the effective dynamics we then make the modified ansatz

$$\begin{aligned} u(x,t) \approx \varepsilon \psi _{\varepsilon }(x,t) = \varepsilon A(\xi ,T) E(x,t)+ c.c. + {\mathcal {O}}(\varepsilon ^3), \end{aligned}$$

(12)

still with the slow time variable $T=\varepsilon ^2 t$, but now with the slow spatial variable $\xi =\varepsilon ^{\theta }(x+c(t) t)$ with $\theta$ suitably chosen below.

We proceed as above. Again at $\varepsilon E$ we find the linear dispersion relation and $\varepsilon ^{1+\theta } E$ determines the linear group velocity c. At $\varepsilon ^3 E$ we find that the modulation A satisfies in lowest order the non-autonomous modulation equation

$$\begin{aligned} i (\nu _{0} + i \varepsilon ^{\theta } \nu _{3} \partial _{\xi })\partial _T A = \nu _{1} \varepsilon ^{2\theta -2} \partial _\xi ^2 A + 3 \nu _{2} A | A|^2, \end{aligned}$$

(13)

with coefficient functions $\nu _{0}$, $\nu _{1}$, and $\nu _2$ as above, and 2L-periodic coefficient function $\nu _3 = \nu _3(t)$ with

$$\begin{aligned} \nu _{3;n} = - 2 c_{;n} - 4 \alpha _{2;n} k_0 \omega _{0;n} . \end{aligned}$$

At a first view it seems that various orders w.r.t. $\varepsilon$ have been mixed up but we kept the higher-order term $\varepsilon ^{\theta } \nu _{3} \partial _{\xi }\partial _T A$ on the left-hand side to compensate below the lower order term $\nu _{1} \varepsilon ^{2\theta -2} \partial _\xi ^2 A$ on the right-hand side. As before the coefficient functions $\nu _j$ in (13) depend periodically on the fast time variable $t=T/\varepsilon ^2$. Inverting formally the operator on the right-hand side by

$$\begin{aligned} (\nu _{0;n} + i \varepsilon ^{\theta } \nu _{3;n} \partial _\xi )^{-1}= \nu _{0;n}^{-1} - i \varepsilon ^{\theta } \nu _{0;n}^{-2} \nu _{3;n} \partial _\xi + {\mathcal {O}}(\varepsilon ^{2\theta } ) \end{aligned}$$

yields formally

$$\begin{aligned} i \partial _T A = \mu _0 \varepsilon ^{2\theta -2} \partial _\xi ^2 A + i \mu _3 \varepsilon ^{3\theta -2} \partial _\xi ^3 A + \mu _1 A |A|^2, \end{aligned}$$

(14)

with 2L-periodic coefficient functions $\mu _0 = \mu _0(t)$ and $\mu _1= \mu _1(t)$ as above, and the 2L-periodic coefficient function $\mu _3= \mu _3(t)$ with $\mu _{3;n} = \nu _{0;n}^{-2} \nu _{3;n} \nu _{1;n}$. In (14) we ignored terms of order ${\mathcal {O}}(\varepsilon ^{\min (\theta ,4 \theta -2, 1)} )$ and higher. The choice $\theta = 1$ has been considered above in Sects. 2.1 and 2.2 and leads to a degenerated equation for vanishing mean dispersion.

Remark 2.1

The higher-order term $+ i \mu _3 \varepsilon ^{3\theta -2} \partial _\xi ^3 A$ in (14) is smaller than ${\mathcal {O}}(1)$ if $\theta > \frac{2}{3}$ and then can be ignored. The term

$$\begin{aligned}\varepsilon ^{2\theta -2} \mu _0(t) \partial _\xi ^2 A = \varepsilon ^{2\theta -2} \mu _0(\varepsilon ^{-2}T) \partial _\xi ^2 A = \varepsilon ^{2\theta -2} {\widetilde{\mu }}_0(\varepsilon ^{2\theta -2}T) \partial _\xi ^2 A \end{aligned}$$

has a prefactor going to infinity if $\theta < 1$. Hence, in case of step functions $\alpha _j = \alpha _j(t) = {\widetilde{\alpha }}_j(\varepsilon ^{2\theta } t)$, with ${\widetilde{\alpha }}_j(\tau ) = {\widetilde{\alpha }}_j(\tau + 2 \pi )$, the scaling as it appears in the dispersion management equation (5) appears with ${\widetilde{\varepsilon }} = \varepsilon ^{2- 2 \theta }$ for $\frac{2}{3}< \theta < 1$ and the periodicity $L = {\mathcal {O}}(\varepsilon ^{-2 \theta })$. This situation will be discussed below in Sect. 7.

In case $\theta = 2/3$ the higher-order linear dispersive term $+ i \mu _3 \varepsilon ^{3\theta -2} \partial _\xi ^3 A$ is of the same order as the nonlinear term $+ \mu _1 A |A|^2$ and appears in the effective modulation equation, cf. Kunze et al. (2005). The modulation equation (14) is then given by

$$\begin{aligned} i \partial _T A = \mu _0 \varepsilon ^{-2/3} \partial _\xi ^2 A + i \mu _3 \partial _\xi ^3 A + \mu _1 A |A|^2. \end{aligned}$$

(15)

In order to have three terms on the right-hand side of the averaged equation of the same order, we assume the following scaling property of the averaged dispersion coefficient $\langle \mu _0\rangle$: There exist a $\mu ^*_0$ and a $C > 0$, which are both independent of $0 < \varepsilon \ll 1$, such that

$$\begin{aligned} | \langle \mu _0 \varepsilon ^{-2/3}\rangle - \mu ^*_0 |= |\frac{1}{2L} \int _0^{2L} \mu _0(t) \varepsilon ^{-2/3} \mathrm{d}t - \mu ^*_0 | \le C \varepsilon ^{2/3} , \end{aligned}$$

(16)

where at this point a rate o(1) on the right-hand side is sufficient. The rate $\varepsilon ^{2/3}$ is chosen to simplify the notation subsequently in Sect. 5.5. As above, it can be expected that the effective dynamics of (14) can be described by the averaged equation

$$\begin{aligned} i \partial _T A_{av} =\mu ^*_0 \partial _\xi ^2 A_{av} + i \langle \mu _3 \rangle \partial _\xi ^3 A_{av} + \langle \mu _1 \rangle A_{av} |A_{av}|^2, \end{aligned}$$

(17)

where $\langle \mu _j\rangle = \frac{1}{2} (\mu _{j;1}+\mu _{j;2})$. Again the question occurs whether for (14) and (17) an approximation result in the sense of Theorem 1.2 can be proven.

3 The Fourier–Floquet Transformed System

Now we change from heuristic to mathematical arguments. In case of comparable wave lengths of light and of fiber periodicity, i.e. $L = {\mathcal {O}}(1)$, we use linear Floquet theory to transfer (1) into a system with autonomous linear part. The resulting system will be the basis of our subsequent analysis.

In the introductory Sect. 1 we considered (1) with step functions $\alpha _j$ in order to simplify our heuristic explanations. For the subsequent analysis we consider smooth periodic functions $\alpha _j$ in (1) in place of (2). This is justified by the fact that all phenomena which we would like to address already appear in smooth systems.

The Fourier transform of (1) w.r.t. x is given by

$$\begin{aligned} \partial ^{2}_{t}{\widehat{u}}(k,t)=-\alpha _{1}k^{2}{\widehat{u}}(k,t)-\alpha _{2}k^{2}\partial ^{2}_{t}{\widehat{u}}(k,t)-\alpha _{3}{\widehat{u}}(k,t)+\alpha _{4}{\widehat{u}}^{*3}(k,t), \end{aligned}$$

(18)

where ${\widehat{u}}^{*3} = {\widehat{u}} *{\widehat{u}} *{\widehat{u}}$ stands for the two-times convolution. Thus, (18) can be written as

$$\begin{aligned} \partial ^{2}_{t}{\widehat{u}}=-{\widehat{\omega }} ^{2}{\widehat{u}}+{\widehat{\rho }} {\widehat{u}}^{*3}, \end{aligned}$$

(19)

with

$$\begin{aligned} {\widehat{\omega }}(k) ^{2}=\frac{\alpha _{3}+ \alpha _{1}k^{2}}{1 + \alpha _{2}k^{2}} \qquad \text {and} \qquad {\widehat{\rho }}(k) =\dfrac{\alpha _{4}}{1+\alpha _{2}k^{2}} . \end{aligned}$$

(20)

In the following we develop our theory for systems of the form (19) with 2L-time periodic coefficient functions ${\widehat{\omega }} = {\widehat{\omega }}(k,t)$ and ${\widehat{\rho }} = {\widehat{\rho }}(k,t)$, whose properties will be specified below. For notational simplicity we choose $L = \pi$ in the following.

We use Floquet theory in order to discuss the dynamics of this time-periodic system. In the following we assume smoothness of ${\widehat{\omega }}$ w.r.t. t and that ${\widehat{\omega }} \ne 0$. Then, we write (19) as a first-order system and introduce ${\widehat{v}}$ by $\partial _{t}{\widehat{u}} = i {\widehat{\omega }} {\widehat{v}}$. This implies $\partial _{t}^2{\widehat{u}} = i (\partial _{t}{\widehat{\omega }}) {\widehat{v}} + i {\widehat{\omega }} \partial _t {\widehat{v}},$ and so

$$\begin{aligned} \partial _{t}{\widehat{v}} = i {\widehat{\omega }} {\widehat{u}}- \frac{1}{{\widehat{\omega }}} (\partial _{t}{\widehat{\omega }}) {\widehat{v}} + \frac{1}{i {\widehat{\omega }}} {\widehat{\rho }} {\widehat{u}}^{*3}. \end{aligned}$$

This resulting system is abbreviated as

$$\begin{aligned} \partial _t {\widehat{U}}(k,t) = {\widehat{{\mathcal {L}}}}(k,t) {\widehat{U}} (k,t) + {\widehat{{\mathcal {N}}}}_3({\widehat{U}}) (k,t), \end{aligned}$$

where

$$\begin{aligned} {\widehat{{\mathcal {L}}}} = \left( \begin{array}{cc} 0 &{} i {\widehat{\omega }} \\ i {\widehat{\omega }} &{} - \frac{1}{{\widehat{\omega }}} (\partial _{t}{\widehat{\omega }}) \end{array} \right) \qquad \text {and}\qquad {\widehat{{\mathcal {N}}}}_3({\widehat{U}}) = \left( \begin{array}{c} 0 \\ \frac{1}{i {\widehat{\omega }}} {\widehat{\rho }} {\widehat{u}}^{*3}\end{array} \right) . \end{aligned}$$

Using the Floquet’s theorem, cf. Verhulst (1996, Theorem 6.5), for each $k \in {\mathbb {R}}$ the solutions of the linear system

$$\begin{aligned} \partial _t {\widehat{U}}(k,t) = {\widehat{{\mathcal {L}}}}(k,t) {\widehat{U}} (k,t) ,\end{aligned}$$

with ${\widehat{{\mathcal {L}}}}(k,t) = {\widehat{{\mathcal {L}}}}(k,t+2\pi )$, can be written as

$$\begin{aligned} {\widehat{U}}(k,t) = {\widehat{P}}(k,t) e^{ {\widehat{{\mathcal {M}}}}(k)t} {\widehat{U}}(k,0), \end{aligned}$$

with invertible ${\widehat{P}}(k,t) \in {{\mathbb {C}}}^{2 \times 2}$ such that ${\widehat{P}}(k,t) ={\widehat{P}}(k,t+2\pi )$ satisfying $\partial _t {\widehat{P}} + {\widehat{P}} {\widehat{{\mathcal {M}}}} = {\widehat{{\mathcal {L}}}} {\widehat{P}}$, and with time-independent matrix ${\widehat{{\mathcal {M}}}}(k) \in {{\mathbb {C}}}^{2 \times 2}$. With the help of the transformation ${\widehat{U}}(k,t) = {\widehat{P}}(k,t) {\widehat{V}}(k,t)$ we obtain the system

$$\begin{aligned} \partial _t {\widehat{V}}(k,t) = {\widehat{{\mathcal {M}}}}(k) {\widehat{V}}(k,t) +{\widehat{P}}^{-1}(k,t) {\widehat{{\mathcal {N}}}}_3({\widehat{P}}(\cdot ,t) {\widehat{V}}(\cdot ,t))(k,t). \end{aligned}$$

The linear part of this system is now autonomous and can be diagonalized (or brought into its Jordan normal form) with ${\widehat{V}}(k,t) = {\widehat{S}}(k) {\widehat{W}}(k,t)$ and ${\widehat{S}}(k) \in {{\mathbb {C}}}^{2 \times 2}$ suitably chosen. For $W = (W_1,W_{-1})$ we find

$$\begin{aligned} \partial _t {W}(x,t) = {\Lambda } {W}(x,t) + {G}({W},{W},{W})(x,t) \end{aligned}$$

(21)

in physical space or

$$\begin{aligned} \partial _t {\widehat{W}}(k,t) = {\widehat{\Lambda }}(k) {\widehat{W}}(k,t) + {\widehat{G}}({\widehat{W}},{\widehat{W}},{\widehat{W}})(k,t) \end{aligned}$$

(22)

in Fourier space, with ${\widehat{\Lambda }}(k)$ a diagonal matrix in case that ${\widehat{{\mathcal {M}}}}$ can be diagonalized.

The nonlinearity ${\widehat{G}}$ is defined through its components²

$$\begin{aligned} ({\widehat{G}}({\widehat{W}},{\widehat{W}},{\widehat{W}})(k,t))_j= & {} ({\widehat{S}}^{-1}(k) {\widehat{P}}^{-1}(k,t) {\widehat{N}}_3({\widehat{P}}(\cdot ,t) {\widehat{S}}(\cdot ) {\widehat{W}}(\cdot ,t))(k,t))_j \\= & {} \sum _{j_1,j_2,j_3=-1,1} \int _{-\infty }^{\infty } \int _{-\infty }^{\infty } i {\widehat{g}}^j_{j_1 ,j_2, j_3}(k,k-l,l-m,m,t) \\&\quad \times {\widehat{W}}_{j_1}(k-l,t) {\widehat{W}}_{j_2}(l-m,t) {\widehat{W}}_{j_3}(m,t) \mathrm{d}m \mathrm{d}l, \end{aligned}$$

for $j = -1,1$. The kernel ${\widehat{g}}^j_{j_1, j_2, j_3}(k,k-l,l-m,m,t) \in {\mathbb {R}}$ is symmetric w.r.t. interchanging the tuples $(j_1,k-l)$, $(j_2,l-m)$, and $( j_3,m)$. This property will simplify the notation in Sect. 5 subsequently. This system will be the basis for our subsequent analysis. It is of the form of all the other original systems for which the NLS approximation has already been justified, provided that

$$\begin{aligned} {\widehat{\Lambda }}(k) = \mathrm {diag}(i{\widehat{\omega }}_b(k) , -i{\widehat{\omega }}_{b}(k)), \end{aligned}$$

for some $i {\widehat{\omega }}_b(k) \in i {{\mathbb {R}}}$ and provided the resonances coming from the time-periodicity of the nonlinear terms can be controlled. What is meant by this will be explained in the next section.

4 Some Preliminary Considerations

Before we derive modulation equations for (21) and later on prove their validity, we make some preliminary considerations about nonlinear resonances and linear instabilities occurring in time-periodic systems.

4.1 Nonlinear Resonances

We explain with a simple example that the time-periodic situation and the autonomous situation are rather different.

Example 4.1

We consider the time-periodic system

$$\begin{aligned} \partial _t^2 u = \partial _x^2 u - u -(1+2 \alpha \cos ( 2 \beta t)) u^3, \end{aligned}$$

(23)

with $\alpha , \beta , t,x,u(x,t) \in {{\mathbb {R}}}$. Inserting the ansatz

$$\begin{aligned} u(x,t) = \varepsilon A( \varepsilon x ,\varepsilon ^2 t) e^{it} + c.c. + {\mathcal {O}}(\varepsilon ^3) \end{aligned}$$

gives

$$\begin{aligned}&\varepsilon ^3 (2 i \partial _T A) e^{it} + {\mathcal {O}}(\varepsilon ^5)+ c.c. \\&\quad = \varepsilon ^3 (\partial _X^2 A) e^{it} - 3 \varepsilon ^3 A|A|^2 e^{it} - \varepsilon ^3 A^3 e^{3it}\\&\qquad - 3 \alpha \varepsilon ^3 {\overline{A}}|A|^2 e^{2i\beta t-it} - \alpha \varepsilon ^3 A^3 e^{2i\beta t+3it} \\&\qquad - 3 \alpha \varepsilon ^3 {\overline{A}}|A|^2 e^{-2i\beta t-it} - \alpha \varepsilon ^3 A^3 e^{-2i\beta t+3it} + {\mathcal {O}}(\varepsilon ^5)+ c.c.. \end{aligned}$$

We obtain the modulation equation for A by equating the coefficient at $\varepsilon ^3 e^{it}$ to zero. If $\beta \ne \pm 1$ the usual NLS equation

$$\begin{aligned} 2 i \partial _T A = \partial _X^2 A - 3 A|A|^2 , \end{aligned}$$

(24)

appears, but in case $\beta = \pm 1$ two of the terms with an $\alpha$ in front are resonant and appear in the modulation equation for A. It reads then

$$\begin{aligned} 2 i \partial _T A = \partial _X^2 A - 3 A|A|^2 - 3 \alpha {\overline{A}}|A|^2 - \alpha A^3. \end{aligned}$$

(25)

With normal form transformations the non-resonant terms can be transformed into higher ${\mathcal {O}}(\varepsilon ^5)$-order terms.

Hence, due to temporal resonances additional nonlinear terms can occur in the modulation equation. Therefore, in order to come to the classical NLS nonlinearity additional non-resonance conditions have to be imposed. However, since our equations do not explicitly depend on x, this problem does not occur for $k_0 > 0$. Hence, w.r.t. to applications in nonlinear optics, where $k_0 > 0$, this problem has an academical character.

4.2 Linear Instabilities

We need that the semigroup generated by the operator $\Lambda$ is uniformly bounded in order to prove bounds for the error made by the NLS approximation, cf. the subsequent Sect. 5. For this we need that the eigenvalues of ${\widehat{\Lambda }}$ are purely imaginary. These eigenvalues are given by the Floquet exponents of the operator ${\widehat{{\mathcal {L}}}}$, respectively of the equation

$$\begin{aligned} \partial ^2_t {\widehat{u}}(k,t) = - {\widehat{\omega }}^2(k,t) {\widehat{u}}(k,t) . \end{aligned}$$

For fixed k such ODEs are well studied in the existing literature. They are studied for instance in the form

$$\begin{aligned} \partial ^2_t {\widehat{u}}(k,t)+(a(k) -2q(k) V(2t)) {\widehat{u}}(k,t) = 0 , \end{aligned}$$

(26)

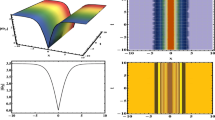
with $V (2 t ) = V (2 t +2 \pi )$. The associated spectral problem is called Hill’s equation. A special example of Hill’s equation is Mathieu’s equation

$$\begin{aligned} \partial ^2_t {\widehat{u}}(k,t)+(a(k)-2q(k) \cos (2t)) {\widehat{u}}(k,t) = 0 \end{aligned}$$

(27)

for which the associated stability picture is plotted in Fig. 2 as a function of a(k) and q(k) . For the Matthieu problem it is well known (Avron and Simon 1981) that the n-th instability gap opens with ${\mathcal {O}}( \delta ^n)$ if $q ={\mathcal {O}}( \delta )$ for $\delta \rightarrow 0$. This means, for a(k) and q(k) in this instability region positive eigenvalues occur. For the Hill problem in general the gaps open with ${\mathcal {O}}( \delta )$, cf. Erdelyi (1934). Thus, in general it cannot be expected that the semigroup generated by $\Lambda$ is uniformly bounded. See Fig. 3. The occurrence of such positive growth rates will prevent the validity of the NLS approximation, cf. the subsequent Sect. 6.

Fig. 2

Stability and instability regions in the (a, q) -plane for Mathieu’s equation (27) alternate. In the regions indicated with ’unstable’, Floquet exponents with positive real part occur, cf. McLachlan (1964)

Fig. 3

For ${\widehat{\omega }}^2(k,t) = 1 +k^2 + 0.25 \cos (2t)+ 0.25 \cos (4t)$ the curves of the imaginary parts of the Floquet exponents $k \mapsto \pm \mathrm {Im}{\widehat{\omega }}_b(k)$ are plotted in blue and the curves of ten times the real parts of the Floquet exponents $k \mapsto \pm 10 \mathrm {Re}{\widehat{\omega }}_b(k)$ are plotted in red (Color figure online)

For time-independent coefficients $\alpha _1 > 0$, $\alpha _2 > 0$, and $\alpha _3 > 0$ no positive growth rates occur, since then ${\widehat{\omega }}(k) ^{2}$ is then given by (20). However, even for small periodic perturbations

$$\begin{aligned} \alpha _j(t) = \alpha _{j,0} + \delta \alpha _{j,per}(t) , \end{aligned}$$

with $\delta > 0$ small, one has to make sure to avoid the instability regions plotted for an example in Fig. 2. Hence, the validity of the NLS approximation can only be expected if a number of assumptions on (21) hold, cf. Sect. 5.2. The assumptions turn out to be sharp in the sense that no approximation property holds if the subsequent Assumptions (ASS1)–(ASS3) do not hold, cf. Sect. 6.

5 Approximation Results

In Sect. 5.1 we derive an NLS equation for (21) which is justified in Sect. 5.4 by proving error estimates for the associated NLS approximation. In order to do so we construct a higher-order approximation in Sect. 5.3 for decreasing the formal error made by this approximation. In Sect. 5.2 we pose a number of assumptions on (21) which allow us to prove the approximation result. Moreover, we check whether these assumptions can be satisfied for (1). In Sect. 5.5 we consider the case ${\widehat{\omega }}_b''(k_0) = 0$ and derive a modulation equation similar to (14). We explain how the approximation proof from Sects. 5.1, 5.2, 5.3 and 5.4 has to be modified for this case.

5.1 Derivation of the NLS Equation

For the derivation of an effective equation in Fourier space we use the NLS ansatz for autonomous systems, although only the linear part of (21) is autonomous. We approximate ${\widehat{W}}_{\pm 1}$ by $\varepsilon {\widehat{\psi }}_{NLS,\pm 1}$ where

$$\begin{aligned} \varepsilon {\widehat{\psi }}_{NLS,1} (k,t)= & {} \varepsilon \varepsilon ^{-1} {\widehat{A}}_1\left( \frac{k-k_0}{\varepsilon },\varepsilon ^2 t \right) e^{i {\widehat{\omega }}_b(k_0) t} e^{i {\widehat{\omega }}'_b(k_0) (k-k_0) t} , \end{aligned}$$

(28)

$$\begin{aligned} \varepsilon {\widehat{\psi }}_{NLS,- 1} (k,t)= & {} \varepsilon \varepsilon ^{-1} {\widehat{A}}_{-1}\left( \frac{k+k_0}{\varepsilon },\varepsilon ^2 t \right) e^{- i {\widehat{\omega }}_b(k_0) t} e^{i {\widehat{\omega }}'_b(k_0) (k+k_0) t}, \end{aligned}$$

(29)

for a $k_0 > 0$, cf. Schneider and Uecker (2017, §11.3). Since ${\widehat{W}}_1$ is then strongly concentrated at the wave number $k_0$ and ${\widehat{W}}_{-1}$ at the wave number $- k_0$ we introduce

$$\begin{aligned} k= k_0 + \varepsilon K, \end{aligned}$$

such that

$$\begin{aligned} {\widehat{\omega }}_b(k) = {\widehat{\omega }}_b(k_0)+ \varepsilon {\widehat{\omega }}_b'(k_0) K + \frac{1}{2} \varepsilon ^2 {\widehat{\omega }}_b''(k_0) K^2 + {\mathcal {O}}(\varepsilon ^3) \end{aligned}$$

and

$$\begin{aligned} {\widehat{g}}^1_{1,1,-1}(k,k-l,l-m,m,t) = {\widehat{g}}^1_{1,1,-1}(k_0,k_0,k_0,-k_0,t) + {\mathcal {O}}(\varepsilon ) , \end{aligned}$$

where we used the expansion $l = \varepsilon L$ and $m = - k_0 + \varepsilon M$ for some $L,M >0$. These point-wise expansions will be transferred into rigorous estimates for the residual terms below. Using this expansion at the wave number $k_0$, in Fourier space we find a cancelation of all terms of order ${\mathcal {O}}(1)$ and of order ${\mathcal {O}}(\varepsilon )$. At ${\mathcal {O}}(\varepsilon ^2) e^{i {\widehat{\omega }}_b(k_0) t}$ and k close to $k_0$ we finally obtain

$$\begin{aligned} \partial _T {\widehat{A}}_1 = \frac{1}{2} i {\widehat{\omega }}''_b(k_0)K^2 {\widehat{A}}_1 + i \gamma {\widehat{A}}_1* {\widehat{A}}_1* {\widehat{A}}_{-1}, \end{aligned}$$

(30)

where $\gamma = 3 {\widehat{g}}^1_{1,1,-1}(k_0,k_0,k_0,-k_0)[0]$ is defined through the Fourier expansion

$$\begin{aligned} {\widehat{g}}^j_{j_1, j_2, j_3} (k,k-l,l-m,m,t) = \sum _{n\in {{\mathbb {Z}}}} {\widehat{g}}^j_{j_1, j_2, j_3} (k,k-l,l-m,m)[n] e^{int} . \end{aligned}$$

We used

$$\begin{aligned}&3 \int \int i {\widehat{g}}^1_{1,1,-1}(k_0,k_0,k_0,-k_0)[0] \\&\qquad \times {\widehat{A}}_1\left( \frac{k-l-k_0}{\varepsilon },\varepsilon ^2 t \right) {\widehat{A}}_1\left( \frac{l-m-k_0}{\varepsilon },\varepsilon ^2 t \right) {\widehat{A}}_{-1}\left( \frac{m+k_0}{\varepsilon },\varepsilon ^2 t \right) \mathrm{d}m \mathrm{d}l \\&= 3 \varepsilon ^2 \int \int {\widehat{g}}^1_{1,1,-1}(k_0,k_0,k_0,-k_0)[0] \\&\qquad \times {\widehat{A}}_1(K-L,T ) {\widehat{A}}_1(L-M,T ) {\widehat{A}}_{-1}(M,T ) \mathrm{d}M \mathrm{d}L \\&= \varepsilon ^2 \gamma {\widehat{A}}_1* {\widehat{A}}_1* {\widehat{A}}_{-1}. \end{aligned}$$

In physical space (30) is given by

$$\begin{aligned} \partial _T {A}_1 = - \frac{1}{2} i {\widehat{\omega }}''_b(k_0)\partial _X^2 {A}_1 + i \gamma |{A}_1|^2 {A}_1 . \end{aligned}$$

(31)

Remark 5.1

In case $k_0 = 0$ additional non-resonance conditions have to be imposed, cf. Example 4.1. Since our original system is real-valued and two-dimensional for fixed $k \in {{\mathbb {R}}}$ we necessarily have ${\widehat{\omega }}'_b(0)=0$. We approximate ${\widehat{W}}_{\pm 1}$ by ${\widehat{\psi }}_{NLS,\pm 1}$ where

$$\begin{aligned} {\widehat{\psi }}_{NLS,\pm 1} (k,t) = \varepsilon \varepsilon ^{-1} {\widehat{A}}_{\pm 1}\left( \frac{k}{\varepsilon },\varepsilon ^2 t \right) e^{\pm i {\widehat{\omega }}_b(k_0) t} . \end{aligned}$$

(32)

We find an NLS equation

$$\begin{aligned} \partial _T {A}_1 = - \frac{1}{2} i {\widehat{\omega }}''_b(0)\partial _X^2 {A}_1 + i \gamma |{A}_1|^2 {A}_1 , \end{aligned}$$

(33)

with $\gamma = 3 {\widehat{g}}^1_{1,1,-1}(0,0,0,0)[0]$, if the non-resonance conditions

$$\begin{aligned} {\widehat{g}}^1_{1,1,-1}(0,0,0,0)[m] \not \in \{2 i \omega _b(0),- 2 i \omega _b(0)\} \end{aligned}$$

are satisfied for all $m \in {{\mathbb {Z}}}$.

5.2 The Linear Assumptions

In order to prove that (30) makes correct predictions about the dynamics of (21), we need a number of estimates for the original system (21). According to our preliminary considerations in Sect. 4.2 we assume

(ASS1) There exists a $C> 0$ such that

$$\begin{aligned} \sup _{t \in {{\mathbb {R}}}} \sup _{k \in {{\mathbb {R}}}} \Vert e^{{\widehat{\Lambda }}(k) t} \Vert _{{{\mathbb {C}}}^2 \rightarrow {{\mathbb {C}}}^2} \le C. \end{aligned}$$

(ASS2) There exists a $C > 0$ such that

$$\begin{aligned} \sup _{t \in [0,2\pi ]} \sup _{k \in {{\mathbb {R}}}}(\Vert {\widehat{P}}(k,t) \Vert _{{{\mathbb {C}}}^2 \rightarrow {{\mathbb {C}}}^2} + \Vert {\widehat{P}}(k,t)^{-1} \Vert _{{{\mathbb {C}}}^2 \rightarrow {{\mathbb {C}}}^2} )\le C. \end{aligned}$$

(ASS3) There exists a $C > 0$ such that

$$\begin{aligned} \sup _{k \in {{\mathbb {R}}}} (\Vert {\widehat{S}}(k) \Vert _{{{\mathbb {C}}}^2 \rightarrow {{\mathbb {C}}}^2} + \Vert {\widehat{S}}(k)^{-1} \Vert _{{{\mathbb {C}}}^2 \rightarrow {{\mathbb {C}}}^2}) \le C. \end{aligned}$$

A direct consequence of the Assumptions (ASS1)–(ASS3) are the following lemmas.

Lemma 5.2

Suppose, (ASS1) holds. Then the operator $\Lambda$ generates a strongly continuous uniformly bounded group $(e^{\Lambda t})_{t \in {{\mathbb {R}}}}$ in every Sobolev space $H^s$ for every $s \ge 0$, given by $e^{\Lambda t} = {\mathcal {F}}^{-1} {e^{{\widehat{\Lambda }} t}} {\mathcal {F}}$. For all $s \ge 0$ there exists a $C_{\Lambda } > 0$ such that

$$\begin{aligned} \sup _{t \in {{\mathbb {R}}}} \Vert e^{\Lambda t} \Vert _{H^s \rightarrow H^s} \le C_{\Lambda } . \end{aligned}$$

Lemma 5.3

Let $P = {\mathcal {F}}^{-1} {\widehat{P}} {\mathcal {F}}$ and suppose, (ASS2) holds. Then for all $s \ge 0$ there exists a $C > 0$ such that

$$\begin{aligned} \sup _{t \in [0,2\pi ]} (\Vert P(t) \Vert _{H^s \rightarrow H^s} + \Vert P(t)^{-1} \Vert _{H^s \rightarrow H^s} ) \le C. \end{aligned}$$

Lemma 5.4

Let $S = {\mathcal {F}}^{-1} {\widehat{S}} {\mathcal {F}}$ and suppose, (ASS3) holds. Then for all $s \ge 0$ there exists a $C > 0$ such that

$$\begin{aligned} \Vert S \Vert _{H^s \rightarrow H^s} + \Vert S^{-1} \Vert _{H^s \rightarrow H^s} \le C. \end{aligned}$$

The assumptions (ASS1)–(ASS3) can easily be satisfied in case of time-independent coefficients $\alpha _1 > 0$, $\alpha _2 > 0$, and $\alpha _3 > 0$. There we have

$$\begin{aligned} {\widehat{\omega }}_b^2(k) = \frac{\alpha _{3} + \alpha _{1} k^2 }{1+ \alpha _{2} k^2}, \quad {\widehat{S}}(k) = \frac{1}{2}\left( \begin{array}{cc} 1 &{} 1 \\ -1 &{} 1 \end{array} \right) , \quad {\widehat{P}}(k,t) = \left( \begin{array}{cc} 1 &{} 0 \\ 0 &{} 1 \end{array} \right) . \end{aligned}$$

However, even for small periodic perturbations

$$\begin{aligned} \alpha _j(t) = \alpha _{j,0} + \delta \alpha _{j,per}(t) , \end{aligned}$$

with $\delta > 0$ small, one has to make sure to avoid the instability regions plotted for instance in Fig. 2 centered at $n^2$ for $n \in {{\mathbb {N}}}_0$. Hence, for $\delta > 0$ a uniformly bounded semigroup only occurs, if the spectrum $\cup _{k \in {{\mathbb {R}}}} {\widehat{\omega }}_b^2(k)$ is disjoint from the resonant wave numbers $n^2$ for $n \in {{\mathbb {N}}}_0$ at $\delta = 0$. For (1) this can be achieved by classical perturbation theory by a suitable choice of $\alpha _{1,0}$, $\alpha _{2,0}$, and $\alpha _{3,0}$ since $\lim _{|k| \rightarrow \infty } {\widehat{\omega }}_b^2(k)$ exists for $\alpha _{2,0} > 0$. What happens, if this assumption is not satisfied, will be discussed in Sect. 6.

5.3 Estimates for the Residual

In order to prove an approximation result for (30) we need that the residual

$$\begin{aligned} \widehat{Res_W(W)}(k,t) = - \partial _t {\widehat{W}}(k,t) +{\widehat{\Lambda }}(k) {\widehat{W}}(k,t) + {\widehat{G}}({\widehat{W}},{\widehat{W}},{\widehat{W}})(k,t), \end{aligned}$$

i.e., the terms which do not cancel after inserting the approximation in (21), are formally of order ${\mathcal {O}}(\varepsilon ^3)$ in Fourier space. By nonlinear interaction of ${\widehat{\psi }}_{NLS,\pm 1}$ through ${\widehat{G}}$ terms of formal order ${\mathcal {O}}(\varepsilon ^2)$ in Fourier space are created which remain in the residual although $A_1$ is chosen to satisfy the NLS equation, cf. the subsequent terms $s_{1,1}$ and $s_{-1,-1}$. In the ${\widehat{W}}_1$-equation, multiplied by $e^{- i {\widehat{\omega }}_b(k_0) t} e^{-i {\widehat{\omega }}'_b(k_0) (k-k_0) t}$, these are

$$\begin{aligned} s_{1,3}= & {} e^{- i {\widehat{\omega }}_b\left( k_0\right) t} \int \int \sum _{n \in {{\mathbb {Z}}}} i {\widehat{g}}^1_{1,1,1}\left( k,k-l,l-m,m\right) [n] e^{int}\\&\times {\widehat{A}}_1\left( \frac{k-l-k_0}{\varepsilon },\varepsilon ^2 t \right) {\widehat{A}}_1\left( \frac{l-m-k_0}{\varepsilon },\varepsilon ^2 t \right) \\&\quad {\widehat{A}}_{1}\left( \frac{m-k_0}{\varepsilon },\varepsilon ^2 t \right) \mathrm{d}m \mathrm{d}l e^{3 i {\widehat{\omega }}_b\left( k_0\right) t} , \\ s_{1,1}= & {} 3 e^{ -i {\widehat{\omega }}_b\left( k_0\right) t }\int \int \sum _{n \in {{\mathbb {Z}}}\setminus \{0\}} i {\widehat{g}}^1_{1,1,-1}\left( k,k-l,l-m,m\right) [n] e^{int} \\&\times {\widehat{A}}_1\left( \frac{k-l-k_0}{\varepsilon },\varepsilon ^2 t \right) {\widehat{A}}_{1}\left( \frac{l-m-k_0}{\varepsilon },\varepsilon ^2 t \right) \\&\quad {\widehat{A}}_{-1}\left( \frac{m+k_0}{\varepsilon },\varepsilon ^2 t \right) \mathrm{d}m \mathrm{d}l e^{ i {\widehat{\omega }}_b\left( k_0\right) t} , \\ s_{1,-1}= & {} 3 e^{ -i {\widehat{\omega }}_b\left( k_0\right) t }\int \int \sum _{n \in {{\mathbb {Z}}}} i {\widehat{g}}^1_{1,-1,-1}\left( k,k-l,l-m,m\right) [n] e^{int} \\&\times {\widehat{A}}_1\left( \frac{k-l-k_0}{\varepsilon },\varepsilon ^2 t \right) {\widehat{A}}_{-1}\left( \frac{l-m+k_0}{\varepsilon },\varepsilon ^2 t \right) \\&\quad {\widehat{A}}_{-1}\left( \frac{m+k_0}{\varepsilon },\varepsilon ^2 t \right) \mathrm{d}m \mathrm{d}l e^{- i {\widehat{\omega }}_b\left( k_0\right) t} , \\ s_{1,-3}= & {} e^{- i {\widehat{\omega }}_b\left( k_0\right) t} \int \int \sum _{n \in {{\mathbb {Z}}}}i {\widehat{g}}^1_{-1,-1,-1}\left( k,k-l,l-m,m\right) [n] e^{int} \\&\times {\widehat{A}}_{-1}\left( \frac{k-l+k_0}{\varepsilon },\varepsilon ^2 t \right) {\widehat{A}}_{-1}\left( \frac{l-m+k_0}{\varepsilon },\varepsilon ^2 t \right) \\&\quad {\widehat{A}}_{-1}\left( \frac{m+k_0}{\varepsilon },\varepsilon ^2 t \right) \mathrm{d}m \mathrm{d}l e^{-3 i {\widehat{\omega }}_b\left( k_0\right) t}. \end{aligned}$$

In the ${\widehat{W}}_{-1}$-equation, multiplied by $e^{i {\widehat{\omega }}_b\left( k_0\right) t} e^{-i {\widehat{\omega }}'_b\left( k_0\right) \left( k-k_0\right) t}$, these are

$$\begin{aligned} s_{-1,3}= & {} e^{ i {\widehat{\omega }}_b\left( k_0\right) t}\int \int \sum _{n \in {{\mathbb {Z}}}} i {\widehat{g}}^{-1}_{1,1,1}\left( k,k-l,l-m,m\right) [n] e^{int} \\&\times {\widehat{A}}_1\left( \frac{k-l-k_0}{\varepsilon },\varepsilon ^2 t \right) {\widehat{A}}_1\left( \frac{l-m-k_0}{\varepsilon },\varepsilon ^2 t \right) \\&\quad {\widehat{A}}_{1}\left( \frac{m-k_0}{\varepsilon },\varepsilon ^2 t \right) \mathrm{d}m \mathrm{d}l e^{3 i {\widehat{\omega }}_b\left( k_0\right) t} , \\ s_{-1,1}= & {} 3 e^{ i {\widehat{\omega }}_b\left( k_0\right) t} \int \int \sum _{n \in {{\mathbb {Z}}}}i {\widehat{g}}^{-1}_{1,1,-1}\left( k,k-l,l-m,m\right) [n] e^{int} \\&\times {\widehat{A}}_1\left( \frac{k-l-k_0}{\varepsilon },\varepsilon ^2 t \right) {\widehat{A}}_{1}\left( \frac{l-m-k_0}{\varepsilon },\varepsilon ^2 t \right) \\&\quad {\widehat{A}}_{-1}\left( \frac{m+k_0}{\varepsilon },\varepsilon ^2 t \right) \mathrm{d}m \mathrm{d}l e^{ i {\widehat{\omega }}_b\left( k_0\right) t} , \\ s_{-1,-1}= & {} 3 e^{ i {\widehat{\omega }}_b\left( k_0\right) t} \int \int \sum _{n \in {{\mathbb {Z}}}\setminus \{0\}}i {\widehat{g}}^{-1}_{1,-1,-1}\left( k,k-l,l-m,m\right) [n] e^{int} \\&\times {\widehat{A}}_1\left( \frac{k-l-k_0}{\varepsilon },\varepsilon ^2 t \right) {\widehat{A}}_{-1}\left( \frac{l-m+k_0}{\varepsilon },\varepsilon ^2 t \right) \\&\quad {\widehat{A}}_{-1}\left( \frac{m+k_0}{\varepsilon },\varepsilon ^2 t \right) \mathrm{d}m \mathrm{d}l e^{ -i {\widehat{\omega }}_b\left( k_0\right) t} , \\ s_{-1,-3}= & {} e^{ i {\widehat{\omega }}_b\left( k_0\right) t} \int \int \sum _{n \in {{\mathbb {Z}}}}i {\widehat{g}}^{-1}_{-1,-1,-1}\left( k,k-l,l-m,m\right) [n] e^{int} \\&\times {\widehat{A}}_{-1}\left( \frac{k-l+k_0}{\varepsilon },\varepsilon ^2 t \right) {\widehat{A}}_{-1}\left( \frac{l-m+k_0}{\varepsilon },\varepsilon ^2 t \right) \\&\quad {\widehat{A}}_{-1}\left( \frac{m+k_0}{\varepsilon },\varepsilon ^2 t \right) \mathrm{d}m \mathrm{d}l e^{-3 i {\widehat{\omega }}_b\left( k_0\right) t}. \end{aligned}$$

In order to get rid of these terms we could add higher-order terms to the NLS approximation ${\widehat{\psi }}_{NLS,\pm 1}$ or, what we will do here, eliminate them by a near identity change of variables. Before we do so we modify ${\widehat{\psi }}_{NLS,\pm 1}$ by some cut-off function in Fourier space. We set

$$\begin{aligned} {\widehat{\psi }}_{\chi ,1} \left( k,t\right)= & {} {\widehat{\psi }}_{NLS,1} \left( k,t\right) \chi _{\delta }\left( k-k_0\right) ,\\ {\widehat{\psi }}_{\chi ,-1}\left( k,t\right)= & {} {\widehat{\psi }}_{NLS,-1} \left( k,t\right) \chi _{\delta }\left( k+k_0\right) , \end{aligned}$$

with $\delta > 0$ small, but independent of $0 < \varepsilon \ll 1$ and where $\chi _{\delta } \in C_0^{\infty }$ satisfies

$$\begin{aligned} \chi _{\delta }\left( k\right) = \left\{ \begin{array}{ll} 1, &{}\quad \text {for } |k| \le \delta , \\ \in [0,1], &{}\quad \text {for } \delta< |k| < 2 \delta , \\ 0 , &{}\quad \text {for } |k| \ge 2 \delta . \end{array} \right. \end{aligned}$$

For ${\widehat{A}}_1 \in L^2_s$ we have

$$\begin{aligned} \Vert {\psi }_{\chi ,\pm 1} \left( \cdot ,t\right) -{\psi }_{NLS,\pm 1} \left( \cdot ,t\right) \Vert _{C^0_b} \le C \varepsilon ^{s+1/2}, \end{aligned}$$

cf. Schneider and Uecker (2017, Lemma 11.5.1). Hence, ${\widehat{\psi }}_{\chi ,\pm 1}$ is close to ${\widehat{\psi }}_{NLS,\pm 1}$, and has the advantage that in the subsequent calculations only a small set of wave numbers has to be considered.

By nonlinear interaction of ${\widehat{\psi }}_{\chi ,\pm 1}$ through ${\widehat{G}}$, which is mainly a two-times convolution of ${\widehat{\psi }}_{\chi ,\pm 1}$, terms of formal order ${\mathcal {O}}(\varepsilon ^2)$ are created in Fourier space which are located in four neighborhoods of length $6 \delta$ centered in $k \in \{ - 3 k_0,-k_0,k_0, 3 k_0 \}$.³ In order to eliminate the oscillatory parts of these terms we make, as already said, a near identity change of variables in

$$\begin{aligned} \partial _t {\widehat{W}}(k,t) = {\widehat{\Lambda }}(k) {\widehat{W}}(k,t) + {\widehat{G}}({\widehat{W}},{\widehat{W}},{\widehat{W}})(k,t). \end{aligned}$$

(34)

We set

$$\begin{aligned} {\widehat{Z}} (k,t) = {\widehat{W}} (k,t) + {\widehat{B}}({\widehat{W}},{\widehat{W}},{\widehat{W}})(k,t), \end{aligned}$$

(35)

with ${\widehat{B}}$ a symmetric trilinear mapping. We find

$$\begin{aligned} \partial _t {\widehat{Z}}= & {} \partial _t {\widehat{W}} + (\partial _t {\widehat{B}})({\widehat{W}},{\widehat{W}},{\widehat{W}},t) \\&+\, {\widehat{B}}(\partial _t {\widehat{W}},{\widehat{W}},{\widehat{W}},t) + {\widehat{B}}({\widehat{W}},\partial _t {\widehat{W}},{\widehat{W}},t) + {\widehat{B}}({\widehat{W}},{\widehat{W}},\partial _t {\widehat{W}},t) \\= & {} {\widehat{\Lambda }} {\widehat{W}} + {\widehat{G}}({\widehat{W}},{\widehat{W}},{\widehat{W}},t)+ (\partial _t {\widehat{B}})({\widehat{W}},{\widehat{W}},{\widehat{W}},t) \\&+\, {\widehat{B}}(\partial _t {\widehat{W}},{\widehat{W}},{\widehat{W}},t) + {\widehat{B}}({\widehat{W}},\partial _t {\widehat{W}},{\widehat{W}},t) + {\widehat{B}}({\widehat{W}},{\widehat{W}},\partial _t {\widehat{W}},t)\\= & {} {\widehat{\Lambda }} {\widehat{W}} + {\widehat{G}}({\widehat{W}},{\widehat{W}},{\widehat{W}},t)+ (\partial _t {\widehat{B}})({\widehat{W}},{\widehat{W}},{\widehat{W}},t) \\&+\, {\widehat{B}}( {\widehat{\Lambda }} {\widehat{W}},{\widehat{W}},{\widehat{W}},t) + {\widehat{B}}({\widehat{W}}, {\widehat{\Lambda }} {\widehat{W}},{\widehat{W}},t) + {\widehat{B}}({\widehat{W}},{\widehat{W}}, {\widehat{\Lambda }} {\widehat{W}},t) + {\mathcal {O}}(\Vert {\widehat{W}}\Vert ^5),\\= & {} {\widehat{\Lambda }} {\widehat{Z}} - {\widehat{\Lambda }} {\widehat{B}}({\widehat{Z}},{\widehat{Z}},{\widehat{Z}},t) + {\widehat{G}}({\widehat{Z}},{\widehat{Z}},{\widehat{Z}},t)+ (\partial _t {\widehat{B}})({\widehat{Z}},{\widehat{Z}},{\widehat{Z}},t) \\&+\, {\widehat{B}}({\widehat{\Lambda }} {\widehat{Z}},{\widehat{Z}},{\widehat{Z}},t) + {\widehat{B}}({\widehat{Z}},{\widehat{\Lambda }} {\widehat{Z}},{\widehat{Z}},t) + {\widehat{B}}({\widehat{Z}},{\widehat{Z}},{\widehat{\Lambda }} {\widehat{Z}},t) + {\mathcal {O}}(\Vert {\widehat{Z}}\Vert ^5), \end{aligned}$$

where we used (34) to replace $\partial _t {\widehat{W}}$ and (35), respectively

$$\begin{aligned} {\widehat{W}} (k,t)= & {} {\widehat{Z}} (k,t) - {\widehat{B}}({\widehat{W}},{\widehat{W}},{\widehat{W}})(k,t)\\= & {} {\widehat{Z}} (k,t) - {\widehat{B}}({\widehat{Z}},{\widehat{Z}},{\widehat{Z}})(k,t)+ {\mathcal {O}}(\Vert {\widehat{Z}}\Vert ^5), \end{aligned}$$

to replace ${\widehat{W}}$. We split the nonlinear terms

$$\begin{aligned} {\widehat{G}} = {\widehat{G}}_0 + {\widehat{G}}_r, \end{aligned}$$

where in $G_r$ stands for the terms which can be eliminated and $G_0$ for the terms which cannot be eliminated via B. In order to do so we have to find a B such that

$$\begin{aligned} 0= & {} - {\widehat{\Lambda }} {\widehat{B}}({\widehat{Z}},{\widehat{Z}},{\widehat{Z}},t) + {\widehat{G}}_r({\widehat{Z}},{\widehat{Z}},{\widehat{Z}},t)+ (\partial _t {\widehat{B}})({\widehat{Z}},{\widehat{Z}},{\widehat{Z}},t) \nonumber \\&+\, {\widehat{B}}({\widehat{\Lambda }} {\widehat{Z}},{\widehat{Z}},{\widehat{Z}},t) + {\widehat{B}}({\widehat{Z}},{\widehat{\Lambda }} {\widehat{Z}},{\widehat{Z}},t) + {\widehat{B}}({\widehat{Z}},{\widehat{Z}},{\widehat{\Lambda }} {\widehat{Z}},t) . \end{aligned}$$

(36)

Since

$$\begin{aligned} ({\widehat{G}}({\widehat{Z}},{\widehat{Z}},{\widehat{Z}})(k,t))_j= & {} \sum _{j_1,j_2,j_3=-1,1} \int _{-\infty }^{\infty } \int _{-\infty }^{\infty } i {\widehat{g}}^j_{j_1, j_2, j_3}(k,k-l,l-m,m,t) \\&\qquad \times {\widehat{Z}}_{j_1}(k-l,t) {\widehat{Z}}_{j_2}(l-m,t) {\widehat{Z}}_{j_3}(m,t) \mathrm{d}m \mathrm{d}l, \end{aligned}$$

for $j = -1,1$, with

$$\begin{aligned} {\widehat{g}}^j_{j_1, j_2, j_3} (k,k-l,l-m,m,t) = \sum _{n\in {{\mathbb {Z}}}} {\widehat{g}}^j_{j_1, j_2, j_3} (k,k-l,l-m,m)[n] e^{int} , \end{aligned}$$

we choose

$$\begin{aligned} ({\widehat{B}}({\widehat{Z}},{\widehat{Z}},{\widehat{Z}})(k,t))_j= & {} \sum _{j_1,j_2,j_3=-1,1} \int _{-\infty }^{\infty } \int _{-\infty }^{\infty } i {\widehat{b}}^j_{j_1, j_2, j_3}(k,k-l,l-m,m,t) \\&\qquad \times {\widehat{Z}}_{j_1}(k-l,t) {\widehat{Z}}_{j_2}(l-m,t) {\widehat{Z}}_{j_3}(m,t) \mathrm{d}m \mathrm{d}l, \end{aligned}$$

with

$$\begin{aligned} {\widehat{b}}^j_{j_1, j_2, j_3} (k,k-l,l-m,m,t) = \sum _{n\in {{\mathbb {Z}}}} {\widehat{b}}^j_{j_1, j_2, j_3} (k,k-l,l-m,m)[n] e^{int} . \end{aligned}$$

Inserting this in (36) yields

$$\begin{aligned}&{\widehat{r}}^j_{j_1, j_2, j_3} (k,k-l,l-m,m)[n] \ {\widehat{b}}^j_{j_1, j_2, j_3} (k,k-l,l-m,m)[n] \\&\qquad = {\widehat{g}}^j_{j_1, j_2, j_3}(k,k-l,l-m,m)[n], \end{aligned}$$

with

$$\begin{aligned} {\widehat{r}}^j_{j_1, j_2, j_3} (k,k-l,l-m,m)[n]= & {} -j \omega _b(k) + in + j_1 \omega _b(k-l)+ j_2 \omega _b(l-m) \\&+j_3 \omega _b(m). \end{aligned}$$

Hence, in order to eliminate the terms collected in $G_r$ we need that for the associated indices and wave numbers

$$\begin{aligned} {\widehat{r}}^j_{j_1, j_2, j_3} (k,k-l,l-m,m)[n] \ne 0 . \end{aligned}$$

(37)

Due to our definition of ${\widehat{\psi }}_{\chi ,\pm 1}$ and the purposes of the transformation, namely the elimination of the terms $s_{ij}$, the factors ${\widehat{r}}^j_{j_1 j_2 j_3} (k,k-l,l-m,m)[n]$ have to be non-zero for wave numbers

$$\begin{aligned} |m \pm k_0| \le 2 \delta , \qquad |l-m \pm k_0| \le 2 \delta , \qquad |k-l \pm k_0| \le 2 \delta . \end{aligned}$$

For continuity reasons (37) follows for $\delta > 0$ sufficiently small, but independent of $0 < \varepsilon \ll 1$, if the following non-resonance conditions are satisfied, see again the terms $s_{ij}$ above.

(NON) We assume that $3 i {\widehat{\omega }}_b(k_0) - i {\widehat{\omega }}_b(3 k_0)$, $- i {\widehat{\omega }}_b(k_0) - i {\widehat{\omega }}_b(- k_0)$, $- 3 i {\widehat{\omega }}_b(k_0) - i {\widehat{\omega }}_b(-3 k_0)$, $3 i {\widehat{\omega }}_b(k_0) + i {\widehat{\omega }}_b(3 k_0)$, $i {\widehat{\omega }}_b(k_0) + i {\widehat{\omega }}_b( k_0)$, and $- 3 i {\widehat{\omega }}_b(k_0) + i {\widehat{\omega }}_b(3 k_0)$ are not elements of ${{\mathbb {Z}}}$.

Thus, only finitely many conditions have to be checked. For the transformed system

$$\begin{aligned} \partial _t {\widehat{Z}} = {\widehat{\Lambda }} {\widehat{Z}} + {\widehat{G}}_0({\widehat{Z}},{\widehat{Z}},{\widehat{Z}},t)+ {\mathcal {O}}(\Vert {\widehat{Z}}\Vert ^5). \end{aligned}$$

(38)

and the associated residual $\widehat{Res_Z(Z)}(k,t)$ we have

Lemma 5.5

Assume the validity of the non-resonance condition (NON). Then there exist $\varepsilon _0 > 0$ and $C > 0$ such that for all $\varepsilon \in (0, \varepsilon _0)$ for the approximation $\varepsilon \psi _{\chi }$ we have

$$\begin{aligned} \sup _{t \in [0,T_0/\varepsilon ^2]} \Vert \varepsilon \psi _{\chi } - \varepsilon \psi _{NLS} \Vert _{H^1} \le C \varepsilon ^{5/2} \end{aligned}$$

and

$$\begin{aligned} \sup _{t \in [0,T_0/\varepsilon ^2]} \Vert Res_Z(\varepsilon \psi _{\chi }) \Vert _{L^2} \le C \varepsilon ^{7/2} \end{aligned}$$

Next we define $\psi _W$ through the solution of

$$\begin{aligned} \widehat{\psi _{\chi }} (k,t) = \widehat{\psi _W} (k,t) + {\widehat{B}}(\widehat{\psi _W},\widehat{\psi _W},\widehat{\psi _W})(k,t). \end{aligned}$$

Then we have

Corollary 5.6

Assume the validity of the non-resonance condition (NON). Then there exist $\varepsilon _0 > 0$ and $C > 0$ such that for all $\varepsilon \in (0, \varepsilon _0)$ the approximation $\varepsilon \psi _W$ satisfies

$$\begin{aligned} \sup _{t \in [0,T_0/\varepsilon ^2]} \Vert \varepsilon \psi _W - \varepsilon \psi _{NLS} \Vert _{H^1} \le C \varepsilon ^{5/2} \end{aligned}$$

and

$$\begin{aligned} \sup _{t \in [0,T_0/\varepsilon ^2]} \Vert Res(\varepsilon \psi _W) \Vert _{L^2} \le C \varepsilon ^{7/2} \end{aligned}$$

The proof of Lemma 5.5 is standard and can be found at various places, cf. Schneider and Uecker (2017). Therefore, we refrain from giving a complete proof, i.e., from showing all estimates. However, for clarity we make a few remarks. We first remark that the scaling properties of the $L^2$-norm w.r.t. $k = \varepsilon K$ leads to a gain of a factor $\varepsilon ^{1/2}$ in Fourier space. Therefore, the formal error ${\mathcal {O}}(\varepsilon ^3)$ of the residual corresponds to ${\mathcal {O}}(\varepsilon ^{7/2})$ in $L^2$ and the formal difference ${\mathcal {O}}(\varepsilon ^2)$ of $\varepsilon \psi - \varepsilon \psi _{NLS}$ corresponds to ${\mathcal {O}}(\varepsilon ^{5/2})$ in $L^2$. Secondly we remark that the near identity change of variables is arbitrarily smooth since only compact sets of wave numbers are involved. For the same reason it can be inverted for $\varepsilon > 0$ sufficiently small. As a consequence $\widehat{\psi _W}$ is well-defined.

5.4 The Error Estimates for the NLS Approximation

We have the following approximation result

Theorem 5.7

Under the validity of (ASS1)–(ASS3) and (NON) the following holds. Fix $T_0 > 0$ and let ${A}_{1} \in C([0,T_0], H^{6})$ be a solution of (31). Then there exist $\varepsilon _0 >0$, $C>0$ such that for all $\varepsilon \in (0,\varepsilon _0)$ there are solutions ${W} \in C([0,T_0/\varepsilon ^2], H^{1})$ of (21) with

$$\begin{aligned} \sup _{t \in [0,T_0/\varepsilon ^2]} \sup _{x \in {{\mathbb {R}}}} |W(x,t) - \varepsilon \psi _{NLS}(x,t) | \le C \varepsilon ^{3/2}, \end{aligned}$$

where $\varepsilon \psi _{NLS}(x,t)$ is defined in (28) and (29).

Proof. Since there is local existence and uniqueness for (21) in $H^1$ the subsequent estimates for the error in $H^1$ guarantee existence and uniqueness of solutions on the long $[0,T_0/\varepsilon ^2]$-time interval. Hence, it is sufficient to establish an error bound in $H^1$. Sobolev’s embedding theorem then will yield the statement of Theorem 5.7.

We introduce the error $\varepsilon ^{\beta } R = W - \varepsilon \psi _W$, with $\beta = 3/2$ and $\varepsilon \psi _W$ the approximation from Corollary 5.6. We find

$$\begin{aligned} \partial _t {\widehat{R}}= & {} {\widehat{\Lambda }} {\widehat{R}} + 3 \varepsilon ^2 {\widehat{G}}({\widehat{\psi }}_W,{\widehat{\psi }}_W,{\widehat{R}}) + 3 \varepsilon ^{1+\beta } {\widehat{G}}({\widehat{\psi }}_W,{\widehat{R}},{\widehat{R}})\nonumber \\&+\, 3 \varepsilon ^{2 \beta } {\widehat{G}}({\widehat{R}},{\widehat{R}},{\widehat{R}}) + \varepsilon ^{-\beta } {\widehat{Res}}_W(\varepsilon \psi _W) . \end{aligned}$$

(39)

We define the energy $E(t) = (R(t) ,R(t) )_{H^1} = ({\widehat{R}}(t) ,{\widehat{R}}(t) )_{L^2_1}$. From (39) we find for any $t \in [0,T_0/\varepsilon ^2]$ that

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} E \le C_1 \varepsilon ^2 E + C_2 \varepsilon ^{\beta +1} E^{3/2} + C_3 \varepsilon ^{2\beta } E^2 + C_4 \varepsilon ^2 (1+E) \end{aligned}$$

(40)

due to the skew symmetry of ${\widehat{\Lambda }}$, with constants $C_j$ which can be chosen independently of $0 < \varepsilon \ll 1$. For the residual terms we used $E^{1/2} \le 1+ E$. We integrate (40) with $E(0) =0$ and find

$$\begin{aligned} E({\widetilde{t}}) \le \int _0^{{\widetilde{t}}} C_1 \varepsilon ^2 E(s) + C_2 \varepsilon ^{\beta +1} E(s)^{3/2} + C_3 \varepsilon ^{2\beta } E(s)^2 + C_4 \varepsilon ^2 (1+E(s)) \mathrm{d}s. \end{aligned}$$

We take $\sup _{{\widetilde{t}} \in [0,t]}$ on both sides and find

$$\begin{aligned} \sup _{{\widetilde{t}} \in [0,t]}E({\widetilde{t}})\le & {} \sup _{{\widetilde{t}} \in [0,t]} \int _0^{{\widetilde{t}}} C_1 \varepsilon ^2 E(s) + C_2 \varepsilon ^{\beta +1} E(s)^{3/2} + C_3 \varepsilon ^{2\beta } E(s)^2\\&+ C_4 \varepsilon ^2 (1+E(s)) \mathrm{d}s. \end{aligned}$$

We introduce $S(t) = \sup _{{\widetilde{t}}\in [0,t]} E({\widetilde{t}})$ and use that $E(s) \le S(s)$ such that

$$\begin{aligned} S(t) \le \sup _{{\widetilde{t}}\in [0,t]} \int _0^{{\widetilde{t}}} C_1 \varepsilon ^2 S(s) + C_2 \varepsilon ^{\beta +1} S(s) ^{3/2} + C_3 \varepsilon ^{2\beta } S(s) ^2 + C_4 \varepsilon ^2 (1+S(s) ) \mathrm{d}s. \end{aligned}$$

Since the integrand increases monotonically we have

$$\begin{aligned} S(t) \le \int _0^t C_1 \varepsilon ^2 S(s) + C_2 \varepsilon ^{\beta +1} S(s) ^{3/2} + C_3 \varepsilon ^{2\beta } S(s) ^2 + C_4 \varepsilon ^2 (1+S(s) ) \mathrm{d}s. \end{aligned}$$

Now set

$$\begin{aligned} M= e^{(C_1+C_4+ 1)T_0} C_4 T_0 \end{aligned}$$

and choose $\varepsilon _0 > 0$ so small that for any $\varepsilon \le \varepsilon _0$

$$\begin{aligned} C_2 \varepsilon ^{\beta -1} M^{1/2} + C_3 \varepsilon ^{2\beta -2} M \le 1. \end{aligned}$$

(41)

We here define

$$\begin{aligned} t^* = \sup \{ t \in [0,T_0/\varepsilon ^2]: S(t) \le M \}. \end{aligned}$$

Note that by this definition $S(t^*)=M$ since S(t) is monotonically increasing, and continuous in t. It remains to prove that in fact $t^* = T_0/\varepsilon ^2$ for any $\varepsilon \le \varepsilon _0$. Suppose now that there would exist $\varepsilon _* \le \varepsilon _0$ such that $t^* < T_0/\varepsilon _{*}^2$, then we may take a $\delta >0$ such that

$$\begin{aligned} \frac{T_0}{\varepsilon _*^2} -\frac{\delta }{\varepsilon _*^2} > t^*. \end{aligned}$$

We then have for any $t \le t^*$,

$$\begin{aligned} S(t) \le \int _0^t (C_1 + C_4 +1 ) \varepsilon _{*}^2 S(s) \mathrm{d}s + C_4 \varepsilon _{*}^2 t. \end{aligned}$$

Gronwall’s inequality yields

$$\begin{aligned} S(t) \le e^{(C_1+C_4+ 1)\varepsilon _{*}^2 t} C_4\varepsilon _{*}^2 t \end{aligned}$$

for any $t \in [0,t^*]$, thus in particular at $t=t^*$, we have

$$\begin{aligned} S(t^*) \le e^{(C_1+C_4+ 1)\varepsilon _{*}^2 t^*} C_4\varepsilon _{*}^2 t^* < e^{(C_1+C_4+ 1)(T_0-\delta )} C_4 (T_0-\delta ) = M -C' \end{aligned}$$

with $C'=e^{(C_1+C_4+ 1)T_0} C_4 \delta >0$, which contradicts the fact $S(t^*)=M$. Hence we have $t^* = T_0/\varepsilon ^2$, for any $\varepsilon \le \varepsilon _0$. Therefore, we have an ${\mathcal {O}}(1)$-bound for the $H^1$-norm of R through the bound on $S(t) = \sup _{s \in [0,t]} E(s)$. The $\sup$-estimate stated in the Theorem follows from this $H^{1}$-estimate by Sobolev’s inequality. $\square$

5.5 The Case of a Vanishing Dispersion Coefficient

As already said the case ${\widehat{\omega }}''_b(k_0) = 0$ is of particular interest since this is the physically desired situation. We follow the calculations in Sect. 2 and in accordance with Assumption (16) we set ${\widehat{\omega }}''_b(k_0) = \varepsilon ^{2/3} \mu _0^*$, with $\mu _0^* \in {{\mathbb {R}}}$ arbitrary, but fixed. By this special choice the second-order spatial derivatives term is included in the limit equations which gives a richer dynamics in the limit equations. In Fourier space the ansatz, corresponding to (12) with $\theta = 2/3$, is given by

$$\begin{aligned} {\widehat{W}}_1(k,t)= & {} \varepsilon \varepsilon ^{-2/3} {\widehat{A}}_1\left( \frac{k-k_0}{\varepsilon ^{2/3}},\varepsilon ^2 t \right) e^{i {\widehat{\omega }}_b(k_0) t} e^{i {\widehat{\omega }}'_b(k_0) (k-k_0) t} , \end{aligned}$$

(42)

$$\begin{aligned} {\widehat{W}}_{-1}(k,t)= & {} \varepsilon \varepsilon ^{-2/3} {\widehat{A}}_{-1}\left( \frac{k+k_0}{\varepsilon ^{2/3}},\varepsilon ^2 t \right) e^{- i {\widehat{\omega }}_b(k_0) t} e^{i {\widehat{\omega }}'_b(k_0) (k+k_0) t} . \end{aligned}$$

(43)

We find a cancelation at ${\mathcal {O}}(1)$ and at ${\mathcal {O}}(\varepsilon ^{2/3})$. At ${\mathcal {O}}(\varepsilon ^{4/3})$ no terms occur and at ${\mathcal {O}}(\varepsilon ^2)$ close to $k_0$ we find

$$\begin{aligned} \partial _T {\widehat{A}}_1 = \frac{1}{2} i \mu _0^* K^2 {\widehat{A}}_1 + \frac{1}{6} i {\widehat{\omega }}'''_b(k_0)K^3 {\widehat{A}}_1 + i \gamma {\widehat{A}}_1* {\widehat{A}}_1* {\widehat{A}}_{-1}, \end{aligned}$$

(44)

or equivalently in physical space

$$\begin{aligned} \partial _T {A}_1 = - \frac{1}{2} i \mu _0^* \partial _X^2 {A}_1 - \frac{1}{6} i {\widehat{\omega }}'''_b(k_0) \partial _X^3 {A}_1 + i \gamma |A_1|^2 A_1. \end{aligned}$$

(45)

We have the following approximation result

Theorem 5.8

Under the validity of (ASS1)–(ASS3) and (NON) the following holds. Fix $T_0 > 0$ and let ${A}_{1} \in C([0,T_0], H^{6})$ be a solution of (45). Then there exist $\varepsilon _0 >0$, $C>0$ such that for all $\varepsilon \in (0,\varepsilon _0)$ there are solutions ${W} \in C([0,T_0/\varepsilon ^2], H^{1})$ of (21) with

$$\begin{aligned} \sup _{t \in [0,T_0/\varepsilon ^2]} \sup _{x \in {{\mathbb {R}}}} |W(x,t) - \varepsilon \psi _{\varepsilon }(x,t) | \le C \varepsilon ^{5/3}, \end{aligned}$$

where $\varepsilon \psi _{\varepsilon }(x,t)$ is defined by the right hand sides of (42) and (43).

Proof. As before we introduce the error $\varepsilon ^{\beta } R = W - \varepsilon \psi$, but now with $\beta = 5/3$. The error function R satisfies

$$\begin{aligned} \partial _t {\widehat{R}}= & {} {\widehat{\Lambda }} {\widehat{R}} + 3 \varepsilon ^2 {\widehat{G}} ({\widehat{\psi }},{\widehat{\psi }},{\widehat{R}}) + 3 \varepsilon ^{1+\beta } {\widehat{G}}({\widehat{\psi }},{\widehat{R}},{\widehat{R}}) \nonumber \\&+\, 3 \varepsilon ^{2 \beta } {\widehat{G}}({\widehat{R}},{\widehat{R}},{\widehat{R}}) + \varepsilon ^{-\beta } {\widehat{Res}}(\varepsilon \psi ) . \end{aligned}$$

(46)

As before we can achieve

$$\begin{aligned} \sup _{t \in [0,T_0/\varepsilon ^2]} \Vert \varepsilon ^{- \beta } Res_W(\varepsilon \psi ) \Vert _{L^2} \le C \varepsilon ^2. \end{aligned}$$

We define the energy $E = (R,R)_{H^1}$. Due to the skew symmetry of ${\widehat{\Lambda }}$ we find

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} E \le C_1 \varepsilon ^2 E + C_2 \varepsilon ^{\beta +1} E^{3/2} + C_3 \varepsilon ^{2\beta } E^2 + C_4 \varepsilon ^2 (1+E), \end{aligned}$$

with constants $C_j$ which can be chosen independently of $0 < \varepsilon \ll 1$. The rest of the proof follows line for line the proof of Theorem 5.7. $\square$

Remark 5.9

At a first view it seems that the approach of Sect. 3 is a short-cut to come directly to the averaged modulation equations (11) and (17) without the detour via (10) and (14) with its highly oscillating coefficients. However, this is not true. A closer look at the non-resonance conditions which occur in both sections shows that these are different. Moreover, the possibility of additional resonant terms in the modulation equations as shown in Example 4.1 is excluded by the approach made in Sect. 2.. These are a number of hints that something must be wrong with the approach presented in Sect. 2. This will be explained in Sect. 7.

6 Failure of the Approximation

It has been rigorously proved in a number of papers that modulation equations can make wrong predictions about the dynamical behavior of the original system. The first result has been shown for the amplitude system describing roll solutions in a rotational symmetric pattern forming system by using a center manifold reduction (Schneider 1995). The failure of the NLS approximation has been established in Schneider et al. (2015) for the water wave problem with small surface tension using the unstable quadratic resonances of the system. See also Bauer et al. (2019). The only existing failure result without imposing periodic boundary conditions on the original system can be found in Haas and Schneider (2020) again using the unstable quadratic resonances of the system.

The present situation is simpler since the failure comes from a linear instability. Statements that a linear instability leads to a failure of modulation equations can be found in a number of papers, cf. Schneider (2016). However, to our knowledge a rigorous proof for failure in such a situation has never been given. This will be done in this section. We construct a simple counter-example in case of periodic boundary conditions which shows that the NLS approximation can fail to make correct predictions if the linear stability assumption (ASS1) is not satisfied. In a number of subsequent remarks we discuss the ingredients for failure in more general situations and we explain how the finite speed of propagation in the original system can be used to prove failure of the NLS approximation without imposing periodic boundary conditions on the original system. The proof of failure of the NLS approximation in case of periodic boundary conditions follows the lines of the instability proof for a spectrally unstable fixed point.

As a counter-example for which the NLS approximation can fail to make correct predictions we consider

$$\begin{aligned} \partial ^{2}_{t}{\widehat{u}}=-{\widehat{\omega }} ^{2}{\widehat{u}}+ {\widehat{u}}^{*3}, \end{aligned}$$

(47)

with

$$\begin{aligned} {\widehat{\omega }}^{2}(k) = 1+ k^2 + \frac{1}{4} \cos (2t) \chi (k) \end{aligned}$$

where $\chi \in C_0^{\infty }$ with

$$\begin{aligned} \chi (k) = \left\{ \begin{array}{cl} 1 , &{}\quad \text {for } |k| \le 2/5, \\ 0, &{}\quad \text {for } |k| \ge 3/5, \\ \in [0,1] , &{}\quad \text {else}. \end{array} \right. \end{aligned}$$

By this choice an instability in the sense of Sect. 4.2 can only occur for wave numbers $|k| < 3/5$. The counter part to (47) in physical space is given by

$$\begin{aligned} \partial ^{2}_{t} {u}=-{\widehat{\omega }}^{2}(-i \partial _x) {u}+ {u}^{3}. \end{aligned}$$

(48)

In the first step we consider (48) with $2 \pi$-spatially periodic boundary conditions and write $u(x,t) = \sum _{k \in {\mathbb {Z}}} {\widehat{u}}_k(t) e^{ikx}$ or restrict (47) to wave numbers $k \in {{\mathbb {Z}}}$. Before we start to derive an NLS equation we remark that by our choice only ${\widehat{u}}_0$ will grow with an exponential rate. All other ${\widehat{u}}_k$ behave oscillatory.

For the NLS approximation we choose the basic wave number $k_0 = 1$. Since we have a cubic nonlinearity by nonlinear interaction only modes ${\widehat{u}}_k$ with odd k will be created. Since $k_0 > 3/5$ the derivation of the NLS equation is not affected by the time-periodic amplification for $|k| < 3/5$. Therefore, the ansatz for the derivation of the NLS equation is the one used for an autonomous system. It is similar to (3) and for the pure derivation of the NLS equation given by

$$\begin{aligned} u(x,t) \approx \varepsilon \psi _{NLS}(x,t) = \varepsilon A_1(T) E(x,t) + c.c. , \end{aligned}$$

(49)

where we recall $E(x,t) = e^{i (k_0 x + \omega _0(t) t)}$. Plugging $\varepsilon \psi _{NLS}(x,t)$ into (48) and equating the coefficient in front $\varepsilon ^3 E$ to zero yields the ODE version

$$\begin{aligned} 2 i \partial _T A_1 = 3 A_1 | A_1|^2, \end{aligned}$$

(50)

of the NLS equation (4). As above for the justification of the NLS approximation by error estimates also for the proof of failure we need an approximation $\varepsilon \psi _{\varepsilon }(x,t)$ nearby $\varepsilon \psi _{NLS}(x,t)$ which is constructed in such a way that the residual is at least of order ${\mathcal {O}}(\varepsilon ^4)$. For our purposes it is sufficient to choose

$$\begin{aligned} \varepsilon \psi _{\varepsilon }(x,t) = \varepsilon A_1(T) E(x,t) + \varepsilon ^3 A_3(T) E^3(x,t) + c.c. . \end{aligned}$$

The equation for $A_3$ is determined by equating the coefficient in front $\varepsilon ^3 E^3$ to zero. We obtain

$$\begin{aligned} - 9 \omega _0^2 A_3 = - 9 k_0^2 A_3 - A_3 + A_1^3. \end{aligned}$$

Since $- 9 \omega _0^2+ 9 k_0^2 + 1 = - 18 + 9 + 1 = - 8 \ne 0$ the function $A_3$ is well-defined and all terms of order ${\mathcal {O}}(\varepsilon ^3)$ have been eliminated from the residual.

In order to show below that (50) makes wrong predictions about the dynamics of (48) we need a small amount of ${\widehat{u}}_0(0)$ initially. Hence we choose for instance

$$\begin{aligned} {u}(x,0) = \varepsilon \psi _{\varepsilon }(x,0) + {\widehat{u}}_0(0) \qquad \text {and} \qquad \partial _t{u}(x,0) = \varepsilon \partial _t \psi _{\varepsilon }(x,0) \end{aligned}$$

as initial condition for (48), with $0 \ne {\widehat{u}}_0(0) = {\mathcal {O}}(\varepsilon ^3)$. Then, we have

$$\begin{aligned} |{u}(x,0) - \varepsilon \psi _{\varepsilon }(x,0) | = {\mathcal {O}}(\varepsilon ^3) \end{aligned}$$

initially. A typical approximation result, cf. Kirrmann et al. (1992), then would show that the NLS approximation makes correct predictions on the NLS time scale of order ${\mathcal {O}}(1/\varepsilon ^2)$, i.e., that the difference between the NLS approximation and true solutions of the original system can be estimated by

$$\begin{aligned} |{u}(x,t) - \varepsilon \psi _{\varepsilon }(x,t) | = {\mathcal {O}}(\varepsilon ^\beta ) \end{aligned}$$

for a $\beta > 1$ and all t on an ${\mathcal {O}}(1/\varepsilon ^2)$-time scale. Hence if we can prove that the difference between the NLS approximation and true solutions of the original system is of the same order as the NLS approximation before the end of the ${\mathcal {O}}(1/\varepsilon ^2)$-time scale we say that NLS approximation fails to make correct predictions. Since in the following we prove

$$\begin{aligned} |{u}(x,t_*) - \varepsilon \psi _{\varepsilon }(x,t_*) | = {\mathcal {O}}(\varepsilon ) \end{aligned}$$

for a $t_* \le {\mathcal {O}}(1/\varepsilon ^{1/2})$, we have the failure of the approximation property. See Fig. 4.

Fig. 4

The mode distribution for $t = 0$ and the mode distribution for $t = {\mathcal {O}}( | \ln \varepsilon |) \ll {\mathcal {O}}( 1/\varepsilon ^{2})$. The NLS approximation is no longer valid in the right picture, since the mode at 0 is of the same order w.r.t. powers of $\varepsilon$ as the NLS modes at $k = \pm 1$

In more detail, we prove

Theorem 6.1

Consider (48) with periodic boundary conditions $u(x ,t) = u(x+ 2\pi ,t)$ for all $x \in {\mathbb {R}}$. Let $A_1 \in C([0,T_0],{\mathbb {C}})$ be a solution of the NLS equation (50). Then there exist $\varepsilon _0 > 0$, $C_1> 0$, and $C_2 > 0$ such that for all $\varepsilon \in (0,\varepsilon _0)$ there is an open set of initial conditions in $H^{1}_{\text {per}} \times L^{2}_{\text {per}}$ for (48) with

$$\begin{aligned} \Vert u(\cdot ,0) - \varepsilon \psi _{\varepsilon } (\varepsilon ,\cdot ,0)\Vert _{H^{1}_{\text {per}}} + \Vert \partial _t u(\cdot ,0) - \varepsilon \partial _t \psi _{\varepsilon } (\varepsilon ,\cdot ,0)\Vert _{L^{2}_{\text {per}}} \le C_1 \varepsilon ^{3} , \end{aligned}$$

for which the associated solutions satisfy

$$\begin{aligned} \sup _{t \in [0,1/\varepsilon ^{1/2}]} \sup _{x \in {{\mathbb {R}}}}| u(x,t) - \varepsilon \psi _{\varepsilon } (\varepsilon ,x,t)| \ge C_2 \varepsilon . \end{aligned}$$

Proof. We split $u(x,t) = u_0(t) + u_h(x,t)$, with $\int u_h(x,t) \mathrm{d}x = 0$, i.e. $u_h (x,t) = \sum _{k \in {\mathbb {Z}}\setminus \{0\}} {\widehat{u}}_k(t) e^{ikx}$. Then we write (48) as

$$\begin{aligned} \partial ^{2}_{t} u_0= & {} -{\widehat{\omega }}_0^{2} {u}_0+ \frac{1}{2\pi } \int _0^{2 \pi } u^3 \mathrm{d}x , \end{aligned}$$

(51)

$$\begin{aligned} \partial ^{2}_{t} u_h= & {} -{\widehat{\omega }}^{2} {u}_h+ u^3 - \frac{1}{2\pi } \int _0^{2 \pi } u^3 \mathrm{d}x , \end{aligned}$$

(52)

with $\omega _0^2(t)= 1+ \frac{1}{4} \cos (2t)$. Thus, for $u_0$ we are in the instability region plotted in Fig. 2, and so one positive Floquet exponent $\lambda _u$ and one negative Floquet exponent $\lambda _s$, occurs. Since the linear part of the $u_h$-equation is autonomous, purely imaginary Floquet exponents occur for the $u_h$-part. We follow the calculations in Sect. 3 and using the notation of Sect. 3 finally write (51) as

$$\begin{aligned} \partial _t R_u = \lambda _u R_u + P_u G(W,W,W), \qquad \partial _t R_s = \lambda _s R_s + P_s G(W,W,W), \end{aligned}$$

where $P_u$ and $P_s$ are the projection on the unstable, respectively stable subspace. We introduce the deviation from the NLS approximation for all other modes by $u_h = \varepsilon \psi _h + R_h$, where $\psi _h$ is the extension of the NLS approximation to the W-variable. We find the system

$$\begin{aligned} \partial _t R_u= & {} \lambda _u R_u + g_u(\psi ,R), \\ \partial _t R_s= & {} \lambda _s R_s + g_s(\psi ,R), \\ \partial _t R_h= & {} \Lambda _h R_h + g_h(\psi ,R), \end{aligned}$$

with $g_u$, $g_s$, and $g_h$ satisfying

$$\begin{aligned} | g_u |= & {} C \varepsilon ^2 \Vert R \Vert _{H_1} + C \varepsilon \Vert R \Vert _{H_1}^2 + C \Vert R \Vert _{H_1}^3, \\ | g_s |= & {} C \varepsilon ^2 \Vert R \Vert _{H_1} + C \varepsilon \Vert R \Vert _{H_1}^2 + C \Vert R \Vert _{H_1}^3, \\ \Vert g_h \Vert _{H_1}= & {} C \varepsilon ^2 \Vert R \Vert _{H_1} + C \varepsilon \Vert R \Vert _{H_1}^2 + C \Vert R \Vert _{H_1}^3 + C \varepsilon ^3 , \end{aligned}$$

where the $C \varepsilon ^3$ in the estimate for $g_h$ comes from the residual which by construction vanishes in the $R_u$- and $R_s$-equation.

We introduce the quantities

$$\begin{aligned} E_{u}=\left| R_{u}\right| ^{2} \qquad \text {and} \qquad E_{s}=\left| R_{s}\right| ^{2}+ \Vert R_h \Vert _{H^1}^2. \end{aligned}$$

For $E= E_u -E_s$ we find with

$$\begin{aligned} \Vert R\Vert _{H^1}^2 = \Vert R_h\Vert _{H^1}^2 + \left| R_{u}\right| ^{2} + \left| R_{s}\right| ^{2} = E_u + E_s \end{aligned}$$

and

$$\begin{aligned} C \varepsilon ^3 \Vert R \Vert _{H_1} \le C \varepsilon ^2 \varepsilon \Vert R \Vert _{H_1} \le C (\varepsilon ^4 + (\varepsilon \Vert R \Vert _{H_1} )^2)\le C \varepsilon ^4 + C \varepsilon ^2 (E_u+ E_s) \end{aligned}$$

that

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}E= & {} 2 \lambda _u E_{u}+ 2 R_u g_u - 2 \lambda _s \left| R_{s}\right| ^{2}- 2 R_s g_s -2 (R_h,g_h)_{H^1} \\\ge & {} 2 \lambda _u E_{u} - 2 |R_u|| g_u| - 2 |R_s|| g_s|- 2 \Vert R_h\Vert _{H^1} \Vert g_h\Vert _{H^1}\\\ge & {} 2 \lambda _u E_{u} - 2 C \varepsilon ^2 \Vert R \Vert _{H_1}^2 - C \varepsilon \Vert R \Vert _{H_1}^3 - C \Vert R \Vert _{H_1}^4 - C \varepsilon ^3 \Vert R \Vert _{H_1}\\\ge & {} 2 \lambda _u E_{u} - 2 C \varepsilon ^2 (E_u + E_s) - C \varepsilon (E_u + E_s)^{3/2} \\&-\, C (E_u + E_s)^2 - C \varepsilon ^4 - C \varepsilon ^2 (E_u + E_s)\\\ge & {} \lambda _u E_{u} - \lambda _u E_{s} - C \varepsilon ^4\\= & {} \lambda _u E - C \varepsilon ^4 \ge \frac{1}{2}\lambda _u E, \end{aligned}$$

under the assumptions

$$\begin{aligned}&2 C \varepsilon ^2 + C \varepsilon (E_u + E_s)^{1/2} + C (E_u + E_s) + C \varepsilon ^2 \le \lambda _u , \end{aligned}$$

(53)

$$\begin{aligned}&C \varepsilon ^4 \le \frac{1}{2}\lambda _u E. \end{aligned}$$

(54)

The assumption (53) follows from the assumptions

$$\begin{aligned}&3 C \varepsilon ^2 + C \varepsilon (E_u + E_s)^{1/2} \le \frac{1}{2} \lambda _u , \end{aligned}$$

(55)

$$\begin{aligned}&C (E_u + E_s) \le \frac{1}{2}\lambda _u . \end{aligned}$$

(56)

Define then

$$\begin{aligned} t_* = \inf \{ t : E(t) \ge \frac{1}{2}\lambda _u \}. \end{aligned}$$

We are done if we prove for instance $t_* \le 1/\varepsilon ^{1/2}$. If the assumption (56) is not satisfied for a $t \in [0,1/\varepsilon ^{1/2}]$ we are done. Hence, we assume in the following that (56) is satisfied. Then choose $\varepsilon > 0$ so small that

$$\begin{aligned} 3 C \varepsilon ^2 + C \varepsilon \left( \frac{1}{2}\lambda _u/C\right) ^{1/2} \le \frac{1}{2} \lambda _u . \end{aligned}$$

Under this assumption also (55) is satisfied.

In order to satisfy (54) we use that for the autonomous case it is well known that we can extend the NLS approximation by higher-order terms such that

$$\begin{aligned} \Vert \text {Res} \Vert _{H_1} = {\mathcal {O}}(\varepsilon ^{n}). \end{aligned}$$

Due to the inequality on E Assumption (54) will follow from

$$\begin{aligned} C \varepsilon ^4 \le \frac{1}{2}\lambda _u E(0) . \end{aligned}$$

(57)

Assumption (57) holds for $\varepsilon _0 > 0$ sufficiently small since if we have chosen $E_u(0) = {\mathcal {O}}(\varepsilon ^{3})$. Thus

$$\begin{aligned} E(t) \ge E(0) e^{ \lambda _u t/2}. \end{aligned}$$

for all $t \in [0,t_*]$. Since ${\mathcal {O}}(\varepsilon ) = {\mathcal {O}}(\varepsilon ^{3})e^{ \lambda _u t/2}$ for $t = {\mathcal {O}}(\ln (1/\varepsilon ^{2})) \ll 1/\varepsilon ^{1/2}$, we are done. See Fig. 5. $\square$

Fig. 5

The solutions leave the sector in the direction of the $R_u$-axis

Remark 6.2

The above idea works whenever (ASS1) is not satisfied, in detail, if there exists at least one interval $[k_-,k_+]$ for which positive growth rates occur. If an integer multiple of $k_0$ does not fall into this interval, then choose an $m \in {{\mathbb {N}}}$ such that $n k_0/m \in [k_-,k_+]$ for an $n \in {{\mathbb {Z}}}$. Then choose $2\pi m$-spatially periodic boundary conditions for (48). The proof for this situation works exactly as before.

Remark 6.3

In order to prove that the NLS approximation $\varepsilon \psi _{\varepsilon }$ also fails for (48) without imposing periodic boundary conditions, we could follow the ideas of Haas and Schneider (2020, Section 5), i.e., we could use the failure of the NLS approximation for (48) with $2 \pi$-spatially periodic boundary conditions and the fact that (48) has a finite speed of propagation of order ${\mathcal {O}}(1)$. Due to the finite ${\mathcal {O}}(1)$-speed of propagation the following holds. If we have initially a spatial domain of size ${\mathcal {O}}(1/\varepsilon ^{1/4})$ filled with $2 \pi$-spatially periodic solutions which are ${\mathcal {O}}(\varepsilon ^{3})$-close to $\psi _{\varepsilon }$, then we know that after a time scale of order ${\mathcal {O}}(\ln (\varepsilon ))$ we still have a domain of size ${\mathcal {O}}(1/\varepsilon ^{1/4})$ filled with $2 \pi$-spatially periodic solutions but which are ${\mathcal {O}}(\varepsilon )$ away from $\psi _{\varepsilon }$. Thus, on this spatial domain this local NLS approximation makes wrong predictions. Due to the scaling of the NLS approximation, cf. (3), this small domain in space and time corresponds in the NLS equation to a spatial domain of size ${\mathcal {O}}(\varepsilon ^{3/4})$ and to a temporal domain of size ${\mathcal {O}}(\varepsilon ^{2}\ln (\varepsilon ))$. Using the variation of constant formula we can guarantee that solutions of the NLS equation, cf. (4), change on this spatial domain only by ${\mathcal {O}}(\varepsilon ^{2}\ln (\varepsilon ))$ which corresponds in (48) to a change of ${\mathcal {O}}(\varepsilon ^{3}\ln (\varepsilon ))$. By the triangle inequality the solution of (48) is still ${\mathcal {O}}(\varepsilon )$ away from the NLS approximation, cf. (3). As a consequence, the NLS approximation, cf. (3), fails to make correct predictions about the dynamics of (48) even without imposing periodic boundary conditions (Fig. 6).

Fig. 6

Left panel: A spatial domain of size ${\mathcal {O}}(1/\varepsilon ^{1/4})$ is not influenced from outside if information is started outside a slightly bigger domain of size ${\mathcal {O}}(1/\varepsilon ^{1/4})$ and if information is transported with velocity ${\mathcal {O}}(1)$ on an ${\mathcal {O}}(|\ln (\varepsilon )|)$-time scale. Right panel: The NLS scaling

7 Discussion

In this last section we begin with a subsection discussing possible generalizations, such as the transfer to original systems with quadratic nonlinearities or replacing the NLS scaling by the N-wave interaction scaling. In the second subsection we discuss time periodicities $L \gg 1$, in particular the case of step functions $\alpha _j$ with period $L = {\mathcal {O}}(\varepsilon ^{-2\theta })$ for $\frac{2}{3}< \theta < 1$, which was the situation where the dispersion management equation (5) occurs, cf. Remark 2.1. The subsequent discussion will make clear that in the modeling used in Nonlinear Optics as described in Fig. 1, the dispersion management equation is at most a phenomenological model which cannot rigorously be derived and justified with some approximation theorem for our toy model (1). We strongly expect that the same holds for the full Maxwell equations.

7.1 Generalizations

We start with the remark that there is a second consistent ansatz for the description of oscillatory wave packets, namely the so called N-wave interaction (NWI) approximation, cf. Craik (1988). For (1) with time-independent coefficients and $N = 1$ it is given by

$$\begin{aligned} u(x,t) = \varepsilon A(\varepsilon ^2 x ,\varepsilon ^2 t) E(x,t) + c.c. + {\mathcal {O}}(\varepsilon ^3), \end{aligned}$$

leading to

$$\begin{aligned} i \nu _{0} \partial _T A= & {} c \partial _{X} A + 3 \nu _{2} A | A|^2 \end{aligned}$$

The justification analysis of the NWI approximation goes very similarly to the NLS approximation (Schneider and Zink 2005). Only in very special situations differences occur (Haas and Schneider 2020). Hence the previous analysis not only applies to NLS scaled wave packets but also to NWI scaled wave packets.

In our considerations we restricted ourselves to an original system with no quadratic terms. With respect to our application to fiber optics this is motivated by the symmetries of the problem which only allow for odd nonlinearities. A simple generalization of our previous toy problem (19) is the consideration of coupled systems

$$\begin{aligned} \partial _t^2 {\widehat{u}}_j = - {\widehat{\omega }}_j^2 {\widehat{u}}_j + {\widehat{f}}_j(u_1,\ldots , u_N) , \end{aligned}$$

for $j=1, \ldots ,N$, with $f_j={\mathcal {O}}(|u_1|^3,\ldots ,|u_N|^3)$ smooth functions from ${{\mathbb {R}}}^N$ to ${{\mathbb {R}}}$. The non-resonance conditions (NON) transfer in an obvious way. The Maxwell-Lorentz system falls into this class, cf. Schneider and Uecker (2017, §11.7).

The case of quadratic nonlinearities is more challenging from a mathematical point of view. In the autonomous case already in the derivation of the modulation equations additional non-resonance conditions are necessary. In the justification analysis the quadratic terms have to be eliminated by near identity changes of variables, cf. Kalyakin (1988) and Schneider (1998). In order to do so even more non-resonance conditions have to be satisfied. The case so-called stable resonances has been handled in Schneider (2005). The handling of nonlinear wave equations with quasilinear quadratic terms was an open problem for a long time and has only been solved recently, cf. Duell (2017) and Hess (2019). We expect that all these existing justification results can be transferred from the autonomous case to the time-periodic case under the validity of assumptions similar to (ASS1)–(ASS3). However, such assumptions would be very restrictive and the related approximations not very helpful.

7.2 Remarks About the Case $L \gg 1$.

For the subsequent discussion we ignore the possibility of linear instabilities in time-periodic systems and explain that, even in the stable case, in the scaling which is necessary for the derivation of the dispersion management equation a behavior occurs which in general cannot be described by a dispersion management equation.

If the time-periodicity 2L is large compared to the wave-length of the underlying carrier wave, i.e., if for instance $L = {\mathcal {O}}(\varepsilon ^{-2 \theta })$ for $\frac{2}{3}< \theta < 1$, then the previous Floquet analysis is no longer of any help, because then the amplitude of the periodic matrices P(t) in Floquet’s theorem also depends singularly on $\varepsilon$ and can be very large. As already said, $L = {\mathcal {O}}(\varepsilon ^{-2 \theta })$ for $\frac{2}{3}< \theta < 1$ is of particular interest due to the formal occurrence of the dispersion management equation (5) for such L, cf. Remark 2.1.

Hence, we come back to the discussion made in Sect. 2 and consider again the situation of 2L-periodic step functions $\alpha _j$ for (1). The main purpose of the subsequent discussion is to explain the influence of the jumps at $t = nL$ on the dynamics. As in Sect. 2 on each of the intervals $(nL,(n+1) L)$ and $((n+1) L,(n+2) L)$ we can derive a NLS equation with constant coefficients. For the description of the effective dynamics we make the ansatz

$$\begin{aligned} u(x,t) \approx \varepsilon \psi _{\varepsilon }(x,t) = \varepsilon A(\xi ,T) E(x,t)+ c.c. + {\mathcal {O}}(\varepsilon ^3), \end{aligned}$$

(58)

with the slow time variable $T=\varepsilon ^2 t$ and the slow spatial variable $\xi =\varepsilon ^{\theta }(x+c(t) t)$ with $\frac{2}{3}< \theta < 1$. As explained in Sect. 2 we obtain the NLS equation

$$\begin{aligned} i \partial _T A = \varepsilon ^{2\theta -2} {\widetilde{\mu }}_0\left( \frac{T}{ \varepsilon ^{2-2\theta }}\right) \partial _\xi ^2 A + {\widetilde{\mu }}_1\left( \frac{T}{ \varepsilon ^{2-2\theta }}\right) A |A|^2 \end{aligned}$$

(59)

with highly oscillatory coefficients. The $2 \pi$-periodic coefficient step functions ${\widetilde{\mu }}_j(\tau )$ are related to the original step functions through $\mu _j(t) = {\widetilde{\mu }}_j(\varepsilon ^{2\theta } t)$.

Remark 7.1

Before we go on, we recall why (58) is exactly the scaling which has to be chosen for a possible derivation of the dispersion management equation (5).

• 1. In order to have the time derivative $\partial _T A$ and the nonlinear terms $A |A|^2$ of the same order, we need that the ratio, coming from $T = \varepsilon ^2 t$ and the scaling $\varepsilon A$, of these two terms is ${\mathcal {O}}(1)$. This is used for the definition of $\varepsilon$.

• 2. The choice $\xi =\varepsilon ^{\theta }(x+c(t) t)$ with $\frac{2}{3}< \theta < 1$ is made to include the term $\partial _\xi ^2 A$ into (59). For $\theta \le \frac{2}{3}$ higher-order terms such as $\partial _\xi ^3 A$ have to be included in (59), too, since they are larger than or equal to $\partial _T A$ and $A |A|^2$. For $\theta > 1$ the term $\partial _\xi ^2 A$ is of higher-order and can be ignored. For $\theta = 1$ it is of the same order as $\partial _T A$ and $A |A|^2$ and a scaling as in (5) cannot be obtained. Thus, we have to choose $\frac{2}{3}< \theta < 1$.

• 3. In order to get a scaling as in (5) we have to set ${\widetilde{\varepsilon }}^{-1} = \varepsilon ^{2 \theta -2}$ and to choose $L = {\mathcal {O}}(\varepsilon ^{-2 \theta })$.

As already discussed in Remark 5.9 this formal derivation of (59) must have ignored a very relevant aspect. What is considered wrong so far is the continuation of the solutions of (1) at the jump points $t = nL$ with $n \in {{\mathbb {N}}}$. For the dispersion management models (10) and (14) the value $A|_{t= nL}$ of the solution at the end of the n-th interval is taken as initial condition for the $(n+1)$-th interval. However, for the original system (1) the two functions $u|_{t= nL}$ and $\partial _t u|_{t= nL}$ at the endpoint of the n-th interval have to be passed as initial conditions to the $n+1$-th interval.

In detail, at the end of the time interval [0, L) we have that

$$\begin{aligned} u(x,L_-)= & {} \varepsilon A(\varepsilon ^{\theta }(x+ c_{;1}L_-),\varepsilon ^2 L_-) e^{ik_0x+ i \omega _{0;1} L_-} + c.c. + {\mathcal {O}}(\varepsilon ^3), \\ \partial _t u(x,L_-)= & {} i \omega _{0;1} \varepsilon A(\varepsilon ^{\theta }(x+ c_{;1}L_-),\varepsilon ^2 L_-) e^{ik_0x+ i \omega _{0;1} L_-} + c.c. + {\mathcal {O}}(\varepsilon ^{1+\theta }), \end{aligned}$$

where $L_-$ stands for the left limit $t \rightarrow L$. However, at the beginning of the next interval we have

$$\begin{aligned} u(x,L_+)= & {} \varepsilon A(\varepsilon ^{\theta }(x+ c_{;2}L_++{\widetilde{x}}_0),\varepsilon ^2 L_+) e^{ik_0x + i \omega _{0;2} L_+ + i {\widetilde{\phi }}_0} + c.c. + {\mathcal {O}}(\varepsilon ^3), \\ \partial _t u(x,L_+)= & {} i \omega _{0;2} \varepsilon A(\varepsilon ^{\theta }(x+ c_{;2}L_++{\widetilde{x}}_0),\varepsilon ^2 L_+) e^{ik_0x+ i \omega _{0;2} L_+ + i {\widetilde{\phi }}_0} \\&+ c.c. + {\mathcal {O}}(\varepsilon ^{1+\theta }), \end{aligned}$$

where $L_+$ stands for the right limit $t \rightarrow L$. Moreover, we introduced the extra phase ${\widetilde{\phi }}_0 \in {{\mathbb {R}}}$ and the extra shift ${\widetilde{x}}_0$ which are chosen in such a way that

$$\begin{aligned} e^{ik_0x + i \omega _{0;1} L_-} = e^{ik_0x + i \omega _{0;2} L_+ + i {\widetilde{\phi }}_0} \end{aligned}$$

and

$$\begin{aligned} x+ c_{;1}L_- = x+ c_{;2}L_++{\widetilde{x}}_0. \end{aligned}$$

It is obvious that the continuity of $\partial _t u$ at $t = L$ cannot be satisfied if $\omega _{0;1} \ne \omega _{0:2}$ and in fact, although the initial conditions at $t = L$ for (1) are concentrated at $k = \pm k_0$ they are no longer of the form which is necessary for the associated solutions to be approximated by a single NLS scaled wave packet on the next interval. A second wave packet propagating in the opposite direction is created. See Figs. 7 and 8.

For $t \in (L,2 L)$ the left and right traveling wave packets can be described by the extended ansatz

$$\begin{aligned} u(x,t)= & {} \varepsilon A_{1,1}(\varepsilon ^{\theta }(x+ c_{;2} t+ x_{1,1}),T) e^{ik_0x+ i \omega _{0;2} t} e^{i \phi _{1,1}}\nonumber \\&+\, \varepsilon A_{1,0}(\varepsilon ^{\theta }(x- c_{;2}t + x_{1,0}),T) e^{ik_0x- i \omega _{0;2} t} e^{i \phi _{1,0}}+ c.c. + {\mathcal {O}}(\varepsilon ^3),\qquad \end{aligned}$$

(60)

with the envelopes $A_{1,j}(X,T) \in {{\mathbb {C}}}$ for $j \in \{0,1\}$. The extra phases $\phi _{1,j}$ and extra shifts $x_{1,j}$ for $j \in \{0,1\}$ are again used to adjust the positions and phases at the jump point $t = L$. They are determined by

$$\begin{aligned} e^{ik_0x + i \omega _{0;1} L_-} = e^{ik_0x+ i \omega _{0;2} L_+} e^{i \phi _{1,1}} = e^{ik_0x- i \omega _{0;2} L_+} e^{i \phi _{10}} \end{aligned}$$

and

$$\begin{aligned} x+ c_{;1}L_- = x+ c_{;2} L_+ + x_{1,1} = x- c_{;2} L_+ + x_{1,0}. \end{aligned}$$

The continuity condition for u at $t = L$ leads to

$$\begin{aligned} u(x,L_-)= & {} \varepsilon A(\varepsilon ^{\theta }(x+ c_{;1}L_-),\varepsilon ^2 L_-) e^{ik_0x+ i \omega _{0;1} L_-} + c.c. + {\mathcal {O}}(\varepsilon ^3) \\= & {} \varepsilon A_{1,1}(\varepsilon ^{\theta }(x+ c_{;2} L_+ + x_{1,1}),\varepsilon ^2 L_+) e^{ik_0x+ i \omega _{0;2} L_+} e^{i \phi _{1,1}}\\&+\, \varepsilon A_{1,0}(\varepsilon ^{\theta }(x- c_{;2} L_+ + x_{1,0}),\varepsilon ^2 L_+) e^{ik_0x- i \omega _{0;2} L_+} e^{i \phi _{1,0}}+ c.c. + {\mathcal {O}}(\varepsilon ^3) \\= & {} u(x,L_+), \end{aligned}$$

respectively to

$$\begin{aligned} A(X,\varepsilon ^2 L_-) = A_{1,1}(X,\varepsilon ^2 L_+) + A_{1,0}(X,\varepsilon ^2 L_+). \end{aligned}$$

(61)

The continuity condition for $\partial _t u$ at $t = L$ leads to

$$\begin{aligned} \partial _t u(x,L_-)= & {} i \omega _{0;1} \varepsilon A(\varepsilon ^{\theta }(x+ c_{;1}L_-),\varepsilon ^2 L_-) e^{ik_0x+ i \omega _{0,1} L_-} + c.c. + {\mathcal {O}}(\varepsilon ^{1+\theta })\\= & {} i \omega _{0,2} \varepsilon A_{1,1}(\varepsilon ^{\theta }(x+ c_{;2} L_+ + x_{1,1}),\varepsilon ^2 L_+) e^{ik_0x+ i \omega _{0;2} L_+} e^{i \phi _{1,1}}\\&-\, i \omega _{0;2} \varepsilon A_{1,0}(\varepsilon ^{\theta }(x- c_{;2} L_+ + x_{1,0}),\varepsilon ^2 L_+) e^{ik_0x- i \omega _{0;2} L_+} e^{i \phi _{1,0}}\\&+\, c.c. + {\mathcal {O}}(\varepsilon ^{1+\theta }) \\= & {} \partial _t u(x,L_+), \end{aligned}$$

respectively to

$$\begin{aligned} i \omega _{0;1} A(X,\varepsilon ^2 L_-) = i \omega _{0;2} A_{1,1}(X,\varepsilon ^2 L_+) - i \omega _{0;2} A_{1,0}(X,\varepsilon ^2 L_+). \end{aligned}$$

(62)

The two conditions (61) and (62) form a linear system for $A_{1,1}(X,\varepsilon ^2 L_+)$ and $A_{1,0}(X,\varepsilon ^2 L_+)$ which can be solved in terms of $A(X,\varepsilon ^2 L_-)$.

Fig. 7

The Fourier mode distribution of the solutions changes at the first jump point. The left panel sketches the distribution for $t \rightarrow L_-$. There are modes associated to the curve $\omega _{0;1}$ concentrated at $k= k_0$ and modes associated to the curve $- \omega _{0;1}$ concentrated at $k= - k_0$. The right panel sketches the distribution for $t \rightarrow L_+$. There are modes associated to the curves $\omega _{0;1}$ and $- \omega _{0;1}$ concentrated at $k= k_0$ and at $k= - k_0$. The modes corresponding to $( \omega _{0;1},k_0)$ and $( -\omega _{0;1},-k_0)$ correspond to left moving waves. The modes corresponding to $( -\omega _{0;1},k_0)$ and $( \omega _{0;1},-k_0)$ correspond to right moving waves

In order to understand the global behavior we have to recall a few facts.

• 1. The modulated wave packets described by (60) move with a velocity $c(t) = {\mathcal {O}}(1)$. Hence on a time interval of length $L = {\mathcal {O}}(\varepsilon ^{-2 \theta })$ the wave packets have moved a distance of order ${\mathcal {O}}(\varepsilon ^{-2 \theta })$. Since the wave packets have a width of order ${\mathcal {O}}(\varepsilon ^{- \theta })$ they are well separated at the end of the time interval, see Fig. 8, if the extended ansatz is a good description of reality, see below.

• 2. Plugging in the ansatz (60) into (1) shows that the amplitudes $A_+$ and $A_-$ satisfy in lowest order

  $$\begin{aligned} i \nu _{0} \partial _T A_{1,1}= & {} \varepsilon ^{2\theta -2} \nu _{1} \partial _X^2 A_{1,1} + 3 \nu _{2} A_{1,1} | A_{1,1}|^2 + 6 \nu _{2} A_{1,1} | A_{1,0}|^2, \nonumber \\ i \nu _{0} \partial _T A_{1,0}= & {} -\varepsilon ^{2\theta -2} \nu _{1} \partial _X^2 A_{1,0} + 3 \nu _{2} A_{1,0}| A_{1,0}|^2 + 6 \nu _{2} A_{1,0} | A_{1,1}|^2. \end{aligned}$$

  (63)

• 3. For $t \in [0,\varepsilon ^{-2 \theta }]$, respectively $T \in [0,\varepsilon ^{2 -2 \theta }]$, the influence of the dispersion is of order ${\mathcal {O}}(1)$ because for the Fourier multiplier we find $e^{i \varepsilon ^{2\theta -2} \nu _{1} K^2 T_0/\nu _0} = e^{i \nu _{1} K^2/\nu _0}$ for $T_0 = \varepsilon ^2 L = \varepsilon ^{2- 2 \theta }$. Therefore, on this time interval the width of the wave packet remains of order ${\mathcal {O}}(\varepsilon ^{- \theta })$. The influence of the nonlinear terms is of order ${\mathcal {O}}(\varepsilon ^{2- 2\theta })$ and therefore of lower order. Hence in lowest order the two wave packets split and separate as predicted by (60). Since the same behavior occurs at the next interval a cascade of wave packets is created. See Fig. 9. For example the ansatz for the four wave packets created at $t = 2 L$ is given by

  $$\begin{aligned} u(x,t)= & {} \varepsilon A_{1,1,1}(\varepsilon ^{\theta }(x+ c_{;1} t+ x_{1,1,1}),T) e^{ik_0x+ i \omega _{0;1} t} e^{i \phi _{1,1,1}}\\&+\, \varepsilon A_{1,1,0}(\varepsilon ^{\theta }(x- c_{;1}t + x_{1,1,0}),T) e^{ik_0x- i \omega _{0;1} t} e^{i \phi _{1,1,0}}\\&+\,\varepsilon A_{1,0,1}(\varepsilon ^{\theta }(x+ c_{;1} t+ x_{1,0,1}),T) e^{ik_0x+ i \omega _{0;1} t} e^{i \phi _{1,0,1}}\\&+\, \varepsilon A_{1,0,0}(\varepsilon ^{\theta }(x- c_{;1}t + x_{1,0,0}),T) e^{ik_0x- i \omega _{0;1} t} e^{i \phi _{1,0,0}}+ c.c. + {\mathcal {O}}(\varepsilon ^3), \end{aligned}$$

  with the envelopes $A_{1,j_1,j_2}(X,T) \in {{\mathbb {C}}}$ for $j_1,j_2 \in \{0,1\}$. The extra phases $\phi _{1,j_1,j_2}$ and extra shifts $x_{1,j_1,j_2}$ for $j_1,j_2 \in \{0,1\}$ are used to adjust the positions and phases at the jump point $t = 2 L$. The wave packet $A_{1,1}$ is split into $A_{1,1,1}$ and $A_{1,1,0}$ and the wave packet $A_{1,0}$ is split into $A_{1,0,1}$ and $A_{1,0,0}$.

• 4. There are various interactions of counter-propagating wave packets in this cascade, cf. Fig. 9. Since $A_{1,\ldots ,1}$ and $A_{1,\ldots ,0}$ depend on the different space variables $X_+ = \varepsilon ^{\theta }(x + c(t) t)$ and $X_- = \varepsilon ^{\theta }(x - c(t) t)$, and since

  $$\begin{aligned} X_+ = \varepsilon ^{\theta }(x + c(t) t) = X_- + 2 c_{;j} \varepsilon ^{\theta -2} T \end{aligned}$$

  the interaction time of the two wave packets is $T = {\mathcal {O}}( \varepsilon ^{2-\theta } )$. Therefore, for localized solutions the interaction terms are of lower order, i.e., in lowest order and localized solutions the two equations decouple, i.e., the dynamics of the wave packets on each interval $(nL,(n+1) L)$ is described by a system of decoupled NLS equations. For instance instead of (63) we can consider

  $$\begin{aligned} i \nu _{0} \partial _T A_{1,1}= & {} \varepsilon ^{2\theta -2} \nu _{1} \partial _X^2 A_{1,1} + 3 \nu _{2} A_{1,1} | A_{1,1}|^2 ,\\ i \nu _{0} \partial _T A_{1,0}= & {} -\varepsilon ^{2\theta -2} \nu _{1} \partial _X^2 A_{1,0} + 3 \nu _{2} A_{1,0}| A_{1,0}|^2 . \end{aligned}$$

  See also Fig. 8. This has been established rigorously in a number of papers (Pierce and Wayne 1995; Babin and Figotin 2006; Chirilus-Bruckner et al. 2008; Chirilus-Bruckner and Schneider 2012). The analysis also applies in our situation, may be not for the long ${\mathcal {O}}(1/\varepsilon ^2)$-time scale but at least for an $\varepsilon$-independent number of interactions which is sufficient for our purposes. Hence, in lowest order the wave packets do not interact.

Fig. 8

The solutions to initial conditions with the scaling necessary for the derivation of the dispersion management equation split in two wave packets, one moving to the left and one moving to the right. At the end of the time interval of length $L = {\mathcal {O}}(\varepsilon ^{-2 \theta })$ they are well separated in space

Fig. 9

The cascade of wave packets created at the jump points $t = nL$

We hope that this discussion convinces the potential reader that for the modeling described in Fig. 1 and in the scaling which is necessary for the derivation of the dispersion management equation a behavior occurs which cannot be described by a single dispersion management equation.

As already said at the beginning of this section in the previous arguments we considered only the best possible situation, i.e., we considered a situation without the possibility of linear instabilities as discussed in Sect. 4.2. Hence, in most cases the situation is even worse.

We finally remark that the dynamics shown in Fig. 9 which reminds us of a sequence of Laplace experiments finally leads to a Gaussian envelope of the wave packets.