The role of natural recovery category in malaria dynamics under saturated treatment

Abstract

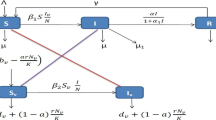
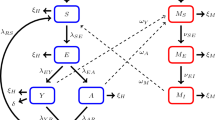
In the process of malaria transmission, natural recovery individuals are slightly infectious compared with infected individuals. Our concern is whether the infectivity of natural recovery category can be ignored in areas with limited medical resources, so as to reveal the epidemic pattern of malaria with simpler analysis. To achieve this, we incorporate saturated treatment into two-compartment and three-compartment models, and the infectivity of natural recovery category is only reflected in the latter. The non-spatial two-compartment model can admit backward bifurcation. Its spatial version does not possess rich dynamics. Besides, the non-spatial three-compartment model can undergo backward bifurcation, Hopf bifurcation and Bogdanov–Takens bifurcation. For spatial three-compartment model, due to the complexity of characteristic equation, we apply Shengjin’s Distinguishing Means to realize stability analysis. Further, the model exhibits Turing instability, Hopf bifurcation and Turing–Hopf bifurcation. This makes the model may admit bistability or even tristability when its basic reproduction number less than one. Biologically, malaria may present a variety of epidemic trends, such as elimination or inhomogeneous distribution in space and periodic fluctuation in time of infectious populations. Notably, parameter regions are given to illustrate substitution effect of two-compartment model for three-compartment model in both scenarios without or with spatial movement. Finally, spatial three-compartment model is used to present malaria transmission in Burundi. The application of efficiency index enables us to determine the most effective method to control the number of cases in different scenarios.

Appendices

Proof of Theorem2

Proof

Due to

$$\begin{aligned} \bar{Q}_{0}>0~\Leftrightarrow \bar{\mathcal {R}}_{0}<1;~~\bar{Q}_{0}=0~\Leftrightarrow \bar{\mathcal {R}}_{0}=1;~~\bar{Q}_{0}<0~\Leftrightarrow \bar{\mathcal {R}}_{0}>1, \end{aligned}$$

$\bar{g}(I_{h})=0$ admits a unique positive solution for $\bar{Q}_{0}<0$. Thereby, as $\bar{\mathcal {R}}_{0}>1$, system admits a unique endemic equilibrium $\bar{E}_{2}$.

If $\bar{\mathcal {R}}_{0}<1$, then (9) has two positive roots when $\bar{Q}_{1}<0$ and $\Delta >0$, and (9) has no positive roots when $\bar{Q}_{1}\ge 0$. Moreover, $\bar{Q}_{1}<0$ if and only if $\bar{\mathcal {R}}_{0}>\bar{P}_0$. Clearly, if $\bar{P}_{0}\ge 1$, then system has no endemic equilibrium when $\bar{\mathcal {R}}_{0}<1$. In addition, one yields that

$$\begin{aligned} \begin{aligned} \bar{P}_{0}<1~\Leftrightarrow ~\alpha>\bar{\alpha }_0,~\Delta>0~\Leftrightarrow ~ 0<\bar{\mathcal {R}}_{0}<\max \{0,~\bar{\mathcal {R}}_{0}^{-}\} ~\textrm{or}~ \bar{\mathcal {R}}_{0}>\bar{\mathcal {R}}_{0}^{+}. \end{aligned} \end{aligned}$$

Thus,  for $\alpha >\bar{\alpha }_0$ and $\bar{\mathcal {R}}_{0}^{+}<\bar{\mathcal {R}}_{0}<1$, there are two endemic equilibria $\bar{E}_{1}$ and $\bar{E}_{2}$.

For $\bar{\mathcal {R}}_{0}=1$ and $\alpha >\bar{\alpha }_0$, $\bar{Q}_{0}=0$ and $\bar{Q}_{1}<0$. Hence, system admits a unique endemic equilibrium $\bar{E}_{2}$.

When $\bar{\mathcal {R}}_{0}=\bar{\mathcal {R}}_{0}^{+}$ and $\alpha >\bar{\alpha }_0$, we have $\Delta =0$,  $\bar{Q}_{0}>0$ and $\bar{Q}_{1}<0$. So, there is a unique endemic equilibrium $\bar{E}_{1}=\bar{E}_{2}$.

When $\alpha >\bar{\alpha }_0$, $\Delta <0$ if $\bar{P}_{0}<\bar{\mathcal {R}}_{0}<\bar{\mathcal {R}}_{0}^{+}$ and $\bar{Q}_{1}\ge 0$ if $\bar{\mathcal {R}}_{0}\le \bar{P}_{0}$. Accordingly, for $\bar{\mathcal {R}}_{0}<\bar{\mathcal {R}}_{0}^{+}$ and $\alpha >\bar{\alpha }_0$, system has no endemic equilibrium.

If $\bar{\mathcal {R}}_{0}\le 1$ and $\alpha \le \bar{\alpha }_0$, then $\bar{Q}_{1}\ge 0$ and $\bar{Q}_{0}\ge 0$. Accordingly, there is no endemic equilibrium. Thereby, we complete the proof. $\square$

Proof of Theorem 4:

Proof

Direct calculation yields the local stability of equilibria. Below, we mainly prove the global stability of $\bar{E}_0$ and $\bar{E}_2$.

When $\bar{E}_0$ is a unique equilibrium of system (10), according to Poincaré-Bendixson Theorem, there is no periodic orbits in $\bar{\Gamma }$. The local stability of $\bar{E}_0$ implies that it is globally asymptotically stable (Brauer and Castillo-Chavez 2012). Thus, Theorem 4 (i) is valid.

Next, Bendixson’s theorem is applied to illustrate the nonexistence of the limit cycle. Let

$$\begin{aligned} \begin{aligned}&\check{P}_1(I_h,I_v)=b\beta _{h}\frac{I_{v}}{N_{h}}(N_{h}-I_{h})-\frac{\delta I_{h}}{1+\alpha I_{h}}-rI_{h}-d_{h}I_{h},\\ {}&\check{Q}_1(I_h,I_v)=b\beta _{v}\frac{I_{h}}{N_{h}}(N_{v}-I_{v})-d_{v}I_{v}. \end{aligned} \end{aligned}$$

One can get

$$\begin{aligned} \begin{aligned}&\frac{\partial \check{P}_1}{\partial I_h}+\frac{\partial \check{Q}_1}{\partial I_v}=-\frac{b\beta _{h}}{N_{h}}I_v-\frac{\delta }{(1+\alpha I_{h})^2}-r-d_{h}-\frac{b\beta _{v}I_{h}}{N_{h}}-d_v<0~in~\bar{\Gamma }. \end{aligned} \end{aligned}$$

This implies that there is no limit cycle in $\bar{\Gamma }$. When $\bar{\mathcal {R}}_{0}>1$, $\bar{E}_2$ is a unique locally asymptotically stable equilibrium of system (10). Accordingly, it must be globally asymptotically stable in $\bar{\Gamma }\setminus \{\bar{E}_0\}$ (Brauer and Castillo-Chavez 2012). Thus, Theorem 4 (iii) is established. $\square$

Proof of Theorem 5:

Proof

System (10) can be written as

$$\begin{aligned} \frac{\text {d}w}{\text {d}t}=\bar{f}(w) \end{aligned}$$

with $w=(w_{1},w_{2})^{\textrm{T}}=(I_{h},I_{v})^{\textrm{T}}$, and $\bar{f}=(\bar{f}_{1},\bar{f}_{2})^{\textrm{T}}$ is shown below

$$\begin{aligned} \left\{ \begin{aligned} \bar{f}_{1}&=\bar{\beta _{h}}w_{2}(N_{h}-w_{1})-\frac{\delta w_{1}}{1+\alpha w_{1}}-rw_{1}-d_{h}w_{1},\\ \bar{f}_{2}&=\bar{\beta _{v}}w_{1}(N_{v}-w_{2})-d_{v}w_{2}. \end{aligned}\right. \end{aligned}$$

Select $\delta$ as the bifurcation parameter. From $\bar{\mathcal {R}}_{0}=1$, we have $\delta =\bar{\delta }_{1}$. Let $\phi =\bar{\delta }_{1}-\delta$. At $\phi =0$, the Jacobian matrix of system (10) at the DFE $\bar{E}_{0}$, denoted by $J(\bar{E}_{0})|_{\phi =0}$, admits a zero eigenvalue and an eigenvalue with negative real part.

The left and right eigenvectors of $J(\bar{E}_{0})|_{\phi =0}$ related to zero eigenvalue are

$$\begin{aligned} \begin{aligned} p=(p_{1},p_{2})=\left( \frac{\bar{\beta _{v}}N_{v}}{r+d_h+\bar{\delta }_1},1\right) p_{2},~ q=(q_{1},q_{2})^{\textrm{T}} =\left( \frac{d_v}{\bar{\beta _h}N_h},1\right) ^{\textrm{T}}q_{2}, \end{aligned} \end{aligned}$$

respectively, where $q_{2}>0$ satisfying Theorem 4.1 in Castillo-Chavez and Song (2004). Furthermore, $p_{2}$ and $q_{2}$ can be selected to satisfy $p_{2}q_{2}=\frac{(r+d_h+\bar{\delta }_1)\bar{\beta _h}N_h}{\bar{\beta _{v}}N_vd_v+(r+d_h+\bar{\delta }_1)\bar{\beta _h}N_h} >0$ such that $p\cdot q=1.$

In addition,

$$\begin{aligned} \begin{aligned}&\frac{\partial ^{2}\bar{f}_{1}}{\partial w_{1}^{2}}(0,0)=2\alpha \bar{\delta }_1,~\frac{\partial ^{2}\bar{f}_{1}}{\partial w_{1}\partial w_{2}}(0,0)=\frac{\partial ^{2}\bar{f}_{1}}{\partial w_{2}\partial w_{1}}(0,0)=-\bar{\beta _{h}},\\&\frac{\partial ^{2}\bar{f}_{2}}{\partial w_{1}\partial w_{2}}(0,0)=\frac{\partial ^{2}\bar{f}_{2}}{\partial w_{2}\partial w_{1}}(0,0)=-\bar{\beta _{v}}, ~\frac{\partial ^{2}\bar{f}_{1}}{\partial w_{1}\partial \phi }(0,0)=1,\\ \end{aligned} \end{aligned}$$

and remaining derivatives are equal to zero.

Based on Theorem 4.1 in Castillo-Chavez and Song (2004), the coefficients $\tilde{a}$ and $\tilde{b}$ are

$$\begin{aligned} \begin{aligned} \tilde{a}&=\sum \limits _{k,i,j=1}^{2}p_{k}q_{i}q_{j}\frac{\partial ^{2}\bar{f}_{k}}{\partial w_{i}\partial w_{j}}(0,0)= \frac{2\bar{\beta _{h}}\bar{\delta }_1 N_{h}d_{v}}{(r+d_h+\bar{\delta }_1)^2}p_2q_2^2(\alpha -\bar{\alpha }_{1}),\\ \tilde{b}&=\sum \limits _{k,i=1}^{2}\bar{p}_{k}\bar{q}_{i} \frac{\partial ^{2}\bar{f}_{k}}{\partial w_{i}\partial \phi }(0,0)= \frac{\bar{\beta _{h}}\bar{\beta _{v}}N_{h}N_{v}}{(r+d_h+\bar{\delta }_1)^2}p_2q_2>0. \end{aligned} \end{aligned}$$

Accordingly, system (10) undergoes, at $\bar{\mathcal {R}}_{0}=1$, a backward bifurcation as $\alpha >\bar{\alpha }_{1}$, and a forward bifurcation as $\alpha <\bar{\alpha }_{1}$. $\square$

Proof of Theorem 10:

Direct calculation can obtain the local stability of equilibria. Next, applying geometric singular perturbation theory (Feng et al. 2004; Fenichel 1979), introduce the reduced system corresponding to system (19)

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\text {d}I_{h}}{\text {d}s}=\bar{\beta }_{h}\frac{\bar{\beta }_{v}(I_{h}+\theta R_{h})N_v}{\bar{\beta }_{v}(I_{h}+\theta R_{h})+d_{v}}(N_{h}-I_{h}-R_{h})-\bar{r}I_{h}-\frac{\bar{\delta } I_{h}}{1+\alpha I_{h}}-\bar{d}_h I_{h},\\&\frac{\text {d}R_{h}}{\text {d}s}=\bar{r}I_{h}-\bar{v}R_{h}-\bar{d}_hR_{h}, \end{aligned}\right. \end{aligned}$$

(D1)

where $\varepsilon =\frac{d_h}{d_v}$, $s=\varepsilon t$, $d_h=\varepsilon \bar{d}_h$, $\frac{b\beta _h}{N_h}=\varepsilon \bar{\beta }_{h}$,  $\delta =\varepsilon \bar{\delta }$, $v=\varepsilon \bar{v}$, $r=\varepsilon \bar{r}$,  $\bar{\beta }_v=\frac{b\beta _v}{N_h}$. Due to the facts that systems (19) and (D1) in this work correspond to systems (58) and (27) in Wang and Zhao (2022), and Wang and Zhao (2022) provides detailed derivation of the dynamics for reduced system (27) that can reveal the dynamics of system (58), we directly apply these results. Specifically, the stability of $\hat{E}_0=(0,0)^\textrm{T}$ in system (D1) is consistent with that of $E_0$ in system (19). Hence, the global stability of the DFE $E_0$ in system (19) is demonstrated by studying the global stability of the DFE $\hat{E}_0$ in reduced system (D1).

For system (D1), $\hat{\Gamma }=\{(I_h,R_h)^\textrm{T}\big |0\le I_h\le N_h,~0\le R_h\le N_h\}$ is positively invariant. If $E_0$ is a unique equilibrium of system (19), then $\hat{E}_0$ is a unique equilibrium of system (D1) Wang and Zhao (2022). According to Poincaré-Bendixson Theorem, system (D1) admits no periodic orbits in $\hat{\Gamma }$. Since the local stability of $E_0$ means the local stability of $\hat{E}_0$, the local stability of $\hat{E}_0$ implies that it is globally asymptotically stable in $\hat{\Gamma }$ (Brauer and Castillo-Chavez 2012). Thus, Theorem 10 is valid.

Proof of Corollary 3:

After some calculations, we obtain the local stability of equilibria. For $\alpha =0$, similar to the proof of Theorem 10, the global stability of $E_0$ and $E_3$ in system (19) is obtained by proving the global stability of $\hat{E}_0$ and $\hat{E}_3=(I_{h3},R_{h3})^\textrm{T}$ in reduced system (D1) (Wang and Zhao 2022).

When $E_0$ is a unique equilibrium of system (19), $\hat{E}_0$ is a unique equilibrium of system (D1). Similar to the proof of Theorem 4 (i) and Theorem 10 (i), its local stability means its global stability. Thus, Corollary 3 (i) is valid.

In the following, Dulac’s criterion is applied to prove the nonexistence of the limit cycle. Let

$$\begin{aligned} \begin{aligned}&\check{P}_2(I_h,R_h)=\bar{\beta }_{h}\frac{\bar{\beta }_{v}(I_{h}+\theta R_{h})N_v}{\bar{\beta }_{v}(I_{h}+\theta R_{h})+d_{v}}(N_{h}-I_{h}-R_{h})-\bar{r}I_{h}-\bar{\delta } I_{h}-\bar{d}_h I_{h},\\ {}&\check{Q}_2(I_h,R_h)=\bar{r}I_{h}-\bar{v}R_{h}-\bar{d}_hR_{h}, \end{aligned} \end{aligned}$$

and take Dulac function $\check{D}=\frac{\bar{\beta }_{v}(I_{h}+\theta R_{h})+d_{v}}{I_{h}+\theta R_{h}}$. We have

$$\begin{aligned} \begin{aligned} \frac{\partial (\check{D}\check{P}_2)}{\partial I_h}+\frac{\partial (\check{D}\check{Q}_2)}{\partial I_v}&=-\bar{\beta }_{h}\bar{\beta }_{v}N_v-\bar{\beta }_{v}(\bar{\delta }+\bar{r}+\bar{d}_{h}) -d_{v}(\bar{\delta }+\bar{r}+\bar{d}_{h})\frac{\theta R_h}{(I_{h}+\theta R_{h})^2}\\ {}&\quad -d_{v}(\bar{r}\theta +\bar{v}+\bar{d}_{h})\frac{I_h}{(I_{h}+\theta R_{h})^2} -\bar{\beta }_{v}(\bar{v}+\bar{d}_{h})<0~in~\hat{\Gamma }\backslash \{\hat{E}_0\}. \end{aligned} \end{aligned}$$

This implies that there is no limit cycle in $\hat{\Gamma }\backslash \{\hat{E}_0\}$. When $\mathcal {R}_{0}>1$, $E_3$ is a unique locally asymptotically stable equilibrium of system (19) with $\alpha =0$. Then $\hat{E}_3$ is a unique locally asymptotically stable equilibrium of system (D1) with $\alpha =0$. Hence, $\hat{E}_3$ must be globally asymptotically stable in $\hat{\Gamma }\backslash \{\hat{E}_0\}$ (Brauer and Castillo-Chavez 2012). Therefore, Corollary 3 (ii) holds.

The definitions of $b_{20}$, $c_{20}$ and $c_{11}$

$$\begin{aligned} \begin{aligned}&a^1_1=-\bar{\beta _h}I_v^*-d_h-r-\frac{\delta }{(1+\alpha I_h^*)^2},~ a^1_2=-\bar{\beta _h}I_v^*,~a^1_3=\bar{\beta _h}(N_h-I_h^*-R_h^*),~ a^2_1=r,\\&a^2_2=-(v+d_h),~a^3_1=\bar{\beta _v}(N_v-I_v^*),~a^3_2=\theta \bar{\beta _v}(N_v-I_v^*),~ a^3_3=-\bar{\beta _v}(I_h^*+\theta R_h^*)-d_v,\\&a^1_{11}=\frac{\delta \alpha }{(1+\alpha I_h^*)^3},~a^1_{13}=-\bar{\beta _h},~ a^1_{23}=-\bar{\beta _h},~a^3_{13}=-\bar{\beta _v},~a^3_{23}=-\theta \bar{\beta _v},\\&v_{11}=a^2_2a^3_3,~v_{21}=-a^2_1a^3_3,~v_{31}=-a^3_1a^2_2+a^3_2a^2_1, ~v_{12}=-a^3_3,~v_{22}=0,~v_{32}=\frac{a^3_3(a_{2}^2+a^1_1)}{a^1_3},\\ \end{aligned} \end{aligned}$$

$$\begin{aligned}&v_{13}=(a^1_1+a^3_3)(a^1_1+a^2_2), ~v_{23}=a^2_1(a^1_1+a^2_2),~v_{33}=a^3_1(a^1_1+a^3_3)+a^3_2a^2_1,\\&T_{11}=-\frac{v_{32}v_{23}}{|T|},~T_{21}=\frac{v_{31}v_{23}-v_{21}v_{33}}{|T|}, ~T_{13}=\frac{v_{12}v_{23}}{|T|},~T_{23}=\frac{v_{21}v_{13}-v_{11}v_{23}}{|T|},\\&b_{20}=T_{11}(a^1_{11}v_{11}^2+a^1_{13}v_{11}v_{31}+a^1_{23}v_{21}v_{31}) +T_{13}(a^3_{13}v_{11}v_{31}+a^3_{23}v_{21}v_{31}),\\&c_{20}=T_{21}(a^1_{11}v_{11}^2+a^1_{13}v_{11}v_{31}+a^1_{23}v_{21}v_{31}) +T_{23}(a^3_{13}v_{11}v_{31}+a^3_{23}v_{21}v_{31}),\\&c_{11}=T_{21}(2a^1_{11}v_{11}v_{12}+a^1_{13}(v_{12}v_{31}+v_{11}v_{32}) +a^1_{23}(v_{31}v_{22}+v_{21}v_{32}))\\&\qquad \quad +T_{23}(a^3_{13}(v_{12}v_{31}+v_{11}v_{32})+a^3_{23}(v_{31}v_{22}+v_{21}v_{32}))\\ \end{aligned}$$

with $|T|=v_{12}(v_{31}v_{23}-v_{21}v_{33})+v_{32}(v_{21}v_{13}-v_{11}v_{23})$.

The normal form of Turing–Hopf bifurcation at $E_2$

Using the method in Song et al. (2016), we derive the normal form of Turing–Hopf bifurcation at $E_2$. We first introduce perturbation vector $\epsilon =(\epsilon _1,\epsilon _2)$ and make $\alpha =\alpha ^*+\epsilon _1$ and $r=r^*+\epsilon _2$. Then system (5) reads as

$$\begin{aligned} \left\{ \begin{aligned} \frac{\partial I_{h}}{\partial t}&=d_1\Delta I_{h}+\bar{\beta _{h}}I_{v}(N_{h}-I_{h}-R_{h}) -\frac{\delta I_{h}}{1+(\alpha ^*+\epsilon _1) I_{h}}\\ {}&\quad -(r^*+\epsilon _2)I_{h}-d_{h}I_{h},&t>0,~x\in \Omega ,\\ \frac{\partial R_{h}}{\partial t}&=d_1\Delta R_{h}+(r^*+\epsilon _2)I_{h}-d_{h}R_{h}-vR_{h},&t>0,~x\in \Omega ,\\ \frac{\partial I_{v}}{\partial t}&=d_{2}\Delta I_{v}+\bar{\beta _{v}}(I_{h}+\theta R_{h})(N_{v}-I_{v}),&t>0,~x\in \Omega ,\\ \frac{\partial I_{h}}{\partial n}&=\frac{\partial R_{h}}{\partial n}=\frac{\partial I_{v}}{\partial n}=0,&x\in \partial \Omega . \end{aligned} \right. \end{aligned}$$

(G2)

Note that $E_2$ is still the endemic equilibrium of system (G2).

Taking the transformation $\xi _1=I_h-I_{h2}$, $\xi _2=R_h-R_{h2}$, $\xi _3=I_v-I_{v2}$, one has

$$\begin{aligned} \left\{ \begin{aligned} \frac{\partial \xi _1}{\partial t}&=d_1\Delta \xi _1+f_1(\xi _1+I_{h2},\xi _2+R_{h2},\xi _3+I_{v2}),&t>0,~x\in \Omega ,\\ \frac{\partial \xi _{2}}{\partial t}&=d_1\Delta \xi _{2}+f_2(\xi _1+I_{h2},\xi _2+R_{h2},\xi _3+I_{v2}),&t>0,~x\in \Omega ,\\ \frac{\partial \xi _{3}}{\partial t}&=d_{2}\Delta \xi _{3}+f_3(\xi _1+I_{h2},\xi _2+R_{h2},\xi _3+I_{v2}),&t>0,~x\in \Omega ,\\ \frac{\partial \xi _{1}}{\partial n}&=\frac{\partial \xi _{2}}{\partial n}=\frac{\partial \xi _{3}}{\partial n}=0,&t>0,~x\in \partial \Omega , \end{aligned} \right. \end{aligned}$$

(G3)

with

$$\begin{aligned} \begin{aligned} f_1(\xi _1+I_{h2},\xi _2+R_{h2},\xi _3+I_{v2})&=\bar{\beta _{h}}(\xi _3+I_{v2})(N_{h}-\xi _1-I_{h2}-\xi _2-R_{h2}) \\ {}&\quad -\frac{\delta (\xi _1+I_{h2})}{1+(\alpha ^*+\epsilon _1) (\xi _1+I_{h2})}\\ {}&\quad -(r^*+\epsilon _2)(\xi _1+I_{h2}) -d_{h}(\xi _1+I_{h2}),\\ f_2(\xi _1+I_{h2},\xi _2+R_{h2},\xi _3+I_{v2})&= (r^*+\epsilon _2)(\xi _1+I_{h2})-(d_{h}+v)(\xi _2+R_{h2}),\\ f_3(\xi _1+I_{h2},\xi _2+R_{h2},\xi _3+I_{v2})&=\bar{\beta _{v}}\left( \xi _1+I_{h2}+\theta (\xi _2+R_{h2})\right) (N_{v}-\xi _3-I_{v2})\\ {}&\quad -d_v(\xi _3+I_{v2}). \end{aligned} \end{aligned}$$

Letting $U=(\xi _1,\xi _2,\xi _3)^{\textrm{T}}$ and

$$\begin{aligned} L(\epsilon ) = \left( \begin{array}{ccc} -\bar{\beta _{h}}I_{v2}-\frac{\delta }{(1+(\alpha ^*+\epsilon _1) I_{h2})^2}-r^* -\epsilon _2-d_h &{} -\bar{\beta _{h}}I_{v2} &{} \bar{\beta _{h}}m_5\\ r^*+\epsilon _2 &{} -v-d_h &{}0 \\ \bar{\beta _{v}}(N_v-I_{v2}) &{} \theta \bar{\beta _{v}}(N_v-I_{v2}) &{} -m_3 \\ \end{array} \right) , \end{aligned}$$

system (G3) takes the following form

$$\begin{aligned} \begin{aligned}&\frac{\partial U}{\partial t}=\mathcal {L}U+\tilde{f}(U,\epsilon ),~t>0,~x\in \Omega , \end{aligned} \end{aligned}$$

(G4)

where

$$\begin{aligned} \mathcal {L}U = \left( \begin{array}{ccc} d_1\Delta &{} 0 &{} 0\\ 0 &{} d_1\Delta &{}0 \\ 0 &{} 0 &{} d_2\Delta \\ \end{array} \right) U+L(0)U, \end{aligned}$$

and

$$\begin{aligned} \begin{array}{lll} \tilde{f}(U,\epsilon ) &{}= L(\epsilon )U-L(0)U+f(U,\epsilon ) \\ {} &{}= \sum \limits _{j_1+j_2+j_3+j_4+j_5\ge 2}\frac{1}{j_1!j_2!j_3!j_4!j_5!} f_{j_1j_2j_3j_4j_5}\xi _1^{j_1}\xi _2^{j_2}\xi _3^{j_3} \epsilon _1^{j_4}\epsilon _2^{j_5} \end{array} \end{aligned}$$

with

$$\begin{aligned} \begin{array}{llll} f(U,\epsilon ) &{}=&{} \left( \begin{array}{c} f^{(1)}(U,\epsilon ) \\ f^{(2)}(U,\epsilon ) \\ f^{(3)}(U,\epsilon ) \\ \end{array} \right) , \end{array} \end{aligned}$$

in which

$$\begin{aligned} \begin{aligned} f^{(1)}(U,\epsilon )&=f_1(\xi _1+I_{h2},\xi _2+R_{h2},\xi _3+I_{v2})+\bar{\beta _{h}}I_{v2}\xi _2 -\bar{\beta _{h}}(N_h-I_{h2}-R_{h2})\xi _3\\&\quad +\left( \bar{\beta _{h}}I_{v2}+\frac{\delta }{(1+(\alpha ^*+\epsilon _1) I_{h2})^2}+r^*+\epsilon _2+d_h\right) \xi _1,\\ f^{(2)}(U,\epsilon )&=0,\\ f^{(3)}(U,\epsilon )&=f_3(\xi _1+I_{h2},\xi _2+R_{h2},\xi _3+I_{v2}) -\bar{\beta _{v}}(N_v-I_{v2})\xi _1-\theta \bar{\beta _{v}}(N_v-I_{v2})\xi _2 \\&\quad +\left( \bar{\beta _{v}}(I_{h2}+\theta R_{h2})+d_v\right) \xi _3. \end{aligned} \end{aligned}$$

For $i\in \mathbb {N}_0$, denote

$$\begin{aligned} \mathcal {M}_i = \left( \begin{array}{ccc} -d_1u_{i}-\bar{\beta _h}I_{v2}-d_h-r^*-\frac{\delta }{(1+\alpha ^* I_{h2})^2} &{} -\bar{\beta _h}I_{v2} &{} \bar{\beta _h}m_5 \\ r^* &{} -d_1u_{i}-(v+d_h) &{} 0 \\ \bar{\beta _v}(N_v-I_{v2}) &{} \theta \bar{\beta _v}(N_v-I_{v2}) &{} -d_2u_{i}-m_3 \\ \end{array} \right) . \end{aligned}$$

For any two vectors $\varphi$, $\psi \in \mathbb {R}^3$, define the product as $\langle \psi ^\textrm{T},\varphi \rangle =\psi ^\textrm{T}\varphi$. Let

$$\begin{aligned} \begin{aligned} \Phi _0=(\varphi _0,\overline{\varphi }_0),~\Phi _{i^*}=\varphi _{i^*},~ \Psi _0=col(\psi ^\textrm{T}_0, \overline{\psi }^\textrm{T}_0), ~\Psi _{i^*}=\psi ^\textrm{T}_{i^*}, \end{aligned} \end{aligned}$$

where $\varphi _0=(\varphi _{01},\varphi _{02},\varphi _{03})^\textrm{T}\in \mathbb {C}^3$, $\varphi _{i^*}=(\varphi _{i^*1},\varphi _{i^*2},\varphi _{i^*3})^\textrm{T}\in \mathbb {R}^3$ are the eigenvectors relevant to the eigenvalues $i\omega _0$ and 0, respectively; $\psi _0=(\psi _{01},\psi _{02},\psi _{03})^\textrm{T}\in \mathbb {C}^3$, $\psi _{i^*}=(\psi _{i^*1},\psi _{i^*2},\psi _{i^*3})^\textrm{T}\in \mathbb {R}^3$ are the corresponding adjoint eigenvectors. After some computations, acquire

$$\begin{aligned} \begin{aligned} \varphi _{01}&=1,~\varphi _{02}=\frac{r^*}{i\omega _0+d_h+v},~ \psi _{01}=\frac{1}{c_1}, ~\psi _{03}=\frac{\bar{\beta _h}m_5}{c_1(m_3-i\omega _0)},\\ \varphi _{03}&=\frac{r^*\bar{\beta _h}I_{v2}}{\bar{\beta _h}m_5(i\omega _0+d_h+v)} +\frac{(\bar{\beta _h}I_{v2}+i\omega _0+d_h+r^*)(1+\alpha ^*I_{h2})^2 +\delta }{\bar{\beta _h}m_5(1+\alpha ^*I_{h2})^2},\\ \end{aligned} \end{aligned}$$

(G5)

$$\begin{aligned} \psi _{02}&=\frac{1}{c_1r^*}\left( \bar{\beta _h}I_{v2}+d_h+r^*+\frac{\delta }{(1+\alpha ^* I_{h2})^2}-i\omega _0-\frac{\bar{\beta _v}\bar{\beta _h}m_5(N_v-I_{v2})}{m_3-i\omega _0}\right) ,~\\ \varphi _{i^*1}&=1,~\varphi _{i^*2}=\frac{r^*}{d_1u_{i^*}+d_h+v}, ~\psi _{i^*1}=\frac{1}{c_2},~\psi _{i^*3}=\frac{\bar{\beta _h}m_5}{c_2(d_2u_{i^*}+m_3)},\\ \varphi _{i^*3}&=\frac{r^*\bar{\beta _h}I_{v2}}{\bar{\beta _h}m_5(d_1u_{i^*}+d_h+v)} +\frac{(\bar{\beta _h}I_{v2}+d_1u_{i^*}+d_h+r^*)(1+\alpha ^*I_{h2})^2 +\delta }{\bar{\beta _h}m_5(1+\alpha ^*I_{h2})^2},\\ \psi _{i^*2}&=\frac{1}{c_2r^*}\left( d_1u_{i^*}+\bar{\beta _h}I_{v2}+d_h+r^*+\frac{\delta }{(1+\alpha ^* I_{h2})^2}-\frac{\bar{\beta _v}\bar{\beta _h}m_5(N_v-I_{v2})}{d_2u_{i^*}+m_3}\right) ,~ \end{aligned}$$

where $c_1$, $c_2$ satisfy $\langle \Psi _0,\Phi _0\rangle =I_2$ and $\langle \Psi _{i^*},\Phi _{i^*}\rangle =1$, respectively, in which $I_2$ is $2\times 2$ identity matrix.

Carrying out Taylor expansion on $f(U,\varepsilon )$, the coefficients of second and third order terms are

$$\begin{aligned} \begin{array}{lll} f_{20000} = \left( \begin{array}{c} \frac{2\delta \alpha ^*}{(1+\alpha ^*I_{h2})^3} \\ 0 \\ 0 \\ \end{array} \right) ,~ f_{10100}= \left( \begin{array}{c} -\bar{\beta _h} \\ 0 \\ -\bar{\beta _v} \\ \end{array} \right) ,~\\ f_{01100}= \left( \begin{array}{c} -\bar{\beta _h} \\ 0 \\ -\theta \bar{\beta _v} \\ \end{array} \right) ,~ f_{30000} = \left( \begin{array}{c} \frac{-6\delta (\alpha ^*)^2}{(1+\alpha ^*I_{h2})^4} \\ 0 \\ 0 \\ \end{array} \right) ,~ \end{array} \end{aligned}$$

and all other coefficients equal $(0,0,0)^\textrm{T}$. In light of the results in Song et al. (2016), acquire the following third-order truncated normal form

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\text {d}z_1}{\text {d}t}= i\omega _0z_1+(B_{11}\epsilon _1+B_{21}\epsilon _2)z_1+B_{210}z_1^2z_2+B_{102}z_1z_3^2,\\&\frac{\text {d}z_2}{\text {d}t}= -i\omega _0z_2+(\bar{B}_{11}\epsilon _1+\bar{B}_{21}\epsilon _2)z_2+\bar{B}_{210}z_1z_2^2+\bar{B}_{102}z_2z_3^2,\\&\frac{\text {d}z_{3}}{\text {d}t}=(B_{13}\epsilon _1+B_{23}\epsilon _2)z_3+B_{111}z_1z_2z_3+B_{003}z_3^3,\\ \end{aligned}\right. \end{aligned}$$

(G6)

where

$$\begin{aligned}&B_{210}=C_{210}+\frac{3}{2}(D_{210}+E_{210}), ~B_{102}=C_{102}+\frac{3}{2}(D_{102}+E_{102}),\\&B_{111}=C_{111}+\frac{3}{2}(D_{111}+E_{111}),~ B_{003}=C_{003}+\frac{3}{2}(D_{003}+E_{003}), \end{aligned}$$

with

$$\begin{aligned} C_{210}= & {} \frac{1}{6l\pi }\psi _0^\textrm{T}A_{210}, ~C_{102}=\frac{1}{6l\pi }\psi _0^\textrm{T}A_{102}, ~C_{111}=\frac{1}{6l\pi }\psi _{i^*}^\textrm{T}A_{111},~ C_{003}=\frac{1}{4l\pi }\psi _{i^*}^\textrm{T}A_{003},\\ D_{210}= & {} \frac{1}{6l\pi \omega _0i}\left( -(\psi _0^\textrm{T}A_{200})(\psi _0^\textrm{T}A_{110})+ |\psi _0^\textrm{T}A_{110}|^2+\frac{2}{3}|\psi _0^\textrm{T}A_{020}|^2\right) ,\\ D_{102}= & {} \frac{1}{6l\pi \omega _0i}\left( -2(\psi _0^\textrm{T}A_{200})(\psi _0^\textrm{T}A_{002})+ (\psi _0^\textrm{T}A_{110})(\overline{\psi }_0^\textrm{T}A_{002})+ 2(\psi _0^\textrm{T}A_{002})(\psi _{i^*}^\textrm{T}A_{101})\right) ,\\ D_{111}= & {} -\frac{1}{3l\pi \omega _0}Im((\psi _{i^*}^\textrm{T}A_{101})(\psi _0^\textrm{T}A_{110})), ~D_{003}=-\frac{1}{3l\pi \omega _0}Im((\psi _{i^*}^\textrm{T}A_{101})(\psi _0^\textrm{T}A_{002})), \end{aligned}$$

$$\begin{aligned} E_{210}&=\frac{1}{3\sqrt{l\pi }}\psi _0^\textrm{T}\left( (f_{20000}\varphi _{01}+ f_{11000}\varphi _{02}+f_{10100}\varphi _{03})h_{0110}^{(1)}\right. \\&\quad \left. +(f_{11000}\varphi _{01}+ f_{02000}\varphi _{02}+f_{01100}\varphi _{03})h_{0110}^{(2)}\right. \\&\quad \left. +(f_{10100}\varphi _{01}+f_{01100}\varphi _{02}+f_{00200}\varphi _{03})h_{0110}^{(3)}\right. \\&\quad \left. +(f_{20000}\overline{\varphi }_{01}+ f_{11000}\overline{\varphi }_{02}+f_{10100}\overline{\varphi }_{03})h_{0200}^{(1)}\right. \\&\quad \left. +(f_{11000}\overline{\varphi }_{01}+ f_{02000}\overline{\varphi }_{02}+f_{01100}\overline{\varphi }_{03})h_{0200}^{(2)}\right. \\&\quad \left. +(f_{10100}\overline{\varphi }_{01}+ f_{01100}\overline{\varphi }_{02}+f_{00200}\overline{\varphi }_{03})h_{0200}^{(3)}\right) , \\ E_{102}&=\frac{1}{3\sqrt{l\pi }}\psi _0^\textrm{T}\left( (f_{20000}\varphi _{01}+ f_{11000}\varphi _{02}+f_{10100}\varphi _{03})h_{0002}^{(1)}\right. \\&\quad \left. +(f_{11000}\varphi _{01}+ f_{02000}\varphi _{02}+f_{01100}\varphi _{03})h_{0002}^{(2)}\right. \\&\quad \left. +(f_{10100}\varphi _{01}+f_{01100}\varphi _{02}+f_{00200}\varphi _{03})h_{0002}^{(3)}\right. \\&\quad \left. +(f_{20000}\varphi _{i^*1}+ f_{11000}\varphi _{i^*2}+f_{10100}\varphi _{i^*3})h_{i^*101}^{(1)}\right. \\&\quad \left. +(f_{11000}\varphi _{i^*1}+ f_{02000}\varphi _{i^*2}+f_{01100}\varphi _{i^*3})h_{i^*101}^{(2)}\right. \\&\quad \left. +(f_{10100}\varphi _{i^*1}+ f_{01100}\varphi _{i^*2}+f_{00200}\varphi _{i^*3})h_{i^*101}^{(3)}\right) , \\ E_{111}&=\frac{1}{3\sqrt{l\pi }}\psi _{i^*}^\textrm{T}\left( (f_{20000}\varphi _{01}+ f_{11000}\varphi _{02}+f_{10100}\varphi _{03})h_{i^*011}^{(1)}\right. \\&\quad \left. +(f_{11000}\varphi _{01}+ f_{02000}\varphi _{02}+f_{01100}\varphi _{03})h_{i^*011}^{(2)}\right. \\&\quad \left. +(f_{10100}\varphi _{01}+f_{01100}\varphi _{02}+f_{00200}\varphi _{03})h_{i^*011}^{(3)}\right. \\&\quad \left. +(f_{20000}\overline{\varphi }_{01}+ f_{11000}\overline{\varphi }_{02}+f_{10100}\overline{\varphi }_{03})h_{i^*101}^{(1)}\right. \\&\quad \left. +(f_{11000}\overline{\varphi }_{01}+ f_{02000}\overline{\varphi }_{02}+f_{01100}\overline{\varphi }_{03})h_{i^*101}^{(2)}\right. \\&\quad \left. +(f_{10100}\overline{\varphi }_{01}+ f_{01100}\overline{\varphi }_{02}+f_{00200}\overline{\varphi }_{03})h_{i^*101}^{(3)}\right) \\&\quad +\psi _{i^*}^\textrm{T}(f_{20000}\varphi _{i^*1}+ f_{11000}\varphi _{i^*2}+f_{10100}\varphi _{i^*3}) \left( \frac{1}{3\sqrt{l\pi }}h_{0110}^{(1)}+ \frac{1}{3\sqrt{2l\pi }}h_{(2i^*)110}^{(1)}\right) \\&\quad +\psi _{i^*}^\textrm{T}(f_{1100}\varphi _{i^*1}+ f_{02000}\varphi _{i^*2}+f_{01100}\varphi _{i^*3}) \left( \frac{1}{3\sqrt{l\pi }}h_{0110}^{(2)}+ \frac{1}{3\sqrt{2l\pi }}h_{(2i^*)110}^{(2)}\right) \\&\quad +\psi _{i^*}^\textrm{T}(f_{10100}\varphi _{i^*1}+ f_{01100}\varphi _{i^*2}+f_{00200}\varphi _{i^*3}) \left( \frac{1}{3\sqrt{l\pi }}h_{0110}^{(3)}+ \frac{1}{3\sqrt{2l\pi }}h_{(2i^*)110}^{(3)}\right) , \\ \end{aligned}$$

$$\begin{aligned} \begin{aligned} E_{003}&=\psi _{i^*}^\textrm{T} (f_{20000}\varphi _{i^*1}+ f_{11000}\varphi _{i^*2}+f_{10100}\varphi _{i^*3}) \left( \frac{1}{3\sqrt{l\pi }}h_{0002}^{(1)}+ \frac{1}{3\sqrt{2l\pi }}h_{(2i^*)002}^{(1)}\right) \\&\quad +\psi _{i^*}^\textrm{T}(f_{11000}\varphi _{i^*1}+ f_{02000}\varphi _{i^*2}+f_{01100}\varphi _{i^*3}) \left( \frac{1}{3\sqrt{l\pi }}h_{0002}^{(2)}+ \frac{1}{3\sqrt{2l\pi }}h_{(2i^*)002}^{(2)}\right) \\&\quad +\psi _{i^*}^\textrm{T}(f_{10100}\varphi _{i^*1}+ f_{01100}\varphi _{i^*2}+f_{00200}\varphi _{i^*3}) \left( \frac{1}{3\sqrt{l\pi }}h_{0002}^{(3)}+\frac{1}{3\sqrt{2l\pi }}h_{(2i^*)002}^{(3)}\right) , \end{aligned} \end{aligned}$$

with

$$\begin{aligned} h_{0200}= & {} \frac{1}{\sqrt{l\pi }}(2\omega _0i\mathcal {I}-\mathcal {M}_0)^{-1} (A_{200}-\psi _0^\textrm{T}A_{200}\varphi _0-\overline{\psi }_0^\textrm{T}A_{200} \overline{\varphi }_0), \\ h_{0020}= & {} \frac{1}{\sqrt{l\pi }}(-2\omega _0i\mathcal {I}-\mathcal {M}_0)^{-1} (A_{020}-\psi _0^\textrm{T}A_{020}\varphi _0-\overline{\psi }_0^\textrm{T}A_{020} \overline{\varphi }_0), \\ h_{0002}= & {} \frac{1}{\sqrt{l\pi }}(-\mathcal {M}_0)^{-1} (A_{002}-\psi _0^\textrm{T}A_{002}\varphi _0-\overline{\psi }_0^\textrm{T}A_{002} \overline{\varphi }_0), \\ h_{0110}= & {} \frac{1}{\sqrt{l\pi }}(-\mathcal {M}_0)^{-1} (A_{110}-\psi _0^\textrm{T}A_{110}\varphi _0-\overline{\psi }_0^\textrm{T}A_{110} \overline{\varphi }_0), \\ h_{i^*101}= & {} \frac{1}{\sqrt{l\pi }}(i\omega _0\mathcal {I}-\mathcal {M}_{i^*})^{-1} (A_{101}-\psi _{i^*}^\textrm{T}A_{101}\varphi _{i^*}), \\ h_{i^*011}= & {} \frac{1}{\sqrt{l\pi }}(-i\omega _0\mathcal {I}-\mathcal {M}_{i^*})^{-1} (A_{011}-\psi _{i^*}^\textrm{T}A_{011}\varphi _{i^*}),\\ h_{(2i^*)002}= & {} \frac{1}{\sqrt{2 l\pi }}(-\mathcal {M}_{2i^*})^{-1} A_{002},~h_{(2i^*)110}=(0,0,0)^\textrm{T}. \end{aligned}$$

Moreover,

$$\begin{aligned} A_{200}&=f_{20000}\varphi _{01}^2+2f_{11000}\varphi _{01}\varphi _{02} +2f_{10100}\varphi _{01}\varphi _{03}+f_{02000}\varphi _{02}^2\\&\quad + 2f_{01100}\varphi _{02}\varphi _{03}+f_{00200}\varphi _{03}^2=\overline{A}_{020}, \\ A_{002}&=f_{20000}\varphi _{i^*1}^2+2f_{11000}\varphi _{i^*1}\varphi _{i^*2} +2f_{10100}\varphi _{i^*1}\varphi _{i^*3}+f_{02000}\varphi _{i^*2}^2\\&\quad + 2f_{01100}\varphi _{i^*2}\varphi _{i^*3}+f_{00200}\varphi _{i^*3}^2, \\ A_{110}&=2(f_{20000}|\varphi _{01}|^2+2f_{11000}Re(\varphi _{01}\overline{\varphi }_{02}) +2f_{10100}Re(\varphi _{01}\overline{\varphi }_{03}) +f_{02000}|\varphi _{02}|^2\\&\quad + 2f_{01100}Re(\varphi _{02}\overline{\varphi }_{03})+f_{00200}|\varphi _{03}|^2), \\ A_{101}&=2\left( f_{20000}\varphi _{i^*1}\varphi _{01} +f_{11000}(\varphi _{i^*2}\varphi _{01}+\varphi _{i^*1}\varphi _{02}) +f_{10100}(\varphi _{i^*3}\varphi _{01}+\varphi _{i^*1}\varphi _{03})\right. \\&\quad \left. +f_{02000}\varphi _{i^*2}\varphi _{02} +f_{01100}(\varphi _{i^*3}\varphi _{02}+\varphi _{i^*2}\varphi _{03}) +f_{00200}\varphi _{i^*3}\varphi _{03}\right) =\overline{A}_{011}, \end{aligned}$$

and

$$\begin{aligned} A_{210}= & {} 3\left( f_{30000}|\varphi _{01}|^2\varphi _{01}+ f_{03000}|\varphi _{02}|^2\varphi _{02}+f_{00300}|\varphi _{03}|^2\varphi _{03} \right. \\{} & {} \quad \left. +f_{21000}(2|\varphi _{01}|^2\varphi _{02}+\varphi _{01}^2\overline{\varphi }_{02}) +f_{20100}(2|\varphi _{01}|^2\varphi _{03}+\varphi _{01}^2\overline{\varphi }_{03}) \right. \\{} & {} \quad \left. +f_{12000}(2\varphi _{01}|\varphi _{02}|^2+\overline{\varphi }_{01}\varphi _{02}^2) +f_{10200}(2\varphi _{01}|\varphi _{03}|^2+\overline{\varphi }_{01}\varphi _{03}^2) \right. \\{} & {} \quad \left. +f_{02100}(2|\varphi _{02}|^2\varphi _{03}+\varphi _{02}^2\overline{\varphi }_{03}) +f_{01200}(2\varphi _{02}|\varphi _{03}|^2+\overline{\varphi }_{02}\varphi _{03}^2) \right. \\{} & {} \quad \left. +2f_{11100}(\overline{\varphi }_{01}\varphi _{02}\varphi _{03}+ \varphi _{01}\overline{\varphi }_{02}\varphi _{03}+\varphi _{01}\varphi _{02}\overline{\varphi }_{03})\right) , \\ A_{102}= & {} 3\left( f_{30000}\varphi _{01}\varphi _{i^*1}^2+ f_{03000}\varphi _{02}\varphi _{i^*2}^2+f_{00300}\varphi _{03}\varphi _{i^*3}^2 \right. \\{} & {} \quad \left. +f_{21000}(2\varphi _{01}\varphi _{i^*1}\varphi _{02}+\varphi _{i^*1}^2\varphi _{02}) +f_{20100}(2\varphi _{01}\varphi _{i^*1}\varphi _{03}+\varphi _{i^*1}^2\varphi _{03}) \right. \\{} & {} \quad \left. +f_{12000}(2\varphi _{i^*1}\varphi _{02}\varphi _{i^*2}+\varphi _{01}\varphi _{i^*2}^2) +f_{10200}(2\varphi _{i^*1}\varphi _{03}\varphi _{i^*3}+\varphi _{01}\varphi _{i^*3}^2) \right. \\{} & {} \quad \left. +f_{02100}(2\varphi _{02}\varphi _{i^*2}\varphi _{i^*3}+\varphi _{i^*2}^2\varphi _{03}) +f_{01200}(2\varphi _{i^*2}\varphi _{03}\varphi _{i^*3}+\varphi _{02}\varphi _{i^*3}^2) \right. \\{} & {} \quad \left. +2f_{11100}(\varphi _{01}\varphi _{i^*2}\varphi _{i^*3}+ \varphi _{i^*1}\varphi _{02}\varphi _{i^*3}+\varphi _{i^*1}\varphi _{i^*2}\varphi _{03})\right) , \\ \end{aligned}$$

Fig. 14

When $(\epsilon _1,\epsilon _2)= (8.0559\times 10^{-4},5.2207\times 10^{-5})\in$  II, there are a stable $E_0$ and a stable spatially homogeneous periodic solution

Fig. 15

When $(\epsilon _1,\epsilon _2)= (-7.7102\times 10^{-4},-7.27\times 10^{-5})\in$ IV, system (5) has a stable $E_0$ and a pair of stable spatially inhomogeneous periodic solutions

Fig. 16

When $(\epsilon _1,\epsilon _2) =(-8.9791\times 10^{-4},-5.17\times 10^{-5})\in$ VI, $E_0$ and spatial inhomogeneous steady states are stable

$$\begin{aligned} A_{003}= & {} f_{30000}\varphi _{i^*1}^3+ f_{03000}\varphi _{i^*2}^3+f_{00300}\varphi _{i^*3}^3 +3f_{21000}\varphi _{i^*1}^2\varphi _{i^*2} +3f_{20100}\varphi _{i^*1}^2\varphi _{i^*3}\\{} & {} \quad +3f_{12000}\varphi _{i^*1}\varphi _{i^*2}^2 +3f_{10200}\varphi _{i^*1}\varphi _{i^*3}^2+3f_{02100}\varphi _{i^*2}^2\varphi _{i^*3} \\{} & {} \quad +3f_{01200}\varphi _{i^*2}\varphi _{i^*3}^2 +6f_{11100}\varphi _{i^*1}\varphi _{i^*2}\varphi _{i^*3}, \\ A_{111}= & {} 6\left( f_{30000}|\varphi _{01}|^2\varphi _{i^*1}+ f_{03000}|\varphi _{02}|^2\varphi _{i^*2}+f_{00300}|\varphi _{03}|^2\varphi _{i^*3} \right. \\{} & {} \quad \left. +f_{21000}(2Re(\varphi _{01}\overline{\varphi }_{02})\varphi _{i^*1} +|\varphi _{01}|^2\varphi _{i^*2}) \right. \\{} & {} \quad \left. +f_{20100}(2Re(\varphi _{01}\overline{\varphi }_{03})\varphi _{i^*1} +|\varphi _{01}|^2\varphi _{i^*3}) \right. \\{} & {} \quad \left. +f_{12000}(2Re(\varphi _{01}\overline{\varphi }_{02})\varphi _{i^*2} +|\varphi _{02}|^2\varphi _{i^*1}) \right. \\{} & {} \quad \left. +f_{10200}(2Re(\varphi _{01}\overline{\varphi }_{03})\varphi _{i^*3} +|\varphi _{03}|^2\varphi _{i^*1}) \right. \\{} & {} \quad \left. +f_{02100}(2Re(\varphi _{02}\overline{\varphi }_{03})\varphi _{i^*2} +|\varphi _{02}|^2\varphi _{i^*3}) \right. \\{} & {} \quad \left. +f_{01200}(2Re(\varphi _{02}\overline{\varphi }_{03})\varphi _{i^*3} +|\varphi _{03}|^2\varphi _{i^*2}) \right. \\{} & {} \quad \left. +2f_{11100}(Re(\varphi _{01}\overline{\varphi }_{02})\varphi _{i^*3} +Re(\varphi _{01}\overline{\varphi }_{03})\varphi _{i^*2} +Re(\varphi _{02}\overline{\varphi }_{03})\varphi _{i^*1})\right) . \end{aligned}$$

In addition,

$$\begin{aligned} \begin{aligned}&B_{11}=\psi _0^\textrm{T}L_{1}^{(1,0)}(\varphi _0), ~B_{21}=\psi _0^\textrm{T}L_{1}^{(0,1)}(\varphi _0), \\ {}&B_{13}=\psi _{i^*}^\textrm{T}L_{1}^{(1,0)}(\varphi _{i^*}),~ B_{23}=\psi _{i^*}^\textrm{T}L_{1}^{(0,1)}(\varphi _{i^*}), \end{aligned} \end{aligned}$$

where

$$\begin{aligned} L_1^{(1,0)} = \left( \begin{array}{ccc} \frac{2\delta I_{h2}}{(1+\alpha ^*I_{h2})^3} &{} 0 &{} 0\\ 0 &{} 0 &{}0 \\ 0 &{} 0 &{} 0 \\ \end{array} \right) ,~ L_1^{(0,1)} = \left( \begin{array}{ccc} -1 &{} 0 &{} 0\\ 1 &{} 0 &{}0 \\ 0 &{} 0 &{} 0 \\ \end{array} \right) . \end{aligned}$$

Multi-stability of system (5) in regions II, IV and VI:

The part is devoted to presenting dynamics of system (5) in regions II, IV and VI. If $(\epsilon _1,\epsilon _2)\in$ II, then system (33) admits an unstable equilibrium $J_0$ and a stable equilibrium $J_1$. Correspondingly, when the parameter vector $(\epsilon _1,\epsilon _2)$ passes through curve $F_0$ from I to II, the stability of $E_2$ for system (5) changes and a stable spatially homogeneous periodic solution appears. This indicates that system (5) presents periodic pattern for appropriate initial value. In the case, malaria is mainly manifested as disappearance or periodic outbreak (see Fig. 14).

When $(\epsilon _1,\epsilon _2)\in$ IV, system (33) admits four unstable equilibria $J_0$, $J_1$, $J_2^\pm$, and a pair of stable equilibria $J_3^\pm$. Accordingly, as the parameters $\epsilon _1$, $\epsilon _2$ pass through curve $K_1$ from III to IV, a pair of stable spatially inhomogeneous periodic solutions emerge, and the spatially homogeneous periodic solution becomes unstable at the same time. Besides, the stability of $E_0$ and $E_2$ is same as that in II. This concludes that system (5) exhibits tristability and spatiotemporal patterns with appropriate initial conditions shown in Fig. 15.

When $(\epsilon _1,\epsilon _2)\in$ VI, system (33) admits a unstable equilibria $J_0$, and a pair of stable equilibria $J_2^\pm$. Then, as the parameter vector $(\epsilon _1,\epsilon _2)$ passes through curve $K_2$ and moves to VI, the stable spatially inhomogeneous periodic solution disappears. There are a pair of stable spatial inhomogeneous steady states. Besides, the stability of $E_0$ and $E_2$ is same as that in II. In this case, system (5) also exhibits tristability (see Fig. 16).