Quasi-neutral dynamics in a coinfection system with N strains and asymmetries along multiple traits

Abstract

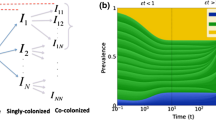
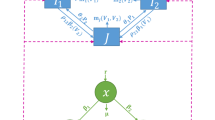
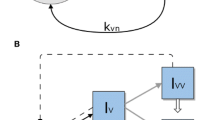
Understanding the interplay of different traits in a co-infection system with multiple strains has many applications in ecology and epidemiology. Because of high dimensionality and complex feedback between traits manifested in infection and co-infection, the study of such systems remains a challenge. In the case where strains are similar (quasi-neutrality assumption), we can model trait variation as perturbations in parameters, which simplifies analysis. Here, we apply singular perturbation theory to many strain parameters simultaneously and advance analytically to obtain their explicit collective dynamics. We consider and study such a quasi-neutral model of susceptible–infected–susceptible (SIS) dynamics among N strains, which vary in 5 fitness dimensions: transmissibility, clearance rate of single- and co-infection, transmission probability from mixed coinfection, and co-colonization vulnerability factors encompassing cooperation and competition. This quasi-neutral system is analyzed with a singular perturbation method through an appropriate slow–fast decomposition. The fast dynamics correspond to the embedded neutral system, while the slow dynamics are governed by an N-dimensional replicator equation, describing the time evolution of strain frequencies. The coefficients of this replicator system are pairwise invasion fitnesses between strains, which, in our model, are an explicit weighted sum of pairwise asymmetries along all trait dimensions. Remarkably these weights depend only on the parameters of the neutral system. Such model reduction highlights the centrality of the neutral system for dynamics at the edge of neutrality and exposes critical features for the maintenance of diversity.

Appendices

Appendix

Neutral system

In Sect. 2.3, we only give formal proof in the analysis of the Neutral system. This formal proof is seen as a guide for the rigorous analysis of the normal form in Sect. 3. However, since we can do it, we give rigorous proof for some results of the neutral system.

We first start with a classical lemma.

Lemma 15

Let a and b belongs to $C^1({\mathbb {R}})$. Let y be a solution of the linear differential equation $y'=a(t)y+b(t)$ with $y(0)=y_0$.

Assume that $a(t)\rightarrow -a^*<0$ and $b(t)\rightarrow 0$. Then $y(t)\rightarrow 0$ as $t\rightarrow +\infty .$

Proof

The proof is classical and we give it for the sake of completeness. We have the explicit formula as follows

$$\begin{aligned} y(t)=e^{A(t)}y_0+\int _0^t e^{A(t)-A(s)}b(s) ds \end{aligned}$$

wherein we have a note

$$\begin{aligned} A(t)=\int _0^t a(s)ds. \end{aligned}$$

Let $0<\epsilon < a^*$ be fixed and choose $t_0>0$ such that for any $t>t_0$, we have $\left| a(t) + a^*\right| <\epsilon$ and $\left| b(t)\right| \le \epsilon$.

We have

$$\begin{aligned} \left| y(t)\right| \le e^{(-a^* +\epsilon )(t-t_0)} e^{A(t_0)}\left( y_0+\int _0^{t_0} e^{-A(s)}|b(s)|ds\right) +\epsilon \int _{t_0}^t e^{(-a^* +\epsilon )(t-s)}ds \end{aligned}$$

This yields $|y(t)|\le C_1e^{(-a^* +\epsilon )\left( t-t_0\right) }+C_2\epsilon$ for some positive constant $C_1$ and $C_2$, which ends the proof by taking $\epsilon \rightarrow 0$ and $t \rightarrow \infty$. $\square$

Lemma 16

Let $S(t)\rightarrow S^*$ and $T(t)\rightarrow T^*$. Let I satisfy $I(0)\ge 0$ and

$$\begin{aligned} \dfrac{dI}{dt} = \beta T S - (m+\beta k T) I \end{aligned}$$

Then $I(t)\rightarrow I^*:= \frac{mT^*}{m + \beta k T^*}$

Proof

Indeed, substitute (S, T) by $\left( S^* + (S - S^*), T^* + (T - T^*)\right)$ into the equation of I in (2.6) to obtain

$$\begin{aligned} \dfrac{dI}{dt}= & {} m T^*-(m+\beta k T^*)I + \left[ \beta S^*\left( T - T^*\right) + \beta T^*\left( S - S^*\right) \right. \nonumber \\{} & {} \left. + \beta \left( T - T^*\right) \left( S - S^*\right) \right] . \end{aligned}$$

(A.1)

Define ${\tilde{I}}$ as the solution of

$$\begin{aligned} \dfrac{d{\tilde{I}}}{dt} = \beta T^* S^* - (m+\beta k T^*) {\tilde{I}}. \end{aligned}$$

It is clear that ${\tilde{I}}(t)\rightarrow I^*$. The equation for $I - {\tilde{I}}$ reads

$$\begin{aligned} \dfrac{d}{dt}\left( I - {\tilde{I}}\right) = g(t)\left( I - {\tilde{I}}\right) + f(t). \end{aligned}$$

(A.2)

Wherein we have set $g(t)= -(m+\beta k T^*+\beta k (T-T^*))$ and $f\left( t\right) = \beta S^*\left( T - T^*\right) + \beta T^*\left( S - S^*\right) + \beta \left( T - T^*\right) \left( S - S^*\right) +\beta k (T-T^*)I^*$.

By Proposition 3, we have $g(t)\rightarrow -(m+\beta k T^*)<0$ and $f\left( t\right) \rightarrow 0$ as $t\rightarrow +\infty$. Thus, by the Lemma 15, we have $I(t)-{\tilde{I}}(t)\rightarrow 0$ as $t\rightarrow +\infty$ which ends the proof. $\square$

Lemma 17

Let $(S(t),T(t),I(t))\rightarrow (S^*,T^*,I^*)$ and define

$$\begin{aligned} A(t)=\begin{pmatrix} -(m+\beta k T(t)&{}\quad m\\ -\frac{\beta k T(t)}{2}&{}\quad -\frac{\beta k I(t)}{2} \end{pmatrix}\quad \text {and}\quad A^*=\begin{pmatrix} -(m+\beta k T^*&{}\quad m\\ -\frac{\beta k T^*}{2}&{}\quad -\frac{\beta k I^*}{2} \end{pmatrix} \end{aligned}$$

Define also

$$\begin{aligned} P = \begin{pmatrix} 2T^*&{}\quad I^* \\ D^*&{}\quad T^* \end{pmatrix}, \qquad P^{-1} = \dfrac{1}{|P|}\begin{pmatrix} T^* &{}\quad -I^* \\ -D^* &{}\quad 2T^* \end{pmatrix} \end{aligned}$$

such that $P^{-1} A P= \begin{pmatrix} -\xi &{}\quad 0\\ 0&{}\quad 0\end{pmatrix}$ with $\xi =m+\beta k T^*-\frac{1}{2} \beta k I^*$.

Let $(v_i,z_i)$ be bounded and verify

$$\begin{aligned} \dfrac{d}{dt}\begin{pmatrix} v_i\\ z_i\end{pmatrix}= P^{-1} A(t) P \begin{pmatrix} v_i\\ z_i\end{pmatrix}. \end{aligned}$$

Then $v_i(t)\rightarrow 0$ and $z_i'(t)\rightarrow 0$.

Proof

This is a direct application of the Lemma 15 on the equation of $v_i$ once we note that $z_i$ is bounded. $\square$

Remark 18

Note that it is wrong that $z_i(t)\rightarrow z_i^*$ for some constant $z_i^*$. Indeed, $z_i$ is susceptible to following very slow dynamics. However, for the application in the slow–fast system ($\epsilon >0$), this very slow perturbation is below the order $\epsilon$ and has no effect.

Lemma 19

Let $I_{ij}$, $i,j \in \{1,\dots ,N\}$, satisfy the neutral system (2.14) and $z_i$ verify the system (2.13). Assume that for each (i, j), $\left( {\tilde{I}}_i (t),{\tilde{J}}_j(t)\right) = \left( I^*z_i(t), T^*z_j(t)\right)$, satisfy that $\left| I_i(t) - {\tilde{I}}_i(t)\right| \rightarrow 0$ and $\left| J_j(t) - {\tilde{J}}_j(t) \right| \rightarrow 0$. Then $\left| I_{ij}(t) - \frac{\beta k}{m}I^*T^*z_i(t) z_j(t)\right| \rightarrow 0$ as $t \rightarrow \infty$.

Proof

Consider the equation

$$\begin{aligned} \dfrac{d{\tilde{I}}_{ij}}{dt} = - m {\tilde{I}}_{ij} + \beta k {\tilde{I}}_i {\tilde{J}}_j \end{aligned}$$

(A.3)

then we can obtain the differential equation for $I_{ij} - {\tilde{I}}_{ij}$, recall $I_{ij}$ satisfies (2.14),

$$\begin{aligned} \dfrac{d}{dt}\left( I_{ij} - {\tilde{I}}_{ij}\right)= & {} - m \left( I_{ij} - {\tilde{I}}_{ij}\right) + \beta k \left[ \left( I_i - {\tilde{I}}_i\right) {\tilde{J}}_j \right. \nonumber \\{} & {} \left. + \left( J_j - {\tilde{J}}_j\right) {\bar{I}}_i + \left( I_i - {\tilde{I}}_i\right) \left( J_j - {\tilde{J}}_j\right) \right] . \end{aligned}$$

(A.4)

Since $\left| I_i(t) - {\tilde{I}}_i(t)\right| \rightarrow 0$ and $\left| J_i(t) - {\tilde{J}}_i(t)\right| \rightarrow 0$, then

$$\begin{aligned} \left| \left( I_i - {\tilde{I}}_i\right) {\tilde{J}}_j + \left( J_j - {\tilde{J}}_j\right) {\bar{I}}_i + \left( I_i - {\tilde{I}}_i\right) \left( J_j - {\tilde{J}}_j\right) \right| \rightarrow 0. \end{aligned}$$

Using Lemma 15, we have that $\left| I_{ij}(t) - {\tilde{I}}_{ij}(t)\right| \rightarrow 0$ as $t \rightarrow +\infty$.

We then compute the solution ${\tilde{I}}_{ij}$ of (A.3) to be

$$\begin{aligned} {\tilde{I}}_{ij}\left( t\right)&= e^{-mt}\left( \beta k I^*T^*\int _{0}^{t}e^{ms}z_i\left( s\right) z_j\left( s\right) ds + C\right) , \qquad C\in {\mathbb {R}}. \nonumber \\&= e^{-mt}\left( \dfrac{\beta k I^*T^*}{m}\left( e^{mt}z_i(t)z_j(t) - z_i(0)z_j(0) \right. \right. \nonumber \\&\quad \left. \left. - \int _{0}^{t}e^{ms}\dfrac{d}{dt}\left[ z_i\left( s\right) z_j\left( s\right) \right] ds\right) + C \right) , \end{aligned}$$

(A.5)

by integrating by parts. Note that $z_i'(t) \rightarrow 0$, $\forall i$ (Lemma 17), by a similar proof in Lemma 15, we can prove that $e^{-mt}\int _{0}^{t}e^{ms}\frac{d}{dt}\left[ z_i\left( s\right) z_j\left( s\right) \right] ds \rightarrow 0$. Hence ${\tilde{I}}_{ij} \rightarrow \frac{\beta k I^* T^*}{m}z_i z_j$ as $t \rightarrow \infty$, implying $I_{ij} \rightarrow \frac{\beta k I^* T^*}{m}z_i z_j$, which ends this proof. $\square$

Tychonov’s theorems

Theorem 20

(see Tikhonov 1952) Consider the initial value problem

$$\begin{aligned} \left\{ \begin{aligned} \epsilon&\dfrac{dx}{d\tau } = f(x,y,\tau ) + \epsilon \dots , \quad&x(0) = x_0, \quad&x \in D \subset {\mathbb {R}}^n,\\&\dfrac{dy}{d\tau } = g(x,y,\tau ) + \epsilon \dots , \quad&y(0) = y_0,\quad&y \in G \subset {\mathbb {R}}^n. \end{aligned} \right. \end{aligned}$$

(B.1)

For f and g, we take sufficiently smooth vector functions in x, y and t; the dots represent (smooth) higher-order terms in $\epsilon$.

• (a) We assume that a unique solution to the initial value problem exists and suppose this also holds for the reduced problem

  $$\begin{aligned} \left\{ \begin{aligned}&0= f(x,y,\tau ),\\&\dfrac{dy}{d\tau } = g(x,y,\tau ), \quad&y(0) = y_0, \end{aligned} \right. \end{aligned}$$

  (B.2)

  with solution ${\bar{x}}(\tau )$, ${\bar{y}}(\tau )$.

• (b) Suppose that $0 = f(x,y,\tau )$ is solved by ${\bar{x}} = \phi (y,\tau )$, where $\phi (y,\tau )$ is a continuous function and an isolated root, i.e., there exists a neighborhood of $\phi (y,\tau )$ such that there is no other solution for $0 = f(x,y,\tau )$ in this vicinity. Also, suppose that ${\bar{x}} = \phi (y,t)$ is an asymptotically stable solution⁷ of the equation $\frac{dx}{dt} = g(x,y,\tau )$, where $\tau = \epsilon t$, that is uniform in the parameters $y \in G$ and $\tau \in {\mathbb {R}}^+$.

• (c) x(0) is contained in an interior subset of the domain of attraction of ${\bar{x}} = \phi (y,\tau )$ in the case of initial conditions $y = y(0)$, $\tau = 0$.

Then, we have

$$\begin{aligned} \begin{aligned}&\lim \limits _{\epsilon \rightarrow 0} x_\epsilon (\tau ) = {\bar{x}}(\tau ), \quad&0 <\tau _0 \le \tau \le T,\\&\lim \limits _{\epsilon \rightarrow 0} y_\epsilon (\tau ) = {\bar{y}}(\tau ), \quad&0 \le \tau \le T, \end{aligned} \end{aligned}$$

(B.3)

with $\tau _0$ and T are constants independent on $\epsilon$.

Besides this Tychonov’s theorem, it needs to use another result that allows us to approximate the original system by the slow–fast form. The following error estimate gives a more precise description of these limits. (theorem 9.1, Verhulst 1996 adapted here for the simple case $m=0$).

Theorem 21

(see Verhulst 1996) Consider the initial value problem

$$\begin{aligned} \dfrac{dx}{dt} = f_0(t,x) +\epsilon R(t,x,\epsilon ) \end{aligned}$$

(B.4)

with $x(t_0) = \eta$ and $|t - t_0| \le h$, $x \in D \subset {\mathbb {R}}^n$, $0 \le \epsilon \le \epsilon _0$. Assume that in this domain we have

• (a) f(t, x) continuous in t and x, 2 times continuously differentiable in x;

• (b) $R(t,x,\epsilon )$ continuous in t, x and $\epsilon$, Lipschitz-continuous in x.

Let $x_0(t)$ be the solution of

$$\begin{aligned} \dfrac{dx}{dt} = f_0(t,x) \end{aligned}$$

(B.5)

with $x_0(t_0) = \eta$ Let $T>0$ and assume that both x and $x_0$ are defined on [0, T] for any $\epsilon \in (0,\epsilon _0)$. There exist $C>0$ (depending on T) such that for any $\epsilon \in (0,\epsilon _0)$, and $t\in (0,T)$, we have the estimate

$$\begin{aligned} \left\| x(t) -x_0(t) \right\| \le C \epsilon \end{aligned}$$

(B.6)

1.1 Proof of Lemma 7 of error estimate

In this subsection, we estimate error through three steps when $\epsilon$ is small enough as follows.

• 1. Lemma 22: approximate the solution S, $I_i$ of the original dynamics (2.1) using the solution of the slow–fast form (3.9)

• 2. Lemma 23: approximate the solution of the slow–fast form (3.9) using the solution of the slow system (3.14)

• 3. Lemma 24: approximate the solution $\left( I_{ij}\right) _{i,j}$ of (2.1) using the solution ${\textbf{z}}$ of (3.14).

Lemma 22

Under our assumptions, for any initial values of (2.1), there exists $\tau _0 > 0$ and initial value ${\textbf{z}}\left( \tau _0\right)$ of (3.9), such that for any $T>\tau _0$, there are $\epsilon _0 > 0$ and $C_T > 0$ which satisfy that $\forall \epsilon < \epsilon _0$

$$\begin{aligned} \left| S\left( \dfrac{\tau }{\epsilon } \right) - S^*\right| + \sum _{i=1}^{N}\left| I^*z_i(\tau ) - I_i\left( \dfrac{\tau }{\epsilon } \right) \right| + \sum _{i=1}^{N}\left| T^*z_i(\tau ) - J_i\left( \dfrac{\tau }{\epsilon } \right) \right| \le \epsilon C_T,\nonumber \\ \end{aligned}$$

(B.7)

for all $\tau _0 \le \tau \le T$, where $\left( S, I_i, J_i\right) _{i = 1,\dots ,N}$ verifies (2.1) and $(z_1, \dots , z_N)$ is the solution of (3.9).

Proof

• First step, we wish to estimate the error between $S^*$, $T^*$, $I^*$ and the solution $\left( S,T,I\right)$ of (2.5).

  Denote $x = \left( S, I_1, \dots , I_N, J_1, \dots , J_N \right)$, by (2.5), we can rewrite the system for x in the form of $\frac{dx}{dt} = f_0(t,x) + \epsilon f_1(t,x)$, where $f_0(t,x)$ and $f_1(t,x)$ are polynomial in multiple variables $\left( S, T, I_i, J_i \right)$, $i = 1,\dots ,N$, implying that $f_0(t,x)$ and $f_1(t,x)$ satisfy conditions of Theorem 21.

  Hence, if $x^r = \left( S^r, T^r, I^r_i, J^r_i \right)$ satisfies the neutral system (2.6) and $x = \left( S, T, I_i, J_i \right) _{1\le i \le N}$ satisfies (2.5), then $\left\| x - x^r\right\| _{{\mathbb {R}}^{2N+2}} = O(\epsilon )$.

  Combine with the arguments in Sect. 2.3, the approximation of solution (S, T, I) of (2.5) by $\left( S^*,T^*,I^*\right)$ is accordingly plausible in the sense of $O\left( \epsilon \right)$. We have done our first step.

• Second step, we claim that all the algebraic and linear transformations from (2.5) to (3.9) are equivalent with error estimate $O\left( \epsilon \right)$, including changing $\left( S,T,I\right)$ to $\left( X,Y\right)$ using $S^*, T^*, I^*$ (proved in the first part), changing $\begin{pmatrix} I_i \\ J_i \end{pmatrix}$ to $\begin{pmatrix} v_i \\ z_i \end{pmatrix}$ (linear operator) and changing to time scale $\tau = \epsilon t$ with re-denote $z\left( \tau \right)$ (see the argument in (3.9)).

  By a similar argument to verify the conditions of Expansion Theorem 21, and note that $v\left( \tau \right) \rightarrow 0$ asymptotically, by Theorem 21 we have that

  $$\begin{aligned} \sum _{i=1}^{N}\left| I^*z_i(\tau ) - I_i\left( \dfrac{\tau }{\epsilon } \right) \right| + \sum _{i=1}^{N}\left| T^*z_i(\tau ) - J_i\left( \dfrac{\tau }{\epsilon } \right) \right| = O\left( \epsilon \right) , \end{aligned}$$

  for all $\tau _0 \le \tau \le T$, where $\left( I_i, J_i\right) _{i=1,\dots ,N}$ verify (2.1) and $(z_1, \dots , z_N)$ is the solution of (3.9).

Combining two parts, we have the conclusion for this lemma. $\square$

Lemma 23

The solution ${\textbf{z}} = \left( z_i\right)$ of the slow–fast form system (3.9) tends to the solution of the slow system (3.14) as $\epsilon \rightarrow 0$ locally uniformly in time on $[\tau _0,T]$, with $\tau _0 > 0$, $T > \tau _0$ arbitrarily and independent on $\epsilon$.

Proof

It suffices to verify the conditions for Tychonov’s theorem; see Theorem (20).

• Firstly, we prove that (3.9) and (3.14) with initial values possess the unique solution.

  The right-hand side of (3.9) is a vector function with all the components being polynomials of variables $\left( X,Y,{\textbf{L}},{\textbf{v}},{\textbf{z}}\right)$ (explicitly computed in Sects. 2.4, 3.3 and 3.3.1) in the bounded set [0, T] of time. Hence, it is global Lipschitz and continuously differentiable, implying the uniqueness of solution for (3.9), according to the Picard–Lindelof Theorem (Theorem 2.2 in Teschl 2010). Similarly, (3.14) has the unique solution

• Secondly, by the proof of Lemma 6, we have that the solution $(X,Y,{\textbf{L}},{\textbf{v}},{\textbf{z}})$ of (3.7) with any initial condition $(X,Y,{\textbf{L}},{\textbf{v}},{\textbf{z}})(0)=(X_0,Y_0,{\textbf{L}}_0,{\textbf{v}}_0,{\textbf{z}}_0)\in {\mathbb {R}}\times {\mathbb {R}}\times \left( {\mathbb {R}}^n\right) ^3$ verifies ${\textbf{z}}(t)={\textbf{z}}_0$ for all $t\ge 0$ and $\lim _{t\rightarrow +\infty }(X,Y,{\textbf{L}},{\textbf{v}})(t)={\varvec{\Phi }}({\textbf{z}}_0)$ asymptotically, in which, $\varPhi \left( {\textbf{z}}\right) = \left( X^*({\textbf{z}}),Y^*({\textbf{z}}),\chi _3{\textbf{L}}^*({\textbf{z}}),0\right)$, satisfy the system (3.9) in slow timescale, with $\epsilon = 0$ as follows

  $$\begin{aligned} \left\{ \begin{aligned}&0 = -\beta T^*X +\chi _1 F_X^1\left( {\textbf{v}},{\textbf{z}}\right) +\chi _2 F_X^2\left( {\textbf{v}},{\textbf{z}}\right) +\chi _3 F_X^3\left( {\textbf{L}}\right) + O(\epsilon )\\&0 = \beta (S^* - T^* -k I^*)X - (m+\beta k T^*)Y +\chi _1 F_Y^1\left( {\textbf{v}},{\textbf{z}}\right) \\&\qquad \qquad +\chi _2 F_Y^2\left( {\textbf{v}},{\textbf{z}}\right) +\chi _5 F_Y^5\left( {\textbf{v}},{\textbf{z}}\right) \\&0 =-m L_i + \chi _3 F_{L_i} \left( {\textbf{v}},{\textbf{z}}\right) \\&0 = -\xi v_i \end{aligned} \right. \end{aligned}$$

  (B.8)

Applying Tychonov’s Theorem, we have the required conclusion. $\square$

By two Lemmas 23 and 24, we have that

$$\begin{aligned} \left| S\left( \dfrac{\tau }{\epsilon } \right) - S^*\right| + \sum _{i=1}^{N}\left| I^*z_i(\tau ) - I_i\left( \dfrac{\tau }{\epsilon } \right) \right| + \sum _{i=1}^{N}\left| T^*z_i(\tau ) - J_i\left( \dfrac{\tau }{\epsilon } \right) \right| \le \epsilon C_T,\nonumber \\ \end{aligned}$$

(B.9)

for all $\tau _0 \le \tau \le T$, where $\left( S, I_i, J_i\right) _{i = 1,\dots ,N}$ verifies (2.1) and $(z_1, \dots , z_N)$ is the solution of (3.14).

Finally, we will find an approximation of $I_{ij}$, $1 \le i \le N$ and estimate the error.

Lemma 24

Under our assumptions, for any initial values of (2.1), there exists $\tau _0 > 0$ and initial value ${\textbf{z}}\left( \tau _0\right)$ of (3.14), such that for any $T>\tau _0$, there is $\epsilon _0 > 0$ and $C_T > 0$, which satisfy that $\forall \epsilon < \epsilon _0$

$$\begin{aligned} \sum _{i,j = 1}^{N}\left| I_{ij}\left( \dfrac{\tau }{\epsilon }\right) - D^*z_i\left( \tau \right) z_j\left( \tau \right) \right| \le \epsilon C_T, \end{aligned}$$

(B.10)

for all $\tau _0 \le \tau \le T$, $(I_{ij})_{1 \le i,j \le N}$ satisfying (2.1) and $(z_1, \dots , z_N)$ is the solution of the reduced system (3.14).

Proof

This proof is similar to the proof of Lemma 19. Denoting ${\textbf{z}}$ be the solution of (3.14), for $1 \le i,j \le N$, denote $I^r_{ij}$ to be the solution of

$$\begin{aligned} \dfrac{dI^r_{ij}\left( t\right) }{dt} = - mI^r_{ij}\left( t\right) + \beta k I^*T^*z_i\left( \epsilon t\right) z_j\left( \epsilon t\right) , \end{aligned}$$

(B.11)

Then, for each $\tau _0>0$ and $T>\tau _0$, after the changing time scale $\tau = \epsilon t$, from (2.1) and (B.11), we have that

$$\begin{aligned} \begin{aligned} \dfrac{d}{dt}\left( I_{ij}\left( \dfrac{\tau }{\epsilon } \right) - I^r_{ij}\left( \dfrac{\tau }{\epsilon } \right) \right) = -&m\left( I_{ij}\left( \dfrac{\tau }{\epsilon }\right) - I^r_{ij}\left( \dfrac{\tau }{\epsilon } \right) \right) - \epsilon \gamma u_{ij} I_{ij}\left( \dfrac{\tau }{\epsilon }\right) \\&+ \left( \beta _jk_{ij}I_i\left( \dfrac{\tau }{\epsilon } \right) J_j\left( \dfrac{\tau }{\epsilon } \right) - \beta k I^* T^* z_i\left( \tau \right) z_j\left( \tau \right) \right) . \end{aligned}\nonumber \\ \end{aligned}$$

(B.12)

By (B.9), we have that $\left| \beta _jk_{ij} I_i\left( \frac{s}{\epsilon }\right) J_j\left( \frac{s}{\epsilon }\right) - \beta k I^* T^* z_i(s) z_j(s)\right| = O(\epsilon )$ uniformly for $s \in [\tau _0,T]$. Note that $\left| I_{ij}\right| \le 1$, then using the expansion theorem- Theorem 21, we observe that $\left| I_{ij}\left( \frac{\tau }{\epsilon }\right) - I^r_{ij}\left( \frac{\tau }{\epsilon }\right) \right| = O(\epsilon )$.

We then compute the solution $\left( I^r_{ij}\right) _{1\le i,j \le N}$ of (B.11) to be

$$\begin{aligned} I^r_{ij}\left( t\right) = e^{-mt}\left( \beta k I^*T^*\int _{0}^{t}e^{ms}z_i\left( \epsilon s\right) z_j\left( \epsilon s\right) ds + C\right) , \qquad C\in {\mathbb {R}}. \end{aligned}$$

(B.13)

Using integrating by parts, (B.13) becomes

$$\begin{aligned} I^r_{ij}(t)= & {} e^{-mt}\left( \beta k I^*T^*\cdot \dfrac{1}{m}\left( e^{mt}z_i(\tau )z_j(\tau ) - z_i(0)z_j(0) \right. \right. \nonumber \\{} & {} \left. \left. - \int _{0}^{t}e^{ms}\dfrac{d}{dt}\left[ z_i\left( \epsilon s\right) z_j\left( \epsilon s\right) \right] ds\right) + C \right) \end{aligned}$$

(B.14)

By (3.14), we deduce that $\dfrac{d}{dt}\left[ z_i\left( \epsilon s\right) z_j\left( \epsilon s\right) \right] = O\left( \epsilon \right)$, implying $\left| I^r_{ij}\left( \frac{\tau }{\epsilon }\right) - k\frac{I^*T^*}{S^*}\right. \left. z_i(\tau )z_j(\tau )\right| \rightarrow O\left( \epsilon \right)$ as $t \rightarrow \infty$. Hence, noting that $k\frac{I^*T^*}{S^*} = D^*$, we have $\left| I^r_{ij}\left( t\right) - D^*z_i\left( \epsilon t\right) z_j\left( \epsilon t\right) \right| = O\left( \epsilon \right)$, implying $\left| I_{ij}\left( \frac{\tau }{\epsilon } \right) - D^*z_i\left( \tau \right) z_j\left( \tau \right) \right| = O\left( \epsilon \right)$, for all $1 \le i,j \le N$. $\square$