Dynamics of a new HIV model with the activation status of infected cells

Abstract

The activation status can dictate the fate of an HIV-infected CD4+ T cell. Infected cells with a low level of activation remain latent and do not produce virus, while cells with a higher level of activation are more productive and thus likely to transfer more virions to uninfected cells during cell-to-cell transmission. How the activation status of infected cells affects HIV dynamics under antiretroviral therapy remains unclear. We develop a new mathematical model that structures the population of infected cells continuously according to their activation status. The effectiveness of antiretroviral drugs in blocking cell-to-cell viral transmission decreases as the level of activation of infected cells increases because the more virions are transferred from infected to uninfected cells during cell-to-cell transmission, the less effectively the treatment is able to inhibit the transmission. The basic reproduction number $R_{0}$ of the model is shown to determine the existence and stability of the equilibria. Using the principal spectral theory and comparison principle, we show that the infection-free equilibrium is locally and globally asymptotically stable when $R_{0}$ is less than one. By constructing Lyapunov functional, we prove that the infected equilibrium is globally asymptotically stable when $R_{0}$ is greater than one. Numerical investigation shows that even when treatment can completely block cell-free virus infection, virus can still persist due to cell-to-cell transmission. The random switch between infected cells with different activation levels can also contribute to the replenishment of the latent reservoir, which is considered as a major barrier to viral eradication. This study provides a new modeling framework to study the observations, such as the low viral load persistence, extremely slow decay of latently infected cells and transient viral load measurements above the detection limit, in HIV-infected patients during suppressive antiretroviral therapy.

1 Introduction

Human immunodeficiency virus (HIV) is the pathogenic agent of the acquired immunodeficiency syndrome (AIDS). It infects CD4+ T cells, an important component of the immune system, leading to patient death eventually caused by opportunistic infection. According to the World Health Organization, there were approximately 36.9 million people living with HIV by the end of 2017 (WHO 2018). It was estimated that about 25% of people infected with HIV did not know their infection status (WHO 2018). There has been constant interest in the study of HIV infection dynamics, mechanisms for disease progression, antiretroviral treatment and vaccine development. Mathematical models have been increasingly used to study these issues (Perelson and Ribeiro 2013).

Perelson et al. (1996) used a basic viral dynamic model to study the interaction between viruses and host CD4+ T cells. An extension of this model including a secondary source of viral production such as activation of latently infected cells was proposed to explain the second-phase viral load decline after administration of antiretroviral drug combination (Perelson et al. 1997). Latently infected cells can escape antiretroviral drug treatment and immune surveillance. They do not produce virus unless they are activated by relevant antigens. Multiple cellular and molecular mechanisms might be involved in the establishment of HIV latency (Donahue and Wainberg 2013). For example, the HIV transactivator of transcription (Tat) protein plays an essential role in viral transcription regulation, and may affect the formulation and reversal of HIV latency (Jordan et al. 2001; Lin et al. 2003). Weinberger et al. (2005) showed that cells with intermediate Tat concentrations could be driven by stochastic fluctuations to either revert to the latent status or turn to highly activated and productive status. Wang and Rong (2014) developed a mathematical model that includes such stochastic population switch, and showed that the model can explain the stability of the latent reservoir (i.e. a group of latently infected CD4+ T cells) and emergence of viral blips (i.e. transient viral load measurements above the detection limit). However, the status of the activation of infected cells (or the level of Tat concentration) can be continuous, more than the three levels (low, intermediate and high) studied in Wang and Rong (2014). In this paper, we include continuous activation status of infected cells in models to study the virus dynamics of HIV infection under antiretroviral therapy.

In addition to the infection of target CD4+ T cells by cell-free virus, HIV can also be transmitted directly from infected to uninfected cells (Martin and Sattentau 2009; Sattentau 2008; Talbert-Slagle et al. 2014). Cell-to-cell transmission may take place when infected cells encounter the uninfected and form the virological synapses (Hübner et al. 2009; Sato et al. 1992). Because of the reduced possibility of being neutralized by antibodies, virus transmitted via cell-to-cell transmission may be more efficient in establishing successful infection than cell-free virus infection (Johnson and Huber 2002; Mazurov et al. 2010). Iwami et al. (2015) estimated that approximately 60% of viral infection may be attributed to cell-to-cell transmission. When multiple virions are transmitted from infected to uninfected cells, antiretroviral drugs may not inhibit the infection by all virions, leading to a higher probability of successful infection. Thus, cell-to-cell transmission may explain the viral persistence in patients under antiretroviral therapy (Sigal et al. 2011).

Mathematical models have been developed to study virus infection dynamics (see a review in Perelson and Ribeiro (2013)). In addition to the basic viral dynamic model (Perelson et al. 1996) and its many variations (reviewed in Rong and Perelson (2009b)), some other models have also been developed, such as the multiple target cell population model (Wang et al. 2016a), multiple stage model (Hernandez-Vargas and Middleton 2013; Wang et al. 2016b) and multiple patch model (Kheiri and Jafari 2019). Both deterministic and stochastic models have also been developed to study the dynamics of HIV latent infection (Archin et al. 2012; Conway and Coombs 2011; Conway and Perelson 2015; Forde et al. 2012; Hill et al. 2014; Smith and Aggarwala 2009). However, very few models, if any, considered the continuous activation status of infected cells. Because cells with a higher activation status are more likely to produce more virions, resulting in a higher probability of successful infection via cell-to-cell transmission, incorporation of the continuous status of activation provides a unique modeling framework to study the viral transmission dynamics. In this paper, we assume that the treatment efficacy of blocking cell-to-cell viral transmission is a decreasing function of the activation status because the more virions are transmitted by infected cells, the less effectively the treatment can block the transmission. We will analyze the model by deriving the basic reproduction number and studying the local and global stability of equilibria. We will evaluate the sensitivity of the basic reproduction number and steady-state viral load with respect to the drug efficacy and study whether cell-to-cell transmission can explain the viral persistence in patients receiving suppressive antiretroviral therapy. Including antigen-stimulated activation of infected cells that have a low level of activation status, we will test whether the model can generate low-level persistent viremia, intermittent viral blips and stable latent reservoir under suppressive therapy. We will also perform numerical simulations to evaluate the relative contribution of cell-to-cell transmission, transfer between cells with different statuses and proliferation of latently infected cells to the maintenance of the latent reservoir.

2 Model formulation and preliminary results

2.1 Model

To study the effect of infected cell status on cell-to-cell viral transmission, we develop a status-dependent HIV infection model that includes both cell-free virus infection and cell-to-cell transmission. The population of infected cells is structured continuously according to their activation status. The model is described by the following system:

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{H}(t)=\lambda -cH(t)-\int _{0}^{1}(1-\epsilon (y))k_{1}H(t)I(t,y)dy-(1-\xi )k_{2}H(t)V(t), \\ I_{t}(t,x)=\beta (x)\left[ \int _{0}^{1}(1-\epsilon (y))k_{1}H(t)I(t,y)dy+(1-\xi )k_{2}H(t)V(t)\right] \\ \qquad +\int _{0}^{1}p(y,x)\delta (y)I(t,y)dy \\ \qquad \quad -\delta (x)I(t,x)-\alpha (x)I(t,x), \\ \dot{V}(t)=\int _{0}^{1}\eta (y)I(t,y)dy-dV(t), \\ \end{array} \right. \end{aligned}$$

(1)

with the initial conditions

$$\begin{aligned} H(0)=H_{0}\ge 0, \quad I(0,\cdot )=I_{0}(\cdot )\ge 0, \quad V(0)=V_{0}\ge 0. \end{aligned}$$

H(t) and V(t) are the concentrations of uninfected CD4+ T cells and viruses at time t, respectively. I(t, x) represents the concentration of infected CD4+ T cells with the activation status x at time t. The variable $x\in [0,1]$ represents the normalized status of activation of infected cells. The value $x=0$ means that the infected cell is in the completely latent status and the value 1 means that the infected cell is in the maximumly activated or productive status. Uninfected cells are generated at rate $\lambda$, die naturally at rate c per cell, become infected via cell-to-cell transmission by infected cells at rate $k_{1}$ or by cell-free virus infection at rate $k_{2}$. Constant d is the viral clearance rate.

Antiretroviral drugs can block viral infection or inhibit viral production. Here we use $\xi$ to represent the overall effectiveness of the treatment in blocking cell-free virus infection (Rong and Perelson 2009a). During cell-to-cell transmission, infected cells with a higher level of activation are more likely to produce and transfer more virions, leading to a lower probability that the therapy simultaneously blocks the infection by all the transmitted virions. Thus, we assume that $\epsilon (y)$, the efficacy of antiretroviral therapy in blocking cell-to-cell transmission by infected cells at status y, is a decreasing function of the status y. The integral $\int _{0}^{1}(1-\epsilon (y))k_{1}H(t)I(t,y)dy$ gives the total generation of infected cells per unit time via the route of cell-to-cell transmission. The infection rate $k_{1}$ can be assumed to be status-dependent without bringing any challenge to mathematical analysis. However, for simplicity we assume that it is a constant and only focus on the effect of status-dependent drug therapy $\epsilon (y)$ on cell-to-cell transmission.

The parameter $\beta (x)$ denotes the probability of the activation status x for newly infected cells. Hence, the production rate of infected cells with the activation status x is given by $\beta (x)\bigg \{\int _{0}^{1}(1-\epsilon (y))k_{1}H(t)I(t,y)dy+(1-\xi )k_{2}H(t)V(t)\bigg \}$. Infected cells at one status can switch to another status (Wang and Rong 2014; Weinberger et al. 2005). The parameter $\delta (y)$ represents the switch rate of infected cells from the activation status y to other statuses and p(y, x) denotes the probability that an infected cell switches from the status y to x. For the convenience of expression, we let

$$\begin{aligned} \gamma (y,x)=p(y,x)\delta (y), \end{aligned}$$

which represents the switch rate of infected cells from the activation status y to x. We note that this switch does not have direction, i.e. there is a chance for a state y to change to any other state x due to random intracellular perturbation. However, it is more likely for an infected cell to change from a state to its close state and the switch rate decreases as the distance between y and x increases. Thus, it is possible that a fully activated infected cell becomes latent although the probability is very low. We also note that the random switch between different status is different from the antigen-induced activation of latently infected cells in which infected cells only change from the latent to activated state (directional). The activation of latently infected cells by relevant antigens will be further studied in a later section.

The integral $\int _{0}^{1}\gamma (x,y)dy$ is the switch rate of infected cells from status x to all the other statuses. Thus, it is equal to $\delta (x)$, i.e., for any $x,y\in [0,1]$, $\gamma (x,y)$ satisfies the balance condition $\int _{0}^{1}\gamma (x,y)dy=\delta (x)$. We also assume that $\gamma (x,x)>0$. The parameter $\alpha (x)$ is the death rate of infected cells with status x and $\eta (y)$ is the production rate of virions by infected cells with status y. All status-dependent parameters are assumed to be nonnegative and continuous.

The status-dependent parameters $\epsilon (y)$ and $\beta (x)$ have the following assumptions:

• (A1) $\epsilon (0)=1$;

• (A2) $\int _{0}^{1}\beta (x)dx=1$;

Assumption (A1) assures that there is no viral transmission from latently infected cells (i.e. $x=0$) to uninfected cells because latently infected cells do not produce virions. The assumption (A2) is trivial. The parameters and their description are summarized in Table 1.

Table 1 Summary of parameters and values used in models (1), (13), (14) and simulations

2.2 Preliminary results

In this section, we derive the basic reproduction number and investigate the existence of equilibria. Define the phase space of model (1) as $\mathbb {X}=\mathbb {R}\times C([0,1])\times \mathbb {R}$ with the norm given by

$$\begin{aligned} \begin{aligned} \Vert (H,I(\cdot ),V)^{T}\Vert _{\mathbb {X}}=|H|+\Vert I(\cdot )\Vert _{C([0,1])}+|V|, \qquad (H,I(\cdot ),V)^{T}\in \mathbb {X}, \end{aligned} \end{aligned}$$

where $(\cdot )^T$ means the transpose. Let $\mathbb {X}_{+}=\mathbb {R}_{+}\times C_{+}([0,1])\times \mathbb {R}_{+}$, where $\mathbb {R}_{+}=[0,+\infty )$ and $C_{+}([0,1])=\big \{I(\cdot )\in C([0,1]): I(\cdot )\ge 0\big \}$. Defining $z(t)=(H(t),I(t,\cdot ),V(t))^{T}$, model (1) can be reformulated as the following abstract Cauchy problems:

$$\begin{aligned} \frac{dz}{dt}=Az(t)+F(z(t)) \end{aligned}$$

for $t\ge 0$ and $z_{0}:=(H_{0},I_{0}(\cdot ),V_{0})^{T}\in \mathbb {X}_+$, where

$$\begin{aligned}&\displaystyle \begin{array}{rcl} A\left( \begin{array}{c} H\\ I\\ V \end{array}\right) =\left( \begin{array}{c} -c H\\ -(\delta (\cdot )+\alpha (\cdot )) I\\ -d V \end{array}\right) , \end{array}\\&\displaystyle \begin{array}{rcl} F\left( \begin{array}{c} H\\ I\\ V \end{array}\right) =\left( \begin{array}{c} \lambda -\int _{0}^{1}(1-\epsilon (y))k_{1}H(t)I(t,y)dy-(1-\xi )k_{2}H(t)V(t)\\ \beta (\cdot )\left[ \int _{0}^{1}(1-\epsilon (y))k_{1}H(t)I(t,y)dy+(1-\xi )k_{2}H(t)V(t)\right] \\ \qquad +\int _{0}^{1}\gamma (y,\cdot )I(t,y)dy\\ \int _{0}^{1}\eta (y)I(t,y)dy \end{array}\right) . \end{array} \end{aligned}$$

By using the theory of abstract Cauchy problems and the similar arguments as in the proof of Theorem 2.1 in Qiu et al. (2018b), system (1) has a unique global classical solution $z(t)=(H(t),I(t,\cdot ),V(t))^{T}$: $[0,+\infty )\rightarrow \mathbb {X}_+$ satisfying $z(0)=z_{0}$. Furthermore, system (1) generates a continuous semiflow defined by $\phi _{t}z_0=z(t;z_0),t\ge 0, z_0\in \mathbb {X}_+$ on $\mathbb {X}_+$.

It is easy to see that the infection-free equilibrium $E^{0}=(H^{0},I^{0}(x),V^{0})^{T}=(\frac{\lambda }{c},0,0)^{T}$ always exists. In addition to $E^{0}$, there may exist the infected equilibrium $E^{*}=(H^{*},I^{*}(x),V^{*})^{T}$ with $I^{*}(x)\ne 0$. In order to obtain the existence condition of the equilibrium $E^{*}$, we define an operator $\mathcal {L}:C([0.1])\rightarrow C([0,1])$, given by

$$\begin{aligned} \begin{aligned} \mathcal {L}[I](x)=&\frac{\beta (x)}{\alpha (x)+\delta (x)}\int _{0}^{1}(1-\epsilon (y))k_{1}H^{0}I(y)dy\\&+\frac{\beta (x) (1-\xi )k_{2}H^{0}}{d(\alpha (x)+\delta (x))}\int _{0}^{1}\eta (y)I(y)dy\\&+\frac{\int _{0}^{1}\gamma (y,x)I(y)dy}{\alpha (x)+\delta (x)}.\\ \end{aligned} \end{aligned}$$

(2)

Using a similar argument as in the proof of lemma 3.5 in Diekmann et al. (1990), we can prove that the operator $\mathcal {L}$ is compact and non-supporting. The operator $\mathcal {L}$ is called non-supporting if there exists $n_0=n_0(I, \kappa )$ such that $\int _0^1 \mathcal L^n[I](x)d\kappa (x)>0$ for any $I\in C_+([0,1])\backslash \big \{0\big \},\kappa \in (C([0,1]))^*_+ \backslash \big \{0\big \}$ and $n\ge n_0$. It follows from Theorem 2.3 in Marek (1970) that $\rho (\mathcal L)$ is a positive and algebraically simple eigenvalue of $\mathcal L$ with an eigenfunction in Int$C_+([0,1])$. Moreover, if $\lambda$ is an eigenvalue of $\mathcal L$ with an eigenfunction in $C_+([0,1]){\setminus }\{0\}$, then $\lambda =\rho (\mathcal L)$. Thus, the basic reproduction number is defined as

$$\begin{aligned} R_0=\rho (\mathcal L). \end{aligned}$$

Moreover, we have the following theorem on the existence of infected equilibrium $E^{*}$. The proof is given in the “Appendix A”.

Theorem 1

If $R_{0}>1$, there exists an infected equilibrium $E^{*}$ with $I^{*}(x)\ne 0$.

Note that this theorem only ensures the existence of an infected equilibrium. We will show later in Theorem 5 that the infected equilibrium $E^{*}$ is unique and globally asymptotically stable in $\mathrm{Int}\mathbb {X}_{+}$ when $R_{0}>1$.

3 Stability of the infection-free equilibrium $E^{0}$

In this section, we study the local and global stability of the infection-free equilibrium $E^{0}$.

3.1 Local stability of equilibrium $E^{0}$

Linearizing system (1) at $E^{0}$ leads to

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{H}(t)=-cH(t)-\int _{0}^{1}(1-\epsilon (y))k_{1}H^{0}I(t,y)dy-(1-\xi )k_{2}H^{0}V(t), \\ I_{t}(t,x)=\beta (x)\left[ \int _{0}^{1}(1-\epsilon (y))k_{1}H^{0}I(t,y)dy+(1-\xi )k_{2}H^{0}V(t)\right] \\ \qquad +\int _{0}^{1}\gamma (y,x)I(t,y)dy\\ \qquad \quad -\delta (x) I(t,x)-\alpha (x)I(t,x), \\ \dot{V}(t)=\int _{0}^{1}\eta (y)I(t,y)dy-dV(t). \\ \end{array} \right. \end{aligned}$$

(3)

Let

$$\begin{aligned} \begin{aligned} \bar{L}\begin{pmatrix} H\\ I\\ V\\ \end{pmatrix} =\begin{pmatrix} -cH-\int _{0}^{1}(1-\epsilon (y))k_{1}H^{0}I(y)dy-(1-\xi )k_{2}H^{0}V \\ L\begin{pmatrix} I\\ V\\ \end{pmatrix} \end{pmatrix}, \qquad \begin{pmatrix} H\\ I\\ V\\ \end{pmatrix}\in \mathbb {X}, \end{aligned} \end{aligned}$$

(4)

where

$$\begin{aligned} \begin{aligned} L\begin{pmatrix} I\\ V\\ \end{pmatrix}&=\begin{pmatrix} \beta (x)\left[ \int _{0}^{1}(1-\epsilon (y))k_{1}H^{0}I(y)dy+(1-\xi )k_{2}H^{0}V\right] +\int _{0}^{1}\gamma (y,x)I(y)dy-\delta (x) I(x)-\alpha (x) I(x)\\ \int _{0}^{1}\eta (y)I(y)dy-dV\\ \end{pmatrix}, \\&\quad \begin{pmatrix} I\\ V\\ \end{pmatrix}\in C([0,1])\times \mathbb {R}.\\ \end{aligned} \end{aligned}$$

Denote the spectral bound of the operator $\mathbb {A}$ by $s(\mathbb {A})=\sup \big \{\mathfrak {R}\varsigma :\varsigma \in \sigma (\mathbb {A})\big \}$, where $\sigma (\mathbb {A})$ is the spectral set of $\mathbb {A}$ and $\mathfrak {R}\varsigma$ is the real part of eigenvalue $\varsigma$. Then we have

Theorem 2

$s(\bar{L})<0$, $s(\bar{L})=0$ and $s(\bar{L})>0$ if and only if $R_0<1,R_0=1$ and $R_0>1$, respectively.

Proof

We claim that $s(\bar{L})=s(L)$. To verify this, we first show that $s(\bar{L})\le s(L)$. Let $\lambda \in \mathbb {C}$ with $\mathfrak {R}\lambda >s(L)$. Then, for any $(\bar{H},\bar{I}(\cdot ),\bar{V})^{T}$, the unique solution of the equation

$$\begin{aligned} (\lambda -\bar{L})\begin{pmatrix} H\\ I(\cdot )\\ V\\ \end{pmatrix}= & {} \begin{pmatrix} \lambda H+cH+\int _{0}^{1}(1-\epsilon (y))k_{1}H^{0}I(y)dy+(1-\xi )k_{2}H^{0}V \\ (\lambda -L)\begin{pmatrix} I(\cdot )\\ V\\ \end{pmatrix} \end{pmatrix}\\= & {} \begin{pmatrix} \bar{H}\\ \bar{I}(\cdot )\\ \bar{V}\\ \end{pmatrix}, \end{aligned}$$

is given by

$$\begin{aligned} \begin{pmatrix} I(\cdot )\\ V\\ \end{pmatrix}&=(\lambda -L)^{-1}\begin{pmatrix} \bar{I}(\cdot )\\ \bar{V}\\ \end{pmatrix} \quad and \quad \\ H&=\frac{\bar{H}-\int _{0}^{1}(1-\epsilon (y))k_{1}H^{0}I(y)dy-(1-\xi )k_{2}H^{0}V}{\lambda +c}. \end{aligned}$$

Thus, $(\lambda -\bar{L})^{-1}$ is well-defined and bounded, which implies that $\lambda \in \mathbb {C}{\setminus } \sigma (\bar{L})$, and hence, $s(\bar{L})\le s(L)$.

Next, we show that $s(\bar{L})=s(L)$. Assume that $s(\bar{L})<s(L)$. We decompose the operator L into two linear operators J and U, where

$$\begin{aligned} J\begin{pmatrix} I\\ V\\ \end{pmatrix}=\begin{pmatrix} -\alpha (x) I(x)-\delta (x) I(x)\\ -dV\\ \end{pmatrix} \end{aligned}$$

and

$$\begin{aligned} U\begin{pmatrix} I\\ V\\ \end{pmatrix}=\begin{pmatrix} \beta (x)\left[ \int _{0}^{1}(1-\epsilon (y))k_{1}H^{0}I(y)dy+(1-\xi )k_{2}H^{0}V\right] +\int _{0}^{1}\gamma (y,x)I(y)dy\\ \int _{0}^{1}\eta (y)I(y)dy\\ \end{pmatrix}. \end{aligned}$$

Clearly, J generates a uniformly continuous, positive and uniformly exponentially stable semigroup $\big \{e^{Jt}\big \}_{t\ge 0}$ on $C_{+}([0,1])\times \mathbb {R}_{+}$, and U is positive and compact. This, together with the assumption $\gamma (x,x)>0$, implies that U is irreducible. Therefore, it follows from Theorem 2.2 in Bürger (1988) that s(L) is an isolated and simple eigenvalue of L, whose eigenspace is spanned by some $(\tilde{I},\tilde{V})^{T}\in C_{++}([0,1])\times \mathbb {R}_{++}$ (where $C_{++}([0,1])=\big \{I(\cdot )\in C([0,1]): \inf _{[0,1]}I(\cdot )>0\big \}$ and $\mathbb {R}_{++}=(0,+\infty )$), i.e.,

$$\begin{aligned} \left\{ \begin{array}{ll} \beta (x)\left[ \int _{0}^{1}(1-\epsilon (y))k_{1}H^{0}\tilde{I}(y) dy+(1-\xi )k_{2}H^{0}\tilde{V} \right] +\int _{0}^{1}\gamma (y,x)\tilde{I}(y) dy-(\delta (x)+\alpha (x)) \tilde{I}(x)=s(L)\tilde{I}(x),\\ \int _{0}^{1}\eta (y)\tilde{I} (y) dy-d \tilde{V}=s(L)\tilde{V}. \end{array} \right. \end{aligned}$$

Setting $\tilde{H}=-\frac{\int _{0}^{1}(1-\epsilon (y))k_{1}H^{0}\tilde{I}(y)dy+(1-\xi )k_{2}H^{0}\tilde{V}}{c+s(L)}$, we have

$$\begin{aligned} \bar{L}\begin{pmatrix} \tilde{H}\\ \tilde{I}(\cdot )\\ \tilde{V}\\ \end{pmatrix}&=\begin{pmatrix} -c\tilde{H}-\int _{0}^{1}(1-\epsilon (y))k_{1}H^{0}\tilde{I}(y)dy-(1-\xi )k_{2}H^{0}\tilde{V} \\ (\lambda -L)\begin{pmatrix} \tilde{I}(\cdot )\\ \tilde{V}\\ \end{pmatrix} \end{pmatrix}\\&=s(L) \begin{pmatrix} \tilde{H}\\ \tilde{I}(\cdot )\\ \tilde{V}\\ \end{pmatrix}. \end{aligned}$$

Thus, s(L) is an eigenvalue of the operator $\bar{L}$, i.e. $s(L)\in \sigma (\bar{L})$. It is a contradiction with $s(\bar{L})<s(L)$. Thus, we have $s(\bar{L})=s(L)$.

In the following, we only need to prove that $s(L)<0$, $s(L)=0$ and $s(L)>0$ if and only if $R_0<1,R_0=1$ and $R_0>1$, respectively. We first show that $s(L)=0$ if and only if $R_0=1$. Assume that $s(L)=0$. Using the same argument as in the above proof, we can show that s(L) is an isolated and simple eigenvalue of L. Moreover, if $\varsigma \in \sigma (L)$ and $\varsigma \ne s(L)$, then $\mathfrak {R}\varsigma <s(L)$ and the eigenspace of s(L) is spanned by some $(\varphi ,\theta )^{T}\in C_{++}([0,1])\times \mathbb {R}_{++}$, i.e.,

$$\begin{aligned} \left\{ \begin{array}{ll} \beta (x)\left[ \int _{0}^{1}(1-\epsilon (y))k_{1}H^{0}\varphi (y) dy+(1-\xi )k_{2}H^{0}\theta \right] +\int _{0}^{1}\gamma (y,x)\varphi (y) dy-(\delta (x)+\alpha (x)) \varphi (x)=0,\\ \int _{0}^{1}\eta (y)\varphi (y) dy-d \theta =0. \end{array} \right. \end{aligned}$$

(5)

The second equation in (5) implies that $\theta =\frac{\int _{0}^{1}\eta (y)\varphi (y) dy}{d}$. Substituting this into the first equation of (5), we have $\mathcal L[\varphi ](x)=\varphi (x)$. It then follows that $R_0=\rho (\mathcal L)=1$.

Next, we assume that $R_0=1$. Then there exists an eigenfunction $\varphi ^*(x)\in C_{++}([0,1])$ such that $\mathcal {L}[\varphi ^*](x)=\varphi ^*(x)$. Let $\theta ^*=\frac{\int _{0}^{1}\eta (y)\varphi ^* (y) dy}{d}>0$. We have

$$\begin{aligned} \left\{ \begin{array}{ll} \beta (x)\left[ \int _{0}^{1}(1-\epsilon (y))k_{1}H^{0}\varphi ^*(y) dy+(1-\xi )k_{2}H^{0}\theta ^* \right] +\int _{0}^{1}\gamma (y,x)\varphi ^*(y) dy-(\delta (x)+\alpha (x)) \varphi ^*(x)=0,\\ \int _{0}^{1}\eta (y)\varphi ^* (y) dy-d \theta ^*=0.\\ \end{array} \right. \end{aligned}$$

This implies that $0\in \sigma (L)$ and $0\le s(L)$. Define $\big \{e^{Lt}\big \}_{t\ge 0}$ as the uniformly continuous semigroup generated by L. Clearly, we have $e^{Lt}(\varphi ^*(x),\theta ^*)^{T}=(\varphi ^*(x),\theta ^*)^{T}$ for all $t\ge 0$. Since $\big \{e^{Lt}\big \}_{t\ge 0}$ is a positive semigroup, it follows that

$$\begin{aligned} \begin{aligned} e^{Lt}(I_{0}(\cdot ),V_{0})^{T}&\le \frac{1}{\min \big \{\inf _{[0,1]}\varphi ^* (x),\theta ^* \big \}}e^{Lt}(\varphi ^*(x),\theta ^*)^{T}\\&=\frac{1}{\min \big \{\inf _{[0,1]}\varphi ^*(x),\theta ^*\big \}} (\varphi ^*(x),\theta ^*)^{T},\\ \end{aligned} \end{aligned}$$

for any $(I_{0}(\cdot ),V_{0})^{T}\in C_{+}([0,1])\times \mathbb {R}_{+}$ with $\Vert (I_{0}(\cdot ), V_{0})^{T}\Vert _{C([0,1])\times \mathbb {R}}\le 1$ and $t\ge 0$. This implies that $\Vert e^{Lt}\Vert \le \frac{\Vert (\varphi ^*(x),\theta ^*)^{T}\Vert _{C([0,1])\times \mathbb {R}}}{\min \big \{\inf _{[0,1]}\varphi ^*(x),\theta ^*\big \}}$ for all $t\ge 0$. Since s(L) is equal to the growth bound of $\big \{e^{Lt}\big \}_{t\ge 0}$, we have $s(L)\le 0$. Therefore, we conclude that $s(L)=0$.

Now let us show that $s(L)>0$ if and only if $R_0>1$. Suppose that $s(L)>0$. Then s(L) is an isolated and simple eigenvalue of L. If $\varsigma \in \sigma (L)$ and $\varsigma \ne s(L)$, then $\mathfrak {R}\varsigma <s(L)$. Moreover, the eigenspace of s(L) is spanned by some $(\varphi ,\theta )^{T}\in C_{++}([0,1])\times \mathbb {R}_{++}$, i.e.,

$$\begin{aligned} \left\{ \begin{array}{ll} \beta (x)\left[ \int _{0}^{1}(1-\epsilon (y))k_{1}H^{0}\varphi (y) dy+(1-\xi )k_{2}H^{0}\theta \right] +\int _{0}^{1}\gamma (y,x)\varphi (y) dy-(\delta (x)+\alpha (x)) \varphi (x)=s(L)\varphi (x),\\ \int _{0}^{1}\eta (y)\varphi (y) dy-d \theta =s(L)\theta . \end{array} \right. \end{aligned}$$

(6)

The second equation in (6) implies that $\theta =\frac{\int _{0}^{1}\eta (y)\varphi (y) dy}{s(L)+d}$. Substituting this into the first equation of (6), we have $\mathcal L[\varphi ](x)\ge (1+s(L))\varphi (x)$. It then follows that $R_0=\rho (\mathcal L)>1$. Let $R_0=\rho (\mathcal L)>1$. Then there exists $\varphi ^*(x)\in C_{++}([0,1])$ such that $\mathcal L[\varphi ^*](x)=R_0 \varphi ^*(x)$. Let $\theta ^*=\frac{\int _{0}^{1}\eta (y)\varphi ^* (y) dy}{d}$. We have that

$$\begin{aligned} L\begin{pmatrix} \varphi ^*\\ \theta ^*\\ \end{pmatrix}=\begin{pmatrix} (\alpha (x)+\delta (x))(R_0-1)\varphi ^*(x)\\ 0\\ \end{pmatrix}. \end{aligned}$$

If $s(L)<0$, then $0\in \mathbb C{\setminus }\sigma (L)$ and $(-L)^{-1}$ is a positive operator as L generates a positive semigroup. Solving the above equation, we obtain

$$\begin{aligned} \begin{pmatrix} \varphi ^*\\ \theta ^*\\ \end{pmatrix}=-(-L)^{-1}\begin{pmatrix} (\alpha (x)+\delta (x))(R_0-1)\varphi ^*(x)\\ 0\\ \end{pmatrix}\le 0, \end{aligned}$$

which leads to a contradiction with $\varphi ^*(x)\in C_{++}([0,1])$. Thus, $s(L)\ge 0$, where the case of $s(L)=0$ has been excluded from the above discussion. The proof is completed. $\square$

Since the sign of $s(\bar{L})$ determines the local stability of the equilibrium $E^0$, we have

Theorem 3

The infection-free equilibrium $E^{0}$ is locally asymptotically stable if the basic reproduction number $R_{0}<1$ and unstable if $R_{0}>1$.

3.2 Global stability of equilibrium $E^{0}$

For the global asymptotic stability of the infection-free equilibrium $E^{0}$, it suffices to show that $E^{0}$ is a global attractor based on the local stability results given in Theorem 3.

Theorem 4

If $R_{0}<1$, then the infection-free equilibrium $E^{0}$ is globally asymptotically stable.

Proof

We only need to show that $(H(t),I(t,\cdot ),V(t))^{T}\rightarrow (H^{0},0,0)^{T}$ as $t\rightarrow +\infty$ for any initial value in $\mathbb X_+$. From $H'(t)\le \lambda -cH(t)$, we have that $H(t)\le H^{0}+\epsilon ^{0}$ for all sufficiently large t. Without loss of generality, we assume that $H(t)\le H^{0}+\epsilon ^{0}$ for all $t\ge 0$. Thus, for any solution $(H,I(\cdot ),V)^{T}$ of (1), we have

$$\begin{aligned} \begin{aligned} I_{t}(t,x)&\le \beta (x)\left[ \int _{0}^{1}(1-\epsilon (y))k_{1}(H^{0}+\epsilon ^{0})I(y)dy+(1-\xi )k_{2}(H^{0}+\epsilon ^{0})V\right] \\&\quad +\int _{0}^{1}\gamma (y,x)I(y)dy\\&\qquad \quad -\delta (x)I(x)-\alpha (x)I(x), \\ \dot{V}(t)&=\int _{0}^{1}\eta (y)I(y)dy-dV. \end{aligned} \end{aligned}$$

Define the operators $\mathcal L_{\epsilon _0}:C([0,1])\rightarrow C([0,1])$ and $L_{\epsilon _0}:C([0,1])\times \mathbb {R}\rightarrow C([0,1])\times \mathbb {R}$ by

$$\begin{aligned} \begin{aligned} \mathcal {L}_{\epsilon _0}[I](x)&=\frac{\beta (x)}{\alpha (x)+\delta (x)}\int _{0}^{1}(1-\epsilon (y))k_{1}(H^{0}+\epsilon ^{0})I(y)dy+\frac{\int _{0}^{1}\gamma (y,x)I(y)dy}{\alpha (x)+\delta (x)}\\&+\frac{\beta (x) (1-\xi )k_{2}(H^{0}+\epsilon ^{0})}{d(\alpha (x)+\delta (x))}\int _{0}^{1}\eta (y)I(y)dy,\\ \end{aligned} \end{aligned}$$

(7)

and

$$\begin{aligned} \begin{aligned} L_{\epsilon _0}\begin{pmatrix} I\\ V\\ \end{pmatrix}=\begin{pmatrix} \beta (x)\left[ \int _{0}^{1}(1-\epsilon (y))k_{1}(H^{0}+\epsilon ^{0})I(y)dy+(1-\xi )k_{2}(H^{0}+\epsilon ^{0})V\right] \\ \qquad +\int _{0}^{1}\gamma (y,x)I(y)dy-\delta (x) I(x)-\alpha (x) I(x)\\ \int _{0}^{1}\eta (y)I(y)dy-dV\\ \end{pmatrix}. \end{aligned} \end{aligned}$$

Because $R_{0}<1$ (i.e. $\rho (\mathcal {L})<1$) and $\mathcal L_{\epsilon _0}\rightarrow \mathcal L$ in the operator norm as $\epsilon ^0\rightarrow 0$, we can choose $\epsilon ^{0}>0$ small enough such that $\rho (\mathcal {L}_{\epsilon _0})<1$. It follows from Theorem 2 that $s(L_{\epsilon _0})<0$.

By the comparison principle, one obtains

$$\begin{aligned} 0\le \begin{pmatrix} I(t,x)\\ V(t)\\ \end{pmatrix}\le e^{L_{\epsilon _0}t}\begin{pmatrix} I_{0}(x)\\ V_{0}\\ \end{pmatrix}. \end{aligned}$$

Because the growth bound of $\big \{e^{L_{\epsilon _0}t}\big \}_{t\ge 0}$ is equal to $s(L_{\epsilon _0})$, we conclude that $e^{L_{\epsilon _0}t}\begin{pmatrix} I_{0}(x)\\ V_{0}\\ \end{pmatrix}\rightarrow 0$ as $t\rightarrow +\infty$, which means that $\begin{pmatrix} I(t,x)\\ V(t)\\ \end{pmatrix}\rightarrow 0$ as $t\rightarrow +\infty$. Together with the first equation of (1), we have $H(t)\rightarrow H^{0}$ as $t\rightarrow +\infty$. This completes the proof. $\square$

4 Global stability of the infected equilibrium $E^{*}$

According to Theorem 1 and Theorem 4, we know that $E^{0}$ becomes unstable and the infected equilibrium $E^{*}$ emerges when $R_{0}>1$. In this section, we study the global stability of equilibrium $E^{*}$. The method of proof is to use Lyapunov functionals and LaSalle’s invariance principle.

To show that the Lyapunov functional is well defined, we need to establish the uniform persistence of system (1) when $R_{0}>1$. Using the method in Thieme (2000), the proof is divided into three steps: Step 1, the solution of (1) is strictly positive when $R_{0}>1$; Step 2, system (1) is uniformly weakly persistent; Step 3, by bounded dissipativity and asymptotic compactness of solution semi-flow $\big \{\phi _{t}\big \}_{t\ge 0}$, system (1) has a global attractor $\mathcal {Y}$. The detailed proof is given in “Appendix B”. With the above results, we have the following theorem.

Theorem 5

When $R_{0}>1$, the infected equilibrium $E^{*}$ is globally asymptotically stable in $\mathrm{Int}\mathbb {X}_{+}$.

Proof

From Theorem 1.3.11 in Zhao (2017), the system (1) has a global attractor $\mathcal {Y}$ in $\mathrm{Int}\mathbb {X}_{+}$. Moreover, for any $(\tilde{H},\tilde{I}(\cdot ),\tilde{V})\in \mathcal {Y}$, there exist $\varrho _{1},\varrho _{2}>0$ such that

$$\begin{aligned} \begin{aligned} \varrho _{1}\le \tilde{H}\le \varrho _{2}, \quad \varrho _{1}\le \inf _{x\in [0,1]}\tilde{I}(x)\le \sup _{x\in [0,1]}\tilde{I}(x)\le \varrho _{2} \quad \hbox {and} \quad \varrho _{1}\le \tilde{V}\le \varrho _{2}, \quad \forall t\ge 0. \end{aligned} \end{aligned}$$

When $R_{0}>1$, system (1) has an unstable equilibrium $E^0$ and a positive equilibrium $E^{*}$. To prove the theorem, we only need to show that $E^{*}$ is the global attractor of system (1) in $\mathrm{Int}\mathbb {X}_{+}$, i.e. $\mathcal {Y}=\big \{E^{*}\big \}$. Let $z(t)=(H(t),I(t,\cdot ),V(t))^{T}$ be a complete solution to system (1) that lies in $\mathcal {Y}$. Then there exist $m>0$ and $M>0$ such that

$$\begin{aligned} \begin{aligned}&m\le \frac{H(t)}{H^{*}}\le M, \quad m\le \inf _{x\in [0,1]}\frac{I(t,x)}{I^{*}(x)}\le \sup _{x\in [0,1]}\frac{I(t,x)}{I^{*}(x)}\le M, \\&\quad m\le \frac{V(t)}{V^{*}}\le M \quad \hbox {for} \; \hbox {all} \; t\ge 0. \end{aligned} \end{aligned}$$

Define

$$\begin{aligned} \begin{aligned} \psi (x,y)=&\left[ \beta (x)\eta (y)(1-\xi )k_{2}H^{*}+d\gamma (y,x)\right] I^{*}(y)\\&+d\beta (x)(1-\epsilon (y))k_{1}H^{*}I^{*}(y), \quad x,y\in [0,1]. \end{aligned} \end{aligned}$$

It is clear that $\psi$ is continuous and $\psi (x,x)>0$ for all $x\in [0,1]$. Then $\mathcal {X}(x)=\int _{0}^{1}\psi (x,y)dy$ defines a continuous positive function, that is, $\mathcal {X}\in C_{++}([0,1])$. Using the Proposition 11.1 in Thieme (2011), there exists a non-negative Borel measurable function w on [0, 1] such that $\mathcal {X}w$ is integrable and

$$\begin{aligned} \begin{aligned} \int _{0}^{1}w(x)\int _{0}^{1}\psi (x,y)[\nu (x)-\nu (y)]dydx=0, \quad \hbox {for} \, \hbox {all} \, \nu \in L^{\infty }([0,1]). \end{aligned} \end{aligned}$$

(8)

Let $\kappa (a)=a-1-\ln a$. It is obvious that the function $\kappa$ is continuously differentiable and attains its global minimum at 1 with $\kappa (1)=0$. We define a Lyapunov functional

$$\begin{aligned} \begin{aligned} G(t)&=G(H(t),I(t,x),V(t))\\&=\int _{0}^{1}w(x)\left[ dH^{*}\beta (x)\kappa (\frac{H(t)}{H^{*}})+dI^{*}(x)\kappa (\frac{I(t,x)}{I^{*}(x)})\right. \\&\quad \left. +(1-\xi )k_{2}H^{*}V^{*}\beta (x)\kappa (\frac{V(t)}{V^{*}})\right] dx. \end{aligned} \end{aligned}$$

(9)

Clearly, the function G(t) is continuously differentiable. Calculating the derivative of G(t) along the solution of model (1) yields

$$\begin{aligned} \frac{dG}{dt}=&-\int _{0}^{1}w(x)\Bigg [d\beta (x)(1-\frac{H^{*}}{H})(cH-cH^{*})\Bigg ]dx\nonumber \\&-\int _{0}^{1}w(x)d\beta (x)(1-\xi )k_{2}H^{*}V^{*}\Bigg [\kappa (\frac{H^{*}}{H})\nonumber \\&+\kappa (\frac{I^{*}(x)}{I(x)}\frac{HV}{H^{*}V^{*}})\Bigg ]dx-\int _{0}^{1}w(x)d\beta (x) \int _{0}^{1}(1-\epsilon (y))k_{1}H^{*}I^{*}(y)\nonumber \\&\quad \Bigg [\kappa (\frac{H^{*}}{H})+\kappa (\frac{HI(y)}{H^{*}I^{*}(y)}\nonumber \\&\cdot \frac{I^{*}(x)}{I(x)})\Bigg ]dydx-\int _{0}^{1}w(x)d\int _{0}^{1}\gamma (y,x)I^{*}(y) \kappa (\frac{I^{*}(x)}{I(x)}\frac{I(y)}{I^{*}(y)})dydx\nonumber \\&-\int _{0}^{1}w(x)\beta (x)(1-\xi )k_{2}H^{*}\nonumber \\&\quad \cdot \int _{0}^{1}\eta (y)I^{*}(y)\kappa (\frac{V^{*}}{V}\frac{I(y)}{I^{*}(y)})dydx\nonumber \\&+\int _{0}^{1}w(x)\int _{0}^{1}\Bigg [\beta (x)k_{2} (1-\xi )H^{*}\eta (y)I^{*}(y)+d\gamma (y,x)I^{*}(y)\nonumber \\&+d\beta (x)(1-\epsilon (y))k_{1}H^{*}I^{*}(y)\Bigg ]\Bigg [\ln \frac{I(x)}{I^{*}(x)}-\frac{I(x)}{I^{*}(x)}-\ln \frac{I(y)}{I^{*}(y)}+\frac{I(y)}{I^{*}(y)}\Bigg ]dydx. \end{aligned}$$

(10)

Detailed calculation is available in “Appendix C”. In view of $(1-\frac{H^{*}}{H})(cH-cH^{*})\ge 0$ and $\kappa (a)$ is nonnegative for all $a>0$, the first five terms on the right-hand side of (10) are non-positive. By (8), the last term on the right-hand side of (10) is 0. Thus, $\frac{dG}{dt}\le 0$ with equality if and only if $H=H^{*}$, $I(x)=I^{*}(x)$ and $V=V^{*}$. Thus, the largest invariant set in $\Big \{(H,I(x),V)^{T}\in \mathbb {X}_{+}: \frac{dG}{dt}\big |_{(2.1)}=0\Big \}$ is the singleton $E^{*}$. Therefore, $\mathcal {Y}=\big \{E^{*}\big \}$, which implies that $E^{*}$ is unique and globally asymptotically stable. $\square$

5 Numerical investigations

We choose specific functions for the status-dependent parameters, examine the effect of cell-to-cell transmission on the basic reproduction number and steady-state viral load, explore if the continuous status-structured model (1) with cell-to-cell transmission can describe the viral load persistence in patients under effective drug treatment, and test whether the viral and latent reservoir persistence, as well as intermittent viral blips can be generated by occasional activation of latently infected cells upon encounter with relevant antigens.

5.1 Parameter values and functions

Based on experimental data and previous modeling literature (Rong and Perelson 2009a, b, c), we fix some parameter values. In the absence of infection, the CD4+ T cell level is approximately $10^{6}$ $ml^{-1}$ (Bofill et al. 1992). The death rate of uninfected CD4+ T cells (c) is 0.01 $day^{-1}$ (Perelson et al. 1993). Thus, from the equilibrium of target cells in the absence of infection, we obtain that the generation rate of uninfected cells is $\lambda =10^{6}\times 0.01=10^{4}$ $ml^{-1}day^{-1}$. The infection rate and clearance rate of virions are chosen to be $k_{2}=2.4\times 10^{-8}$ ml/day and $d=23$ $day^{-1}$ (Rong and Perelson 2009b), respectively. The rate of cell-to-cell viral transmission is $k_{1}=2\times 10^{-6}$ ml/day (Wang et al. 2017b). Antiretroviral drugs can block both cell-free virus infection and cell-to-cell viral transmission. However, multiple viral genomes can be transmitted simultaneously during cell-to-cell transmission. Thus, antiretroviral drugs may not completely block the infection caused by all the virions. Compared with cell-free virus infection, the same antiretroviral drugs have lower treatment efficacy for cell-to-cell viral transmission. To rule out the potential influence of cell-free virus infection and only focus on the effect of cell-to-cell transmission on HIV infection, we study an extreme case, i.e. letting the overall drug efficacy of inhibiting cell-free virus infection $\xi$ be 1. The function of the drug efficacy blocking cell-to-cell viral transmission $\epsilon (y)$ will be further discussed below.

The probability function $\beta (x)$ of generating newly infected cells with the activation status x satisfies the condition (A2), i.e. $\int _{0}^{1}\beta (x)dx=1$, but its functional form remains unknown. Although there are some data on the cells with low, intermediate and high concentration of Tat (Weinberger et al. 2005) , it is not sufficient to justify the choice of a specific function $\beta (x)$. Here we choose the following function as an example

$$\begin{aligned} \begin{aligned} \beta (x)=\frac{1}{\int _{0}^{1}B(x)dx}\times B(x), \end{aligned} \end{aligned}$$

(11)

where $B(x)=\frac{1}{\sqrt{2\pi }r_{1}}e^{-\frac{(x-\beta _{1})^{2}}{2r_{1}^{2}}}$ is the probability density function of a normal distribution with the location parameter $\beta _{1}$ and the scale parameter $r_{1}$. HIV latent infection accounts for a small fraction of the new infection (Rong and Perelson 2009b). Thus, we assume the location parameter $\beta _{1}$ to be greater than one half, and choose $\beta _{1}=0.8$ and $r_{1}=0.2$ as an example in the simulation. More data on the distribution of the activation status would be useful in determining the status-dependent function $\beta (x)$.

Parameter $\gamma (y,x)=\delta (y)p(y,x)$ represents the switch rate of infected cells from status y to status x. Because it is more likely for an infected cell to change from one status to its closer status, this switch rate should decrease as the distance between y and x increases. We choose the following function

$$\begin{aligned} \begin{aligned} \gamma (y,x)=\frac{1}{\sqrt{2\pi }r_{2}}e^{-\frac{(y-x)^{2}}{2r_{2}^{2}}} \end{aligned} \end{aligned}$$

(12)

as an example with the scale parameter $r_{2}=0.1$. The switch rate of infected cells from status x to other statuses is calculated by the balance condition $\delta (x)=\int _{0}^{1}\gamma (x,y)dy$. Latently infected cells have a much longer lifespan than activated cells (Chun et al. 1995). Thus, we assume the death rate of infected cells $\alpha (x)$ to be larger when the infected cell has a higher activation status. The death rate of completely latently infected cells and productively infected cells are 0.001 $day^{-1}$ (i.e. $\alpha (0)=0.001$) and 1 $day^{-1}$ (i.e. $\alpha (1)=1$) (Rong and Perelson 2009c), respectively. Thus, a simple example of the increasing function $\alpha (x)$ is $\alpha (x)=1.001-0.001^{x}$. Because infected cells with a higher activation status can produce more virions, the viral production rate $\eta (y)$ of an infected cell with the activation status y is also an increasing function of the status y. A completely latently infected cell does not produce virus, that is, $\eta (0)=0$. The viral production rate of fully productively infected cells is chosen to be 2000 virus/cell (Wang et al. 2017a). Hence, we assume the status-dependent viral production rate to be $\eta (y)=200\times (11^{y}-1)$ such that $\eta (0)=0$ and $\eta (1)=2000$. These parameters and their values are summarized in Table 1.

5.2 Effect of cell-to-cell viral transmission on HIV persistence

In this section, we study the effect of cell-to-cell transmission on the basic reproduction number $R_{0}$ and the steady-state viral load. The status-dependent drug efficacy of blocking cell-to-cell transmission, i.e. the function $\epsilon (y)$, is assumed to be a decreasing function of the status y and also satisfy the condition (A1) (i.e. $\epsilon (0)=1$). However, the exact functional form remains unknown. We performed simulations using two different functions for $\epsilon (y)$. One is the exponential decay function $\epsilon (y)=e^{-ay}$ and the other is a linear function $\epsilon (y)=\max \big \{1-by,0\big \}$, where $a>0$ and $b>0$ are constants that characterize how fast the drug efficacy declines as the level of activation of infected cells increases.

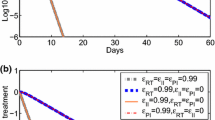
Figure 1a shows that the basic reproduction number $R_{0}$ is an increasing function of the decay constant a or b. A larger value of a or b implies that the treatment effectiveness in blocking cell-to-cell transmission declines faster given the same level of infected cell activation. Thus, as a or b increases, the treatment efficacy decreases and the basic reproduction number increases. Moreover, $R_{0}$ becomes less sensitive to the increase of the decay constant. The simulations also show a threshold value for the decay constant, below which the basic reproduction number is less than 1 (i.e. viral eradication) and above which $R_{0}$ is greater than 1 (i.e. viral persistence). Therefore, even when the treatment can completely inhibit cell-free virus infection, cell-to-cell viral transmission can still lead to viral persistence. Note that the threshold value of a is greater than that of b. This is because the linear function of drug efficacy $\epsilon (y)$ declines faster than the exponential function as y increases for the same decay rates. Thus, a larger threshold value of a is needed for the basic reproduction number to reach 1.

We also investigate the steady-state viral load as a function of the decay constant a or b (see Fig. 1b). Similar to the change of the basic reproduction number, the steady-state viral load also increases as the decay constant a or b increases but it is sensitive to the decay constant near the threshold value for the equilibrium to reach the detection limit. Also note that the threshold value of the decay constant for the viral load to reach the detection limit is larger than that for the basic reproduction number to reach 1.

Fig. 1

Sensitivity of the basic reproduction number and viral load equilibrium with respect to the drug efficacy $\epsilon (y)$ of blocking cell-to-cell transmission by infected cells at status y. Different functions are used for the drug efficacy $\epsilon (y)$, $\epsilon (y)=e^{-ay}$ and $\epsilon (y)=\max \big \{1-by,0\big \}$. The other parameters are listed in Table 1. a How the basic reproduction number $R_{0}$ changes with the decay constant a or b in the drug efficacy function $\epsilon (y)$. b How the viral load equilibrium changes as the decay constants increase. Red and black horizontal lines in (a) and (b) represent $R_{0}=1$ and the detection limit of standard assays, respectively. Vertical dash-dotted line in (a) indicates the threshold value of the decay constant a or b corresponding to $R_{0}=1$

5.3 Activation of latently infected cells by relevant antigens

In addition to the ongoing viral replication induced by cell-to-cell viral transmission, activation of latently infected cells can also serve as a source of persistent viremia. In model (1), we did not have a separable variable for latently infected cells. We only assumed that the lower the activation status, the more likely the infected cell remains in the latent status. If we specify an interval of the activation status over which the infected cell is considered to be latent, for example [0, 1/2], then we can study the dynamics of virus and latent reservoir. In this extreme case, we assume that the remaining activation status interval [1/2, 1] represents productively infected cells, which can produce virions and transfer to uninfected cells during cell-to-cell transmission. This is similar to the discrete case in which infected cells are either latent or productive. In addition to the switch of infected cells with different activation statuses due to intrinsic random perturbations (Wang and Rong 2014; Weinberger et al. 2005), latently infected cells can also be activated and become productively infected cells when they encounter their relevant antigens. Taking this into consideration, model (1) with antigenic activation can be described by the following equations:

$$\begin{aligned}&\dot{H}(t)=\lambda -cH(t)-\int _{1/2}^{1}(1-\epsilon (y))k_{1}H(t)I(t,y)dy-(1-\xi )k_{2}H(t)V(t), \nonumber \\&I_{t}(t,x)=\beta (x)\left[ \int _{1/2}^{1}(1-\epsilon (y))k_{1}H(t)I(t,y)dy+(1-\xi )k_{2}H(t)V(t)\right] \nonumber \\&\quad +\int _{0}^{1}\gamma (y,x)I(t,y)dy \nonumber \\&\quad -\delta (x)I(t,x)-\alpha (x)I(t,x)-r(x)I(t,x), \qquad \qquad \qquad \qquad \quad \qquad x\in [0,1/2), \nonumber \\&I_{t}(t,x)=\beta (x)\left[ \int _{1/2}^{1}(1-\epsilon (y))k_{1}H(t)I(t,y)dy+(1-\xi )k_{2}H(t)V(t)\right] \nonumber \\&\quad +\int _{0}^{1}\gamma (y,x)I(t,y)dy \nonumber \\&\quad -\delta (x)I(t,x)-\alpha (x)I(t,x)+r(x-1/2)I(t,x-1/2), \qquad \qquad \qquad x\in [1/2,1],\nonumber \\&\dot{V}(t)=\int _{1/2}^{1}\eta (y)I(t,y)dy-dV(t). \end{aligned}$$

(13)

Because latently infected cells do not produce virus, the total virus generated by productively infected cells per unit time is $\int _{1/2}^{1}\eta (y)I(t,y)dy$. Further, latently infected cells cannot transfer virions to uninfected cells. Thus, uninfected cells are infected via cell-to-cell transmission at a rate $\int _{1/2}^{1}(1-\epsilon (y))k_{1}H(t)I(t,y)dy$. The function r(x) is the rate at which infected cells with status x are activated by their relevant antigens. For simplicity, we assume that r(x) is status-independent in the simulation. When latently infected cells encounter their specific antigens, r is assumed to increase from 0 to 0.3 $day^{-1}$ (Rong and Perelson 2009b). We will study if model (13) with antigenic activation of latently infected cells can explain the emergence of viral blips during treatment and how the activation affects the dynamics of the latent reservoir. The other parameters and variables are the same as those in Eq. (1).

We use the exponential function $\epsilon (y)=e^{-ay}$ as the efficacy of treatment in blocking cell-to-cell transmission. Other functions that decrease as the level of activation of infected cells increases and that satisfy the condition (A1) can also be used, e.g. the linear function $\epsilon (y)=\max \big \{1-by,0\big \}$ we used in Sect. 5.2. The value of the function $\epsilon (y)$ depends on the activation status y and the choice of the decay constant a or b. When $0.5<y<1$, any value of the parameter a or b that can generate low steady-state viral load can also be used in the simulation. For the exponential function $\epsilon (y)=e^{-ay}$, when $a=1.05687$, model (13) has a unique infected equilibrium, in which the viral load is suppressed to below the detection limit (i.e. 43 RNA copies/ml). To test the sensitivity of viral blips and the latent reservoir size with respect to drug efficacy, we also show another example with a slightly smaller decay rate, $a=1.05686$, in which the model has a lower level of steady-state viral load, 40 RNA copies/ml. These equilibria are set as the initial values when performing simulations in response to antigenic stimulation.

Fig. 2

Viral load and the latent reservoir dynamics predicted by the model with antigenic activation of latently infected cells (Eq. (13)). To test the sensitivity of model prediction to the treatment, we plot the viral load and cell changes with different decay constants a in the exponential drug efficacy $\epsilon (y)=e^{-ay}$. Simulations are performed before antigen activation (0 to day 50, i.e. steady-state level), under antigen activation (day 50 to 55) and post-activation (after day 55). The predicted dynamics of a viral load, b total latently infected cells, c total productively infected cells, and d the relative contributions of cell-to-cell transmission and infected cell switch between different statuses to the latent reservoir are shown. When activation occurs, i.e. $50\le t\le 55$ days, r was chosen to be 0.3 $day^{-1}$ and it was 0 elsewhere. The other parameter values used are listed in Table 1. The black solid horizontal line in (a) represents the detection limit of 50 RNA copies/ml

Figure 2 shows the changes of viral load, latent reservoir, productively infected cells, and the contributions of cell-to-cell transmission and infected cell transfer between statuses to the latent reservoir during an antigenic activation of latently infected cells. Latently infected cells and productively infected cells are given by $\int _{0}^{1/2}I(t,x)dx$ and $\int _{1/2}^{1}I(t,x)dx$, respectively. Upon activation, latently infected cells decline quickly (Fig. 2b), leading to an increase of productively infected cells (Fig. 2c), which in turn produce more virions and generate a viral blip above the detection limit (Fig. 2a). The change of viral load is synchronized with that of productively infected cells because productively infected cells are the only source of viral production. Interestingly, the decline of latently infected cells is transient, followed by an increase to an even higher level than that before activation (Fig. 2b). The increase of latently infected cells after activation comes from two sources. One is the replenishment by productively infected cells via cell-to-cell transmission (i.e. $\beta (x)[\int _{1/2}^{1}(1-\epsilon (y))k_{1}H(t)I(t,y)dy]$, where $x\in [0,1/2)$). Note that we assume $\xi =1$ in the simulation so there is no contribution to the latent reservoir from ongoing viral replication induced by cell-free virus infection. The other source contributing to the increase of latently infected cells is the switch of infected cells between different statuses (i.e. $\int _{0}^{1}\gamma (y,x)I(t,y)dy$, where $x\in [0,1/2)$). Productively infected cells increase following latently infected cell activation and revert to the latent status due to random perturbations, which provides an avenue to replenish the latent reservoir. We also note that the decay constant a in the drug efficacy function $\epsilon (y)=e^{-ay}$ plays an important role in the prediction of viral blips. With a smaller decay constant, the initial viral load (i.e. the steady-state viral load of the model before activation) is lower. In this scenario, a burst of viral production following the activation of latently infected cells cannot generate a viral blip above the detection limit (Fig. 2a).

To compare the relative contributions to the latent reservoir from cell-to-cell transmission and infected cell switch between different statuses, we plot the following ratio

$$\begin{aligned}&\int _{0}^{1/2}\beta (x)\int _{1/2}^{1}(1-\epsilon (y))k_{1}H(t)I(t,y)dydx :\\&\qquad \int _{0}^{1/2} \left[ \int _{0}^{1}\gamma (y,x)I(t,y)dy-\delta (x)I(t,x)\right] dx \end{aligned}$$

in Fig. 2d The denominator in the ratio is the net increase of latently infected cells due to switch. The simulation shows that cell-to-cell transmission contributes more than the switch between infected cells. This result is supported by some other studies showing that cell-to-cell transmission accounts for over half of virus infection (Chen et al. 2007; Dimitrov et al. 1993; Iwami et al. 2015). Figure 2d also shows that the curves with different decay constants overlap. Thus, changing the decay constant in the drug efficacy function of blocking cell-to-cell transmission does not have any visible influence on the relative contributions to the latent reservoir. However, it should be noted that the quantitative comparison of the relative contributions depends on the choice of other parameters. In summary, we showed that when the viral load is successfully suppressed (assuming no cell-free virus infection of CD4+ T cells), cell-to-cell transmission and the random switch between infected cells can play a critical role in the maintenance of the latent reservoir.

5.4 Emergence of viral blips and latent reservoir stability

From the simulation in Fig. 2a, we find that a small change of the decay constant in the drug efficacy function affects the emergence of viral blips, which suggests that the viral load depends heavily on the therapeutic efficacy. After latently infected cell activation, the decay of virus and infected cells is extremely slow (Fig. 2a–c). If we increase the decay constant in the exponential drug efficacy function, i.e. decrease the drug efficacy in blocking cell-to-cell transmission, then the viral load will increase and stay above the detection limit for a long time. Thus, the viral load above the detection limit is not transient and cannot be considered as a viral blip. The latent reservoir will also increase and stay at a higher level after the antigenic activation, which does not agree with the stability (or extremely slow decay) of the latent reservoir observed in patients under long-term suppressive therapy. On the contrary, if we decrease the decay constant, then the level of virus and latently infected cells will decline quickly after the initial increase following activation. Therefore, viral blip above the detection limit will not appear and the size of the latent reservoir cannot be maintained. This suggests that the emergence of transient viral blips and the size of the latent reservoir are sensitive to small changes in the decay constant in the exponential drug efficacy function.

To overcome these limitations, we include a logistic term representing the homeostatic proliferation of latently infected cells, which was proposed in a viral dynamic model (Rong and Perelson 2009c) and confirmed in experiments (Chomont et al. 2009). With the logistic term, the second equation of model (13) becomes

$$\begin{aligned} \begin{aligned} I_{t}(t,x)=&\beta (x)\left[ \int _{1/2}^{1}(1-\epsilon (y))k_{1}H(t)I(t,y)dy+(1-\xi )k_{2}H(t)V(t)\right] \\&+\int _{0}^{1}\gamma (y,x)I(t,y)dy \\&-\delta (x)I(t,x)-\alpha (x)I(t,x)-r(x)I(t,x)\\&+p(x)I(t,x)[1-I(t,x)/I_{max}(x)] \\ \end{aligned} \end{aligned}$$

(14)

for $x\in [0,1/2)$, where p(x) and $I_{max}(x)$ are the maximum proliferation rate and carrying capacity of latently infected cells with the activation status $x\in [0,1/2)$, respectively. For simplification, we assume that they are constants and choose $p=1$ $day^{-1}$ and $I_{max}=64$ cells/ml in the simulation (Rong and Perelson 2009c). The other equations remain unchanged as in model (13).

Fig. 3

The effect of varying the decay constant a in drug efficacy $\epsilon (y)$ on the dynamics predicted by the model with homeostatic proliferation of latently infected cells during antigen activation (model (13) with the second equation replaced by Eq. (14)). We used $a=0.2$ and $a=0.1$ in the simulations. The dynamics of a viral load, b latently and c productively infected cells, and d the relative contribution of homeostatic proliferation of latently infected cells and cell-to-cell transmission to the latent reservoir were plotted before, during and after antigen activation. When $t<50$ days and $t>53$ days, the activation rate is $r=0$ $day^{-1}$; when $50\le t\le 53$ days, r is chosen to be 0.2 $day^{-1}$. The other parameters are the same as those in Fig. 2. The black solid horizontal line in (a) represents the detection limit of 50 RNA copies/ml

Using the model with homeostatic proliferation of latently infected cells, we study the influence of drug efficacies on the viral load and latent reservoir dynamics during antigenic activation. We choose two decay constants $a=0.2$ and $a=0.1$, which correspond to two drug efficacy functions $e^{-0.2y}$ and $e^{-0.1y}$ with the treatment effectiveness of blocking cell-to-cell transmission from completely productively infected cells (i.e. $y=1$) as 0.82 and 0.90, respectively. The steady-state viral loads before activation with these two decay constants are 8.7 and 7.1 RNA copies/ml, respectively. This shows that the new model can robustly describe the viral load persistence at a low level. We choose these equilibria before activation to be the initial conditions for the simulation with antigen activation. Assuming the activation rate $r=0.2$ $day^{-1}$ and a duration of 3 days for the activation, we found that viral loads increase to above the detection limit in the two cases (Fig. 3a). Moreover, after the activation the viral load declines to the pre-activation level because of the suppressive therapy. Viral blips occurs when antigen activation takes places and the emergence of viral blips is not sensitive to the changes in the decay constant or the drug efficacy of blocking cell-to-cell transmission (note that cell-free virus infection is still assumed to be completely blocked). The activation consumes latently infected cells, resulting in a decline of the latent reservoir size. However, homeostatic proliferation replenishes the latent reservoir when the activation is over (Fig. 3b). This explains the stability of the latent reservoir. In summary, model (13) with the second equation replaced by Eq. (14) is not sensitive to the changes in drug efficacy. It can robustly generate the viral blips and persistent viremia after occasional antigenic stimulation and maintain the stability of the latent reservoir. This is consistent with the observation in patients receiving long-term combination therapy (Siliciano et al. 2003).

In addition to the cell-to-cell transmission and infected cell switch between different activation statuses, homeostatic proliferation of latently infected cells can also replenish the latent reservoir. Because the contribution from the transfer between statuses is minor in this case, we only plot the relative contribution to the latent reservoir from homeostatic proliferation of latently infected cells and cell-to-cell transmission (given by the following ratio) in Fig. 3d:

$$\begin{aligned}&\int _{0}^{1/2}p(x)I(t,x)(1-I(t,x)/I_{max}(x))dx : \int _{0}^{1/2}\beta (x)\\&\quad \Big [\int _{1/2}^{1}(1-\epsilon (y))k_{1}H(t)I(t,y)dy\Big ]dx. \end{aligned}$$

The simulation shows that homeostatic proliferation of latently infected cells plays a dominant role in the maintenance of the latent reservoir. As the decay constant a increases, the drug efficacy of blocking cell-to-cell transmission decreases, leading to an increase of the relative contribution to the latent reservoir from cell-to-cell transmission. Thus, the ratio of the contribution from homeostatic proliferation to that from cell-to-cell transmission decreases.

6 Discussion

In addition to the direct cell-free virus infection, cell-to-cell transmission from infected to uninfected CD4+ T cells is another route of HIV spread. Virions transmitted via cell-to-cell transmission evade the antibody neutralization and may be more efficient in establishing viral infection. During cell-to-cell transmission, when multiple virions are tranferred, antiretroviral drugs may not be able to block the infection by all the virions. Thus, cell-to-cell transmission may permit ongoing viral replication despite effective antiretroviral therapy (Sigal et al. 2011). Mathematical models have been developed to include cell-to-cell viral transmission (Allen and Schwartz 2015; Culshaw et al. 2003; Komarova and Wodarz 2013; Lai and Zou 2014; Pourbashash et al. 2014; Shu et al. 2018; Yang et al. 2015). In a recent study (Wang and Rong 2019), we developed a model that includes cell-to-cell viral transmission to study HIV persistence. We assumed that variable number of virions are transmitted with different probabilities and antiretroviral therapy has different effectiveness in blocking their infection. The model contains many variables for different classes of cells that are infected by multiple virions transferred via cell-to-cell transmission. An interesting question arises: can we develop a population-structured model of cell-to-cell transmission that does not contain so many variables but can still be used to study the contributions of cell-free infection and cell-to-cell transmission to HIV persistence? Ideally, this modeling framework can also be used to study other observations, such as the extremely slow decay of the latent reservoir and emergence of intermittent viral blips during long-term suppressive therapy.

There are a lot of population dynamics models (mostly in epidemiology) that are structured by age, size, and spatial position (Auger et al. 2008; Qiu et al. 2018b). However, no models have included the structure of cells or virus that can be used to study cell-to-cell transmission within infected individuals. The difficulty is to find a status variable that can biologically link the population (i.e. infected cells) with cell-to-cell transmission. The activation status of infected cells is a good candidate. Infected cells with a low level of activation stay in the latent state and do not produce virus, while infected cells with a higher level of activation are more productive and thus more likely to transmit virions to uninfected cells during cell-to-cell transmission.

Another reason we choose the activation status of infected cells as the status variable is that it is related to HIV latency, which is considered as a major obstacle to viral elimination. Mathematical models have been developed to study HIV latent infection (see review in Rong and Perelson (2009b)). Most models assumed only two statuses of infection: one is latent and the other is productive infection. However, infected cells do not have to be either completely latent or productive. The activation status of infected cells can be continuous. Using the HIV regulatory protein Tat as the activation marker of infected CD4+ T cells (Karn 1999), it was shown that infected cells can be driven by random intracellular perturbations to switch to other activation statuses (Weinberger et al. 2005). Because cells with a higher activation status are likely to produce more virions, resulting in a larger probability of successful infection via cell-to-cell transmission, incorporation of the continuous status of activation turns out to be a convenient way to study the viral transmission dynamics. In this paper, we developed a new mathematical model that includes continuous status structure of infected cells to study the effect of the switch between infected cells with different activation statuses on virus dynamics. In the model, we assumed that the treatment effectiveness of blocking cell-to-cell transmission declines as the number of virions transmitted per time increases. Because highly activated infected cells produce and transmit more virions, we further assumed that the drug efficacy of inhibiting cell-to-cell transmission is a decreasing function of the level of activation of infected cells.

In the absence of drug treatment, model (1) is similar to the status-dependent epidemiological model (Qiu et al. 2018b). Qiu et al. (2018b) studied an SIR model with a conceptual continuous status and only focused on the mathematical analysis. The status in the model is also vague. In comparison, the status variable in our within-host model is very specific, has a clear biomarker, and provides a new avenue to study some critical issues during HIV treatment. In particular, the transfer between infected cells with different statuses can be used to study the contribution from infected cell population switch that would be difficult to address using a within-host model without the status structure, including the model developed in Wang and Rong (2019).

Mathematical analysis of the model with continuous status structure is more challenging than that given by a system of ordinary differential equations. However, we can still obtain the basic reproduction number $R_{0}$ by defining an operator on viral infection and transfer. The basic reproduction number was shown to completely govern the existence and stability of the equilibria. The model always admits an infection-free equilibrium. When $R_{0}$ is greater than one, the model also has an infected equilibrium. We further proved the stability of the equilibria. When $R_{0}<1$, the infection-free equilibrium is locally and globally asymptotically stable and HIV infection is predicted to die out; when $R_{0}>1$, the infected equilibrium is globally asymptotically stable and HIV establishes chronic infection. In the proof of the stability of equilibria, we used the methods for monotone dynamical system, principal spectral theory and Lyapunov direct method. These methods were also used when analyzing the epidemic model in Qiu et al. (2018b). A further analysis of the steady-state viral load and the basic reproduction number of model (1) shows that cell-to-cell viral transmission can establish infection even when the treatment can completely block the cell-free virus infection. Thus, cell-to-cell transmission alone can lead to viral persistence during suppressive therapy. However, the viral load is sensitive to the changes in the decay constant of the drug efficacy of blocking the cell-to-cell tranmission (Fig. 1).

The latent reservoir plays an essential role in HIV persistence during therapy. When latently infected cells are activated by relevant antigens, they become productive and produce virions, which can fuel ongoing viral replication (Chun et al. 1998). Although the activation consumes latently infected cells, the latent reservoir is very stable or decays extremely slowly during long-term therapy (Siliciano et al. 2003). The mechanisms underlying the stability of the latent reservoir are not fully understood. Different mechanisms have been proposed and tested using mathematical models, such as the programmed expansion and contraction (Rong and Perelson 2009c) or asymmetric cell division of latently infected cells (Rong and Perelson 2009a) upon antigen stimulation. More mechanisms and mathematical models for the latent reservoir stability can be found in the review article (Rong and Perelson 2009b).

To study the dynamics of the latent reservoir using this status-dependent model, we need to specify an interval over which infected cells are latently infected cells. We use [0, 1/2) and [1/2, 1] as an example that resembles the discrete case of infected cells being either latent or productive. Upon activation, the latent reservoir undergoes a temporary decline, followed by a rapid replenishment to reach an even higher level (Fig. 2b). This replenishment is mainly due to the latent infection that comes from cell-to-cell transmission by productively infected cells. However, the transfer between infected cells with different activation statuses also contributes to the maintenance of the latent reservoir (Fig. 2d).

Intermittent viral blips are observed in many antiretroviral-treated patients with plasma viral load suppressed to below the detection limit for many years (Ramratnam et al. 2000; Sklar et al. 2002). This implies that there must be some factors leading to a sudden burst of viral replication that would otherwise be well suppressed. The activation of latently infected cells can explain the emergence of intermittent viral blips (Rong and Perelson 2009a, c). In our status-dependent model, we included an extra activation rate during a period of time (when latently infected cells encounter their recall antigens) and found that the model is able to describe the emergence of viral blips after antigenic activation (Fig. 2a). This antigen-induced activation of latently infected cells is different from the stochastic population switch between infected cells that can generate viral blips (Wang and Rong 2014). Other studies showed that simple deterministic models without forcing functions or stochastic elements can also display viral blips (Zhang et al. 2014).

Model (13) can achieve a low viral load equilibrium, generate viral blips, and replenish the latent reservoir when antigenic activation of latently infected cells takes place. However, the model prediction is sensitive to the drug efficacy of blocking cell-to-cell viral transmission (Fig. 2). To reduce this sensitivity, we modify the model by including the homeostatic proliferation of latently infected cells. The new model was shown to robustly generate viral load persistence at a low level. In fact, even when the antiretroviral therapy completely inhibits cell-to-cell transmission and cell-free virus infection, a low steady-state viral load (i.e. 0.12 RNA copies/ml using the parameter values in Fig. 3) still persists. When activation of latently infected cells occurs, viral blips appear and their emergence is not sensitive to the changes in drug treatment effectiveness. The latent reservoir can be maintained at a stable level, mainly due to the proliferation of latently infected cells (Fig. 3).

In the simulation of antigen activation, we assumed that all latently infected cells have the same activation rate r. However, latently infected cells with different activation statuses have different transcriptional availability and thus may respond differently to antigen, suggesting that they have different activation rates. Similarly, they may have different maximum proliferation rate p and carrying capacity $I_{max}$ with different activation statuses. The heterogeneity of latently infected cells with respect to these parameters may reduce the sensitivity of model prediction. Using status-dependent distributions of these rates, whether the model without homeostatic proliferation of latently infected cells can describe low viral persistence and the latent reservoir stability remains to be further investigated.

Viruses can be consumed when attacking uninfected cells and the cell-free virus infection term $(1-\xi )k_{2}H(t)V(t)$ should be subtracted from both uninfected CD4+ T cells and viruses. We did not subtract this term in the virus equation due to the following considerations. First, HIV is a “fast” virus and has a large clearance rate. The loss of virus due to infection may be minor compared with death and antibody-induced viral neutralization. This has also been assumed in the basic viral dynamic model. Second, including $-(1-\xi )k_{2}H(t)V(t)$ in the virus equation makes mathematical analysis of the full model more complex (for example, see the analysis of a viral dynamic model with immune response (Wang et al. 2013)). For simplicity, we removed the cell-free virus infection term from the V equation. This has also been assumed in some other mathematical models (Perelson et al. 1993, 1996; Perelson and Ribeiro 2013; Pourbashash et al. 2014; Qiu et al. 2018a, b; Ramratnam et al. 2000; Rong and Perelson 2009a, b, c). Lastly, to exclude the influence of cell-free virus infection and only focus on the effect of cell-to-cell transmission on HIV infection, we studied an extreme case in the numerical simulations, i.e. letting the overall drug efficacy of inhibiting cell-free virus infection $\xi$ be 1. In this case, $(1-\xi )k_{2}H(t)V(t)=0$ for any t. Thus, neglecting the loss of virus due to infection does not affect the numerical investigations and conclusions in Sect. 5.

Taken together, we developed and analyzed a new mathematical model that structures the population of infected cells continuously according to their activation status. This provides a new modeling framework that can be used to study the virus dynamics in patients receiving long-term antiretroviral therapy. Even when treatment can completely block the cell-free virus infection, virus can persist due to the cell-to-cell transmission from infected to uninfected cells. In addition to the ongoing viral replication induced by cell-to-cell transmission, the transfer between infected cells with different statuses of activation is able to replenish the latent reservoir. By including the homeostatic proliferation of latently infected cells, the status-dependent model provides a robust model to describe low viral load persistence, extremely slow decay of the latent reservoir and emergence of intermittent viral blips during suppressive therapy. Once beyond a threshold value of the drug efficacy, drug treatment does not play an important role in affecting the viral load and latent reservoir dynamics. Therefore, treatment intensification would not achieve viral eradication, in agreement with the prediction from another modeling study of LTR (long terminal repeats) generation during treatment with integrase inhibitor (Wang et al. 2017a). Other treatment strategies such as blocking the proliferation of latently infected cells or even preventing the establishment of the latent reservoir using very early treatment have to be developed for the elimination of the virus (Vaidya and Rong 2017).

Appendices

Appendix A: Proof of Theorem 1

Proof

Any equilibrium of system (1) satisfies

$$\begin{aligned} \left\{ \begin{array}{ll} \lambda -cH-\int _{0}^{1}(1-\epsilon (y))k_{1}HI(y)dy-(1-\xi )k_{2}HV=0, \\ \beta (x)\left[ \int _{0}^{1}(1-\epsilon (y))k_{1}HI(y)dy+(1-\xi )k_{2}HV\right] +\int _{0}^{1}\gamma (y,x)I(y)dy-\delta (x) I(x)\\ \qquad -\alpha (x) I(x)=0, \\ \int _{0}^{1}\eta (y)I(y)dy-dV=0. \\ \end{array} \right. \end{aligned}$$

(15)

According to the third equation of (15), we have $V=\frac{1}{d}\int _{0}^{1}\eta (y)I(y)dy$. Thus, (15) is equivalent to

$$\begin{aligned} \left\{ \begin{array}{ll} \lambda -cH-\int _{0}^{1}f(y,H,I(y))dy-g(H,I(y))=0,&{} \\ \beta (x)\left[ \int _{0}^{1}f(y,H,I(y))dy+g(H,I(y))\right] +\int _{0}^{1}\gamma (y,x)I(y)dy-\delta (x) I(x)-\alpha (x) I(x)=0, &{}\\ \end{array} \right. \end{aligned}$$

(16)

where $f(y,H,I(y))=(1-\epsilon (y))k_{1}HI(y)$ and $g(H,I(y))=\frac{(1-\xi )k_{2}H}{d}\int _{0}^{1}\eta (y)I(y)dy$. Define

$$\begin{aligned} f_{n}(y,H,I)=f(y,H,\min \big \{I,n\big \}), \quad g_{n}(H,I)=g(H,\min \big \{I,n\big \}), \quad n\in \mathbb {N}_{+}, \end{aligned}$$

and consider the following approximating system

$$\begin{aligned} \left\{ \begin{array}{ll} \lambda -cH-\int _{0}^{1}f_{n}(y,H,I(y))dy-g_{n}(H,I(y))=0, \\ \beta (x)\left[ \int _{0}^{1}f_{n}(y,H,I(y))dy+g_{n}(H,I(y))\right] \\ \qquad +\int _{0}^{1}\gamma (y,x)\min \big \{I(y),n\big \}dy-\delta (x) I(x)-\alpha (x) I(x)\\ \qquad +\varepsilon _{n}[\alpha (x)+\delta (x)]=0, \\ \end{array} \right. \end{aligned}$$

(17)

where $\big \{\varepsilon _{n}\big \}_{n}$ is a decreasing sequence with $\varepsilon _{n}\rightarrow 0$ as $n\rightarrow +\infty$.

To simplify (17), we define $j_{n}: \mathbb {R}_{+}\times C_{+}([0,1])\rightarrow \mathbb {R}$ such that

$$\begin{aligned} \begin{aligned} j_{n}(H,I(y))=\lambda -cH-\int _{0}^{1}f_{n}(y,H,I(y))dy-g_{n}(H,I(y)). \end{aligned} \end{aligned}$$

Since $j_{n}(0,I(y))=\lambda >0$, $j_{n}(H^{0}+1,I(y))<0$ and

$$\begin{aligned} \begin{aligned} \frac{dj_{n}(H,I(y))}{dH}=&-c-\int _{0}^{1}\frac{f_{n}(y,H,I(y))}{dH}dy-\frac{g_{n}(H,I(y))}{dH}\\ =&-c-\int _{0}^{1}(1-\epsilon (y))k_{1}\min \big \{I(y),n\big \}dy\\&-\frac{(1-\xi )k_{2}}{d}\int _{0}^{1}\eta (y)\min \big \{I(y),n\big \}dy\\ <\;&0, \end{aligned} \end{aligned}$$

there exists a unique $\breve{H}_{n}$ such that $j_{n}(\breve{H}_{n},I(y))=0$. Furthermore, for all $I(y)\in C_{+}([0,1])$, $\breve{H}_{n}\le H^{0}$. Hence, (17) can be rewritten as

$$\begin{aligned} \begin{aligned}&\beta (x)\left[ \int _{0}^{1}f_{n}(y,\breve{H}_{n},I(y))dy+g_{n}(\breve{H}_{n},I(y))\right] \\&\quad +\int _{0}^{1}\gamma (y,x)\min \big \{I(y),n\big \}dy-\delta (x) I(x) -\alpha (x) I(x)\\&\quad +\varepsilon _{n}\left[ \alpha (x)+\delta (x)\right] =0, \end{aligned} \end{aligned}$$

(18)

which suggests that we consider the following operator $\mathscr {F}_{n}$

$$\begin{aligned} \begin{aligned} \mathscr {F}_{n}[I]=&\frac{\beta (x)\int _{0}^{1}f_{n}(y,\breve{H}_{n},I(y))dy}{\alpha (x)+\delta (x)}+\frac{\beta (x) g_{n}(\breve{H}_{n},I(y))}{\alpha (x)+\delta (x)}\\&+\frac{\int _{0}^{1}\gamma (y,x)\min \big \{I(y),n\big \}dy}{\alpha (x)+\delta (x)}+\varepsilon _{n},\\&I(y)\in C_{+}([0,1]). \end{aligned} \end{aligned}$$

Obviously, $\mathscr {F}_{n}$ is well-defined, continuous and compact. Notice that

$$\begin{aligned} \begin{aligned} \mathscr {F}_{n}[I]\le&\frac{\beta (x)\int _{0}^{1}f_{n}(y,H^{0},n)dy}{\alpha (x)+\delta (x)}+\frac{\beta (x) g_{n}(H^{0},n)}{\alpha (x)+\delta (x)}\\&+\frac{n\int _{0}^{1}\gamma (y,x)dy}{\alpha (x)+\delta (x)}+\varepsilon _{n}, \, I(y)\in C_{+}([0,1]). \end{aligned} \end{aligned}$$

The inequality $r_{n}\gg 1$ implies that $\mathscr {F}_{n}$ maps $C_{n}$ into itself, where $C_{n}=\big \{I(y)\in C_{+}([0,1]): \sup _{[0,1]}I(y)\le r_{n}\big \}$. As $C_{n}$ is closed and convex, it follows from Schauder fixed point theorem that there exists some $I_{n}(y)\in C_{n}$ such that $\mathscr {F}_{n}[I_{n}(y)]=I_{n}(y)$.

Suppose $H_{n}$ is solution of $j_{n}(H,I_{n}(y))=0$, that is, $(H_{n},I_{n}(y))^{T}$ satisfies

$$\begin{aligned} \left\{ \begin{array}{ll} \lambda -cH_{n}-\int _{0}^{1}f_{n}(y,H_{n},I_{n}(y))dy-g_{n}(H_{n},I_{n}(y))=0, \\ \beta (x)\left[ \int _{0}^{1}f_{n}(y,H_{n},I_{n}(y))dy+g_{n}(H_{n},I_{n}(y))\right] +\int _{0}^{1}\gamma (y,x)\min \big \{I_{n}(y),n\big \}dy\\ \quad -\delta (x) I_{n}(x)\\ -\alpha (x) I_{n}(x)+\varepsilon _{n}[\alpha (x)+\delta (x)]=0. \\ \end{array} \right. \end{aligned}$$

(19)

Integrating the second equation of (19) over [0, 1] and adding the resulting equation to the first equation of (19), we have that

$$\begin{aligned} \begin{aligned}&\lambda -cH_{n}+\int _{0}^{1}\delta (x)\min \big \{I_{n}(x),n\big \}dx-\int _{0}^{1}\delta (x)I_{n}(x)dx-\int _{0}^{1}\alpha (x) I_{n}(x)dx\\&\quad +\varepsilon _{n}\int _{0}^{1}[\alpha (x)+\delta (x)]dx=0,\\ \end{aligned} \end{aligned}$$

where assumption (A2) and the balance condition $\int _{0}^{1}\gamma (x,y)dy=\delta (x)$ have been used. Because $\int _{0}^{1}\delta (x)\min \big \{I_{n}(x),n\big \}dx\le \int _{0}^{1}\delta (x)I_{n}(x)dx$, we have

$$\begin{aligned} \begin{aligned} \int _{0}^{1}\alpha (x)I_{n}(x)dx&\le \lambda -cH_{n}+\varepsilon _{n}\int _{0}^{1}[\alpha (x)+\delta (x)]dx\\&\le \lambda +\varepsilon _{1}\int _{0}^{1}[\alpha (x)+\delta (x)]dx. \end{aligned} \end{aligned}$$

Thus, $\big \{\int _{0}^{1}I_{n}(x)dx\big \}_{n}$ is bounded. This, together with equation $\mathscr {F}_{n}[I_{n}(x)]=I_{n}(x)$, implies that $\big \{I_{n}(x)\big \}_{n}$ is bounded in $C_{+}([0,1])$. According to $\mathscr {F}_{n}[I_{n}(x)]=I_{n}(x)$, we also have $\big \{I_{n}(x)\big \}_{n}$ is equi-continuous, which shows that $\big \{I_{n}(x)\big \}_{n}$ is compact in $C_{+}([0,1])$. Therefore, there exists a sequence $(H_{n},I_{n}(x))^{T}\in \mathbb {R}_{+}\times C_{+}([0,1])$ and $(H^{*},I^{*}(x))^{T}\in \mathbb {R}_{+}\times C_{+}([0,1])$ such that $(H_{n},I_{n}(x))^{T}\rightarrow (H^{*},I^{*}(x))^{T}$ as $n\rightarrow +\infty$. Taking limit in (19), we conclude that $(H^{*},I^{*}(x))^{T}$ is a solution of (16). Let $V^{*}=\frac{1}{d}\int _{0}^{1}\eta (x)I^{*}(x)dx$. $E^{*}$ is a equilibrium of (1).

The result that $I^{*}(x)\ne 0$ follows from the similar arguments in page 3784 of Thieme (2011). Therefore, it is omitted here. $\square$

Appendix B: Uniform persistence when $R_{0}>1$

We first prove the strict positivity of solutions.

Theorem 6

When $R_{0}>1$, let $(H(t),I(t,x),V(t))^{T}$ be the unique solution of (1) with initial value $(H_{0},I_{0}(\cdot ),V_{0})^{T}\in \mathbb {X}\backslash \big \{(H^{0},0,0)^{T}\big \}$. Then we have $I(t,x)>0$ and $V(t)>0$ for all $t>0$ and $x\in [0,1]$.

Proof

When $I_{0}(\cdot )\ne 0$, we suppose that R(t, x) is the unique solution for

$$\begin{aligned} \left\{ \begin{array}{ll} R_{t}(t,x)=\int _{0}^{1}\gamma (y,x)R(t,y)dy-\delta (x)R(t,x)-\alpha (x)R(t,x), &{} \\ R(0,x)=I_{0}(x). &{}\\ \end{array} \right. \end{aligned}$$

It follows from the comparison principle that $I(t,x)\ge R(t,x)$ for all $t>0$ and $x\in [0,1]$. Using a similar argument as in the proof of proposition 2.2 of Shen and Zhang (2010), we can show that $R(t,x)>0$. Thus, $I(t,x)>0$ for all $t>0$ and $x\in [0,1]$. From this, we obtain $V(t)>0$ for $t>0$.

When $V_{0}\ne 0$, in view of $I(t,x)\ge 0$ for $t>0$ and $x\in [0,1]$, we deduce from the third equation in (1) that $V(t)>0$ for $t>0$. Using system (1) and $H(t)>0$, it can be demonstrated that $I(t,x)\ne 0$ for $t>0$. Next, for any $t_{1}>0$, let $R(t,x;t_{1})$ be the unique solution of

$$\begin{aligned} \left\{ \begin{array}{ll} R_{t}(t,x;t_{1})=\int _{0}^{1}\gamma (y,x)R(t,y;t_{1})dy-\delta (x)R(t,x;t_{1})-\alpha (x)R(t,x;t_{1}), &{} \\ R(t_{0},x;t_{1})=I_{0}(t_{1},x). &{}\\ \end{array} \right. \end{aligned}$$

By applying similar approach presented in the above case, we obtain that $R(t,x)>0$ for $t>t_{1}$ and $x\in [0,1]$. Because $t_{1}$ is arbitrary, we have $I(t,x)>0$ for $t>0$ and $x\in [0,1]$. This completes the proof. $\square$

We have the following result about the weak uniform persistence.

Theorem 7

If $R_{0}>1$, then there exists a constant $\epsilon _{1}>0$ such that any solution $(H(t),I(t,x),V(t))^{T}$ of (1) with initial value $(H_{0},I_{0}(x),V_{0})^{T}\in \mathbb {X}\backslash \big \{(H^{0},0,0)^{T}\big \}$ satisfies

$$\begin{aligned} \begin{aligned} \limsup _{t\rightarrow +\infty }\max \big \{\sup _{x\in [0,1]}I(t,x),V(t)\big \}\ge \epsilon _{1}.\\ \end{aligned} \end{aligned}$$

Proof

Suppose the contrary that the disease dies out, that is, for any $\upsilon >0$, there exists $(H_{0\upsilon },I_{0\upsilon }(x),V_{0\upsilon })^{T}\in \mathbb {X}\backslash \big \{(H^{0},0,0)^{T}\big \}$ such that the corresponding solution

$(H_{\upsilon }(t),I_{\upsilon }(t,x),V_{\upsilon }(t))^{T}$ of (1) satisfies

$$\begin{aligned} \begin{aligned} \limsup _{t\rightarrow +\infty }\max \big \{\sup _{x\in [0,1]}I_{\upsilon }(t,x),V_{\upsilon }(t)\big \}<\upsilon . \end{aligned} \end{aligned}$$

Using Theorem 6, we can assume that

$$\begin{aligned} \begin{aligned} 0<I_{\upsilon }(t,x)<\upsilon , \qquad 0<V_{\upsilon }(t)<\upsilon , \quad t>0, \; x\in [0,1]. \end{aligned} \end{aligned}$$

(20)

Because $H'_{\upsilon }(t)\le \lambda -cH_{\upsilon }(t)$, there exists a sufficiently small number $\epsilon _{2}$ such that $H_{\upsilon }(t)\le H^{0}+\epsilon _{2}$ for all sufficiently large t. Replacing $(H_{0\upsilon },I_{0\upsilon }(x),V_{0\upsilon })^{T}$ with $(H_{\upsilon }(t_{\upsilon }),I_{\upsilon }(t_{\upsilon },x),V_{\upsilon }(t_{\upsilon }))^{T}$ and choosing $t_{\upsilon }$ to be further large, we can assume that $H_{\upsilon }(t)\le H^{0}+\epsilon _{2}$ for all $t\ge 0$. From the first equation in (1), it follows that

$$\begin{aligned} \begin{aligned} H'_{\upsilon }(t)\ge \lambda -cH_{\upsilon }(t)-\mu (\upsilon ), \end{aligned} \end{aligned}$$

where $\mu (\upsilon )=\int _{0}^{1}(1-\epsilon (y))k_{1}(H^{0}+\epsilon _{2})\upsilon dy+(1-\xi )k_{2}(H^{0}+\epsilon _{2})\upsilon$. For equation

$$\begin{aligned} \begin{aligned} \hat{H}'(t)=\lambda -c\hat{H}(t)-\mu (\upsilon ), \end{aligned} \end{aligned}$$

it has a unique equilibrium $H^{0}-\frac{\mu (\upsilon )}{c}$ attracting all positive solutions. Using comparison principle and choosing $t_{\upsilon }$ to be further large, we have $H_{\upsilon }(t)\ge H^{0}-\frac{\mu (\upsilon )}{c}$ for all $t\ge 0$.

It is easy to check that

$$\begin{aligned} \left\{ \begin{array}{llll} \partial _{t}I_{\upsilon }(t,x)\ge \beta (x)\left[ \int _{0}^{1}(1-\epsilon (y))k_{1}(H^{0}-\frac{\mu (\upsilon )}{c})I_{\upsilon }(t,y)dy+(1-\xi )k_{2}(H^{0}-\frac{\mu (\upsilon )}{c})V_{\upsilon }(t)\right] \\ \qquad \quad \, +\int _{0}^{1}\gamma (y,x)I_{\upsilon }(t,y)dy-\alpha (x)I_{\upsilon }(t,x)-\delta (x)I_{\upsilon }(t,x), \\ \quad \, \dot{V}_{\upsilon }(t)=\int _{0}^{1}\eta (y)I_{\upsilon }(t,y)dy-dV_{\upsilon }(t). \\ \end{array} \right. \end{aligned}$$

(21)

Define the following operators $L_{\upsilon }$ and $\mathcal {L}_{\upsilon }$ on $C_{+}([0,1])\times \mathbb {R}_{+}$ and $C_{+}([0,1])$, respectively,

$$\begin{aligned} \begin{aligned}&L_{\upsilon }\begin{pmatrix} I\\ V\\ \end{pmatrix}\\&=\begin{pmatrix} \beta (x)\left[ \int _{0}^{1}(1-\epsilon (y))k_{1}(H^{0}-\frac{\mu (\upsilon )}{c})I(y)dy+(1-\xi )k_{2}(H^{0}-\frac{\mu (\upsilon )}{c})V(t)\right] \\ \qquad +\int _{0}^{1}\gamma (y,x)I(y)dy-\alpha (x) I(x)-\delta (x) I(x)\\ \int _{0}^{1}\eta (y)I(y)dy-dV\\ \end{pmatrix}, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \mathcal {L}_{\upsilon }(I)=&\frac{\beta (x)}{\alpha (x)+\delta (x)}\int _{0}^{1}(1-\epsilon (y))k_{1}(H^{0}-\frac{\mu (\upsilon )}{c})I(y)dy+\frac{\int _{0}^{1}\gamma (y,x)I(y)dy}{\alpha (x)+\delta (x)}\\&+\frac{\beta (x) (1-\xi )k_{2}(H^{0}-\frac{\mu (\upsilon )}{c})}{d(\alpha (x)+\delta (x))}\int _{0}^{1}\eta (y)I(y)dy. \end{aligned} \end{aligned}$$

Because $R_{0}=\rho (\mathcal {L})>1$, we can choose a small $\epsilon _{3}$ such that $\rho (\mathcal {L}_{\epsilon _{3}})>1$. By Theorem 2, we see that $s(L_{\epsilon _{3}})>0$. Moreover, $s(L_{\epsilon _{3}})$ is an isolated and simple eigenvalue of $L_{\epsilon _{3}}$ with eigenfunction $(\varphi _{3},\theta _{3})^{T}\in C_{++}([0,1])\times \mathbb {R}_{++}$.

Let $\big \{e^{L_{\epsilon _{3}}t}\big \}_{t\ge 0}$ be the semigroup on $C_{+}([0,1])\times \mathbb {R}_{+}$ generated by $L_{\epsilon _{3}}$. For any $\varepsilon _{3}>0$, we can choose a corresponding $\xi _{3}$ such that $\xi _{3}\varphi _{3}\le I_{0\epsilon _{3}}$ and $\xi _{3}\theta _{3}\le V_{0\epsilon _{3}}$. Using these inequalities, we have

$$\begin{aligned} \begin{aligned} e^{L_{\epsilon _{3}}t}(I_{0\epsilon _{3}},V_{0\epsilon _{3}})^{T}\ge e^{L_{\epsilon _{3}}t}\xi _{3}(\varphi _{3},\theta _{3})^{T}=e^{s(L_{\epsilon _{3}})t}\xi _{3}(\varphi _{3},\theta _{3})^{T}, \quad t\ge 0, \end{aligned} \end{aligned}$$

which means that $\Vert e^{L_{\epsilon _{3}}t}(I_{0\epsilon _{3}},V_{0\epsilon _{3}})^{T}\Vert _{C_{+}([0,1])\times \mathbb {R}_{+}}\rightarrow +\infty$ as $t\rightarrow +\infty$. Utilizing the comparison principle, we obtain from (21) that

$$\begin{aligned} \begin{aligned}&\Vert (I_{\epsilon _{3}}(t,x),V_{\epsilon _{3}}(t))\Vert _{C_{+}([0,1])\times \mathbb {R}_{+}}\\&\qquad \ge \Vert e^{L_{\epsilon _{3}}t}(I_{0\epsilon _{3}},V_{0\epsilon _{3}})^{T}\Vert _{C_{+}([0,1])\times \mathbb {R}_{+}}\rightarrow +\infty \quad as \; t\rightarrow +\infty . \end{aligned} \end{aligned}$$

This contradicts (20). Hence the proof of Theorem 7 is completed. $\square$

Lastly, we prove that system (1) has a global attractor $\mathcal {Y}$. To this end, we need to show the bounded dissipativity and asymptotic compactness of $\big \{\phi _{t}\big \}_{t\ge 0}$.

Theorem 8

The semi-flow $\big \{\phi _{t}\big \}_{t\ge 0}$ is bounded dissipative and asymptotically compact.

Proof

Due to the global well-posedness of (1), for any bounded subset $N\subset \mathbb {X}$, there exist $t^{*}(N)>0$ and $K>0$ such that

$$\begin{aligned} \begin{aligned} \sup _{(H_{0},I_{0}(x),V_{0})^{T}\in N}[H(t)+\Vert I(t,x)\Vert _{L_{+}^{1}[0,1]}+V(t)]\le K, \quad t\ge t^{*}. \end{aligned} \end{aligned}$$

Thus, for any $x\in [0,1]$ and $t\ge t^{*}$

$$\begin{aligned} \begin{aligned} I_{t}(t,x)=&\beta (x)\left[ \int _{0}^{1}(1-\epsilon (y))k_{1}H(t)I(t,y)dy+(1-\xi )k_{2}H(t)V(t)\right] \\&+\int _{0}^{1}\gamma (y,x)I(t,y)dy\\&-[\delta (x)+\alpha (x)]I(t,x)\\&\le \sup _{[0,1]}\beta (x)\left[ \int _{0}^{1}(1-\epsilon (y))k_{1}H(t)I(t,y)dy+(1-\xi )k_{2}H(t)V(t)\right] \\&+\sup _{[0,1] \times [0,1]}\gamma \int _{0}^{1}I(t,y)dy\\&-\inf _{[0,1]}[\alpha (x)+\delta (x)]I(t,x)\\ \le&\check{K}-\check{a}I(t,x), \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \check{K}= & {} K\Bigg \{\sup _{[0,1]}\beta (x)\left[ \sup _{(y,H)\in [0,1]\times [0,K]}(1-\epsilon (y))k_{1}H+\sup _{H\in [0,K]}(1-\xi )k_{2}H\right] \\&+\sup _{[0,1] \times [0,1]}\gamma \Bigg \} \end{aligned}$$

and $\check{a}=\inf _{[0,1]}[\alpha (x)+\delta (x)]$. Therefore, we have that

$$\begin{aligned} \begin{aligned} I(t,x)\le e^{-\check{a}(t-t^{*})}I(t^{*},x)+\frac{\check{K}}{\check{a}}, \quad x\in [0,1], \quad t\ge t^{*}. \end{aligned} \end{aligned}$$

Because $\sup _{(H_{0},I_{0}(x),V_{0})^{T}\in N}\Vert I(t^{*},x)\Vert _{C([0,1]}<+\infty$, there exists some $t(N)\gg t^{*}(N)$ such that $\Vert I(t,x)\Vert _{C([0,1]}\le \frac{\check{K}}{\check{a}}+1$ for all $t\ge t^{*}$. Let $\mathcal {N}=\big \{(H,I,V)\in \mathbb {X}: H+\Vert I(t,x)\Vert _{C([0,1])}+V\le K+\frac{\check{K}}{\check{a}}+1\big \}$, we have $\phi _{t}N\subset \mathcal {N}$ for all $t\ge t^{*}$. That is, the semi-flow $\big \{\phi _{t}\big \}_{t\ge 0}$ is bounded dissipative.

In the following, we prove the asymptotic compactness of $\big \{\phi _{t}\big \}_{t\ge 0}$. Because of the bounded dissipativity of $\big \{\phi _{t}\big \}_{t\ge 0}$, we only need to show that for any bounded sequence $\big \{k_{n}\big \}_{n}\subset \mathbb {X}$ and any time sequence $\big \{t_{n}\big \}_{n}$ with $t_{n}\rightarrow +\infty$ as $n\rightarrow +\infty$, the sequence $\big \{\phi _{t_{n}}k_{n}\big \}_{n}$ has a converging subsequence in $\mathbb {X}$.

Let $\big \{(H_{0}^{n},I_{0}^{n}(x),V_{0}^{n})^{T}\big \}_{n}$ be a bounded sequence in $\mathbb {X}$ and the sequence $\big \{t_{n}\big \}_{n}\in \mathbb {R}_{+}$ satisfy $t_{n}\rightarrow +\infty$ as $n\rightarrow +\infty$. Denote the unique solution of (1) with initial value $(H_{0}^{n},I_{0}^{n}(x),V_{0}^{n})^{T}$ by $(H^{n}(t),I^{n}(t,x),V^{n}(t))^{T}$, namely,

$$\begin{aligned} \begin{aligned} \phi _{t}(H_{0}^{n},I_{0}^{n}(x),V_{0}^{n})^{T}=(H^{n}(t),I^{n}(t,x),V^{n}(t))^{T}, \qquad t\ge 0. \end{aligned} \end{aligned}$$

In particular,

$$\begin{aligned} \begin{aligned} \phi _{t_{n}}(H_{0}^{n},I_{0}^{n}(x),V_{0}^{n})^{T}=(H^{n}(t_{n}),I^{n}(t_{n},x), V^{n}(t_{n}))^{T}. \end{aligned} \end{aligned}$$

Due to the bounded dissipativity of $\big \{\phi _{t}\big \}_{t\ge 0}$ and the boundness of $\big \{(H_{0}^{n},I_{0}^{n}(x),V_{0}^{n})^{T}\big \}_{n}$,

$$\begin{aligned} \begin{aligned} \bigcup _{t\ge 0}\bigcup _{n}(H^{n}(t),I^{n}(t,x),V^{n}(t))^{T} =\bigcup _{t\ge 0}\bigcup _{n}\phi _{t}(H_{0}^{n},I_{0}^{n}(x),V_{0}^{n})^{T} \end{aligned} \end{aligned}$$

is bounded in $\mathbb {X}$. In particular, $\big \{H^{n}(t_{n})\big \}_{n}$ and $\big \{V^{n}(t_{n})\big \}_{n}$ are bounded. We only need to show the equi-continuity of $\big \{I^{n}(t_{n},x)\big \}_{n}$ on the basis of the Arzelà-Ascoli theorem.

Define $l(x)=\alpha (x)+\delta (x)$. Using (1), we have

$$\begin{aligned} \begin{aligned}&\frac{d}{dt}[I^{n}(t_{n}+t,x)-I^{n}(t_{n}+t,s)]^{2}\\&\quad =2[I^{n}(t_{n}+t,x)-I^{n}(t_{n}+t,s)][I_{t}^{n}(t_{n}+t,x)-I_{t}^{n}(t_{n}+t,s)]\\&\quad =2[I^{n}(t_{n}+t,x)-I^{n}(t_{n}+t,s)]\Bigg \{-\left[ l(x)I^{n}(t_{n}+t,x) -l(s)I^{n}(t_{n}+t,s)\right] \\&\quad +[\beta (x)-\beta (s)]\\&\quad \cdot \left[ \int _{0}^{1}(1-\epsilon (y))k_{1}H^{n}(t_{n}+t)I^{n}(t_{n}+t,y)dy +(1-\xi )k_{2}H^{n}(t_{n}+t)V^{n}(t_{n}+t)\right] \\&\quad +\int _{0}^{1}\left[ \gamma (y,x)-\gamma (y,s)\right] I^{n}(t_{n}+t,y)dy\Bigg \}. \end{aligned} \end{aligned}$$

Notice that

$$\begin{aligned} \begin{aligned}&-\left[ l(x)I^{n}(t_{n}+t,x)-l(s)I^{n}(t_{n}+t,s)\right] \\&\quad =-l(x)\left[ I^{n}(t_{n}+t,x)-I^{n}(t_{n}+t,s)\right] -\left[ l(x)-l(s)\right] I^{n} (t_{n}+t,s)\\&\quad \le -l(x)\left[ I^{n}(t_{n}+t,x)-I^{n}(t_{n}+t,s)\right] +Q_{1}|l(x)-l(s)|, \end{aligned} \end{aligned}$$

where $Q_{1}=\sup _{n}\sup _{t\ge -t_{n}}\Vert I^{n}(t_{n}+t,\cdot )\Vert _{C_{+}([0,1])}<+\infty$, and that

$$\begin{aligned} \begin{aligned}&{[}\beta (x)-\beta (s)]\left[ \int _{0}^{1}(1-\epsilon (y))k_{1}H^{n}(t_{n}+t)I^{n}(t_{n} +t,y)dy\right. \\&\quad \left. +(1-\xi )k_{2}H^{n}(t_{n}+t)V^{n}(t_{n}+t)\right] \\&\quad \le Q_{2}|\beta (x)-\beta (s)|, \end{aligned} \end{aligned}$$

where

$$\begin{aligned} Q_{2}= & {} \sup _{n}\sup _{t\ge -t_{n}}\left[ \int _{0}^{1}(1-\epsilon (y))k_{1}H^{n}(t_{n}+t)I^{n} (t_{n}+t,y)dy\right. \\&\quad \left. +(1-\xi )k_{2}H^{n}(t_{n}+t)V^{n}(t_{n}+t)\right] . \end{aligned}$$

Moreover, we have

$$\begin{aligned} \begin{aligned} \int _{0}^{1}\left[ \gamma (y,x)-\gamma (y,s)\right] I^{n}(t_{n}+t,y)dy\le Q_{1}\int _{0}^{1}|\gamma (y,x)-\gamma (y,s)|dy. \end{aligned} \end{aligned}$$

Let $Q_{3}=\max \big \{Q_{1},Q_{2}\big \}$ and $m(x,s)=|l(x)-l(s)|+|\beta (x)-\beta (s)|+\int _{0}^{1}|\gamma (y,x)-\gamma (y,s)|dy$. We find

$$\begin{aligned} \begin{aligned}&\frac{d}{dt}[I^{n}(t_{n}+t,x)-I^{n}(t_{n}+t,s)]^{2}\\&\quad \le -l(x)\left[ I^{n}(t_{n}+t,x)-I^{n}(t_{n}+t,s)\right] ^{2}+2Q_{3}|I^{n}(t_{n}+t,x)\\&\quad -I^{n}(t_{n}+t,s)|m(x,s)\\&\quad \le -\frac{\inf _{[0,1]}l}{2}\left[ I^{n}(t_{n}+t,x)-I^{n}(t_{n}+t,s)\right] ^{2}+Q_{4}m^{2}(x,s) \end{aligned} \end{aligned}$$

for some $Q_{4}>0$, where we used Young’s inequality. We integrate the above inequality from $-t_{n}$ to 0, and obtain

$$\begin{aligned} \begin{aligned}&\left[ I^{n}(t_{n},x)-I^{n}(t_{n},s)\right] ^{2}\le e^{-\frac{\inf _{[0,1]}l}{2}t_{n}} [I^{n}(0,x)-I^{n}(0,s)]^{2}\\&\quad +\int _{-t_{n}}^{0}e^{\frac{\inf _{[0,1]}l}{2}h}Q_{4}m^{2}(x,s)dh\\&\quad \le e^{-\frac{\inf _{[0,1]}l}{2}t_{n}}[I_{0}^{n}(x)-I_{0}^{n}(s)]^{2}+\frac{2Q_{4}}{\inf _{[0,1]}l} m^{2}(x,s). \end{aligned} \end{aligned}$$

It follows that $\big \{I^{n}(t_{n},\cdot )\big \}_{n}$ is equi-continuous. This completes the proof. $\square$

Now we can establish the uniform persistence of (1), which is stated in the following theorem.

Theorem 9

Assuming that $R_{0}>1$, there exists a constant $\epsilon ^{*}>0$ such that any solution $(H(t),I(t,x),V(t))^{T}$ of system (1) with initial value $(H_{0},I_{0}(x),V_{0})^{T}\in \mathbb {X}\backslash \big \{(H^{0},0,0)^{T}\big \}$ satisfies

$$\begin{aligned} \begin{aligned} \liminf _{t\rightarrow +\infty }H(t)\ge \epsilon ^{*}, \quad \liminf _{t\rightarrow +\infty }\inf _{x\in [0,1]} I(t,x)\ge \epsilon ^{*}, \quad and \quad \liminf _{t\rightarrow +\infty }V(t)\ge \epsilon ^{*}. \end{aligned} \end{aligned}$$

Proof

Because system (1) is bounded dissipative, there exists constant $b>0$ such that $H'(t)\ge \lambda -cH(t)-bH(t)$ for all large t. Therefore, we have $\limsup _{t\rightarrow +\infty }H(t)\ge \liminf _{t\rightarrow +\infty }H(t)\ge \frac{\lambda }{b+c}$.

Next, we need to prove that there exists constant $\epsilon ^{*}$ such that

$$\begin{aligned} \begin{aligned} \liminf _{t\rightarrow +\infty }\min \big \{\inf _{x\in [0,1]}I(t,x),V(t)\big \}>\epsilon ^{*}. \end{aligned} \end{aligned}$$

(22)

Define

$$\begin{aligned} \begin{aligned} \check{\rho }((H,I,V)^{T})=\max \big \{\sup _{x\in [0,1]}I(x),V\big \}, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \tilde{\rho }((H,I,V)^{T})=\min \big \{\inf _{x\in [0,1]}I(x),V\big \}, \end{aligned} \end{aligned}$$

for $(H,I,V)^{T}\in \mathbb {X}$. Obviously, the functions $\check{\rho }$ and $\tilde{\rho }$ are continuous. From Theorem 6, $\check{\rho }((H_{0},I_{0}(x),V_{0})^{T})>0$ implies $\check{\rho }(\phi _{t}(H_{0},I_{0}(x),V_{0})^{T})=\max \big \{\sup _{x\in [0,1]}I(t,x),V(t)\big \}>0$ for all $t\ge 0$. Theorem 7 indicates that the semi-flow $\big \{\phi _{t}\big \}_{t\ge 0}$ is uniformly weakly $\check{\rho }-persistent$. From Theorem 8, we know that the semi-flow has a global attractor, which means that the compactness assumption of Thieme (2003) (Theorem A.34) is satisfied.

Let $(\tilde{H}(t),\tilde{I}(t,x),\tilde{V}(t))^{T}$ be a bounded total orbit of $\big \{\phi _{t}\big \}_{t\ge 0}$ and $\check{\rho }((\tilde{H}(t),\tilde{I}(t,x),\tilde{V}(t))^{T})>0$ for all $t\in \mathbb {R}$. In this case, $\check{\rho }((\tilde{H}(t_{0}),\tilde{I}(t_{0},x),\tilde{V}(t_{0}))^{T})=\max \big \{\sup _{x\in [0,1]}\tilde{I}(t_{0},x),\tilde{V}(t_{0})\big \}>0$ for some $t_{0}<0$. Applying Theorem 6 again, the equation $\tilde{\rho }((\tilde{H}(0),\tilde{I}(0,x),\tilde{V}(0))^{T})=\min \big \{\inf _{x\in [0,1]}\tilde{I}(0,x),\tilde{V}(0)\big \}>0$ is ensured. The above conditions meet the requirements of Theorem A.34 in Thieme (2003). Thus, inequality (22) is satisfied. This completes the proof of Theorem 9. $\square$

Appendix C: Calculation of the derivative of G(t)

The derivative of G(t) along the solution of model (1) is

$$\begin{aligned} \begin{aligned}&\frac{dG}{dt}=\int _{0}^{1}w(x)\left[ d\beta (x)(1-\frac{H^{*}}{H})\frac{dH}{dt}\right] dx +\int _{0}^{1}w(x)\left[ d(1-\frac{I^{*}(x)}{I(x)})\frac{\partial I(x)}{\partial t}\right] dx\\&\qquad +\int _{0}^{1}w(x)\Bigg [\beta (x)(1-\xi )k_{2}H^{*}(1-\frac{V^{*}}{V})\frac{dV}{dt} \Bigg ]dx\\&\quad =\int _{0}^{1}w(x)\Bigg [d\beta (x)(1-\frac{H^{*}}{H})(\lambda -cH\\&\qquad -\int _{0}^{1} (1-\epsilon (y))k_{1}HI(y)dy-(1-\xi )k_{2}HV)\Bigg ]dx\\&\qquad +\int _{0}^{1}w(x)\Bigg [d(1-\frac{I^{*}(x)}{I(x)})\bigg (\beta (x)\Big [\int _{0}^{1} (1-\epsilon (y))k_{1}HI(y)dy+(1-\xi )k_{2}HV\Big ]\\&\qquad +\int _{0}^{1}\gamma (y,x)I(y)dy-\delta (x)I(x)-\alpha (x)I(x)\bigg )\Bigg ]dx\\&\qquad +\int _{0}^{1}w(x)\Bigg [\beta (x)(1-\xi )k_{2}H^{*}(1\\&\qquad -\frac{V^{*}}{V})(\int _{0}^{1}\eta (y)I(y)dy-dV)\Bigg ]dx. \end{aligned} \end{aligned}$$

It follows from (15) that

$$\begin{aligned} \frac{dG}{dt}=&\int _{0}^{1}w(x)\Bigg [d\beta (x)(1-\frac{H^{*}}{H})(cH^{*}-cH)\Bigg ]dx\nonumber \\&+\int _{0}^{1}w(x)d\beta (x)(1-\xi )k_{2}H^{*}V^{*}\Bigg [2-\frac{H^{*}}{H} +\frac{V}{V^{*}}\nonumber \\&-\frac{I^{*}(x)}{I(x)}\frac{HV}{H^{*}V^{*}} -\frac{I(x)}{I^{*}(x)}\Bigg ]dx+\int _{0}^{1}w(x)d\beta (x) \int _{0}^{1} (1-\epsilon (y))k_{1}H^{*}I^{*}(y)\nonumber \\&\quad \Bigg [2-\frac{H^{*}}{H} +\frac{I(y)}{I^{*}(y)}\nonumber \\&-\frac{I(x)}{I^{*}(x)}-\frac{I^{*}(x)}{I(x)} \frac{HI(y)}{H^{*}I^{*}(y)}\Bigg ]dydx\nonumber \\&+\int _{0}^{1}w(x)d\int _{0}^{1}\gamma (y,x)I^{*}(y)\Bigg [1 +\frac{I(y)}{I^{*}(y)}-\frac{I(x)}{I^{*}(x)}-\frac{I^{*}(x)}{I(x)}\nonumber \\&\cdot \frac{I(y)}{I^{*}(y)}\Bigg ]dydx+\int _{0}^{1}w(x)\beta (x)(1-\xi )k_{2}H^{*} \int _{0}^{1}\eta (y)I^{*}(y)\nonumber \\&\quad \Bigg [1+\frac{I(y)}{I^{*}(y)}-\frac{V^{*}}{V} \frac{I(y)}{I^{*}(y)}-\frac{V}{V^{*}}\Bigg ]dydx. \end{aligned}$$

(23)

Using $\kappa$ to group terms, (23) can be rewritten as

$$\begin{aligned} \frac{dG}{dt}&=-\int _{0}^{1}w(x)\Bigg [d\beta (x)(1-\frac{H^{*}}{H})(cH-cH^{*})\Bigg ]dx\nonumber \\&-\int _{0}^{1}w(x)d\beta (x)(1-\xi )k_{2}H^{*}V^{*}\Bigg [\kappa (\frac{H^{*}}{H})\nonumber \\&+\kappa (\frac{I^{*}(x)}{I(x)}\frac{HV}{H^{*}V^{*}})\Bigg ]dx-\int _{0}^{1} w(x)d\beta (x) \int _{0}^{1}(1-\epsilon (y))k_{1}H^{*}I^{*}(y)\nonumber \\&\quad \Bigg [\kappa (\frac{H^{*}}{H})+\kappa (\frac{I^{*}(x)}{I(x)}\nonumber \\&\cdot \frac{HI(y)}{H^{*}I^{*}(y)})\Bigg ]dydx-\int _{0}^{1}w(x)d\int _{0}^{1} \gamma (y,x)I^{*}(y)\kappa (\frac{I^{*}(x)}{I(x)}\frac{I(y)}{I^{*}(y)})dydx\nonumber \\&-\int _{0}^{1}w(x)\beta (x)\nonumber \\&\cdot (1-\xi )k_{2}H^{*}\int _{0}^{1}\eta (y)I^{*}(y)\kappa (\frac{V^{*}}{V} \frac{I(y)}{I^{*}(y)})dydx\nonumber \\&+\int _{0}^{1}w(x)d\beta (x) (1-\xi )k_{2}H^{*}V^{*}\nonumber \\&\cdot \Bigg [-\ln \frac{H^{*}}{H}+\frac{V}{V^{*}}-\ln \frac{I^{*}(x)}{I(x)} \frac{HV}{H^{*}V^{*}}-\frac{I(x)}{I^{*}(x)}\Bigg ]dx\nonumber \\&+\int _{0}^{1}w(x)d\beta (x) \int _{0}^{1}(1-\epsilon (y))k_{1}\nonumber \\&\cdot H^{*}I^{*}(y)\Bigg [-\ln \frac{H^{*}}{H}+\frac{I(y)}{I^{*}(y)} -\frac{I(x)}{I^{*}(x)}-\ln \frac{I^{*}(x)}{I(x)}\frac{HI(y)}{H^{*}I^{*}(y)} \Bigg ]dydx\nonumber \\&+\int _{0}^{1}w(x)d\nonumber \\&\int _{0}^{1}\gamma (y,x)I^{*}(y)\Bigg [\frac{I(y)}{I^{*}(y)}-\ln \frac{I^{*}(x)}{I(x)} \frac{I(y)}{I^{*}(y)}-\frac{I(x)}{I^{*}(x)}\Bigg ]dydx\nonumber \\&+\int _{0}^{1}w(x)\beta (x) (1-\xi )k_{2}H^{*}\nonumber \\&\cdot \int _{0}^{1}\eta (y)I^{*}(y)\Bigg [\frac{I(y)}{I^{*}(y)}-\ln \frac{V^{*}}{V} \frac{I(y)}{I^{*}(y)}-\frac{V}{V^{*}}\Bigg ]dydx. \end{aligned}$$

(24)

After collecting and rearranging terms on the right-hand side of (24), we obtain

$$\begin{aligned} \frac{dG}{dt}=&-\int _{0}^{1}w(x)\Bigg [d\beta (x)(1-\frac{H^{*}}{H})(cH-cH^{*})\Bigg ]dx\nonumber \\&-\int _{0}^{1}w(x)d\beta (x)(1-\xi )k_{2}H^{*}V^{*}\Bigg [\kappa (\frac{H^{*}}{H})\nonumber \\&+\kappa (\frac{I^{*}(x)}{I(x)}\frac{HV}{H^{*}V^{*}})\Bigg ]dx-\int _{0}^{1}w(x)d \beta (x) \int _{0}^{1}(1-\epsilon (y))k_{1}H^{*}I^{*}(y)\nonumber \\&\quad \Bigg [\kappa (\frac{H^{*}}{H}) +\kappa (\frac{I^{*}(x)}{I(x)}\nonumber \\&\cdot \frac{HI(y)}{H^{*}I^{*}(y)})\Bigg ]dydx\nonumber \\&-\int _{0}^{1}w(x)d\int _{0}^{1}\gamma (y,x)I^{*} (y) \kappa (\frac{I^{*}(x)}{I(x)}\frac{I(y)}{I^{*}(y)})dydx-\int _{0}^{1}w(x)\beta (x)\nonumber \\&\cdot (1-\xi )k_{2}H^{*}\int _{0}^{1}\eta (y)I^{*}(y)\kappa (\frac{V^{*}}{V} \frac{I(y)}{I^{*}(y)})dydx\nonumber \\&+\int _{0}^{1}w(x)d\beta (x) (1-\xi )k_{2}H^{*}V^{*} \Bigg [\frac{V}{V^{*}}\nonumber \\&-\ln \frac{V}{V^{*}}\Bigg ]dx+\int _{0}^{1}w(x)d\beta (x)(1-\xi )k_{2}H^{*}V^{*} \Bigg [\ln \frac{I(x)}{I^{*}(x)}-\frac{I(x)}{I^{*}(x)}\Bigg ]dx\nonumber \\&+\int _{0}^{1}w(x)\beta (x) d\nonumber \\&\cdot \int _{0}^{1}(1-\epsilon (y))k_{1}H^{*}I^{*}(y)\Bigg [\ln \frac{I(x)}{I^{*}(x)} -\frac{I(x)}{I^{*}(x)}-\ln \frac{I(y)}{I^{*}(y)}+\frac{I(y)}{I^{*}(y)}\Bigg ]dydx\nonumber \\&+\int _{0}^{1}w(x)d\int _{0}^{1}I^{*}(y)\nonumber \\&\cdot \gamma (y,x)\Bigg [\frac{I(y)}{I^{*}(y)}-\ln \frac{I(y)}{I^{*}(y)} +\ln \frac{I(x)}{I^{*}(x)}-\frac{I(x)}{I^{*}(x)}\Bigg ]dydx\nonumber \\&+\int _{0}^{1}w(x) \beta (x)(1-\xi )k_{2}H^{*}\int _{0}^{1}I^{*}(y)\nonumber \\&\cdot \eta (y)\Bigg [\frac{I(y)}{I^{*}(y)}-\ln \frac{I(y)}{I^{*}(y)}\Bigg ]dydx +\int _{0}^{1}w(x)\beta (x)(1-\xi )k_{2}H^{*}\int _{0}^{1}\eta (y)I^{*}(y)\nonumber \\&\quad \Bigg [\ln \frac{V}{V^{*}}-\frac{V}{V^{*}}\Bigg ]dydx.\nonumber \\ \end{aligned}$$

(25)

Recalling $d V^{*}=\int _{0}^{1}\eta (y)I^{*}(y)dy$, the seventh and eleventh terms on the right-hand side of (25) can be rewritten as

$$\begin{aligned} \begin{aligned}&\int _{0}^{1}w(x)\beta (x)(1-\xi )k_{2}H^{*}\int _{0}^{1}\eta (y)I^{*}(y) \Bigg [\ln \frac{I(x)}{I^{*}(x)}-\frac{I(x)}{I^{*}(x)}\Bigg ]dydx,\\&\quad \int _{0}^{1}w(x)\beta (x)(1-\xi )k_{2}H^{*}dV^{*}\Bigg [\ln \frac{V}{V^{*}} -\frac{V}{V^{*}}\Bigg ]dx. \end{aligned} \end{aligned}$$

(26)

Substituting (26) into (25), we have

$$\begin{aligned} \begin{aligned} \frac{dG}{dt}=&-\int _{0}^{1}w(x)\Bigg [d\beta (x)(1-\frac{H^{*}}{H})(cH-cH^{*})\Bigg ] dx\\&-\int _{0}^{1}w(x)d\beta (x)(1-\xi )k_{2}H^{*}V^{*}\Bigg [\kappa (\frac{H^{*}}{H})\\&+\kappa (\frac{I^{*}(x)}{I(x)}\frac{HV}{H^{*}V^{*}})\Bigg ]dx-\int _{0}^{1}w(x)d \beta (x) \int _{0}^{1}(1-\epsilon (y))k_{1}H^{*}I^{*}(y)\\&\quad \Bigg [\kappa (\frac{H^{*}}{H}) +\kappa (\frac{HI(y)}{H^{*}I^{*}(y)}\\&\cdot \frac{I^{*}(x)}{I(x)})\Bigg ]dydx-\int _{0}^{1}w(x)d\int _{0}^{1}\gamma (y,x)I^{*}(y) \kappa (\frac{I^{*}(x)}{I(x)}\frac{I(y)}{I^{*}(y)})dydx\\&-\int _{0}^{1}w(x)\beta (x) (1-\xi )k_{2}H^{*}\\&\cdot \int _{0}^{1}\eta (y)I^{*}(y)\kappa (\frac{V^{*}}{V}\frac{I(y)}{I^{*}(y)})dydx\\&+\int _{0}^{1}w(x)\int _{0}^{1}\Bigg [\beta (x)k_{2} (1-\xi )H^{*}\eta (y)I^{*}(y)+d\gamma (y,x)I^{*}(y)\\&+d\beta (x)(1-\epsilon (y))k_{1}H^{*}I^{*}(y)\Bigg ]\\&\quad \times \Bigg [\ln \frac{I(x)}{I^{*}(x)} -\frac{I(x)}{I^{*}(x)}-\ln \frac{I(y)}{I^{*}(y)}+\frac{I(y)}{I^{*}(y)}\Bigg ]dydx. \end{aligned} \end{aligned}$$

(27)