Population abundance of two-patch competitive systems with asymmetric dispersal

Abstract

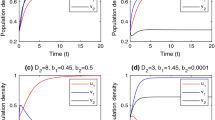
This paper considers two-species competitive systems with two patches, in which one of the species can move between the patches. One patch is a source where each species can persist alone, but the other is a sink where the mobile species cannot survive. Based on rigorous analysis on the model, we show global stability of equilibria and bi-stability in the first octant Int$R_+^3$. Then total population abundance of each species is explicitly expressed as a function of dispersal rates, and the function of the mobile species displays a distorted surface, which extends previous theory. A novel prediction of this work is that appropriate dispersal could make each competitor approach total population abundance larger than if non-dispersing, while the dispersal could reverse the competitive results in the absence of dispersal and promote coexistence of competitors. It is also shown that intermediate dispersal is favorable, large or small one is not good, while extremely large or small dispersal will result in extinction of species. These results are important in ecological conservation and management.

Appendices

Appendix A

The proof of Proposition 2.1

Proof

Since $y=0$ is a solution of the third equation of (2.1), $x_1x_2$-plane is invariant, which implies $y(t) \ge 0$ as $t> 0$.

On the boundary $x_1=0$, from the first equation of (2.1) we have $dx_1/dt = D_2 x_2$. If $x_2>0$, then $dx_1/dt >0$, which implies that $x_1(t)$ is nonnegative when t increases. Assume $x_2=0$. Then we have $x_1=x_2=0$. Since y-axis is an invariant set of system (2.1), no orbit could pass through the invariant set, which implies that $x_1(t) \equiv 0$. Thus $x_1(t)\ge 0$ when $t>0$. Similarly, $x_2(t)\ge 0$ when $t>0$. Hence, solutions of systems (2.1) are nonnegative.

Boundedness of the solutions is shown as follows. From the first and second equations of (2.1), we have

$$\begin{aligned} \dfrac{d(x_1 + x_2) }{dt}\le & {} -r_1 x_1 +r_2 x_2 \left( 1- \frac{x_2 }{K_2}\right) \le x_2 ({{\bar{r}}}_2- \frac{r_2 x_2 }{K_2}) -r_1 (x_1 + x_2)\\\le & {} \frac{K_2 {{\bar{r}}}_2^2 }{4r_2} -r_1 (x_1 + x_2), \end{aligned}$$

where ${{\bar{r}}}_2 = r_2 +r_1$. By the comparison theorem (Hale 1969), we obtain

$$\begin{aligned} \limsup _{t\rightarrow \infty } x_1(t) + x_2(t) \le \frac{K_2 {{\bar{r}}}_2^2 }{4r_1 r_2}, \end{aligned}$$

which implies that $x_1(t), x_2(t)$ are bounded since they are nonnegative.

From the third equation of (2.1), we have

$$\begin{aligned} \dfrac{dy }{dt} \le r y ( 1- \frac{y}{K}), \end{aligned}$$

which means $\limsup _{t\rightarrow \infty } y(t) \le K$ by the comparison theorem (Hale 1969). Thus, y(t) is bounded since it is nonnegative. This completes the proof. $\square$

Appendix B

The proof of Theorem 3.1

Proof

Denote

$$\begin{aligned} V(x_1, x_2, y) = \frac{ D_1}{r_1 + D_1 } x_1 +x_2. \end{aligned}$$

Since $D_2 \ge {{\bar{D}}}_2$, we have

$$\begin{aligned} \frac{d V(x_1, x_2, y)}{dt }|_{(2.1) } = x_2 \left( r_2- \frac{ r_1D_2}{r_1 + D_1 } - \frac{ r_2}{K_2 } x_2 \right) - c_{23} x_2 y \le 0. \end{aligned}$$

Let $\dfrac{d V}{dt }|_{(2.1) } =0$. Then we obtain $x_i=0, i = 1,2$, which means that all positive solutions of (2.1) converge to the y-axis where $P_3(0,0,K)$ is globally asymptotically stable on the positive y-axis. We need to show equilibrium O(0, 0, 0) has no stable manifold in Int$R_+^3$, which implies that equilibrium $P_3$ is globally asymptotically stable in Int$R_+^3$ by the LaSalle Invariance Principle. Indeed, the Jacobian matrix of system (2.1) at O is

$$\begin{aligned} J_0= \left( \begin{array}{lcccr} -r_1 - D_1 &{}D_2 &{} 0 \\ D_1 &{} r_2 - D_2 &{} 0 \\ 0 &{}0 &{} r \\ \end{array} \right) . \end{aligned}$$

Then $J_0$ has an eigenvalue $\lambda _1 =r>0$. The other two eigenvalues $\lambda _2, \lambda _3$ satisfy

$$\begin{aligned}&\lambda ^2 +b \lambda +c =0,~b = D_1 - r_2+ D_2 + r_1,~ c = - r_1r_2 -r_2 D_1 + r_1 D_2,\\&\lambda _2 = \frac{1}{2}(-b+ \sqrt{b^2-4c}),~ \lambda _3 = \frac{1}{2}(-b- \sqrt{b^2-4c}),~ \end{aligned}$$

A direct computation shows

$$\begin{aligned} b^2-4c = (D_1 - r_2)^2+ (D_2 - r_1)^2+ 2(D_1 - r_2) +4(r_1r_2 + r_2 D_1) \ge 4 (r_1+ r_2 )D_1 >0. \end{aligned}$$

Since $D_2 \ge {{\bar{D}}}_2$, we have $b>0, c>0$ and $\lambda _{2,3} <0$, which implies that O is a saddle point. We show that the eigenvector of $J_0$ corresponding to $\lambda _2$ does not direct towards Int$R_+^3$, while a similar discussion can be given for $\lambda _3$. In fact, the eigenvector $u(u_1,u_2,u_3)$ satisfies

$$\begin{aligned} (-r_1 - D_1- \lambda _2) u_1 +D_2 u_2=0,~ (r-\lambda _2)u_3=0. \end{aligned}$$

A direct computation shows $-r_1 - D_1- \lambda _2>0$. Then we obtain the eigenvector $u=(-D_2,-r_1 - D_1- \lambda _2,0)$, which does not direct towards Int$R_+^3$. This completes the proof. $\square$

Appendix C

The proof of Theorem 3.2

Proof

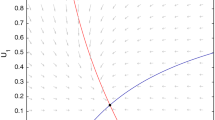
(i) From $\lambda _3^{(12)}>0$ and $\lambda _{12}^{(3)} >0$ we have

$$\begin{aligned} r r_2- c_{23}c_{32} K K_2 = \frac{ c_{32} K_2 r_1D_2}{r_2 (r_1+ D_1)} \left( r_2- c_{23} K - \frac{ r_1D_2}{r_2 (r_1+ D_1)} \right) >0. \end{aligned}$$

Since $\lambda _3^{(12)}>0$, the numerator of $x_2^*$ in (3.1) is positive. Since $\lambda _{12}^{(3)} >0$, the numerator of $y^*$ in (3.1) is positive. Thus, system (2.1) has a unique positive equilibrium $P^*(x_1^*,x_2^*,y^*)$.

By Lyapunov theory, we construct Lyapunov function in each patch and then combine them by $\alpha$ via graph method (see Li and Shuai 2010; Hofbauer and Sigmund 1998), which is shown as follows. Denote

$$\begin{aligned} W_1(x_1)= & {} \frac{ D_1 x_1^*}{D_2 x_2^* } \left( x_1- x_1^* -x_1^* \ln \frac{x_1}{x_1^* }\right) ,~~ W_2(x_2)= x_2- x_2^* -x_2^* \ln \frac{x_2}{x_2^* },~~\\ W_3(y)= & {} \alpha (y- y^* -y^* \ln \frac{y}{y^* }),~~ \alpha = \frac{r r_2}{K K_2 c_{32}^2 }. \end{aligned}$$

Let $V(x_1, x_2, y)=W_1(x_1) +W_2(x_2)+W_3(y)$. Then

$$\begin{aligned} \frac{d V(x_1, x_2, y)}{dt }|_{(2.1) }= & {} - \frac{r_2}{K_2 } (x_2- x_2^* )^2 - (\alpha c_{32} + c_{23} ) (x_2- x_2^* )(y- y^* ) \\&- \frac{r \alpha }{K } (y- y^* )^2 + D_1 x_1^* \left( 2- \frac{x_1 x_2^* }{x_1^* x_2 } - \frac{x_1^* x_2 }{x_1 x_2^* } \right) . \end{aligned}$$

From $r r_2 \ge c_{23}c_{32}K K_2$ we obtain $(c_{23} +\alpha c_{32} )^2 - 4 r r_2 \alpha /(K K_2) \le 0$, which implies that for all $x_2\ge 0, y\ge 0$, we have

$$\begin{aligned} - \frac{r_2}{K_2 } (x_2- x_2^* )^2 - (\alpha c_{32} + c_{23} ) (x_2- x_2^* )(y- y^* ) - \frac{r \alpha }{K } (y- y^* )^2 \le 0. \end{aligned}$$

By using the inequality $2- u - \dfrac{1}{u } \le 0$ as $u >0$, we obtain $\dfrac{d V}{dt }|_{(2.1) } \le 0$.

Let $\dfrac{d V}{dt }|_{(2.1) } =0$. Then we obtain $x_2 = x_2^*$ and $y = y^*$, which means $x_1 = x_1^*$ by the second equation of (2.1). By the LaSalle Invariance Principle, equilibrium $P^*$ is globally asymptotically stable in Int$R_+^3$.

(ii) The Jacobian matrix of system (2.1) at $P_3$ is

$$\begin{aligned} J_3= \left( \begin{array}{lcccr} -r_1 - D_1 &{}D_2 &{} 0 \\ D_1 &{} r_2 - D_2 - c_{23} K &{} 0 \\ 0 &{} - c_{32} K &{} -r \\ \end{array} \right) . \end{aligned}$$

Then $J_3$ has an eigenvalue $\lambda _1 =-r<0$. The other two eigenvalues $\lambda _2, \lambda _3$ satisfy

$$\begin{aligned} \lambda ^2 +a \lambda - \lambda _3^{(12)} =0,~a = r_1 + D_1 + D_2 + c_{23} K- r_2. \end{aligned}$$

From $\lambda _3^{(12)}<0$, we obtain $c_{23} K- r_2 >- D_2$, which implies $a>0$. Then the eigenvalues $\lambda _2, \lambda _3$ have negative real parts, which implies that equilibrium $P_3$ is asymptotically stable in Int$R_+^3$.

(iii) The Jacobian matrix of system (2.1) at $P_{12}$ is

$$\begin{aligned} J_{12}= \left( \begin{array}{lcccr} -r_1 - D_1 &{}D_2 &{} 0 \\ D_1 &{} r_2 (1- \frac{2x_2^+ }{K_2} ) - D_2 &{} - c_{23} x_2^+ \\ 0 &{} 0 &{} r - c_{32} x_2^+ \\ \end{array} \right) . \end{aligned}$$

Then $J_{12}$ has an eigenvalue $\lambda _{12}^{(3)}= r - c_{32} x_2^+ <0$. Since $D_2 < {{\bar{D}}}_2$, the other two eigenvalues satisfy

$$\begin{aligned}&\lambda ^2 +a_1 \lambda + a_2 =0,\\&a_1 = r_1 + D_1+ \frac{D_1 D_2 }{r_1 + D_1} +r_2 - \frac{r_1 D_2 }{r_1 + D_1}>0,~ a_2 = r_2 (r_1 + D_1) -r_1 D_2 >0, \end{aligned}$$

which implies that the other two eigenvalues of $J_{12}$ have negative real parts. Then $P_{12}$ is asymptotically stable in Int$R_+^3$. Thus, system (2.1) is not persistent. $\square$

Appendix D

The proof of Theorem 3.3

Proof

(i) We use functions $U_1$ and $U_2$ in the proof of Theorem 2.2 and form the following function by graph method and Lyapunov theory

$$\begin{aligned} V_I(x_1, x_2, y)= & {} U_1(x_1) +U_2(x_2) + \alpha y = \frac{ D_1 x_1^+}{D_2 x_2^+ } \left( x_1- x_1^+ -x_1^+ \ln \frac{x_1}{x_1^+ }\right) \\&+ x_2- x_2^+ -x_2^+ \ln \frac{x_2}{x_2^+ } + \alpha y, \end{aligned}$$

where $\alpha =r r_2/(K K_2 c_{32}^2 )$. Then

$$\begin{aligned} \frac{d V_I(x_1, x_2, y)}{dt }|_{(2.1) }= & {} D_1 x_1^+ \left( 2- \frac{x_1 x_2^+ }{x_1^+ x_2 } - \frac{x_1^+ x_2 }{x_1 x_2^+ } \right) + \alpha (r- c_{32} x_2^+) y \\&- \frac{r_2}{K_2 } (x_2- x_2^+ )^2 - (c_{23} +\alpha c_{32} ) (x_2- x_2^+ ) y - \frac{\alpha r}{K } y^2. \end{aligned}$$

From $r r_2 \ge c_{23}c_{32}K K_2$ we obtain $(c_{23} +\alpha c_{32} )^2 - 4 r r_2 \alpha /(K K_2) \le 0$, which implies that for all $x_2\ge 0, y\ge 0$, we have

$$\begin{aligned} - \frac{r_2}{K_2 } (x_2- x_2^+ )^2 - (c_{23} +\alpha c_{32} ) (x_2- x_2^+ ) y - \frac{\alpha r}{K } y^2 \le 0. \end{aligned}$$

Since $\lambda _{12}^{(3)} = r- c_{32} x_2^+<0$, we obtain $\dfrac{d V_I}{dt }|_{(2.1) } \le 0$ by using the inequality $2- u - \dfrac{1}{u } \le 0$ as $u >0$.

Let $\dfrac{d V_I}{dt }|_{(2.1) } =0$. Then we obtain $x_i = x_i^+$ and $y = 0, i=1,2$. By the LaSalle Invariance Principle, equilibrium $P_{12}$ is globally asymptotically stable in Int$R_+^3$.

(ii) By graph method and Lyapunov theory, we form the following function

$$\begin{aligned} V_{II}(x_1, x_2, y) = \frac{D_1 }{r_1+ D_1 } x_1 +x_2 + \alpha \left( y- K -K \ln \frac{y}{K }\right) ,~~ \alpha = \frac{r r_2}{K K_2 c_{32}^2 }. \end{aligned}$$

Then

$$\begin{aligned} \frac{d V_{II}(x_1, x_2, y)}{dt }|_{(2.1) } = \lambda _3^{(12)} x_2 - \frac{r_2}{K_2 } x_2^2 - (c_{23} +\alpha c_{32} ) x_2 (y- K) - \frac{\alpha r}{K } (y- K)^2. \end{aligned}$$

From $r r_2 \ge c_{23}c_{32}K K_2$ we obtain $(c_{23} +\alpha c_{32} )^2 - 4 r r_2 \alpha /(K K_2) <0$, which implies that for all $x_2\ge 0, y\ge 0$, we have

$$\begin{aligned} - \frac{r_2}{K_2 } x_2^2 - (c_{23} +\alpha c_{32} ) x_2 (y- K) - \frac{\alpha r}{K } (y- K)^2 \le 0. \end{aligned}$$

Since $\lambda _3^{(12)} <0$, we obtain $\dfrac{d V_{II}}{dt }|_{(2.1) } \le 0$.

Let $\dfrac{d V_{II}}{dt }|_{(2.1) } =0$. We obtain $x_2 = 0, y = K,$ which implies $x_1 = 0$ by the second equation of (2.1). By the LaSalle Invariance Principle, equilibrium $P_3$ is globally asymptotically stable in Int$R_+^3$. $\square$

Appendix E

The proof of Theorem 3.4

Proof

(i) Denote

$$\begin{aligned} \epsilon _0= & {} \frac{K K_2 c_{32} \lambda _3^{(12)} }{2 (c_{23}c_{32}K K_2 -r r_2 ) } >0,\\ {{\bar{\alpha }}}= & {} \frac{1}{ c_{32}^2 } \left[ \frac{2 r r_2}{K K_2 } - \frac{2 r_2 \lambda _{12}^{(3)}}{K_2 (K + \epsilon _0)} - c_{23}c_{32}\right] . \end{aligned}$$

Let $(x_1(t),x_2(t), y(t) )$ be a positive solution of (2.1). Observe that for fixed $x_2$, the third equation of (2.1) satisfies

$$\begin{aligned} \frac{dy }{dt} \le r y ( 1- \frac{y}{K}), \end{aligned}$$

which implies that $\limsup _{t\rightarrow \infty }y(t)\le K$. Then there exists $T>0$ such that $y(t)\le K + \epsilon _0$ when $t>T$.

We use a revised version of function $V_I$ (with different $\bar{\alpha }$) in the proof of Theorem 3.3(i), i.e.,

$$\begin{aligned} V_{III}(x_1, x_2, y) = \frac{ D_1 x_1^+}{D_2 x_2^+ } \left( x_1- x_1^+ -x_1^+ \ln \frac{x_1}{x_1^+ }\right) + x_2- x_2^+ -x_2^+ \ln \frac{x_2}{x_2^+ } + {{\bar{\alpha }}} y. \end{aligned}$$

Assume $t>T$. Then

$$\begin{aligned}&\frac{d V_{III}(x_1, x_2, y) }{dt }|_{(2.1) } = D_1 x_1^+ \left( 2- \frac{x_1 x_2^+ }{x_1^+ x_2 } - \frac{x_1^+ x_2 }{x_1 x_2^+ } \right) +a (x_2- x_2^+ )^2 +b(x_2- x_2^+ )+c,\\&a=- \frac{r_2}{K_2 },~~ b=- (c_{23} +{{\bar{\alpha }}} c_{32} ) y,~~ c= {{\bar{\alpha }}} \lambda _{12}^{(3)} y - \frac{{{\bar{\alpha }}} r}{K } y^2, \end{aligned}$$

so that

$$\begin{aligned} b^2-4ac =y\left\{ \left[ (c_{23} +{{\bar{\alpha }}} c_{32} )^2 - \frac{4rr_2\bar{\alpha }}{K K_2 } \right] y + \frac{4 r_2 {{\bar{\alpha }}} \lambda _{12}^{(3)} }{K_2} \right\} , \end{aligned}$$

where we have $(c_{23} +\alpha c_{32} )^2 - \dfrac{4rr_2\alpha }{K K_2 } >0$ for all $\alpha$ by $r r_2 < c_{23}c_{32}K K_2$. Since

$$\begin{aligned} K +\epsilon _0 < \frac{- r_2 K {{\bar{\alpha }}} \lambda _{12}^{(3)} }{ c_{23}c_{32}K K_2 -r r_2 }, \end{aligned}$$

we have

$$\begin{aligned} \frac{rr_2 }{K K_2 } - \frac{ r_2 \lambda _{12}^{(3)} }{K_2 (K +\epsilon _0 )} - c_{23}c_{32} >0, \end{aligned}$$

so that ${{\bar{\alpha }}} >0$ and

$$\begin{aligned} c_{32}^2 {{\bar{\alpha }}}^2 +\left[ 2 c_{23}c_{32} - \frac{4rr_2 }{K K_2 } + \frac{4 r_2 \lambda _{12}^{(3)} }{K_2 (K +\epsilon _0 )}\right] {{\bar{\alpha }}} +c_{23}^2 <0 \end{aligned}$$

which implies $b^2-4ac \le 0.$ By using the inequality $2- u - \dfrac{1}{u } \le 0$ as $u >0$, we obtain $\dfrac{d V_{III}}{dt }|_{(2.1) } \le 0$.

Let $\dfrac{d V_{III}}{dt }|_{(2.1) } =0$. We obtain $y = 0, x_i = x_i^+, i=1,2$. By the LaSalle Invariance Principle, equilibrium $P_{12}$ is globally asymptotically stable in Int$R_+^3$.

(ii) Denote

$$\begin{aligned} \epsilon _0= & {} \frac{1}{2 } \left[ \frac{-r K_2 \lambda _3^{(12)} }{(r_1+ D_1) (c_{23}c_{32}K K_2 -r r_2 ) } - x_2^+ \right] ,\\ {{\hat{\alpha }}}= & {} \frac{1}{ c_{32}^2 } \left[ \frac{2 r r_2}{K K_2 } - \frac{2 r \lambda _3^{(12)}}{K (r_1+ D_1) (x_2^+ + \epsilon _0)} - c_{23}c_{32}\right] . \end{aligned}$$

Then a direct computation shows

$$\begin{aligned} \epsilon _0 = \frac{K K_2 c_{23} \lambda _{12}^{(3)} }{2(c_{23}c_{32}K K_2 -r r_2 ) } >0. \end{aligned}$$

Since $D_2 < {{\bar{D}}}_2$, the boundary equilibrium $P_{12}$ is globally asymptotically stable in Int$R_+^2$ when $y=0$. Let $(x_1(t),x_2(t), y(t) )$ be a positive solution of (2.1). Observe that for fixed y, the $(x_1,x_2 )$ subsystem of (2.1) is cooperative with

$$\begin{aligned} \begin{aligned} \frac{dx_1}{dt}&\le -r_1 x_1 + D_2x_2 -D_1x_1 \\ \frac{dx_2}{dt}&\le r_2 x_2 ( 1- \frac{x_2}{K_2}) +D_1x_1 - D_2x_2. \end{aligned} \end{aligned}$$

Consider a planar system

$$\begin{aligned} \begin{aligned} \frac{dX_1}{dt}&= -r_1 X_1 + D_2X_2 -D_1X_1 \\ \frac{dX_2}{dt}&= r_2 X_2 ( 1- \frac{X_2}{K_2}) +D_1X_1 - D_2X_2. \end{aligned} \end{aligned}$$

(5.1)

By Theorem 2.2, all positive solutions of (5.1) converge to equilibrium $E_{12}(x_1^+,x_2^+)$. Let $(x_1(t),x_2(t),y(t))$ be a positive solution of (2.1). Since (5.1) is cooperative, we have $\limsup _{t\rightarrow \infty }x_i(t)\le x_i^+, i=1,2$ (cf. Appendix B, Smith and Waltman 1995). Then there exists $T>0$ such that $x_2(t)\le x_2^+ + \epsilon _0$ when $t>T$.

Assume $t>T$. Denote

$$\begin{aligned} V_{IV}(x_1, x_2, y) =x_1 +x_2 + {{\hat{\alpha }}} (y- K -K \ln \frac{y}{K }). \end{aligned}$$

Then we have

$$\begin{aligned} \frac{d V_{IV}(x_1, x_2, y)}{dt }|_{(2.1) } =a (y- K)^2 +b(y- K)+c,~~\end{aligned}$$

$$\begin{aligned} a=- \frac{{{\hat{\alpha }}} r}{K },~~ b=- (c_{23} +{{\hat{\alpha }}} c_{32} ) x_2,~~ c=\frac{\lambda _3^{(12)}}{r_1+ D_1 }x_2 - \frac{r_2}{K_2 } x_2^2, \end{aligned}$$

so that

$$\begin{aligned} b^2-4ac =x_2 \left\{ \left[ (c_{23} +{{\hat{\alpha }}} c_{32} )^2 - \frac{4rr_2\hat{\alpha }}{K K_2 } \right] x_2 - \frac{-4 r {{\hat{\alpha }}}\lambda _3^{(12)} }{K (r_1+ D_1)} \right\} , \end{aligned}$$

where we have $(c_{23} +\alpha c_{32} )^2 - \dfrac{4rr_2\alpha }{K K_2 } >0$ for all $\alpha$ by $r r_2 < c_{23}c_{32}K K_2$. Since

$$\begin{aligned} x_2^+ +\epsilon _0 < \frac{- r K_2 {{\hat{\alpha }}}\lambda _3^{(12)} }{ (r_1+ D_1) (c_{23}c_{32}K K_2 -r r_2 )}, \end{aligned}$$

we have

$$\begin{aligned} \frac{rr_2{{\hat{\alpha }}} }{K K_2 } - \frac{ r \lambda _3^{(12)} }{K (r_1+ D_1)(x_2^+ +\epsilon _0 )} - c_{23}c_{32} >0, \end{aligned}$$

so that ${{\hat{\alpha }}} >0$ and

$$\begin{aligned} c_{32}^2 {{\hat{\alpha }}}^2 +\left[ 2 c_{23}c_{32} - \frac{4rr_2 }{K K_2 } + \frac{4 r \lambda _3^{(12)} }{K (r_1+ D_1)(x_2^+ +\epsilon _0 )}\right] {{\hat{\alpha }}} +c_{23}^2 <0 \end{aligned}$$

which implies

$$\begin{aligned} b^2-4ac \le x_2 \left\{ \left[ (c_{23} +{{\hat{\alpha }}} c_{32} )^2 - \frac{4rr_2{{\hat{\alpha }}} }{K K_2 } \right] (x_2^+ +\epsilon _0 ) - \frac{-4 r {{\hat{\alpha }}}\lambda _3^{(12)} }{K (r_1+ D_1)} \right\} \le 0. \end{aligned}$$

Let $\dfrac{d V_{IV}}{dt }|_{(2.1) } =0$. Then we obtain $y = K, x_i = 0, i=1,2$. By the LaSalle Invariance Principle, equilibrium $P_3$ is globally asymptotically stable in Int$R_+^3$.

(iii) By Theorem 3.2(ii–iii), equilibrium $P_{12}$ and $P_3$ are asymptotically stable in Int$R_+^3$ since $\lambda _{12}^{(3)} <0$ and $\lambda _3^{(12)} <0$, respectively. From (3.1), system (2.1) has a positive equilibrium $P^*(x_1^*,x_2^*,y^*)$. From (2.1), the Jacobian matrix of system (2.1) at $P^*$ is

$$\begin{aligned} J^*= \left( \begin{array}{lcccr} -r_1 - D_1 &{}D_2 &{} 0 \\ D_1 &{} - \frac{r_2}{K_2 } x_2^* - \frac{D_1D_2}{r_1 +D_1 } &{} - c_{23} x_2^* \\ 0 &{} - c_{32} y^* &{} -\frac{r}{K } y^* \\ \end{array} \right) . \end{aligned}$$

The characteristic equation of $J^*$ is

$$\begin{aligned}&\lambda ^3 +a_1 \lambda ^2 +a_2 \lambda +a_3 =0, \\&a_1 = r_1 + D_1 + \dfrac{r_2}{K_2 } x_2^* + \dfrac{D_1D_2}{r_1 +D_1 } + \dfrac{r}{K } y^*>0,\\&a_3 = - x_2^*y^*\dfrac{r_1 + D_1}{K K_2 } (c_{23}c_{32}K K_2 -rr_2)<0. \end{aligned}$$

Thus, the three eigenvalues $\lambda _i$ of $J^*$ satisfy

$$\begin{aligned} \lambda _1+\lambda _2+\lambda _3 =-a_1 <0,~~ \lambda _1\lambda _2\lambda _3 =-a_3 >0, \end{aligned}$$

which implies that one of the eigenvalues is positive and the other two eigenvalues have negative real parts, i.e., Re$\lambda _i<0$ and $\lambda _3> 0, i=1,2$. Thus, equilibrium $P^*$ is a saddle point with a two-dimensional stable manifold. $\square$