Steady-state voltage distribution in three-dimensional cusp-shaped funnels modeled by PNP

Abstract

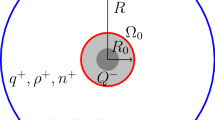
We study here the bulk electro-diffusion properties of micro- and nanodomains containing a cusp-shaped structure in three-dimensions when the cation concentration dominates over the anions. To determine the consequences on the voltage distribution, we use the steady-state Poisson–Nernst–Planck equation with an integral constraint for the number of charges. A non-homogeneous Neumann boundary condition is imposed on the boundary. We construct an asymptotic approximation for certain surface charge distribution that agree with numerical simulations. Finally, we analyze the consequences of several piecewise constant non-homogeneous surface charge densities, motivated by designing new nanopipettes. To conclude, when electro-neutrality is broken at the scale of hundreds of nanometers, the geometry of cusp-shaped domains influences the voltage profile, specifically inside the cusp structure. The main results are summarized in the form of new three-dimensional electrostatic laws for non-electroneutral electrolytes. These formula provide a refined characterization of voltage distribution at steady-state in neuronal microdomains such as dendritic spines, but can also be used to design nanometric patch-pipettes.

5 Appendix

1.1 5.1 Radial derivative under the Mobius map (26)

We present in this appendix the computations to reduce the first order radial derivative from (25) that lead to (37) in Sect. 2.2.

First, we note that in complex coordinates, we have

$$\begin{aligned} \frac{\partial u( \tilde{r}, \tilde{z})}{\partial \tilde{r}}= & {} \mathfrak {R}e \left( \nabla u( \xi )\right) , \end{aligned}$$

(121)

where

$$\begin{aligned} \nabla u(\xi )= & {} \frac{\partial u( \tilde{r}, \tilde{z})}{\partial \tilde{r}} +i\frac{\partial u( \tilde{r}, \tilde{z})}{\partial \tilde{z}}. \end{aligned}$$

(122)

Under the conformal mapping (26), the gradient (122) is transformed into

$$\begin{aligned} \nabla u(\xi )= & {} \nabla _w v(w) \, \overline{w'(\xi )}. \end{aligned}$$

(123)

Using $w=X+iY$, we get

$$\begin{aligned} \nabla _w v(w)= & {} \frac{\partial v(X,Y) }{\partial X } + i \frac{\partial v(X,Y)}{\partial Y }. \end{aligned}$$

(124)

The real functions $w_1(X,Y)$ and $w_2(X,Y)$ satisfy

$$\begin{aligned} \overline{w'(\xi )}=\overline{w'(w^{-1}(X,Y))}=w_1(X,Y)+i\,w_2(X,Y). \end{aligned}$$

(125)

Using the Möbius transformation (26), we get

$$\begin{aligned} \overline{w'(w^{-1}(X,Y))}= & {} \frac{\overline{(1+\alpha w)^2}}{{ 1-\alpha ^2} }. \end{aligned}$$

(126)

Equations (125) and (126) lead to

$$\begin{aligned} \begin{aligned} w_1(X,Y)&= \frac{(1+\alpha X)^2-\alpha ^2Y^2}{1-\alpha ^2}\\ w_2(X,Y)&=-\frac{2\alpha Y(1+\alpha X)}{1-\alpha ^2}. \end{aligned} \end{aligned}$$

(127)

From (121)–(123)–(124)–(125), we obtain

$$\begin{aligned} \frac{\partial u}{\partial \tilde{r}}= & {} w_1(X,Y)\frac{\partial v(X,Y) }{\partial X }-w_2(X,Y)\frac{\partial v(X,Y) }{\partial Y }. \end{aligned}$$

(128)

Due to the geometry of the banana-shaped domain $\Omega _w$, it is convenient to switch from Cartesian (X, Y) to polar coordinates $(\rho , \theta )$. Setting $v(X,Y)=\tilde{v}(\rho , \theta )$, we get

$$\begin{aligned} \begin{aligned} \frac{\partial v(X,Y) }{\partial X }&= \frac{\partial \tilde{v}(\rho ,\theta ) }{\partial \rho }\frac{\partial \rho }{\partial X }+\frac{\partial \tilde{v}(\rho ,\theta ) }{\partial \theta }\frac{\partial \theta }{\partial X }\\ \frac{\partial v(X,Y) }{\partial Y }&=\frac{\partial \tilde{v}(\rho ,\theta ) }{\partial \rho }\frac{\partial \rho }{\partial Y }+\frac{\partial \tilde{v}(\rho ,\theta ) }{\partial \theta }\frac{\partial \theta }{\partial Y } \end{aligned} \end{aligned}$$

(129)

where,

$$\begin{aligned} \begin{aligned} \frac{\partial \rho }{\partial X } = \cos (\theta ),&\quad \frac{\partial \rho }{\partial Y } =\sin (\theta ) \\ \frac{\partial \theta }{\partial X } = -\frac{\sin (\theta )}{\rho },&\quad \frac{\partial \theta }{\partial Y } = \frac{\cos (\theta )}{\rho }. \end{aligned} \end{aligned}$$

(130)

Using (129) and (130) in (128), it follows that

$$\begin{aligned} \frac{\partial \tilde{u}(\tilde{r}, \tilde{z})}{\partial \tilde{r}}= & {} \frac{\partial \tilde{v}(\rho ,\theta )}{\partial \rho }\left( \cos (\theta ) \tilde{w}_1(\rho ,\theta ) - \sin (\theta )\tilde{w}_2(\rho ,\theta ) \right) \nonumber \\&-\frac{1}{\rho }\frac{\partial \tilde{v}(\rho ,\theta ) }{\partial \theta }\left( \sin (\theta )\tilde{w}_1(\rho ,\theta ) +\cos (\theta ) \tilde{w}_2(\rho ,\theta ) \right) , \end{aligned}$$

(131)

where we set $\tilde{w}_i(\rho ,\theta )=w_i(X,Y)$ for $i\in \{1,\,2\}$, such as

$$\begin{aligned} \begin{aligned} \tilde{w}_1(\rho ,\theta )&= \frac{1-\alpha ^2 \rho ^2 +2\alpha \rho \cos (\theta )(1+ \alpha \rho \cos (\theta )) }{1-\alpha ^2}\\ \tilde{w}_2(\rho ,\theta )&= -2\alpha \rho \sin (\theta )\frac{ 1 + \alpha \rho \cos (\theta ) }{1-\alpha ^2}. \end{aligned} \end{aligned}$$

(132)

Using (132) and (131), we obtain to leading order

$$\begin{aligned} \frac{1}{\tilde{r}}\frac{\partial \tilde{u}(\tilde{r},\tilde{z})}{\partial \tilde{r}}= & {} - \frac{ \rho (1-\cos (\theta ))^2}{\varepsilon ^{3/2}}\frac{\partial \tilde{v} (\rho ,\theta z)}{\partial \rho } - \frac{\sin (\theta )(1-\cos (\theta ))}{\varepsilon }\frac{\partial \tilde{v} (\rho ,\theta z)}{\partial \theta }.\nonumber \\ \end{aligned}$$

(133)

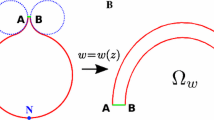
1.2 5.2 Field lines in the regions A and B

We present here the line field that lead to splitting the mapped domain into the two regions A and B (Fig. 8).

Fig. 8

Field lines in the domains $\Omega$ and $\Omega _w$. a Field lines $\left( \frac{\partial u}{\partial x}, \frac{\partial u}{\partial y} \right)$ are computed numerically inside $\Omega$. The inset in a represents a magnification near the end of the cusp. The grey lines originate from the bulk, while the orange and green start in the cusp. The blue arrows represent the direction of the Neumann boundary condition at the surface. b Field line and arrows from a mapped into $\Omega _w$ using the Mobius transformation (26). c The two subregions A (blue) and B (magenta) of $\Omega _w$. d Magnification near $\theta =\pi$ showing region B (magenta) of size $\sqrt{\varepsilon }$. The arrows show the direction of the Neumann boundary condition, parallel to the radial (blue) and the angular (magenta) coordinates (color figure online)

1.3 5.3 PNP solutions (2) and (4) for several values of $\varepsilon$

We present here additional results to Figs. 4 and 6 where we vary the size of the cusp opening $\varepsilon$. We compare in Fig. 9, the analytical solutions (68) and (108) with numerical simulations (22) for several values $\varepsilon =\{ 0.2; 0.1, 0.02; 0.01\}$.

Fig. 9

Numerical versus analytical solutions computed in $\Omega _w$. a, b Analytical (Eq. 68, dashed green) and numerical solutions (22) (blue), computed in 3D for several values of $\varepsilon =0.2; 0.1; 0.02; 0.01$, $\sigma =100$ (a) and $\sigma =1000$ (b). c–f Analytical (Eq. 108, dashed green) and numerical solutions (22) (blue) computed for $\sigma _{cusp}=0$ and the 1D reduced Eq. 93 (dashed red). Here $\sigma =1000$

1.4 5.4 The numerical procedure

Numerical solutions were constructed by the COMSOL Multiphysics 5.0 (BVP problems), Maple 2015 (Shooting problems) and Matlab R2015 (Conformal mapping). The boundary value problems in 1D, 2D, and 3D were solved by the finite elements method in the COMSOL ’Mathematics’ package. We used an adaptive mesh refinement to ensure numerical convergence for large value of the parameters $\sigma$, $\sigma _{\varepsilon }$, $\sigma _{bulk}$ and $\sigma _{cusp}$. We solved the PDEs by the shooting procedure for boundary value problems using Runge-Kutta fourth-order method.