Skip to main content
Springer Nature Link
Log in

Signaling networks and cell motility: a computational approach using a phase field description

  • Published:
Journal of Mathematical Biology Aims and scope Submit manuscript

Abstract

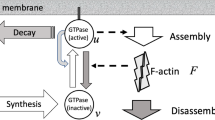
The processes of protrusion and retraction during cell movement are driven by the turnover and reorganization of the actin cytoskeleton. Within a reaction–diffusion model which combines processes along the cell membrane with processes within the cytoplasm a Turing type instability is used to form the necessary polarity to distinguish between cell front and rear and to initiate the formation of different organizational arrays within the cytoplasm leading to protrusion and retraction. A simplified biochemical network model for the activation of GTPase which accounts for the different dimensionality of the cell membrane and the cytoplasm is used for this purpose and combined with a classical Helfrich type model to account for bending and stiffness effects of the cell membrane. In addition streaming within the cytoplasm and the extracellular matrix is taken into account. Combining these phenomena allows to simulate the dynamics of cells and to reproduce the primary phenomenology of cell motility. The coupled model is formulated within a phase field approach and solved using adaptive finite elements.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  • Allain J, Ben Amar M (2004) Biphasic vesicle: instability induced by adsorption of proteins. Phys A 337:531–545

    Google Scholar 

  • Altschuler SJ, Angenent SB, Wang Y, Wu LF (2008) On the spontaneous emergence of cell polarity. Nature 454:886–889

    Article  Google Scholar 

  • Barnhart E, Lee KC, Keren K, Mogilner A, Theriot J (2011) An adhesion-dependent switch between mechanisms that determine mitile cell shape. PLOS Biol 9:e1001,059

    Article  Google Scholar 

  • Biben T, Kassner K, Misbah C (2005) Phase-field approach to three-dimensional vesicle dynamics. Phys Rev E 72:1–15

    Article  Google Scholar 

  • Bonito A, Nochetto R, Pauletti M (2011) Dynamics of biomembranes: effect of the bulk fluid. Math Model Nat Phenom 6:25–43

    Article  MATH  MathSciNet  Google Scholar 

  • Das S, Du Q (2008) Adhesion of vesicles to curved substrates. Phys Rev E 77

  • Du Q, Li M, Liu C (2007) Analysis of a phase field Navier–Stokes vesicle–fluid interaction model. Discrete Contin Dyn Syst Ser B 8:539–556

    Article  MATH  MathSciNet  Google Scholar 

  • Du Q, Liu C, Ryham R, Wang X (2005) A phase field formulation of the Willmore problem. Nonlinearity 18:1249

    Article  MATH  MathSciNet  Google Scholar 

  • Du Q, Liu C, Ryham R, Wang X (2005) Modeling the spontaneous curvature effects in static cell membrane deformations by a phase field formulation. Commun Pure Appl Anal 4:537–548

    Article  MATH  MathSciNet  Google Scholar 

  • Du Q, Liu C, Ryham R, Wang X (2009) Energetic variational approaches in modeling vesicle and fluid interactions. Phys D 238:923–930

    Article  MATH  MathSciNet  Google Scholar 

  • Du Q, Liu C, Wang X (2006) Simulating the deformation of vesicle membranes under elastic bending energy in three dimensions. J Comput Phys 212:757–777

    Article  MATH  MathSciNet  Google Scholar 

  • Du Q, Zhang J (2008) Adaptive finite element method for a phase field bending elasticity model of vesicle membrane deformations. SIAM J Sci Comput 30:1634–1657

    Article  MATH  MathSciNet  Google Scholar 

  • Elliott C, Stinner B (2010) A surface phase field model for two-phase biological membranes. SIAM J Appl Math 70:2904–2928

    Article  MATH  MathSciNet  Google Scholar 

  • Elliott CM, Stinner B, Venkataraman C (2012) Modelling cell motility and chemotaxis with evolving surface finite elements. J R Soc Interface 9:3027-3044

    Google Scholar 

  • Enculescu M, Gholami A, Falcke M (2008) Dynamic regimes and bifurcations in a model of actin-based motility. Phys Rev E 78:031,915

    Article  MathSciNet  Google Scholar 

  • Enculescu M, Sabouri-Ghorni M, Danuser G, Falcke M (2010) Modeling of protrution phenotypes driven by the actin–membrane interaction. Biophys J 98:1571–1581

    Article  Google Scholar 

  • Evans E, Rawicz W (1990) Entropy-driven tension and bending elasticity in condensed-fluid membranes. Phys Rev Lett 64:2094–2097

    Article  Google Scholar 

  • Goryachev AB, Pokhilko AV (2008) Dynamics of Cdc42 network embodies a Turing-type mechanism of yeast cell polarity. FEBS Lett 582:1437–1443

    Article  Google Scholar 

  • Haußer F, Li S, Lowengrub J, Marth W, Rätz A, Voigt A (2013) Thermodynamically consistent models for two-component vesicles (submitted)

  • Helfrich W (1973) Elastic properties of lipid bilayers: theory and possible experiments. Z Naturforsch 28:693–703

    MathSciNet  Google Scholar 

  • Jilkine A, Edelstein-Keshet L (2011) A comparison of mathematical models for polarization of single eukaryotic cells in response to guided cues. PLoS Comput Biol 7:e1001121

    Google Scholar 

  • Landsberg C, Stenger F, Deutsch A, Gelinsky M, Roesen-Wolff A, Voigt A (2011) Chemotaxis of mesenchymal stem cells within 3D biomimetic scaffolds—a modeling approach. J Biomech 44: 359–364

    Article  Google Scholar 

  • Levine H, Rappel WJ (2005) Membrane-bound turing patterns. Phys Rev E 72:061,912

    Article  MathSciNet  Google Scholar 

  • Li X, Lowengrub J, Raetz A, Voigt A (2009) Solving pde’s in complex geometries: a diffuse domain approach. Commun Math Sci 7:81–107

    Article  MATH  MathSciNet  Google Scholar 

  • Lowengrub J, Xu J, Voigt A (2007) Surface phase separation and flow in a simple model of multicomponent drops and vesicles. Fluid Dyn Math Proc 3:13–28

    MathSciNet  Google Scholar 

  • Lowengrub JS, Rätz A, Voigt A (2009) Phase-field modeling of the dynamics of multicomponent vesicles: spinodal decomposition, coarsening, budding, and fission. Phys Rev E 79:031,926

    Article  Google Scholar 

  • Maree AFM, Jilkine A, Dawes A, Grieneisen VA, Edelstein-Keshet L (2006) Polarization and movement of keratocytes: a multiscale modelling approach. Bull Math Biol 68:1169–1211

    Article  Google Scholar 

  • McMahon H, Gallop J (2005) Membrane curvature and mechanisms of dynamic cell membrane remodelling. Nature 438:590–596

    Article  Google Scholar 

  • Rätz A, Röger M (2012) Turing instabilities in a mathematical model for signaling networks. J Math Biol 65:1215–1244

    Article  MATH  MathSciNet  Google Scholar 

  • Rätz A, Röger M (2013) Symmetry breaking in a bulk-surface reaction-diffusion model for signaling networks (preprint)

  • Rätz A, Voigt A (2006) Pde’s on surfaces—a diffuse interface approach. Commun Math Sci 4:575–590

    Article  MATH  MathSciNet  Google Scholar 

  • Ryham R, Cohen FS, Eisenberg R (2012) A dynamic model of open vesicles in fluids. Commun Math Sci 10:1273–1285

    Article  MATH  MathSciNet  Google Scholar 

  • Salac D, Miksis M (2011) A level set projection model of lipid vesicles in general flows. J Comput Phys 230:8192–8215

    Article  MATH  MathSciNet  Google Scholar 

  • Seifert U (1997) Configurations of fluid membranes and vesicles. Adv Phys 46:13–137

    Article  Google Scholar 

  • Seifert U, Lipowsky R (1990) Adhesion of vesicles. Phys Rev A 42:4768–4771

    Article  Google Scholar 

  • Shao D, Levine H, Rappel WJ (2012) Coupling actin flow, adhesion, and morphology in a computational cell motility model. PNAS 109:6851–6856

    Article  Google Scholar 

  • Shao D, Rappel WJ, Levine H (2010) Computational model for cell morphodynamics. Phys Rev Lett 105:108,104

    Article  Google Scholar 

  • Simson R, Wallraff E, Faix J, Niewohner J, Gerisch G, Sackmann E (1998) Membrane bending modulus and adhesion energy of wild-type and mutant cells of Dictyostelium lacking talin or cortexillins. Biophys J 74:514–522

    Article  Google Scholar 

  • Sohn JS, Tseng YH, Li S, Voigt A, Lowengrub JS (2010) Dynamics of multicomponent vesicles in a viscous fluid. J Comput Phys 229:119–144

    Article  MATH  MathSciNet  Google Scholar 

  • Strey H, Peterson M (1995) Measurment of erythrocyte-membrane elasticity by flicker eigenmode decomposition. Biophys J 69:478–488

    Article  Google Scholar 

  • Teigen KE, Li X, Lowengrub J, Wang F, Voigt A (2009) A diffuse-interface approach for modeling transport, diffusion and adsorption/desorption of material quantities on a deformable interface. Commun Math Sci 7:1009–1037

    Article  MATH  MathSciNet  Google Scholar 

  • Teigen KE, Song P, Lowengrub J, Voigt A (2011) A diffuse-interface method for two-phase flows with soluble surfactants. J Comput Phys 230(2):375–393

    Article  MATH  MathSciNet  Google Scholar 

  • Vanderlei B, Feng JJ, Edelstein-Keshet L (2011) A computational model of cell polarization and motility coupling mechanics and biochemistry. Multiscale Model Simul 9:1420–1443

    Article  MATH  MathSciNet  Google Scholar 

  • Veksler A, Gov NS (2007) Phase transitions of the coupled membrane-cytoskeleton modify cellular shape. Biophys J 93:3798–3810

    Article  Google Scholar 

  • Vey S, Voigt A (2007) Amdis: adaptive multidimensional simulations. Comput Visual Sci 10:57–67

    Article  MathSciNet  Google Scholar 

  • Voigt A, Witkowski T (2012) A multi-mesh finite element method for lagrange elements of arbitrary degree. J Comput Sci 3:420–428

    Article  Google Scholar 

  • Wang X, Du Q (2008) Modelling and simulations of multi-component lipid membranes and open membranes via diffuse interface approaches. J Math Biol 56:347–371

    Article  MATH  MathSciNet  Google Scholar 

  • Wedlich-Soldner R, Altschuler S, Wu L, Li R (2003) Spontaneous cell polarization through actomyosin-based delivery of the Cdc42 GTPase. Science 299:1231–1235

    Article  Google Scholar 

  • Wedlich-Soldner R, Wai S, Schmidt T, Li R (2004) Robust cell polarity is a dynamic state established by coupling transport and GTPase SIGNALING. J Cell Biol 166:889–900

    Article  Google Scholar 

  • Zhelev DV, Needham D, Hochmuth R (1994) A novel micropipet method for measuring the bending modulus for vesicle membranes. Biophys J 67:720–727

    Article  Google Scholar 

  • Ziebert F, Swaminathan S, Aranson IS (2012) Model for self-polarization and motility of keratocyte fragments. J Roy Soc Interface 9:1084–1092

    Article  Google Scholar 

Download references

Acknowledgments

The work has been funded through grant DFG Vo899/6 and FP7 IRSES 247504. We further acknowledge the provided computing resources at ZIH at TU Dresden.

Author information

Authors and Affiliations

  1. Department of Mathematics, TU Dresden, 01062 , Dresden, Germany

    Wieland Marth & Axel Voigt

Authors
  1. Wieland Marth
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Axel Voigt
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Axel Voigt.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Marth, W., Voigt, A. Signaling networks and cell motility: a computational approach using a phase field description. J. Math. Biol. 69, 91–112 (2014). https://doi.org/10.1007/s00285-013-0704-4

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00285-013-0704-4

Keywords

Mathematics Subject Classification