Analysis of a stochastic predator–prey model with applications to intrahost HIV genetic diversity

Abstract

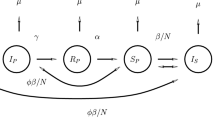
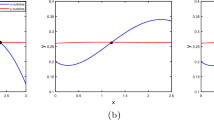
During an infection, HIV experiences strong selection by immune system T cells. Recent experimental work has shown that MHC escape mutations form an important pathway for HIV to avoid such selection. In this paper, we study a model of MHC escape mutation. The model is a predator–prey model with two prey, composed of two HIV variants, and one predator, the immune system CD8 cells. We assume that one HIV variant is visible to CD8 cells and one is not. The model takes the form of a system of stochastic differential equations. Motivated by well-known results concerning the short life-cycle of HIV intrahost, we assume that HIV population dynamics occur on a faster time scale then CD8 population dynamics. This separation of time scales allows us to analyze our model using an asymptotic approach. Using this model we study the impact of an MHC escape mutation on the population dynamics and genetic evolution of the intrahost HIV population. From the perspective of population dynamics, we show that the competition between the visible and invisible HIV variants can reach steady states in which either a single variant exists or in which coexistence occurs depending on the parameter regime. We show that in some parameter regimes the end state of the system is stochastic. From a genetics perspective, we study the impact of the population dynamics on the lineages of an HIV sample taken after an escape mutation occurs. We show that the lineages go through severe bottlenecks and that in certain parameter regimes the lineage distribution can be characterized by a Kingman coalescent. Our results depend on methods from diffusion theory and coalescent theory.