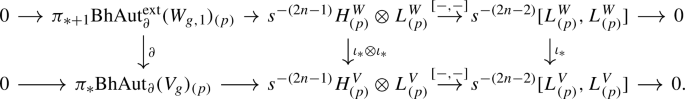A homological approach to pseudoisotopy theory. I

Abstract

We construct a zig–zag from the once delooped space of pseudoisotopies of a closed 2n-disc to the once looped algebraic K-theory space of the integers and show that the maps involved are p-locally $(2n-4)$-connected for $n\,{>}\,3$ and large primes p. The proof uses the computation of the stable homology of the moduli space of high-dimensional handlebodies due to Botvinnik–Perlmutter and is independent of the classical approach to pseudoisotopy theory based on Igusa’s stability theorem and work of Waldhausen. Combined with a result of Randal-Williams, one consequence of this identification is a calculation of the rational homotopy groups of $\mathrm {BDiff}_\partial (D^{2n+1})$ in degrees up to $2n-5$.

The homotopy type of the group of smooth pseudoisotopies, or concordance diffeomorphisms,

$$\begin{aligned} \mathrm {C}(M)=\{\phi :M\times [0,1]\overset{\cong }{\longrightarrow } M\times [0,1]\mid \phi |_{M\times \{0\}\cup \partial M\times [0,1]}=\mathrm {id}\}, \end{aligned}$$

of a smooth compact d-dimensional manifold M in the smooth topology has been an object of interest to geometric topologists for many years, not least because of its intimate connection to algebraic K-theory already visible on the level of path components. Building on Cerf’s proof that $\mathrm {C}(M)$ is connected if M is simply connected and $d\ge 5$ [11], Hatcher and Wagoner [20] computed the group $\pi _0\mathrm {C}(M)$ of isotopy classes of concordances in high dimensions by relating it to the lower algebraic K-groups of the integral group ring $\mathbf {Z}[\pi _1M]$ of the fundamental group of M.¹ Beyond its components, the homotopy type of the space of concordances $\mathrm {C}(M)$ and its relation to K-theory has so far been studied in two steps: deep work of Igusa [22] shows that the stabilisation map

$$\begin{aligned} \mathrm {C}(M)\longrightarrow \mathrm {C}(M\times [0,1]) \end{aligned}$$

induced by crossing with an interval is $\min (\frac{d-4}{3},\frac{d-7}{2})$-connected, so in this range up to about a third of the dimension, one may consider the stable concordance space $\mathrm {colim}_k\mathrm {C}(M\times [0,1]^k)$ instead, which in turn admits a complete description in terms of Waldhausen’s generalised algebraic K-theory for spaces by Waldhausen, Jahren, and Rognes’ foundational stable parametrised h-cobordism theorem [48].

In this work, we focus on the case $M=D^{2n}$ of a closed disc of even dimension and study its space of concordances via a new route—independent of the classical approach—which does not involve stabilising the dimension and is, vaguely speaking, homological instead of homotopical; we shall elaborate on this at a later point. Our main result relates the delooped concordance space $\mathrm {BC}(D^{2n})$ to the once looped algebraic K-theory space of the integers $\Omega ^{\infty +1}\mathrm {K}(\mathbf {Z})$ in a range up to approximately the dimension, p-locally for primes p that are large with respect to the dimension and the degree.

FormalPara Theorem A

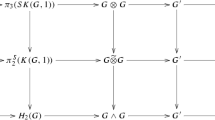
For $n>3$, there exists a zig–zag

$$\begin{aligned} \mathrm {BC}(D^{2n})\longrightarrow \cdot \longleftarrow \Omega ^{\infty +1}_0\mathrm {K}(\mathbf {Z})\end{aligned}$$

whose maps are p-locally $\min (2n-4,2p-4-n)$-connected for primes p.

FormalPara Remark

The result we prove is slightly stronger than stated here (see Theorem 5.1) and implies for instance that $\pi _{2n-4}\mathrm {BC}(D^{2n})\otimes \mathbf {Q}$ surjects onto $K_{2n-3}(\mathbf {Z})\otimes \mathbf {Q}$ as long as $n>3$.

When combined with Borel’s work on the stable rational cohomology of arithmetic groups [9], Theorem A provides an isomorphism

$$\begin{aligned}\pi _*\mathrm {BC}(D^{2n})\otimes \mathbf {Q}\cong & {} K_{*+1}(\mathbf {Z})\otimes \mathbf {Q}\\ {}\cong & {} {\left\{ \begin{array}{ll}\mathbf {Q}&{}{}\text{ if } *\equiv 0\ (\mathrm {mod}\ 4)\\ 0&{}{}\text{ otherwise }\end{array}\right. }\quad \text{ for } 0<*<2n-4,\end{aligned}$$

and an epimorphism $\pi _*\mathrm {BC}(D^{2n})\otimes \mathbf {Q}\rightarrow K_{*+1}(\mathbf {Z})\otimes \mathbf {Q}$ in degree $2n-4$, which goes significantly beyond the range that was previously accessible by relying on Igusa’s stability result and shows for instance that $\mathrm {BC}(D^{8})$ is nontrivial, even rationally. Given that the K-groups $K_{*}(\mathbf {Z})$ are known to contain p-torsion for comparatively large primes with respect to the degree due to contributions from Bernoulli numbers, Theorem A also exhibits many new torsion elements in $\pi _*\mathrm {BC}(D^{2n})$, such as one of order 691 in $\pi _{21}\mathrm {BC}(D^{2n})$ as long as $n>12$ resulting from the fact that $K_{22}(\mathbf {Z})$ is cyclic of that order.

In the remainder of this introduction, we explain more direct applications of Theorem A and conclude by indicating some ideas that go into its proof.

Diffeomorphisms and concordances of odd discs

Restricting a concordance to the moving part of its boundary induces a homotopy fibre sequence

$$\begin{aligned}\mathrm {Diff}_\partial (D^{d+1})\longrightarrow \mathrm {C}(D^{d})\longrightarrow \mathrm {Diff}_\partial (D^{d})\end{aligned}$$

that compares the group of concordances $\mathrm {C}(D^{d})$ of a d-disc to its group of its diffeomorphisms $\mathrm {Diff}_\partial (D^d)$ fixing the boundary pointwise. By a result of Randal-Williams [37, Thm 4.1] based on Morlet’s lemma of disjunction and work of Berglund and Madsen [8] (a combination which incidentally inspired parts of our strategy to prove Theorem A), the space $\mathrm {BDiff}_\partial (D^{2n})$ is rationally $(2n-5)$-connected, so the delooped maps

$$\begin{aligned}\mathrm {BDiff}_\partial (D^{2n+1})\longrightarrow \mathrm {BC}(D^{2n})\quad \text {and}\quad \mathrm {BC}(D^{2n+1})\longrightarrow \mathrm {BDiff}_\partial (D^{2n+1})\end{aligned}$$

are rationally $(2n-5)$-connected as well, resulting in the following corollary of Theorem A.

FormalPara Corollary B

There exist isomorphisms

$$\begin{aligned}\pi _*\mathrm {BDiff}_\partial (D^{2n+1})\otimes \mathbf {Q}\cong \pi _*\mathrm {BC}(D^{2n+1})\otimes \mathbf {Q}\cong K_{*+1}(\mathbf {Z})\otimes \mathbf {Q}\end{aligned}$$

in degrees $*<2n-5$ and epimorphisms

$$\begin{aligned}&\pi _*\mathrm {BDiff}_\partial (D^{2n+1})\otimes \mathbf {Q}\rightarrow K_{*+1}(\mathbf {Z})\otimes \mathbf {Q}\quad \pi _*\mathrm {BC}(D^{2n+1})\otimes \mathbf {Q}\rightarrow K_{*+1}(\mathbf {Z})\otimes \mathbf {Q}\ \end{aligned}$$

in degree $2n-5$.

FormalPara Remark

• (i) The range in Corollary B is nearly optimal: by work of Watanabe [45] or as consequence of Weiss’ results on topological Pontryagin classes [46], the group $\pi _{2n-2}\mathrm {BDiff}_\partial (D^{2n+1})\otimes \mathbf {Q}$ is known to be nontrivial for many values of n for which $K_{2n-1}(\mathbf {Z})\otimes \mathbf {Q}$ vanishes by Borel’s work.

• (ii) A combination of the strengthening of Theorem A mentioned earlier with recent work of Kupers and Randal-Williams [27] improves the range of Corollary B by one degree from $2n-5$ to $2n-4$.

• (iii) In the range captured by Igusa’s stability result, i.e. up to approximately degree 2n/3, Corollary B was previously known as a result of a classical computation due to Farrell and Hsiang [16] based on Waldhausen’s approach to pseudoisotopy theory (of which the proof of Corollary B is independent).

Homeomorphisms of Euclidean spaces

By an enhancement of a result due to Morlet (see e.g. [5, Thm 4.4]), there are homotopy equivalences

$$\begin{aligned}\mathrm {BDiff}_\partial (D^d)&\simeq \Omega ^d_0\mathrm {Top}(d)/\mathrm {O}(d)\quad \text{ and }\\\mathrm {BC}(D^d)&\simeq \Omega ^d\mathrm {hofib}\Big (\mathrm {Top}(d)/\mathrm {O}(d)\rightarrow \mathrm {Top}(d+1)/\mathrm {O}(d+1)\Big )\end{aligned}$$

for $d\ge 5$ that relate the groups of diffeomorphisms and concordances of a d-disc to the homotopy fibre $\mathrm {Top}(d)/\mathrm {O}(d)$ of the map $\mathrm {BO}(d)\rightarrow \mathrm {BTop}(d)$ that classifies the inclusion of the orthogonal group $\mathrm {O}(d)$ into the topological group $\mathrm {Top}(d)$ of homeomorphisms of $\mathbf {R}^d$, and to its stabilisation map $\mathrm {Top}(d)/\mathrm {O}(d)\rightarrow \mathrm {Top}(d+1)/\mathrm {O}(d+1)$ induced by taking products with $\mathbf {R}$. Theorem A and Corollary B can thus be reformulated in terms of these equivalent spaces and result in particular in the following corollary, using the fact that $\pi _*\mathrm {Top}(d)/\mathrm {O}(d)$ is finite for $*<d+2$ and $d\ne 4$ [28, Essay V, 5.0].

FormalPara Corollary C

There exists an isomorphism

$$\begin{aligned}&\pi _*\mathrm {Top}(2n+1)/\mathrm {O}(2n+1)\otimes \mathbf {Q}\\&\quad \cong {\left\{ \begin{array}{ll}0&{}\text{ for } *\le 2n+1\\ K_{*+2n+2}(\mathbf {Z})\otimes \mathbf {Q}&{}\text{ for } 2n+1<*< 4n-4\end{array}\right. }\end{aligned}$$

and an epimorphism $\pi _*\mathrm {Top}(2n+1)/\mathrm {O}(2n+1)\otimes \mathbf {Q}\rightarrow K_{*+2n+2}(\mathbf {Z})\otimes \mathbf {Q}$ in degree $4n-4$.

FormalPara Remark

As per item (ii) of the previous remark, this range can be improved by one degree.

Idea of proof

Instead of sketching the proof of Theorem A, we outline a strategy to achieve a seemingly different task: relating the p-local homology of $\mathrm {BC}(D^{2n})$ to K-theory in a range of degrees. This should, however, convey the main ideas; the actual proof of Theorem A uses a similar strategy to construct a zig–zag between $\mathrm {BC}(D^{2n})$ and $\Omega ^{\infty +1}_0\mathrm {K}(\mathbf {Z})$ that consists of maps that are p-local homology isomorphisms in a range and then argues that the maps are actually p-locally highly connected. In the sketch that follows, we allow ourselves to be somewhat vague; full details shall be given in the body of this work.

The root of the proof of Theorem A is to consider the odd-dimensional disc $D^{2n+1}$ as the 0th member of a whole family of manifolds—the high-dimensional handlebodies

$$\begin{aligned}V_g:=\natural ^gD^{n+1}\times S^n\end{aligned}$$

given as iterated boundary connected sums of $D^{n+1}\times S^n$. Comparing the groups of diffeomorphisms $\mathrm {Diff}_{D^{2n}}(V_g)$ that pointwise fix a chosen disc $D^{2n}\subset \partial V_g$ in the boundary to the corresponding block diffeomorphism groups yields homotopy fibre sequences

$$\begin{aligned}\widetilde{\mathrm {Diff}}_{D^{2n}}(V_g)/\mathrm {Diff}_{D^{2n}}(V_g)\longrightarrow \mathrm {BDiff}_{D^{2n}}(V_g)\longrightarrow \mathrm {B\widetilde{Diff}}_{D^{2n}}(V_g),\end{aligned}$$

one for each g. Varying g, these fibre sequences are connected by stabilisation maps induced by extending (block) diffeomorphisms along the inclusion $V_g\subset V_{g+1}$ by the identity, and Morlet’s lemma of disjunction ensures that the map between homotopy fibres

$$\begin{aligned}\widetilde{\mathrm {Diff}}_{D^{2n}}(V_g)/\mathrm {Diff}_{D^{2n}}(V_g)\longrightarrow \widetilde{\mathrm {Diff}}_{D^{2n}}(V_{g+1})/\mathrm {Diff}_{D^{2n}}(V_{g+1})\end{aligned}$$

is highly connected. It is not hard to see that the space $\mathrm {BC}(D^{2n})$ of interest is equivalent to this fibre for $g=0$, so to access $\mathrm {BC}(D^{2n})$ in a range, we may as well study the homotopy fibre of the sequence obtained from the previous one by taking homotopy colimits,

$$\begin{aligned} \widetilde{\mathrm {Diff}}_{D^{2n}}(V_\infty )/\mathrm {Diff}_{D^{2n}}(V_\infty )\longrightarrow \mathrm {BDiff}_{D^{2n}}(V_\infty )\longrightarrow \mathrm {B\widetilde{Diff}}_{D^{2n}}(V_\infty ).\end{aligned}$$

(1)

By work of Botvinnik and Perlmutter [10], the homology of $\mathrm {BDiff}_{D^{2n}}(V_\infty )$ has a surprisingly simple description in homotopy theoretical terms, so to compute the homology of the fibre of (1) and hence that of $\mathrm {BC}(D^{2n})$ in a range, one might try to compute the homology of $\mathrm {B\widetilde{Diff}}_{D^{2n}}(V_\infty )$ and analyse the Serre spectral sequence of (1). This is essentially what we do, and it involves several steps of which some might be of independent interest:

• (i) In Sect. 2, we use surgery theory to express the space of block diffeomorphisms of a general manifold triad satisfying a $\pi$-$\pi$-condition p-locally for large primes in terms of its homotopy automorphisms covered by certain bundle data. A similar result in the rational setting which inspired ours but applies to another class of triads was obtained by Berglund and Madsen [8] (see also Remark 2.3).

• (ii) Sect. 3 serves to compute variants of the mapping class group $\pi _0\mathrm {Diff}_{D^{2n}}(V_g)$ up to extensions in terms of automorphisms groups of the integral homology of $V_g$.

• (iii) In Sect. 4, we calculate the p-local homotopy and homology groups of the delooped space of homotopy automorphisms $\mathrm {BhAut}_{D^{2n}}(V_g,W_{g,1})$ of $V_g$ that fix $D^{2n}$ and restrict to a homotopy automorphism of the complement of the boundary as a module over the group $\pi _0\mathrm {hAut}_{D^{2n}}(V_g,W_{g,1})$ in a range of degrees. This uses some pieces of the apparatus of rational homotopy theory, as well as an ad-hoc p-local generalisation we provide along the way.

• (iv) The action on the nth homology group $\mathrm {H}_n(V_g;\mathbf {Z})\cong \mathbf {Z}^g$ induces a map

  $$\begin{aligned}\mathrm {B\widetilde{Diff}}_{D^{2n}}(V_\infty )\longrightarrow \mathrm {BGL}_\infty (\mathbf {Z})^+\simeq \Omega ^{\infty }_0 \mathrm {K}(\mathbf {Z}),\end{aligned}$$

  a variant of which we show in Sect. 5 with the help of all previous steps to be a p-local homology isomorphism in a range of degrees.

Outlook

In [24], we will take a different approach and study concordance spaces $\mathrm {C}(M)$ without restriction on the p-torsion. As a byproduct, the setup of [24] will also make apparent that the zig–zag of Theorem A is compatible with the iterated stabilisation map $\mathrm {C}(D^{2n})\rightarrow \mathrm {C}(D^{2n}\times [0,1]^2)\simeq \mathrm {C}(D^{2n+2})$ and agrees up to equivalence with the zig–zag

$$\begin{aligned}&\mathrm {BC}(D^{2n})\rightarrow \Omega ^{\infty +1}_0\mathrm {Wh}^{\mathrm {Diff}}(*)=\Omega ^{\infty }_0\mathrm {fib}\big (\mathbf {S}\rightarrow K(\mathbf {S})\big )\\&\quad \rightarrow \Omega _0^{\infty }\mathrm {fib}\big (\mathbf {S}\rightarrow K(\mathbf {Z})\big )\leftarrow \Omega _0^{\infty +1}K(\mathbf {Z}) \end{aligned}$$

known from Waldhausen’s work [42] (see also Sect. 5.4).

1 Preliminaries

We start off with a lemma on semi-simplicial actions and a short recollection on nilpotent spaces for later reference, followed by foundational material on various types automorphisms of manifolds with bundle data. Primarily, this serves us to set up a convenient theory of block automorphism spaces with tangential structures.

1.1 Semi-simplicial monoids and their actions

The homotopy quotient of a semi-simplicial set $X_\bullet$ semi-simplicially acted upon by a semi-simplicial monoid $M_\bullet$ from the right is the semi-simplicial space $X_\bullet /\!/M_\bullet$whose space of p-simplices is defined as the bar-construction $\mathrm {B}(X_p,M_p,*)$, with face maps induced by the face maps of $M_\bullet$ and $X_\bullet$. For $X_\bullet =*_\bullet$ the semi-simplicial point, i.e. $*_p$ a singleton for all p, we abbreviate $X_\bullet /\!/M_\bullet$ by $\mathrm {B}M_\bullet$. The unique semi-simplicial map $X_\bullet \rightarrow *_\bullet$ induces a natural map $X_\bullet /\!/M_\bullet \rightarrow \mathrm {B}M_\bullet$ which is well-known to geometrically realise to a quasi-fibration with fibre the realisation of $X_\bullet$ if $M_\bullet$ is a group-like simplicial monoid acting simplicially on a simplicial set $X_\bullet$. To explain a generalisation of this fact for semi-simplicial $M_\bullet$ and $X_\bullet$, we denote the geometric realisation by $|-|$ and consider the natural zig–zag

$$\begin{aligned} |X_\bullet |\times |M_\bullet |\longleftarrow |X_\bullet \times M_\bullet |\longrightarrow |X_\bullet |\end{aligned}$$

whose left map is induced by the projections and the right map by the action. If the underlying semi-simplicial sets of $M_\bullet$ and $X_\bullet$ admit degeneracies, i.e. if they agree (as semi-simplicial sets) with the underlying semi-simplicial sets of simplicial sets, then the left arrow is an equivalence (see e.g. [15, Thm 7.2]), so a contractible choice of a homotopy inverse yields an action map $\mu :|X_\bullet |\times |M_\bullet |\rightarrow |X_\bullet |$. In this situation, we say that $M_\bullet$ acts on $X_\bullet$ by equivalences if $\mu (-,m):|X_\bullet |\rightarrow |X_\bullet |$ is an equivalence for all $m\in |M_\bullet |$. The following lemma shows that this is sufficient to conclude that the natural map $X_\bullet /\!/M_\bullet \rightarrow \mathrm {B}M_\bullet$ realises to a quasi-fibration.

Lemma 1.1

For a semi-simplicial monoid $M_\bullet$ acting on a semi-simplicial set $X_\bullet$ such that $M_\bullet$ and $X_\bullet$ admit degeneracies and the action of $M_\bullet$ on $X_\bullet$ is by equivalences, the sequence

$$\begin{aligned}X_\bullet \longrightarrow X_\bullet //M_\bullet \longrightarrow \mathrm {B}M_\bullet \end{aligned}$$

induces a quasi-fibration on geometric realisations.

Remark 1.2

• (i) In all situations we encounter, the condition that $M_\bullet$ and $X_\bullet$ admit degeneracies is ensured by them being Kan (every semi-simplicial Kan complex admits degeneracies [23]) and the condition that $M_\bullet$ acts on $X_\bullet$ by equivalences by $M_\bullet$ being group-like, i.e. the monoid $\pi _0|M_\bullet |$ having inverses. Note that Lemma 1.1 neither requires the degeneracies of $M_\bullet$ to be compatible with the monoid structure nor those of $X_\bullet$ with the action.

• (ii) The condition that $M_\bullet$ and $X_\bullet$ admit degeneracies is crucial, even if $M_\bullet =G_\bullet$ is a simplicial group. For an instructive example, consider the semi-simplicial set $X_\bullet =G_\bullet ^{\le 0}$ which agrees with $G_0$ in degree 0 and is empty otherwise, semi-simplicially acted upon by $G_\bullet$ via right translations. In this case, the realisation $|X_\bullet /\!/G_\bullet |$ is contractible, but $|G_\bullet ^{\le 0}|\simeq G_0$ is rarely equivalent to $\Omega |\mathrm {B}G_\bullet |\simeq |G_\bullet |$.

• (iii) Under the assumption of Lemma 1.1, the long exact sequence induced by the quasi-fibration yields a bijection $\pi _0|X_\bullet |/ \pi _0|M_\bullet |\cong \pi _0|X_\bullet /\!/M_\bullet |$

Proof of Lemma 1.1

The sequence in question is the geometric realisation of a sequence

(2)

of simplicial semi-simplicial sets, where the simplicial (bar-)direction is indicated by the square and the semi-simplicial direction by the bullet $\bullet$; the fibre $X_\bullet$ is constant in the -direction. Since the realisation of a simplicial set is canonically equivalent to the realisation of its underlying semi-simplicial set [15, Lem. 1.7] and the realisation of a bi-semi-simplicial sets is independent of which direction one realises first [15, p. 2106], we may rely on a result of Segal [15, Thm 2.12] and the second part of its simplification from [15, Lem. 2.11] to reduce the claim to showing that the commutative squares

obtained from the simplicial structure of by realising the $\bullet$-direction are homotopy cartesian for $p\ge 0$. For the left square, this follows directly from the definition of the bar-construction together with the above mentioned fact that the realisation of the product of two semi-simplicial sets that admit degeneracies is canonically equivalent to the product of their realisations. Spelling out the definition of the bar-construction, the right hand square is given as

involving the action $\mu _\bullet$ and the projection $(\mathrm {pr}_2)_\bullet$ on the second coordinate, so we are left to show that the shear map $(|\mu _\bullet |, |(\mathrm {pr}_2)_\bullet |):|X_\bullet \times M_\bullet |\rightarrow |X_\bullet |\times |M_\bullet |$ is an equivalence. This map fits into a commutative triangle

whose map on diagonal homotopy fibres at $m\in |M_\bullet |$ agrees up to equivalence with the action map $\mu (-,m):|X_\bullet |\rightarrow |X_\bullet |$. The latter is an equivalence by assumption, so the shear map is an equivalence and the claim follows. $\square$

1.2 Nilpotent spaces

A space is nilpotent if it is path connected and its fundamental group is nilpotent and acts nilpotently on all higher homotopy groups. Such spaces have an unambiguous p-localisation at a prime p, which on homology and homotopy groups (including the fundamental group) has the expected effect of p-localisation in the algebraic sense [31, Thm 6.1.2]. Localisations are defined in terms of a universal property [31, Def. 5.2.3], which ensures that they are unique and functorial up to homotopy. A map between nilpotent spaces is p-locally k-connected for a prime p and $k\ge 1$ if the induced map on p-localisations is k-connected in the usual sense.

Lemma 1.3

For a map $X\rightarrow Y$ between nilpotent spaces, a prime $p\ge 2$, and $k\ge 1$, the following statements are equivalent:

• (i) The map $X\rightarrow Y$ is p-locally k-connected.

• (ii) The induced map on p-localised homotopy groups $(\pi _*X)_{(p)}\rightarrow (\pi _*Y)_{(p)}$ is an isomorphism for $*<k$ and surjective for $*=k$.

• (iii) The induced map on p-local homology groups $\mathrm {H}_*(X;\mathbf {Z}_{(p)})\rightarrow \mathrm {H}_* (Y;\mathbf {Z}_{(p)})$ is an isomorphism for $*< k$ and surjective for $*=k$.

Proof

The above mentioned fact that p-localisation of nilpotent spaces commutes with taking homotopy groups shows that the first two items are equivalent. The equivalence between the second two follows for $k=1$ from the well-known fact that a morphism $G\rightarrow H$ between nilpotent groups is surjective if and only if it is surjective on abelianisations which one sees as follows: writing $\Gamma ^1(G)=G$ and $\Gamma ^n(G)=[\Gamma ^{n-1}(G),G]$ for the lower central series, there is a natural epimorphism $\otimes ^n_{\mathbf {Z}}G^{\mathrm {ab}}\rightarrow \Gamma ^{n}(G)/\Gamma ^{n+1}(G)$ induced by taking left-normed commutators (see e.g. [44, Thm 3.1]), so one may prove the claim by an induction on the nilpotence degree. For $k\ge 2$, the equivalence between the second two items is a consequence of the relative Hurewicz theorem for nilpotent spaces (see e.g. [19, Cor. 3.4]) applied to the p-localisation of the map in question. $\square$

At several points in this work, we will make use of the fact that nilpotent spaces behave well with respect to taking homotopy fibres (see e.g. [31, Prop. 4.4.1] for a proof).

Lemma 1.4

Let $\pi :E\rightarrow B$ be a fibration, $e\in E$ a point, and $E_e\subset E$ and $F_e\subset \pi ^{-1}(\pi (e))$ the respective path components containing e. If $E_e$ is nilpotent, then $F_e$ is nilpotent as well.

1.3 Block spaces

As is customary, we denote the standard p-simplex by $\Delta ^p\subset \mathbf {R}^{p+1}$ and identify its faces $\sigma :\Delta ^q\rightarrow \Delta ^p$ with their images. A p-block space is a space X together with a map $\pi :X\rightarrow \Delta ^p$. For a q-face $\sigma \subset \Delta ^p$, the preimage $X_\sigma :=\pi ^{-1}(\sigma )$ becomes a q-block space by pulling back $\pi$ along $\sigma$. A block map between block p-spaces is a map $f:X\rightarrow Y$ between underlying spaces such that $f(X_\sigma )\subset Y_{\sigma }$ for all faces $\sigma \subset \Delta ^p$ and a block homotopy equivalence is a block map $f:X\rightarrow Y$ such that the induced map $f_\sigma :X_\sigma \rightarrow Y_\sigma$ is a homotopy equivalence for all faces $\sigma \subset \Delta ^p$. Spaces of the form $\Delta ^p\times M$ are implicitly considered as p-block spaces via the projection. For $i=0,\ldots ,p$, the map

$$\begin{aligned}c_{i}:\begin{array}{rcl} [0,1]\times \Delta ^{p-1} &{} \longrightarrow &{} \Delta ^p \\ [0.3em] (s,t_0,\ldots ,t_{p-1}) &{} \longmapsto &{} ((1-s)t_0,\ldots ,(1-s)t_{i-1},s,(1-s)t_{i},\ldots ,(1-s)t_{p-1} ) \end{array}\end{aligned}$$

induces for $0<\epsilon \le 1$ a diffeomorphism of manifolds with corners

$$\begin{aligned}c_{i,\epsilon }:[0,\varepsilon )\times \Delta ^{p-1}\longrightarrow c_i([0,\epsilon )\times \Delta ^{p-1})=:\Delta ^p_{i,\epsilon }\end{aligned}$$

onto an open neighborhood $\Delta ^p_{i,\epsilon }$ of the ith codimension 1 face $\Delta ^p_i\subset \Delta ^p$. A block map $f:\Delta ^p\times M\rightarrow \Delta ^p\times N$ for spaces M and N is collared if there exists an $\varepsilon >0$ such that

• (i) $f(\Delta ^p_{i,\epsilon }\times M)\subset \Delta ^p_{i,\varepsilon }\times N$ and

• (ii) $(c_{i,\epsilon }^{-1}\times \mathrm {id}_N)\circ f|_{\Delta ^p_{i,\epsilon }\times M}\circ (c_{i,\epsilon }\times \mathrm {id}_M)=f_{\Delta _i^p}\times \mathrm {id}_{[0,\epsilon )}$

are satisfied for $i=0,\ldots ,p$.

1.4 Diffeomorphisms

For a compact smooth d-manifold W and two compact submanifolds $M,N\subset W$, we denote by $\widetilde{\mathrm {Diff}}_M(W,N)_\bullet$ the semi-simplicial group of block diffeomorphisms whose p-simplices consists of all diffeomorphisms of $\Delta ^p\times W$ that are collared block maps, fix $\Delta ^p\times N$ setwise, and fix a neighborhood of $\Delta ^p\times M$ pointwise. The semi-simplicial structure is induced by restricting diffeomorphisms of $\Delta ^p\times M$ to $\sigma \times M$ for faces $\sigma \subset \Delta ^p$. Whenever one of the submanifolds is empty, we omit it from the notation and in the case $M=\partial W$, we write $\widetilde{\mathrm {Diff}}_\partial (W,N)$ instead of $\widetilde{\mathrm {Diff}}_M(W,N)$. Making use of the collaring condition, one shows that $\widetilde{\mathrm {Diff}}_M(W,N)_\bullet$ satisfies the Kan property (see [18, p. 58-59] for a proof in the case $M=N=\varnothing$; the general case follows in the same way²). The semi-simplicial subgroup of diffeomorphisms

$$\begin{aligned}\mathrm {Diff}_M(W,N)_\bullet \subset \widetilde{\mathrm {Diff}}_M(W,N)_\bullet \end{aligned}$$

is defined by requiring the diffeomorphisms of $\Delta ^p\times M$ to commute with the projection to the simplex $\Delta ^p$ instead of just preserving its faces. This semi-simplicial subgroup agrees with the (collared and smooth) singular set of the topological group $\mathrm {Diff}_M(W,N)$ of diffeomorphisms by which we mean the set of 0-simplices $\mathrm {Diff}_M(W,N)_0$ equipped with the smooth Whitney topology, so there is a canonical weak equivalence $|\mathrm {Diff}_M(W,N)_\bullet |\rightarrow \mathrm {Diff}_M(W,N)$ and we shall not distinguish between these spaces.

1.5 Homotopy automorphisms

The p-simplices of the semi-simplicial monoid of block homotopy automorphisms $\mathrm {\widetilde{hAut}}_M(W,N)_\bullet$ are the block homotopy automorphisms of $\Delta ^p\times W$ that fix $\Delta ^p\times M$ pointwise and restrict to homotopy automorphisms of $\Delta ^p\times N$. Unlike for $\widetilde{\mathrm {Diff}}_M(W,N)_\bullet$, it is straight-forward to see that $\mathrm {\widetilde{hAut}}_M(W,N)_\bullet$ is Kan: a map from the semi-simplicial horn $(\Lambda _i^p)_\bullet$ is represented by a homotopy equivalence $\psi :\Lambda _i^p\times W\rightarrow \Lambda _j^p\times W$ and a lift to a p-simplex $\Delta ^p\times W\rightarrow \Delta ^p\times W$ is given by $(\varphi _i\times \mathrm {id}_W)\circ (\mathrm {id}_{[0,1]}\times \psi )\circ (\varphi _i^{-1}\times \mathrm {id}_W)$, where $\varphi _i:[0,1]\times \Lambda _i^p\rightarrow \Delta ^p$ is any homeomorphism that extends the inclusion on $\{0\}\times \Lambda _i^p\subset \Delta ^p$ and restricts to a homeomorphism from $[0,1]\times \partial \Lambda _i^p\cup \{1\}\times \Lambda _i^p$ onto the ith face $\Delta ^p_i\subset \Delta ^p$. As for diffeomorphisms, insisting that the homotopy equivalences of $\Delta ^p\times M$ be over $\Delta ^p$ defines a sub semi-simplicial monoid of homotopy automorphisms

$$\begin{aligned} \mathrm {hAut}_M(W,N)_\bullet \subset \mathrm {\widetilde{hAut}}_M(W,N)_\bullet , \end{aligned}$$

(3)

which agrees with the singular set of the space $\mathrm {hAut}_M(W,N)$ obtained by equipping the set of homotopy equivalences $\mathrm {hAut}_M(W,N)_0$ with the compact open topology, so also $|\mathrm {hAut}_M(W,N)_\bullet |$ and $\mathrm {hAut}_M(W,N)$ are canonically equivalent. An aspect which distinguishes the situation for homotopy automorphisms from that for diffeomorphisms is that the inclusion (3) of Kan complexes induces an equivalence on geometric realisation, which one can see from the combinatorial description of their homotopy groups together with the contractibility of $\mathrm {hAut}_{\partial \Delta ^p}(\Delta ^p)$.

1.6 Bundle maps, unstably

A bundle map between two vector bundles $\xi \rightarrow X$ and $\nu \rightarrow Y$ over CW complexes X and Y is a commutative square of the form

whose induced maps on vertical fibres are linear isomorphisms. Of course the underlying map of spaces $\bar{\phi }$ can be recovered from $\phi$, so we often omit it. Given a subcomplex $A\subset X$ and a bundle map $\ell _0:\xi |_{A}\rightarrow \nu$ defined on the restriction of $\xi$ to A, the semi-simplicial set of block bundle maps $\mathrm {\widetilde{Bun}}_A(\xi ,\nu ;\ell _0)_\bullet$ has as its p-simplices the bundle maps $\Delta ^p\times \xi \rightarrow \Delta ^p\times \nu$ that agree with $\mathrm {id}_{\Delta ^p}\times \ell _0$ on $\Delta ^p\times \xi |_{A}$ and whose underlying map $\Delta ^p\times X\rightarrow \Delta ^p\times Y$ is a block map. As before, the semi-simplicial structure is induced by restriction to subspaces $\sigma \times X$ for faces $\sigma \subset \Delta ^p$. Insisting that the underlying map between base spaces be over $\Delta ^p$ defines the sub semi-simplicial set

$$\begin{aligned}\mathrm {Bun}_A(\xi ,\nu ;\ell _0)_\bullet \subset \mathrm {\widetilde{Bun}}_A(\xi ,\nu ;\ell _0)_\bullet \end{aligned}$$

of bundle maps, which agrees with the singular set of the space $\mathrm {Bun}_A(\xi ,\nu ;\ell _0)$ obtained by equipping the set $\mathrm {Bun}_A(\xi ,\nu ;\ell _0)_0$ of bundle maps $\xi \rightarrow \nu$ relative to $\ell _0$ with the compact-open topology. If $\xi =\nu$ and $\ell _0=\mathrm {inc}$ then the semi-simplicial sets of (block) bundle maps $\mathrm {\widetilde{Bun}}_A(\xi ,\xi ;\mathrm {inc})_\bullet$ and $\mathrm {Bun}_A(\xi ,\xi ;\mathrm {inc})_\bullet$ are semi-simplicial monoids under composition, and they act by precomposition on $\mathrm {\widetilde{Bun}}_A(\xi ,\nu ;\ell _0)_\bullet$ respectively $\mathrm {Bun}_A(\xi ,\nu ;\ell _0)_\bullet$ for any bundle $\nu$ and bundle map $\ell _0:\xi |_{A}\rightarrow \nu$. For a subcomplex $C\subset X$, we denote by

$$\begin{aligned}\mathrm {\widetilde{hAut}}_A(\xi ,C)_\bullet \subset \mathrm {\widetilde{Bun}}_A(\xi ,\xi ;\mathrm {inc})_\bullet \end{aligned}$$

the submonoid of block bundle maps whose underlying selfmap of $\Delta ^p\times X$ is a homotopy equivalence that restricts to an equivalence of $\Delta ^p\times C$. The submonoid

$$\begin{aligned}\mathrm {hAut}_A(\xi ,C)_\bullet \subset \mathrm {Bun}_A(\xi ;\xi ,\mathrm {inc})_\bullet \end{aligned}$$

is defined analogously.

1.6.1 Tangential bundle maps

Introducing yet another variant of bundle maps, we define the semi-simplicial set of tangential block bundle maps $\mathrm {\widetilde{Bun}}_A(\xi ,\nu ;\ell _0)^\tau _\bullet$ as follows: writing $\tau _{M}$ for the tangent bundle of a manifold M and $\varepsilon$ for the trivial line bundle, the p-simplices of $\mathrm {\widetilde{Bun}}_A(\xi ,\nu ;\ell _0)^\tau _\bullet$ are the bundle maps $\varphi :\tau _{\Delta ^p}\times \xi \rightarrow \tau _{\Delta ^p}\times \nu$ that agree with $\mathrm {id}_{\tau _{\Delta ^p}}\times \ell _0$ on $\tau _{\Delta ^p}\times \xi |_A$, satisfy $\varphi (\tau _{\Delta _i^p}\times \xi )\subset \tau _{\Delta _i^p}\times \nu$ for $0\le i\le p$, and make the diagram

(4)

commute, where the bottom horizontal map is given by the restriction of $\varphi$ on $\tau _{\Delta ^p_i}\times \xi$ and the identity on $\varepsilon$, and the vertical maps are induced by the canonical trivialisation of $\tau _{[0,1]}$ and the derivative of the map $c_i$ defined in Sect. 1.3. Requiring the underlying map $\Delta ^p\times X\rightarrow \Delta ^p\times Y$ to be over $\Delta ^p$ defines the sub semi-simplicial set

$$\begin{aligned} \mathrm {Bun}_A(\xi ,\nu ;\ell _0)^\tau _\bullet \subset \mathrm {\widetilde{Bun}}_A(\xi ,\nu ;\ell _0)^\tau _\bullet \end{aligned}$$

(5)

of tangential bundle maps. As before, we have a chain of semi-simplicial monoids

$$\begin{aligned}\mathrm {hAut}_A(\xi ,C)^\tau _\bullet \subset \mathrm {\widetilde{hAut}}_A(\xi ,C)^\tau _\bullet \subset \mathrm {\widetilde{Bun}}_A(\xi ,\xi ;\mathrm {inc})^\tau _\bullet \end{aligned}$$

which are defined in the same way as for non-tangential (block) bundle maps. Note that there is a canonical map

$$\begin{aligned} \mathrm {Bun}_A(\xi ,\nu ;\ell _0)_\bullet \longrightarrow \mathrm {Bun}_A(\xi ,\nu ;\ell _0)_\bullet ^\tau \end{aligned}$$

(6)

given by extending a bundle map $\Delta ^p\times \xi \rightarrow \Delta ^p\times \nu$ over $\Delta ^p$ to $\tau _{\Delta ^p}\times \xi \rightarrow \tau _{\Delta ^p}\times \nu$ by the identity. This map is not an equivalence, but we shall see in the next paragraph that it becomes one after stabilisation.

Remark 1.5

Note that the map (6) does not extend to a map $\mathrm {\widetilde{Bun}}_A(\xi ,\nu ;\ell _0)_\bullet \rightarrow \mathrm {\widetilde{Bun}}_A(\xi ,\nu ;\ell _0)_\bullet ^\tau$ in an obvious way. This is because, for a bundle map $\phi :\Delta ^p\times \xi \rightarrow \Delta ^p\times \nu$ covering a block map, the map $\tau _{\Delta ^p}\times \xi \rightarrow \tau _{\Delta ^p}\times \nu$ that maps (x, y) to $(x,\phi (\overline{x},y))$ is not a bundle map unless $\phi$ commutes with the projection on $\Delta ^p$. Here $\overline{x}\in \Delta ^p$ is the underlying point of $x\in \tau _{\Delta ^p}$.

1.7 Bundle maps, stably

A stable vector bundle is a sequence of vector bundles $\psi =\{\psi _k\rightarrow B_k\}_{k\ge l}$ for some $l\ge 0$, where $\psi _k$ is k-dimensional, together with structure maps $\psi _k\oplus \varepsilon \rightarrow \psi _{k+1}$ for $k\ge l$, covering maps of the form $B_{k}\rightarrow B_{k+1}$. Given a d-dimensional vector bundle $\xi$, its stabilisation is the stable vector bundle $\xi ^s$ with $\xi ^s_{d+k}=\xi \oplus \epsilon ^k$ and the identity as structure maps. For a d-dimensional vector bundle $\xi \rightarrow X$, a stable vector bundle $\psi$, and a bundle map $\ell _0:\xi |_{A}\oplus \varepsilon ^k\rightarrow \psi _{d+k}$ for some k, the semi-simplicial set of stable bundle maps is the colimit

$$\begin{aligned}\mathrm {Bun}_A(\xi ^s,\psi ;\ell _0)_\bullet :=\mathrm {colim}_{m\ge k}\mathrm {Bun}_A(\xi \oplus \varepsilon ^m,\psi _{d+m};\ell _0)_\bullet \end{aligned}$$

over the stabilisation maps

$$\begin{aligned}\mathrm {Bun}_A(\xi \oplus \varepsilon ^m,\psi _{d+m};\ell _0)_\bullet \longrightarrow \mathrm {Bun}_A(\xi \oplus \varepsilon ^{m+1},\psi _{d+m+1};\ell _0)_\bullet \end{aligned}$$

given by adding a trivial line bundle followed by postcomposition with the structure map $\psi _{d+m}\oplus \varepsilon \rightarrow \psi _{d+m+1}$. Analogously, we define stable tangential bundle maps as the colimit

$$\begin{aligned}\mathrm {Bun}_A(\xi ^s,\psi ;\ell _0)^\tau _\bullet :=\mathrm {colim}_{m\ge k}\mathrm {Bun}_A(\xi \oplus \varepsilon ^m,\psi _{d+m};\ell _0)^\tau _\bullet .\end{aligned}$$

As in Section 1.6, there are semi-simplicial sub-monoids

$$\begin{aligned}&\mathrm {hAut}_A(\xi ^s;C)_\bullet \subset \mathrm {Bun}_A(\xi ^s,\xi ^s;\mathrm {inc})_\bullet \quad \text {and}\\&\mathrm {hAut}_A(\xi ^s;C)_\bullet ^\tau \subset \mathrm {Bun}_A(\xi ^s,\xi ^s;\mathrm {inc})^\tau _\bullet ,\end{aligned}$$

and also block variants of these semi-simplicial sets, defined by adding appropriate tildes. As the extension map (6) is compatible with the stabilisation maps, it gives rise to maps

(7)

which we show in Lemma A.4 to be equivalences if X is a finite CW complex.

1.8 Tangential structures

A d-dimensional tangential structure is a fibration $\theta :B_d\rightarrow \mathrm {BO}(d)$ whose target is the base of the universal d-dimensional vector bundle $\gamma _d\rightarrow \mathrm {BO}(d)$. The semi-simplicial set of $\theta$-structures on a d-dimensional vector bundle $\xi$ over a CW complex X is the semi-simplicial set of bundle maps $\mathrm {Bun}_A(\xi ,\theta ^*\gamma _d;\ell _0)$ from $\xi$ to the pullback $\theta ^*\gamma _d$ of the universal bundle along $\theta$, relative to a fixed bundle map $\ell _0:\xi |_A\rightarrow \theta _d^*\gamma _d$. We denote the homotopy quotient (in the sense of Sect. 1.1) of the action of $\mathrm {hAut}_A(\xi ,C)_\bullet \subset \mathrm {Bun}_A(\xi ;\xi ,\mathrm {inc})_\bullet$ on the semi-simplicial set of $\theta$-structures by

$$\begin{aligned}\mathrm {BhAut}^{\theta }_A(\xi ,C;\ell _0)_\bullet :=\mathrm {Bun}_A(\xi ,\theta ^*\gamma _d;\ell _0)_\bullet //\mathrm {hAut}_A(\xi ,C)_\bullet .\end{aligned}$$

Remark 1.6

Note that $\mathrm {BhAut}^{\theta }_A(\xi ,C;\ell _0)_\bullet$ is in many cases empty or disconnected, so despite the suggestive notation, it is in general not the classifying space of any kind of group or monoid, (semi-)simplicial or topological.

1.8.1 Stable tangential structures

A stable tangential structure is a fibration of the form $\Xi :B\rightarrow \mathrm {BO}$, which induces a d-dimensional tangential structure $\Xi _d:B_d\rightarrow \mathrm {BO}(d)$ for any $d\ge 0$ by pulling back $\Xi$ along the stabilisation map $\mathrm {BO}(d)\rightarrow \mathrm {BO}$. Note, however, that not all d-dimensional tangential structures arise this way, for instance the tangential structure $\mathrm {EO}(d)\rightarrow \mathrm {BO}(d)$ encoding unstable framings does not. A stable tangential structure defines a stable vector bundle $\Xi ^*\gamma =\{\Xi _{d}^*\gamma _d\}_{d\ge 0}$ whose structure maps are induced by the canonical bundle map $\gamma _d\oplus \varepsilon \rightarrow \gamma _{d+1}$ covering the usual stabilisation map $\mathrm {BO}(d)\rightarrow \mathrm {BO}(d+1)$. Given a stable bundle map $\ell _0:\xi ^s|_{A}\rightarrow \Xi ^*\gamma$, we call $\mathrm {Bun}_A(\xi ^s,\Xi ^*\gamma ;\ell _0)$ the semi-simplicial set of stable $\theta$-structures on $\xi$. As in the unstable case, we abbreviate

$$\begin{aligned} \mathrm {BhAut}^{\Xi }_A(\xi ^s,C;\ell _0)_\bullet :=\mathrm {Bun}_A(\xi ^s,\Xi ^*\gamma ;\ell _0)_\bullet //\mathrm {hAut}_A(\xi ^s,C)_\bullet .\end{aligned}$$

(8)

Tangential and or block variants of the previous definitions are defined by using the respective variants of bundle maps and adding appropriate tildes and or $\tau$-superscripts.

1.8.2 Forgetting tangential structures

It follows from Lemma 1.1 that the sequence of semi-simplicial spaces

$$\begin{aligned} \mathrm {Bun}_A(\xi ,\theta ^*\gamma _d;\ell _0)_\bullet \longrightarrow \mathrm {BhAut}^{\theta }_A(\xi ,C;\ell _0)_\bullet \longrightarrow \mathrm {BhAut}_A(\xi ,C)_\bullet \end{aligned}$$

(9)

realises to a quasi-fibration, because $\mathrm {Bun}_A(\xi ,\theta ^*\gamma _d;\ell _0)_\bullet$ and $\mathrm {hAut}_A(\xi ,C)_\bullet$ admit degeneracies since they satisfy the Kan property (they agree with the singular complex of a space, see Sect. 1.6) and the action is by equivalences as $\mathrm {hAut}_A(\xi ,C)_\bullet$ is group-like. The same argument applies to the stable analogue of this sequence involving (8) and, using Corollary A.2 (assuming that X is a finite complex), also to its variants involving tangential and or block bundle maps. By definition of the universal bundle, the semi-simplicial set $\mathrm {Bun}_A(\xi ,\theta ^*\gamma _d;\ell _0)_\bullet$ is contractible in the case $\theta =\mathrm {id}$, so the second map in (9) is an equivalence for this particular choice of $\theta$. The analogous statement holds in the stable case as well and, as a result of Lemmas A.3 and A.4, also for the tangential and or block variants.

1.9 The derivative maps

Taking fibrewise derivatives of diffeomorphisms $\varphi :\Delta ^p\times W\rightarrow \Delta ^p\times W$ over $\Delta ^p$ induces a canonical semi-simplicial map

$$\begin{aligned} \mathrm {Diff}_M(W,N)_\bullet \longrightarrow \mathrm {hAut}_M(\tau _W,N)_\bullet ,\end{aligned}$$

(10)

which we call the derivative map. Furthermore, the notion of a tangential bundle map is designed exactly so that there is a block derivative map

$$\begin{aligned} \widetilde{\mathrm {Diff}}_M(W,N)_\bullet \longrightarrow \mathrm {\widetilde{hAut}}_M(\tau ^s_W,N)^\tau _\bullet .\end{aligned}$$

(11)

given by assigning a block diffeomorphism $\Delta ^p\times W\rightarrow \Delta ^p\times W$ its derivative $\tau _{\Delta ^p}\times \tau _W\rightarrow \tau _{\Delta ^p}\times \tau _W,$ which indeed makes the square (4) commute as $\varphi$ is assumed to be collared in the sense of Section 1.3.

Remark 1.7

• (i) A different model of the block derivative map (11) was considered by Berglund and Madsen in their prominent study of the rational homotopy type of spaces of block diffeomorphisms of manifolds with certain boundary conditions [8] (see Section 4.3 loc. cit. and Remark 2.3 below).

• (ii) Lemmas A.3 and A.4 provide an equivalence

  $$\begin{aligned}\mathrm {\widetilde{hAut}}_M(\tau ^s_W,N)^\tau _\bullet \simeq \mathrm {hAut}_M(\tau ^s_W,N)_\bullet ,\end{aligned}$$

  so the delooped space $\mathrm {B\widetilde{hAut}}_M(\tau ^s_W,N)^\tau _\bullet$ classifies fibrations $\pi _W: E\rightarrow B$ with fibre W together with the following data:

  • (1) maps of fibrations $\pi _M\rightarrow \pi _W\leftarrow \pi _N$ over the identity whose induced maps on fibres is equivalent to the system of inclusions $M\subset W\supset N$,

  • (2) a trivialisation of $\pi _M$, and

  • (3) a stable vector bundle $E\rightarrow \mathrm {BO}$ over the total space of $\pi _W$ whose restriction to each fibre agrees with the stable tangent bundle of W.

  From this point of view, the block derivative (11) comes as no surprise: it is reminiscent of the fact that a block bundle has an underlying fibration and a stable vertical tangent bundle by [14]. However, somewhat curiously, the block derivative map (11) obviously factors over the variant $\mathrm {\widetilde{hAut}}_M(\tau _W,N)^\tau _\bullet$ involving the unstable tangent bundle of W, giving rise to an unstable block derivative map

  $$\begin{aligned}\mathrm {B\widetilde{Diff}}_M(W,N)_\bullet \longrightarrow \mathrm {B\widetilde{hAut}}_M(\tau _W,N)^\tau _\bullet .\end{aligned}$$

  The target of this map is neither equivalent to $\mathrm {BhAut}_M(\tau ^s_W,N)_\bullet$ nor $\mathrm {BhAut}_M(\tau _W,N)_\bullet$, and it would be interesting to have a good description of what it classifies.

We denote the submonoids of the components hit by the derivative maps by

$$\begin{aligned} \begin{aligned} \mathrm {hAut}^{\cong }_{M}(\tau _W,N)_\bullet&\subset \mathrm {hAut}_M(\tau _W,N)_\bullet \quad \text {and}\\ \mathrm {\widetilde{hAut}}^{\cong }_M(\tau ^s_W,N)^\tau _\bullet&\subset \mathrm {\widetilde{hAut}}_M(\tau ^s_W,N)^\tau _\bullet \end{aligned}\end{aligned}$$

(12)

and add the same $\cong$-superscript to (8) and its tangential block variant to indicate when we take homotopy quotients by the submonoids (12) instead of the full monoids. Defining

$$\begin{aligned} \mathrm {B\widetilde{Diff}}_M^{\Xi }(W,N;\ell _0)_\bullet :=\mathrm {\widetilde{Bun}}_M(\tau ^s_W,{\Xi }^*\gamma ;\ell _0)^\tau _\bullet //\widetilde{\mathrm {Diff}}_M(W,N)_\bullet \end{aligned}$$

(13)

for a stable tangential structure $\Xi$ and a $\Xi$-structure $\ell _0$ on $\tau ^s_W|_M$ and

$$\begin{aligned}\mathrm {BDiff}_M^{\theta }(W,N;\ell _0)_\bullet :=\mathrm {Bun}_M(\tau _W,\theta ^*\gamma _d;\ell _0)_\bullet //\mathrm {Diff}_M(W,N)_\bullet \end{aligned}$$

in the unstable case, the two derivative maps fit into a commutative square

(14)

whose vertical maps are induced by the composition

$$\begin{aligned} \mathrm {Bun}_M(\tau _W,\Xi _d^*\gamma _d;\ell _0)_\bullet\rightarrow & {} \mathrm {Bun}_M(\tau ^s_W,\Xi ^*\gamma ;\ell _0)_\bullet \\\rightarrow & {} \mathrm {Bun}_M(\tau ^s_W,\Xi ^*\gamma ;\ell _0)^\tau _\bullet \subset \mathrm {\widetilde{Bun}}_M(\tau ^s_W,{\Xi }^*\gamma ;\ell _0)^\tau _\bullet . \end{aligned}$$

All maps in this composition are equivalences, the first one by an exercise in obstruction theory and the second map as well as the final inclusion as a result of Lemmas A.3 and A.4. The composition of equivalences just discussed also induces the vertical maps in the commutative diagram

(15)

whose horizontal maps are induced by forgetting tangential structures.

Lemma 1.8

The geometric realisation of (15) is homotopy cartesian.

Proof

By construction the induced map on horizontal strict fibres agrees with the composition of equivalences discussed above (15), so it suffices to show that the horizontal maps of the square realise to quasi-fibrations. As $\mathrm {Diff}_M(W,N)_\bullet$ and $\widetilde{\mathrm {Diff}}_M(W,N)_\bullet$ are Kan and group-like (see Section 1.4), this follows from Lemma 1.1 and Corollary A.2. $\square$

2 Surgery theory and spaces of block diffeomorphisms

We use surgery theory to give a partial p-local description of the space $\mathrm {B\widetilde{Diff}}^\Xi _{\partial _0W}(W,\partial _1W)$ of block diffeomorphisms with tangential structures in terms of spaces of homotopy automorphisms with bundle data for manifold triads $(W;\partial _0W,\partial _1W)$ of dimension $d\ge 6$ satisfying a $\pi$-$\pi$-condition.

Notation

As a point of notation, we refer to the geometric realisation of any of the semi-simplicial sets or spaces of the previous sections by omitting their $\bullet$-subscripts.

2.1 A reminder of surgery theory

A d-dimensional manifold triad is a triple $W=(W;\partial _0W,\partial _1W)$ consisting of a compact smooth d-manifold W (possibly with corners) and (possibly empty) submanifolds $\partial _0W\subset W$ and $\partial _1W\subset W$ such that

$$\begin{aligned}\partial W=\partial _0 W\cup \partial _1 W\quad \text {and}\quad \partial (\partial _0W)=\partial _0W\cap \partial _1W=\partial (\partial _1W).\end{aligned}$$

A diffeomorphism or (simple) homotopy equivalence $(W;\partial _0W,\partial _1W)\rightarrow (W';\partial _0W',\partial _1W')$ between two manifold triads is a diffeomorphism or (simple) homotopy equivalence $W\rightarrow W'$ which restricts to a map of this kind between $\partial _0W$ and $\partial _0W'$, between $\partial _1W$ and $\partial _1W'$, and between their intersections. At times, we omit $\partial _0W$ and $\partial _1W$ from the notation and abbreviate a triad $(W;\partial _0W,\partial _1W)$ simply by W. The smooth structure set $\mathcal {S}(W)$ of a triad W (see e.g. [43, Ch. 10]) is the collection of equivalence classes of simple homotopy equivalences of triads $N\rightarrow W$ that restrict to a diffeomorphism $\partial _0N\rightarrow \partial _0W$, where two such equivalences $N\rightarrow W$ and $N'\rightarrow W$ are equivalent if there exists a diffeomorphism of triads $N\rightarrow N'$ that makes the triangle of triads

homotopy commute relative to $\partial _0N$. The structure set $\mathcal {S}(W)$ is canonically based; the identity serves as basepoint. The main tool to access $\mathcal {S}(W)$ is the surgery exact sequence

(16)

which relates the structure sets $\mathcal {S}(W\times D^k)$ of the triads

$$\begin{aligned}W\times D^k=(W\times D^k;\partial _0W\times D^k\cup W\times \partial D^k;\partial _1W\times D^k)\end{aligned}$$

to the sets of normal invariants $\mathcal {N}(W\times D^k)$ and the L-groups $\mathcal {L}(W\times D^k)$. Assuming $d\ge 6$, this sequence is an exact sequence of abelian groups until $\mathcal {L}(W\times D^1)$ where it continues as an exact sequence of based sets (see e.g. [43, Ch. 10]). The similarity with the long exact sequence of homotopy groups induced by a fibration is no coincidence: Quinn’s surgery fibration [34, 35] is a homotopy fibration of based spaces

$$\begin{aligned} \tilde{\mathbf {S}}(W)\longrightarrow \mathbf {N}(W)\longrightarrow \mathbf {L}(W)\end{aligned}$$

(17)

that induces (16) on homotopy groups (see also [43, Ch. 17A], or [32] for a detailed account in the topological category). We refrain from describing (16) or (17) in detail; all we shall need to know are a few basic properties, which we explain in the following.

2.1.1 The block structure space

Assuming $d\ge 6$, an application of the s-cobordism theorem results in a preferred homotopy equivalence

$$\begin{aligned} \mathrm {\widetilde{hAut}}^{\cong }_{\partial _0W}(W,\partial _1W)/\widetilde{\mathrm {Diff}}_{\partial _0W}(W)\simeq \tilde{\mathbf {S}}(W)_{\mathrm {id}}\end{aligned}$$

(18)

between the homotopy fibre of the map $\mathrm {B\widetilde{Diff}}_{\partial _0W}(W)\rightarrow \mathrm {B\widetilde{hAut}}^{\cong }_{\partial _0W}(W,\partial _1W)$ induced by inclusion and the basepoint component $\tilde{\mathbf {S}}(W)_{\mathrm {id}}\subset \tilde{\mathbf {S}}(W)$ of the block structure space (cf. [43, Ch. 17A] or [7, p. 33-34]). Here

$$\begin{aligned} \mathrm {\widetilde{hAut}}^{\cong }_{\partial _0W}(W,\partial _1W)\subset \mathrm {\widetilde{hAut}}_{\partial _0W}(W,\partial _1W)\end{aligned}$$

(19)

are the components in the image of the map $\widetilde{\mathrm {Diff}}_{\partial _0W}(W)\rightarrow \!\!\mathrm {\widetilde{hAut}}_{\partial _0W}(W,\partial _1W)$. Note that a diffeomorphism of W that fixes $\partial _0W$ pointwise automatically preserves $\partial _1W$ setwise, since $\partial _1W$ is the complement of the interior of $\partial _0W\subset \partial W$. On homotopy groups, the equivalence (18) can be described as follows: using the combinatorial description of the relative homotopy groups of a semi-simplicial Kan pair, a class in

$$\begin{aligned}&\pi _k(\mathrm {\widetilde{hAut}}^{\cong }_{\partial _0W}(W,\partial _1W)/\widetilde{\mathrm {Diff}}_{\partial _0W}(W);\mathrm {id})\\&\cong \pi _k(\mathrm {\widetilde{hAut}}^{\cong }_{\partial _0W}(W,\partial _1W),\widetilde{\mathrm {Diff}}_{\partial _0W}(W);\mathrm {id})\end{aligned}$$

is represented by a simple homotopy equivalence of triads $W\times D^k\rightarrow W\times D^k$ which is the identity on $\partial _0W\times D^k$ and restricts to a diffeomorphism on $W\times \partial D^k$, so it defines a class in the structure set $\mathcal {S}(W\times D^k)\cong \pi _k(\tilde{\mathbf {S}}(W); \mathrm {id})$.

2.1.2 The space of normal invariants

The space of normal invariants $\mathbf {N}(W)$ admits a preferred homotopy equivalence to the pointed mapping space $\mathrm {Maps}_*(W/\partial _0W,\mathrm {G}/\mathrm {O})$ based at the constant map, where $\mathrm {G}/\mathrm {O}$ is the homotopy fibre of the canonical map $\mathrm {BO}\rightarrow \mathrm {BG}$ witnessing the fact that a stable vector bundle has an underlying stable spherical fibration (see e.g. [34] or [43, Ch. 10, 17A]). This map is one of infinite loop spaces, so its homotopy fibre $\mathrm {G}/\mathrm {O}$ is an infinite loop space and hence so is the mapping space $\mathrm {Maps}_*(W/\partial _0W,\mathrm {G}/\mathrm {O})$. On homotopy groups, the composition

$$\begin{aligned}\tilde{\mathbf {S}}(W)\rightarrow \mathbf {N}(W)\simeq \mathrm {Maps}_*(W/\partial _0W,\mathrm {G}/\mathrm {O})\rightarrow \mathrm {Maps}_*(W/\partial _0W,\mathrm {BO})\end{aligned}$$

has the following geometric description (see e.g. [43, p. 113-114]): given a class in the structure set $\pi _k(\tilde{\mathbf {S}}(W);*)\cong \mathcal {S}(W\times D^k)$ represented by a simple homotopy equivalence $\varphi :N\rightarrow W\times D^k$, choose a homotopy inverse $\tilde{\varphi }:W\times D^k\rightarrow N$ of triads that agrees with $(\varphi |_{\partial _0N})^{-1}$ on $\partial _0(W\times D^k)$. Writing $\nu ^s$ and $\tau ^s$ for the stable normal respectively tangent bundle the stable vector bundle $(\tilde{\varphi }^*\nu ^s_N)\oplus \tau ^s_{W\times D^k}$ on $W\times D^k$ comes with a trivialisation on the subspace

$$\begin{aligned}\partial _0(W\times D^k)=\partial _0W\times D^k\cup W\times \partial D^{k}\end{aligned}$$

by making use of the diffeomorphism $\tilde{\varphi }|_{\partial _0(W\times D^k)}$, and hence gives a class

$$\begin{aligned}\in \pi _k(\mathrm {Maps}_*(W/\partial _0W,\mathrm {BO});*).\end{aligned}$$

2.1.3 The L-theory space

The L-theory space $\mathbf {L}(W)$ is an infinite loop space as well (see e.g. [32, Prop. 2.2.2]), and its homotopy groups are canonically isomorphic to Wall’s quadratic L-groups (see e.g. [32, Prop. 2.2.4]). We shall not need to know much about these groups, except that $\pi _k(\mathbf {L}(W);*)\cong \mathcal {L}(W\times D^k)$ vanishes if W satisfies the $\pi$-$\pi$-condition, i.e. if the inclusion $\partial _1W\subset W$ induces an equivalence on fundamental groupoids. This is a consequence of the exact sequence of L-groups of a triad (or more generally, n-ad) described for instance in [43, Thm 3.1]. In other words, under these assumptions, the L-theory space $\mathbf {L}(W)$ is weakly contractible, so (17) induces a preferred equivalence $\tilde{\mathbf {S}}(W)\simeq \mathbf {N}(W)$—an instance of the so-called $\pi$-$\pi$-theorem.

2.2 The block derivative map of a triad

With these basics of space-level surgery theory in mind, we now turn towards studying connectivity properties of the block derivative map resulting from (11) and (12)

$$\begin{aligned}\mathrm {B\widetilde{Diff}}_{\partial _0W}(W)\longrightarrow \mathrm {B\widetilde{hAut}}^{\cong }_{\partial _0W}(\tau _W^s,\partial _1W)^\tau \end{aligned}$$

and its enhancement involving tangential structures (i.e. the realisation of the bottom row of (14)), beginning with a technical but useful lemma on the homotopy fibre featuring in (18). We refer Sect. 1.2 for a recollection on nilpotent spaces.

Lemma 2.1

For a manifold triad $(W;\partial _0W,\partial _1W)$ of dimension $d\ge 6$, the homotopy fibre

$$\begin{aligned}&\mathrm {\widetilde{hAut}}^{\cong }_{\partial _0W}(W,\partial _1W)/\widetilde{\mathrm {Diff}}_{\partial _0W}(W)\\&\quad =\mathrm {hofib}(\mathrm {B\widetilde{Diff}}_{\partial _0W}(W)\rightarrow \mathrm {B\widetilde{hAut}}^{\cong }_{\partial _0W}(W,\partial _1W))\end{aligned}$$

is a nilpotent space.

Proof

By definition of the subspace $\mathrm {\widetilde{hAut}}^{\cong }_{\partial _0W}(W,\partial _1W)\subset \mathrm {\widetilde{hAut}}_{\partial _0W}(W,\partial _1W)$ in Sect. 2.1.1, the map $\mathrm {B\widetilde{Diff}}_{\partial _0W}(W)\rightarrow \mathrm {BhAut}^{\cong }_{\partial _0W}(W,\partial _1W)$ is surjective on fundamental groups, so its homotopy fibre is connected. To see that it is nilpotent, we use the equivalence (18) to the identity component $\tilde{\mathbf {S}}(W)_{\mathrm {id}}$ of the block structure space, which is itself equivalent to a component of the homotopy fibre of the surgery obstruction map $\mathbf {N}(W)\rightarrow \mathbf {L}(W)$ of (17). Given this description of the space in consideration, the claim follows from an application of Lemma 1.4, using the fact that, being an infinite loop space, the space of normal invariants $\mathbf {N}(W)$ is nilpotent (see Sect. 2.1.2). $\square$

To state the main result of this section, some notation is in order. For a stable tangential structure $\Xi :B\rightarrow \mathrm {BO}$ and a $\Xi$-structure $\ell :\tau ^s_W\rightarrow \Xi ^*\gamma$ (see Sect. 1.8.1), we write $\ell _0$ for the restriction of $\ell$ to $\tau ^s_{W}|_{\partial _0W}$ and denote by

$$\begin{aligned}\mathrm {B\widetilde{Diff}}^\Xi _{\partial _0W}(W;\ell _0)_\ell \quad \text {and}\quad \mathrm {B\widetilde{hAut}}^{\Xi ,\cong }_{\partial _0W}(\tau _W^s,\partial _1W;\ell _0)^\tau _\ell \end{aligned}$$

the components of the spaces (see Sects.1.8.1 and 1.9 for the notation)

$$\begin{aligned}\mathrm {B\widetilde{Diff}}^\Xi _{\partial _0W}(W;\ell _0)=\mathrm {\widetilde{Bun}}_{\partial _0W}(\tau ^s_W,{\Xi }^*\gamma ;\ell _0)^\tau //\widetilde{\mathrm {Diff}}_{\partial _0W}(W) \end{aligned}$$

and

$$\begin{aligned}\mathrm {B\widetilde{hAut}}^{\Xi ,\cong }_{\partial _0W}(\tau _W^s,\partial _1W;\ell _0)^\tau =\mathrm {\widetilde{Bun}}_{\partial _0W}(\tau ^s_W,{\Xi }^*\gamma ;\ell _0)^\tau //\mathrm {\widetilde{hAut}}^{\cong }_{\partial _0W}(\tau _W^s,\partial _1W)^\tau \end{aligned}$$

that correspond to $\ell$ under the bijection

$$\begin{aligned} \pi _0\mathrm {B\widetilde{hAut}}^{\Xi ,\cong }_{\partial _0W}(\tau _W^s,\partial _1W;\ell _0)^\tau\cong & {} \pi _0\mathrm {B\widetilde{Diff}}^\Xi _{\partial _0W}(W;\ell _0)\\\cong & {} \pi _0\mathrm {\widetilde{Bun}}_{\partial _0W}(\tau ^s_W,{\Xi }^*\gamma ;\ell _0)^\tau /\pi _0\widetilde{\mathrm {Diff}}_{\partial _0W}(W)\end{aligned}$$

resulting from Remark 1.21.2 and the discussion in Sects.1.8.1 and 1.9, using that the map induced by the block derivative

$$\begin{aligned}\pi _0\widetilde{\mathrm {Diff}}_{\partial _0W}(W)\longrightarrow \pi _0\mathrm {\widetilde{hAut}}^{\cong }_{\partial _0W}(\tau _W^s,\partial _1W)^\tau \end{aligned}$$

is surjective by the definition of the target in (12). Recall from Sects.2.1.3 that a manifold triad $W=(W;\partial _0W,\partial _1W)$ satisfies the $\pi$-$\pi$-condition if the inclusion $\partial _1W\subset W$ induces an equivalence on fundamental groupoids.

Theorem 2.2

Let $d\ge 6$ and W be a d-dimensional triad satisfying the $\pi$-$\pi$-condition. For a stable tangential structure $\Xi$ and a $\Xi$-structure $\ell$ on $\tau _W^s$, the homotopy fibre of the map

$$\begin{aligned}\mathrm {B\widetilde{Diff}}^\Xi _{\partial _0W}(W;\ell _0)_\ell \longrightarrow \mathrm {B\widetilde{hAut}}^{\Xi ,\cong }_{\partial _0W}(\tau _W^s,\partial _1W;\ell _0)^\tau _\ell \end{aligned}$$

is nilpotent and has finite homotopy groups. Moreover, this fibre is p-locally $(2p-4-k)$-connected for primes p, where k is the relative handle dimension of the inclusion $\partial _0W\subset W$.

Remark 2.3

Theorem 2.2 is inspired by a similar result of Berglund and Madsen [8, Thm 1.1], which applies to a different class of triads, namely those satisfying $\partial _0W=\partial W\cong S^{d-1}$. Another point in which their result differs from ours is that it is purely rational, and does in fact not seem to admit a p-local refinement analogous to Theorem 2.2. This is because p-torsion occurs for primes p that can be rather large with respect to the degree, originating from contributions of numerators of divided Bernoulli numbers to the homotopy groups of the homotopy fibre $\mathrm {Top}/\mathrm {O}$ of the canonical map $\mathrm {BO}\rightarrow \mathrm {BTop}$.

Proof of Theorem 2.2

Using Corollary A.2, an application of Lemma 1.1 to the horizontal arrows of the canonical square

(20)

identifies the horizontal homotopy fibres with the union of components of the space $\mathrm {\widetilde{Bun}}_{\partial _0W}(\tau ^s_W,{\Xi }^*\gamma ;\ell _0)^\tau$ given by the $\pi _0\widetilde{\mathrm {Diff}}_{\partial _0W}(W)$-orbit of the $\Xi$-structure $\ell$, so (20) is homotopy cartesian, which reduces the proof to the case $\Xi =\mathrm {id}$ in which both rows of the square are equivalences (see Sect. 1.8.1). To settle the case $\Xi =\mathrm {id}$, we consult the map of fibre sequences induced by the block derivative map

(21)

in order to see that the homotopy fibre in question agrees with the homotopy fibre of the left vertical map and is therefore nilpotent by Lemmas 1.4 and 2.1. The bottom right horizontal map of (21) forms the rightmost column of a commutative diagram

(22)

whose right horizontal maps are induced by inclusion and are equivalences; the upper by Lemma A.3 and the lower by the discussion in Sect. 1.5. The left upper horizontal map is the equivalence from (7) and the leftmost vertical arrow fits into a commutative square induced by inclusion

(23)

where $\mathrm {hAut}_{\partial _0W}(W,\partial _1W)_{\tau _W^s}$ are the components in the image of the map

$$\begin{aligned} \mathrm {hAut}_{\partial _0W}(\tau _W^s,\partial _1W)\longrightarrow \mathrm {hAut}_{\partial _0W}(W,\partial _1W)\end{aligned}$$

(24)

that forgets bundle data. Before taking geometric realisation, the map (24) is easily seen to be a Kan fibration, so the homotopy fibre of the right vertical map in (23) is equivalent to the classifying space of the gauge group of $\tau _W^s$ relative to $\partial _0W$, which is in turn canonically equivalent to the space $\mathrm {Maps}_{\partial _0W}(W,\mathrm {BO})_{\tau ^s_W}$ of maps homotopic to a choice of classifying map for $\tau _W^s$ relative to $\partial _0W$. The horizontal arrows in (23) are 1-coconnected by construction, so the same holds for the induced map on vertical homotopy fibres. Combining this with Lemma 4.8 (i), we see that the left vertical map in (21) agrees, up to canonical equivalence and postcomposition with a 1-coconnected map, with a map

$$\begin{aligned}\mathrm {\widetilde{hAut}}^{\cong }_{\partial _0W}(W,\partial _1W)/\widetilde{\mathrm {Diff}}_{\partial _0W}(W)\longrightarrow \mathrm {Maps}_{\partial _0W}(W,\mathrm {BO})_{\tau _W^s},\end{aligned}$$

so it suffices to show that this map between nilpotent spaces is p-locally $(2p-3-k)$-connected and that its homotopy fibre has finite homotopy groups. On homotopy groups, this map has the following description: a class in $\pi _k(\mathrm {\widetilde{hAut}}^{\cong }_{\partial _0W}(W,\partial _1W),\widetilde{\mathrm {Diff}}_{\partial _0W}(W);\mathrm {id})$ is represented by a homotopy equivalence of triads $\varphi :W\times D^k\rightarrow W\times D^k$ that is the identity on $D^k\times \partial _0W$ and restricts to a diffeomorphism on $\partial D^k\times W$ that is the identity on $*\times M$ for a base point $*\in \partial D^k$. The pullback $\varphi ^*\tau _{W\times D^k}^s$ is a stable vector bundle over $W\times D^k$ that agrees with $\tau _{W\times D^k}^s$ over $D^k\times \partial _0W\cup \{*\}\times W$ and comes with a canonical identification $\varphi ^*\tau _{W\times D^k}^s|_{\partial D^k\times M}\cong \tau _{W\times D^k}^s|_{\partial D^k\times M}$ given by the derivative of $\varphi |_{\partial D^k\times M}$, so it defines a class in the kth homotopy group of $\mathrm {Maps}_{\partial _0W}(W,\mathrm {BO})_{\tau _W^s}$ based at a choice of classifying map for $\tau _W^s$. Comparing this description with those of the equivalence

$$\begin{aligned}\mathrm {\widetilde{hAut}}^{\cong }_{\partial _0W}(W,\partial _1W)/\widetilde{\mathrm {Diff}}_{\partial _0W}(W)\simeq \tilde{\mathbf {S}}(W)_{\mathrm {id}}\end{aligned}$$

and the map $\tilde{\mathbf {S}}(W)_{\mathrm {id}}\rightarrow \mathrm {Maps}_*(W/\partial _0W,\mathrm {BO})_0$ on homotopy groups explained in Sections 2.1.1 and 2.1.2, one sees that the diagram of nilpotent spaces

commutes upon taking homotopy groups. Here the upper horizontal map is the one we just discussed, the right vertical equivalence is induced by multiplication with the stable normal bundle $\nu ^s_W$ using the infinite loop space structure induced from that of $\mathrm {BO}$ followed by the involution on $\mathrm {Maps}_{\partial _0W}(W,\mathrm {BO})_{0}$ induced by the canonical involution on $\mathrm {BO}$, the left vertical equivalences are induced by the surgery fibration (see Sections 2.1.1 and 2.1.2), and the bottom horizontal is given by postcomposition with the canonical map $\mathrm {G}/\mathrm {O}\rightarrow \mathrm {BO}$. Note that, being an infinite loop space, the mapping space $\mathrm {Maps}_*(W/\partial _0W,\mathrm {BO})_{0}$ is simple, so its homotopy groups at different base points are canonically identified. The bottom arrow is a map of infinite loop spaces and its homotopy fibre equivalent to a collection of components of the infinite loop space $\mathrm {Maps}_*(W/\partial _0W,\mathrm {G})$, so to finish the proof, we are left to show that the homotopy groups of this infinite loop space (including in degree 0) are finite and vanish p-locally in degrees $*<(2p-3-k)$. This follows from an application of obstruction theory, since $W/\partial _0W$ has no cohomology above degree k by the assumption on the relative handle dimension of $\partial _0W\subset W$ and the homotopy groups of $\mathrm {G}$ are $\mathbf {Z}/2$ in degree 0 and agree the stable homotopy groups of spheres in positive degrees, which are finite and p-torsion free in degrees $*<2p-3$ by a result of Serre [38, p. 498, Prop. 5]. $\square$

The stable tangential structure we shall be primarily interested in is the one encoding stable framings, which we denote by $\mathrm {sfr}:\mathrm {EO}\rightarrow \mathrm {BO}$. In this case, the p-local approximation of the space of block diffeomorphisms with tangential structures provided by Theorem 2.2 can be further simplified in terms of the union of components

$$\begin{aligned}\mathrm {\widetilde{hAut}}^{\cong }_{\partial _0W}(W,\partial _1W)_\ell \subset \mathrm {\widetilde{hAut}}^{\cong }_{\partial _0W}(W,\partial _1W)\end{aligned}$$

given by the image of the canonical map that forgets tangential structures

$$\begin{aligned}\mathrm {B\widetilde{hAut}}^{\mathrm {sfr},\cong }_{\partial _0W}(\tau _W^s,\partial _1W;\ell _0)^\tau _\ell \longrightarrow \mathrm {B\widetilde{hAut}}^{\cong }_{\partial _0W}(W,\partial _1W)\end{aligned}$$

on fundamental groups based at a fixed stable framing $\ell$ of $\tau _{W}$ (see (12) and (19) for the notation). Loosely speaking, these are the components of homotopy equivalences of triads that are homotopic to a diffeomorphism preserving the component of the stable framing $\ell$.

Corollary 2.4

Let $d\ge 6$ and W be a d-dimensional manifold triad satisfying the $\pi$-$\pi$-condition. For a stable framing $\ell$ of W, the homotopy fibre of

$$\begin{aligned}\mathrm {B\widetilde{Diff}}^{\mathrm {sfr}}_{\partial _0W}(W;\ell _0)_\ell \longrightarrow \mathrm {B\widetilde{hAut}}^{\cong }_{\partial _0W}(W,\partial _1W)_\ell \end{aligned}$$

is nilpotent and has finite homotopy groups. Moreover, this fibre is p-locally $(2p-4-k)$-connected for primes p, where k is the relative handle dimension of the inclusion $\partial _0W\subset W$.

Proof

Once we show that the map

$$\begin{aligned}\mathrm {B\widetilde{hAut}}^{\mathrm {sfr},\cong }_{\partial _0W}(\tau _W^s,\partial _1W;\ell _0)^\tau _\ell \longrightarrow \mathrm {B\widetilde{hAut}}^{\cong }_{\partial _0W}(W,\partial _1W)_\ell \end{aligned}$$

is an equivalence, the statement is a consequence of Theorem 2.2. By construction, the homotopy fibre of this map is connected. Using (22) and (23), one sees that it is thus sufficient to show that the map

$$\begin{aligned}\mathrm {BhAut}^{\mathrm {sfr}}_{\partial _0W}(\tau _W^s,\partial _1W;\ell _0)_\ell \longrightarrow \mathrm {BhAut}_{\partial _0W}(W,\partial _1W)\end{aligned}$$

is an equivalence. Taking vertical homotopy fibres in the map of fibre sequences

where $\mathrm {Bun}_{\partial _0W}(\tau _W^s,\mathrm {sfr}^*\gamma ;\ell _0)_\ell \subset \mathrm {Bun}_{\partial _0W}(\tau _W^s,\mathrm {sfr}^*\gamma ;\ell _0)$ are the components of the $\ell$-orbit of the $\pi _0\mathrm {hAut}_{\partial _0W}(\tau _W^s,\partial _1W)$-action, we see that it suffices to show that the induced action of the loop space of the homotopy fibre of the right vertical map on $\mathrm {Bun}_{\partial _0W}(\tau _W^s,\mathrm {sfr}^*\gamma ;\ell _0)_\ell$ is a torsor in the homotopical sense, i.e. that the map given by acting on $\ell$ is an equivalence. Since $\mathrm {hAut}_{\partial _0W}(\tau _W^s,\partial _1W)_\bullet \rightarrow \mathrm {hAut}_{\partial _0W}(W,\partial _1W)_\bullet$ is a Kan fibration, this loop space is canonically equivalent to the space of bundle self-maps of $\tau _W^s$ that cover the identity and agree with the identity on $\tau _W^s|_{\partial _0W}$. Moreover, by construction of the top fibration, the induced action on $\mathrm {Bun}_{\partial _0W}(\tau _W^s,\mathrm {sfr}^*\gamma ;\ell _0)_\ell$ is given by precomposition. Suitably modeled, this action is simply transitive, so the assertion follows. $\square$

3 High-dimensional handlebodies and their mapping classes

This section serves to compute variants of the mapping class group of a high-dimensional handlebody up to extensions in terms of automorphisms of the integral homology.

3.1 Automorphisms of handlebodies

The proof of Theorem A relies on considering a more general family of manifold than discs, the boundary connected sums

$$\begin{aligned}V_g:=\natural ^g (D^{n+1}\times S^n),\end{aligned}$$

and their boundaries as well as the manifolds obtained by cutting out a fixed embedded disc $D^{2n}\subset \partial V_g$, denoted by

$$\begin{aligned}W_g:=\partial V_g\cong \sharp ^g(S^n\times S^n)\quad \text {and}\quad W_{g,1}:=W_g\backslash \mathrm {int}(D^{2n}).\end{aligned}$$

This includes the case $g=0$, that is $V_0=D^{2n+1}$, $W_0=S^{2n}$, and $W_{0,1}=D^{2n}$. Using the notation introduced in Sections 1.4 and 1.5, the restriction of diffeomorphisms and relative homotopy automorphisms of $V_g$ to its boundary induces a commutative diagram

(25)

where the right horizontal maps are fibrations and the left maps the inclusions of the fibres over the identity. These fibrations need not be surjective; we denote their images by

$$\begin{aligned}\mathrm {Diff}^{\mathrm {ext}}_{\partial }(W_{g,1})\subset \mathrm {Diff}_\partial (W_{g,1})\quad \text { and }\quad \mathrm {hAut}^{\mathrm {ext}}_{\partial }(W_{g,1})\subset \mathrm {hAut}_{\partial }(W_{g,1}).\end{aligned}$$

Furthermore, in agreement with (19) we write

$$\begin{aligned}\mathrm {hAut}^{\cong }_\partial (V_g),\quad \mathrm {hAut}^{\cong }_{D^{2n}}(V_g,W_{g,1}),\quad \text {and}\quad \mathrm {hAut}^{\cong }_{\partial }(W_{g,1})\end{aligned}$$

for the components hit by the vertical maps. Block variants of all of the above automorphism spaces are defined in the same way.

3.2 The mapping class group

As a first step in our analysis of the mapping class group $\pi _0\mathrm {Diff}_{D^{2n}}(V_g)$, we observe that we may equally study orientation-preserving diffeomorphisms of $V_g$ that do not necessarily fix the embedded disc in the boundary $D^{2n}\subset \partial V_{g}$, or diffeomorphisms that preserve a disc $D^{2n+1}\subset \mathrm {int}(V_g)$ in the interior set- or pointwise.

Lemma 3.1

For $n\ge 2$ and discs $D^{2n}\subset \partial V_g$ and $D^{2n+1}\subset \mathrm {int}(V_g)$, the compositions induced by inclusion

consist of isomorphisms.

Proof

Up to isotopy, preserving a disc in the interior setwise is equivalent to preserving a point, so the group agrees with the group of path components of the subgroup of diffeomorphisms that fix the centre $*\in D^{2n+1}\subset \mathrm {int}(V_g)$. As $V_g$ is $(n-1)$-connected, the long exact sequence of the fibration given by evaluating diffeomorphisms at $*$ implies that agrees with , so the second map in the first composition in the statement is an isomorphism. Taking derivatives at $*$ yields a homotopy fibre sequence of the form

(26)

and hence an exact sequence

On the subgroup $\mathrm {SO}(n)\subset \mathrm {SO}(2n+1)$, the derivative map d has a section since $V_g$ admits a smooth $\mathrm {SO}(n)$-action with fixed point $*\in V_g$ whose tangential representation agrees with the restriction of the standard representation to the subgroup $\mathrm {SO}(n)$: take the g-fold equivariant boundary connected sums of $D^{n+1}\times S^{n}$ with $\mathrm {SO}(n)$ acting by rotating $S^n$ along an axis. As $\mathrm {SO}(n)\subset \mathrm {SO}(2n+1)$ is $(n-1)$-connected, this section ensures that the long exact sequence on homotopy groups of (26) splits in degrees $*\le n-1$ into short exact sequences and shows in particular that t is trivial for $n\ge 2$, so holds as claimed. Replacing (26) by the fibration sequence induced by taking the derivative at the centre $*\in D^{2n}\subset \partial V_g$ of the disc in the boundary, the proof of the claim regarding the maps in the second composition of the statement proceeds analogous to the first part of the proof. $\square$

3.2.1 The homology action

To obtain further information on the mapping class group $\pi _0\mathrm {Diff}_{D^{2n}}(V_g)$, we consider its action on the nth integral homology of $V_g$ and its boundary $\partial V_g=W_{g}$, which we abbreviate by

$$\begin{aligned}H_{W_{g,1}}:=\mathrm {H}_n(W_{g,1};\mathbf {Z})\quad \text {and}\quad H_{V_{g}}:=\mathrm {H}_n(V_{g};\mathbf {Z}).\end{aligned}$$

This action preserves further structure, such as the intersection pairing

$$\begin{aligned}\lambda :H_{W_{g,1}}\otimes H_{W_{g,1}}\longrightarrow \mathbf {Z},\end{aligned}$$

which equips $H_{W_{g,1}}$ with a nondegenerate $(-1)^n$-symmetric form by Poincaré duality. In addition, any automorphism of $H_{W_{g,1}}$ induced by an orientation-preserving diffeomorphism of $W_{g,1}$ has to preserve the function

$$\begin{aligned}\alpha :H_{W_{g,1}}\longrightarrow \pi _{n}\mathrm {BSO}(n)\end{aligned}$$

given by representing a homology class by an embedded n-sphere and taking its normal bundle. Wall [39, Thm 2] has shown that $\lambda$ and $\alpha$ satisfy the relations

• (i) $\lambda (x,x)=\partial _n \alpha (x)$

• (ii) $\alpha (x+y)=\alpha (x)+\alpha (y)+\lambda (x,y)\cdot \tau _{S^n}$

as long as $n\ge 3$, where

$$\begin{aligned}\partial _n:\pi _n\mathrm {BSO}(n)\longrightarrow \pi _{n-1}S^{n-1}\cong \mathbf {Z}\end{aligned}$$

is induced by the fibration $S^{n-1}\rightarrow \mathrm {BSO}(n-1)\rightarrow \mathrm {BSO}(n)$ and $\tau _{S^n}\in \pi _n\mathrm {BSO}(n)$ is the class representing the tangent bundle of the n-sphere. In sum, we arrive at a morphism

$$\begin{aligned}\pi _0\mathrm {Diff}(W_{g,1})\longrightarrow G_g:=\mathrm {Aut}(H_{W_{g,1}},\lambda ,\alpha )\end{aligned}$$

to the subgroup $G_g\subset \mathrm {GL}(H_{W_g})$ of automorphisms preserving $\lambda$ and $\alpha$, which is surjective by [40, Lem. 10]. However, we are interested in the mapping class group $\pi _0\mathrm {Diff}_{D^{2n}}(V_g)$ and not every automorphism in $G_g$ is realised by a diffeomorphism of $W_{g,1}$ that extends to one of $V_g$; it would at least have to preserve the Lagrangian subspace

$$\begin{aligned}K_g:=\ker \big (H_{W_{g,1}}\rightarrow H_{V_{g}}\big ),\end{aligned}$$

so there is a canonical map $\pi _0\mathrm {Diff}_{D^{2n}}(V_g)\rightarrow G_g^{\mathrm {ext}}$ to the subgroup

$$\begin{aligned}G_g^{\mathrm {ext}}:=\{\Phi \in G_g\mid \Phi (K_g)\subset K_g\}\end{aligned}$$

of automorphisms that preserve this Lagrangian, given by acting on the homology of the boundary. Using the canonical isomorphism $H_{W_{g,1}}/K_g\cong H_{V_g}$, the subgroup $G^{\mathrm {ext}}_g$ maps further to $\mathrm {GL}(H_{V_g})$. The resulting composition

$$\begin{aligned} \pi _0\mathrm {Diff}_{D^{2n}}(V_g)\longrightarrow G_g^{\mathrm {ext}}\longrightarrow \mathrm {GL}(H_{V_g})\end{aligned}$$

(27)

agrees with the action on the homology of $V_g$ and one may ask for the (co)kernel of the three maps involved. Extending work of Wall [40, 41], we express the answer in Theorem 3.3 below in terms of an exact sequence

$$\begin{aligned} 0\longrightarrow H_{V_g}^{\vee }\otimes S\pi _n\mathrm {SO}(n)\longrightarrow N_g\longrightarrow M_g\longrightarrow 0,\end{aligned}$$

(28)

of $\mathrm {GL}(H_{V_g})$-modules where

• (1) $S\pi _n\mathrm {SO}(n)\subset \pi _n\mathrm {SO}(n+1)$ is the image of the stabilisation map $\pi _n\mathrm {SO}(n)\rightarrow \pi _n\mathrm {SO}(n+1)$,

• (2) $M_g\subset (H_{V_g}\otimes H_{V_g})^{\vee }$ is the submodule of bilinear forms $\mu \in (H_{V_g}\otimes H_{V_g})^{\vee }$ that are

  • $(-1)^{n+1}$-symmetric and satisfy

  • $\mu (x,x)\in \mathrm {im}(\partial _{n+1}:\pi _{n}\mathrm {SO}(n+1)\rightarrow \mathbf {Z})$ for $x\in H_{V_g}$, and

• (3) $N_g\subset M_g\oplus (\pi _n\mathrm {SO}(n+1))^{H_{V_g}}$ is the submodule of pairs $(\mu ,\beta )$ of a bilinear form $\mu \in M_g$ and a function $\beta :H_{V_g}\rightarrow \pi _n\mathrm {SO}(n+1)$ that fulfil the conditions

  • $\mu (x,x)=\partial _{n+1}\beta (x)$ for $x\in H_{V_g}$ and

  • $\beta (x+y)=\beta (x)+\beta (y)+\mu (x,y)\cdot \tau _{S^{n+1}}$ for $x,y\in H_{V_g}$,

all equipped with the evident $\mathrm {GL}(H_{V_g})$-action through $H_{V_g}$. Here we denoted the integral dual of a G-module M by $M^\vee :=\mathrm {Hom}(M,\mathbf {Z})$.

Remark 3.2

The image of the map $\partial _{n+1}:\pi _{n}\mathrm {SO}(n+1)\rightarrow \pi _nS^n\cong \mathbf {Z}$ is generated by the order of the tangent bundle $\tau _{S^n}\in \pi _{n-1}\mathrm {SO}(n)$, so we have (see [29, §1B)])

$$\begin{aligned} \mathrm {im}(\partial _{n+1})= {\left\{ \begin{array}{ll} 0&{}\text{ for } n\text { even}\\ \mathbf {Z}&{}\text{ for } n=1,3,7\\ 2\cdot \mathbf {Z}&{}\text{ otherwise }, \end{array}\right. }\end{aligned}$$

(29)

which exhibits the condition $\mu (x,x)\in \mathrm {im}(\partial _{n+1})$ in (2) as vacuous unless $n\ne 1,3,7$ is odd. Moreover, this shows that, after choosing a basis $H_{V_g}\cong \mathbf {Z}^{g}$, the module $M_g$ can be described equivalently in terms of $(-1)^{n+1}$-symmetric integral $(g\times g)$-matrices, with even diagonal entries if $n\ne 1,3,7$ is odd.

Theorem 3.3

Let $n\ge 3$.

• (1) The action of $\pi _0\mathrm {Diff}_{D^{2n}}(V_g)$ on $H_{V_g}$ gives rise to an extension

  $$\begin{aligned}0\longrightarrow N_g\longrightarrow \pi _0\mathrm {Diff}_{D^{2n}}(V_g)\longrightarrow \mathrm {GL}(H_{V_g})\longrightarrow 0.\end{aligned}$$

• (2) The morphism $G_g^{\mathrm {ext}}\rightarrow \mathrm {GL}(H_{V_g})$ fits into an extension of the form

  $$\begin{aligned}0\longrightarrow M_g\longrightarrow G^{\mathrm {ext}}_g\longrightarrow \mathrm {GL}(H_{V_g})\longrightarrow 0.\end{aligned}$$

• (3) The action of $\pi _0\mathrm {Diff}_{D^{2n}}(V_g)$ on $H_{W_{g,1}}$ induces an extension

  $$\begin{aligned}0\longrightarrow H_{V_g}^\vee \otimes S\pi _n\mathrm {SO}(n)\longrightarrow \pi _0\mathrm {Diff}_{D^{2n}}(V_g)\longrightarrow G^{\mathrm {ext}}_g\longrightarrow 0.\end{aligned}$$

Moreover, the induced outer actions of these extensions is as specified above and the second extension admits a preferred splitting.

Remark 3.4

For a complete description of $\pi _0\mathrm {Diff}_{D^{2n}}(V_g)$, one still needs to determine the extension problems of the first or third part of the theorem, which we do not pursue at this point. Similar extensions by Kreck [26] describing the closely related mapping class group $\pi _0\mathrm {Diff}_\partial (W_{g,1})$ for $n\ge 3$ have been resolved in [25] for n odd.

Proof of Theorem 3.3

We begin with three preparatory remarks.

• (1) Results of Wall we shall use rely on are phrased in terms of pseudoisotopy instead of isotopy, but these notions agree in our situation by [11].

• (2) Justified by Lemma 3.1, we do not distinguish between seemingly different variants of $\pi _0\mathrm {Diff}_{D^{2n}}(V_g)$ fixing various discs point- or setwise.

• (3) We identify $K_g$ canonically with the dual ${H_{V_g}}^\vee$ as a $G^{\mathrm {ext}}_g$-module via the isomorphism induced by the form $\lambda$, and dually $H_{V_g}$ with $K_g^\vee$.

Wall [40, Lem. 10] showed that the action $\pi _0\mathrm {Diff}_{D^{2n}}(V_g)\rightarrow \mathrm {GL}(H_{V_g})$ is surjective and identified its kernel with those isotopy classes of diffeomorphisms $\varphi$ that are homotopic to the identity. Moreover, in [41, p. 298], he defined a complete obstruction $(\mu _\varphi ,\beta _\varphi )\in N_g$ for such a homotopically trivial diffeomorphism to be isotopic to the identity. By [40, Lem. 12–13], these obstructions are additive and exhaust $N_g$, so the resulting function

$$\begin{aligned} \ker \big (\pi _0\mathrm {Diff}(V_g)\rightarrow \mathrm {GL}(H_{V_g})\big )\longrightarrow N_g\end{aligned}$$

(30)

is an isomorphism of groups, which establishes the first of the three claims. To demonstrate the second, note that, as automorphisms in $G_g^{\mathrm {ext}}$ preserve the form $\lambda$, the composition

$$\begin{aligned}G^{\mathrm {ext}}_g\longrightarrow \mathrm {GL}(H_{V_g})\overset{((-)^{-1})^{\vee }}{\longrightarrow }\mathrm {GL}(K_g)\end{aligned}$$

agrees with the restriction to $K_g$. In particular, this shows that the kernel of the first map in this composition acts trivially on $K_g$, so there is a canonical monomorphism

defined by sending $\phi \in G_g^{\mathrm {ext}}$ to the linear map $\Psi (\phi ):H_{V_g}\rightarrow K_g$ induced by the difference $(\phi -\mathrm {id}):H_{W_{g,1}}\rightarrow K_g$. This leaves us with identifying the image of $\Psi$ with $M_g$ for which it is helpful to note that a morphism $f\in \mathrm {Hom}(H_{V_g},K_g)$ lies in the subspace

$$\begin{aligned}M_g\subset (H_{V_g}\otimes H_{V_g})^\vee \cong \mathrm {Hom}(H_{V_g},K_g)\end{aligned}$$

if and only if $f^{\vee }=(-1)^{n+1}f$ and $\lambda (f(x),\tilde{x})\in \mathrm {im}(\partial _{n+1})$ holds for all $x\in H_{V_g}$. Here $\tilde{x}\in H_{W_{g,1}}$ is a choice of preimage of x under the projection $H_{W_{g,1}}\rightarrow H_{V_g}$, but the value $\lambda (f(x),\tilde{x})$ is independent of this choice $\tilde{x}$ since $K_g$ is Lagrangian. For elements of the form $\Psi (\phi )$, the first property $\Psi (\phi )^{\vee }=(-1)^{n+1}\Psi (\phi )$ follows from the fact that $\phi$ preserves the form $\lambda$. To see the second, we note that, since $K_g$ is Lagrangian, the function $\alpha$ is additive on $K_g$, so it vanishes on it since the images of the second $S^n$-factors of the connected sum $W_{g,1}\cong \sharp ^g(S^n\times S^n)\backslash D^{n}$ in $V_g=\natural ^g (D^{n+1}\times S^n)$ induce a basis of $K_g$ and have trivial normal bundle. Using the fact that $\phi \in G_g^{\mathrm {ext}}$ preserves $\alpha$ and property (ii) of $\alpha$, we compute

$$\begin{aligned} \alpha (\tilde{x})=\alpha \big (\Psi (\phi )(x)+\tilde{x}\big )= & {} \alpha \big (\Psi (\phi )(x)\big )+\alpha (\tilde{x})+\lambda \big (\Psi (\phi )(x),\tilde{x}\big )\cdot \tau _{S^n}\\= & {} \alpha (\tilde{x})+\lambda \big (\Psi (\phi )(x),\tilde{x}\big )\cdot \tau _{S^n}\end{aligned}$$

and conclude that $\lambda \big (\Psi (\phi )(x),\tilde{x}\big )\cdot \tau _{S^n}$ vanishes, so $\lambda \big (\Psi (\phi )(x),\tilde{x}\big )\in \mathrm {im}(\partial _{n+1})$ holds as claimed. This proves that the image of $\Psi$ is contained in $M_g$, and to show that it agrees with it, we consider the commutative diagram

whose vertical arrow $N_g\rightarrow \ker (G_g^{\mathrm {ext}}\rightarrow \mathrm {GL}(H_{V_g}))$ is induced by the isomorphism (30). By [41, Lem. 24], the vertical composition in the diagram agrees with the projection $N_g\rightarrow M_g$ in (28), so it is surjective. Consequently, $\Psi$ is surjective as well and hence an isomorphism, which proves the second claim of the statement. To show the third, we observe that, given that $\Psi$ is an isomorphism and $N_g\rightarrow M_g$ is surjective, the diagram implies that $\pi _0\mathrm {Diff}(V_g)\rightarrow G_g^{\mathrm {ext}}$ is surjective and moreover that its kernel agrees with the kernel of $N_g\rightarrow M_g$, which is $H_{V_g}^\vee \otimes S\pi _n\mathrm {SO}(n)$ as claimed.

We now identify the actions as asserted. For the second extension, one can argue as follows: an automorphism $\varphi \in \mathrm {GL}(H_{V_g})$ acts on $\ker (G_g^{\mathrm {ext}}\rightarrow \mathrm {GL}(H_{V_g}))$ by conjugating with a choice of lift $\widetilde{\varphi }\in G_g^{\mathrm {ext}}$, so the isomorphism $\Psi$ is equivariant simply because of the identity $(\widetilde{\varphi }(\phi -\mathrm {id})\widetilde{\varphi }^{-1})=(\widetilde{\varphi }\phi \widetilde{\varphi }^{-1}-\mathrm {id})$ in $\mathrm {Hom}(H_{V_g},K_g)$ for all $\phi \in \mathrm {Hom}(H_{V_g},K_g)$. For the first extension, we use that the left vertical composition in the diagram above agrees with the projection $N_g\rightarrow M_g$, so it suffices to show that the composition

$$\begin{aligned} \ker (\pi _0\mathrm {Diff}_{D^{2n}}(V_g)\rightarrow \mathrm {GL}(H_{V_g}))\overset{\cong }{\longrightarrow } N_g\longrightarrow (\pi _n\mathrm {SO}(n+1))^{H_{V_g}}\end{aligned}$$

(31)

of (30) with the projection is equivariant. From Wall’s definition [40, p. 267] of the invariant $\beta _\varphi$ of an element $\varphi$ in the kernel, we see that this composition can be described as follows: representing a homology class $[e]\in H_{V_g}$ by an embedded sphere $e:S^n\rightarrow V_g$, we can alter $\varphi$ by an isotopy such that it preserves e pointwise. In this case, the derivative of $\varphi$ restricts an automorphism of the normal bundle $\nu (e)\cong \varepsilon ^{n+1}$ which induces an element $\beta _\varphi ([e])\in \pi _n\mathrm {SO}(n+1)$. This uses a trivialisation of $\nu (e)$, but the resulting element $\beta _\varphi ([e])$ is independent of this choice. From this description, the claimed equivariance is straight-forward to check, and the identification of the action of the last sequence follows from that of the first two by chasing through the diagram obtained by extending the diagram above by taking vertical kernels.

To see that the second extension splits, note that the second $S^n$-factors in the connected sum decomposition of $W_{g,1}=\sharp ^gS^n\times S^n\backslash \mathrm {int}(D^{2n})\subset \natural ^g D^{n+1}\times S^n=V_g$ induce a splitting of the canonical map $H_{W_{g,1}}\rightarrow H_{V_g}$ and thus an isomorphism of the form $K_g\oplus H_{V_g}\cong H_{W_{g,1}}$. Using this splitting of the homology, we can define a morphism $\mathrm {GL}(H_{V_g})\rightarrow G_{g}^{\mathrm {ext}}$ by assigning $\phi \in \mathrm {GL}(H_{V_g})$ the automorphism

$$\begin{aligned}H_{W_{g,1}}\cong K_g\oplus H_{V_g}\xrightarrow {(\phi ^{-1})^{\vee }\oplus \phi }K_g\oplus H_{V_g}\cong H_{W_{g,1}},\end{aligned}$$

which clearly preserves $K_g$. Moreover, its induced automorphism of $H_{W_{g,1}}$ agrees with $\phi$ by construction, so we obtain a splitting as desired. $\square$

Remark 3.5

With respect to the basis $H_{W_{g,1}}\cong \mathbf {Z}^{2g}$ suggested by the connected sum decomposition $W_{g,1}\cong \sharp ^g(S^n\times S^n)\backslash \mathrm {int}(D^{2n})$, the subgroup $G_g^{\mathrm {ext}}\subset \mathrm {GL}(H_{W_{g,1}})\cong \mathrm {GL}_{2g}(\mathbf {Z})$ agrees with the group of block matrices of the form

$$\begin{aligned}\left( \begin{matrix} A&{}M\\ 0 &{}(A^{-1})^T\end{matrix}\right) \end{aligned}$$

with $M\in M_g$, using the matrix description of $M_g$ explained in Remark 3.2. From this point of view, the splitting $\mathrm {GL}_g(\mathbf {Z})\rightarrow G_g^{\mathrm {ext}}$ described in the proof of Theorem 3.3 is the obvious one that sends a matrix $A\in \mathrm {GL}_g(\mathbf {Z})$ to the block diagonal matrix with $M=0$.

3.3 Stable framings

Choosing the canonical map $\mathrm {sfr}:\mathrm {EO}\rightarrow \mathrm {BO}$ as a stable tangential structure in the sense of Section 1.8.1, the space of $\mathrm {sfr}$-structures

$$\begin{aligned}\mathrm {Bun}_{D^{2n}}(\tau _{V_g}^s,\mathrm {sfr}^*\gamma ;\ell _0)\end{aligned}$$

as defined in that section is the space of stable framings of $V_g$ relative to a fixed stable framing $\ell _0:\tau _{V_g}^s|_{D^{2n}}\rightarrow \mathrm {sfr}^*\gamma$. We denote the stabiliser of the canonical action of $\pi _0\mathrm {Diff}_{D^{2n}}(V_g)$ on the set of components $\pi _0\mathrm {Bun}_{D^{2n}}(\tau _{V_g}^s,\mathrm {sfr}^*\gamma ;\ell _0)$ and its image in $G_g^{\mathrm {ext}}$ by

$$\begin{aligned}\pi _0\mathrm {Diff}_{D^{2n}}(V_g)_\ell \subset \pi _0\mathrm {Diff}_{D^{2n}}(V_g)\quad \text {and}\quad G_{g,\ell }^{\mathrm {ext}}\subset G_g^{\mathrm {ext}}.\end{aligned}$$

Note that $\pi _0\mathrm {Diff}_{D^{2n}}(V_g)_\ell$ agrees with the image of the canonical map $\mathrm {BDiff}^{\mathrm {sfr}}_{D^{2n}}(V_g)\rightarrow \mathrm {BDiff}_{D^{2n}}(V_g)$ on fundamental groups based at the point induced by the stable framing $\ell$, or equivalently, with the kernel of the crossed homomorphism

$$\begin{aligned} \pi _0\mathrm {Diff}_{D^{2n}}(V_g)\longrightarrow H_{V_g}^\vee \otimes \pi _n\mathrm {SO}\end{aligned}$$

(32)

given by acting on $\ell$. This uses the identification

$$\begin{aligned}H_{V_g}^\vee \otimes \pi _n\mathrm {SO}\cong & {} \mathrm {Hom}(H_{V_g},\pi _n\mathrm {SO})\\ {}\cong & {} \pi _0\mathrm {Maps}_{D^{2n}}(V_g,\mathrm {SO})\cong \pi _0\mathrm {Bun}_{D^{2n}}(\tau _{V_g}^s,\theta ^*\gamma ;\ell _0)\end{aligned}$$

whose first two isomorphisms are the evident ones and whose third is induced by the choice of stable framing $\ell$, using that $\pi _0\mathrm {Bun}_{D^{2n}}(\tau _{V_g}^s,\mathrm {sfr}^*\gamma ;\ell _0)$ is a torsor over $\pi _0\mathrm {Maps}_{D^{2n}}(V_g,\mathrm {SO})$ with pointwise multiplication.

Remark 3.6

As the stabilisation map $\mathrm {SO}(2n+1)\rightarrow \mathrm {SO}$ is 2n-connected, the induced map $\mathrm {Maps}_{D^{2n}}(V_g,\mathrm {SO}(2n+1))\rightarrow \mathrm {Maps}_{D^{2n}}(V_g,\mathrm {SO})$ is n-connected, which implies that there is no difference between equivalence classes of stable and unstable framings, so the discussion of this subsection applies equally well to unstable framings instead of stable ones.

To relate the subgroups $\pi _0\mathrm {Diff}_{D^{2n}}(V_g)_\ell \subset \pi _0\mathrm {Diff}_{D^{2n}}(V_g)$ and $G_{g,\ell }^{\mathrm {ext}}\subset G_{g}^{\mathrm {ext}}$ to the sequences of Theorem 3.3, we define the $\mathrm {GL}(H_{V_g})$-submodule

• (1) $N_g^{\mathrm {sfr}}\subset N_g$ as the intersection of $N_g$ with $M_g\oplus \langle \tau _{S^{n+1}} \rangle ^{H_{V_g}}$, where $\langle \tau _{S^{n+1}} \rangle$ is the subgroup of $\pi _n\mathrm {SO}(n+1)$ generated by the tangent bundle $\tau _{S^{n+1}}$

• (2) $M_g^{\mathrm {sfr}}\subset M_g$ as the collection of $(-1)^{n+1}$-symmetric bilinear forms $\mu \in (H_{V_g}\otimes H_{V_g})^{\vee }$ that are even, i.e. $\mu (x,x)\in 2\cdot \mathbf {Z}$ for all $x\in H_{V_g}$, which is automatic if n is even.

Standard arguments involving the long exact sequences in homotopy groups of the usual fibration $\mathrm {SO}(d)\rightarrow \mathrm {SO}(d+1)\rightarrow S^d$ (cf. [29, §1B)]) show that the sequence (28) restricts to an exact sequence of $\mathrm {GL}(H_{V_g})$-modules

$$\begin{aligned}0\longrightarrow H_{V_g}^\vee \otimes \ker \big (S\pi _n\mathrm {SO}(n)\rightarrow \pi _n\mathrm {SO}\big )\longrightarrow N_g^{\mathrm {sfr}}\longrightarrow M_g^{\mathrm {sfr}}\longrightarrow 0.\end{aligned}$$

Proposition 3.7

Let $n\ge 3$.

• (i) The action of $\pi _0\mathrm {Diff}_{D^{2n}}(V_g)$ on the set $\pi _0\mathrm {Bun}_{D^{2n}}(\tau _{V_g}^s,\mathrm {sfr}^*\gamma ;\ell _0)$ of equivalence classes of stable framings is transitive.

• (ii) For any stable framing $\ell :\tau _{V_g}^s\rightarrow \mathrm {sfr}^*\gamma$, the sequences of Theorem 3.3 restrict to exact sequences of the form

  $$\begin{aligned} 0\longrightarrow & {} N_g^{\mathrm {sfr}}\longrightarrow \pi _0\mathrm {Diff}_{D^{2n}}(V_g)_\ell \longrightarrow \mathrm {GL}(H_{V_g})\longrightarrow 0,\\ 0\longrightarrow & {} M_g^{\mathrm {sfr}}\longrightarrow G_{g,\ell }^{\mathrm {ext}}\longrightarrow \mathrm {GL}(H_{V_g})\longrightarrow 0,\text { and}\\ 0\longrightarrow & {} H_{V_g}^\vee \otimes \ker \big (S\pi _n\mathrm {SO}(n)\rightarrow \pi _n\mathrm {SO}\big )\longrightarrow \pi _0\mathrm {Diff}_{D^{2n}}(V_g)_\ell \longrightarrow G_{g,\ell }^{\mathrm {ext}}\longrightarrow 0. \end{aligned}$$

Remark 3.8

The calculation of $\mathrm {im}(\partial _{n+1})$ in Remark 3.2 shows that the inclusion $M_g^{\mathrm {sfr}}\subset M_g$ is an equality for $n\ne 1,3,7$, so the same holds for $G_{g,\ell }^{\mathrm {ext}}\subset G^{\mathrm {ext}}_g$ as a result of Proposition 3.7.

Proof of Proposition 3.7

The first sequence of Theorem 3.3 fits into a diagram

where $\tau$ is the crossed homomorphism (32), which is up to isomorphism given by the action of $\pi _0\mathrm {Diff}_{D^{2n}}(V_g)$ on $\ell$, so the first part of the statement is equivalent to the surjectivity of $\tau$. The diagonal arrow is the morphism which assigns an element $(\mu ,\beta )\in N_g$ the composition of $\beta :H_{V_g}\rightarrow \pi _n\mathrm {SO}(n+1)$ with the stabilisation map $\pi _n\mathrm {SO}(n+1)\rightarrow \pi _n\mathrm {SO}$. As $\tau _{S^{n+1}}\in \pi _n\mathrm {SO}(n+1)$ is stably trivial, it follows from the second defining property of $N_g$ that this composition is additive, so indeed defines an element of ${H_{V_g}}^\vee \otimes \pi _n\mathrm {SO}\cong \mathrm {Hom}(H_{V_g},\pi _n\mathrm {SO})$. As a next step, observe that the diagonal map is surjective, since the projection

$$\begin{aligned}N_g\subset M_g\oplus (\pi _n\mathrm {SO}(n+1))^{H_{V_g}}\rightarrow (\pi _n\mathrm {SO}(n+1))^{H_{V_g}}\end{aligned}$$

has a section over the subspace of linear maps ${H_{V_g}}^\vee \otimes \pi _n\mathrm {SO}(n+1)\subset (\pi _n\mathrm {SO}(n+1))^{H_{V_g}}$ by setting the $M_g$-coordinate to zero and because the stabilisation map $\pi _n\mathrm {SO}(n+1)\rightarrow \pi _n\mathrm {SO}$ is surjective. This reduces the first claim of the statement to the commutativity of the triangle, which follows from the geometric description of the composition (31) we gave in the proof of Theorem 3.3 in a straight-forward manner.

The kernel of the vertical map agrees with the stabiliser $\pi _0\mathrm {Diff}_{D^{2n}}(V_g)_\ell$, so the surjectivity of the diagonal arrow in the diagram also shows that this stabiliser surjects onto $\mathrm {GL}(H_{V_g})$ and that the kernel of the restriction $\ker (\tau )\rightarrow \mathrm {GL}(H_{V_g})$ agrees with the kernel of the diagonal arrow. But this kernel is exactly the submodule $N_g^{\mathrm {sfr}}\subset N_g$, because the kernel of the stabilisation map $\pi _n\mathrm {SO}(n+1)\rightarrow \pi _n\mathrm {SO}$ agrees with the kernel of $\pi _n\mathrm {SO}(n+1)\rightarrow \pi _n\mathrm {SO}(n+2)$, i.e. the subgroup generated by $\tau _{S^{n+1}}$. This establishes the first sequence of the second claim. For the second, note that the surjectivity of the morphism

$$\begin{aligned}\pi _0\mathrm {Diff}_{D^{2n}}(V_g)_\ell \longrightarrow \mathrm {GL}(H_{V_g})\end{aligned}$$

implies that also the morphism

$$\begin{aligned}G_{g,\ell }^{\mathrm {ext}}\longrightarrow \mathrm {GL}(H_{V_g})\end{aligned}$$

is surjective. Comparing the first two sequences of Theorem 3.3, we see that its kernel agrees with the image of $N_g^{\mathrm {sfr}}$ in $M_g$ under the projection $N_g\rightarrow M_g$, i.e. with those bilinear forms $\mu \in M_g$ that satisfy $\mu (x,x)\in \mathrm {im}(\partial _{n+1}\langle \tau _{S^{n+1}}\rangle )$. The image of $\tau _{S^{n+1}}\in \pi _n\mathrm {SO}(n+1)$ under $\partial _{n+1}$ is the Euler characteristic of $S^{n+1}$ (see [29, §1B)]), so the kernel in question agrees with $M_g^{\mathrm {sfr}}$ as claimed. To establish the last sequence, one first observes that

$$\begin{aligned}\pi _0\mathrm {Diff}_{D^{2n}}(V_g)_\ell \longrightarrow G_{g,\ell }^{\mathrm {ext}}\end{aligned}$$

is surjective by definition of the target, and then compares the first two sequences in the claim to see that its kernel agrees with the kernel of $N_g^{\mathrm {sfr}}\rightarrow M_g^{\mathrm {sfr}}$, which agrees with $H_{V_g}^\vee \otimes \ker (S\pi _n\mathrm {SO}(n)\rightarrow \pi _n\mathrm {SO})$ as already noted in the discussion prior to this proof. $\square$

Lemma 3.9

The negative of the identity $-\mathrm {id}\in \mathrm {GL}(H_{W_g})$ is contained in the subgroup $G_{g,\ell }^{\mathrm {ext}}\subset \mathrm {GL}(H_{W_g})$ for all stable framings $\ell :\tau _{V_g}^s\rightarrow \mathrm {sfr}^*\gamma$.

Proof

We first restrict to the case $g=1$ and a particular choice of stable framing, namely that induced by the standard embedding $D^{n+1}\times S^n\subset \mathbf {R}^{n+1}\times \mathbf {R}^{n+1}$. The diffeomorphism

$$\begin{aligned} \begin{array}{rcl} D^{n+1}\times S^n &{} \longrightarrow &{} D^{n+1}\times S^n \\ [0.3em] ((x_1,\ldots ,x_{n+1}),(y_1,\ldots ,y_{n+1})) &{} \longmapsto &{} ((-x_1,x_2,\ldots ,x_{n+1}),(-y_1,y_2,\ldots ,y_{n+1})) \end{array}\end{aligned}$$

(33)

is orientation preserving, maps to $-\mathrm {id}\in \mathrm {GL}(H_{W_1})$, and has constant derivative, so it preserves the stable framing as required. It does not preserve a disc in the boundary, but by Lemma 3.1, we can rectify this by an isotopy. To extend this argument to higher genera, we take the boundary connected sum of two copies of this diffeomorphism using the fixed discs in the boundary to obtain a diffeomorphism of $V_2$ whose image in $\mathrm {GL}(H_{W_2})$ is $-\mathrm {id}$, which we can again isotope so it preserves a disc as required. Continuing like this yields a sequence of isotopy classes in $\pi _0\mathrm {Diff}_{D^{2n}}(V_g)$ for all $g\ge 0$ that satisfy the requirements of the claim. This establishes the statement for one specific stable framing for each g, but implies the general case, the reason being that $-\mathrm {id}\in \mathrm {GL}(H_{W_g})$ is central and all subgroups $G_{g,\ell }^{\mathrm {ext}}\subset G_g^{\mathrm {ext}}$ are conjugate, because the different stabilisers $\pi _0\mathrm {Diff}_{D^{2n}}(V_g)_\ell$ are, as the action is transitive by Proposition 3.7. This concludes the proof. $\square$

3.4 The homotopy mapping class group

Not only the smooth mapping class groups $\pi _0\mathrm {Diff}_{D^{2n}}(V_g)$ and $\pi _0\mathrm {Diff}_\partial (W_{g,1})$ act on the homology $H_{W_{g,1}}$, also their homotopical cousins $\pi _0\mathrm {hAut}_{D^{2n}} (V_g,W_{g,1})$ and $\pi _0\mathrm {hAut}_\partial (W_{g,1})$ do. Restricting these actions to the images

$$\begin{aligned} \pi _0\mathrm {hAut}^{\cong }_{D^{2n}}(V_g,W_{g,1})\subset & {} \pi _0\mathrm {hAut}_{D^{2n}}(V_g,W_{g,1})\quad \text { and }\\ \pi _0\mathrm {hAut}^{\cong }_\partial (W_{g,1})\subset & {} \pi _0\mathrm {hAut}_\partial (W_{g,1})\end{aligned}$$

of the canonical maps

$$\begin{aligned} \pi _0\mathrm {Diff}_{D^{2n}}(V_g,W_{g,1})\rightarrow & {} \pi _0\mathrm {hAut}_{D^{2n}}(V_g,W_{g,1})\quad \text {and}\\ \pi _0\mathrm {Diff}_\partial (W_{g,1})\rightarrow & {} \pi _0\mathrm {hAut}_\partial (W_{g,1}),\end{aligned}$$

they land in the subgroups $G_g^{\mathrm {ext}}$ and $G_g$ of $\mathrm {GL}(H_{W_{g,1}})$, respectively.

Lemma 3.10

Let $n\ge 3$. The morphisms induced by the action on $H_{W_{g,1}}$

$$\begin{aligned}\pi _0\mathrm {hAut}_{\partial }^{\cong }(W_{g,1})\longrightarrow G_g\quad \text { and }\quad \pi _0\mathrm {hAut}_{D^{2n}}^{\cong }(V_g,W_{g,1})\longrightarrow G_g^{\mathrm {ext}}\end{aligned}$$

are surjective. Moreover, their kernels are finite and p-torsion free as long as $n<2p-4$.

Proof

In the course of this proof, we shall make frequent use of the fact that the homotopy groups $\pi _{n+k}(\vee ^hS^n)$ with $n\ge 3$ are p-torsion free for $k<2p-3$ as a result of the Hilton–Milnor theorem (see (37) below) and the case $h=1$ due to Serre [38, p. 498, Prop. 5].

To begin with the actual proof, note that the two morphisms of the statement are certainly surjective, since this holds already for $\pi _0\mathrm {Diff}_{\partial }(W_{g,1})\rightarrow G_g$ and $\pi _0\mathrm {Diff}(V_g)\rightarrow G_g^{\mathrm {ext}}$ by Theorem 3.3 and the discussion it precedes. Evidently, the kernel of the first morphism of the statement is contained in that of $\pi _0\mathrm {hAut}_{\partial }(W_{g,1})\rightarrow \mathrm {GL}(H_{W_{g,1}})$, which enjoys the claimed finiteness and torsion property by an application of the fibre sequence induced by restriction along the boundary inclusion

$$\begin{aligned}\mathrm {hAut}_{\partial }(W_{g,1})\longrightarrow \mathrm {hAut}_{*}(W_{g,1})\longrightarrow \mathrm {Maps}_{*}(\partial W_{g,1},W_{g,1}),\end{aligned}$$

using the isomorphism $\pi _0\mathrm {hAut}_{*}(W_{g,1})\cong \mathrm {GL}(H_{W_{g,1}})$ induced by the homology action and the fact that the group $\pi _1\mathrm {Maps}_{*}(\partial W_{g,1},W_{g,1})\cong \pi _{2n}(\vee ^{2g}S^n)$ is finite and without p-torsion for $n<2p-3$. To deduce the claim for the kernel of second morphism from this, we consult the fibre sequence $\mathrm {hAut}_{\partial }(V_{g})\rightarrow \mathrm {hAut}_{D^{2n}}(V_{g},W_{g,1})\rightarrow \mathrm {hAut}_{\partial }(W_{g,1})$ to realise that it suffices to show that $\pi _0\mathrm {hAut}_{\partial }(V_{g})$ is finite and p-torsion free for $n<2p-4$. Using the fibre sequence $\mathrm {hAut}_{\partial }(V_{g})\rightarrow \mathrm {hAut}_{*}(V_{g})\rightarrow \mathrm {Maps}(W_g,V_g)$ and the observation that its fibre inclusion is trivial on path components since $\pi _0\mathrm {hAut}_{\partial }(V_{g})$ acts trivially on homology and $\pi _0\mathrm {hAut}_{*}(V_{g})\cong \mathrm {GL}(H_{V_g})$, we see that $\pi _0\mathrm {hAut}_{\partial }(V_{g})$ is a quotient of the fundamental group $\pi _1\mathrm {Maps}_*(W_g,V_g)$ based at the inclusion $\iota$. Finally, note that the fibre sequence $\mathrm {Maps}_*(W_g,V_g)\rightarrow \mathrm {Maps}_*(W_{g,1},V_g)\rightarrow \mathrm {Maps}_*(\partial W_{g,1},V_g)$ induces an exact sequence

$$\begin{aligned}\pi _{2n+1}(\vee ^gS^n)^{\oplus g}\longrightarrow \pi _1(\mathrm {Maps}_*(W_g,V_g);\iota )\longrightarrow \pi _{n+1}(\vee ^gS^n)^{\oplus 2g}\end{aligned}$$

whose outer groups are finite and p-torsion free for $n<2p-4$, so we can conclude the claim. $\square$

3.5 Stabilisation

To relate the automorphism spaces of the handlebody $V_g=\natural ^gD^{n+1}\times S^n$ relative to the disc $D^{2n}\subset \partial V_g$ fixed in Section 3.1 to the ones of $V_{g+1}$, it is convenient to modify $V_g$ by introducing codimension 2 corners at the boundary of the disc $D^{2n}\subset V_g$ in the boundary so that there is smooth boundary preserving embedding $c:(-1,0]\times D^{2n}\rightarrow V_g$ whose restriction to ${\{0\}\times D^{2n}}$ agrees with the chosen disc. Abusing common terminology, we call such an embedding a collar. Fixing another disc $D^{2n-1}\subset \partial D^{2n}$, we consider

$$\begin{aligned}H:=([0,1]\times D^{2n})\natural (D^{n+1}\times S^n),\end{aligned}$$

where the boundary connected sum is performed away from the union

$$\begin{aligned}D:=\{0,1\}\times D^{2n}\cup [0,1]\times D^{2n-1}\subset [0,1]\times D^{2n},\end{aligned}$$

and think of $V_{g+1}$ as being obtained by gluing $V_g$ to H along the two collared discs $D^{2n}\subset V_g$ and $\{0\}\times D^{2n}\subset H$, where we declare $\{1\}\times D^{2n}\subset H\subset V_{g+1}$ to the new distinguished disc in the boundary, which comes with a preferred collar. Given a tangential structure $\theta :B\rightarrow \mathrm {BO}(d)$, a choice of bundle map $\ell _0:\varepsilon \oplus \tau _{D^{2n}}\rightarrow \theta ^*\gamma _{2n+1}$ induces canonical $\theta$-structures on $\tau _{V_g}|_{D^{2n}}$ and $\tau _{V_{g+1}}|_{D^{2n}}$ by using the fixed collars, and also one on $\tau _{H}|_{D}$ by making use of the canonical trivialisation of $\tau _{[0,1]}$. With respect to these $\theta$-structures, generically denoted by $\ell _0$, there is an evident gluing map for tangential structures

$$\begin{aligned}&\mathrm {Bun}_{D^{2n}}(\tau _{V_g},\theta ^*\gamma _{2n+1};\ell _0)\times \mathrm {Bun}_{D}(\tau _{H},\theta ^*\gamma _{2n+1};\ell _0)\longrightarrow \mathrm {Bun}_{D^{2n}}(\tau _{V_{g+1}},\theta _{2n+1}^*\gamma ;\ell _0)\end{aligned}$$

that is equivariant with respect to the gluing morphism

$$\begin{aligned} \mathrm {Diff}_{D^{2n}}(V_g)\times \mathrm {Diff}_{D}(H)\longrightarrow \mathrm {Diff}_{D^{2n}}(V_{g+1})\end{aligned}$$

(34)

for diffeomorphisms. Taking homotopy orbits, this induces a map of the form

$$\begin{aligned}\mathrm {BDiff}_{D^{2n}}^\theta (V_g;\ell _0)\times \mathrm {BDiff}_{D}^\theta (H;\ell _0)\longrightarrow \mathrm {BDiff}_{D^{2n}}^\theta (V_{g+1};\ell _0)\end{aligned}$$

and hence a homotopy class of stabilisation maps

$$\begin{aligned} \mathrm {BDiff}_{D^{2n}}^\theta (V_g;\ell _0)\rightarrow \mathrm {BDiff}_{D^{2n}}^\theta (V_{g+1};\ell _0)\end{aligned}$$

(35)

that in general depends on the choice of a component of $\mathrm {BDiff}_{D}^\theta (H;\ell _0)$, but not in any of the cases we shall be interested in, because of the following.

Lemma 3.11

If B is n-connected, then the space $\mathrm {BDiff}_{D}^\theta (H;\ell _0)$ is nonempty and connected.

Proof

Up to smoothing corners, the pairs (H, D) and $(V_1,D^{2n})$ are diffeomorphic, so there we have an equivalence $\mathrm {BDiff}_{D}^\theta (H;\ell _0)\simeq \mathrm {BDiff}_{D^{2n}}^\theta (V_1;\ell _0)$, which shows that the claim is equivalent to the transitivity of the action of $\pi _0\mathrm {Diff}_{D^{2n}}(V_1)$ on $\pi _0\mathrm {Bun}_{D^{2n}}(\tau _{V_1},\theta ^*\gamma _{2n+1};\ell _0)$, using that the latter set is nonempty as $V_1$ is parallelizable. As B is n-connected, it is a consequence of obstruction theory that every $\theta$-structure on $V_g$ is induced by a framing, so it suffices to consider the case $\theta :\mathrm {EO}(2n+1)\rightarrow \mathrm {BO}(2n+1)$, which we have already settled as the first part of Proposition 3.7 (see also Remark 3.6). $\square$

A similar discussion results in analogous stabilisation maps of the form

$$\begin{aligned}\mathrm {B\widetilde{Diff}}^\Xi _{D^{2n}}(V_g;\ell _0)\longrightarrow \mathrm {B\widetilde{Diff}}^\Xi _{D^{2n}}(V_{g+1};\ell _0)\end{aligned}$$

for stable tangential structures $\Xi :B\rightarrow \mathrm {BO}$ and bundle maps $\ell _0:\tau _{V_g}^s\rightarrow \Xi ^*\gamma$, which are compatible with the non-block variants defined above and are again unique up to homotopy if B is n-connected. Moreover, using the splittings of the inclusions $H_{W_{g,1}}\rightarrow H_{W_{g+1,1}}$ and $H_{V_g}\rightarrow H_{V_{g+1}}$ suggested by the decomposition $V_{g+1}=V_g\cup H$, there are stabilisation maps for the respective linear groups on $H_{W_{g,1}}$ and $H_{V_g}$ given by extending automorphisms by the identity and these are related to the stabilisation maps described above via the action on the homology of $V_g$ and $W_{g,1}$ (see Section 3.2), so there is a commutative diagram of compatible stabilisation maps that has the form

4 Relative homotopy automorphisms of handlebodies

Theorem 2.2 illustrates that the space of block diffeomorphisms $\widetilde{\mathrm {Diff}}_{D^{2n}}(V_g)$ is closely related to the space $\mathrm {\widetilde{hAut}}_{D^{2n}}(V_g,W_{g,1})$ of relative block homotopy automorphisms or, equivalently, to its non-block variant $\mathrm {hAut}_{D^{2n}}(V_g,W_{g,1})$ (see Section 1.5). To access the homology of the classifying space of this space of homotopy automorphisms, one might try to study the Serre spectral sequence of the fibration sequence induced by taking components

$$\begin{aligned}\mathrm {BhAut}^{\mathrm {id}}_{D^{2n}}(V_g,W_{g,1})\longrightarrow \mathrm {BhAut}_{D^{2n}}(V_g,W_{g,1})\longrightarrow \mathrm {B}\pi _0\mathrm {hAut}_{D^{2n}}(V_g,W_{g,1})\end{aligned}$$

for which one ought to know at least the homology of the fibre as a module over the group $\pi _0\mathrm {hAut}_{D^{2n}}(V_g,W_{g,1})$. This is what this section aims to compute—p-locally and in a range of degrees—by first calculating the p-local homotopy groups in a range using some tools from rational homotopy theory combined with an ad-hoc extension to the p-local setting tailored to our situation, and then pass from homotopy to homology groups.

4.1 Conventions on gradings

Essentially all objects in this section carry a $\mathbf {Z}$-grading, and we shall keep track of it throughout. For instance, we consider the (reduced) homology of a space X always with its natural grading, even if it is supported in a single degree.

We denote the k-fold suspension of a graded R-module A over some commutative ring R by $s^kA$, the graded R-module whose degree k piece consists of R-module morphisms raising the degree by k by $\mathrm {Hom}(A,B)$ for graded modules A and B, the graded R-dual of A by $A^\vee :=\mathrm {Hom}(A,R[0])$ where R[0] is the base ring concentrated in degree zero, and the subspace of elements of strictly positive degrees by $A^+\subset A$. For an ungraded R-module M we write M[k] for the graded R-module which is trivial in all degrees but k where it agrees with M. The graded tensor product $A\otimes B$ is defined in the usual way. Note that $(s^kA)\otimes B=s^k(A\otimes B)=A\otimes (s^kB)$. The degreewise rationalisation or p-localisation of a graded $\mathbf {Z}$-module A is denoted by $A_\mathbf {Q}$ or $A_{(p)}$ respectively, and we view it as a graded $\mathbf {Q}$- respectively $\mathbf {Z}_{(p)}$-module.

4.2 Lie algebras and their derivations

We consider differential graded (short dg) Lie algebras over a commutative ring R. However, most of the dg Lie algebras which we shall encounter actually have trivial differential. Examples include the free graded Lie algebra $\mathbf {L}(V)$ on a graded R-module A or the onefold shift of the homotopy groups $\pi _{*+1}X$ of a based space X with its canonical Lie algebra structure over $\mathbf {Z}$ given by the Whitehead bracket (except for a 2-torsion subtlety that will not play a role for us). Given a dg Lie algebra L, we write $[L,L]\subset L$ for the graded subspace generated by brackets. An important principle in this section is that the homotopy type of mapping spaces is closely related to certain chain complexes of f-derivations by which we mean the following: for a morphism $f:(L,d_L)\rightarrow (L',d')$ of dg Lie algebras, an f-derivation of degree k is a linear map $\theta :L\rightarrow L'$ that raises the degree by k and satisfies

$$\begin{aligned}\theta ([x,y])=[\theta (x),f(y)]+(-1)^{k|x|}[f(x),\theta (y].\end{aligned}$$

These derivations form the degree k piece of the chain complex $\mathrm {Der}^f(L,L')$ of f-derivations over R whose differential is defined as $d(\theta )=d_{L'}\theta -(-1)^{|\theta |}\theta d_L$, so it vanishes if both L and $L'$ have trivial differential. Given a cycle $\omega \in L$, we denote the subcomplex of f-derivations that vanish on $\omega$ by $\mathrm {Der}^f_{\omega }(L,L')\subset \mathrm {Der}^f(L,L')$. In the case $L=L'$ and $f=\mathrm {id}$, we abbreviate the complex of $\mathrm {id}$-derivations $\mathrm {Der}^{\mathrm {id}}(L,L)$ by $\mathrm {Der}(L)$.

4.3 Rational homotopy theory, Quillen style

Recall from [33] Quillen’s functor $\lambda$, which assigns a simply connected based space X a dg Lie algebra $\lambda (X)$ over the rationals, one of whose many properties is that it captures the rationalised homotopy Lie algebra of X via a natural isomorphism $\mathrm {H}_*(\lambda (X))\cong \pi _{*+1}(X)_\mathbf {Q}$ of graded Lie algebras, where $\mathrm {H}_*(\lambda (X))=\ker (d_{\lambda (X)})/\mathrm {im}(d_{\lambda (X)})$ is the homology Lie algebra of $\lambda (X)$. A Lie model of X is a rational dg Lie algebra $L_\mathbf {Q}^X$ quasi-isomorphic to $\lambda (X)$. Such a model is called free if the underlying graded Lie algebra of $L_\mathbf {Q}^X$ is isomorphic to a free graded Lie algebra $\mathbf {L}(V)$ on a graded $\mathbf {Q}$-vector space V and minimal if it is free and has decomposable differential, i.e. $d(L_\mathbf {Q}^X)\subset [L_\mathbf {Q}^X,L_\mathbf {Q}^X]$. Any simply connected based space has a minimal Lie model $L_\mathbf {Q}^X$, unique up to (non-canonical) isomorphism, and a based map between such spaces $f:X\rightarrow Y$ gives rise to a map $f:L_\mathbf {Q}^X \rightarrow L_\mathbf {Q}^Y$ between their minimal models.

4.4 Derivations and mapping spaces

As mentioned earlier, the homotopy theory of mapping spaces is tightly connected to derivations of dg Lie algebras. In the rational setting, this is made precise for instance by a result of Lupton–Smith [30, Thm 3.1]. The version of their result we shall need is marginally stronger than stated in [30], but follows from the given proof in a straight-forward way (see also [8, Thm 3.6]).

Theorem 4.1

(Lupton–Smith) Let $f:X\rightarrow Y$ be a map between simply connected finite based CW-complexes, with minimal Lie model $f:L_\mathbf {Q}^X\rightarrow L_\mathbf {Q}^Y$. There is an isomorphism

$$\begin{aligned}\pi _*(\mathrm {Maps}_*(X,Y);f)_\mathbf {Q}\overset{\cong }{\longrightarrow }\mathrm {H}_*(\mathrm {Der}^{f}(L_\mathbf {Q}^X,L_\mathbf {Q}^Y))\end{aligned}$$

for $*\ge 2$, which is natural in both X and Y. For X a co-H-space, this also holds for $*=1$.

4.5 A p-local generalisation

From the point of view of Quillen’s approach to rational homotopy theory, the spaces we shall be applying Theorem 4.1 to are of the simplest nature possible: they are homotopy equivalent to boquets of equidimensional spheres. The minimal model of such a space $X\simeq \vee ^gS^n$ for $n\ge 2$ agrees with the free graded Lie algebra

$$\begin{aligned} L_\mathbf {Q}^{X}:=\mathbf {L}(s^{-1}H_\mathbf {Q}^X)\cong \pi _{*+1}X_\mathbf {Q}\quad \text {on}\quad H_\mathbf {Q}^X:=\widetilde{\mathrm {H}}_*(X;\mathbf {Q}),\end{aligned}$$

(36)

equipped with the trivial differential. Given a map between spaces of this kind, the induced map on minimals models is simply given by the induced map on rational homotopy groups. It is a consequence of the Hilton–Milnor theorem that, p-locally in small degrees with respect to p, the homotopy Lie algebra $\pi _{*+1}X$ is free even before rationalisation. To make this precise, we abbreviate the integral and p-local analogue of (36) by

$$\begin{aligned}&L^X:=\mathbf {L}(s^{-1}H^{X})\text { and }L_{(p)}^X:=\mathbf {L}(s^{-1}H_{(p)}^{X})\text { where }\\&H^X:=\widetilde{\mathrm {H}}_*(X;\mathbf {Z})\text { and }H^X_{(p)}:=\widetilde{\mathrm {H}}_*(X;\mathbf {Z}_{(p)}).\end{aligned}$$

The inverse of the Hurewicz map $\mathrm {H}_n(X;\mathbf {Z}_{(p)})\cong \pi _nX_{(p)}$ induces a map $L_{(p)}^X\rightarrow \pi _{*+1}X_{(p)}$ of graded Lie algebras over $\mathbf {Z}_{(p)}$, which turns out to be an isomorphism in a range of degrees.

Lemma 4.2

For an odd prime p and a based space X that is homotopy equivalent to $\vee ^gS^n$ with $n\ge 2$, the morphism

$$\begin{aligned}L_{(p)}^X\longrightarrow \pi _{*+1}X_{(p)}\end{aligned}$$

is an isomorphism on torsion free quotients. Moreover, the right hand side is torsion free in degrees $*<2p-4+n$, so the map is an isomorphism in this range.

Proof

As a preparation to the proof, note that by specialising the Hilton–Milnor theorem to $\vee ^gS^n$, we have an isomorphism

$$\begin{aligned} \textstyle {\pi _{i+1}(\vee ^gS^n)\cong \bigoplus _{\omega \in L_g}\pi _{i+1}(S^{l(\omega )(n-1)+1})}\end{aligned}$$

(37)

where $L_g$ denotes a Hall basis for the free ungraded Lie algebra in g ordered generators and $l(\omega )$ is the word-length of $\omega$. Here the map $\pi _{i+1}(S^{l(\omega )(n-1)+1})\rightarrow \pi _{i+1}(\vee ^gS^n)$ corresponding to $\omega \in L_g$ is given by mapping a class $x\in \pi _{i+1}(S^{l(\omega )(n-1)+1})$ to the composition $(\iota _\omega \circ x)$, where $\iota _\omega \in \pi _{l(\omega )(n-1)+1}(\vee ^gS^{n})$ is the class obtained by taking Whitehead products of the canonical classes $\iota _i \in \pi _{n}(\vee ^gS^n)$ for $1\le i\le g$ represented by the inclusions of the summands as guided by the Lie word $\omega \in L_g$. A proof can be extracted from [47]: combine XI.6.6 and the subsequent discussion with VII.2.6 and X.7.10.

To prove the asserted claim, we use that source and domain of the morphism in the statement are both degreewise finitely generated and that the rationalisation of this morphism agrees with (36), so to prove the first part of the claim, it suffices to show that all classes in $\pi _{*+1}X_{(p)}$ of infinite order are in the image. From (37), we see every class in $\pi _{k}X_{(p)}$ is a composition $(y \circ x)$ of some $x\in \pi _kS^m_{(p)}$ with $m\ge n$ and a class $y\in \pi _mX_{(p)}$ in the image of the map in question. The group $\pi _kS^m_{(p)}$ is finite unless $k=m$, where it is generated by the identity, or $m=2l$ and $k=4l-1$, where it is is generated by $[\mathrm {id}_{S^{2l}},\mathrm {id}_{S^{2l}}]$, since this element has Hopf invariant 2 and we assumed p to be odd. As $y\circ [\mathrm {id}_{S^{2l}},\mathrm {id}_{S^{2l}}]=[y,y]$ in $\pi _{4l-1}X_{(p)}$ and the image of $L_{(p)}^X\rightarrow \pi _{*+1}X_{(p)}$ is closed under taking brackets, this implies the first part of the claim. The second part follows from Serre’s result [38, p. 498, Prop. 5] that $\pi _kS^m$ is p-torsion free for $k-m<2p-3$ together with another application of (37). $\square$

As a result of Lemma 4.2, every map $f:X\rightarrow Y$ between bouquets of equidimensional spheres induces a morphism $f_*:L^X_{(p)}\rightarrow L^Y_{(p)}$ by taking torsion free quotients of p-local homotopy groups, so the following extension of Theorem 4.1 might not come as a surprise.

Proposition 4.3

For an odd prime p and a map $f:X\rightarrow Y$ between based spaces $X\simeq \vee ^g S^n$ and $Y\simeq \vee ^h S^m$ with $n,m\ge 2$ , the map of Theorem 4.1 fits into a commutative square

which is natural in X and Y and whose upper arrow is an isomorphism for $*<2p-3-(n-m)$.

Remark 4.4

Dwyer’s tame homotopy theory [13] provides a p-local generalisation of Quillen’s rational homotopy theory for primes p that are just large enough with respect to the degree to prevent stable k-invariants from appearing. It is not unlikely that Theorem 4.1 could be generalised to this setting, but our layman extension Proposition 4.3 for bouquets of spheres suffices for the applications we have in mind.

Proof of Proposition 4.3

We begin with a twofold simplification of the statement. Firstly, the claimed naturality is automatic, since the vertical maps are evidently natural, the bottom map is natural by Theorem 4.1, and the right vertical map is injective, so it suffices to construct a top arrow with the desired properties for $X=\vee ^gS^n$. Secondly, there is a commutative diagram

induced by restricting derivations to generators, which shows that it is enough to produce a dashed arrow making the diagram

(38)

commute. To do so, we consider the composition

$$\begin{aligned} \pi _*(\mathrm {Maps}_*(X,Y);f)\xrightarrow [\cong ]{(-f)_*}\pi _*(\mathrm {Maps}_*(X,Y);*)\cong \mathrm {Hom}(s^{-1}H^X,\pi _{*+1}Y)^+\end{aligned}$$

(39)

whose first isomorphism is given by acting with the inverse of f, using the loop space structure on $\mathrm {Maps}_*(X,Y)$, and whose second isomorphism is induced by mapping a class in $\pi _k(\mathrm {Maps}_*(X,Y);*)$ represented by a pointed map $g:S^k\rightarrow \mathrm {Maps}_*(X,Y)$ to the composition

$$\begin{aligned}\mathrm {H}_n(X)\cong \mathrm {H}_{n+k}(S^k\wedge X)\cong \pi _{n+k}(S^k\wedge X)\overset{g_*}{\longrightarrow }\pi _{n+k}(Y),\end{aligned}$$

involving the suspension isomorphism, the inverse of the Hurewicz map, and the adjoint of g. Postcomposing (39) with the map given by p-localising and taking torsion free quotients results by Lemma 4.2 in a dashed map with the claimed connectivity property, so we are left to show that this choice does make the diagram (38) commute, i.e. that the rationalisation of (39) agrees with the bottom map of (38). The adjoint of a map $h:S^k\rightarrow \mathrm {Maps}_*(X,Y)$ representing a class in $\pi _*(\mathrm {Maps}_*(X,Y);f)$ forms the top arrow of the diagram

(40)

whose middle diagonal arrow is induced by h via the canonical homeomorphism $(S^k\times X)/(S^k\vee *)\cong S^k_+\wedge X$ and whose vertical equivalence is given as the composition

$$\begin{aligned}S^k_+\wedge X\xrightarrow {\mathrm {id}_{S^k_+}\wedge \nabla } S^k_+\wedge X\vee S^k_+ \wedge X\xrightarrow {c}X\vee S^k \wedge X\end{aligned}$$

using the co-H-space structure $\nabla$ of X and the evident collapse map c. The map $(-f)_*(h)$ is the adjoint of a representative of the image of h under the first map in (39), so (40) commutes up to changing h within its class in $\pi _k(\mathrm {Maps}_*(X,Y);f)$. We thus obtain a rational model for the top arrow in (40) as the composition

$$\begin{aligned} \begin{aligned}&\left( \mathbf {L}\left( s^{-1}H^X_{\mathbf {Q}}\oplus s^{-1+k}H_\mathbf {Q}^X\oplus s^{-1}H_\mathbf {Q}^{S^k}\right) ,d \right) \\ {}&\quad \longrightarrow L_\mathbf {Q}^{S^k\vee S^k\wedge X}\xrightarrow {\pi _{*+1}(f\vee (-f)_*(g))\otimes \mathbf {Q}} L_{\mathbf {Q}}^Y,\end{aligned}\end{aligned}$$

(41)

where the source is the Lie model of $S^k\times X$ described in [30, Cor. 2.2], i.e. its differential d is trivial on $s^{-1}H^X_{\mathbf {Q}}\oplus s^{-1}H_\mathbf {Q}^{S^k}$ and is on $s^{-1+k}H_\mathbf {Q}^X$ given as

$$\begin{aligned} s^{-1+k}H_\mathbf {Q}^X\cong s^{-1}H^X_{\mathbf {Q}}\xrightarrow {(-1)^{k-1}[z,-]}\mathbf {L}\left( s^{-1}H^X_{\mathbf {Q}}\oplus s^{-1+k}H_\mathbf {Q}^X\oplus s^{-1}H_\mathbf {Q}^{S^k}\right) \end{aligned}$$

where the first isomorphism is the canonical identification as ungraded vector spaces induced by the identity and $z\in s^{-1}H_\mathbf {Q}^{S^k}$ denotes the standard generator. The first map in the composition (41) takes the quotient by the dg Lie ideal generated by the subspace $s^{-1}H_\mathbf {Q}^{S^k}$ and the second map is defined as indicated. Using this particular choice of rational model in the definition of the isomorphism of Theorem 4.1 in [30, p. 176–177], the image of the class defined by h under the bottom horizontal composition in (38) is precisely its image under (39) after rationalisation, so the claim follows. $\square$

4.6 p-local homotopy groups of $\mathrm {BhAut}^{\mathrm {id}}_{D^{2n}}(V_g,W_{g,1})$

The theory set up in the previous paragraphs will allow us to compute the p-local homotopy groups of the classifying space $\mathrm {BhAut}^{\mathrm {id}}_{D^{2n}}(V_g,W_{g,1})$ of the identity component of the topological monoid of relative homotopy automorphisms as defined in Sect. 3.1 as a module over the group

$$\begin{aligned}\pi _1\mathrm {BhAut}_{D^{2n}}(V_g,W_{g,1})\cong \pi _0\mathrm {hAut}_{D^{2n}}(V_g,W_{g,1}).\end{aligned}$$

More generally, we will compute the p-local homotopy groups of the spaces participating in the fibration sequence (see Section 3.1 for the notation)

$$\begin{aligned} \mathrm {BhAut}_{\partial }(V_g)\longrightarrow \mathrm {BhAut}_{D^{2n}}(V_g,W_{g,1})\longrightarrow \mathrm {BhAut}^{\mathrm {ext}}_{\partial }(W_{g,1}) \end{aligned}$$

(42)

induced by restriction, together with the induced action of $\pi _0\mathrm {hAut}_{D^{2n}} (V_g,W_{g,1})$. To state the answer (and give the proof), we adopt the notation of in the previous subsection for the three manifolds $W_{g,1}$, $V_g$, and $\partial W_{g,1}$ involved, which are homotopy equivalent to bouquets of spheres. We do however omit the g-superscripts to increase readability, so write

$$\begin{aligned} H_{(p)}^W= & {} \widetilde{\mathrm {H}}_*(W_{g,1};\mathbf {Z}_{(p)}), L_{(p)}^W=\mathbf {L}(s^{-1}H_{(p)}^W),\\ H_{(p)}^V= & {} \widetilde{\mathrm {H}}_*(V_{g};\mathbf {Z}_{(p)}),\quad \text {and} \quad L_{(p)}^V=\mathbf {L}(s^{-1}H_{(p)}^V) \end{aligned}$$

and omit the (p)-subscripts to denote the integral analogues. Moreover, we generically write $\iota$ for any combination of the inclusions

$$\begin{aligned}\partial W_{g,1}\subset W_{g,1}\subset W_g\subset V_g.\end{aligned}$$

Finally, we let $\omega \in L_{W_{g,1}}$ be the class that represents the inclusion $S^{2n-1}=\partial W_{g,1}\subset W_{g,1}$ of the boundary of $W_{g,1}=\sharp ^g(S^n\times S^n)\backslash \mathrm {int}(D^{2n})$, i.e. the attaching map

$$\begin{aligned} \textstyle {\omega =\sum _{i=1}^{g}[e_i,f_i]\in \pi _{2n-1}W_{g,1}},\end{aligned}$$

(43)

where $e_i,f_i\in \pi _nW_{g,1}$ correspond to the first respectively second $S^n$-summand in the ith summand of

$$\begin{aligned}W_{g,1}\cong \sharp ^{g}S^n\times S^n\backslash \mathrm {int}(D^{2n})\simeq \vee ^g (S^n\vee S^n).\end{aligned}$$

Note that the inclusion $\partial W_{g,1}\subset V_g$ is trivial, since it factors over $W_g=W_{g,1}\cup _{\partial W_{g,1}}D^{2n}$.

Remark 4.5

Note that $H^{W}$ and $H^{V}$ stand for the graded $\mathbf {Z}$-module given by the reduced homology of $W_{g,1}$ and $V_g$, which shall not be confused with the ungraded middle dimensional integral homology groups of these spaces that featured in Section 3.2.1 as $H_{W_{g,1}}$ and $H_{V_g}$.

Theorem 4.6

Let $n\ge 2$ and p an odd prime.

• (i) The inclusion $\pi _{0}\mathrm {Maps}_{\partial }(V_{g},V_g)\subset \pi _{0}\mathrm {hAut}_{\partial }(V_{g})$ is an equality. This group is abelian.

• (ii) In degrees $0<*<2p-3-n$, the boundary map of the fibration (42) fits into a commutative diagram of graded $\mathbf {Z}_{(p)}$-modules with exact rows

  

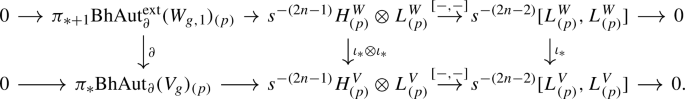
  which is $\pi _0\mathrm {hAut}_{D^{2n}}(V_g,W_{g,1})$-equivariant with respect to the action on the leftmost column induced by (42) and by the action through $H^{W}$ and $H^{V}$ on the other columns.

• (iii) Rationally, the conclusion of (ii) holds in all positive degrees.

A splitting of the canonical projection $\iota _*:H_{W_{g,1}}\rightarrow H_{V_g}$ induces compatible splittings of the rightmost two columns of the diagram in Theorem 4.6 (ii), so the boundary map $\partial$ of the fibration (42) is p-locally split surjective in a range and we conclude the following.

Corollary 4.7

Let $n\ge 2$ and p an odd prime. In degrees $0<*<2p-4-n$, the graded $\mathbf {Z}_{(p)}[\pi _0\mathrm {hAut}_{D^{2n}}(V_g,W_{g,1})]$-module $\pi _{*+1}\mathrm {BhAut}_{D^{2n}}(V_g,W_{g,1})_{(p)}$ is isomorphic to the common kernel of the maps

$$\begin{aligned}&s^{-(2n-1)}H^{W}_{(p)}\otimes L_{(p)}^{W}\overset{\left[ -,-\right] }{\longrightarrow } s^{-(2n-2)}[L_{(p)}^{W}, L_{(p)}^{W}] \quad \text {and}\\&s^{-(2n-1)}H^{W}_{(p)}\otimes L_{(p)}^{W}\overset{\iota _*\otimes \iota _*}{\longrightarrow }s^{-(2n-1)}H^{V}_{(p)}\otimes L_{(p)}^{V}.\end{aligned}$$

Rationally, this holds in all positive degrees.

In particular, Theorem 4.6 and Corollary 4.7 imply that the $\pi _0\mathrm {hAut}_{D^{2n}}(V_g,W_{g,1})$-action on the p-local higher homotopy groups of the spaces participating in (42) factors in a range of degrees through the morphism (recall $K_g=\ker (\mathrm {H}_n(W_{g,1})\rightarrow \mathrm {H}_n(V_g))$ from Section 3.2.1)

$$\begin{aligned}\pi _0\mathrm {hAut}_{D^{2n}}(V_g,W_{g,1})\longrightarrow \{\phi \in \mathrm {GL}(H_{W_{g,1}})\mid \phi (K_g)\subset K_g\}\end{aligned}$$

induced by the action on the homology of $W_{g,1}$. During the proof of Theorem 4.6 and the preceding Lemma 4.8, we frequently use Proposition 4.3 to implicitly identify p-local homotopy groups of path components of pointed mapping spaces between bouquets of equidimensional spheres with derivations of free graded Lie algebras in a range of degrees. We denote by $\mathrm {Maps}_*^f(X,Y)$ for a map of based spaces $f:X\rightarrow Y$ the corresponding component of the mapping space, pointed by f. Reminding the reader of our notation for spaces of derivations in Section 4.2, we begin with the following lemma, whose first part is rationally due to Berglund and Madsen [8, Prop. 5.6].

Lemma 4.8

Let $n\ge 2$ and p an odd prime.

• (i) In degrees $*<2p-3-n$, the morphism induced by relaxing the boundary condition

  $$\begin{aligned}\pi _*\mathrm {Maps}_\partial ^{\mathrm {id}}(W_{g,1},W_{g,1})_{(p)}\longrightarrow \pi _*\mathrm {Maps}_*^{\mathrm {id}}(W_{g,1},W_{g,1})_{(p)}\cong \mathrm {Der}(L_{(p)}^{W})^+\end{aligned}$$

  is injective and has image $\mathrm {Der}_{\omega }(L_{(p)}^{W})^+\subset \mathrm {Der}(L_{(p)}^{W})^+$.

• (ii) In the range $*<2p-3-n$, the morphism induced by $W_{g,1}\subset W_g$

  $$\begin{aligned}\pi _*\mathrm {Maps}_*^{\iota }(W_{g},V_g)_{(p)}\longrightarrow \pi _*\mathrm {Maps}_*^{\iota }(W_{g,1},V_g)_{(p)}\cong \mathrm {Der}^{\iota }(L_{(p)}^{W},L_{(p)}^{V})^+\end{aligned}$$

  is injective and has image $\mathrm {Der}^{\iota }_{\omega }(L_{(p)}^{W},L_{(p)}^{V})^+\subset \mathrm {Der}^{\iota }(L_{(p)}^{W},L_{(p)}^{V})^+$.

Proof

Restriction along the inclusion $\partial W_{g,1}\subset W_{g,1}$ yields a fibration

$$\begin{aligned} \mathrm {Maps}_*(W_{g,1},W_{g,1})\longrightarrow \mathrm {Maps}_*(\partial W_{g,1},W_{g,1})\end{aligned}$$

(44)

whose fibre at $\iota$ is $\mathrm {Maps}_\partial (W_{g,1},W_{g,1})$. The induced maps on homotopy groups fits in the range $0<*<2p-2-n$ into a diagram of the form

(45)

whose top square is provided by Proposition 4.3, so commutes. The bottom square is given as follows: the bottom right vertical map is the evaluation at the fundamental class

$$\begin{aligned}\in s^{-1}H_{(p)}^{\partial W_{g,1}}\cong \mathbf {Q}[2n-2],\end{aligned}$$

which factors as a composition of isomorphisms

$$\begin{aligned} \mathrm {Der}^{\iota }(L_{(p)}^{\partial W_{g,1}},L_{(p)}^{W})^+&\overset{\cong }{\longrightarrow }&\mathrm {Hom}(s^{-1}H_{(p)}^{\partial W_{g,1}}, L_{(p)}^{W})^+\\&\overset{\cong }{\longrightarrow }&\big (s^{-(2n-2)}L_{(p)}^{W}\big )^+=\big (s^{-(2n-2)}{[L_{(p)}^{W},L_{(p)}^{W}]}\big )^+\end{aligned}$$

where the first isomorphism restricts to generators, the second isomorphism evaluates at the fundamental class, and the final equality holds for degree reasons. The latter is because elements of degree $>0$ in $s^{-(2n-2)}L_{(p)}^{W}$ correspond to elements of degree $>2n-2$ in $L_{(p)}^{W}$, so are sums of brackets since this Lie algebra is generated in degree $n-1$ as $H_W$ is supported in degree n. The bottom left vertical map is the restriction to positive degrees of the map

$$\begin{aligned} \begin{aligned}\mathrm {Der}(L_{(p)}^{W})\overset{\cong }{\longrightarrow }\mathrm {Hom}(s^{-1}H_{(p)}^{W},L_{(p)}^{W})\cong&L_{(p)}^{W}\otimes (s^{-1}H_{(p)}^{W})^{\vee }\\\cong&s^{-(2n-1)}L_{(p)}^{W}\otimes H_{(p)}^{W}, \end{aligned} \end{aligned}$$

(46)

where the first isomorphism is given by restricting to generators, the second is the canonical one, and the third is induced by the intersection form on $s^{-1}H_{W_{g,1}}$ (see Example B.1). By construction, the composition

$$\begin{aligned} \mathrm {Der}(L_{(p)}^{W})^+\longrightarrow \big (s^{-(2n-2)}[L_{(p)}^{W},L_{(p)}^{W}]\big )^+\end{aligned}$$

(47)

coincides with the evaluation at the class $\omega$ that represents the inclusion $\partial W_{g,1}\subset W_{g,1}$, so it follows from Lemma 1 that this square commutes up to a sign, since $\omega =\sum _{i=1}^{g}[e_i,f_i]\in L_{W_{g,1}}$ agrees up to a sign with the element (76) from the appendix as $e_i^{\#}= f_i$ and $f_i^{\#}= e_i$ holds in the notation of the appendix up to a fixed sign depending on n (which does not play a role in the argument). As the bottom horizontal map is surjective as a consequence of the graded Jacobi identity, the middle horizontal arrow is surjective as well, and hence so is the top one. A consultation of the long exact sequence in homotopy groups induced by the fibration (44) thus proves (i) since the kernel of the middle horizontal arrow of the diagram is $\mathrm {Der}_{\omega }(L_{(p)}^{W})$ as (47) is given by the evaluation at $\omega$. This finishes the proof of (i). The proof of (ii) is completely analogous, based on the fibration sequence obtained by applying $\mathrm {Maps}_*(-,V_g)$ to the cofibration sequence $\partial W_{g,1}\rightarrow W_{g,1}\rightarrow W_g$ instead of (44). The bottom square of the diagram corresponding to (45) is now given by

(48)

whose vertical arrows are given by the composition

$$\begin{aligned} \mathrm {Der}^{\iota }(L_{(p)}^{\partial W_{g,1}},L_{(p)}^{V})^+&\overset{\cong }{\longrightarrow }&\mathrm {Hom}(s^{-1}H_{(p)}^{\partial W_{g,1}},L_{(p)}^{V})^+\\&\overset{\cong }{\longrightarrow }&\big (s^{-(2n-2)}L_{(p)}^{V}\big )^+=\big (s^{-(2n-2)}{[L_{(p)}^{V},L_{(p)}^{V}]}\big )^+\end{aligned}$$

and the restriction to elements of positive degrees of the composition

$$\begin{aligned} \begin{aligned} \mathrm {Der}^\iota (L_{(p)}^{W},L_{(p)}^{V})\xrightarrow {\cong }\mathrm {Hom}(s^{-1}H_{(p)}^{W},L_{(p)}^{V})\cong&L_{(p)}^{V}\otimes (s^{-1}H_{(p)}^{W})^{\vee }\\\cong&s^{-(2n-1)}L_{(p)}^{V}\otimes H_{(p)}^{W},\end{aligned}\end{aligned}$$

(49)

both completely analogous to the two compositions explained below (45). $\square$

Proof of Theorem 4.6

We consider the map of horizontal fibration sequences

(50)

where the top right horizontal arrow is induced by restriction and the rightmost vertical arrow is given by extending a selfmap of $W_{g,1}$ relative to the boundary over the complement of $W_{g,1}\subset W_{g}$ by the identity, followed by postcomposition with the inclusion $W_{g}\subset V_g$. The induced morphism $\pi _*\mathrm {Maps}^{\mathrm {id}}_*(V_g,V_g)\rightarrow \pi _*\mathrm {Maps}^{\iota }_*(W_g,V_g)$ is injective because its composition with the morphism $\pi _*\mathrm {Maps}^{\iota }_*(W_g,V_g)\rightarrow \pi _*\mathrm {Maps}^{\iota }_*(W_{g,1},V_g)$ induced by restriction along the inclusion $W_{g,1}\subset W_g$ is a retract since the composition

$$\begin{aligned}\vee ^g(S^n\vee S^n)\simeq W_{g,1}\subset W_g\subset V_g\simeq \vee ^gS^n\end{aligned}$$

is a homotopy retraction. From the long exact sequence in homotopy groups of the bottom fibration, we see that the monoid $\pi _0\mathrm {Maps}_{\partial }(V_g,V_g)$ receives a surjection from $\pi _1\mathrm {Maps}_*^{\iota }(W_g,V_g)$, and this is a monoid homomorphism as it agrees with the map induced on $\pi _0(-)$ by the homotopy fibre inclusion of the fibre sequence of $A_\infty$-spaces

$$\begin{aligned}\big (\Omega \mathrm {Maps}_*^{\iota }(W_g,V_g) \simeq \mathrm {hofib}_{\mathrm {id}}(\mathrm {inc})\big )\longrightarrow \mathrm {Maps}_{\partial }(V_g,V_g)\overset{\mathrm {inc}}{\longrightarrow }\mathrm {Maps}_{*}(V_g,V_g).\end{aligned}$$

The group $\pi _1\mathrm {Maps}_*^{\iota }(W_g,V_g)$ is abelian since we have

$$\begin{aligned} \pi _1\mathrm {Maps}_*^{\iota }(W_g,V_g)\cong [S^1\wedge W_g,V_g]_*\cong & {} [S^1\wedge (\vee ^{2g} S^n\vee S^{2n}),V_g]_*\\\cong & {} \pi _{n+1}(V_g)^{\oplus 2g}\oplus \pi _{2n+1}(V_g),\end{aligned}$$

using $S^1\wedge W_g\simeq S^1\wedge (\vee ^{2g} S^n\vee S^{2n})$ due to the fact that the attaching map (43) of the top-dimensional cell in the usual CW-decomposition of $W_g$ is a sum of Whitehead-brackets and thus nullhomotopic after suspension. Being surjected upon by an abelian group, the monoid $\pi _0\mathrm {Maps}_{\partial }(V_g,V_g)$ is itself an abelian group and hence agrees with $\pi _0\mathrm {hAut}_{\partial }(V_g)$, as claimed in (i). To prove (ii), we combine the injectivity we just observed with Lemma 4.8 (ii) and the long exact sequence of the bottom row in (50) to obtain a short exact sequence

$$\begin{aligned} 0\longrightarrow \mathrm {Der}(L_{(p)}^{V})^+&\overset{(-)\circ \iota _*}{\longrightarrow }&\mathrm {Der}^{\iota }_{\omega }(L_{(p)}^{W},L_{(p)}^{V})^+\nonumber \\\longrightarrow & {} \pi _{*-1}\mathrm {Maps}_\partial ^{\mathrm {id}}(V_g,V_g)_{(p)}\longrightarrow 0\end{aligned}$$

(51)

in the range $*<2p-3-n$. Combining this with Lemma 4.8 (i), we see that the boundary map in the long exact sequence in homotopy groups of the upper fibration of (50) fits in degrees $*<2p-3-n$ into a commutative diagram

(52)

where $\pi$ is the quotient map and the right vertical map is induced by (51). To finish the proof of (ii), we thus need to show that the bottom composition of (52) fits as the left vertical arrow in a diagram as in (ii). To see this, we first combine the bottom square of (45) with the compatible square (48) to obtain a commutative diagram with exact rows

(53)

Next, writing

$$\begin{aligned}K:=\ker (\iota _*:H^W\rightarrow H^V),\end{aligned}$$

we note that there is a chain of natural isomorphisms

$$\begin{aligned} \mathrm {Der}(L_{(p)}^{V}){\cong }\mathrm {Hom}(H_{(p)}^{V},L_{(p)}^{V}){\cong } L_{(p)}^{V}{\otimes } (s^{-1}H_{(p)}^{V})^\vee {\cong } s^{-(2n-1)}L_{(p)}^{V}{\otimes } K_{(p)}\qquad \end{aligned}$$

(54)

defined analogously to (and compatible with) (49), using that the isomorphism $(H^{W})^\vee \cong H^{W}$ induced by the intersection form (neglecting grading shifts) sends $(H^{V})^\vee \subset (H^{W})^\vee$ to $K\subset H^{W}$. Except for the equivariance claim, (ii) now follows by combining the chain of isomorphisms (54) with the diagrams (52)–(53) and the chain of isomorphisms

$$\begin{aligned}&\big (s^{-(2n-1)}L_{(p)}^{V}\otimes H_{(p)}^{W}\big )/\big ( s^{-(2n-1)}L_{(p)}^{V}\otimes K_{(p)} \big )\\&\quad \cong s^{-(2n-1)}L_{(p)}^{V}\otimes \big (H_{(p)}^{W}/ K_{(p)} \big )\cong s^{-(2n-1)}L_{(p)}^{V}\otimes H_{(p)}^{V}. \end{aligned}$$

This uses that the inclusion $\mathrm {hAut}^{\mathrm {ext}}_\partial (W_{g,1})\subset \mathrm {Maps}_\partial (W_{g,1},W_{g,1})$ is 0-coconnected and that we have $\mathrm {hAut}_\partial (V_g)=\mathrm {Maps}_\partial (V_g,V_g)$ by (i). To see the equivariance, note that all vertical maps in the diagram of (ii) are equivariant by construction. Since they are also surjective (see the discussion after the statement), it suffices to show that the top row is equivariant. This is clear for the second map in the top row, so we are left with showing equivariance of the first map

$$\begin{aligned} \pi _{*+1}\mathrm {BhAut}_\partial (W_{g,1})_{(p)}\longrightarrow s^{2n-1}H_{(p)}^{W}\otimes L_{(p)}^{W}.\end{aligned}$$

(55)

With respect to the canonical isomorphisms in positive degrees

$$\begin{aligned}\pi _{*+1}\mathrm {BhAut}_\partial (W_{g,1})_{(p)}\cong \pi _{*}\mathrm {hAut}_\partial (W_{g,1})_{(p)}\cong \pi _*\mathrm {Maps}_\partial (W_{g,1},W_{g,1})_{(p)},\end{aligned}$$

the action on the domain of (55) is induced by conjugation. Going through the proof, we see that (55) arises as a composition of the form

$$\begin{aligned} \pi _{*}\mathrm {Maps}^{\mathrm {id}}_\partial (W_{g,1},W_{g,1})_{(p)}\longrightarrow & {} \pi _{*}\mathrm {Maps}^{\mathrm {id}}_*(W_{g,1},W_{g,1})_{(p)}\\\longrightarrow & {} \mathrm {Der}(L_{(p)}^{W})\cong s^{2n-1}H_{(p)}^{W}\otimes L_{(p)}^{W}.\end{aligned}$$

The first map relaxes the boundary condition, which is equivariant. The second map is given by the isomorphism in Proposition 4.3, and its equivariance follows from the naturality part of that proposition. The third map is provided by the chain of isomorphisms (46), which is equivariant by the naturality of the intersection form. This finishes the proof of (ii). To see (iii), note that all restrictions on the degree in the proof of (ii) originated from the assumption on the degree in Proposition 4.3. This proposition holds rationally without that assumption, so the proof of 4.6 also applies to 4.6. $\square$

In a range of degrees, the particular shape of the p-local homotopy groups of the space $\mathrm {BhAut}^{\mathrm {id}}_{D^{2n}}(V_g,W_{g,1})$ ensured by Corollary 4.7 allows us to pass from homotopy to homology groups, which is what we are actually interested in. In the following statement, we consider the module $\mathrm {H}_n(W_{g,1};\mathbf {Z}_{(p)})$ as ungraded.

Corollary 4.9

For $n\ge 2$, there is an injection of graded $\pi _0\mathrm {hAut}_{D^{2n}} (V_g,W_{g,1})$-modules

in degrees $*< \min (2n-1,2p-3-n)$ for primes p.

Proof

We may assume $p> 3$, since otherwise the claim has no content. As a result of Corollary 4.7, there is an injective map of graded $\pi _0\mathrm {hAut}_{D^{2n}}(V_g,W_{g,1})$-modules

in degrees $0<*< 2p-4-n$. Using that we have

$$\begin{aligned}&[s^{-1}H^{W}_{(p)},s^{-1}H^{W}_{(p)}]\subset (s^{-1}H^{W}_{(p)})^{\otimes 2}\end{aligned}$$

by antisymmetrisation and that $H^{W}_{(p)}=\widetilde{\mathrm {H}}_*(W_{g,1};\mathbf {Z}_{(p)})$ is concentrated in degree n, we obtain

$$\begin{aligned} s^{-(2n-1)}H^{W}_{(p)}\otimes \mathbf {L}(s^{-1}H^{W}_{(p)})\subset & {} s^{-(2n-1)}H^{W}_{(p)}\otimes (s^{-1}H^{W}_{(p)})^{\otimes 2}\\= & {} \big (\mathrm {H}_n(W_{g,1};\mathbf {Z}_{(p)})^{\otimes 3}\big )[n-1],\end{aligned}$$

in degrees $*<2n-2$, so the claim holds for homotopy instead of homology groups. This leaves us with showing that the p-local Hurewicz homomorphism

$$\begin{aligned} \pi _{*}\mathrm {BhAut}^{\mathrm {id}}_{D^{2n}}(V_g,W_{g,1})_{(p)}\longrightarrow \widetilde{\mathrm {H}}_*(\mathrm {BhAut}^{\mathrm {id}}_{D^{2n}}(V_g,W_{g,1})_{(p)};\mathbf {Z}_{(p)}) \end{aligned}$$

is an isomorphism in degree $*< m:=\min (2n-1,2p-3-n)$. Since submodules of free $\mathbf {Z}_{(p)}$-modules are free, it follows from the first part of the proof that n-truncation induces a p-locally m-connected map of the form

$$\begin{aligned}\mathrm {BhAut}^{\mathrm {id}}_{D^{2n}}(V_g,W_{g,1})\longrightarrow K(A,n)\end{aligned}$$

where A is a free $\mathbf {Z}_{(p)}$-module, so it suffices to show that K(A, n) has trivial $\mathbf {Z}_{(p)}$-homology in the range $n<*<m$. Since A is free, it is enough to show that $\mathrm {H}_*(K(\mathbf {Z}_{(p)},n);\mathbf {Z}_{(p)})\cong \mathrm {H}_*(K(\mathbf {Z},n);\mathbf {Z}_{(p)})$ vanishes in this range, which is certainly true rationally, so we may instead prove that $\mathrm {H}^*(K(\mathbf {Z},n);\mathbf {F}_{p})$ vanishes for $n+1<*<m+1$. As the natural map

$$\begin{aligned}\mathbf {HF}_p^*(\mathbf {HZ})={\lim }_n\mathrm {H}^{*+n}(K(\mathbf {Z},n);\mathbf {F}_p)\longrightarrow \mathrm {H}^{*+n}(K(\mathbf {Z},n);\mathbf {F}_p)\end{aligned}$$

is an isomorphism in degrees $*<n$, this follows from showing that the spectrum cohomology $\mathbf {HF}_p^*(\mathbf {HZ})$ vanishes in degrees $0<*<\min (n,2p-2-2n)$. But $\mathbf {HF}_p^*(\mathbf {HZ})$ is a quotient of the mod p Steenrod algebra $\mathbf {HF}_p^*(\mathbf {HF}_p)$ by an ideal containing the Bockstein, so $\mathbf {HF}_p^*(\mathbf {HZ})$ vanishes in degrees $0<*<2p-2$ and we conclude the assertion. $\square$

5 The proof of Theorem A

This section is devoted to the proof of the following refinement of Theorem A.

Theorem 5.1

For $n>3$, there is a nilpotent space X and a zig–zag

$$\begin{aligned}\mathrm {BC}(D^{2n})\overset{\phi }{\longrightarrow } X\overset{\psi }{\longleftarrow } \Omega _0^{\infty +1}\mathrm {K}(\mathbf {Z})\end{aligned}$$

such that p-locally, $\phi$ is $\min (2n-4,2p-4-n)$-connected and $\psi$ is $\min (2n,2p-4)$-connected.

Remark 5.2

As remarked in the introduction, our proof is independent of Waldhausen’s work on pseudoisotopy theory. If one is willing to invest Dwyer–Weiss–Williams’ index theorem [12] (which relies in parts of Waldhausen’s work), then it takes little effort to also explicitly identify X and $\psi$ in terms of well-known infinite loop spaces, see Section 5.4.

As a first step towards proving Theorem 5.1, we replace $\mathrm {BC}(D^{2n})$ by an equivalent space that is more convenient to compare to the various automorphism spaces of high-dimensional handlebodies $V_g=\natural ^gD^{n+1}\times S^n$ we studied in the previous sections.

Lemma 5.3

For $d\ge 5$, there exists a homotopy equivalence

$$\begin{aligned} \mathrm {BC}(D^{d})\simeq & {} \widetilde{\mathrm {Diff}}_{D^{d}}(D^{d+1})/\mathrm {Diff}_{D^{d}}(D^{d+1})\\= & {} \mathrm {hofib}(\mathrm {BDiff}_{D^{d}}(D^{d+1})\rightarrow \mathrm {B\widetilde{Diff}}_{D^{d}}(D^{d+1}))\end{aligned}$$

Proof

A choice of identification $D^{d}\times [0,1]\cong D^{d+1}$ by smoothing corners induces an equivalence $\mathrm {BC}(D^{d})\simeq \mathrm {BDiff}_{D^{d}}(D^{d+1})$, so the claim is equivalent to showing that the space of block diffeomorphisms $\widetilde{\mathrm {Diff}}_{D^{d}}(D^{d+1})$ is contractible. This follows from Cerf’s result that every concordance of a manifold of dimension at least 5 is isotopic to the identity [11], together with the isomorphisms $\pi _k(\widetilde{\mathrm {Diff}}_{D^{d}}(D^{d+1});\mathrm {id})\cong \pi _0\mathrm {Diff}_{D^{d+k}}(D^{d+k+1})\cong \pi _0\mathrm {C}(D^{d+k})$ which is most easily seen by using the combinatorial description of the homotopy groups of the Kan complex $\widetilde{\mathrm {Diff}}_{D^{d}}(D^{d+1})_\bullet$ (see Section 1.4). $\square$

The alternative point of view on $\mathrm {BC}(D^{2n})$ as the homotopy fibre

$$\begin{aligned}\widetilde{\mathrm {Diff}}_{D^{2n}}(D^{2n+1})/\mathrm {Diff}_{D^{2n}}(D^{2n+1})=\widetilde{\mathrm {Diff}}_{D^{2n}}(V_0)/\mathrm {Diff}_{D^{2n}}(V_0)\end{aligned}$$

is advantageous as it makes a stabilisation map of the form

$$\begin{aligned} \mathrm {BC}(D^{2n})\simeq \widetilde{\mathrm {Diff}}_{D^{2n}}(V_0)/\mathrm {Diff}_{D^{2n}}(V_0)\longrightarrow \widetilde{\mathrm {Diff}}_{D^{2n}}(V_g)/\mathrm {Diff}_{D^{2n}}(V_g),\end{aligned}$$

(56)

apparent, which is induced by iterating the stabilisation maps for $\mathrm {BDiff}_{D^{2n}}(V_g)$ and its block analogue explained in Section 3.5. It is a consequence of Morlet’s lemma of disjunction that this map is highly connected:

Lemma 5.4

The stabilisation map (56) is $(2n-4)$-connected.

Proof

Taking vertical homotopy fibres in the diagram (see Section 3.1 for the notation)

of fibre sequences whose diagonal arrows are given by the iterated stabilisation maps results in a map of fibre sequences of the form

whose inner diagonal map is the map in question and whose rightmost equivalences follow from another application of Cerf’s result mentioned in the previous proof. As the manifolds $V_g$ and $W_{g,1}$ are $(n-1)$-connected, the two outer diagonal maps are $(2n-4)$-connected by a form of Morlet’s lemma of disjunction [6, p. 29, Cor. 3.2], so the claim follows from the induced ladder of long exact sequences in homotopy groups. $\square$

Combining the previous two lemmas results in a $(2n-4)$-connected map

$$\begin{aligned}&\mathrm {BC}(D^{2n})\rightarrow \widetilde{\mathrm {Diff}}_{D^{2n}}(V_\infty )/\mathrm {Diff}_{D^{2n}}(V_\infty ):=\mathrm {hocolim}_g\widetilde{\mathrm {Diff}}_{D^{2n}}(V_g)/\mathrm {Diff}_{D^{2n}}(V_g)\end{aligned}$$

(57)

to the homotopy colimit over the stabilisation maps, so in order to prove Theorem 5.1, it remains to establish a zig–zag with the claimed connectivity properties between this homotopy colimit and the zero component of the once looped algebraic K-theory space of the integers $\Omega _0^{\infty +1}\mathrm {K}(\mathbf {Z})$, which we model as the plus-construction³

$$\begin{aligned}\Omega _0^{\infty +1}\mathrm {K}(\mathbf {Z})\simeq \mathrm {BGL}_\infty (\mathbf {Z})^+\end{aligned}$$

of the homotopy colimit $\mathrm {BGL}_\infty (\mathbf {Z}):=\mathrm {hocolim}_g\mathrm {BGL}_g(\mathbf {Z})$ over the stabilisation maps induced by the usual block inclusions $\mathrm {GL}_g(\mathbf {Z})\subset \mathrm {GL}_{g+1}(\mathbf {Z})$. The zig–zag we construct arises as part of a commutative zig–zag of horizontal homotopy fibre sequences of the form

(58)

which we explain now. Denoting the tangential structure encoding stable framings by $\mathrm {sfr}:\mathrm {EO}\rightarrow \mathrm {BO}$, the upper right corner is defined as

$$\begin{aligned}\mathrm {B\widetilde{Diff}}^{\mathrm {sfr}}_{D^{2n}}(V_\infty ;\ell _0)_\ell :=\mathrm {hocolim}_g\mathrm {B\widetilde{Diff}}^{\mathrm {sfr}}_{D^{2n}}(V_g;\ell _0)_\ell \end{aligned}$$

along the stabilisation maps explained in Section 3.5, and the space $\mathrm {BDiff}^{\mathrm {sfr}}_{D^{2n}}(V_\infty ;\ell _0)_\ell$ is defined analogously, using the unstable $(2n+1)$-dimensional tangential structure induced by $\mathrm {sfr}:\mathrm {EO}\rightarrow \mathrm {BO}$, which we denote by the same symbol (see Section 1.8.1). The upper right horizontal map is the homotopy colimit of the comparison map

$$\begin{aligned}\mathrm {BDiff}^{\mathrm {sfr}}_{D^{2n}}(V_g;\ell _0)_\ell \longrightarrow \mathrm {B\widetilde{Diff}}^{\mathrm {sfr}}_{D^{2n}}(V_g;\ell _0)_\ell \end{aligned}$$

whose homotopy fibre at the base point is canonically equivalent to $\widetilde{\mathrm {Diff}}_{D^{2n}}(V_\infty )/\mathrm {Diff}_{D^{2n}}(V_\infty )$ in view of Lemma 1.8 and the fact that homotopy fibres commute with sequential homotopy colimits. Using a functorial model of the plus-construction (see e.g. [4, VII.6.2]), the upper right square of (58) is induced by the homotopy colimit of the composition

$$\begin{aligned}&\mathrm {BDiff}^{\mathrm {sfr}}(V_g;\ell _0)_\ell \rightarrow \mathrm {B\widetilde{Diff}}^{\mathrm {sfr}}(V_g;\ell _0)_\ell \rightarrow \mathrm {BGL}(H_{V_g}) =\mathrm {BGL}(\mathrm {H}_n(V_g;\mathbf {Z}))\cong \mathrm {BGL}_g(\mathbf {Z}) \end{aligned}$$

(59)

along the stabilisation maps (see Section 3.5), where the second map is induced by the action on the middle homology of $V_g$. The space X is defined as the homotopy fibre of the map $\mathrm {BDiff}^{\mathrm {sfr}}(V_\infty ;\ell _0)_\ell ^+\rightarrow \mathrm {BGL}_\infty (\mathbf {Z})^+$, and it receives a map from the top left corner induced by the commutativity of the upper right square. The bottom row is induced by the inclusion of the basepoint in the universal cover $\mathrm {BGL}_\infty (\mathbf {Z})^+\langle 1\rangle$ whose homotopy fibre agrees with the base point component of $\Omega \mathrm {BGL}_\infty (\mathbf {Z})^+$. This explains the diagram (58), aside from the map of fibre sequences from the bottom to the middle row, which is induced by the universal cover $\mathrm {BGL}_\infty (\mathbf {Z})^+\langle 1\rangle \rightarrow \mathrm {BGL}_\infty (\mathbf {Z})^+$ and the basepoint inclusion of $\mathrm {BDiff}^{\mathrm {sfr}}(V_\infty ;\ell _0)_\ell ^+$.

In the two following subsections, we continue the preparations of the proof of Theorem 5.1 by analysing the vertical maps and .

5.1 The stable homology of $\mathrm {BDiff}_{D^{2n}}(V_g)$ and the map

Botvinnik and Perlmutter [10] have computed the stable homology of $\mathrm {BDiff}^\theta _{D^{2n}}(V_g;\ell _0)_\ell$ in homotopy theoretical terms for all tangential structures $\theta :B\rightarrow \mathrm {BSO}(2n+1)$ whose space B is n-connected. For us, their main result [10, Cor. 6.8.1, Prop. 6.14] is most conveniently expressed as an identification of the group completion of the disjoint union

$$\begin{aligned}\textstyle {\mathcal {M}_{\theta }:=\coprod _{g\ge 0}\mathrm {BDiff}_{D^{2n}}^{\theta }(V_g;\ell _0)_\ell },\end{aligned}$$

which becomes a homotopy commutative topological monoid under boundary connected sum when choosing an appropriate point-set model (see [10, Prop. 6.11, Prop. 6.14]).

Theorem 5.5

(Botvinnik–Perlmutter)For $n>3$, a tangential structure $\theta :B\rightarrow \mathrm {BSO}(2n+1)$ for which B is n-connected, there is a homotopy equivalence of the form

$$\begin{aligned}\Omega \mathrm {B}\mathcal {M}_{\theta }\simeq \Omega ^\infty \Sigma ^\infty _+B.\end{aligned}$$

The equivalence they produce factors as a composition

$$\begin{aligned} \Omega \mathrm {B} \mathcal {M}_{\theta }\overset{\simeq }{\longrightarrow }\Omega \mathrm {B}\mathcal {C}^\partial _\theta \overset{\simeq }{\longrightarrow }\Omega ^\infty \Sigma ^\infty _+B\end{aligned}$$

(60)

whose intermediate terms is the group-completion of a topological category $\mathcal {C}_\theta ^\partial$ of bordisms between 2n-manifolds with $\theta$-structures, possibly with boundary. This category was studied by Genauer [17], who established the final equivalence in (60) as a parametrised form of the Pontryagin–Thom construction. Botvinnik and Perlmutter showed that $\mathcal {M}_{\theta }$ can be seen as a submonoid of the endomorphism monoid $\mathcal {C}_\theta ^\partial (D^{2n},D^{2n})$ of the closed disc $D^{2n}$ with some $\theta$-structure and that the chain of inclusions $\mathcal {M}_{\theta }\subset \mathcal {C}_\theta ^\partial (D^{2n},D^{2n})\subset \mathcal {C}_\theta ^\partial$ is an equivalence upon taking classifying spaces (see [10, Thm 6.3, Prop. 6.14]).

As $\mathcal {M}_\theta$ is homotopy commutative, Randal-Williams’ elucidation of the group completion theorem [36, Cor. 1.2] moreover provides an equivalence

$$\begin{aligned} \mathrm {BDiff}_{D^{2n}}^{\theta }(V_\infty ;\ell _0)_\ell ^+\simeq \Omega _0\mathrm {B}\mathcal {M}_\theta ,\end{aligned}$$

(61)

which leads to the following consequence of Theorem 5.5 when specialised to the tangential tangential structure encoding stable framings.

Corollary 5.6

The space $\mathrm {BDiff}_{D^{2n}}^{\mathrm {sfr}}(V_\infty ;\ell _0)_\ell ^+$ is nilpotent and p-locally $\min (2n,2p-4)$-connected as long as $n>3$.

Proof

Connected H-spaces are nilpotent, so (61) settles the nilpotency claim. Regarding the connectivity part of the statement, note that the unstable $(2n+1)$-dimensional tangential structure $(\mathrm {sfr})_{2n+1}$ induced by the stable structure $\mathrm {sfr}:\mathrm {EO}\rightarrow \mathrm {BO}$ (see Section 1.8.1) is equivalent to the inclusion $\mathrm {O}/\mathrm {O}(2n+1)\rightarrow \mathrm {BO}(2n+1)$ of the homotopy fibre of the stabilisation $\mathrm {BO}(2n+1)\rightarrow \mathrm {BO}$, so Theorem 5.5 and the discussion preceding this corollary show that the space in question is equivalent to $\Omega ^\infty _0\Sigma ^\infty _+\mathrm {O}/\mathrm {O}(2n+1)$. As $\mathrm {O}/\mathrm {O}(2n+1)$ is 2n-connected, the homotopy groups of $\Omega ^\infty _0\Sigma ^\infty _+\mathrm {O}/\mathrm {O}(2n+1)$ agree in positive degrees less than $2n+1$ with the stable homotopy groups of spheres which are free of p-torsion in degrees less than $2p-3$ by a result of Serre [38, p. 498, Prop. 5], so the claim follows. $\square$

Said differently Corollary 5.6 shows that the base point inclusion in (58) is p-locally $\min (2n,2p-4)$-connected for $n>3$.

5.2 The homology action and the map

As a consequence of Proposition 3.7 (ii), the map on fundamental group induced by is infinite abelian, so the map is as far from being highly connected as possible, even p-locally for any p. Nevertheless, it turns out that it does induce an isomorphism on p-local homology groups in a range, which we shall prove by separately studying the effect on homology of the two maps in the factorisation

$$\begin{aligned} \mathrm {B\widetilde{Diff}}^{\mathrm {sfr}}_{D^{2n}}(V_g;\ell _0)_{\ell }\longrightarrow \mathrm {BG}^{\mathrm {ext}}_{g,\ell }\longrightarrow \mathrm {BGL}(H_{V_g}),\end{aligned}$$

(62)

of the second map in (59). Here $G_{g,\ell }^{\mathrm {ext}}\subset \mathrm {GL}(H_{W_{g,1}})$ is the subgroup considered in Sect. 3.3.

Lemma 5.7

For $n\ge 3$ and any prime p, the induced map

$$\begin{aligned}\mathrm {H}_*\big (\mathrm {B\widetilde{Diff}}^{\mathrm {sfr}}_{D^{2n}}(V_g;\ell _0)_\ell ;\mathbf {Z}_{(p)}\big )\longrightarrow \mathrm {H}_*\big (\mathrm {BG}^{\mathrm {ext}}_{g,\ell };\mathbf {Z}_{(p)}\big )\end{aligned}$$

is an isomorphism for $*<\min (2n-1,2p-3-n)$ and a surjection in that degree.

Proof

The claim is vacuous for $p=2$, so we assume otherwise. Consider the factorisation of the map in question

$$\begin{aligned} \begin{aligned} \mathrm {B\widetilde{Diff}}^{\mathrm {sfr}}_{D^{2n}}(V_g;\ell _0)_\ell&\rightarrow \mathrm {B\widetilde{hAut}}^{\cong }_{D^{2n}}(V_g,W_{g,1})_\ell \\ {}&\rightarrow \mathrm {B}\pi _0\mathrm {\widetilde{hAut}}^{\cong }_{D^{2n}}(V_g,W_{g,1})_\ell \rightarrow \mathrm {BG}^{\mathrm {ext}}_{g,\ell },\end{aligned} \end{aligned}$$

(63)

where the first map is that of Corollary 2.4 applied to the triad $(V_g;D^{2n},W_{g,1})$, the second map is induced by taking path components, and the third is given by acting on the homology of $W_{g,1}\subset \partial V_g$ (see Section 3.3). It follows from the corollary just mentioned that the first map induces an isomorphism in homology with $\mathbf {Z}_{(p)}$-coefficients in degrees $*<2p-3-n$ and a surjection in that degree since $V_g$ is obtained from $D^{2n}$ by attaching n-handles and the triad $(V_g;D^{2n},W_{g,1})$ satisfies the $\pi$-$\pi$-condition as $W_{g,1}$ and $V_g$ are simply connected for $n\ge 2$. To study the remaining maps, we may replace the space of block homotopy automorphisms by its equivalent non-block analogue $\mathrm {BhAut}^{\cong }_{D^{2n}}(V_g,W_{g,1})_\ell$ (see Section 1.5), so the $E_2$-page of the p-local Serre spectral sequence of the second map has the form

$$\begin{aligned} E_{k,l}^2\cong \mathrm {H}_k\Big (\pi _0\mathrm {hAut}^{\cong }_{D^{2n}}(V_g,W_{g,1})_\ell ;\mathrm {H}_l \big (\mathrm {BhAut}^{\mathrm {id}}_{D^{2n}}(V_g,W_{g,1});\mathbf {Z}_{(p)} \big ) \Big ).\end{aligned}$$

(64)

To compute $E_{k,l}^2$, we employ the Serre spectral sequence of the extension

$$\begin{aligned} 0\longrightarrow L_g\longrightarrow \pi _0\mathrm {hAut}^{\cong }_{D^{2n}}(V_g,W_{g,1})_\ell \longrightarrow G^{\mathrm {ext}}_{g,\ell }\longrightarrow 0,\end{aligned}$$

(65)

with coefficients in $\mathrm {H}_l(\mathrm {BhAut}^{\mathrm {id}}_{D^{2n}}(V_g,W_{g,1});\mathbf {Z}_{(p)})$, where $L_g$ is the kernel as indicated. The $E_2$-page of this spectral sequence has the form

$$\begin{aligned}E_{s,t}^2\cong \mathrm {H}_s\Big (G^{\mathrm {ext}}_{g,\ell };\mathrm {H}_t\big (L_g;\mathrm {H}_l(\mathrm {BhAut}^{\mathrm {id}}_{D^{2n}}(V_g,W_{g,1});\mathbf {Z}_{(p)})\big )\Big ).\end{aligned}$$

The kernel $L_g$ of the extension (65) is a subgroup of the kernel of the analogous extension without the $\ell$-subscripts, and as the latter is finite and p-torsion free for $n<2p-4$ by Lemma 3.10, so is the former. The group $L_g$ thus has no nontrivial homology in positive degrees with coefficients in a $\mathbf {Z}_{(p)}[L_g]$-module if $n<2p-4$, so in this case the spectral sequence $E_{s,t}^2$ is concentrated in the bottom row and we conclude that

$$\begin{aligned} E_{k,l}^2\cong \mathrm {H}_k\Big (G^{\mathrm {ext}}_{g,\ell };\mathrm {H}_l\big (\mathrm {BhAut}^{\mathrm {id}}_{D^{2n}}(V_g,W_{g,1});\mathbf {Z}_{(p)}\big )_{L_g}\Big )\quad \text {for }n<2p-4,\end{aligned}$$

(66)

where $(-)_{L_g}$ stands for taking coinvariants. By Lemma 3.9, the group $G^{\mathrm {ext}}_{g,\ell }$ contains the negative of the identity, which is central and acts on the coefficients in (66) by $-1$ as long as $0<l<m:=\min (2n-1,2p-3-n)$ as a result of Corollary 4.9, since it acts by $-1$ on $\mathrm {H}_n(W_{g,1};\mathbf {Z})^{\otimes 3}$ as $(-1)^3=(-1)$. This allows us to apply the “centre kills”-trick⁴ to conclude that the $E_2$-page $E_{k,l}^2$ is 2-torsion for $0<l<m$ (which implies $n<2p-4$) and is therefore trivial as p was assumed to be odd. In this range, the spectral sequence (64) is therefore concentrated at the bottom row, so the second map in (63) induces an isomorphism on $\mathbf {Z}_{(p)}$-homology in degrees $*<m$ and a surjection in that degree. This leaves us with arguing that the final map in (63) also has this property. But we already observed that the kernel in (65) is p-locally acyclic for $n<2p-4$, so in this case the third map is in fact a p-local homology isomorphism. As the statement is vacuous unless $1<m$ and thus $n<2p-4$, this finishes the proof. $\square$

In contrast to the first map in (62), the second map might not induce a p-local homology isomorphism in a range of degrees, but we will see below that its homotopy colimit $\mathrm {BG}^{\mathrm {ext}}_{\infty ,\ell }\rightarrow \mathrm {BGL}(H_{V_\infty })$ with respect to the stabilisation maps explained in Section 3.5 does.

Lemma 5.8

For odd primes p, the induced map

$$\begin{aligned}\mathrm {H}_*\big (\mathrm {BG}^{\mathrm {ext}}_{\infty ,\ell };\mathbf {Z}_{(p)}\big )\longrightarrow \mathrm {H}_*\big (\mathrm {BGL}(H_{V_\infty });\mathbf {Z}_{(p)}\big )\end{aligned}$$

is an isomorphism.

Proof

By an application of the Serre spectral sequence of the extension

$$\begin{aligned}0\longrightarrow M_g^{\mathrm {sfr}}\longrightarrow G_{g,\ell }^{\mathrm {ext}}\longrightarrow \mathrm {GL}(H_{V_g})\longrightarrow 0\end{aligned}$$

established in Proposition 3.7 (ii), it suffices to show that the colimit induced by stabilisation

$$\begin{aligned}&\mathrm {colim}_g\mathrm {H}_*\big (\mathrm {GL}(H_{V_g});\widetilde{\mathrm {H}}_*(M_g^{\mathrm {sfr}};\mathbf {Z}_{(p)})\big )\\&\quad \cong \mathrm {colim}_g\mathrm {H}_*\big (\mathrm {GL}(H_{V_g});\widetilde{\mathrm {H}}_*(M_g^{\mathrm {sfr}}\otimes \mathbf {Z}_{(p)};\mathbf {Z}_{(p)})\big )\end{aligned}$$

vanishes; the isomorphism can be viewed as being induced by the p-localisation of $K(M_g^{\mathrm {sfr}},1)$, see Section 1.2. Recall from Section 3.3 that the $\mathrm {GL}(H_{V_g})$-module $M^{\mathrm {sfr}}_g\subset (H_{V_g}\otimes H_{V_g})^\vee$ consists of all even $(-1)^{n+1}$-symmetric bilinear forms $\mu \in (H_{V_g}\otimes H_{V_g})^\vee$, so as p is assumed to be odd, its p-localisation $M_g^{\mathrm {sfr}}\otimes \mathbf {Z}_{(p)}$ is isomorphic to the dual of the symmetric square $\mathrm {Sym}^2(H_{V_g})^\vee \otimes \mathbf {Z}_{(p)}$ if n is odd and the dual of the exterior square $\Lambda ^2(H_{V_g})^\vee \otimes \mathbf {Z}_{(p)}$ if n is even. In particular, by antisymmetrisation, the $\mathrm {GL}(H_{V_g})$-module $M_g^{\mathrm {sfr}}\otimes \mathbf {Z}_{(p)}$ is a direct summand of $(H_{V_g}\otimes H_{V_g})^{\vee }\otimes \mathbf {Z}_{(p)}$. Choosing a basis $H_{V_g}\cong \mathbf {Z}^g$ compatible with the stabilisation maps, this shows that it suffices to show that the stable $\mathrm {GL}_g(\mathbf {Z})$-homology with coefficients in $\mathrm {H}_k((\mathbf {Z}^{g}\otimes \mathbf {Z}^{g})^{\vee };\mathbf {Z})\cong \Lambda ^{k}(\mathbf {Z}^{g}\otimes \mathbf {Z}^{g})^{\vee }$ vanishes for $k>0$. Pulling back this module along the automorphism of $\mathrm {GL}_g(\mathbf {Z})$ given by taking transpose inverse, we see that we may replace this module by its dual $\Lambda ^{k}(\mathbf {Z}^{g}\otimes \mathbf {Z}^{g})$ whose $\mathrm {GL}_g(\mathbf {Z})$-homology for large g with respect to k does indeed vanish by an application of a result due to Betley [1, Thm 3.1]. $\square$

Corollary 5.9

Let $n\ge 3$ and p a prime. The map on homology induced by the map ,

$$\begin{aligned}\mathrm {H}_*(\mathrm {B\widetilde{Diff}}^{\mathrm {sfr}}_{D^{2n}}(V_\infty ;\ell _0)_\ell ;\mathbf {Z}_{(p)})\longrightarrow \mathrm {H}_*(\mathrm {BGL}_\infty (\mathbf {Z})^+;\mathbf {Z}_{(p)}),\end{aligned}$$

is an isomorphism for $*<\min (2n-1,2p-3-n)$ and a surjection in that degree.

Proof

This is free of content if p is even and follows for p odd from a combination of Lemmas 5.7 and 5.8, using that the canonical map $\mathrm {BGL}_\infty (\mathbf {Z})\rightarrow \mathrm {BGL}_\infty (\mathbf {Z})^+$ is acyclic. $\square$

5.3 Proof of Theorem 5.1

As in the previous proofs, we assume $p>2$; the claim is vacuous otherwise. Our goal is to demonstrate that the precomposition of the left column in (58) with the $(2n-4)$-connected map (57) provides a zig–zag as promised by Theorem 5.1. As a result of the discussion in Section 5.1, the space X is the homotopy fibre of a map out of an infinite loop space which is moreover surjective on fundamental groups as a result of Proposition 3.7, so it follows from Lemma 1.4 that X is nilpotent. That the map is p-locally $\min (2n,2p-4)$-connected is a consequence of having this property by Corollary 5.6 and the 1-connected cover $\mathrm {BGL}_\infty (\mathbf {Z})^+\langle 1 \rangle \rightarrow \mathrm {BGL}_\infty (\mathbf {Z})^+$ being a p-local equivalence as $\pi _1\mathrm {BGL}_\infty (\mathbf {Z})^+\cong \mathbf {Z}/2$ and p is odd. This leaves us with showing that the composition

$$\begin{aligned}\mathrm {BC}(D^{2n})\longrightarrow \widetilde{\mathrm {Diff}}_{D^{2n}}(V_\infty )/\widetilde{\mathrm {Diff}}_{D^{2n}}(V_\infty )\longrightarrow X\end{aligned}$$

is p-locally $\min (2n-4,2p-4-n)$-connected, which we can test on p-local homology groups by Lemma 1.1 as source and target are nilpotent. The first map in this composition is $(2n-4)$-connected by Lemma 5.4, so we may focus on the second and show that it induces an isomorphism in p-local homology in the required range. Since plus-constructions do not affect homology groups and is an isomorphism in homology with $\mathbf {Z}_{(p)}$-coefficients in degrees less than $\min (2n-1,2p-3-n)$ and an epimorphism in that degree by Corollary 5.9, the claim follows from an application of Zeeman’s comparison theorem (see e.g. [19, Thm. 3.2]) to the map of Serre spectral sequences induced by the first two rows of (58), provided we ensure that the actions of the fundamental groups of the bases of both fibre sequences on the $\mathbf {Z}_{(p)}$-homology of the respective fibres are trivial in this range. For the second row, this follows from the p-local high connectivity of the map established in the first part of the proof, using that the canonical action of $\pi _1\mathrm {BGL}_\infty (\mathbf {Z})^+$ on the homology of $\Omega \mathrm {BGL}_\infty (\mathbf {Z})^+$ is trivial as $\mathrm {BGL}_\infty (\mathbf {Z})^+\simeq \Omega _0 \mathrm {B}(\coprod _g\mathrm {BGL}_g(\mathbf {Z}))$ is a loop space (in fact, an infinite one). For the first row, the triviality of the action is a consequence of Lemma 5.4 together with the observation that any element in $\pi _0\mathrm {Diff}_{D^{2n}}(V_g)$ can be represented by a diffeomorphism that fixes $D^{2n+1}=V_0\subset V_g$ pointwise, so commutes with any diffeomorphism in the image of the iterated stabilisation map $\mathrm {C}(D^{2n})\simeq \mathrm {Diff}_{D^{2n}}(D^{2n+1})\rightarrow \mathrm {Diff}_{D^{2n}}(V_g)$. This finishes the proof of Theorem 5.1, which in particular implies Theorem A.

5.4 A reformulation

Although not necessary for the proof of Theorem 5.1 or Theorem A, we shall explain in Section 5.4.2 below how an instance of the Dwyer–Weiss–Williams index theorem [12] shows that the plus constructed stable homology action

$$\begin{aligned} \mathrm {BDiff}^{\mathrm {sfr}}_{D^{2n}}(V_\infty )_\ell ^+\longrightarrow \mathrm {BGL}_{\infty }(\mathbf {Z})^+\end{aligned}$$

(67)

featuring in (58) agrees with respect to the equivalence $\mathrm {BDiff}^{\mathrm {sfr}}_{D^{2n}}(V_\infty )_\ell ^+\simeq \Omega ^\infty _0\Sigma _+^\infty \mathrm {O}/\mathrm {O}(2n+1)$ explained in Section 5.1 with the map obtained by applying $\Omega ^\infty _0(-)$ to the composition

$$\begin{aligned} \Sigma _+^\infty \mathrm {O}/\mathrm {O}(2n+1)\overset{\mathrm {pr}}{\longrightarrow }\mathbf {S}{\overset{\iota }{\longrightarrow }}K(\mathbf {Z})\overset{(-1)^n}{\longrightarrow }K(\mathbf {Z}), \end{aligned}$$

(68)

where $\mathrm {pr}$ is the projection and $\iota$ the unit. This identifies the homotopy fibre X in (58) as the space

$$\begin{aligned}X\simeq \Omega ^\infty _+\mathrm {hofib}\big (\Sigma _+^\infty \mathrm {O}/\mathrm {O}(2n+1)\xrightarrow {\mathrm {pr}}\mathbf {S}\xrightarrow {\iota } K(\mathbf {Z})\big ),\end{aligned}$$

so we may postcompose the map $\phi$ from Theorem 5.1 with the $(2n+1)$-connected map $\mathrm {hofib}(\iota \circ \mathrm {pr})\rightarrow \mathrm {hofib}(\iota )$ induced by the projection to arrive at a cleaner formulation of Theorem A: there is a p-locally $\min (2n-4,2p-4-n)$-connected map

$$\begin{aligned} \mathrm {BC}(D^{2n})\longrightarrow \Omega _0^\infty \mathrm {hofib}(\mathbf {S}\xrightarrow {\iota } K(\mathbf {Z})).\end{aligned}$$

(69)

5.4.1 Relation to Waldhausen’s work

It is reasonable to expect that the map (69) agrees up to equivalences with the composition

$$\begin{aligned} \begin{aligned}\mathrm {BC}(D^{2n})&\longrightarrow \Omega _0^\infty \mathrm {Wh}^{\mathrm {Diff}}(*)=\Omega _0^\infty \mathrm {hofib}\big (\mathbf {S}\rightarrow K(\mathbf {S})\big )\\ {}&\longrightarrow \Omega _0^\infty \mathrm {hofib}\big (\mathbf {S}\rightarrow K(\mathbf {Z})\big )\end{aligned} \end{aligned}$$

(70)

of the map known from Waldhausen’s work [42] with the map induced by linearisation. While it is not hard to show that the map (69) does indeed factor over the second map in (70), a convincing comparison between (69) and (70) appears to be more laborious and we will not go into this matter at this point (however, see the final remark of the introduction).

5.4.2 An application of the index theorem

To justify the claimed identification of (67) with the map resulting from applying $\Omega ^\infty _0(-)$ of (68), one can argue as follows: firstly, it suffices to show that these maps agree when precomposed with an arbitrary map $B\rightarrow \mathrm {BDiff}^{\mathrm {sfr}}_{D^{2n}}(V_\infty )_\ell ^+$ that classifies a smooth $V_g$-bundle $\pi :E\rightarrow B$ for some $g\ge 0$ together with a trivial $D^{2n}$-subbundle and stably framed vertical tangent bundle $T_\pi E$. Tracing through the equivalences featuring in Section 5.1, one finds that the composition

$$\begin{aligned} B\longrightarrow \mathrm {BDiff}^{\mathrm {sfr}}_{D^{2n}}(V_\infty )_\ell ^+\simeq \Omega ^\infty _0\Sigma ^\infty _+(\mathrm {O}/\mathrm {O}(2n+1)) \end{aligned}$$

(71)

represents the class

$$\begin{aligned}\circ \mathrm {BG}(\pi )-\chi (V_g)\in [\Sigma _+^\infty B, \Sigma ^\infty _+(\mathrm {O}/\mathrm {O}(2n+1)]\end{aligned}$$

where $\chi (-)$ is the Euler characteristic, $\mathrm {BG}(\pi )\in [\Sigma _+^\infty B, \Sigma ^\infty _+E]$ is the Becker–Gottlieb transfer of the bundle $\pi$ described in terms of the Pontryagin–Thom construction [2, 3], and the class $[T_\pi E]\in [\Sigma _+^\infty E, \Sigma ^\infty _+\mathrm {O}/\mathrm {O}(2n+1)]$ is induced by the vertical tangent bundle of $\pi$ together with its stable framing. It thus suffices to show that the class

$$\begin{aligned} (-1)^n(\iota \circ \mathrm {pr})^* (\mathrm {BG}(\pi )-\chi (V_g))\in [\Sigma _+^\infty B, K(\mathbf {Z})]\end{aligned}$$

(72)

agrees with the class represented by the composition

$$\begin{aligned}B\longrightarrow \mathrm {BDiff}^{\mathrm {sfr}}_{D^{2n}}(V_\infty )_\ell ^+\longrightarrow \mathrm {BGL}_{\infty }(\mathbf {Z})^+\simeq \Omega ^{\infty }_0K(\mathbf {Z}).\end{aligned}$$

The latter can be identified with the class

$$\begin{aligned}{}[H_n(\pi )]-g\in [\Sigma ^\infty _+B,K(\mathbf {Z})]\end{aligned}$$

(73)

where $H_n(\pi )$ is the local system over B of fibrewise middle-dimensional homology groups of $\pi$. Dwyer–Weiss–Williams’ improved Riemann–Roch theorem [12, p. 2] gives

$$\begin{aligned}(\iota \circ \mathrm {pr})^* \mathrm {BG}(\pi )=1+(-1)^n\cdot [H_n(\pi )]\in [\Sigma ^\infty _+B,K(\mathbf {Z})],\end{aligned}$$

so using $\chi (V_g)=1+(-1)^ng$ it follows that (72) and (73) indeed agree.

6 Appendix A. Stable tangential bundle maps are stable bundle maps

Fix a d-dimensional vector bundle $\xi$ over a space X, a stable vector bundle $\{\psi _k\rightarrow B_k\}_{k\ge 0}$, subcomplexes $A,C\subset X$, and a bundle map $\ell _0:\xi |_A\oplus \varepsilon ^k\rightarrow \psi _{d+k}$ covering a map $\bar{\ell }_0:X\rightarrow B_{d+k}$ for some $k\ge 0$. In addition to the notation for various types of bundle maps in Section 1, we abbreviate

$$\begin{aligned}\widetilde{\mathrm {Map}}_A(X,B;\bar{\ell }_0)_\bullet :=\mathrm {colim}_{m\ge k}\widetilde{\mathrm {Map}}_A(X,B_m;\bar{\ell }_0)_\bullet ,\end{aligned}$$

where $\widetilde{\mathrm {Map}}_A(X,B_m;\bar{\ell }_0)_\bullet$ is the semi-simplicial set whose p-simplices are block maps $\Delta ^p\times X\rightarrow \Delta ^p\times B_{m}$ which agree with $\mathrm {id}_{\Delta ^p}\times \bar{\ell }_0$ on $\Delta ^p\times A$. The colimit is taken over the maps induced by post-composition with the maps $B_m\rightarrow B_{m+1}$ underlying the structure maps of $\psi$. The sub semi-simplicial set of maps $\Delta ^p\times X\rightarrow \Delta ^p\times B_m$ over $\Delta ^p$ is denoted by $\mathrm {Maps}_A(X,B;\bar{\ell }_0)_\bullet \subset \widetilde{\mathrm {Map}}_A(X,B;\bar{\ell }_0)_\bullet$.

Lemma A.1

If the base X of $\xi$ is a finite CW-complex, then the maps

$$\begin{aligned}\mathrm {\widetilde{Bun}}_A(\xi ^s,\psi ;\ell _0)^\tau _\bullet\longrightarrow & {} \widetilde{\mathrm {Map}}_A(X,B;\bar{\ell }_0)_\bullet \quad \text {and}\quad \\\mathrm {\widetilde{hAut}}_A(\xi ^s;C)^\tau _\bullet\longrightarrow & {} \mathrm {\widetilde{hAut}}_A(X;C)_\bullet \end{aligned}$$

induced by forgetting bundle maps are Kan fibrations.

Proof

For $\psi =\xi ^s$ and $\ell _0=\mathrm {inc}$ the inclusion, the second map agrees with the pullback of the first map along the inclusion $\mathrm {\widetilde{hAut}}_A(X;C)_\bullet \subset \widetilde{\mathrm {Map}}_A(X,X;\mathrm {inc})_\bullet$, so it suffices to show that the first map is a Kan fibration. We shall do so in the case where A is empty; the argument for general A is similar. The upper horizontal map in a lifting problem

induces bundle maps

$$\begin{aligned}\phi _i:\tau _{\Delta ^p_i}\times \xi \oplus \varepsilon ^k\longrightarrow \tau _{\Delta ^p_i}\times \psi _{d+k}\end{aligned}$$

for $i\ne j$ that agree on their faces and cover the restriction of the map $\bar{\phi }:\Delta ^p\times X\rightarrow \Delta ^p\times B_{d+k}$ induced by the bottom horizontal arrow to $\Delta ^p_i\times X$. By replacing $\xi$ with its stabilisation $\xi \oplus \varepsilon ^k$, we may assume $k=0$. There is an extension of $\phi _i$ to $\tau _{\Delta ^p}|_{\Delta ^p_i}$ given by the composition

$$\begin{aligned}\tau _{\Delta ^p}|_{\Delta ^p_i} \times \xi \xrightarrow {\cong }\varepsilon \oplus \tau _{\Delta ^p_i} \times \xi \xrightarrow {\mathrm {id}_\varepsilon \oplus \phi _i } \varepsilon \oplus \tau _{\Delta ^p_i}\times \psi _{d}\xrightarrow {\cong }\tau _{\Delta ^p}|_{\Delta ^p_i} \times \psi _{d}\end{aligned}$$

whose outer isomorphisms are induced by the differential of the diffeomorphism $c_{i,\epsilon }$ of Section 1.3. The condition (4) in the definition of tangential bundle maps is made precisely such that these extensions agree on their intersections, so they assemble to a bundle map

$$\begin{aligned}\phi _{\Lambda ^p_j}:\tau _{\Delta ^p}|_{\Lambda ^p_j}\times \xi \longrightarrow \tau _{\Delta ^p}|_{\Lambda ^p_j}\times \psi _{d} \end{aligned}$$

that covers the restriction of $\bar{\phi }$ to $\Lambda ^p_j\times X$ and we are left to argue that this bundle map is the restriction of a p-simplex in $\mathrm {Bun}(\xi ^s,\psi )^\tau _\bullet$ covering $\bar{\phi }$. As the inclusion $\Lambda ^p_j\times X\subset \Delta ^p\times X$ is a trivial cofibration, obstruction theory provides an extension of $\phi _{\Lambda ^p_j}$ to a bundle map

$$\begin{aligned}\phi _{\Delta ^p}:\tau _{\Delta ^p}\times \xi \longrightarrow \tau _{\Delta ^p}\times \psi _{d}\end{aligned}$$

that covers $\bar{\phi }$, but this extension might violate condition (4) on the jth face, i.e. the map

$$\begin{aligned}\phi _j:\varepsilon \oplus \tau _{\Delta ^p_j}\times \xi \longrightarrow \varepsilon \oplus \tau _{\Delta ^p_j}\times \psi _{d}\end{aligned}$$

obtained by restricting $\phi _{\Delta ^p}$ to $\Delta ^p_j\times X$ and using the isomorphism $\tau _{\Delta ^p}|_{\Delta ^p_j}\cong \varepsilon \oplus \tau _{\Delta ^p_j}$ induced by the derivative of $c_{j,\epsilon }$ need not have the form $\mathrm {id}_\varepsilon \oplus \phi _j$ for a bundle map

$$\begin{aligned}\phi _j:\tau _{\Delta ^p_j}\times \xi \longrightarrow \tau _{\Delta ^p_j}\times \psi _{d}.\end{aligned}$$

Nevertheless, its restriction to $\partial \Delta ^p_j\times X$ does have this form and we will argue that after adding a trivial bundle of sufficiently large dimension, say n, we can alter $\phi _j$ by a homotopy of bundle maps relative to $\partial \Delta ^p_i\times X$ that covers $\bar{\phi }|_{\Delta ^p_i}$ so that it does have the required form. This would show the claim because we can use this homotopy to change $\phi _{\Delta ^p}\oplus \mathrm {id}_{\varepsilon ^n}$ to a p-simplex in $\mathrm {Bun}(\xi \oplus \varepsilon ^n,\psi _{d}\oplus \varepsilon ^n)^\tau _\bullet$ that covers $\bar{\phi }$ and extends $\phi _{\Lambda ^p_j}\oplus \mathrm {id}_{\varepsilon ^n}$ and thus provides a lift as required. To this end, we denote by $\mathrm {Iso}(\nu ,\eta )\rightarrow Y$ for vector bundles $\nu$ and $\eta$ over a space Y the fibre bundle whose sections correspond to bundle morphisms $\nu \rightarrow \eta$ over the identity, so the fibre over $y\in Y$ is the space of isomorphisms $\nu _y\rightarrow \eta _y$ between the fibres of $\nu$ and $\eta$. Abbreviating $\nu :=\tau _{\Delta _j^p}\times \xi$ and $\eta :=\bar{\phi }^*(\tau _{\Delta _j^p}\times \psi _d)$, we consider the diagram

in which the solid diagonal arrow is induced by $\phi _j\oplus \mathrm {id}_{\varepsilon ^n}$ and the upper left horizontal one by its restriction to $\partial \Delta ^p_j\times X$, which makes the subdiagram of solid arrows commute strictly. From this point of view, the task we set us is equivalent to constructing a dashed arrow for some n that makes the upper leftmost triangle commutes strictly and the one formed by the two diagonal arrows up to homotopy relative $\partial \Delta ^p_j\times X$. Using that X is a finite CW complex and that the connectivity of the map on vertical homotopy fibres of the right square increases in n as it agrees with the inclusion $\mathrm {O}(p+d+n)\subset \mathrm {O}(p+d+n+1)$ up to equivalence, this follows from obstruction theory. $\square$

Remark

We learnt the “stabilisation trick” of the previous proof from Appendix D of [8], which contains results similar to those of this appendix.

Corollary A.2

If the base X of $\xi$ is a finite CW-complex, then the following semi-simplicial sets satisfy the Kan property.

• (i) $\mathrm {\widetilde{Bun}}_A(\xi ^s,\psi ;\ell _0)^\tau _\bullet$

• (ii) $\mathrm {Bun}_A(\xi ^s,\psi ;\ell _0)^\tau _\bullet$

• (iii) $\mathrm {\widetilde{hAut}}_A(\xi ^s;C)_\bullet ^\tau$

• (iv) $\mathrm {hAut}_A(\xi ^s;C)_\bullet ^\tau$

Proof

It is straight-forward to see that $\widetilde{\mathrm {Map}}_A(X,B;\bar{\ell }_0)_\bullet$ is Kan, so the first part follows from Lemma A.1 and the fact that the domain of a Kan fibration over a Kan complex is Kan. The same reasoning applies to the second semi-simplicial set, using that $\mathrm {Bun}_A(\xi ^s,\psi ;\ell _0)^\tau _\bullet \rightarrow \mathrm {Maps}_A(X,B;\bar{\ell }_0)_\bullet$ is a Kan fibration because it is the pullback of the first map of Lemma A.1 along the inclusion $\mathrm {Maps}_A(X,B;\bar{\ell }_0)_\bullet \subset \widetilde{\mathrm {Map}}_A(X,B;\bar{\ell }_0)_\bullet$. Also the semi-simplicial sets $\mathrm {hAut}_A(X;C)_\bullet$ and $\mathrm {\widetilde{hAut}}_A(X;C)_\bullet$ are easily seen to be Kan (see Section 1.5), so the remaining claims can be proved in the same way. $\square$

Lemma A.3

If the base X of $\xi$ is a finite CW-complex, then the inclusions

$$\begin{aligned}\mathrm {Bun}_A(\xi ^s,\psi ;\ell _0)_\bullet ^\tau\subset & {} \mathrm {\widetilde{Bun}}_A(\xi ^s,\psi ;\ell _0)_\bullet ^\tau \quad \text {and}\\ \mathrm {hAut}_A(\xi ^s;C)_\bullet ^\tau\subset & {} \mathrm {\widetilde{hAut}}_A(\xi ^s;C)_\bullet ^\tau \end{aligned}$$

are equivalences.

Proof

These inclusions are pullbacks of the inclusions

$$\begin{aligned} \begin{aligned}&\mathrm {Maps}_A(X,B;\bar{\ell }_0)_\bullet \subset \widetilde{\mathrm {Map}}_A(X,B;\bar{\ell }_0)_\bullet \quad \text { and }\\&\quad \mathrm {hAut}_A(X;C)_\bullet \subset \mathrm {\widetilde{hAut}}_A(X;C)_\bullet \end{aligned}\end{aligned}$$

(74)

along the two Kan fibrations discussed in Lemma A.1, so the claim follows from showing that the inclusions (74) are equivalences. As already mentioned in the previous proof, it is straight-forward to show that these semi-simplicial sets are Kan. Using the combinatorial description of their homotopy groups, the claim follows from the contractibility of the mapping space $\mathrm {Maps}_{\partial \Delta ^p}(\Delta ^p,\Delta ^p)$ (cf. Section 1.5). $\square$

Lemma A.4

If the base X of $\xi$ is a finite CW-complex, then the extension maps of (7)

$$\begin{aligned}\mathrm {Bun}_A(\xi ^s,\psi ;\ell _0)_\bullet\rightarrow & {} \mathrm {Bun}_A(\xi ^s,\psi ;\ell _0)_\bullet ^\tau \quad \text {and}\\ \mathrm {hAut}_A(\xi ^s;C)_\bullet\rightarrow & {} \mathrm {hAut}_A(\xi ^s;C)_\bullet ^\tau \end{aligned}$$

are equivalences.

Proof

The proof for the two maps are essentially identical; we restrict our attention to the first map. Its source and target have the Kan property (the source because it is the singular complex of a space, the target by Corollary A.2), so we may test the claim on semi-simplicial homotopy groups. The two semi-simplicial sets involved have the same 0-simplices, so the map is clearly surjective on path components. To show that it is surjective on homotopy groups in positive degrees, we fix a semi-simplicial base point in $\mathrm {Bun}_A(\xi ^s,\psi ;\ell _0)_\bullet$ by choosing a 0-simplex $\ell :\xi \oplus \varepsilon ^l\rightarrow \psi _{d+l}$ and taking products with the tangent bundles $\tau _{\Delta ^p}$. Let

$$\begin{aligned}\phi :\xi \oplus \varepsilon ^k\times \tau _{\Delta ^p} \longrightarrow \psi _{d+k}\times \tau _{\Delta ^p}\end{aligned}$$

be a p-simplex that represents a class in $\pi _p(\mathrm {Bun}_A(\xi ^s,\psi ;\ell _0)^\tau _\bullet ;\ell )$. Up to changing $\phi$ within its homotopy class, we may assume that the underlying map $\bar{\phi }:X\times \Delta ^p\rightarrow B_{d+k}\times \Delta ^p$ satisfies the collaring condition from Section 1.3 for some $0<\epsilon <1/2$. By replacing $\xi$ with $\xi \oplus \epsilon ^k$, we may assume $k=0$. Fixing a trivialisation $F:\tau _{\Delta ^p}\cong \mathbf {R}^p\times \Delta ^p$, our candidate for a preimage in $\pi _p(\mathrm {Bun}_A(\xi ^s,\psi ;\ell _0)_\bullet ;\ell )$ is the class defined by the composition

$$\begin{aligned} \begin{aligned} \xi \oplus \varepsilon ^p\times \Delta ^p&\overset{\mathrm {id}_{\xi }\times F^{-1}}{\longrightarrow }\xi \times \tau _{\Delta ^p}\overset{\phi }{\longrightarrow }\psi _{d}\times \tau _{\Delta ^p}\\ {}&\overset{\mathrm {id}_{\psi _{d}}\times F}{\longrightarrow } \psi _d\oplus \varepsilon ^p\times \Delta ^p\longrightarrow \psi _{d+p}\times \Delta ^p,\end{aligned}\end{aligned}$$

(75)

where the last arrow is induced by the structure map of $\psi$. To justify this, we will show the existences of a $(p+1)$-simplex in $\mathrm {Bun}_A(\xi \oplus \varepsilon ^p\oplus \varepsilon ^2,\psi _{d+p+2};\ell _0)^\tau _\bullet$ which on the pth face agrees with the $(p+2)$-fold stabilisation of $\phi$, on the $(p+1)$st face with the image $\phi ^F\in \mathrm {Bun}_A(\xi \oplus \epsilon ^p\oplus \epsilon ^2,\psi _{d+p+2};\ell _0)_p^\tau$ of the 2-fold stabilisation of the composition (75) and on the remaining faces with the basepoint. To this end, we consider the linear map

$$\begin{aligned}\Lambda :\begin{array}{rcl} \mathbf {R}^p\times \mathbf {R}\times \mathbf {R}\times \mathbf {R}^p &{} \longrightarrow &{} \mathbf {R}^p\times \mathbf {R}\times \mathbf {R}\times \mathbf {R}^p \\ [0.3em] (x,u,v,y) &{} \longmapsto &{} {\left\{ \begin{array}{ll}(y,u,v,x)&{}\text {if }p\text { is even}\\ (y,v,u,x)&{}\text {if }p\text { is odd}, \end{array}\right. } \end{array},\end{aligned}$$

which has determinant 1 (this is the reason we introduced the additional $(\mathbf {R}\times \mathbf {R})$-coordinate), so there exists a path $\gamma :[0,1]\rightarrow \mathrm {GL}(\mathbf {R}^p\times \mathbf {R}\times \mathbf {R}\times \mathbf {R}^p)$ from the identity to $\Lambda$, which we may choose to be constant in a neighborhood of $[0,\epsilon ]\cup [1-\epsilon ,1]$. In terms of this path, we define a homotopy $H_t$ of bundle automorphisms of $\varepsilon ^p\oplus \tau _{\Delta ^p}$ covering the identity by

$$\begin{aligned} \varepsilon ^p\oplus \varepsilon ^2\oplus \tau _{\Delta ^p}&\xrightarrow {\mathrm {id}_{\mathbf {R}^p\times \mathbf {R}^2}\times F}&\mathbf {R}^p\times \mathbf {R}^2\times \mathbf {R}^p\times \Delta ^p\\&\xrightarrow {\gamma _t\times \mathrm {id}_{\Delta ^p}}&\mathbf {R}^p\times \mathbf {R}^2\times \mathbf {R}^p\times \Delta ^p\xrightarrow {\mathrm {id}_{\mathbf {R}^p\times \mathbf {R}^2}\times F^{-1}}\varepsilon ^p\oplus \tau _{\Delta ^p}.\end{aligned}$$

Using H, we define a homotopy $\widetilde{H}$ of bundle maps as the composition

$$\begin{aligned} \xi \oplus \varepsilon ^p\oplus \varepsilon ^2\times \tau _{\Delta ^p}&\overset{\mathrm {id}_{\xi }\times H_t}{\longrightarrow }&\xi \oplus \varepsilon ^p\oplus \varepsilon ^2\times \tau _{\Delta ^p}\xrightarrow {\phi }\psi _{d}\oplus \varepsilon _p\oplus \varepsilon ^2 \times \tau _{\Delta ^p}\\&\overset{\mathrm {id}_{\psi _d}\times H_t^{-1}}{\longrightarrow }&\psi _{d}\oplus \varepsilon _p\oplus \varepsilon ^2\times \tau _{\Delta ^p}\rightarrow \psi _{d+p+2}\times \tau _{\Delta ^p},\end{aligned}$$

where the last map is induced by the structure map of $\psi$. Going through the definitions, one checks that this is a homotopy from the stabilisation of $\phi$ to $\phi ^F$ and that its underlying homotopy of maps of spaces is constantly $\bar{\phi }$. Using the canonical trivialisation of $\tau _{[0,1]}$, this homotopy gives rise to a bundle map $\widetilde{H}:\xi \oplus \varepsilon ^p\oplus \varepsilon ^2\times \tau _{\Delta ^p\times [0,1]}\rightarrow \psi _{d+p+2}\times \tau _{\Delta ^p\times [0,1]}$ which one checks to descend uniquely to a dashed arrow making the diagram

commute, where c is the map

$$\begin{aligned}c:\begin{array}{rcl} \Delta ^p\times [0,1] &{} \longrightarrow &{} \Delta ^{p+1} \\ [0.3em] ((x_0,\ldots ,x_p),s) &{} \longmapsto &{} (x_0,\ldots ,x_{p-1},s\cdot x_p,(1-s)\cdot x_{p}) \end{array}\end{aligned}$$

whose derivative is surjective (though not fibrewise). The resulting bundle map $\bar{H}$ has the correct behaviour on all faces, so almost provides a $(p+1)$-simplex in $\mathrm {Bun}_A(\xi \oplus \varepsilon ^p\oplus \varepsilon ^2,\psi _{d+p+2};\ell _0)^\tau _\bullet$ as wished. The only problem is that it does not satisfy the collaring condition (4) for $i=p$, but this can be rectified as follows: choosing a block diffeomorphism $\alpha :\Delta ^{p+1}\rightarrow \Delta ^{p+1}$ which agrees with the identity on $\Delta ^{p+1}_{p+1, \delta }$ for some $\delta >0$ (see Section 1.3 for the notation) and makes the diagram

commute for some $\delta '>\epsilon$, the composition

$$\begin{aligned} \xi \oplus \varepsilon ^p\oplus \varepsilon ^2\times \tau _{\Delta ^{p+1}}&\overset{\mathrm {id}_{\xi \oplus \varepsilon ^p\oplus \varepsilon ^2}\times \mathrm {d}\alpha }{\longrightarrow }\xi \oplus \varepsilon ^p\oplus \varepsilon ^2\times \tau _{\Delta ^{p+1}}\overset{\bar{H}}{\longrightarrow }\psi _{d+p+2}\times \tau _{\Delta ^{p+1}}\\&\overset{\mathrm {id}_{\xi \oplus \varepsilon ^p\oplus \varepsilon ^2}\times \mathrm {d}\alpha ^{-1}}{\longrightarrow }\psi _{d+p+2}\times \tau _{\Delta ^{p+1}}\end{aligned}$$

defines a $(p+1)$-simplex as required. This finishes the proof of surjectivity of the map on homotopy groups and injectivity follows from a relative version of the argument. $\square$

7 Appendix B. A lemma on symplectic derivations

This appendix serves to record a minor generalisation of Proposition 3.9 in [8]. We adopt the notation and conventions introduced in Sections 4.1 and 4.2 and fix a principal ideal domain R with $2\in R^\times$, an integer $k\in \mathbf {Z}$, and a graded R-module V that is degreewise free, together with map $\lambda :V\otimes V\rightarrow R[0]$ of degree $-k$ such that the adjoint map $s^{-k} V\rightarrow V^\vee$ given by mapping v to $\lambda (v,-)$ is an isomorphism. We moreover assume that $\lambda$ is graded antisymmetric, i.e. that $\lambda (x,y)=-(-1)^{|x||y|}\lambda (y,x)$ holds for all $x,y\in V$.

Example B.1

Let M be a compact R-oriented d-manifold whose R-homology is free. If $\partial M\simeq S^{d-1}$, then the desuspension $s^{-1}\widetilde{\mathrm {H}}_*(M;R)$ of the reduced homology qualifies as an example of V as above where $k=d-2$ and $\lambda$ is induced by the intersection form. Concretely, $\lambda$ is defined to vanish on elements $s^{-1}x\otimes s^{-1}y$ unless $|x|+|y|=d$ in which case it is given by $\lambda (s^{-1}x\otimes s^{-1}y)=(-1)^{|x|}\langle D(x)\cup D(y),[M,\partial M]\rangle$, where $D(-)$ denotes the Poincaré duality isomorphism.

Following [8, Sec. 3.5], given a homogenous basis $\{a_i\}$ of V, we use the dual basis $\{a_i^\#\}$ determined by $\lambda (a_i,a_j^\#)=\delta _{ij}$ to define an element $\omega :=\sum _ia_i^\#\otimes a_i\in V\otimes V$. This element can be seen to be independent of the chosen basis (see p. 91 loc.cit. for a proof for $R=\mathbf {Q}$, which generalises) and to be homogenous of degree k, since $|a_i^{\#}|=k-|a_i|$. We identify [V, V] with a subspace of $V\otimes V$ via the antisymmetrisation map $[V,V]\rightarrow V\otimes V$ mapping [x, y] to $x\otimes y-(-1)^{|x||y|}y\otimes x$, which is injective since its composition with the bracket is multiplication by $2\in R^\times$. Under this identification, one verifies

$$\begin{aligned} \textstyle {\omega =\tfrac{1}{2}\sum _i[a_i^{\#},a_i]\in [V,V]}.\end{aligned}$$

(76)

as in p. 91 loc.cit. Given a dg Lie algebra K over R and a map $f:V\rightarrow K$ of graded R-modules, we consider the diagram of graded R-modules

(77)

whose vertical isomorphism is given by the composition

$$\begin{aligned} \mathrm {Der}^f(\mathbf {L}(V),K)\overset{\cong }{\longrightarrow }\mathrm {Hom}(V,K)&\overset{\cong }{\longrightarrow }&K\otimes V^\vee \\ {}&\overset{\cong }{\longrightarrow }&K\otimes s^{-k}V=s^{-k}K\otimes V, \end{aligned}$$

where the first map is given by restriction to generators, the second map is the canonical isomorphism, and the third map is induced by the inverse of the adjoint map of $\lambda$.

The following lemma is a straight-forward extension of Proposition 3.9 of [8], which corresponds to the case $R=\mathbf {Q}$, $K=\mathbf {L}(V)$, and $f=\mathrm {inc}_{V\subset \mathbf {L}(V)}$.

Lemma 1

The diagram (77) is commutative.

Proof

Following the beginning of the proof of [8, Prop. 3.9], one sees that a derivation $\theta \in \mathrm {Der}^f(\mathbf {L}(V),K)$ evaluates on the special element $\omega$ as $\theta (\omega )=\sum _i[\theta (a_i^{\#}),f(a_i)]$. We will use this to show the equivalent claim that the inverse of the vertical map in (77) followed by $\mathrm {ev}_\omega$ agrees with $[-,f(-)]$. This inverse assigns an element $k\otimes v\in s^{-k}K\otimes V$ the unique f-derivation $\theta _{k,v}$ that extends the linear map $\lambda (v,-)\cdot k:V\rightarrow K$. Using that for $v\in V$, we have $v=\sum _i\lambda (v,a_i^{\#})\cdot a_i$ by the definition of the dual basis, we compute

$$\begin{aligned} \theta _{k,v}(\omega )= & {} \sum _i[\theta _{k,v}(a_i^{\#}),f(a_i)]=\sum _i[\lambda (v,a_i^{\#})\cdot k,f(a_i)]\\= & {} [k,f(\sum _i\lambda (v,a_i^{\#})\cdot a_i)]=[k,v],\end{aligned}$$

which implies the claim. $\square$