Abstract
We show that the statement analogous to the Mumford–Tate conjecture for Abelian varieties holds for 1-motives on unipotent parts. This is done by comparing the unipotent part of the associated Hodge group and the unipotent part of the image of the absolute Galois group with the unipotent part of the motivic fundamental group.
Similar content being viewed by others
Notes
This is nonstandard terminology. By a semiabelian scheme over S one usually understands a group scheme over S each of whose fibres is an extension of an Abelian scheme by a torus. This is the right thing to consider in order to study degenerations of Abelian schemes.
Recall that we have chosen to place the complexes [Y→G] associated with 1-motives in degrees 0 and 1. With this convention the 1-motive [ℤ→0] is a neutral object for the tensor product of complexes, as it should be.
Actually: a \(\pi_{1}^{\mathrm {mot}}(M)\)-equivariant derivation.
References
Andreatta, F., Bertapelle, A.: Crystalline realisation of 1-motives. J. Pure Appl. Algebra 215, 1919–1944 (2011)
Bertolin, C.: Le radical unipotent du groupe de Galois motivique d’un 1-motif. Math. Ann. 327(3), 585–607 (2003)
Bertrand, D.: Special points and Poincaré biextensions. arXiv:1104.5178
Brylinski, J.L.: 1-Motifs et Formes Automorphes (théorie Arithmétique des Domaines de Siegel), Publ. Univ. Paris VII, vol. 15 (1983)
Barbieri-Viale, L., Srinivas, V.: Albanese and Picard 1-Motives. Mémoires Société Mathématique de France, vol. 87. Soc. Math. France, Paris (2001), vi+104 pages
Deligne, P.: Théorie de Hodge III. Publ. Math. Inst. Hautes Études Sci. 44, 5–77 (1974)
Charles, F., Schnell, C.: Notes on absolute Hodge classes. arXiv:1101.3647v1 50 p
Deligne, P.: Hodge cycles on Abelian varieties. In: Deligne, P., Milne, J.S., Ogus, A., Shih, K. (eds.) Hodge Cycles, Motives, and Shimura Varieties. Lecture Notes in Math., vol. 900. Springer, Berlin (1982)
Hindry, M.: Autour d’une conjecture de Serge Lang. Invent. Math. 94, 575–603 (1988)
Jacquinot, O., Ribet, K.: Deficient points on extensions of Abelian varieties by 𝔾 m . J. Number Theory 25(2), 133–151 (1987)
Jannsen, U.: Mixed motives, motivic cohomology and ext-groups. In: Proceedings of the ICM, vol. I, pp. 667–679. Birkhäuser, Basel (1994)
Jossen, P.: Detecting linear dependence on a simple Abelian variety. Comment. Math. Helv., to appear, 24 p
Lazard, M.: Groupes analytiques p-adiques. Publ. Math. Inst. Hautes Études Sci. 26, 5–219 (1965)
Pink, R.: ℓ-adic algebraic monodromy groups, cocharacters and the Mumford–Tate conjecture. J. Reine Angew. Math. 495, 187–237 (1998)
Pohlmann, H.: Algebraic cycles on Abelian varieties of complex multiplication type. J. Ann. Math. (2) 88, 161–180 (1968)
Ribet, K.: Dividing rational points on Abelian varieties of CM-type. Compos. Math. 33(1), 69–74 (1976)
Ribet, K.: Kummer theory on an extension of an Abelian variety by tori. Duke Math. J. 46, 745–761 (1979)
Ribet, K.: Review of Abelian ℓ-adic representations and elliptic curves by J.-P. Serre. Bull. Am. Math. Soc. (N.S.) 22(1), 214–218 (1990)
Serre, J.-P.: Abelian ℓ-Adic Representations and Elliptic Curves. Benjamin, New York (1968)
Serre, J.-P.: Sur les groupes de congruence des variétés abéliennes II. Izv. Akad. Nauk SSSR 35, 731–735 (1971)
Serre, J.-P.: Cours au collège de France, 1984–1985
Serre, J.-P.: Lettres à Marie–France Vignéras du 10 février et à Ken Ribet du 7 mai 1986. Oeuvres IV, 38–65 (2003)
Vasiu, A.: Some cases of the Mumford–Tate conjecture and Shimura varieties. Indiana Univ. Math. J. 57, 1–76 (2008)
Acknowledgements
I am indebted to the University of Regensburg, who kindly supported me for quite some time now without ever seriously complaining. I am grateful to Tamás Szamuely who suggested valuable improvements to earlier versions of the text, and to Pierre Deligne who contributed an essential complement and generously permitted me to propagate it. This work was initiated in July 2010 while attending a workshop on Tannakian categories in Lausanne, I wish to thank the EPFL and in particular Varvara Karpova for kindest hospitality.
Author information
Authors and Affiliations
Corresponding author
Appendix: The Tannakian construction of P(M) (following P. Deligne)
Appendix: The Tannakian construction of P(M) (following P. Deligne)
I reproduce here in almost unaltered form a comment of P. Deligne, explaining our construction of the Lie algebra of the unipotent motivic fundamental group P(M) of a 1-motive M in terms of Tannakian formalism. I alone am to blame for mistakes.
The starting point is that in Definition 4.3 the point \(\overline{u}\) should be seen as an extension of \(W_{-1}\mathcal {E}\mathit {nd}(M)\) by the unit object ℤ. This extension can be constructed in a general setting as follows:
A.1
Let \(\mathcal{T}\) be a Tannakian category in characteristic zero with unit object  . Suppose each object of \(\mathcal{T}\) has a functorial exhaustive filtration W compatible with tensor products and duals, the functor \(\mathrm{gr}^{W}_{\ast}\) being exact. For any object M, the object \(\mathcal {E}\mathit {nd}(M) = M^{\vee}\otimes M\) contains the subobject \(W_{-1}\mathcal {E}\mathit {nd}(M)\). The filtration of \(\mathcal {E}\mathit {nd}(M)\) is deduced from the filtration of M, hence
. Suppose each object of \(\mathcal{T}\) has a functorial exhaustive filtration W compatible with tensor products and duals, the functor \(\mathrm{gr}^{W}_{\ast}\) being exact. For any object M, the object \(\mathcal {E}\mathit {nd}(M) = M^{\vee}\otimes M\) contains the subobject \(W_{-1}\mathcal {E}\mathit {nd}(M)\). The filtration of \(\mathcal {E}\mathit {nd}(M)\) is deduced from the filtration of M, hence
As  , we can take the class of M in each of the vector spaces Ext1(M/W
p
M,W
p
M), interpret it as a class in
, we can take the class of M in each of the vector spaces Ext1(M/W
p
M,W
p
M), interpret it as a class in  , take the sum of those and push to \(W_{-1}\mathcal {E}\mathit {nd}(M)\) by functoriality of Ext1. We get a class
, take the sum of those and push to \(W_{-1}\mathcal {E}\mathit {nd}(M)\) by functoriality of Ext1. We get a class

which is natural in M under taking subobjects and quotients.
A.2
Let G be the fundamental group of \(\mathcal{T}\). It has an invariant unipotent subgroup W
−1(G) with Lie algebra \(W_{-1}(\operatorname{Lie} G)\). Thus, for all objects M, the group G acts on M respecting the filtration W, and the unipotent subgroup W
−1(M) acts trivially on \(\mathrm{gr}^{W}_{\ast}M\). Let w:𝔾
m
→G/W
−1(G) be the cocharacter defined by the numbering of the filtration of W of M, for any M. This means that for a∈𝔾
m
, the automorphism w(a) of \(\mathrm{gr}^{W}_{\ast}(M)\) acts as multiplication with a
n on \(\mathrm{gr}^{W}_{n}(M)\). Let us consider the inverse image of this 𝔾
m
in G, or more precisely \(\mathbb {G}_{m}\times_{G/W_{-1}G}G\). Its Lie algebra \(\mathfrak{L}\) is an extension of  by \(\operatorname{Lie} W_{-1}(G)\).
by \(\operatorname{Lie} W_{-1}(G)\).
For any object M of \(\mathcal{T}\), let \(\mathfrak{u}_{M}\) be the image in \(W_{-1}\mathcal {E}\mathit {nd}(M)\) of \(\operatorname{Lie} W_{-1}(G)\). The extension \(\mathfrak{L}\) gives us by functoriality a quotient \(\mathfrak{L}_{M}\) of \(\mathfrak{L}\) acting on M, which is an extension of  by \(\mathfrak{u}_{M}\).
by \(\mathfrak{u}_{M}\).
In the setting of Sect. 4, U(M) corresponds to \(W_{-1}\mathcal {E}\mathit {nd}(M)\), and the subobject P(M) of U(M) corresponds to the subobject \(\mathfrak{u}_{M}\) of \(W_{-1}\mathcal {E}\mathit {nd}(M)\). We have a 1-motive [ℤ→U(M)] given by the point \(\overline{u}\), which has to be seen as an extension of [0→U(M)] by [ℤ→0], and P(M) was defined to be the smallest subobject of U(M) from which this extension comes, say after passing to ℚ-coefficients. Exactly in this way the two stories A.1 and A.2 are related:
Proposition A.3
-
(1)
The extension cl(M) is the push out of the extension \(\mathfrak{L}_{M}\) via the inclusion \(\mathfrak{u}_{M}\to W_{-1}\mathcal {E}\mathit {nd}(M)\).
-
(2)
If \(\mathfrak{v}\) is a subobject of \(\mathfrak{u}_{M}\) such that cl(M) is the image of a class in
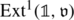 , then
\(\mathfrak{v} = \mathfrak{u}_{M}\).
, then
\(\mathfrak{v} = \mathfrak{u}_{M}\).
I claim in (1) an equality in  . As
. As  is 0 for weight reasons, it is the same as an (unique) isomorphism of actual extensions.
is 0 for weight reasons, it is the same as an (unique) isomorphism of actual extensions.
A first computation, which was helpful for understanding but now has disappeared from the proof, was to consider the category of graded representations of a graded Lie algebra \(\mathfrak{g}\) with degrees <0, and wondering what cocycle \(c:\mathfrak{g}\to W_{-1} \mathcal {E}\mathit {nd}(M)\) was giving me cl(M) in \(H^{1}(\mathfrak{g}, W_{-1}\mathcal {E}\mathit {nd}(M))\). The answer is the composite map \(\mathfrak{g}\to \mathfrak{g}\to W_{-1} \mathcal {E}\mathit {nd}(M)\), where the first map is multiplication by n in degree −n, and the second map is given by the action of \(\mathfrak{g}\) on M.
Proof of Proposition A.3
(1) For each integer n we have a map

The push-out by \(\mathfrak{u}_{M} \to W_{-1}\mathcal {E}\mathit {nd}(M)\) of the extension  is the pull-back of the extension
is the pull-back of the extension
by ∑
n
ne
n
. Indeed, ∑
n
ne
n
gives the action of  on \(\mathrm{gr}^{W}_{\ast}\!M\) corresponding to the grading. Define E
p
:=∑
n>p
e
n
and let A≤B be integers such that W
A
M=0 and W
B
M=M. We have then
on \(\mathrm{gr}^{W}_{\ast}\!M\) corresponding to the grading. Define E
p
:=∑
n>p
e
n
and let A≤B be integers such that W
A
M=0 and W
B
M=M. We have then
for some integer m depending on the choice of A and B. The map ∑
n
e
n
lifts to the identity morphism of M, viewed as a map  which factors over \(W_{0}\mathcal {E}\mathit {nd}(M)\). The pull-back of (∗) by m∑
n
e
n
is hence trivial, and the push-out of \(\mathfrak{L}_{M}\) by the inclusion \(\mathfrak{u}_{M} \to W_{-1}\mathcal {E}\mathit {nd}(M)\) is the sum of the pull-backs of (∗) by the E
p
. This pull-back by E
p
comes from an extension of
which factors over \(W_{0}\mathcal {E}\mathit {nd}(M)\). The pull-back of (∗) by m∑
n
e
n
is hence trivial, and the push-out of \(\mathfrak{L}_{M}\) by the inclusion \(\mathfrak{u}_{M} \to W_{-1}\mathcal {E}\mathit {nd}(M)\) is the sum of the pull-backs of (∗) by the E
p
. This pull-back by E
p
comes from an extension of  by \(\mathcal {H}\mathit {om}(M/W_{p}M,W_{p}M)\), which I would like to call Endomorphisms of
M
respecting
W
p
(M), inducing a multiple of the identity on
M/W
p
M
and 0 on
W
p
M. At least, that is what it becomes in any realisation. This is the extension already considered in A.1, corresponding to the class of M in Ext1(M/W
p
M,W
p
M). The sum of those extension classes, pushed to \(W_{-1}\mathcal {E}\mathit {nd}(M)\), had been defined to be cl(M).
by \(\mathcal {H}\mathit {om}(M/W_{p}M,W_{p}M)\), which I would like to call Endomorphisms of
M
respecting
W
p
(M), inducing a multiple of the identity on
M/W
p
M
and 0 on
W
p
M. At least, that is what it becomes in any realisation. This is the extension already considered in A.1, corresponding to the class of M in Ext1(M/W
p
M,W
p
M). The sum of those extension classes, pushed to \(W_{-1}\mathcal {E}\mathit {nd}(M)\), had been defined to be cl(M).
(2) On objects N of weights <0, i.e. such that N=W
−1
N, the functor  is left exact. For any class α in
is left exact. For any class α in  , there is hence a smallest sub-object N
0 of N such that α comes from a class in
, there is hence a smallest sub-object N
0 of N such that α comes from a class in  . Indeed, if α comes from N′ and from N″, the short exact sequence
. Indeed, if α comes from N′ and from N″, the short exact sequence
shows after applying  that α also comes from N′∩N″. It remains to show that the class of \(\mathfrak{L}_{M}\) in
that α also comes from N′∩N″. It remains to show that the class of \(\mathfrak{L}_{M}\) in  does not come from any \(\mathfrak{v} \subsetneq \mathfrak{u}_{M}\). Indeed, any subobject of \(\mathfrak{L}_{M}\) is stable by the action of \(\mathfrak{L}_{M}\) because G and \(\operatorname{Lie} G\) act on everything. □
does not come from any \(\mathfrak{v} \subsetneq \mathfrak{u}_{M}\). Indeed, any subobject of \(\mathfrak{L}_{M}\) is stable by the action of \(\mathfrak{L}_{M}\) because G and \(\operatorname{Lie} G\) act on everything. □
Proposition A.4
Any Lie-subobject of
\(\mathfrak{L}_{M}\)
mapping onto
 is equal to
\(\mathfrak{L}_{M}\). In other words, the extension
is equal to
\(\mathfrak{L}_{M}\). In other words, the extension
 is essential.
is essential.
Proof
The bracket of \(\mathfrak{L}_{M}\) passes to the quotients by W and defines brackets
and this bracket  is the multiplication by p. For any subobject \(\mathfrak{L}'\) of \(\mathfrak{L}_{M}\) mapping onto the quotient
is the multiplication by p. For any subobject \(\mathfrak{L}'\) of \(\mathfrak{L}_{M}\) mapping onto the quotient  , the stability of \(\mathfrak{L}'\) by the action of \(W_{p} \mathfrak{L}_{M}\) hence gives a surjectivity
, the stability of \(\mathfrak{L}'\) by the action of \(W_{p} \mathfrak{L}_{M}\) hence gives a surjectivity
from which the equality \(\mathfrak{L}' = \mathfrak{L}_{M}\) follows. □
Rights and permissions
About this article
Cite this article
Jossen, P. On the Mumford–Tate conjecture for 1-motives. Invent. math. 195, 393–439 (2014). https://doi.org/10.1007/s00222-013-0459-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00222-013-0459-y



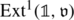 , then
, then