Abstract
We investigate the notion of real form of complex Lie superalgebras and supergroups, both in the standard and graded version. Our functorial approach allows most naturally to go from the superalgebra to the supergroup and retrieve the real forms as fixed points, as in the ordinary setting. We also introduce a more general notion of compact real form for Lie superalgebras and supergroups, and we prove some existence results for Lie superalgebras that are simple contragredient and their associated connected simply connected supergroups.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The study of real forms of complex contragredient Lie superalgebras was initiated by V. G. Kac in his foundational work [14] and then carried out by M. Parker in [19] and V. Serganova in [21], where also symmetric superspaces were accounted for. Later on, Chuah in [6] gave another thorough classification of such real forms using Vogan diagrams and Cartan automorphisms. In fact, as it happens for the ordinary setting, we have a one to one correspondence between real structures on a contragredient Lie superalgebra \( \mathfrak {g}\, \), and its Cartan automorphisms \( \textrm{aut}_{2,4}(\mathfrak {g}) \, \), that is automorphisms that are involutions on the even part and whose square is the identity on the odd part of \( \mathfrak {g}\, \). This translates to a bijection between the antilinear involutions \( \mathrm {\overline{aut}}_{2,2}(\mathfrak {g}) \) of \( \mathfrak {g}\) and the linear automorphisms \( \textrm{aut}_{2,4}(\mathfrak {g}) \, \). In the ordinary setting, that is for \( \, \mathfrak {g}= \mathfrak {g}_{\bar{0}}\, \), this correspondence is explicitly obtained through the Cartan antiinvolution \( \omega _{\bar{0}}\, \), whose fixed points give the compact form of \( \mathfrak {g}_{\bar{0}}\, \). In the supersetting, as we shall see, such antiinvolution is replaced by an antilinear automorphism \( \, \omega \in \mathrm {\overline{aut}}_{2,4}(\mathfrak {g}) \, \). This prompts for a more general treatment of real structures and real forms of superspaces and superalgebras, together with their global versions, where we consider both cases \( \, \mathrm {\overline{aut}}_{2,s}(\mathfrak {g}) \, \) and \( \, \textrm{aut}_{2,s}(\mathfrak {g}) \, \), for \( \, s = 2, 4 \, \). We shall refer to such real structures and real forms as standard and graded; they were introduced in [20, 21].
The paper is organized as follows. Section 2 contains preliminaries that help to establish our notation. In Sect. 3, we begin by defining the notion of standard and graded real structure on a superspace V as a pair \( (V,\phi ) \) with \( \, \phi \in \mathrm {\overline{aut}}_{2,2}(\mathfrak {g}) \, \) or \( \, \mathrm {\overline{aut}}_{2,4}(\mathfrak {g}) \, \), respectively. We obtain two categories, \( \mathrm {(smod)}_\mathbb {C}^\textrm{st}\) and \( \, \mathrm {(smod)}_\mathbb {C}^\textrm{gr}\, \), that we compactly denote \( \mathrm {(smod)}_\mathbb {C}^\bullet \, \) whenever there is no need to remark the difference; similarly, we define the corresponding categories of superalgebras \( \mathrm {(salg)}_\mathbb {C}^\bullet \, \). As expected, given a real structure, the associated real form is given by the fixed points of the antiautomorphism, however in the graded case, the functorial point of view is most fruitful, because such points cannot be seen over the complex field. After establishing the terminology and definitions, we can then give naturally the notion of real structures and real forms of Lie superalgebras, following and extending the work [20]. These real structures and real forms do integrate: thus, in Sect. 4, we obtain the category of complex supergroups with standard or graded real structures, that we denote with \( \mathrm {(sgrps)}_\mathbb {C}^\textrm{st}\) and \( \mathrm {(sgrps)}_\mathbb {C}^\textrm{gr}\, \), or more compactly \( \mathrm {(sgrps)}_\mathbb {C}^\bullet \, \). We also briefly discuss the super Harish-Chandra pairs (sHCp) approach in this context (see also [3, 11, 17]). Our main result for this part is the following (see Theorem 3.12).
Theorem A
If \( \, \big (\textbf{G},\Phi \big ) \in \mathrm {(sgrps)}_\mathbb {C}^\bullet \, \), the real form \( \, \textbf{G}^\Phi \) of \( \, \textbf{G}\, \), given by the fixed points of \( \, \Phi \, \), is
where \( \, G_+^{\Phi _+} \) is the ordinary underlying real form of \( G_+ \) and \( \, {\mathbb {A}}_{\bullet ,\mathbb {C}}^{0\,|d_1} \, \) is a real form of a purely odd affine superspace. In particular, the supergroup functor \( \, \textbf{G}^\Phi \) is representable.
In the remaining part of the paper, we discuss compact real forms of contragredient complex Lie superalgebras and the corresponding supergroups, using the results detailed above.
In the ordinary setting, a real Lie algebra is compact if it is embedded into some orthogonal or equivalently unitary Lie algebra. For a Lie superalgebra \( \mathfrak {g}\, \), many authors (see [2, 4, 6]) replace this notion with the requirement that \( \, \mathfrak {g}= \mathfrak {g}_0 \, \) and the latter compact. We take a more general approach, allowing \( \mathfrak {g}\) to have odd elements. For this reason, in Sect. 5, we need to examine super Hermitian forms, in the standard and graded context, and the corresponding unitary Lie superalgebras. In our Sect. 6.1, we retrieve in our language the physicists’ definition of unitary Lie superalgebra (see [21] and references therein), but also a graded version of it, obtained as fixed points of the superadjoint—that is, the supertranspose complex conjugate. We regard this example very significant and natural, since it is obtained via an antilinear morphism in \( \, \mathrm {\overline{aut}}_{2,4}(\mathfrak {gl}(m|n)) \, \), which has a categorical motivation (see [10], Ch. 1, and also [20, 21]).
In Sect. 6, we formulate our notion of compact Lie superalgebra as one admitting an embedding into a unitary Lie superalgebra for a suitable positive definite super Hermitian form. We shall call this super-compact. Then, we are finally able to introduce \( \, \omega \in \mathrm {\overline{aut}}_{2,4}(\mathfrak {g}) \, \), generalizing the Cartan antiinvolution \( \omega _{\bar{0}}\) mentioned above, and to prove the correspondence between \( \, \mathrm {\overline{aut}}_{2,4}(\mathfrak {g}) \, \) and \( \, \textrm{aut}_{2,2}(\mathfrak {g}) \, \) and between \( \, \mathrm {\overline{aut}}_{2,2}(\mathfrak {g}) \, \) and \( \, \textrm{aut}_{2,4}(\mathfrak {g}) \, \). Our main result for this part is the following (see Theorems 5.10 and 5.11):
Theorem B
Let \( \mathfrak {g}\) be a simple complex contragredient Lie superalgebra. Then:
- (a):
-
\( \mathfrak {g}\) admits a graded, super-compact real form, given via \( \, \omega \in \mathrm {\overline{aut}}_{2,4}(\mathfrak {g}) \, \);
- (b):
-
if \( \mathfrak {g}\) is of type 1, then \( \mathfrak {g}\) admits a standard, compact real form;
- (c):
-
if \( \mathfrak {g}\) is of type 2, then \( \mathfrak {g}\) has no standard, compact real form. In all cases, such super-compact or compact forms are unique up to inner automorphisms.
We end our treatment giving a global version of the previous results (see Theorems 6.4, 6.5).
Theorem C
Let \( \, \textbf{G}\) be a complex supergroup with \( \, \mathfrak {g}= \textrm{Lie}(G) \, \) being simple contragredient. Then \( \, \textbf{G}\) admits a graded, super-compact real form, which is unique up to inner automorphisms.
If \( \, \mathfrak {g}\) is of type 1, then \( \, \textbf{G}\) admits a standard, compact real form, unique up to inner automorphisms. If \( \, \mathfrak {g}\) is of type 2, then \( \, \textbf{G}\) has no standard, compact real form.
2 Real Structures of Superspaces and Superalgebras
Let our ground field \( \, \Bbbk = \mathbb {C}\, \). For notation and basic facts on supergeometry, see [1, 8, 16].
2.1 Real structures of super vector spaces
Definition 2.1
Let \( \, V \,\) be a complex super vector space. We call (generalized) real structure, of standard or graded type respectively, on V any \( \mathbb {C}\)–antilinear super vector space morphism \( \, \phi : V \longrightarrow V \, \) such that
(1) \( \phi ^2\big |_{V_{\bar{0}}} = \, \text { id}_{V_{\bar{0}}} \,\, \),
(2.s) \( \phi ^2\big |_{V_{\bar{1}}} = \, +\text { id}_{V_{\bar{1}}} \,\, \) (standard real structure),
(2.g) \( \phi ^2\big |_{V_{\bar{1}}} = \, -\text { id}_{V_{\bar{1}}} \,\, \) (graded real structure).
Note that giving a real structure on V is the same as giving on it a \( \mathbb {C}\)–antilinear action of the cyclic group \( \mathbb {Z}_4 \) which on the even part \( V_{\bar{0}}\) factors through its quotient \( \mathbb {Z}_2 \, \). The action factors through \( \mathbb {Z}_2 \) on all of V if and only if the corresponding real structure is standard.
We call the subspace \( V^\phi \) of fixed points standard or graded real form of \( V \, \). This \( V^\phi \) is a real form of V in the usual sense if and only if \( \phi \) is an involution, i.e. in the standard case.
If in addition V is a Lie superalgebra, we require \( \phi \) to be a Lie superalgebra (anti-linear) morphism, i.e. to preserve the Lie (super)bracket of V. Similarly, we require the analogous property when \( \phi \) is an associative superalgebra, a superbialgebra, a Hopf superalgebra, etc.
Definition 2.2
We define the categories \( \mathrm {(smod)}^\textrm{st}_\mathbb {C}\) and \( \mathrm {(smod)}^\textrm{gr}_\mathbb {C}\) of \( \mathbb {C}\)–supermodules with standard or graded real structure as follows. The objects are pairs \( (V,\phi ) \), where V is any \( \mathbb {C}\)–supermodule with \( \phi \) as its real structure (standard or graded). The morphisms from an object \( \big (V',\phi '\big ) \) to an object \( \big (V'',\phi ''\big ) \)—both either standard or graded—are those morphisms of \( \mathbb {C}\)–supermodules \( \, f : V' \longrightarrow V'' \, \) such that \( \, f \circ \phi ' = \phi '' \circ f \, \); in short, any such f preserves the \( \mathbb {Z}_4 \)–action. We use notation \( \mathrm {(smod)}^\bullet _\mathbb {C}\) to denote either one of these categories, with \( \, \bullet \in \{\textrm{st},\textrm{gr}\} \, \).
If \( \, (V,\phi ) \in \mathrm {(smod)}^\bullet _\mathbb {C}\, \) and \( \, V' \subseteq V \, \) is a super vector subspace of \( V \, \), with \( \, \phi (V') = V' \, \), we say that the real structure \( (V',\phi |_{V'}) \) is induced by \( (V,\phi ) \) and we write \( (V',\phi |_{V'})\!\! \subseteq (V,\phi ) \).
We can similarly define the categories \( \mathrm {(salg)}^\textrm{st}\) and \( \mathrm {(salg)}^\textrm{gr}\) of all unital associative commutative superalgebras with a standard or graded real structure and the categories \( \mathrm {(sLie)}^\textrm{st}\) and \( \mathrm {(sLie)}^\textrm{gr}\) of all Lie \( \mathbb {C}\)–superalgebras with a standard or graded real structure.
As customary with superalgebras—cf. [20]—for \( \, A \in \mathrm {(salg)}_\mathbb {C}^\bullet \, \) we denote the real structure with the notation \( \, a \mapsto {\widetilde{a}} \, \) , and we call such map standard or graded conjugation.
Remark 2.3
By its very construction, \( \mathrm {(smod)}_\mathbb {C}^\bullet \) is a subcategory of the category \( \mathrm {(smod)}_\mathbb {C}^{\mathbb {Z}_4} \) of supervector spaces with a \( \mathbb {Z}_4 \)–action. Moreover, the latter is also a tensor category, and then \( \mathrm {(smod)}_\mathbb {C}^\bullet \) is actually a tensor subcategory: namely, if \( \, \big (V',\phi '\big ), \big (V'',\phi ''\big ) \in \mathrm {(smod)}_\mathbb {C}^\bullet \, \), then \( \, \phi ' \otimes \phi '' \, \) is a real structure—of the correct type, i.e. either standard or graded—on \( \, V' \otimes V'' \, \).
2.2 Real structures and real forms of functors
We now want to express functorially the notion of (generalized) real structure described in the previous section. Assume that V is a complex super vector space and consider the functor

(the definition on the morphisms being clear), the
\( \mathbb {Z}_2 \)–grading being given by
\( \, {\big (h_V(A)\big )}_{\overline{z}} := A_{\overline{z}} \otimes V_{\overline{z}} \, \) for each
\( \, \overline{z} \in \mathbb {Z}_2 \, \). This in fact is identified with the functor of points of the affine superspace
\( \mathbb {A}(V) \)—see [1], Ch. 10. When in addition
\( \, V = \mathfrak {g}\in \mathrm {(sLie)}_\mathbb {C}\, \) is a complex Lie superalgebra, the associated functor
\( \, h_\mathfrak {g}\, \) is actually valued in the category
\( {(\mathbb {Z}_2\text {--Lie})}_\mathbb {C}\) of complex,
\( \mathbb {Z}_2 \)–graded Lie algebras, i.e. it is a functor
 .
.
Definition 2.4
Let V a complex super vector space. For
\( \, \bullet \in \{\textrm{st},\textrm{gr}\} \, \), let
\( \, {\mathcal {L}}_V \! := {\mathcal {R}} \circ h_V \circ {\mathcal {F}} \, \) where
\( \, {\mathcal {F}} : \mathrm {(salg)}^\bullet _\mathbb {C}\!\longrightarrow \! \mathrm {(salg)}_\mathbb {C}\, \) is the obvious forgetful functor and
\( \, {\mathcal {R}} : \mathrm {(smod)}_\mathbb {C}\!\longrightarrow \! \mathrm {(smod)}_\mathbb {R}\, \) is the obvious functor of scalar restriction. We call real structure on
\( {\mathcal {L}}_V \) any natural transformation
 such that for each
\( \, A \in \mathrm {(salg)}^\bullet _\mathbb {C}\, \) the map
such that for each
\( \, A \in \mathrm {(salg)}^\bullet _\mathbb {C}\, \) the map
 is
is
- (1):
-
conjugate \( A_{\bar{0}}\)–linear, i.e. \( \,\, \varphi _A(a_1 X_1 + a_2 X_2) = {\widetilde{a}}_1 \, \varphi _A(X_1) + {\widetilde{a}}_2 \, \varphi _A(X_2) \, \) for all \( \, a_i \in A_{\bar{0}}\, \), \( \, X_i \in {\mathcal {L}}_V(A) \, \),
- (2):
-
parity-preserving, i.e. \( \,\, \varphi _A\big ( A_{\overline{a}} \otimes V_{\overline{a}} \big ) \, \subseteq \, A_{\overline{a}} \otimes V_{{\overline{a}}} \,\, \),
- (3):
-
involutive, i.e. \( \, \varphi _{\!A}^{\,\,2} = 1 \,\, \).
Such a \( \varphi \) is called standard, resp. graded, if \( \, \bullet = \textrm{st} \, \), resp. \( \, \bullet = \textrm{gr} \, \).
If in addition \( \, V = \mathfrak {g}\in \mathrm {(sLie)}_\mathbb {C}\) is a Lie superalgebra, we define a real structure on \( {\mathcal {L}}_{\mathfrak {g}} \) as above, but adding the further condition that each \( \varphi _A \) be a morphism of ( \( \mathbb {Z}_2 \)–graded) Lie algebras, i.e.
Theorem 2.5
For every \( \, \mathfrak {g}\in \mathrm {(sLie)}_\mathbb {C}\), there exists a canonical, bijection between standard, resp. graded, real structures on \( {\mathcal {L}}_{\mathfrak {g}} \) and standard, resp. graded, real structures on \( \mathfrak {g}\, \). Furthermore, this bijection induces an equivalence between the category of functors \( {\mathcal {L}}_{\mathfrak {g}} \) with standard, resp. graded, real structures and \( \mathrm {(sLie)^{\textrm{st}}_\mathbb {C}}\, \), resp. \( \mathrm {(sLie)^{\textrm{gr}}_\mathbb {C}}\)—and similarly for \( {\mathcal {L}}_V \) and \( \mathrm {(smod)^{\textrm{st}}_\mathbb {C}}\, \), resp. \( \mathrm {(smod)^{\textrm{gr}}_\mathbb {C}}\, \).
Proof
If \( \varphi \) is a real structure on \( \mathcal {L}_V \), we have a corresponding real structure \( \, \phi : V \rightarrow V \, \) on V defined by \( \, \phi (v) := \varphi _\mathbb {C}(v) \, \). Conversely, if \( \phi \) is a real structure on V, for each \( \, A \in \mathrm {(salg)}_\mathbb {C}^\bullet \, \) we define a corresponding \( \varphi _A \) by \( \, \varphi _A(a \otimes v) := {\widetilde{a}} \otimes \phi (v) \, \). Details can be found in [20], Theorem 2.6. \(\square \)
We now turn to examine generalized real forms in the functorial language.
Definition 2.6
Let V be a complex super vector space with real structure \( \phi \, \), and \( \varphi \) the corresponding real structure on the functor \({\mathcal {L}}_{V} \, \), as in Theorem 2.5. We define real form (standard or graded) of \( {\mathcal {L}}_{V} \) as being the functor \( \, {\mathcal {L}}_{V}^{\,\varphi } : {\mathrm {(salg)}}^\bullet _\mathbb {C}\!\longrightarrow {\mathrm {(smod)}}_\mathbb {R}\, \) given on objects by
—in other words, \( \mathcal {L}_V^{\,\varphi }(A) \) is the submodule of \( \varphi _A \)–invariants, i.e. the fixed points of \( \varphi _A \, \), in \( \mathcal {L}_V(A) \, \)—and in the obvious way on morphisms. Note also that if \( \, V = \mathfrak {g}\in \mathrm {(sLie)}_\mathbb {C}\, \) is in fact a complex Lie superalgebra, and \( \phi \) is a real structure in the Lie sense, then each \( \, \mathcal {L}_\mathfrak {g}^{\,\varphi }(A) \, \) is automatically a \( \mathbb {Z}_2 \)–graded real Lie subalgebra in \( \mathcal {L}_\mathfrak {g}(A) \, \), so that \( \mathcal {L}_\mathfrak {g}^{\,\varphi } \) is actually a functor from \( \mathrm {(salg)}^\bullet _\mathbb {C}\) to \( {(\mathbb {Z}_2\text {--Lie})}_\mathbb {R}\, \), the category of \( \mathbb {Z}_2 \)–graded real Lie algebras.
Proposition 2.7
With notation as above, assume V is finite dimensional. Then the functor \( {\mathcal {L}}^{\,\varphi }_V \) is representable and it is represented by the symmetric superalgebra \( \, S(V^*) \in \mathrm {(salg)}^\bullet _\mathbb {C}\, \).
Proof
It is immediate by the following chain of equalities:
\(\square \)
Remarks 2.8
The following are alternative, equivalent ways to introduce the notion of “real structure” on the functor \(\mathcal {L}_V\) for any \( \, V \in \mathrm {(smod)}_\mathbb {C}\, \):
- (a):
-
Let \( {\overline{V}} \) be the complex-conjugate of V, that is V itself as real vector space endowed with the conjugate complex structure. Let \( \, {\mathcal {F}} : \mathrm {(salg)}^\bullet _\mathbb {C}\!\longrightarrow \! \mathrm {(salg)}_\mathbb {C}\, \) be the forgetful functor considered above, and \( \, {\mathcal {C}} : \mathrm {(salg)}^\bullet _\mathbb {C}\!\longrightarrow \! \mathrm {(salg)}^\bullet _\mathbb {C}\, \) be the functor given on objects by \( \, {\mathcal {C}}(A) := {\overline{A}} \, \) and on morphisms by \( \, {\mathcal {C}}(f) := f \, \); then, setting \( \, \mathcal {L}'_V := h_V \circ {\mathcal {F}} \, \) and \( \, \mathcal {L}'_{{\overline{V}}} := h_{{\overline{V}}} \circ {\mathcal {F}} \, \) we have \( \, h_{{\overline{V}}} = h_V \circ {\mathcal {C}} \, \) and \( \, \mathcal {L}'_{{\overline{V}}} = \mathcal {L}'_V \circ {\mathcal {C}} \, \). Using this language, giving a real structure on \( \mathcal {L}_V \) is equivalent to giving a pair of natural transformations
 and
and 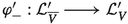 that are parity preserving and such that \( \, \varphi '_- \circ \varphi '_+ = \textrm{id}_{\mathcal {L}'_V} \, \) and \( \, \varphi '_+ \circ \varphi '_- = \textrm{id}_{\mathcal {L}'_{{\overline{V}}}} \, \).
that are parity preserving and such that \( \, \varphi '_- \circ \varphi '_+ = \textrm{id}_{\mathcal {L}'_V} \, \) and \( \, \varphi '_+ \circ \varphi '_- = \textrm{id}_{\mathcal {L}'_{{\overline{V}}}} \, \). - (b):
-
If \( \varphi \) is a real structure on \( \mathcal {L}_V \, \), then
 —for each \( \, A \in \mathrm {(salg)}_\mathbb {C}^\bullet \, \)—is a real structure, in classical sense, on the \( \mathbb {Z}_2 \)–graded complex vector space \( \mathcal {L}_V(A) \, \), which is conjugate \( A_{\bar{0}}\)–linear and preserves the \( \mathbb {Z}_2 \)–grading. Now, let \( {(\mathbb {Z}_2\text {--mod})}_\mathbb {C}^{\text {rs}} \) be the category of \( \mathbb {Z}_2 \)–graded complex vector spaces with a conjugate \( A_{\bar{0}}\)–linear, \( \mathbb {Z}_2 \)–graded real structure, and
—for each \( \, A \in \mathrm {(salg)}_\mathbb {C}^\bullet \, \)—is a real structure, in classical sense, on the \( \mathbb {Z}_2 \)–graded complex vector space \( \mathcal {L}_V(A) \, \), which is conjugate \( A_{\bar{0}}\)–linear and preserves the \( \mathbb {Z}_2 \)–grading. Now, let \( {(\mathbb {Z}_2\text {--mod})}_\mathbb {C}^{\text {rs}} \) be the category of \( \mathbb {Z}_2 \)–graded complex vector spaces with a conjugate \( A_{\bar{0}}\)–linear, \( \mathbb {Z}_2 \)–graded real structure, and 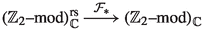 the obvious forgetful functor. Then, just rephrasing the Definition 2.4, we can quickly find that giving a real structure on \( \mathcal {L}_V \) is actually equivalent to giving a functor
the obvious forgetful functor. Then, just rephrasing the Definition 2.4, we can quickly find that giving a real structure on \( \mathcal {L}_V \) is actually equivalent to giving a functor  such that \( \, \mathcal {F}_* \circ {\dot{\mathcal {L}}} = \mathcal {L}_V \circ \mathcal {F}\, \).
such that \( \, \mathcal {F}_* \circ {\dot{\mathcal {L}}} = \mathcal {L}_V \circ \mathcal {F}\, \).
Indeed, roughly speaking the condition \( \, \mathcal {F}_* \circ {\dot{\mathcal {L}}} = \mathcal {L}_V \circ \mathcal {F}\, \) means that “\( {\dot{\mathcal {L}}} \) coincides with \( \mathcal {L}_V \) up to forgetting any real structure”, hence we can say that, in a nutshell, any such functor \( {\dot{\mathcal {L}}} \) is (sort of) “\( \mathcal {L}_V \) endowed with a pointwise real structure”.
2.3 Real affine superspaces
Let V be a complex super vector space of finite (super) dimension \( r|s \, \); its associated affine superspace \( \mathbb {A}(V) \) is the complex superspace described by the functor \( \, \mathcal {L}_V : \mathrm {(salg)}_\mathbb {C}\!\longrightarrow \mathrm {(smod)}_\mathbb {C}\, \), which is represented by the complex commutative superalgebra \( S(V^*) \, \). If in addition \( \phi \) is a real structure on V, we define the real affine superspace \( \mathbb {A}(V,\phi ) \) associated to \( (V,\phi ) \) as the “superspace with real structure” whose functor of points is \( \mathcal {L}_V^\varphi \) (as in Proposition 2.7 above), represented by the symmetric superalgebra \( S(V^*) \) with real structure canonically induced by that of V. We will also write \( \, \mathbb {A}_{\bullet ,\mathbb {C}}^{d_0|d_1} \! := \mathbb {A}(V, \phi ) \, \) if \( \, d_0\big |d_1 \, \, \) is the superdimension of \( V \, \), with \( \bullet \) denoting the type of \( \phi \, \).
Now observe that for any graded real structure \( \phi \) on a finite-dimensional complex superspace V, from \( \, \phi {\big |}_{V_{\bar{1}}}^2 = -\text {id}_{V_{\bar{1}}} \, \) it easily follows that \( V_{\bar{1}}\) has a \( \mathbb {C}\)–basis \( \, \big \{ u_1 , \dots , u_\delta , w_1 , \dots , w_\delta \big \} \, \) such that \( \, \phi (u_i) = +w_i \, \), \( \, \phi (w_i) = -u_i \, \), for all \( \, i = 1 , \dots , \delta \, \). In particular, \( \, d_1 := { dim}(V_{\bar{1}}) = 2\,\delta \, \) is even, and \( \, \phi {\big |}_{V_{\bar{1}}} \, \) is described—as a \( \mathbb {C}\)–linear map from \( V_{\bar{1}}\) to \( {\overline{V}}_{\bar{1}}\, \), that is \( V_{\bar{1}}\) endowed with the conjugate complex structure—by the \( 2 \times 2 \) block matrix \( \, \begin{pmatrix} \, 0 &{} -I_\delta \, \\ +I_\delta &{} 0 \, \end{pmatrix} \, \).
In particular, if V is a complex super vector space which is entirely odd, i.e. \( \, V = V_{\bar{1}}\, \), \( \, V_{\bar{0}}= 0 \, \), with graded real structure \( \phi \, \), then \( S(V^*) \) is isomorphic to the complex Grassmann algebra \( \, \Lambda _\mathbb {C}\big ( \xi _1^+ , \dots , \xi _\delta ^+ , \xi _1^- , \dots , \xi _\delta ^- \big ) \, \) in \( \, 2\,\delta = d_{\bar{1}}\, \) odd indeterminates—where \( \, \delta := d_1\big /2 = { dim}(V_{\bar{1}}) \big / 2 \, \)—with graded real structure given by \( \, \phi \big ( \xi _i^\pm \big ) := \pm \xi _i^\mp \, \) for all \( \, i = 1 , \dots , \delta \, \). Note that the A–points—for any \( \, A \in \mathrm {(salg)}_\mathbb {C}^{\text {gr}} \, \)—of \( \, \mathbb {A}_{\text {gr},\mathbb {C}}^{0|d_1} := \mathbb {A}(V, \phi ) \, \) are given by
or
When a real structure \( \varphi \) on \( \mathcal {L}_V \) is standard, we have the following characterization of \( {\mathcal {L}}_V^{\,\varphi } \, \):
Proposition 2.9
Let \( \varphi \) be a standard real form on \( {\mathcal {L}}_V \, \), and \( \phi \) the corresponding real structure on V. Then
- (a):
-
\({\mathcal {L}}_V^{\,\varphi }(A) \, := \, {(A \otimes V)}_{\bar{0}}^{\varphi _A} \, = \, {\big ( A^\textrm{re}\otimes V^\phi \,\big )}_{\bar{0}}\, \), with \( \, A^\textrm{re}= \big \{\, a \! \in \! A \,\big |\, a = \tilde{a} \,\big \} \quad \forall \, A \in \mathrm {(salg)}_\mathbb {C}^\textrm{st}\, \);
- (b):
-
\( {\mathcal {L}}_V^{\,\varphi }(R \otimes \mathbb {C}) \, = \, {\textrm{Hom}\,}_{\mathrm {(salg)}^\textrm{st}_\mathbb {C}}\big ( \mathbb {C}[V] , R \otimes \mathbb {C}\,\big ) \, = \, {\textrm{Hom}\,}_{\mathrm {(salg)}_\mathbb {R}}\big ( \mathbb {R}\big [V^\phi \big ] , R \,\big ) \quad \forall \, R \in \mathrm {(salg)}_\mathbb {R}\, \).
Proof
- (a):
-
Definitions give \( \, {(A \otimes V)}_{\bar{0}}^{\varphi _A} = \big \{\, a \otimes v + \varphi _A (a\otimes v) \,\big |\, |a| = |v| \,\big \} \, \). Let \( \, a = a_1 + i\,a_2 \, \), \( \, v = v_1 + i\,v_2 \, \), so that \( \, {\widetilde{a}} = a_1 - i\,a_2 \, \) and \( \, \phi (v) = v_1 - i\,v_2 \, \). Then
$$\begin{aligned}{} & {} (a_1+ia_2) \otimes (v_1+iv_2) + (a_1-ia_2) \otimes (v_1-iv_2) \\{} & {} \quad = \, 2a_1 \otimes v_1-2a_2 \otimes v_2 \in {\big ( A^\textrm{re}\otimes V^\phi \,\big )}_{\bar{0}}\end{aligned}$$ - (b):
-
By Proposition 2.7 we have
$$\begin{aligned}{} & {} {\mathcal {L}}_V^{\,\varphi }(R \otimes \mathbb {C}) \, = \, {\big ( (R \otimes _\mathbb {R}\mathbb {C}) \otimes _\mathbb {C}V \,\big )}_{\bar{0}}^{\varphi _{R \otimes \mathbb {C}}} \, = \, {\textrm{Hom}\,}_{\mathrm {(smod)}^\textrm{st}_\mathbb {C}} \big ( V^* , R \otimes _\mathbb {R}\mathbb {C}\big ) \, = \quad \\{} & {} \quad = \, {\textrm{Hom}\,}_{\mathrm {(salg)}^\textrm{st}_\mathbb {C}} \big ( S(V^*), R \otimes _\mathbb {R}\mathbb {C}\,\big ) \, = \, {\textrm{Hom}\,}_{\mathrm {(salg)}^\textrm{st}_\mathbb {C}} \big ( \mathbb {C}[V], R \otimes _\mathbb {R}\mathbb {C}\,\big ) \end{aligned}$$
On the other hand, by claim (a) we have
\(\square \)
Notice that, by claim (b) of the previous proposition, we have that \( \, {\mathcal {L}}_V^{\,\varphi }(A) \, = \, h_{V^\phi }(A^\textrm{re}) \, \) because in the standard case we have \( \, A = A^\textrm{re}\otimes \mathbb {C}\, \); therefore we can identify \( {\mathcal {L}}_V^{\,\varphi } \) with the functor \( h_{V^\phi } \) representing the real super vector space \( V^\phi \, \).
Observations 2.10
- (a):
-
If \( \, V' \subseteq V \, \) is a super vector subspace with real structure induced by \( (V,\phi ) \, \), then \( \, \mathcal {L}_{V'}^\varphi (A) \subseteq \mathcal {L}_V^\varphi (A) \, \ \text { for all} \,\ A \in {\mathrm {(salg)}}_{\mathbb C}^\bullet \, \).
- (b):
-
If \( \, V' \subseteq V \, \) is a super vector subspace with standard real structure induced by \( (V,\phi ) \, \), then \( \, (V')^\phi \subseteq V^\phi \, \) as real super vector spaces.
3 Real Structures and Real Forms of Supergroups
We now want to define the notion of real structure and real form of a supergroup, from different points of view. Let \( \mathrm {(sgrps)}_\mathbb {C}\, \) denote the category of complex supergroups.
3.1 Real structures on supergroups
We shall give our definition of real structure using both the sHCp’s and the functor of points approach. We first record a couple of auxiliary observations.
Observation 3.1
Let \( \textbf{G}\) be a complex supergroup, and \( \textrm{Lie}(\textbf{G}) \) its Lie superalgebra. Let \( \, {\mathcal {F}} : \mathrm {(salg)}_\mathbb {C}^\bullet \longrightarrow \mathrm {(salg)}_\mathbb {C}\, \) be the obvious forgetful functor, and \( \, {\mathcal {R}} : \mathrm {(smod)}_\mathbb {C}\!\longrightarrow \! \mathrm {(smod)}_\mathbb {R}\, \) be the obvious functor of scalar restriction. Thinking of \( \, \textbf{G}\, \) as a functor defined on \( \mathrm {(salg)}_\mathbb {C}\, \), we use notation \( \, \textbf{G}^\bullet := \textbf{G}\circ {\mathcal {F}} \, \). Then in particular we have—with notation of Definition 2.4—\( \, \mathcal {L}_{\textrm{Lie}(\textbf{G})} := {\mathcal {R}} \circ h_{\textrm{Lie}(\textbf{G})} \circ {\mathcal {F}} = {\mathcal {R}} \circ \mathcal {L}_{\textrm{Lie}(\textbf{G}^\bullet )} \, \).
Similarly, for the complex conjugate supergroup \( {\overline{\textbf{G}}} \) we have a parallel functor \( \overline{\textbf{G}^\bullet } \, \).
Lemma 3.2
Let \( \textbf{G}\) be a complex supergroup and \( \textrm{Lie}(\textbf{G}) \) its Lie superalgebra, and consider any natural transformation  —which loosely speaking can be equivalently seen as
—which loosely speaking can be equivalently seen as  . Then the following are equivalent (notations as in Observation 3.1 above):
. Then the following are equivalent (notations as in Observation 3.1 above):
- (a):
-
 is a real structure for \( \mathcal {L}_{\textrm{Lie}(\textbf{G})} \, \).
is a real structure for \( \mathcal {L}_{\textrm{Lie}(\textbf{G})} \, \). - (b):
-
\( \, \big ( \Phi _{\!A[\epsilon ]} \circ \textbf{G}^\bullet (v_a) \big )(z) \, = \, \big (\textbf{G}^\bullet (v_{\,{\widetilde{a}}}) \circ \Phi _{\!A[\epsilon ]} \big )(z) \, \) for \( \, A \in \mathrm {(salg)}_\mathbb {C}^\bullet \, \), \( \, a \in A_0 \, \), \( \, z \in {\textrm{Lie}(\textbf{G})}^\bullet (A) \, \), with
 given by \( \, v_a(x+\epsilon \,y) := x + \epsilon \,a\,y \, \).
given by \( \, v_a(x+\epsilon \,y) := x + \epsilon \,a\,y \, \).
Proof
By definition of \({\textbf{G}}^\bullet (v_a) \)—see [1], §11.3—we have \( \,\, \textbf{G}(v_a)(z) = a\,.\,z \, \) for all \( \, z \in \textrm{Lie}\big (\textbf{G}^\bullet \big )(A) \, \), that is \( \textbf{G}^\bullet (v_a) \) gives the action of \( \, a \in \mathcal {A}_0 \, \) onto \( \, \textrm{Lie}\big (\textbf{G}^\bullet \big )(A) \, \). Moreover, by [1], Ch. 11, we have \( \, \Phi _{\!A[\epsilon ]}(z) = {\textrm{Lie}(\Phi )}_A(z) \, \) for all \( \, z \in \textrm{Lie}\big (\textbf{G}^\bullet \big )(A) \, \). But then the condition in (b) reads \( \, {\textrm{Lie}(\Phi )}_A(a\,.\,z) \, = \, {\widetilde{a}}\,.\,{\textrm{Lie}(\Phi )}_A(z) \, \) which (applying \( {\mathcal {R}} \)) is equivalent to the conditions in (a). \(\square \)
The following definition is inspired by [20]:
Definition 3.3
(a) Let \( \textbf{G}\) be a complex supergroup and \( \textrm{Lie}(\textbf{G}) \) its Lie superalgebra. We call (generalized) real structure on \( \textbf{G}\) any natural transformation  such that
such that
(a.1) \( \, \Phi \) is an involution, i.e. \( \,\, \Phi ^2 = \text {id}_{{}_{\scriptstyle \textbf{G}^\bullet }}\),
(a.2)  is a real structure for \( \mathcal {L}_{\textrm{Lie}(\textbf{G})}\).
is a real structure for \( \mathcal {L}_{\textrm{Lie}(\textbf{G})}\).
(b) The pairs \( (\textbf{G},\Phi ) \) consisting of a complex supergroup with a real structure on it, along with all morphisms among them that respect the real structures on both sides, form a category that we denote hereafter by \( \mathrm {(sgrps)}_\mathbb {C}^\bullet \, \); moreover, we also denote by  , slightly abusing the notation, the natural forgetful functor, see Observation 3.1(b).
, slightly abusing the notation, the natural forgetful functor, see Observation 3.1(b).
As complex supergroups correspond to sHCp’s (via a category equivalence), we introduce the notion of generalized real structure for the latter.
Definition 3.4
Let \( (G_+,\mathfrak {g}) \) be a complex sHCp. We call (generalized) sHCp real structure on \( (G_+,\mathfrak {g}) \) any pair \( (\Phi _+,\phi ) \) such that
- (a):
-
\( \Phi _+ \) is a real structure (in the classical sense) on the complex algebraic group \( G_+ \, \);
- (b):
-
\( \phi \, \) is a real structure on the complex Lie superalgebra \( \mathfrak {g}\, \);
- (c):
-
\( \, {\big ( \textrm{Lie}(\Phi _+) \big )}_{1_{G_+}} \!\! = \, \phi {\big |}_{\mathfrak {g}_{\bar{0}}} \).
Then, we can define the category of standard or graded real sHCp’s \( \mathrm {(sHCp)}_\mathbb {C}^\bullet \, \), according to the type of \( \phi \, \), whose morphisms are morphisms of sHCp’s which preserve the real structures on either side; in addition, once more we have a natural forgetful functor  , again with a small abuse of notation—see Observation 3.1(b).
, again with a small abuse of notation—see Observation 3.1(b).
Remark 3.5
Just like a real structure on a complex vector superspace V can be thought of as a special \( \mathbb {C}\)–linear map from V to its complex-conjugate \( {\overline{V}} \), or viceversa, similarly a real structure on a complex supergroup \( \textbf{G}\) can be seen as a special morphism from \( \textbf{G}^\bullet \) to its complex-conjugate, denoted by \( \overline{\textbf{G}^\bullet } \, \). In the same way, a real structure on a complex sHCp \( (G_+,\mathfrak {g}) \) can be seen as a particular morphism from \( (G_+,\mathfrak {g}) \) to its complex-conjugate \( \overline{(G_+,\mathfrak {g})} \)—see [3, 8] for more details.
We show now that the two notions of real structure, that we have introduced, are indeed equivalent, through the above mentioned correspondence between supergroups and sHCp’s.
Proposition 3.6
Let \( \textbf{G}\) be a complex supergroups and \( (G_+,\mathfrak {g}) \) a complex sHCp that correspond to each other. Then there is a one-to-one correspondence between real structures on \( \textbf{G}\) and real structures on \( (G_+,\mathfrak {g}) \, \). This induces an equivalence of the corresponding categories \( \mathrm {(sgrps)}_\mathbb {C}^\bullet \) and \( \mathrm {(sHCp)}^\bullet \, \), which is consistent—via the natural forgetful functors—with the equivalence between supergroups and sHCp’s: in other words, the following diagram of functors (whose horizontal arrows are the above mentioned equivalences) is commutative

Proof
One way it is clear: if we have a real structure \( \Phi \) on \( \textbf{G}\) then via the equivalence  we define the pair \( \, (\Phi _+ , \phi ) := \big ( \Phi {|}_{G_+} , \textrm{Lie}(\Phi ) \big ) \, \).
we define the pair \( \, (\Phi _+ , \phi ) := \big ( \Phi {|}_{G_+} , \textrm{Lie}(\Phi ) \big ) \, \).
In the reverse direction, for a real structure \( (\Phi _+,\phi ) \) on \( (G_+,\mathfrak {g}) \) we define  via the reverse equivalence
via the reverse equivalence  . Using the explicit form of such an equivalence provided in [11] or [12], we only need to define \( \Phi _A \)—for each \( \, A \in \mathrm {(salg)}_\mathbb {C}^\bullet \, \)—on special elements in \( \, \textbf{G}^\bullet (A) := \textbf{G}(A) \, \) of the form \( \, (1 + \xi \,X) \, \), with \( \, \xi \in A_{\bar{1}}\, \), \( \, X \in \mathfrak {g}_{\bar{1}}\, \); then the recipe in [11, 13] for them prescribes \( \,\, \Phi ( 1 + \xi \,X ) \, := \, 1 + {\widetilde{\xi }} \, \phi (X) \, \). \(\square \)
. Using the explicit form of such an equivalence provided in [11] or [12], we only need to define \( \Phi _A \)—for each \( \, A \in \mathrm {(salg)}_\mathbb {C}^\bullet \, \)—on special elements in \( \, \textbf{G}^\bullet (A) := \textbf{G}(A) \, \) of the form \( \, (1 + \xi \,X) \, \), with \( \, \xi \in A_{\bar{1}}\, \), \( \, X \in \mathfrak {g}_{\bar{1}}\, \); then the recipe in [11, 13] for them prescribes \( \,\, \Phi ( 1 + \xi \,X ) \, := \, 1 + {\widetilde{\xi }} \, \phi (X) \, \). \(\square \)
In the next result we explain real structures for supergroups described as super-ringed spaces.
Proposition 3.7
Let \( \textbf{G}= \big ( |G|, \mathcal {O}_\textbf{G}\big ) \, \), be a complex algebraic supergroup, \( \, G_+ = \big ( |G|, \mathcal {O}_\textbf{G}/\mathcal {J}\big ) \, \) its reduced subgroup, and \( \Phi _+ \) a real structure on \( G_+ \, \). Then there exists a bijection between
- (i):
-
real standard, resp. graded, structures \( \Phi \) on \( \textbf{G}\) such that \( \, \Phi {\big |}_{G_+} = \Phi _+ \, \);
- (ii):
-
antilinear sheaf morphisms \( \, {\big \{ \mathcal {O}_\textbf{G}\big (\Phi _+^{-1}(U)\big ) \!\longrightarrow \mathcal {O}_\textbf{G}(U) \,\big \}} \, \) which are involutions on the even part and whose square is plus the identity, resp. minus the identity, on the odd part.
In particular, when \( \textbf{G}\) is affine, a real structure on \( \textbf{G}\) is equivalently given by an antilinear morphism \( \, \mathbb {C}[\textbf{G}] \longrightarrow \mathbb {C}[\textbf{G}] \, \), where \( \mathbb {C}[\textbf{G}] \) is the superalgebra of global sections on \( \textbf{G}\, \), which reduces to \( \Phi _+^* \) on the reduced algebra \( \, \mathbb {C}[\textbf{G}]\big /J \, \).
Proof
We give just a sketch of the argument (for more details, see [3, 8]). By Proposition 3.6, \( \textbf{G}\) corresponds to the sHCp \( (G_+,\mathfrak {g}) \)—where \( \, \mathfrak {g}= \textrm{Lie}(\textbf{G}) \, \) as usual—and any real structure \( \Phi \) on \( \textbf{G}\) as in (i) corresponds to a real structure \( (\Phi _+,\phi ) \) on the sHCp \( (G_+,\mathfrak {g}) \, \). In this setup, the structure sheaf \( \mathcal {O}_\textbf{G}\) of \( \textbf{G}\) can be described (cf. [2]) as
Now, starting from a real structure \( \Phi \) on \( \textbf{G}\) as in (i), hence from a real structure \( (\Phi _+,\phi ) \) on \( (G_+,\mathfrak {g}) \, \), note that the antilinear morphism \( \, \phi : \mathfrak {g}\longrightarrow \mathfrak {g}\, \) extends uniquely to an antilinear morphism \( \, {\mathfrak {U}}(\phi ) : {\mathfrak {U}}(\mathfrak {g}) \longrightarrow {\mathfrak {U}}(\mathfrak {g}) \, \). For each open U in \( G_+ \, \), this gives a map \( \, f \mapsto \! {\big (\Phi _+^*\big )}_U \circ f \circ \, {\mathfrak {U}}(\phi ) \, \) from \( \, \mathcal {O}_{\textbf{G}}(U) := {\textrm{Hom}\,}_{{\mathfrak {U}}(\mathfrak {g}_0)}\big ( {\mathfrak {U}}(\mathfrak {g}), \mathcal {O}_{G_+}(U) \!\big ) \, \) to \( \, \mathcal {O}_{\textbf{G}}\big (\Phi _+^{-1}(U)\!\big ) := {\textrm{Hom}\,}_{{\mathfrak {U}}(\mathfrak {g}_0)}\big ( {\mathfrak {U}}(\mathfrak {g}), \mathcal {O}_{G_+\!}\big (\Phi _+^{-1}(U)\big ) \big ) \, \)—where \( \, {\big \{ {\big (\Phi _+^*\big )}_U : \mathcal {O}_{G_+}(U) \longrightarrow \mathcal {O}_{G_+\!}\big (\Phi _+^{-1}(U)\big ) \big \}}_U \, \) is the built-in, antilinear sheaf morphism.
The construction of the inverse map is left to the reader. \(\square \)
Remark 3.8
Let \( \textbf{G}\) be an affine complex (algebraic or Lie) supergroup, and let \( \mathbb {C}[\textbf{G}] \) be the corresponding Hopf superalgebra. Then Proposition 3.7 guarantees that any (generalized) real structure on \( \textbf{G}\, \), say \( \Phi \, \), bijectively corresponds to a (generalized) real structure on the Hopf superalgebra \( \mathbb {C}[\textbf{G}] \)—cf. Definition 2.1; we denote this last structure by  .
.
As now \( \textbf{G}\) is affine, its functor of points is representable, and we can describe it in detail. Identifying \( \textbf{G}\) with its functor of points, and the real structure \( \Phi \) with a natural transformation
 , the real structure
, the real structure
 corresponding to
\( \Phi \) is given by
\( \, \varphi := {\Phi _{\mathbb {C}[\textbf{G}]}\big ( { id}_{\mathbb {C}[\textbf{G}]} \big )}^{-1} \, \). Conversely, given
corresponding to
\( \Phi \) is given by
\( \, \varphi := {\Phi _{\mathbb {C}[\textbf{G}]}\big ( { id}_{\mathbb {C}[\textbf{G}]} \big )}^{-1} \, \). Conversely, given
 , the corresponding real structure
\( \Phi \) on
\( \textbf{G}\) is given (as a natural transformation) by
\( \, \Phi _A := (-) \circ \varphi ^{-1} \, \), i.e.
, the corresponding real structure
\( \Phi \) on
\( \textbf{G}\) is given (as a natural transformation) by
\( \, \Phi _A := (-) \circ \varphi ^{-1} \, \), i.e.

for all \( \, A \in \mathrm {(salg)}_\mathbb {C}\, \), taking into account—cf. Remark 3.5—that any real structure on \( \textbf{G}\) can be seen as a special supergroup morphism from \( \, \textbf{G}^\bullet \, \) to \( \, \overline{\textbf{G}^\bullet } \, \) (the complex-conjugate of \( \, \textbf{G}^\bullet \, \)).
Now we modify the natural transformation
 above, by setting
\( \, \Phi ^\bullet _A := \widetilde{(\ )}_A \circ \Phi _A \, \) for all
\( \, A \in \mathrm {(salg)}_\mathbb {C}^\bullet \, \), that is in detail
above, by setting
\( \, \Phi ^\bullet _A := \widetilde{(\ )}_A \circ \Phi _A \, \) for all
\( \, A \in \mathrm {(salg)}_\mathbb {C}^\bullet \, \), that is in detail
since
\( \, \textbf{G}^\bullet (A) := \textbf{G}(A) \, \). Note that
\( \, \Phi ^\bullet _{\!A}(g_{{}_A}) \in {\textrm{Hom}\,}_{\mathrm {(salg)}_\mathbb {C}}\big ( \mathbb {C}[\textbf{G}] \, , A \big ) =: \textbf{G}^\bullet (A) \, \) since each
\( \Phi ^\bullet _{\!A}(g_{{}_A}) \) is now
\( \mathbb {C}\)–linear, so
\( \, \Phi ^\bullet _{\!A} \, \) is a group morphism from
\( \textbf{G}^\bullet (A) \) to
\( \textbf{G}^\bullet (A) \, \). All these
\( \Phi ^\bullet _{\!A} \)’s define a natural transformation
\( \, \Phi ^\bullet := {\big \{ \Phi ^\bullet _{\!A} \big \}}_{A \in \mathrm {(salg)}_\mathbb {C}^\bullet } \, \) from
\( \textbf{G}^\bullet \) to itself: in the following, whenever
\( \textbf{G}\) is affine by real structure on
\( \textbf{G}^\bullet \) we shall mean exactly this supergroup endomorphism
 .
.
3.2 Real forms of supergroups
We now turn to the definition of (generalized) real forms for supergroups.
Definition 3.9
Let \( \, (\textbf{G},\Phi ) \) be a complex supergroup with real structure, and \( \, \textbf{G}^\bullet := \textbf{G}\circ \mathcal {F}\, \) as above. We define (generalized) real form functor (“standard/graded”, according to \( \Phi \)) of \( \, (\textbf{G},\Phi ) \, \), or “real form functor of \( \textbf{G}\) with respect to \( \Phi \)”, the subgroup functor \( \textbf{G}^\Phi \) of \( \textbf{G}^\bullet \) defined by
—for every \( \, A, B \in \mathrm {(salg)}_\mathbb {C}^\bullet \, \), \( \, f \in {\textrm{Hom}\,}_{\mathrm {(salg)}_\mathbb {C}^\bullet }(A\,,B\,) \, \)—where we denote by
the subgroup of \( \Phi ^\bullet _{\!A} \)–invariants. Hereafter we are tacitly identifying—as it is always possible, by general theory—the abstract groups \( \, \textbf{G}^\bullet (A) := \textbf{G}(A) \, \) and \( \, \overline{\textbf{G}^\bullet }(A) := {\overline{\textbf{G}}}(A) \, \).
Proposition 3.10
Let \( \textbf{G}\) be an affine complex supergroup with (generalized) real structure \( \Phi \, \). Then the functor \( \textbf{G}^\Phi \) is representable.
Proof
As
\( \textbf{G}\) is affine, let
\( \, \mathbb {C}[\textbf{G}] \in \mathrm {(salg)}_\mathbb {C}\, \) be the Hopf superalgebra representing it, as a functor from
\( \mathrm {(salg)}_\mathbb {C}\) to
\( \mathrm {(grps)}\, \): then by Proposition 3.7, there exists a real structure
 —which corresponds uniquely to
\( \Phi \)—so that
\( \, \big (\mathbb {C}[\textbf{G}], \varphi \big ) \in \mathrm {(salg)}_\mathbb {C}^\bullet \, \). Now Definition 3.9 together with Remark 3.8 yield—for every
\( \, A \in \mathrm {(salg)}_\mathbb {C}^\bullet \, \)—
—which corresponds uniquely to
\( \Phi \)—so that
\( \, \big (\mathbb {C}[\textbf{G}], \varphi \big ) \in \mathrm {(salg)}_\mathbb {C}^\bullet \, \). Now Definition 3.9 together with Remark 3.8 yield—for every
\( \, A \in \mathrm {(salg)}_\mathbb {C}^\bullet \, \)—
because the condition
\( \, \widetilde{g(u)} = g\big (\varphi (u)\big ) \, \)—for
\( \, u \in \mathbb {C}[\textbf{G}] \, \)—means that the superalgebra morphism
 preserves the real structure on both sides, hence
\( \, g \in {\textrm{Hom}\,}_{\mathrm {(salg)}_\mathbb {C}^\bullet }\big ( \mathbb {C}[\textbf{G}], A \big ) \, \).
\(\square \)
preserves the real structure on both sides, hence
\( \, g \in {\textrm{Hom}\,}_{\mathrm {(salg)}_\mathbb {C}^\bullet }\big ( \mathbb {C}[\textbf{G}], A \big ) \, \).
\(\square \)
Observation 3.11
Let us consider a standard real structure \( \Phi \) on a complex affine supergroup \( \textbf{G}\, \), i.e. \( \, (\textbf{G}, \Phi ) \in \mathrm {(sgrps)}_\mathbb {C}^\textrm{st}\, \), and let \( \varphi \) be the corresponding real structure on \( \mathbb {C}[\textbf{G}] \, \). As \( \Phi \) is standard, the same is true for \( \varphi \) as well: then each \( \, f \in \mathbb {C}[\textbf{G}] \, \) has a unique splitting as \( \, f = f_+ + i \, f_- \, \) with \( \, \varphi (f_\pm ) = f_\pm \, \). Using this, the relation (2) and—for all \( \, A \in \mathrm {(salg)}_\mathbb {C}^\textrm{st}\, \)—the identity \( \, {\textrm{Hom}\,}_{\mathrm {(salg)}_\mathbb {C}^\textrm{st}}\big (\, \mathbb {C}[\textbf{G}], A \,\big ) \, = \, {{\textrm{Hom}\,}_{\mathrm {(salg)}_\mathbb {C}}\big (\, \mathbb {C}[\textbf{G}], A \,\big )}^{\Phi _{\!A}^\bullet } \, \) and Proposition 3.10, one finds that
for all \( \, R \in \mathrm {(salg)}_\mathbb {R}\, \). This gives us a description of the real supergroup functor \( \, R \mapsto \textbf{G}^\Phi \big ( \mathbb {C}\otimes _\mathbb {R}R \,\big ) \, \)—for all \( \, R \in \mathrm {(salg)}_\mathbb {R}\, \) —which is the real form \( \textbf{G}^\Phi \) (of \( \textbf{G}\, \)) when seen as a real supergroup.
This is the analog, in some sense, of Proposition 2.9 for super vector spaces.
3.3 Functor of points of real forms
In this section we describe in detail the real form of a supergroup, using the functor of points approach. To begin with, we shortly recall the following.
For the standard functor
 we choose a specific quasi-inverse functor
we choose a specific quasi-inverse functor
 , namely the second one described in [12], therein denoted by
\( \Psi ^e \). Via the latter, for every
\( \, \textbf{G}\in \mathrm {(sgrps)}_\mathbb {C}\, \) and
\( \, A \in \mathrm {(salg)}_\mathbb {C}\, \) the group
\( \textbf{G}(A) \) is described as
, namely the second one described in [12], therein denoted by
\( \Psi ^e \). Via the latter, for every
\( \, \textbf{G}\in \mathrm {(sgrps)}_\mathbb {C}\, \) and
\( \, A \in \mathrm {(salg)}_\mathbb {C}\, \) the group
\( \textbf{G}(A) \) is described as
where \( \, \exp \!\big ( A_{\bar{1}}\!\otimes _\mathbb {C}\mathfrak {g}_{\bar{1}}\big ) \! := \! \big \{ \exp (\mathcal {Y}) \,\big |\, \mathcal {Y}\! \in \! A_{\bar{1}}\!\otimes _\mathbb {C}\mathfrak {g}_{\bar{1}}\big \} \, \), \( \, d_{\bar{1}}:= { dim}(\mathfrak {g}_{\bar{1}}) \, \), and the symbol “ \( \, \cong \, \)” on the right just means that \( \textbf{G}\) and \( \, G_+ \times {\mathbb {A}}_\mathbb {C}^{0\,|d_{\bar{1}}} \, \) are isomorphic as supermanifolds. In particular, formula (3) means that each \( \, g \in \textbf{G}(A) \, \) has a unique expression of the form
for some unique \( \, g_+ \in G_+(A) \, \) and \( \, \mathcal {Y}\in A_{\bar{1}}\!\otimes _\mathbb {C}\mathfrak {g}_{\bar{1}}\, \). Now, let \( \Phi \) be the chosen real structure on \( \textbf{G}\, \), and \( \, \big ( \Phi _+, \phi \big ) \, \) its corresponding real structure on \( \, \big ( G_+, \mathfrak {g}\big ) \, \); then the action of \( \Phi \) on \( \, g \in \textbf{G}(A) \, \) reads—through (4), and setting \( \, \varphi _A := \widetilde{( - )} \otimes \phi \, \) (cf. Theorem 2.5)—as follows:
We are now ready for the main result in this section, which is Theorem A in Sect. 1.
Theorem 3.12
Let \( \, \big (\textbf{G},\Phi \big ) \in \mathrm {(sgrps)}_\mathbb {C}^\bullet \, \). Then the real form \( \, \textbf{G}^\Phi \) of \( \, \textbf{G}\) is explicitly described as
Moreover, the factorization is direct: each \( \, g \in \textbf{G}(A)\) has a unique factorization of the form
In particular we have \( \, \textbf{G}^\Phi \cong \, G_+^{\Phi _+} \! \times {\mathbb {A}}_{\bullet ,\mathbb {C}}^{0\,|d_1} \, \) (cf. § 2.3), hence the functor \( \, \textbf{G}^\Phi \) is representable.
Proof
Given \( \, g \in \textbf{G}(A) \, \), with factorization \( \, g = g_+ \!\cdot \exp (\mathcal {Y}) \, \) as in (4), by (5) we have
and the rightmost condition is equivalent to \( \, \Phi _+(g_+) = g_+ \, \) together with \( \, \exp \!\big (\varphi _A(\mathcal {Y})\big ) = \exp (\mathcal {Y}) \, \), i.e. \( \, \Phi _+(g_+) = g_+ \, \) and \( \, \varphi _A(\mathcal {Y}) = \mathcal {Y}\, \), which means \( \, g_+ \in G_+^{\Phi _+}(A) \, \) and \( \, \mathcal {Y}\in {( A_{\bar{1}}\!\otimes _\mathbb {C}\mathfrak {g}_{\bar{1}})}^{\varphi _A} \, \). Then
as claimed. Moreover, the factorization \( \, g = g_+ \!\cdot \exp (\mathcal {Y}) \, \) is unique by construction. \(\square \)
We end this section with a remark regarding the more general setting of supermanifolds, that we shall not pursue directly in this paper.
Remark 3.13
The sheaf theoretic characterization of standard and graded real forms of a supergroup as in Proposition 3.7 can be extended, almost immediately, to give a well posed more general definition of real forms (standard and graded) of supermanifolds.
4 Hermitian Forms and Unitary Lie Superalgebras
We introduce now a suitable notion of unitary Lie superalgebra, which is a special real form of \( \mathfrak {gl}(V) \) associated with a Hermitian form on the superspace \( V \, \).
4.1 Super Hermitian Forms
We begin with the definition of super Hermitian form on a complex super vector space \( V \, \): this is a map  which is \( \mathbb {C}\)–linear in the first entry, \( \mathbb {C}\)–antilinear in the second entry, and such that
which is \( \mathbb {C}\)–linear in the first entry, \( \mathbb {C}\)–antilinear in the second entry, and such that
In addition, we say that B is consistent if \( \, B(x,y) = 0 \, \) for any homogeneous x and y of different parity (see [21], pg. 112, for more details). From now on we assume B to be consistent.
We can write any consistent super Hermitian form B as \( \, B = B_{\bar{0}}+ i \, B_{\bar{1}}\, \), where each \( \, B_{{\overline{z}}} := {(-i)}^{{\overline{z}}} \, B{\Big |}_{V_{{\overline{z}}} \times V_{{\overline{z}}}} \, \) is an Hermitian form (in the classical, non-super sense) on the vector space \( V_{{\overline{z}}} \, \), for \( \, {\overline{z}} \in \mathbb {Z}_2 \, \). Notice then that \( \, B' = B_{\bar{0}}- i \, B_{\bar{1}}\, \) is also another super Hermitian form on \( V \, \).
We say that B is non degenerate if both the \( B_{{\overline{z}}} \)’s are non degenerate; similarly, B is positive definite if both the \( B_{{\overline{z}}} \)’s are positive definite: in this case we write \( \, B > 0 \, \). If instead \( \, B_{\bar{0}}> 0 \, \) and \( \, B_{\bar{1}}< 0 \, \), then \( B' \) (as defined above) is a positive definite super Hermitian form, instead of \( B \, \).
Example 4.1
Let \( \, V := \mathbb {C}^{m|n} \, \). We can define on V two super Hermitian forms, say \( B^+_V \) and \( B^-_V \, \), given by
where \( \, z , z' \in \mathbb {C}^m \, \), \( \, \zeta , \zeta ' \in \mathbb {C}^n \, \), while \( \, z \cdot z' \, \) and \( \, \zeta \!\cdot \zeta ' \, \) are the usual scalar products in \( \mathbb {C}^m \) and \( \mathbb {C}^n \).
We recall also the notion of supersymmetric (bilinear) form on a complex super vector space \( V \, \): it is a \( \mathbb {C}\)–bilinear map \( \, \langle \,\ ,\ \rangle : V \times V \longrightarrow \mathbb {C}\, \) such that
Again, we say that the form \( \, \langle \,\ ,\ \rangle \, \) is consistent if \( \, \langle x, y \rangle = 0 \, \) for any homogeneous x and y of different parity. From now on we assume any such form \( \, \langle \,\ ,\ \rangle \, \) to be consistent.
Now let \( \phi \) be a real structure on V and \( \, \langle \,\ , \ \rangle \, \) be any \( \mathbb {C}\)–bilinear form on \( V \, \). We say that the form \( \, \langle \,\ , \ \rangle \, \) is \( \phi \)–invariant—or just invariant—if it is a morphism of superspaces with real structures (i.e. of \( \mathbb {Z}_4 \)–modules), that is \( \,\, \overline{\langle \, v \,, w \,\rangle } \, = \, \big \langle \phi (v) \,, \phi (w) \big \rangle \,\, \) for all \( \, v, w \in V \, \). Then we have the following link with Hermitian forms on \( V \, \), which follows by direct computation:
Proposition 4.2
Let \( \, (V,\phi ) \in \mathrm {(smod)}_\mathbb {C}^\bullet \, \) and let \( \, \langle \,\ , \ \rangle \, \) be a \( \phi \)–invariant, consistent, supersymmetric, \( \mathbb {C}\)–bilinear form on \( V \, \). Then
defines two consistent super Hermitian forms \( B^+_\phi \) and \( B^-_\phi \) on V (which coincide if \( \phi \) is standard).
Observation 4.3
When \( \phi \) is graded, we can write the super Hermitian form \( B^\pm _\phi \) in (8) as
where \( \, B_0(x_0,y_0) := \big \langle x_0 \,, \phi (y_0) \big \rangle \, \) and \( \, B_1(x_1,y_1) := \big \langle x_1 \,, \phi (y_1) \big \rangle \, \) are ordinary Hermitian forms (in the classical, non-super sense) on \( V_0 \) and \( V_1 \) both considered as plain complex vector spaces—i.e. forgetting their super structure. Similarly, if \( \phi \) is standard we can write \( \, B_\phi := B^\pm _\phi \, \) as
where \( \, B_0(x_0,y_0) := \big \langle x_0 \,, \phi (y_0) \big \rangle \, \) and \( \, B_1(x_1,y_1) := -i \, \big \langle x_1 \,, \phi (y_1) \big \rangle \, \) are both ordinary Hermitian forms on \( V_0 \) and \( V_1 \) respectively (now seen as plain complex vector spaces).
We end this section with some examples of real structures in \( \mathbb {C}^{m|n} \), to be used later on.
Examples 4.4
Let \( \, V := \mathbb {C}^{m|n} = \mathbb {C}^{m|2t} \, \) with \( \, n = 2\,t \in 2\,\mathbb {N}_+ \, \); we consider on it the standard and graded real structures \( \phi _\textrm{gr}\) defined by


Now we fix in \(\mathbb {C}^{m|2t} \) the bilinear form  defined by
defined by
(notation as before). A moment’s check shows that the form \( \, {\langle \,\ ,\ \rangle }_V \, \) fulfills the following:
— (1) it is supersymmetric,
— (2) \( \overline{\langle x, y \rangle _V} \, = \, {\big \langle \phi (x), \phi (y) \big \rangle }_V \,\, \) for all \( \, x , y \in V \), for both \( \, \phi \in \big \{ \phi _\textrm{st}, \phi _\textrm{gr}\big \} \, \).
According to Proposition 4.2, there exist two pairs of super Hermitian forms on \( \, V := \mathbb {C}^{m|2t} \, \) associated with the form \( \, {\langle \,\ ,\ \rangle }_V \, \) and the real structures \( \phi _\textrm{st}\) and \( \phi _\textrm{gr}\, \), namely
-
Standard case (the sign being irrelevant):
$$\begin{aligned} B^\pm _{\phi _\textrm{st}}\!\big ( (z,\zeta _+,\zeta _-), \big (z',\zeta '_+,\zeta '_-\big ) \big ) \,\, = \,\, z \cdot \overline{z'} \, + \, \zeta _+ \cdot \overline{\zeta '_-} \, - \, \zeta _- \cdot \overline{\zeta '_+} \quad \end{aligned}$$(11) -
Graded case:
$$\begin{aligned} B^\pm _{\phi _\textrm{gr}}\!\big ( (z,\zeta _+,\zeta _-), \big (z',\zeta '_+,\zeta '_-\big ) \big ) \,\, = \,\, z \cdot \overline{z'} \, \mp \, i \, \big (\, \zeta _+ \!\cdot \overline{\zeta '_+} \, + \, \zeta _- \!\cdot \overline{\zeta '_-} \,\big ) \end{aligned}$$(12)
Note that, using the compact notation \( \, \zeta := (\zeta _+ , \zeta _-) \, \), we can re-write the forms \( B^\pm _{\phi _\textrm{gr}} \) as
which looks like (7) in the standard case, up to switching signs.
Remark 4.5
It is worth stressing that not all Hermitian forms can be realized as \( B_\phi \) as in Proposition 4.2; in fact, for any such \( B_\phi \) the odd part of the superspace V must be even dimensional. So, for example, the forms in (7) on \( \mathbb {C}^{m|n} \) for odd n cannot be realized as a \( B_\phi \, \).
Nevertheless, we will have a particular interest for Hermitian forms on \( \mathfrak {gl}(m|n) \, \): note that for this superspace the odd part has dimension \( 2\,m\,n \, \).
4.2 Functorial Hermitian forms
We introduce now the functorial counterpart of the notion of super Hermitian form.
Definition 4.6
Given \( \, (V,\phi ) \in \mathrm {(smod)}^\bullet _\mathbb {C}\, \)—for any \( \, \bullet \in \{\text { st} , \text { gr}\} \, \)—recall that the functor \( \, \mathcal {L}_V : \mathrm {(salg)}_\mathbb {C}^\bullet \longrightarrow \mathrm {(smod)}_\mathbb {R}\, \) has values into the category \( \mathrm {(smod)}_\mathbb {R}\) of real super vector spaces with \( \mathbb {Z}_2 \)–grading given by \( \, {\big ( \mathcal {L}_V(A) \big )}_{{\overline{z}}} := A_{{\overline{z}}} \otimes _\mathbb {C}V_{{\overline{z}}} \, \)—for each \( \, {{\overline{z}}} \in \mathbb {Z}_2 \, \); for this grading, we denote with \( \, [v] := {\overline{z}} \, \) the degree of a homogeneous vector \( \, v \in {\big ( \mathcal {L}_V(A) \big )}_{{\overline{z}}} \, \).
We call functorial Hermitian form (or just Hermitian form) \( \mathcal {B}\) on \( \, \mathcal {L}_V : \mathrm {(salg)}_\mathbb {C}^\bullet \longrightarrow \mathrm {(smod)}_\mathbb {R}\, \) any natural transformation \( \, \mathcal {B}: \mathcal {L}_V \times \mathcal {L}_V \longrightarrow \mathcal {L}_\mathbb {C}\, \) such that
-
1.
\( \, \mathcal {B}\, \) is \( \mathcal {A}_{\bar{0}}\)–linear on the left, i.e. it is left-additive and such that \( \, \mathcal {B}(a\,X,Y)\, = \, a \, \mathcal {B}(X,Y) \, \) for all \( \, a \in A_{\bar{0}}\, \), \( \, X , Y \in \mathcal {L}_V(A) \, \), \( \, A \in \mathrm {(salg)}^\bullet _\mathbb {C}\, \);
-
2.
\( \, \mathcal {B}\, \) is \( A_{\bar{0}}\)–antilinear on the right, i.e. it is right-additive and such that \( \, \mathcal {B}(X,a\,Y) \, = \, {\widetilde{a}} \, \mathcal {B}(X,Y) \, \) for all \( \, a \in A_{\bar{0}}\, \), \( \, X , Y \in \mathcal {L}_V(A) \, \), \( \, A \in \mathrm {(salg)}^\bullet _\mathbb {C}\, \);
-
3.
\( \mathcal {B}(X,Y) \, = \, {\left\{ \begin{array}{ll} \, {(-1)}^{[X]\,[Y]} \, \widetilde{\mathcal {B}(Y,X)} &{} \ \text {if} \, \phi \, \text {is } { standard} \\ \,\,\, \widetilde{\mathcal {B}(Y,X)} &{} \ \text { if } \, \phi \, \text { is } { graded} \end{array}\right. } \) for all \( \, X , Y \in \mathcal {L}_V(A) \, \), \( \, A \in \mathrm {(salg)}^\bullet _\mathbb {C}\, \). In short, using notation as in (8) we can write \( \,\, \mathcal {B}(X,Y) \, = \, {(-1)}^{(\,{\bar{1}}-\nu _\phi )\,[X]\,[Y]} \, \widetilde{\mathcal {B}(Y,X)} \,\, \) for any \( \phi \, \).
In addition, we say that \( \mathcal {B}\) is consistent if \( \, \mathcal {B}(Y,X) = 0 \, \) for all homogeneous X, Y with different parity, i.e. \( \, [X] \not = [Y] \, \).
Lemma 4.7
Let \( \, (V,\phi ) \in \mathrm {(smod)}^\bullet _\mathbb {C}\, \), and let \( \, B_V : V \times V \longrightarrow \mathbb {C}\, \) be a consistent super Hermitian form on the super vector space \( V \, \). Then the natural transformation  defined on objects—for \( \, A \in \mathrm {(salg)}^\bullet _\mathbb {C}\, \) and homogeneous \( \, a \in A_{{\overline{z}}} \, \), \( \, x \in V_{{\overline{z}}} \, \), \( \, b \in A_{{\overline{s}}} \, \), \( \, y \in V_{{\overline{s}}} \, \)—by
defined on objects—for \( \, A \in \mathrm {(salg)}^\bullet _\mathbb {C}\, \) and homogeneous \( \, a \in A_{{\overline{z}}} \, \), \( \, x \in V_{{\overline{z}}} \, \), \( \, b \in A_{{\overline{s}}} \, \), \( \, y \in V_{{\overline{s}}} \, \)—by
is a consistent Hermitian form for \( \mathcal {L}_V \, \).
Proof
The proof is a matter of sheer computation. \(\square \)
Proposition 4.8
Let \( \, (V,\phi ) \in \mathrm {(smod)}^\bullet _\mathbb {C}\, \). Then formula (13) realizes a bijection between
-
(a)
the set of all consistent super Hermitian forms on V,
-
(b)
the set of all consistent Hermitian forms for \( \mathcal {L}_V \, \).
Proof
After Lemma 4.7, we only need to show that if a form \( \mathcal {B}_{\mathcal {L}_V} \) as in (b) is given, then we can find a unique \( B_V \) on V satisfying (13). Indeed, such a \( B_V \) is defined as follows. Consider \( \, A_{\,\xi _+,\xi _-} := \mathbb {C}\big [ \xi _+ , \xi _- \,\big ] \in \mathrm {(salg)}_\mathbb {C}\, \): this superalgebra has a “canonical” standard real structure defined by \( \, \xi _\pm \mapsto \widetilde{\xi _\pm } := \xi _\mp \, \), and a “canonical” graded one given by \( \, \xi _\pm \mapsto \widetilde{\xi _\pm } := \pm \xi _\mp \, \). Then also  is defined, taking values in \( \, \mathcal {L}_\mathbb {C}\big ( A_{\,\xi _+,\xi _-} \big ) = \mathbb {C}\oplus \mathbb {C}\,\xi _+\,\xi _- \, \), which has \( \mathbb {C}\)–basis \( \, \{ 1, \xi _+\,\xi _- \} \, \); thus we can use (13) with respect to \( A_{\,\xi _+,\xi _-} \) to define \( B_V \) on \( V \, \), and then easily verify that it has all the required properties. \(\square \)
is defined, taking values in \( \, \mathcal {L}_\mathbb {C}\big ( A_{\,\xi _+,\xi _-} \big ) = \mathbb {C}\oplus \mathbb {C}\,\xi _+\,\xi _- \, \), which has \( \mathbb {C}\)–basis \( \, \{ 1, \xi _+\,\xi _- \} \, \); thus we can use (13) with respect to \( A_{\,\xi _+,\xi _-} \) to define \( B_V \) on \( V \, \), and then easily verify that it has all the required properties. \(\square \)
Definition 4.9
We say that an Hermitian form \( \mathcal {B}_{\mathcal {L}_V} \) for \( \mathcal {L}_V \) is non degenerate, or that it is positive definite, if its associated \( B_V \) is.
Observation 4.10
Let \( \, (V,\phi ) \in \mathrm {(smod)}^\bullet _\mathbb {C}\, \) and let \( \langle \,\ ,\ \rangle \) be a consistent supersymmetric bilinear form on V. Then we can associate to it a natural transformation

where \( \, a , b \in A_{{\overline{z}}} \, \) and \( \, x , y \in V_{{\overline{z}}} \, \), for all \( \, z \in \mathbb {Z}_2 \, \). By Proposition 4.2, there exist two super Hermitian forms \( B^\pm _V \) associated to \( \, \langle \,\ ,\ \rangle \, \), and by Lemma 4.7 there exists a unique \( \mathcal {B}^\pm _{\mathcal {L}_V} \) associated to \( B^\pm _V \, \). Therefore we can write \( \mathcal {B}^\pm _{\mathcal {L}_V} \) directly from \( \, \langle \,\ ,\ \rangle _{\mathcal {L}_V} \, \), namely (with notation as in (8))
4.3 Unitary Lie superalgebras
In this section we introduce a general notion of unitary superalgebras; in the subsequent subsection then we will also present some relevant examples.
Definition 4.11
Let \( \, (V,\phi ) \in \mathrm {(smod)}^\bullet _\mathbb {C}\, \), and let \( \mathcal {B}\) be a non-degenerate, consistent Hermitian form on \( \, \mathcal {L}_V : \mathrm {(salg)}_\mathbb {C}^\bullet \longrightarrow \mathrm {(smod)}_\mathbb {R}\, \). We define the adjoint (w.r.t. \( \mathcal {B}\, \)) of \( \, M \in \big ({ End}\,(V)\big )(A) \, \) as the unique \( \, M^\star \in \big ({ End}\,(V)\big )(A) \, \) defined by
for all \( \, x, y \in V(A) \, \), \( \, M \in \big ({ End}(V)\big )(A) \, \)—which in the standard case are taken homogeneous with respect to the \( \mathbb {Z}_2 \)–grading whose degree is denoted by “\( \, [\ \ ] \, \)”, cf. Definition 4.6. Like before, the condition (16) reads \( \,\, \mathcal {B}\big ( x , M^\star (y) \big ) = {(-1)}^{(\,{\bar{1}}\,-\,\nu _\phi )\,[x]\,[M]} \, \mathcal {B}\big (M(x), y\big ) \) with notation as in (8).
The key properties of the adjoint are the following, proved by straightforward check:
Lemma 4.12
With notation as in Definition 4.11 above, we have
for all \( \, a \in A_{\bar{0}}\, \), all \( \, M , N \in \big ({ End}\,(V)\big )(A) \, \) and all \( \, J \in \big (\textbf{GL}(V)\big )(A) \, \).
Proposition 4.13
Let the notation be as above, and identify \( \, \big (\mathcal {L}_{\mathfrak {gl}(V)}\big )(A) = \big ({ End}\,(V)\big ) (A)\). Then the natural transformation  defined on objects by
defined on objects by
and by
is a real structure on the functor \(\mathcal {L}_{\mathfrak {gl}(V)} \,\), hence—via Theorem 2.5—defines a real structure on the complex Lie superalgebra \( \mathfrak {gl}(V) \, \).
Proof
By Definition 2.4, we have to verify properties (1)–(3) therein and also that \( \, \circledast \, \) preserves the Lie bracket. All this follows easily from direct calculations that use Lemma 4.12. \(\square \)
Definition 4.14
Let \( \mathcal {B}\) be a non-degenerate, consistent Hermitian form on \( \mathcal {L}_V \, \). We define the unitary Lie superalgebra \( \, \mathfrak {u}_\mathcal {B}(V) \, \) as the functor of fixed points of  , hereafter denoted \( \mathcal {L}_{\mathfrak {gl}(V)}^{\,\circledast } \)—in the sense of Definition 2.6—given on objects by
, hereafter denoted \( \mathcal {L}_{\mathfrak {gl}(V)}^{\,\circledast } \)—in the sense of Definition 2.6—given on objects by
Note then that \( \mathfrak {u}_\mathcal {B}(V)(A) \) is a \( \mathbb {Z}_2 \)–graded Lie algebra—for all \( \, A \in \mathrm {(salg)}_\mathbb {C}^\bullet \, \)—just because \( \mathcal {L}_{\mathfrak {gl}(V)}(A) \) is a \( \mathbb {Z}_2 \)–graded Lie algebra, cf. Definition 2.6.
Remark 4.15
By Proposition 2.7, the functor \( \mathfrak {u}_\mathcal {B}(V) \) is always representable. In addition, in the standard case, i.e. when \( \, (V,\phi ) \in \mathrm {(smod)}^\textrm{st}_\mathbb {C}\, \), by Proposition 2.9 the representable functor \( \mathfrak {u}_\mathcal {B}(V) \) is represented by the super vector space of all \( \, \text { m} \in \mathfrak {gl}(V) \, \) such that (see [21], pg. 111):
Observation 4.16
Let \( \mathfrak {u}_\mathcal {B}(V) \) be a unitary Lie superalgebra as in Definition 4.14; let also B be the consistent super Hermitian form on V which corresponds to \( \mathcal {B}\) via Proposition 4.8, which we write as \( \, B = B_{\bar{0}}+ B_{\bar{1}}\, \) as in Sect. 4.1. For each \( \, {\overline{s}} \in \mathbb {Z}_2 \, \), let \( \, \mathfrak {u}_{B_{{\overline{s}}}}(V_{{\overline{s}}}) \) be the classical unitary Lie algebra associated to \( V_{{\overline{s}}} \) with the non-degenerate Hermitian form \( B_{{\overline{s}}} \, \). Then the even part of \( \mathfrak {u}_\mathcal {B}(V) \) is the functor of points of the direct sum Lie algebra \( \, \mathfrak {u}_{B_{\bar{0}}}(V_{\bar{0}}) \oplus \mathfrak {u}_{B_{\bar{1}}}(V_{\bar{1}}) \, \).
4.4 Examples of unitary Lie superalgebras
We provide now some examples of real structures, super Hermitian forms and associated unitary Lie superalgebras.
4.17 Standard real structures on \( \varvec{\, \mathfrak {gl}_{m|n} \,} \). Let \( \, V := \mathbb {C}^{m|n} \, \) be endowed—like in Example 4.1 — with the standard real structure  given by \( \, \phi _\textrm{st}(z,\zeta ) := \big (\,\overline{z}\,,\overline{\zeta }\,\big ) \, \), and the two super Hermitian forms given by
given by \( \, \phi _\textrm{st}(z,\zeta ) := \big (\,\overline{z}\,,\overline{\zeta }\,\big ) \, \), and the two super Hermitian forms given by
Following Lemma 4.7 , the super Hermitian forms \( B^\pm _V \) on \( \, V := \mathbb {C}^{m|n} \, \) correspond to Hermitian forms \( \mathcal {B}^\pm _{\mathcal {L}_V} \) on \( \, \mathcal {L}_V \, \), defined through (13): in detail, these read explicitly
Now, according to Definition 4.11 we can consider the adjoint of any \( \, u \in \mathcal {L}_{\mathfrak {gl}(V)}(A) = \mathfrak {gl}(m|n)(A) \, \) with respect to either \( \mathcal {B}^+_{\mathcal {L}_V} \) or \( \mathcal {B}^-_{\mathcal {L}_V} \, \), that we will denote by \( \, u^\star _+ \, \) and \( \, u^\star _- \, \), respectively. After Proposition 4.13, we also have corresponding real structures \( \circledast _\pm \) on \( \mathcal {L}_{\mathfrak {gl}(V)} \, \): in turn, by Definition 4.14 these will define two unitary real forms of \( \mathcal {L}_{\mathfrak {gl}(V)} \, \), hence of \( \, \mathfrak {gl}(V) = \mathfrak {gl}(m|n) \, \) as well. They are given as follows. The explicit form of the adjoint maps is
from which we infer the explicit formula of the associated real structures, namely
With these real structures, the associated unitary real forms—cf. Definition 4.14—are
Notice that the real structures considered above were defined for the functor of points \( \mathcal {L}_{\mathfrak {gl}(V)} \, \). If instead we look at the Lie superalgebra \( \, \mathfrak {gl}(V) = \mathfrak {gl}(m|n) \, \) as a superspace, then the real structures (22) on \( \mathcal {L}_{\mathfrak {gl}(V)} \) corresponds to the real structures \( \, *_\pm \, \) on \( \, \mathfrak {gl}(V) = \mathfrak {gl}(m|n) \, \) given by
which have been previously introduced in [21], §3.4.
Similarly, the unitary Lie (sub)superalgebra of \( \mathfrak {gl}(m|n) \) associated with the real form in (23) , and representing the functor \( \mathfrak {u}_{\mathcal {B}^\pm _V}(V) \, \), is
4.18 Graded real structures on \( \varvec{\, \mathfrak {gl}_{m|n} \,} \). Let again \( \, V := \mathbb {C}^{m|n} \, \) but consider now its associated functor \( \mathcal {L}_V \) as being defined on commutative superalgebras with a graded real structure, hence  —just like in Definition 4.6. Then we have two natural, consistent, non-degenerate Hermitian forms on \( \mathcal {L}_V \, \), denoted \( \mathcal {B}^\pm _\textrm{gr}\, \), which are defined on objects by
—just like in Definition 4.6. Then we have two natural, consistent, non-degenerate Hermitian forms on \( \mathcal {L}_V \, \), denoted \( \mathcal {B}^\pm _\textrm{gr}\, \), which are defined on objects by
Note that (25) looks exactly like (21)—where the functor is defined \( \mathrm {(salg)}_\mathbb {C}^\textrm{st}\) instead. With the same arguments as in §4.17 above, we find the following explicit form of the adjoint maps
from which we get:
With these real structures, the associated unitary real forms (via Definition 4.14) are given by
which can be re-written as
Finally, although we have introduced the real structures directly on the functor \( \, \mathcal {L}_{\mathfrak {gl}(V)} \, \), we can easily see that these structures \( \, \circledast _\pm \, \) on \( \mathcal {L}_{\mathfrak {gl}(V)} \) actually correspond to the real structures  on the Lie superalgebra \( \, \mathfrak {gl}(V) = \mathfrak {gl}(m|n) \, \) given by
on the Lie superalgebra \( \, \mathfrak {gl}(V) = \mathfrak {gl}(m|n) \, \) given by
In particular, \( \, *_+ \, \) has a neat expression in terms of “supertranspose” as \( \, M^{*_+} = -{\overline{M}}^{\,st} \, \) commonly used by physicists (see [10] and also [20, 21]).
4.19 Standard and graded real structures induced by a supersymmetric form. For \( \, n = 2\,t \, \), let \( \, \phi _\textrm{st}\, \) be the standard real structure on \( \, V := \mathbb {C}^{m|2t} \, \) considered in §4.17. For \( \, A \in \mathrm {(salg)}^\textrm{st}_\mathbb {C}\, \), we write any element of \( \, V(A) = \mathbb {C}^{m|2t}(A) = A_{\bar{0}}^{\,m} \times A_{\bar{1}}^{\,2t} \, \) as a triple \( \, (x\,,\xi _+\,,\xi _-) \, \) with \( \, x \in A_{\bar{0}}^{\,m} \, \) and \( \, \xi _\pm \in A_{\bar{1}}^{\,t} \, \). Accordingly, any \( \, u \in \mathcal {L}_{\mathfrak {gl}(V)}(A) = \mathfrak {gl}(m|\,2\,t)(A) \, \)—for \( \, A \in \mathrm {(salg)}^\textrm{st}_\mathbb {C}\, \)—will be written as a block matrix \( \, u \, = \begin{pmatrix} a &{} \beta _+ &{} \beta _- \, \\ \, \gamma _+ &{} d_{\scriptscriptstyle +,+} &{} d_{\scriptscriptstyle +,-} \, \\ \, \gamma _- &{} d_{\scriptscriptstyle -,+} &{} d_{\scriptscriptstyle -,-} \, \end{pmatrix} \, \) where a and \( d_{\scriptscriptstyle \pm ,\pm } \) have entries in \( A_{\bar{0}}\) and \( \beta _\pm \) and \( \gamma _\pm \) have them in \( A_{\bar{1}}\, \); in turn, we will write its adjoint as \( \, u^\star _\pm \, = \begin{pmatrix} a^\star &{} \beta ^\star _+ &{} \beta ^\star _- \, \\ \, \gamma ^\star _+ &{} d^\star _{\scriptscriptstyle +,+} &{} d^\star _{\scriptscriptstyle +,-} \, \\ \, \gamma ^\star _- &{} d^\star _{\scriptscriptstyle -,+} &{} d^\star _{\scriptscriptstyle -,-} \, \end{pmatrix} \, \). With these conventions, the (unique!) Hermitian form \( \mathcal {B}^\pm _{\mathcal {L}_V} \) on \( \, \mathcal {L}_V \, \), that by Lemma 4.7—via (13)—correspond to \( B^\pm _{\phi _\textrm{st}} \) on V is given explicitly by
(we still write a superscript “\( \, \pm \, \)”, yet it is irrelevant). Using it, we compute the “adjoint” \( \, u^\star := u^\star _\pm \, \) (again unique!) applying the defining conditions (16) to the nine homogeneous summands (that here we read as block-entries) of the matrix \( \, u \, = \begin{pmatrix} a &{} \beta _+ &{} \beta _- \, \\ \, \gamma _+ &{} d_{\scriptscriptstyle +,+} &{} d_{\scriptscriptstyle +,-} \, \\ \, \gamma _- &{} d_{\scriptscriptstyle -,+} &{} d_{\scriptscriptstyle -,-} \, \end{pmatrix} \, \). The explicit calculations follow again the same arguments as in §4.17 above; eventually, we find the following explicit form of the adjoint maps
and then from the latter we deduce the the associated real structure—as in (17)—namely
Finally, the unitary real form associated—by Definition 4.14—with this real structure is
Note that the map \( \, u \mapsto u^\circledast \, \) is the real structure for the functor of points \( \mathcal {L}_{\mathfrak {gl}(V)} \, \). If instead we look at the Lie superalgebra \( \, \mathfrak {gl}(V) = \mathfrak {gl}(m|\,2\,t) \, \) as a superspace, then the real structure (29) on \( \mathcal {L}_{\mathfrak {gl}(V)} \) corresponds to the real structure on \( \, \mathfrak {gl}(V) = \mathfrak {gl}(m|\,2\,t) \, \) described by
Similarly, the unitary Lie (sub)superalgebra of \( \mathfrak {gl}(m|\,2\,t) \) associated with this real form, and representing the functor \( \mathfrak {u}_{\mathcal {B}^\pm _{\phi _\textrm{st}}}\!(V) \, \), is
Finally, a parallel construction starting from the graded real structure  given by \( \, \phi _\textrm{gr}(z,\zeta _+,\zeta _-) := \big (\,\overline{z}\,,+\overline{\zeta _-}\,,-\overline{\zeta _+}\,\big ) \, \) provides again, in the first steps, the Hermitian forms (25) of §4.18, hence the final outcome will be a special instance of what we found therein.
given by \( \, \phi _\textrm{gr}(z,\zeta _+,\zeta _-) := \big (\,\overline{z}\,,+\overline{\zeta _-}\,,-\overline{\zeta _+}\,\big ) \, \) provides again, in the first steps, the Hermitian forms (25) of §4.18, hence the final outcome will be a special instance of what we found therein.
5 Compact Real Forms
In this section we describe real forms of basic Lie superalgebras (see [19, 21], we give a new notion of “super compactness”, going beyond [4, 6], and we describe the associated real structures in the graded and standard case. We begin with some notation.
Definition 5.1
Let V be any complex super vector space. For any \( \, s \in \{2\,,4\} \, \), let \( \, \textrm{aut}^{\,{}_\mathbb {R}}_{2,s}(V) \, \) be the set of automorphisms \( \vartheta \) of V as a real vector superspace such that \( \, \vartheta \big |_{V_{{\overline{z}}}} \not = \, \text { id}_{V_{{\overline{z}}}} \, \) for \( \, {{\overline{z}}} \in \mathbb {Z}_2 \, \), \( \, \vartheta ^2\big |_{V_{\bar{0}}} = \, \text { id}_{V_{\bar{0}}} \, \) and \( \, \vartheta ^2\big |_{V_{\bar{1}}} = \, +\text { id}_{V_{\bar{0}}} \, \) for \( \, s := 2 \, \) while \( \, \vartheta ^2\big |_{V_{\bar{1}}} = \, -\text { id}_{V_{\bar{0}}} \, \) for \( \, s := 4 \, \). Then we set:
- (a):
-
\( \mathrm {\overline{aut}}_{2,s}(V) \, := \, \big \{\, \theta \in \textrm{aut}^{\,{}_\mathbb {R}}_{2,s}(V) \,\big |\, \theta \ \text {is}\ \mathbb {C}--\text {antilinear} \,\big \} \, \);
- (b):
-
\( \textrm{aut}_{2,s}(V) \, := \, \big \{\, \sigma \in \textrm{aut}^{\,{}_\mathbb {R}}_{2,s}(V) \,\big |\, \sigma \ \text {is}\ \mathbb {C}--\text {linear} \,\big \} \, \). If in addition \( \, V = {\mathfrak {A}} \, \) is a complex associative superalgebra, resp. a complex Lie superalgebra, by \( \, \mathrm {\overline{aut}}_{2,s}({\mathfrak {A}}) \, \) and \( \, \textrm{aut}_{2,s}({\mathfrak {A}}) \, \) we mean the similar objects defined as above but starting from the set \( \, \textrm{aut}^{\,{}_\mathbb {R}}_{2,s}({\mathfrak {A}}) \, \) of automorphisms of \( {\mathfrak {A}} \) as a real (associative, resp. Lie) superalgebra with the extra conditions specified above.
According to Definition 2.1, the elements of \( \mathrm {\overline{aut}}_{2,s}(V) \) are exactly the real structures on \( V \, \); we will presently show that these can also be classified by the elements of \( \textrm{aut}_{2,s}(V) \) as well.
5.1 Real structures of basic (simple) Lie superalgebras
Let \( \mathfrak {g}\) be a complex Lie superalgebra which is contragredient, in the sense of [14], §2.5. Thus \( \mathfrak {g}\) is defined via a Cartan matrix \( \, A := {\big ( a_{i,j} \big )}_{i,j \in I} \, \)—with \( \, I = \{1,\dots ,r\} \, \)—with entries in \( \mathbb {C}\, \), a set of generators \( \, x^+_i \, \), \( x^-_i \, \), \( h_i \) (for all \( \, i \in I := \{1,\dots ,r\} \, \)), of parity \( \, |h_i| := {\bar{0}}\, \), \( \, \big | x^\pm _i \big | := {\bar{0}}\, \) if \( \, i \not \in \tau \, \), \( \, \big | x^\pm _i \big | := {\bar{1}}\, \) if \( \, i \in \tau \, \), for some fixed subset \( \, \tau \subseteq I \, \).
In addition, we shall say that the set of generators \( \, {\big \{ x^+_i, h_i, x^-_i \big \}}_{i \in I} \, \) is distinguished if \( \, |\tau | = 1 \, \)—in other words, there exists one and only one positive simple root which is odd—cf. [6, 14].
Proposition 5.2
Let \( \, \mathfrak {g}\) be contragredient, built out of a Cartan matrix A with entries in \( {\mathbb {R}} \, \). Then there exists a unique \( \, \omega \in \mathrm {\overline{aut}}_{2,4}(\mathfrak {g}) \, \) such that
Proof
This is the “antilinear counterpart” of a well-known result which guarantees the existence and uniqueness of a \( \mathbb {C}\)–linear automorphism \( \omega ' \) of \( \mathfrak {g}\) whose action on the generators is the same as \( \omega \)’s. One proves it along the same lines as in [18], Proposition 5.1.3 and 5.2.1. \(\square \)
Note that when \( \mathfrak {g}\) is a semisimple Lie algebra, then \( \omega _{\bar{0}}\) is the classical Cartan involution corresponding to its compact form (see [15], VI, §1).
From now on, we assume our complex Lie superalgebra \( \mathfrak {g}\) to be simple of basic type, hence—according to the classification \( \mathfrak {g}\) is of one of the following types:
Moreover, for type D(2, 1; a) we assume that \( \, a \in {\mathbb {R}} \, \). In particular, our \( \mathfrak {g}\) is contragredient, and Proposition 5.2 above applies.
We shall now collect a few technical results that we need later.
Lemma 5.3
Let \( \mathfrak {g}\) be simple of basic type as in (30) above, with \( \, a \in {\mathbb {R}} \, \) for type \( D(2,1;a) \, \). Then there exists a suitable positive system \( \Delta ^+ \) and suitable root vectors \( x_{\pm \alpha } \, \big (\, \pm \alpha \in \Delta ^\pm = \Delta _{\bar{0}}^\pm \cup \Delta _{\bar{1}}^\pm \,\big ) \, \) for which \( \omega \) as in Proposition 5.2 gives
Proof
Indeed, for \( \mathfrak {g}\) as in the claim it is known that we can select a distinguished Dynkin diagram, as in [14], p. 56, Table VI. Accordingly, we have unique associated sets of simple roots, of simple root vectors, and of positive/negative roots, as well as a unique associated Cartan matrix. Then the claim follows as a special instance of Proposition 5.2. \(\square \)
Lemma 5.4
Any inner automorphism \( \phi _{\bar{0}}\) of \( \mathfrak {g}_{\bar{0}}\) can be extended to an inner automorphism \( \phi \) of \( \mathfrak {g}\)—i.e. one of the form \( \, \phi = \exp \big (\textrm{ad}(n)\big ) \, \) with \( \, n \in \mathfrak {g}_{\bar{0}}\, \).
Proof
This is proved, in the standard case, by Proposition 2.1 in [19]. In short, given \( \, \phi _{\bar{0}}= \exp \big (\textrm{ad}(n)\big ) \, \) on \( \mathfrak {g}_{\bar{0}}\) (with \( \, n \in \mathfrak {g}_{\bar{0}}\, \)), we can take \( \, \phi _{\bar{1}}:= \exp \big (\textrm{ad}_{\bar{1}}(n)\big ) \, \), where \( \textrm{ad}_{\bar{1}}\) denotes the adjoint action of \( \mathfrak {g}_{\bar{0}}\, \) on \( \mathfrak {g}_{\bar{1}}\, \). In addition, by a straightforward analysis one checks that the very same method actually applies to the graded case as well. \(\square \)
The previous lemma has an immediate consequence, whose proof is straightforward.
Lemma 5.5
Let \( \, \sigma \in \mathrm {\overline{aut}}_{2,s}(\mathfrak {g}) \, \)—or \( \, \sigma \in \textrm{aut}_{2,s}(\mathfrak {g}) \, \)—\( \, s \in \{2\,,4\} \, \), and let \( \, \sigma '_{\bar{0}}\in \mathrm {\overline{aut}}_2(\mathfrak {g}_{\bar{0}}) \, \)—or \( \, \sigma '_{\bar{0}}\in \textrm{aut}_2(\mathfrak {g}_{\bar{0}}) \, \), respectively. If \( \, \sigma '_{\bar{0}}= \phi _{\bar{0}}\circ \sigma _{\bar{0}}\circ \phi _{\bar{0}}^{-1} \, \) for an inner automorphism \( \phi _{\bar{0}}\) of \( \mathfrak {g}_{\bar{0}}\, \), then \( \sigma '_{\bar{0}}\) extends to \( \, \sigma ' = \sigma '_{\bar{0}}+ \sigma '_{\bar{1}}\in \mathrm {\overline{aut}}_{2,s}(\mathfrak {g}) \, \)—or to \( \, \sigma ' = \sigma '_{\bar{0}}+ \sigma '_{\bar{1}}\in \textrm{aut}_{2,s}(\mathfrak {g}) \, \), respectively—given by \( \, \sigma ' := \phi \circ \sigma \circ \phi ^{-1} \, \), with \( \, \phi = \phi _{\bar{0}}+ \phi _{\bar{1}}\, \) as in Lemma 5.4 above.
When \( \, \sigma ' = \phi \circ \sigma \circ \phi ^{-1} \, \), with \( \, \sigma \in \mathrm {\overline{aut}}_{2,s}(\mathfrak {g}) \, \), \( \, s \in \{2\,,4\} \, \), for an inner automorphism \( \phi \), we will say that \( \sigma \) and \( \sigma ' \) are inner-isomorphic, and we will write \( \, \sigma \simeq \sigma ' \, \).
Lemma 5.6
Let \( \, \sigma , \sigma ' \in \mathrm {\overline{aut}}_{2,s}(\mathfrak {g}) \, \), \( \, s \in \{2\,,4\} \, \), with \( \, \sigma _{\bar{0}}= \sigma '_{\bar{0}}\, \). Then:
-
(a)
if \( \mathfrak {g}\) is of type 1, then \( \, \sigma ' \, \simeq \, \sigma _{\bar{0}}\pm \sigma _{\bar{1}}\, \);
-
(b)
if \( \mathfrak {g}\) is of type 2, then \( \, \sigma ' \, = \, \sigma _{\bar{0}}\pm \sigma _{\bar{1}}\, \).
Proof
For the standard case, the claim is proved in Lemma 2.3 and Lemma 2.4 of [19]. The same arguments work in the graded case too. \(\square \)
Lemma 5.7
Let \( \, \theta , \theta ' \in \textrm{aut}_{2,s}(\mathfrak {g}) \, \) with \( \, s \in \{2\,,4 \} \, \). If \( \, \theta _{\bar{0}}= \theta '_{\bar{0}}\, \), then \( \, \theta _{\bar{1}}= \pm \theta '_{\bar{1}}\, \).
Proof
This is Proposition 2.3 of [7] for the standard case; the graded case is just an exercise, where one replaces \( \, \pm \,i \, \) therein with \( \, \pm \,1 \, \). \(\square \)
At last, we have an important result.
Proposition 5.8
Let \( \, \mathfrak {g}\) and \( \, \omega \in \mathrm {\overline{aut}}_{2,4}(\mathfrak {g}) \, \) be defined as in Proposition 5.2. Then there exist mutually inverse bijections

and

and also mutually inverse bijections

and

Proof
It is enough to show that the given maps are actually well-defined —namely, their images do lie in the expected target set—since then they will clearly be pairwise mutually inverse.
It follows from definitions and from the explicit description of \( \, \textrm{aut}_{2,s}(\mathfrak {g}) \, \)—see [6]—that \( \omega \) commutes with every \( \, \eta \in \textrm{aut}_{2,s}(\mathfrak {g}) \, \) and every \( \, \gamma \in \mathrm {\overline{aut}}_{2,s}(\mathfrak {g}) \, \). This implies (for all \( \, z \in \mathbb {Z}\, \))
Using these identities, a trivial check shows that
which means that the maps \( \Phi _{\scriptscriptstyle \wedge } \, \), \( \Psi _{\scriptscriptstyle \wedge } \, \), \( \Phi _{\scriptscriptstyle \vee } \) and \( \Psi _{\scriptscriptstyle \vee } \) are well defined, q.e.d. \(\square \)
5.2 Compact forms of basic Lie superalgebras
We want to define the notion of compact real form of a (complex) Lie superalgebra. Our notion differs from [2, 4, 6], where compact superalgebras are assumed to be even.
Definition 5.9
Let \( \mathfrak {g}\) be a complex Lie superalgebra with a real structure \( \phi \) on it, and let \( \mathcal {L}_\mathfrak {g}^\varphi \)—see Definition 2.6—be the associated real form (in functorial sense).
- (a):
-
We say that \( \mathcal {L}_\mathfrak {g}^\varphi \) is super-compact if there exists a suitable superspace V with a positive definite, consistent Hermitian form \( \mathcal {B}\) such that \( \, \mathcal {L}_\mathfrak {g}^\varphi \subseteq \mathfrak {u}_\mathcal {B}(V) \, \)—cf. Definition 4.14;
- (b):
-
We say that \( \mathcal {L}_\mathfrak {g}^\varphi \) is compact if its even part \( {\big ( \mathcal {L}_\mathfrak {g}^\varphi \big )}_{\bar{0}}\) is compact in the classical sense, that is—as \( {\big ( \mathcal {L}_\mathfrak {g}^\varphi \big )}_{\bar{0}}\) is (always) represented by \( \, {(\mathfrak {g}_{\bar{0}})}^\phi = {\big ( \mathfrak {g}^\phi \big )}_{\bar{0}}\, \)—if the real Lie algebra \( \, {(\mathfrak {g}_{\bar{0}})}^\phi = {\big ( \mathfrak {g}^\phi \big )}_{\bar{0}}\,\) is compact in the classical sense.
- (c):
-
We say that a (graded or standard) real structure \( \phi \) on \( \mathfrak {g}\) is super-compact, resp. is compact, if the associated real form \( {\big ( \mathcal {L}_\mathfrak {g}^\varphi \big )}_{\bar{0}}\) of \( \mathcal {L}_\mathfrak {g}^\varphi \) is super-compact, resp. is compact. N.B.: it follows at once from Observation 4.16 that super-compactness implies compactness.
The following existence result proves the key importance of the notion of graded real structures. Theorem B in Sect. 1 consists of the statements of Theorem 5.10 and Theorem 5.11.
Theorem 5.10
Let \( \mathfrak {g}\) be a simple complex Lie superalgebra of basic type, with the additional assumption that \( \, a \in {\mathbb {R}} \, \) if \( \, \mathfrak {g}\) is of type \( D(2,1;a) \, \). Then \( \mathfrak {g}\) has a graded, super-compact real structure \( \omega \) (hence a graded, super-compact real form \( \mathcal {L}_\mathfrak {g}^\omega \, \)) which is unique up to inner automorphisms.
Proof
Let \( \, \omega \in \mathrm {\overline{aut}}_{2,4}(\mathfrak {g}) \, \) be given as in Proposition 5.2, and let \( \kappa \) be the Cartan-Killing form of \( \mathfrak {g}\) (see [18], Sect. 6.1, Ch. 5): by Theorem 5.4.1 in [18], this \( \kappa \) is non-degenerate. Using this and other properties of \( \omega \) and \( \kappa \, \), one easily checks that
Thus the condition of Proposition 4.2 is satisfied, and therefore
is a consistent super Hermitian form, which in addition is also positive definite.
Now consider the associated Hermitian form (following Lemma 4.7)
for all homogeneous \( \, a \in A_{{\overline{z}}} \, \), \( \, x \in V_{{\overline{z}}} \, \), \( \, b \in A_{{\overline{s}}} \, \), \( \, y \in V_{{\overline{s}}} \, \) and all \( \, A \in \mathrm {(salg)}^\textrm{gr}_\mathbb {C}\, \); more directly, according to (15) we can also write
We want to show that the functor \( \mathcal {L}_\mathfrak {g}^\omega \) embeds into \( \mathfrak {u}_\mathcal {B}(\mathfrak {g}) \, \): this is equivalent to showing that
for all \( \, X , Y \in \mathcal {L}_\mathfrak {g}(A) \, \) and \( \, U \in \mathcal {L}_\mathfrak {g}^\omega (A) \, \), where \( \, U \!\cdot \! X := [U,X] \, \). Note that in the present case the super vector space V of Definition 4.14 is just \( \mathfrak {g}\) itself. Now, thanks to (35) we have
since \( \kappa \) is ad–invariant and \( \, \omega _A(U) = U \, \) by assumption; thus (36) is proved.
We now come to uniqueness. By the ordinary theory, a real structure \( \, \phi _{\bar{0}}\, \) on \( \mathfrak {g}_{\bar{0}}\) giving a compact real form of the latter is unique up to inner automorphism, i.e. we can write any other real structure \( \, \phi '_{\bar{0}}\, \) on \( \mathfrak {g}_{\bar{0}}\) yielding another compact form as \( \, \phi '_{\bar{0}}= \psi _{\bar{0}}\circ \phi _{\bar{0}}\circ \psi _{\bar{0}}^{-1} \, \) for some inner automorphism \( \psi _{\bar{0}}\, \). Thanks to this, if \( \, \phi ' \, \) is any real structure on \( \mathfrak {g}\) giving a compact form \( \mathfrak {k}' \, \), then Lemma 5.5 applies and we conclude our proof. \(\square \)
We now turn our attention to the standard case.
Theorem 5.11
Let \( \mathfrak {g}\) be a simple complex Lie superalgebra of basic type. Then:
- (a):
-
if \( \mathfrak {g}\) is of type 1 (i.e., of type A or \( C \, \)), then it admits a standard, compact real structure, which is unique up to inner automorphisms;
- (b):
-
if \( \mathfrak {g}\) is of type 2 (i.e., of type \( B \, \), \( D \, \), F or \( G \, \)), then it has no standard, compact real structure.
Proof
- (a):
-
If \( \mathfrak {g}\) is of type \( A \, \), then \( \, \mathfrak {g}= \mathfrak {sl}(m\!+\!1|\,n\!+\!1) \, \) or \( \, \mathfrak {g}= \mathfrak {psl}(m\!+\!1|\,m\!+\!1) \, \). In both cases, one easily sees that the standard structures in \( \mathfrak {gl}(m\!+\!1|\,n\!+\!1) \) described in §4.17 induce similar structures on \( \mathfrak {g}\, \), and we are done. Finally, uniqueness follows as in the proof of Theorem 5.10. If \( \mathfrak {g}\) is of type C instead, we find an explicit \( \, \sigma \in \mathrm {\overline{aut}}_{2,2}(C(n)) \, \) making explicit use of Proposition 5.8, namely in the form \( \, \sigma := \omega \circ \theta \, \); here \( \omega \) is as in Proposition 5.2, while \( \, \theta \in \textrm{aut}_{2,4}\big (C(n)\big ) \, \) is chosen to be the identity on \( {C(n)}_{\bar{0}}\) and such that \( \, \theta (X_\beta ) := i\,X_\beta \, \) for \( \beta \) the odd simple root in a positive system with preferred simple system (i.e., a simple system with one odd root, now denoted \( \beta \)). Once we describe \( \mathfrak {g}\) of type C(n) as the Lie superalgebra \( \mathfrak {osp}\big (2\big |2(n\!-\!1)\big ) \, \)—see [14], p. 31—a straightforward analysis yields the following explicit description of \( \sigma \)
$$\begin{aligned} \sigma \begin{pmatrix} \, b &{} 0 &{} x &{} y \,\, \\ \, 0 &{} -b &{} z &{} w \,\, \\ \, w^t &{} y^t &{} A &{} B \,\, \\ \, -z^t &{} -x^t &{} C &{} D \,\, \end{pmatrix} \, = \, \begin{pmatrix} \, -\overline{b}&{} 0 &{} -i\,\overline{w}&{} i\,\overline{z}\,\, \\ \, 0 &{} \overline{b}&{} i\,\overline{y}&{} -i\,\overline{x}\,\, \\ \, -i\,\overline{x}^t &{} i\,\overline{z}^t &{} -\overline{A}^t &{} -\overline{C}\,\, \\ \, -i\,\overline{y}^t &{} i\,\overline{w}^t &{} -\overline{B}^t &{} \overline{A}\,\, \end{pmatrix} \end{aligned}$$(37)—where the above are block matrices with blocks of convenient sizes—from which one can directly check that actually \( \, \sigma \in \mathrm {\overline{aut}}_{2,2}(C(n)) \, \), as required.
As to uniqueness, it follows again as in the proof of Theorem 5.10.
- (b):
-
In this case, the statement is discussed in detail in [5], where the condition of admissible marking—see (1.4) in [5] —prescribes one even root to be non compact. For the reader convenience we briefly recap here the argument. According to Theorem 5.8 a real form corresponds to an automorphism \( \, \theta \in \textrm{aut}_{2,4}(\mathfrak {g}) \, \), assigning the eigenvalue \( \, i \, \) to \( \, x_\beta \in \mathfrak {g}_\beta \, \), with \( \beta \) a simple odd root in the simple system as in Proposition 5.2. Since the lowest root \( \, \varphi = 2\,\beta + \dots \, \) is even, the eigenvalue of \( \varphi \) is \( \, -1 \, \), hence \( \varphi \) is non compact. Hence \( \mathfrak {g}_0 \) is non compact, consequently we cannot have a standard compact real form for \( \mathfrak {g}\, \) (see also [5] Secc. 1, 2). \(\square \)
Remark 5.12
In particular for \( \, \mathfrak {g}= \mathfrak {osp}\big (2\,\big |\,2(n-1)\big ) \, \)—i.e., of type C(n) —one easily sees that the real form defined by the standard real structure \( \sigma \) in (37) —i.e., the real Lie subsuperalgebra of fixed points of \( \sigma \) in \( \mathfrak {g}\)—is given by
5.3 Cartan involutions and decomposition
If \( \mathfrak {g}_{\bar{0}}\) is a complex semisimple Lie algebra, we have a one to one correspondence between non compact real forms of \( \mathfrak {g}_{\bar{0}}\) and involutions \( \theta _{\bar{0}}\) of \( \mathfrak {g}_{\bar{0}}\, \). Now \( \theta _{\bar{0}}\) restricts to a Cartan involution on the corresponding real form, unique up to inner automorphism. We wish to extend this picture to the graded setting.
Let \( \mathfrak {g}\) be a contragredient basic Lie superalgebra, \( \mathfrak {h}\) a Cartan subalgebra and let \( \, \theta \in \textrm{aut}_{2,2}(\mathfrak {g}) \, \) be equal rank, that is \( \, \theta {\big |}_\mathfrak {h}= \textrm{id}_\mathfrak {h}\, \). As in Proposition 5.8, we have that \( \, \sigma = \omega \circ \theta \in \mathrm {\overline{aut}}_{2,4}(\mathfrak {g}) \, \) gives a graded real structure on \( \mathfrak {g}\, \). Let \( \, \mathfrak {k}= \mathfrak {g}^\theta \, \). Since \( \theta \) commutes with \( \omega \, \), we have that \( \theta \) preserves this structure, hence \( \, \big (\, \mathfrak {k}, \sigma {\big |}_\mathfrak {k}\,\big ) \, \) is a well defined graded real structure on \( \mathfrak {k}\, \).
Proposition 5.13
Let the notation be as above. Then \( \, \big (\, \mathfrak {k}, \sigma {\big |}_\mathfrak {k}\,\big ) \, \) is super-compact.
Proof
By the arguments of Theorem 5.10, we immediately see that \( \, \mathcal {L}^\sigma _\mathfrak {k}\subseteq \mathfrak {u}(\kappa ) \, \). \(\square \)
Let \( \mathfrak {p}\) be the eigenspace of \( \theta \) of eigenvalue \( -1 \, \). Then we immediately have the decomposition:
This complex decomposition is preserved by the graded real structure \( \sigma \) and then we shall call it the Cartan decomposition of the graded real form \( (\mathfrak {g},\sigma ) \, \). Notice that, by Lemmas 5.5 and 5.7, the Cartan automorphism \( \theta \) and the corresponding Cartan decomposition are unique up to inner automorphism.
We now turn to examine the standard case (see [6]). When \( \mathfrak {g}\) is of type 2, the lack of compact forms (see Theorem 5.11) makes the case \( \, \mathfrak {k}= \mathfrak {k}_{\bar{0}}\, \) studied in [4, 6] most relevant. We invite the reader to consult those references for more details. So we focus on the case when \( \mathfrak {g}\) is of type 1.
Let \( \, \theta \in \textrm{aut}_{2,4}(\mathfrak {g}) \, \) be an equal rank automorphism. Let \( \mathfrak {k}_{\bar{0}}\, \), \( \mathfrak {p}_{\bar{0}}\) be the eigenspaces of eigenvalues \( \pm 1 \) for \( \theta _{\bar{0}}\, \), let \( \Delta ^k_{\bar{0}}\) the root system of the semisimple part of \( \mathfrak {k}_{\bar{0}}\, \). Choose a distinguished simple system, that is one with only one odd root \( \beta \, \). Define
Then, most immediately we have the decomposition as above:
An easy check shows that it is preserved by the standard real structure \( \sigma \) associated with \( \theta \, \), hence we call it the Cartan decomposition of the standard real form \( (\mathfrak {g},\sigma ) \, \). As before, we notice that by Lemmas 5.5 and 5.7 the Cartan automorphism \( \theta \) and the corresponding Cartan decomposition are unique up to inner automorphism.
6 Real Forms of Basic Supergroups
In this section, we shall provide a global version of the infinitesimal real forms constructed in the previous sections.
6.1 Unitary supergroups
Let \( \, (V,\phi ) \in \mathrm {(smod)}_\mathbb {C}^\bullet \, \) be a complex super vector space with (standard or graded) real structure, and B a consistent, non-degenerate, positive definite super Hermitian form on it. Proposition 4.13 provides a real structure  on \( \mathcal {L}_{\mathfrak {gl}(V)} \, \), which corresponds to a real structure on the Lie superalgebra \( \mathfrak {gl}(V) \, \). By Proposition 3.6, there exists a unique real structure
on \( \mathcal {L}_{\mathfrak {gl}(V)} \, \), which corresponds to a real structure on the Lie superalgebra \( \mathfrak {gl}(V) \, \). By Proposition 3.6, there exists a unique real structure

on the supergroup \( \textbf{GL}(V) \) corresponding to it. In particular, on an element \( \, g = g_+ \cdot \exp (\mathcal {Y}) \in \big (\textbf{GL}(V)\big )(A) \, \)—as in (4)—using the exponential notation, we have
where \( \circledast ^{\scriptscriptstyle G}_{\bar{0}}\) is the ordinary real structure on \( \, \textrm{GL}(V_{\bar{0}}) \times \textrm{GL}(V_{\bar{1}}) \, \), namely
while, by Proposition 4.13 and Lemma 4.12,
—where \( \, \varepsilon := i \, \) or \( \, \varepsilon := -1 \, \) according to whether we are in the standard or the graded case. So
where N is the least non-negative integer such that \( \, {\big (\mathcal {X}^\star \big )}^{N+1} = \, 0 \, \in \, \big ({ End}(V)\big )(A) \, \). Therefore
Note in addition that the graded case—when \( \, \varepsilon = -1 \, \)—also reads
Definition 6.1
We define the unitary supergroup \( \, \textbf{U}_\mathcal {B}(V) \, \), with respect to the super Hermitian form \( \mathcal {B}\, \), as the real form of \( \textbf{GL}(V) \) corresponding to the real structure \( \circledast ^{\scriptscriptstyle \textbf{G}} \, \). Explicitly, it is
N.B.: It follows at once from Observation 4.16 that the even part of a unitary supergroup is the direct product of two ordinary unitary groups.
Examples 6.2
- (a):
-
Let \( \, V := \mathbb {C}^{1|1} \, \) with the standard real structure given in §4.17. Then the associated standard real structure \( \, \circledast ^{\scriptscriptstyle G} \, \) on the supergroup \( \, \textbf{GL}(V) = \textbf{GL}_{1|1} \, \) is given explicitly as follows (see also [9]):
$$\begin{aligned} \begin{pmatrix} \, a &{} \beta \,\, \\ \, \gamma &{} d \,\, \end{pmatrix}^{\!\circledast ^\textbf{G}} \, = \,\, \begin{pmatrix} \, {\widetilde{a}}^{-1} \big (\, 1 + {\widetilde{a}}^{-1} {\widetilde{\beta }} \, {\widetilde{d}}^{-1} \, {\widetilde{\gamma }} \,\big ) &{} \mp \, i \, {\widetilde{a}}^{-1} {\widetilde{d}}^{-1} \, {\widetilde{\gamma }} \,\, \\ \, \mp \, i \, {\widetilde{d}}^{-1} \, {\widetilde{a}}^{-1} {\widetilde{\beta }} &{} {\widetilde{d}}^{-1} \big (\, 1 + {\widetilde{d}}^{-1} \, {\widetilde{\gamma }} \, {\widetilde{a}}^{-1} {\widetilde{\beta }} \,\big ) \, \end{pmatrix} \end{aligned}$$ - (b):
-
Let \( \, V := \mathbb {C}^{m|n} \, \) with the graded real structure given in §4.18. Then the associated graded real structure \( \, \circledast ^{\scriptscriptstyle G} \, \) on the supergroup \( \, \textbf{GL}(V) = \textbf{GL}_{m|n} \, \) is given explicitly as follows:
$$\begin{aligned} \begin{pmatrix} \, a &{} \beta \,\, \\ \, \gamma &{} d \,\, \end{pmatrix}^{\!\circledast ^\textbf{G}} \, = \,\, \begin{pmatrix} \, {\widetilde{a}}^{\,t} &{} \pm \, {\widetilde{\gamma }}^{\,t} \,\, \\ \, \mp \, {\widetilde{\beta }}^{\,t} &{} {\widetilde{d}}^{\,t} \,\, \end{pmatrix}^{\!-1} \end{aligned}$$
6.2 Compact real forms of supergroups
Our notion of compact supergroup will be modelled on the one of Lie superalgebras (cf. Definition 5.9), therefore, it is stronger than the one commonly seen in the literature, which amounts to “topological compactness” only (see [4, 9]).
Definition 6.3
Let \( \textbf{G}\) be a complex Lie supergroups with a real structure \( \Phi \) on it, and let \( \textbf{G}^\Phi \)—see Definition 3.9—be the associated real form.
- (a):
-
We say that \( \textbf{G}^\Phi \) is super-compact if there exists a suitable superspace V with a non-degenerate, positive definite, consistent Hermitian form \( \mathcal {B}\) such that \( \, \textbf{G}^\Phi \le \textbf{U}_\mathcal {B}(V) \, \) (see Definition 6.1).
- (b):
-
We say that \( \textbf{G}^\Phi \) is compact if its even part \( {\big ( \textbf{G}^\Phi \big )}_{\bar{0}}\) is compact in the classical sense.
- (c):
-
We say that a (graded or standard) real structure \( \Phi \) on \( \textbf{G}\) is super-compact, resp. is compact, if the associated real form \( \textbf{G}^\Phi \) is super-compact, resp. is compact.
- N.B. : :
-
it is immediate to see that super-compactness implies compactness.
Let \( \textbf{G}\) be a complex supergroup, with tangent Lie superalgebra \( \, \mathfrak {g}:= \textrm{Lie}(\textbf{G}) \, \). We say that \( \textbf{G}\) is basic if \( \mathfrak {g}\) is simple of basic type. Now assume that a complex supergroup \( \textbf{G}\) is connected and simply connected. Then, it is clear by Sect. 3.1 that any real structure on \( \mathfrak {g}\) integrates to a real structure (of the same order) on \( \textbf{G}\, \). In particular, if \( \textbf{G}\) is also basic, we have the following, direct consequence of Theorem 5.10:
Theorem 6.4
Let \( \textbf{G}\) be a connected, simply connected, basic, complex supergroup, with \( \, a \in \mathbb {R}\, \) if \( \textbf{G}\) is of type \( D(2,1;a) \, \). Then \( \textbf{G}\) admits a graded, super-compact real structure \( \Omega \)—hence a graded, super-compact real form \( \textbf{G}^\Omega \)—which is unique up to inner automorphisms, whose associated real structure on \( \, \mathfrak {g}:= \textrm{Lie}(\textbf{G}) \, \) is the real structure \( \omega \) of Theorem 5.10.
Similarly, we have the following, straightforward consequence of Theorem 5.11:
Theorem 6.5
Let \( \textbf{G}\) be a connected, simply connected, basic, complex supergroup. Then:
- (a):
-
if \( \textrm{Lie}(\textbf{G}) \) is of type 1 (i.e., of type A or \( C \, \)), then G admits a standard, compact real structure, which is unique up to inner automorphisms;
- (b):
-
if \( \textrm{Lie}(\textbf{G}) \) is of type 2 (i.e., of type B, D, F or \( G \, \)), then G has no standard, compact real structure.
Observation 6.6
We can also immediately construct the real forms associated with the real structures \( (\mathfrak {g},\sigma ) \) of Sect. 5.3. It is not difficult to see that we have the standard and graded global Cartan decompositions associated to the Cartan decompositions (39) and (38), that is
where \( \textbf{K}\) is the supergroup associated with the superalgebra \( \, \mathfrak {k}= \mathfrak {g}^\sigma \, \) and \( \, \textbf{P}\, \cong \, \textbf{P}_{\bar{0}}\times \mathbb {A}^{0|d_1}_{\bullet } \, \), while \( \textbf{P}_{\bar{0}}\) is the space appearing in the ordinary global Cartan decomposition (see [15], Ch. VI). Clearly on \( \textbf{G}\) we have the real structure induced by \( \sigma \, \), which restricts also to \( \textbf{K}\) and to \( \textbf{P}\, \).
References
Carmeli, C., Caston, L., Fioresi, R.: Mathematical Foundation of Supersymmetry, EMS Series of Lectures in Mathematics, European Mathematical Society (EMS), Zürich (2011)
Carmeli, C., Fioresi, R.: Superdistributions, analytic and algebraic super Harish-Chandra pairs. Pacific J. Math. 263(1), 29–51 (2013)
Carmeli, C., Fioresi, R., Kwok, S.D.: SUSY structures, representations and Peter-Weyl theorem for \(S^{1|1}\). J. Geom. Phys. 95, 144–158 (2015)
Carmeli, C., Fioresi, R., Varadarajan, V.S.: Highest weight Harish-Chandra supermodules and their geometric realizations. Transf. Groups 25(1), 33–80 (2020)
Chuah, M.K.: Finite order automorphisms on contragredient Lie superalgebras. J. Algebra 351, 138–159 (2012)
Chuah, M.K.: Cartan automorphisms and Vogan superdiagrams. Math. Z. 273, 793–800 (2013)
Chuah, M.K., Fioresi, R.: Real forms of contragredient Lie superalgebras with isomorphic even parts. J. Lie Theory 29(1), 239–246 (2019)
Deligne, P., Morgan, J.: Notes on supersymmetry (following J. Bernstein). In: Quantum fields and strings: a course for mathematicians, vol. 1, 2 (Princeton, NJ, 1996/1997), pp. 41–97. Amer. Math. Soc., Providence, RI (1999)
Fioresi, R.: Compact forms of complex Lie supergroups. J. Pure Appl. Algebra 218(2), 228–236 (2014)
Fioresi, R., Lledo, M.A.: The Minkowski and conformal superspaces. The classical and quantum descriptions. World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ (2015)
Gavarini, F.: Global splittings and super Harish-Chandra pairs for algebraic supergroups. Trans. AMS 368, 3973–4026 (2016)
Gavarini, F.: A new equivalence between super Harish-Chandra pairs and Lie supergroups. Pac. J. Math. 306(2), 451–485 (2020)
Kac, V.G.: Lie superalgebras. Adv. Math. 26, 8–96 (1977)
Knapp, A.W.: Lie Groups beyond an Introduction, 2nd. ed., Progr. Math. 140, Birkhäuser, Boston (2002)
Manin, Y.I.: Gauge field theory and complex geometry, Grundlehren der mathematischen Wissenschaften 289. Springer, Berlin (1997)
Masuoka, A.: Harish-Chandra pairs for algebraic affine supergroup schemes over an arbitrary field’’. Transf. Groups 17, 1085–1121 (2012)
Musson, I.M.: Lie Superalgebras and Enveloping Algebras, Graduate Studies in Mathematics 131. American Mathematical Society, Providence, RI (2012)
Parker, M.: Classification of real simple Lie superalgebras of classical type. J. Math. Phys. 21(4), 689–698 (1980)
Pellegrini, F.: Real forms of complex Lie superalgebras and complex algebraic supergroups. Pac. J. Math. 229, 485–498 (2007)
Serganova, V.: Classification of real simple Lie superalgebras and symmetric superspaces. Funct. Anal. Appl. 17, 200–207 (1983)
Varadarajan, V.S.: Supersymmetry for mathematicians: an introduction, Courant Lecture Notes in Mathematics 11. AMS, Providence, RI (2004)
Acknowledgements
This work was partially supported by the MIUR Excellence Department Project awarded to the Department of Mathematics of the University of Rome “Tor Vergata”, CUP E83C18000100006. The authors thank M.-K. Chuah for helpful comments. R. Fioresi and F. Gavarini thank respectively the department of Mathematics of Rome “Tor Vergata” and of Bologna for the wonderful hospitality while this work was prepared.
Funding
Open access funding provided by Alma Mater Studiorum - Università di Bologna within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Both authors R. Fioresi and F. Gavarini declare there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fioresi, R., Gavarini, F. Real Forms of Complex Lie Superalgebras and Supergroups. Commun. Math. Phys. 397, 937–965 (2023). https://doi.org/10.1007/s00220-022-04502-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-022-04502-x





 and
and 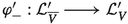 that are parity preserving and such that
that are parity preserving and such that  —for each
—for each 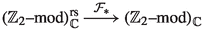 the obvious forgetful functor. Then, just rephrasing the Definition
the obvious forgetful functor. Then, just rephrasing the Definition  such that
such that  is a real structure for
is a real structure for  given by
given by