Abstract
We describe a general approach to the theory of self consistent transfer operators. These operators have been introduced as tools for the study of the statistical properties of a large number of all to all interacting dynamical systems subjected to a mean field coupling. We consider a large class of self consistent transfer operators and prove general statements about existence of invariant measures, speed of convergence to equilibrium, statistical stability and linear response. While most of the results presented in the paper are valid in a weak coupling regime, the existence results for the invariant measures we show also hold outside the weak coupling regime. We apply the general statements to examples of different nature: coupled continuous maps, coupled expanding maps, coupled systems with additive noise, systems made of different maps coupled by a mean field interaction and other examples of self consistent transfer operators not coming from coupled maps. We also consider the problem of finding the optimal coupling between maps in order to change the statistical properties of the system in a prescribed way.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Suppose we have a normed real or complex vector space \(B_{w}\) and a collection of linear operators \(L_{\delta ,f}:B_{w}\rightarrow B_{w}\) depending on some parameter \(\delta \in \mathbb {R}\) and \(f\in B_{w}\). One can consider the nonlinear function \(\mathcal {L}_{\delta }:B_{w}\rightarrow B_{w}\) defined by
These kind of nonlinear functions have been also called self-consistent transfer operators (as the operator itself depends on the point at which it is calculated). In many examples where these operators are used the family \(L_{\delta ,f}\) depends in a Lipschitz way on f and the Lipschitz constant is proportional to \(\delta \). In this context the parameter \(\delta \) represents in some sense a measure of the strength of the nonlinearity of the function \(\mathcal {L}\). These concepts have been introduced and studied as models to describe the collective behavior of a network of interacting systems coupled by a mean field interaction. In the case of operators modeling coupled extended systems the parameter \(\delta \) often represents the strength of the coupling or of the interaction between the systems.
These operators, their invariant measures and their properties have been studied by different techniques in classes of examples. In this paper we attempt a general approach to the study of this kind of operators, and the statistical properties of their dynamics. The main goal is to investigate under which assumptions we can establish some basic important properties of the self-consistent system as the existence of the invariant measure in a certain regularity class, the convergence to equilibrium, the statistical stability and response to perturbation of the system.
We show the flexibility and the effectiveness of the approach applying it to several kinds of self-consistent operators coming from coupled expanding maps, coupled random systems and other examples.
We study the behavior of the invariant measures of these operators, their convergence to equilibrium and their statistical stability mostly in the “weak coupling” regime, in the sense that most of the results presented hold for intervals of values of the type \(\delta \in [0,\overline{\delta } ] \) for a relatively small \(\overline{\delta }\) (with an estimate for the size of \(\overline{\delta }\), hence not only for \(\delta \rightarrow 0\)). Some of the results presented however can be applied even for large values of \(\delta \). In particular, under suitable assumptions, we prove the existence of some invariant probability measure for the self-consistent operator \(\mathcal {L}_{\delta }\), also providing estimates on its regularity imposing no restrictions on the size of \(\delta \) (Theorem 3), such result then also hold in a strong coupling regime, for which very few results are known. Sufficient assumptions for the uniqueness of the invariant measure are then shown in the case of weak coupling regime (Theorem 4). Still in the weak coupling regime we study the attractiveness of the invariant measure as a fixed point of \(\mathcal {L} _{\delta }\), providing exponential convergence to equilibrium results (Theorem 6) and study the response of the invariant measure of the system to changes in the function defining the mean field coupling interaction in the zero coupling limit (Theorems 12 and 14). We also investigate these questions from an optimal control point of view. Suppose we have an initial uncoupled system and we want to introduce a coupling which maximizes certain aspects of the statistical properties of the coupled system, as for example the average of a given observable. What is the best coupling to be introduced in order to do so? This is a problem related to the control of the statistical properties of chaotic and complex systems.
In this paper we have to deal with several concepts: networks of coupled systems; self-consistent transfer operators; linear response; random and deterministic systems; optimal response and control of the statistical properties. To help the reader, each main section dealing with these concepts will have an introductory part trying to explain the concept, the main ideas behind and giving some additional references for its deeper understanding.
Transfer operators. An efficient method for the study of transport and the statistical properties of a dynamical system is to associate to the system a certain transfer operator describing how the dynamics acts on suitable spaces of measures or probability distributions on the phase space. Important properties of the original system are related to fixed points and other properties of these transfer operators. The transfer operator which is convenient to associate to a dynamical system is usually a linear operator. Self-consistent transfer operators are nonlinear operators.
As mentioned before, these operators arise as natural models of extended systems in which there is a large set of interacting dynamical systems and we consider the dynamics of each element of the large set (the local dynamics) as being influenced or perturbed by the state of the other elements in a mean field coupling. This means that the perturbation we apply to the dynamics of each local system depends on the distribution of the states of all the other elements of the large system. This global state will be represented by a probability measure, representing the probability of finding a generic local system in a given set of states of the phase space. If now we consider the transfer operator associated with the dynamics of each local system we have that this linear operator depends on the current global state of the system. One can furthermore suppose all the local systems to be homogeneous and consider again the measure representing the global state of the system as a representative for the probability of finding a local system in a given stateFootnote 1. Applying the transfer operator associated to the local dynamics to see how this probability measure evolves, we have then a transfer operator depending on a certain measure and acting on the measure itself. This naturally brings us to the formalization presented in (1). From a formal point of view this give rise to a nonlinear function to be applied to a certain functional space of measures. In the weak coupling regime however this nonlinear function is a small nonlinear perturbation of a linear one, simplifying the situation and the understanding of the properties of this function.
The use of self-consistent operators for the study of networks of coupled maps was developed from a mathematical point of view in [6, 33]. In Sect. 2 we explain some of the heuristics behind the use of these operators for the study of coupled maps. We refer to [8, 43] for a further discussion on the scientific context in which these concepts appear and for an accurate bibliography on the subject (see also [13, 31] for other approaches to maps in a global coupling). For introductory material we also recommend the reading of the paper [41].
Overview of the main results. In Sect. 3 we show a set of general assumptions on the family of operators \(L_{\delta ,f}\) , ensuring that the nonlinear operator \(\mathcal {L}_{\delta }\) has a fixed point of a certain type and hence the associated system has some invariant probability measure (see Theorem 3). This result is obtained by topological methods, applying the Brouwer fixed point theorem to a suitable sequence of finite dimensional nonlinear operators approximating \( \mathcal {L}_{\delta }\). The assumptions required for this result are related to the regularity of the family of linear operators \(L_{\delta ,f}\) when f varies in a strong-weak topology, the regularity of its invariant measures (see the assumptions (Exi1), (Exi1.b), (Exi2) in Theorem 3) and the existence of a suitable finite dimensional projection, allowing to apply a kind of finite element reduction of the problem. The result also holds outside the weak coupling regime and implies a general statement for the existence of an invariant measure for systems of continuous maps in the mean field coupling (see Proposition 16). We also discuss the uniqueness of the invariant probability measure. This will be proved in the weak coupling regime (see Theorem 4). The set of assumptions for the uniqueness, essentially require that the operators \( L_{\delta ,f}\) and their fixed points depend on f in a Lipschitz way (see assumptions (Exi3) in Theorem 4). The assumptions required to apply these results are not difficult to be verified, and in the following sections we show how to apply this general framework to interacting random and deterministic systems, together with examples of different kind.
In Sect. 4 we take the same point of view with the goal of investigating the convergence to equilibrium: the attractiveness of the invariant measure as a fixed point of \(\mathcal {L}_{\delta }\) and in the weak coupling regime we show assumptions under which we can prove exponential speed of convergence to equilibrium for a general class of self-consistent transfer operators (see Theorem 6). The assumptions we require are related to convergence to equilibrium and a common “one step” Lasota Yorke inequality satisfied by each transfer operator in the family \(L_{\delta ,f}\) (see assumptions \((Con1),\ldots ,(Con3)\) ). The assumptions made are in a certain sense natural when considering suitable coupled dynamical systems like expanding maps or random systems with additive noise, and in the next sections we apply these general results to several classes of examples.
In Sect. 5, after an introduction to the concept of Linear Response and some related bibliography, we prove a general statistical stability result (see Theorem 12) and a linear response result for nonlinear perturbations of linear transfer operators (see Theorem 14), describing the first order change in the invariant measure of the system when an infinitesimal perturbation leading to a nonlinear operator is applied. We remark that this result is similar in the statement and in the proof to many other general linear response results proved for linear transfer operators (see e.g. [15]).
The methods used to establish the general statements in Sects. 3, 4, 5 are related to the classical transfer operator approach, letting the transfer operator associated with the system to act on stronger and weaker spaces (in a way similar to the classical reference [35]), exploiting the fact that the perturbations we are interested in applying to our systems are small when considered in a kind of mixed norm, from the stronger to the weaker space.
We show the flexibility of this general approach applying it to systems of different kind. In particular we will consider coupled deterministic expanding maps and random maps with additive noise, coupling identical maps or different ones in a mean field regime. For these examples we will use simple spaces of functions as \(L^{1},C^{k}\), the Sobolev spaces \( W^{k,1},W^{k,2}\) or the space of Borel signed measures equipped with the total variation or the Wasserstein distance.
In Sect. 6 we consider continuous maps on the circle with a mean field coupling and we prove the existence of an invariant probability measure for the associated self-consistent transfer operators, providing a sort of Krylov-Bogoliubov theorem for this kind of extended systems.
In Sect. 7, after recalling several useful classical results on expanding maps we show that the self-consistent transfer operator associated with a network of coupled expanding maps has an invariant measure in a suitable Sobolev space \(W^{k,1}\) and we show an estimate for its Sobolev norm (see Theorem 23). In the small coupling regime we also show exponential convergence to equilibrium for this kind of systems. This will allow to apply our general linear response statement and get a linear response statement for the zero coupling limit of such systems. Similar results for this kind of systems in the weak coupling regime appear in [41], the spaces used and the methods of proof however are quite different.
In Sect. 8 we consider coupled random maps and we apply our general framework to this case. More precisely, we consider maps with additive noise in which at every iterate of the dynamics a certain deterministic map is applied and then a random i.i.d. perturbation is added. Due to the regularizing effect of the noise at the level of the associated transfer operators we do not need to put particular restrictions on the maps considered. These examples are then particularly interesting for the applications. After recalling the basic properties of these systems and the associated transfer operators we define a self-consistent transfer operator representing the global behavior of a network of coupled random maps. We prove the existence of invariant measures for this self-consistent operator and show an estimate for its \(C^{k}\) norm which is uniform when varying the coupling strength. In the case of weak coupling, we also prove exponential speed of convergence to equilibrium for this globally coupled system. We then apply the general linear response results to this system, obtaining again a linear response result for the system in the zero coupling limit.
In Sect. 9 we consider a class of self-consistent transfer operators where the deterministic part of the dynamics is driven by a certain map whose slope depends on the average of a given observable, in some sense similar to the examples studied in [44]. For these systems we study the existence, uniqueness of the invariant measures and linear response, similarly to what is proved for the systems coming from coupled maps.
In Sect. 10 we consider suitable self-consistent transfer operators to model a mean field interaction of different maps. For simplicity we consider two types of maps. We show that the general framework we are considering also applies to this case, showing the existence and uniqueness of the invariant measure in a weak coupling regime.
In Sect. 11 we consider the linear response results we proved from an optimal control point of view. Suppose we want to introduce in the system a coupling which changes the statistical properties of the dynamics in some desired way. What is the optimal coupling to be considered? Given some observable whose average is meant to be optimized and a convex set P of allowed infinitesimal couplings to be applied, we show conditions under which the problem has a solution in P and this solution is unique. We remark that in [37] the research in this direction of research was motivated, with the goal of the management of the statistical properties of complex systems and in this direction several results for probabilistic cellular automata were shown.
2 Self-Consistent Transfer Operators for Coupled Circle Maps, Heuristics and Formalization
Since the study of self-consistent transfer operators is strongly motivated by the applications to systems of globally interacting maps, in this section we briefly introduce a model representing the dynamics of a large number of coupled maps in a global mean field interaction and the associated self-consistent transfer operators. We will see how the formalization of such interaction leads to the study of a self-consistent transfer operator of the kind defined at the beginning of the introduction.
We remark that in this paper we only consider discrete time dynamical systems. In the continuous time case, the models one is lead to consider are related to the topic of Vlasov-type differential equations, we suggest the recent surveys [12, 23] and the references therein for an introduction to the subject.
We are now going to define more precisely the self-consistent transfer operators associated with a set of dynamical systems coupled by a mean field interaction. One can think the set of interacting systems as a continuum, endowed with a measure, as for instance a swarm of interacting particles distributed by a certain density in different parts of the space. We take this point of view and we consider the case in which the set of systems we consider is a measurable space M with a probability p. The set M can be finite or infinite and in each case we can define the self-consistent transfer operator associated with the system. We remark that one could see the case where M is infinite as a suitable limit of finite sets and define the self-consistent transfer operator associated with the global coupling of infinitely many systems by a suitable limit of finitely many couplings (see [6, 33, 41] and Footnote 2 for further details on this approach).
Let us fix some notation and terminology: let us consider two metric spaces X, Y, the spaces of Borel probability measures PM(X), PM(Y) on X and Y, and a Borel measurable \(F:X\rightarrow Y\). We denote the pushforward of F as \(L_{F}:PM(X)\rightarrow PM(Y)\), defined by the relation
for all \(\mu \in PM(X)\) and measurable set \(A\subseteq Y\). The pushforward can be extended as a linear function \(L_{F}:SM(X)\rightarrow SM(Y)\) from the vector space of Borel signed measures on X to the same space on Y. In this case \(L_{F}\) will be also called as the transfer operator associated with the function F.
We now define a model for the dynamics of a family of dynamical systems interacting in the mean field. For simplicity we will suppose as a phase space for each interacting system the unit circle \(\mathbb {S}^{1}\) and we will equip \(\mathbb {S}^{1}\) with the Borel \(\sigma -\)algebra. We consider an additional metric space M equipped with the Borel \(\sigma -\)algebra and a probability measure \(p\in PM(M)\). Let us consider a collection of identical dynamical systems \((\mathbb {S}^{1},T)_{i}\), with \(i\in M\) and \( T:\mathbb {S}^{1}\rightarrow \mathbb {S}^{1}\) being a Borel measurable function.
The initial state of this collection of interacting systems can be identified by a point \(\mathbf {x}(0)=(x_{i}(0))_{i\in M}\in \) \((\mathbb {S} ^{1})^{M}\) (we suppose \(i\rightarrow x_{i}(0)\) being measurable). Let \( \mathcal {X\subseteq }(\mathbb {S}^{1})^{M}\) be the set of measurable functions \(M\rightarrow \mathbb {S}^{1}\). We now define the dynamics of the interacting systems by defining a global map \(\mathcal {T}:\mathcal {X} \rightarrow \mathcal {X}\) and global trajectory of the system by
where \(\mathbf {x}(t+1)\) is defined on every coordinate by applying at each step the local dynamics T, plus a perturbation given by the mean field interaction with the other systems, by
for all \(i\in M\), where \(\Phi _{\delta ,\mathbf {x}(t)}:\mathbb {S} ^{1}\rightarrow \mathbb {S}^{1}\) represents the perturbation provided by the global mean field coupling with strength \(\delta \ge 0\), defined in the following way: let \(\pi _{\mathbb {S}^{1}}:\mathbb {R}\rightarrow \mathbb {S} ^{1}\) be the universal covering projection, let us consider some continuous function \(h:\mathbb {S}^{1}\times \mathbb {S}^{1}\rightarrow \mathbb {R}\), where h(x, y) represents the way in which the presence of some subsystem in the state \(y\in \mathbb {S}^{1}\) perturbs a certain subsystems in the state \( x\in \mathbb {S}^{1}\); we define \(\Phi _{\delta ,\mathbf {x}(t)}\) as
(\(j\rightarrow h(x,x_{j}(t))\) can be viewed as a function \(:M\rightarrow \mathbb {R}\))Footnote 2. Consider the function \(I_{\mathbf {x},t}:M\rightarrow \mathbb {S}^{1}\) defined by
We remark that with these definitions, for all \(t\in \mathbb {N}\), \(I_{ \mathbf {x},t}\) is also measurable. We say that the global state \(\mathbf {x} (t)\) of the system is represented by a probability measure \(\mu _{\mathbf {x} (t)}\in PM(\mathbb {S}^{1})\) if
(the pushforward of p by the function \(I_{\mathbf {x},t}\)). Now we see how the measures representing given initial conditions evolve with the dynamics.
Lemma 1
Let us consider the system \((\mathcal {X},\mathcal {T})\) defined above. Let \( \mu \in PM(\mathbb {S}^{1}),\) let us consider
Suppose the initial condition of the system \(\mathbf {x}(0)\) is represented by a measure \(\mu _{\mathbf {x}(0)},\) then \(\mathbf {x}(1)=\mathcal {T}(\mathbf { x}(0))\) is represented by
Proof
Since two probability measures are identical if they act in the same way on continuous functions, we prove that for all continuous \(g:\mathbb {S} ^{1}\rightarrow \mathbb {R},\) we have \(\int g~d\mu _{\mathbf {x}(1)}=\int g~dL_{\Phi _{\delta ,\mu _{\mathbf {x}(0)}}\circ T}(\mu _{\mathbf {x}(0)}).\) By applying several times the change of variable formula, we have
But since \(\mathbf {x}(0)\) is represented by \(\mu _{\mathbf {x}(0)}\)
leading to the statement. \(\square \)
Hence the measure representing the current state of the system fully determines the measure which represents the next state of the system, defining a function between measures
This function is an example of what in the following section we will consider as a self-consistent transfer operator. In the case of coupled systems \((\mathcal {X},\mathcal {T})\) described above, to describe the evolution of a certain probability measure representing the global state of the system we hence apply at each time a transfer operator from a family of the kind
Each operator \(L_{\delta ,\mu }\) can be seen as the transfer operator associated with the dynamics of a given node of the network of coupled systems, given that the distribution of the states of the other nodes in the network is represented by the measure \(\mu .\)
We remark that the extended system \((\mathcal {X},\mathcal {T})\) above described can be identified by the choice of the phase space \(\mathbb {S}^{1}\) , the local dynamics T, the strength of coupling \(\delta \) and the coupling function \(\ h.\) Hence it can be identified as the quadruple \(( \mathbb {S}^{1},T,\delta ,h)\).
3 Self-Consistent Operators, the Existence of the Invariant Measure
General standing assumptions and notations. Motivated by the class of examples described in the previous section, given a compact metric space X we consider a family of Markov operators \(L_{\delta ,\mu }:SM(X)\rightarrow SM(X)\) depending on a probability measure \(\mu \in PM(X)\) and \(\delta \ge 0\). In our statements, we will apply the operators \( L_{\delta ,\mu }\) to different strong and weak spaces of measures which are subspaces of SM(X). We now introduce the notations and the basic assumptions to formalize this. Let \((B_{w},||~||_{w})\) be a normed vector subspace of \(\ SM(X)\). In the paper we will suppose that the weak norm \( ||~||_{w}\) is strong enough so that the function \(\mu \rightarrow \mu (X)\) is continuous as a function \(:B_{w}\rightarrow \mathbb {R}\) and that \(||\mu _{n}-\mu ||_{w}\rightarrow 0\) for a sequence of positive measures \(\mu _{n}\) implies that \(\mu \) is positive. Let \(P_{w}:=B_{w}\cap PM(X)\) the set of probability measures in \(B_{w}.\) We will suppose that \(P_{w}\) with the metric induced by \(||~||_{w}\) is a complete metric space.
A self-consistent transfer operator in our context will be the given of a family of Markov linear operators such that \(L_{\delta ,\mu }:\) \( B_{w}\rightarrow B_{w}\) for all \(\mu \in P_{w}\), some \(\delta \ge 0\) and the dynamical system \((P_{w},\mathcal {L}_{\delta })\) where \(\mathcal {L} _{\delta }:P_{w}\rightarrow P_{w}\) is defined by
In the notation \(\mathcal {L}_{\delta }\) we emphasize the dependence on \( \delta \) as in the following we will be interested in the behavior of these operators for certain sets of values of \(\delta \) or in the limit \(\delta \rightarrow 0.\) We also point out that here and in the following we will use the calligraphic notation \(\mathcal {L}\) to denote some operator which is not necessarily linear and the notation L to denote linear operators.
In the following we will apply linear operators on spaces with different topologies. If A, B are two normed vector spaces and \(L:A\rightarrow B\) is a linear operator we denote the mixed norm \(\Vert L\Vert _{A\rightarrow B}\) as
Remark 2
In the case where \(L_{\delta ,\mu }\) is the transfer operator associated with a map \(T_{\delta ,\mu }:X\rightarrow X\) to this dynamical system one can also associate the skew product dynamical system \((A\times X,F)\) on \( A\times X\) where \(F:A\times X\rightarrow A\times X\) is defined by
(see also [5]). One can remark that in the case \(\mu \) is a fixed point for \(\mathcal {L}_{\delta }\) the associated dynamics will be nontrivial only on the second coordinate, where \(T_{\delta ,\mu }\) represents a map for which \(\mu \) is an invariant measure. Hence by the classical ergodic theory results, finding the fixed points of \(\mathcal {L}_{\delta }\) gives important information on the statistical behavior of the second coordinate of the system F.
We will hence be interested in the dynamics \(\mathcal {L}_{\delta }\) considered on a space of measures, and on the properties of its fixed points. In particular we will be interested in the attractiveness of these fixed points (which will determine the convergence to equilibrium of the global system) and to the stability or response of these fixed points with respect to perturbations of the global system.
Standing assumptions 1. In this section we will use the following standing assumptions and notations.
Let \(B_{w}\) as above, and let \(B_{s}\) be a normed vector subspace \( (B_{s},||~||_{s})\subseteq \) \((B_{w},||~||_{w})\). Suppose \(||~||_{s}\ge ||~||_{w}\). We also denote by \(P_{s}:=P_{w}\cap B_{s}\) the set of probability measures in \(B_{s}\). We suppose \(P_{s}\ne \emptyset \). We will also suppose that there is \(M\ge 0\) such that as \(\mu \) varies in \(P_{w}\) the family \(L_{\delta ,\mu }\) is such that \(||L_{\delta ,\mu }||_{B_{w}\rightarrow B_{w}}\le M\) and \(||L_{\delta ,\mu }||_{B_{s}\rightarrow B_{s}}\le M\).
We now prove general statements regarding the existence and uniqueness of regular (and then physically meaningful) invariant measures for self-consistent transfer operators. We remark that since our transfer operators are not linear, the normalization of the measure to a probability one is important in this context. In the case in which we put no restrictions on the size of the parameter \(\delta \) representing the nonlinearity strength, by a topological reasoning we prove a general result on the existence of invariant probability measures (Theorem 3). We then suppose that the parameter \(\delta \) is below a certain threshold, and in this weak coupling regime we also prove some unique existence result (see Theorem 4). We remark that in the weak coupling regime similar results have been proved in several cases of extended systems (see e.g. [6, 26, 34]), also showing the uniqueness of the invariant measure in a certain class. It is known on the other hand that as the coupling strength grows, phase transitions phenomena can occur, leading to the presence of multiple invariant measures (see [4, 44] for a case not arising from coupled maps in which the uniqueness of absolutely continuous invariant measures is lost for all \(\delta >0\)).
Theorem 3
Suppose that there exists \(\pi _{n}:B_{w}\rightarrow B_{s} \), a linear projection of finite rank n which is a Markov operator with the following properties: there is \(M_{0}\ge 0\) and a decreasing sequence \(a(n)\rightarrow 0\) such that for all \(n\ge 0\)
and
Let us suppose that \(\pi _{n}(P_{w})\subseteq P_{s}\) and \(\pi _{n}(P_{w})\) is bounded in \(B_{s}\). Let us fix \(\delta \ge 0\) and suppose furthermore that:
- Exi1:
-
there is \(M_{1}\ge 0\) such that \(\forall \mu _{1}\in P_{w}\) and f \(\in P_{w}\) which is a fixed point of \(L_{\delta ,\mu _{1}}\) it holds
$$\begin{aligned} ||f||_{s}\le M_{1}; \end{aligned}$$ - Exi1.b:
-
\(\forall \mu _{1}\in P_{w},~n\in \mathbb {N}\) and for every f \(\in P_{w}\) which is a fixed point for the finite rank approximation \(\pi _{n}L_{\delta ,\pi _{n}\mu _{1}}\pi _{n}\) of \(\ L_{\delta ,\mu _{1}}\) it holds
$$\begin{aligned} ||f||_{s}\le M_{1}; \end{aligned}$$ - Exi2:
-
there is \(K_{1}\ge 0\) such that \(\forall \mu _{1},\mu _{2}\in P_{w}\)
$$\begin{aligned} ||L_{\delta ,\mu _{1}}-L_{\delta ,\mu _{2}}||_{B_{s}\rightarrow B_{w}}\le \delta K_{1}||\mu _{1}-\mu _{2}||_{w}. \end{aligned}$$
Then there is \(\mu \in P_{s}\) such that
and
To understand the assumptions made we suggest to think of \(B_{w}\) as a weak space, for example \(L^{1}\) and of \(B_{s}\) as a stronger space in which regular fixed points of the linear transfer operators \(L_{\delta ,\mu }\) are contained, for example, in the case of transfer operators associated with expanding maps, one can think of \(B_{s}\) as some Sobolev space. The projection \(\pi _{n}\) allows to reduce the problem to a finite dimensional one and find fixed points of the finite dimensional reduced operators by the Brouwer fixed point theorem. In concrete examples \(\pi _{n}\) could be a finite dimensional discretization, as the Ulam discretization or similar. The assumptions (Exi1), (Exi1.b) tells that the invariant measures of the original and discretized operators are unifornmly regular, and can be verified in concrete examples by showing that these operators satisfy a common Lasota-Yorke inequality. The assumption (Exi2) in some sense says that the family of operators \(L_{\delta ,\mu }\) depends on \(\mu \) in a Lipschitz way, considering a (weak) mixed norm topology. The assumptions made are then quite natural for a family of transfer operators depending on a parameter. An interesting corollary of Theorem 3 is Proposition 16, establishing a general statement for the existence of an invariant probability meaure for general continuous maen field coupled maps, even outside the weak cupling regime.
Proof of Theorem 3 Without loss of generality we can suppose that each operator \(L_{\delta ,\mu }\) is such that \(||L_{\delta ,\mu }||_{B_{s}\rightarrow B_{s}}\le M_{0},\) \( ||L_{\delta ,\mu }||_{B_{w}\rightarrow B_{w}}\le M_{0}\). First we prove that under the assumptions of the theorem, given a sequence \(\mu _{i}\) of probability measures which is bounded in \(B_{s}\) there is \(\mu \in P_{w}\) and converging subsequence \(\mu _{i_{k}}\rightarrow \mu \), converging in the weak topology. Indeed let \(\mu _{i}\) be such a sequence, with \(||\mu _{i}||_{s}\le M_{2}\), let us consider \(\nu _{n,i}:=\pi _{n}\mu _{i}\). Since \(\pi _{n}\) is Markov this is a sequence of probability measures. By (6) this sequence is bounded in \(B_{w}\) and belongs to the finite dimensional space \(\pi _{n}B_{w}\), then it has a converging subsequence \( \nu _{n,i_{n,k}}\rightarrow \nu _{n}\) where we denote by \(i_{n,k}\) a sequence of indices for which we have this convergence. We remark that this indices can depend on n. Since \(P_{w}\) is complete for the weak norm (see Standing assumptions 1) we also have that \(\nu _{n}\in P_{w}.\) By (7), for all n and k we have \(||\nu _{n,i_{n,k}}-\mu _{i_{n,k}}||_{w}\le a(n)M_{2}.\) Without loss of generality we can suppose that \(i_{n,k}\) is a subsequence of \(i_{n-1,k}\) (suppose we selected the sequence of indices \(i_{n-1,k}\), then we can select the subsequence \(\nu _{n,i_{n,k}}\rightarrow \nu _{n}\) only from the indices belonging to \( i_{n-1,k}\) since \(\nu _{n-1,i_{n-1,k}}\) is also a bounded sequence, and so on for all n by induction). In this case, for \(m\ge n\) we have
Since this is true for all k, by taking the limits it holds that \(||\nu _{n}-\nu _{m}||_{w}\le 2a(n)M_{2}\) and hence \(\nu _{n}\) is a Cauchy sequence of probability measures in \(P_{w}\). By the completeness of \(P_{w}\), the sequence \(\nu _{n}\) will then converge to some \(\nu \in P_{w}\). We also have that \(\nu _{k,i_{k,k}}\rightarrow \nu \) in \(B_{w}\) and since \( ||\nu _{k,i_{k,k}}-\mu _{i_{k,k}}||_{w}\le a(k)M_{2}\) we also have \(\mu _{i_{k,k}}\rightarrow \nu \) in \(B_{w}\), finding a converging subsequence as claimed.
Let us consider a finite rank approximation of \(\mathcal {L}_{\delta },\) defined by
We now prove that \(\mathcal {L}_{\delta ,n}\) is a continuous function \( P_{w}\rightarrow P_{w}\), indeed let \(\mu \in P_{w},\nu \in B_{w}\) such that \( \mu +\nu \in P_{w},\) we have
and
while using (Exi2)
hence
By assumption \(\pi _{n}P_{w}\) is bounded in \(B_{s}\), this shows that \(||\pi _{n}\mu ||_{s}\) is uniformly bounded as \(\mu \) ranges in \(P_{w}\) and then \( \mathcal {L}_{\delta ,n}(\mu )\) is Lipschitz continuous \(P_{w}\rightarrow P_{w}.\) Note that since \(P_{w}\) is a convex set, \(\pi _{n}P_{w}\) is a finite dimensional convex and bounded set. Now let us see that this is also a closed set in \(B_{w}\). We will deduce that it is compact. Suppose \(p_{i}\in \pi _{n}P_{w}\subseteq P_{w}\) is a Cauchy sequence for the \(B_{w}\) norm. Since \(P_{w}\) is complete this will converge to a point w of \(P_{w}\). But \( \pi _{n}B_{w},\) being a finite dimensional vector space, is a closed space, then \(w\in \pi _{n}B_{w}\). Suppose \(w=\pi _{n}(u)\) with \(u\in B_{w},\) since \(w=\pi _{n}(\pi _{n}u)=\pi _{n}(w)\) and \(w\in P_{w}\) then \(w\in \pi _{n}P_{w}.\) By this \(\pi _{n}P_{w}\) is a closed subspace of \(B_{w}.\) Since \(\pi _{n}P_{w}\) is a bounded, convex and closed subset of a finite dimensional space, then it is homeomorphic to a closed disc (see e.g. [14], Corollary 1.1.1). We have that \(\mathcal {L}_{\delta ,n}\) is continuous on \(\pi _{n}P_{w}\) and \(\mathcal {L}_{\delta ,n}(\pi _{n}P_{w})\subseteq \pi _{n}P_{w}\). Then by the Brouwer fixed point theorem there is \(\mu _{n}\in \pi _{n}P_{w}\) such that
This means that \(\pi _{n}L_{\delta ,\pi _{n}\mu _{n}}\pi _{n}(\mu _{n})=\mu _{n}\) and then by Exi1.b we have that for all \(n\in \mathbb {N}\), \(||\mu _{n}||_{s}\le M_{1}.\) As we proved above \(\mu _{n}\) has then a converging subsequence \(\mu _{n_{k}}\rightarrow \hat{\mu }\) in the weak norm to some element \(\hat{\mu }\in P_{w}.\)
Now let us prove that
In fact we have for all \(k\ge 0\)
Since \(||\hat{\mu }-\mu _{n_{k}}||_{w}\rightarrow 0,\) and the operator \( L_{\delta ,\hat{\mu }}\) is bounded then
in the weak norm. By Exi2
which by Exi1.b becomes
and then
in the weak norm. Since \(\mu _{n_{k}}=\pi _{n_{k}}\mu _{n_{k}}\) we also have that
and then by (7)
We then proved that
Since
then we get
proving the invariance of \(\hat{\mu }.\)
Now we are only left to prove that \(||\hat{\mu }||_{s}\le M_{1}\). Since \( L_{\delta ,\hat{\mu }}(\hat{\mu })=\hat{\mu }\) this directly follows from (Exi1). \(\square \)
Theorem 3 gives general, sufficient conditions for the existence of the invariant probability measure of a self-consistent operator, but it is hard to apply it constructively to approximate the invariant measure. Furthermore it does not give information about the uniqueness.
Now we prove a kind of constructive existence and uniqueness result in the case of weak coupling. Before stating the result, as a general remark on the uniqueness of the invariant probability measure we show that when \( \delta \) is small and the operators \(L_{\delta ,\mu }\) are statistically stable in some sense, different invariant probability measures in \(B_{w}\) of the associated \(\mathcal {L}_{\delta }\) must be near each other. Indeed, suppose that each operator of the family \(L_{\delta ,\mu }\) with \(\delta \ge 0\) and \(\mu \in P_{w}\) has a unique fixed probability measure in \(B_{w}\) which we denote by \(f_{\mu }\in P_{w}\) and suppose there is \(F:\mathbb {R}\rightarrow \mathbb {R}\) such that \(\forall \mu _{1},\mu _{2}\in P_{w}\)
If \(\mu \), \(\nu \in P_{w}\) are invariant measures for \(\mathcal {L}_{\delta },\) this implies that \(\mu =f_{\mu }\) and \(\nu =f_{\nu }\). Then we have
In the case \(\lim _{\delta \rightarrow 0}F(\delta )=0\) we see that when \( \delta \) is small different invariant measures of \(\mathcal {L}_{\delta }\) must be near each other. In the following statement we then suppose a strong stability property (see (Exi3)) for the invariant measures of the operators \(L_{\delta ,\mu }\) as \(\mu \) vary.
Theorem 4
Suppose there is \(\overline{\delta }\ge 0\) such that for all \(0\le \delta <\overline{\delta }\) the family \(L_{\delta ,\mu }\) satisfies (Exi1) and (Exi2) uniformly (with the same constants for each such \(\delta \)). Suppose that \(P_{w}\) contains some probability measure \(\mu \) with \(||\mu ||_{w}\le M_{1}\) (where \(M_{1}\) is the constant coming from (Exi1)). Suppose that for all \(0\le \delta <\overline{\delta }\) and \( \mu \in P_{w}\) with \(||\mu ||_{w}\le M_{1}\), \(L_{\delta ,\mu }\) has a unique fixed probability measure in \(P_{w}\) which we denote by \(f_{\mu }.\) Suppose furthermore that the family \(L_{\delta ,\mu }\) satisfies the following:
- Exi3:
-
there is \(K_{2}\ge 1\) such that \(\forall \mu _{1},\mu _{2}\in P_{w}\) with \(\max (||\mu _{1}||_{w},||\mu _{2}||_{w})\le M_{1}\)
$$\begin{aligned} ||f_{\mu _{1}}-f_{\mu _{2}}||_{w}\le \delta K_{2}||\mu _{1}-\mu _{2}||_{w}. \end{aligned}$$
Then for all \(0\le \delta \le \min (\overline{\delta },\frac{1}{K_{2}})\), there is a unique \(\mu \in P_{w}\) such that
Furthermore \(\mu =\lim _{k\rightarrow \infty }\mu _{k}\) where \(\mu _{k}\) is any sequence defined inductively in the following way: let \(\mu _{0}\) be some probability measure in \(P_{w}\) with \(||\mu _{0}||_{w}\le M_{1}\), then \( \mu _{1}\) is the fixed probability measure of \(L_{\delta ,\mu _{0}},\) \(\mu _{i}\) in \(\ P_{w}\); \(\mu _{i}\) is the fixed probability measure of \( L_{\delta ,\mu _{i-1}}\) in \(\ P_{w}\) and so on.
While the assumptions (Exi1), (Exi2) and the uniqueness of the fixed probability measure in \(P_{w}\) for the family \(L_{\delta ,\mu }\) can be easily verified for a large class of examples, including families of transfer operators coming from piecewise expanding maps, the assumption (Exi3) imposes some stronger requirements on the kind of systems we can consider when applying this statement.
The assumption (Exi3) correspond to a Lipschitz quantitative stability for the fixed points of the operators in the family \(L_{\delta ,\mu }\) when the operators are perturbed by changing \(\mu \). This is a strong assumption which is however satisfied for many interesting systems, as expanding and uniformly hyperbolic or many random ones, but it is not satisfied for other systems like piecewise expanding maps for perturbations changing their turning points. We remark that indeed self-consistent transfer operators arising from piecewise expanding maps show a complicated behavior from the point of view of the uniqueness of the invariant measure [44].
Proof of Theorem 4
Let us consider \(\overline{\delta }\) such that
Let us consider some \(0<\delta \le \overline{\delta }.\) Let \(f_{0}\in P_{w}\) with \(||f_{0}||_{w}\le M_{1}\). Let \(f_{1}\in P_{s}\) be the fixed probability measure of \(L_{\delta ,f_{0}}\) in \(B_{w}\), again \( ||f_{1}||_{w}\le M_{1}\). Now, \(L_{\delta ,f_{1}}\) has a fixed probability measure which we will denote by \(f_{2}.\) We also have \(||f_{2}||_{w}\le M_{1}\). By (Exi3)
Now let us consider the linear operator \(L_{\delta ,f_{2}}\), this operator has a fixed probability measure \(f_{3}\in B_{s}\) with \(||f_{3}||_{w}\le M_{1}\). We get
Continuing as before, this will lead to a new fixed probability measure \( f_{4}\) with \(||f_{4}-f_{3}||_{w}\le (K_{2}\delta )^{3}||f_{0}-f_{1}||_{w}\) and so on, defining a sequence \(f_{k}\) with \(||f_{k}||_{w}\le M_{1}\) and \( ||f_{k}-f_{k-1}||_{w}\le (K_{2}\delta )^{k-1}||f_{0}-f_{1}||_{w}\). Since \( (K_{2}\delta )^{k}\) is summable, \(f_{k}\) is a Cauchy sequence in \(P_{w}.\)
Since \(P_{w}\) is complete this sequence has a limit. Let \( f:=\lim _{k\rightarrow \infty }f_{k}\in P_{w}.\) By (Exi1), \(f_{k}\) is also uniformly bounded in \(B_{s}.\) Now we can prove that \(\mathcal {L}_{\delta }(f)=L_{\delta ,f}(f)=f\). Indeed
because of the continuity of \(L_{\delta ,f}\) in the weak norm. Furthermore
because \(L_{\delta ,f_{k-1}}(f_{k})=f_{k}.\) However, by (Exi2) there is \( K_{1}\ge 0\) such that \(||L_{\delta ,\mu _{1}}-L_{\delta ,\mu _{2}}||_{B_{s}\rightarrow B_{w}}\le K_{1}\delta ||\mu _{1}-\mu _{2}||_{w}\) and using this together with (Exi1) we get
Then in the \(B_{w}\) topology
Regarding the uniqueness, suppose \(\mu _{1},\mu _{2}\in P_{w}\) are invariant for \(\mathcal {L}_{\delta }\). Then \(L_{\delta ,\mu _{1}}(\mu _{1})=\mu _{1}\) and \(L_{\delta ,\mu _{2}}(\mu _{2})=\mu _{2}.\) By (Exi1) we have \(\max (||\mu _{1}||_{w},||\mu _{2}||_{w})\le M_{1}\) and then by (Exi3) we have \(||\mu _{1}-\mu _{2}||_{w}\le \delta K_{2}||\mu _{1}-\mu _{2}||_{w}\), implying \(||\mu _{1}-\mu _{2}||_{w}=0\) because \(K_{2}\delta <1 \). \(\square \)
Remark 5
The way the fixed point f is found in the previous proof is constructive, provided we have a mean of finding the invariant measures of the various operators \(L_{\delta ,f_{k}}\) (which is possible in many interesting cases by some suitable finite element reduction). In this case f can be approximated by the sequence \(f_{k}\rightarrow f\) and the proof also provides an explicit way to estimate the convergence rate of this sequence, which is exponential.
4 Self-Consistent Operators, Exponential Convergence to Equilibrium
Theorems 3 and 4 give information about the existence of fixed probability measures for the self-consistent operators but gives no information on whether they are attractive fixed points. In this section we address this question, giving general sufficient conditions for this to hold. In the case where the invariant probability measure is attractive we have that the associated system has convergence to equilibrium in some sense, since iterates of some initial probability measure will converge to the invariant one. It is important to estimate the speed of this convergence. In the case of weak coupling we will show a set of general conditions implying exponential speed of convergence to equilibrium for self-consistent transfer operators.
Standing assumptions 2. In this section we will consider a setup similar to the one in the previous section, with strong and weak spaces \(B_{s}\) and \(B_{w}\) and a family of Markov bounded operators \( L_{\delta ,\mu }\) satistyfing the General Standing assumptions and the Standing assumptions 1 stated at beginning of Sect. 3. We will also consider a stronger space \((B_{ss},||~||_{ss})\) with norm satisfying \( ||~||_{ss}\ge ||~||_{s}\). We denote by \(P_{ss}\) the set of probability measures in \(B_{ss}\). We will suppose that for all \(\mu \in P_{w}\) and \( \delta \ge 0\) the operators \(L_{\delta ,\mu }:B_{ss}\rightarrow B_{ss}\) are bounded and that \(P_{w}\) is a bounded set for the \(B_{w}\) norm. We will consider furthermore the following assumptions:
- Con1:
-
The operators \(L_{\delta ,\mu }\) satisfy a common “one step” Lasota Yorke inequality. There are constants \(\hat{\delta },B,\lambda _{1}\ge 0\) with \(\lambda _{1}<1\) such that for all \(f\in B_{s},\) \(\mu \in P_{w},\) \(0\le \delta \le \hat{\delta }\)
$$\begin{aligned} \left\{ \begin{array}{c} ||L_{\delta ,\mu }f||_{w}\le ||f||_{w} \\ ||L_{\delta ,\mu }f||_{s}\le \lambda _{1}||f||_{s}+B||f||_{w}. \end{array} \right. \end{aligned}$$(11) - Con2:
-
The family of operators satisfy an extended (Exi2) property: there is \(K\ge 1\) such that for all \(f\in B_{s},\) \(\mu ,\nu \in P_{w}\), \(0\le \delta \le \hat{\delta }\)
$$\begin{aligned} ||(L_{\delta ,\mu }-L_{\delta ,\nu })(f)||_{B_{s}\rightarrow B_{w}}\le \delta K||\mu -\nu ||_{w} \end{aligned}$$(12)and \(\forall f\in B_{ss},\) \(\mu ,\nu \in P_{w}\)
$$\begin{aligned} ||(L_{\delta ,\mu }-L_{\delta ,\nu })(f)||_{B_{ss}\rightarrow B_{s}}\le \delta K||\mu -\nu ||_{w}. \end{aligned}$$We remark that by (12), when \(\delta =0\) \(\ \ L_{\delta ,\mu },\) \( L_{\delta ,\nu }:B_{s}\rightarrow B_{s}\) are identical operators for all \( \mu ,\nu \in B_{w}\). We hence denote this operator as \(L_{0}\). We also suppose that for all \(f\in B_{s},\) \(\nu \in P_{w}\), \(0\le \delta \le \hat{ \delta }\)
$$\begin{aligned} ||(L_{0}-L_{\delta ,\nu })(f)||_{B_{s}\rightarrow B_{w}}\le \delta K||\nu ||_{w}. \end{aligned}$$(13) - Con3:
-
The operator \(L_{0}:B_{s}\rightarrow B_{s}\) has convergence to equilibrium: there exists \(a_{n}\ge 0\) with \(a_{n}\rightarrow 0\) such that for all \(n\in \mathbb {N}\) and \(v\in V_{s}\)
$$\begin{aligned} ||L_{0}^{n}(v)||_{w}\le a_{n}||v||_{s} \end{aligned}$$(14)where
$$\begin{aligned} V_{s}=\{\mu \in B_{s}|\mu (X)=0\} \end{aligned}$$
We remark that the assumption (Con1) implies that the family of operators \( L_{\delta ,\mu }\) is uniformly bounded when acting on \(B_{s}\) and on \(B_{w} \) as \(\mu \) varies in \(P_{w}\)Footnote 3.
We also remark that the convergence to equilibrium assumption is sometimes not trivial to be proved in a given system, but it is somehow expected in systems having some sort of indecomposability and chaotic behavior (for instance some kind of topological mixing, expansion, hyperbolicity or presence of noise, see also Remark 40).
The following statement estimates the speed of convergence to equilibrium for self-consistent transfer operators \(\mathcal {L}_{\delta }\) when \( \delta \) is small.
Theorem 6
Let \(L_{\delta ,\mu }\) be a family of Markov operators satisfying the Standing assumptions 2 (including (Con1), ..., (Con3)) for some \(\hat{\delta }>0\) and that
Let us consider for all \(\delta \le \hat{\delta }\) the self-consistent operator \(\mathcal {L}_{\delta }\) defined as in (5), suppose that for each such \(\delta \) there is an invariant probability measure \(\mu _{\delta }\in P_{ss}\) for \(\mathcal {L}_{\delta }\) and suppose that
Then there exists \(\overline{\delta }\) such that \(0<\overline{\delta }<\hat{ \delta }\) and there are \(C,\gamma \ge 0\) such that for all \(n\in \mathbb {N}\) , \(0<\delta <\overline{\delta },\) \(\nu \in P_{ss}\) we have
We remark that the convergence speed estimates provided in (17) are in the strong norm. These estimates are uniform for \(\delta \) small enough and uniform in \(\nu \). We also remark that since there is the strong norm on both sides of the inequality, (17) is similar to a spectral gap estimate, rather than a convergence to equilibrium estimate (where the regularity of the measure is estimated in the strong norm and the convergence is in the weak one, resulting in a weaker estimate).
Before the proof of Theorem 6 we prove several results on the convergence to equilibrium of a sequential composition of operators in the family \(L_{\delta ,\mu }\). In particular it will be useful to prove a Lasota Yorke inequality for such a composition.
Lemma 7
Let \(L_{\delta ,\mu }\) be a family of Markov operators satisfying (Con1). Let \(\mu _{1},...,\mu _{n}\in P_{w}\) and
be a sequential composition of operators in such family, then
and
Proof
The first inequality is straightforward from (Con1). Let us now prove (20). We have
thus
Continuing the composition we get (20). \(\square \)
Lemma 8
Let \(\delta \ge 0\) and let \(\ L(n)\) be a sequential composition of operators \(L_{\delta ,\mu _{i}}\) as in (18) with \(i\in \{1,...,n\}\) and \(\mu _{i}\in P_{w}\) satisfying the above Standing assumptions 2 (including (Con1),...,(Con3)). Let \(L_{0}\) be the operator in the family for \(\delta =0\) as defined in (Con2). Since \(P_{w}\) is bounded, let us denote by \(Q:=\sup _{\mu \in P_{w}}||\mu ||_{w}\). Then there is \(C\ge 0\) such that \(\forall g\in B_{s},\forall n\ge 0\)
where B is the second coefficient of the Lasota Yorke inequality (11).
Proof
To shorten notation let us denote for \(i\in \{1,...,n\},\) \(L_{i}:=L_{\delta ,\mu _{i}}\). By (Con2), equation (13) we get
The case \(n=1\) of (21) directly follows from (13). Let us now suppose inductively
then
The statement follows from the observation that continuing the composition, \( C_{n}\) remains being bounded by the sum of a geometric series. \(\square \)
Next statement is inspired by the methods developed in [18] and allows to estimate the speed of convergence to equilibrium of a sequential composition of linear operators satisfying the Standing assumptions 2 (including (Con1),...,(Con3)). The statement is in some sense homologous to Proposition 2.7 in [11].
Proposition 9
Let us consider \(\delta \ge 0\) and a family of operators \( L_{\delta ,\mu }\) satisfying the Standing assumptions 2 (including (Con1) ,...,(Con3)). Let us consider a sequential composition L(n) as above. Let us fix \(n_{1}>0\) and consider the \(2\times 2\) matrix M defined by
Under the previous assumptions for any \(g\in V_{s}\) the following holds:
(i) for all integer \(i\ge 0\) the norms of the iterates \(L(in_{1})g\) are bounded by
Here \(\preceq \) indicates the componentwise \(\le \) relation (both coordinates are less or equal).
(ii) Let \(\rho \) be the maximum eigenvalue of \(M^{T}\), with eigenvector \( \left( \begin{array}{c} a \\ b \end{array} \right) .\) Suppose \(a,b\ge 0\) and \(a+b=1,\) let us define the (a, b) balanced-norm as
In this case we have
Furthermore, the situation in which \(\rho <1\), \(a,b\ge 0\) can be achieved if \(n_{1}\) is big enough and \(\delta \) small enough. More precisely, fixing \( n_{1}\) large enough we have that \(\rho =\rho (\delta )\) can be seen as a function of \(\delta \). There is some \(\delta _{1}<1\) such that
and there is a positive eigenvector of \(\rho (\delta )\) for \(\delta \le \delta _{1}\).
As a consequence we also have
and
For the proof of Proposition 9 the following lemma will be useful
Lemma 10
Let us consider real sequences \(a_{n},b_{n}\) such that \( a_{n}\ge 0,~b_{n}\ge 0\) for all \(n\in \mathbb {N}\) and \( a_{n},b_{n}\rightarrow 0\), real numbers \(\delta ,A,B,C\ge 0\) and a real matrix of the form
Then there is \(n_{1}\ge 0\), \(\overline{\delta }\ge 0\) and \(0\le \overline{ \rho }<1\) such that for all \(0\le \delta \le \overline{\delta }\) the matrix
has largest eigenvalue \(\rho \) such that \(0\le \rho \le \overline{\rho }\) and an associated eigenvector (a, b), such that \(a,b\ge 0.\)
Proof
Fixing n and letting \(\delta \rightarrow 0\), the matrix \(\left( \begin{array}{cc} b_{n} &{} a_{n} \\ A &{} 0 \end{array} \right) \), has maximum right eigenvalue \(\frac{1}{2}b_{n}+\frac{1}{2}\sqrt{ b_{n}^{2}+4Aa_{n}}\) with eigenvector \(\left( \begin{array}{c} \frac{1}{2A}\left( b_{n}+\sqrt{b_{n}^{2}+4Aa_{n}}\right) \\ 1 \end{array} \right) .\) Now if we take \(n_{1}\) big enough we can let \(0\le \frac{1}{2} b_{n_{1}}+\frac{1}{2}\sqrt{b_{n_{1}}^{2}+4Aa_{n_{1}}}<1\) and then for sufficiently small \(\delta \) the statement holds. \(\square \)
Now we are ready to prove Proposition 9.
Proof of Proposition 9
For the proof of (i): let us consider \(n_{1}\ge 0\) and \(g_{0}\in V_{s}\) and let us denote \(g_{i}=L(in_{1})g_{0}.\) By Lemma 7 we have
By Lemma 8, assumption (Con3) and (14) we get
Compacting (24) and (25) into a vector notation, setting \(v_{i}=\left( \begin{array}{c} ||g_{i}||_{s} \\ ||g_{i}||_{w} \end{array} \right) \) we get
We remark that the matrix M does not depend on \(g_{0}\) and depend on the operators in the family \(L_{\delta ,\mu }\), composing the sequential composition L(n) only by their common coefficients \(\lambda _{1},a_{n_{1}},K,B\) coming from the assumptions (Con1), ..., (Con3). Furthermore, since M is positive, \(v_{1}\preceq v_{2}\) implies \( Mv_{1}\preceq Mv_{2}\). Hence the inequality can be iterated and we have
proving (i). To prove (ii) let us consider the (a, b) balanced-norm: \( ||g||_{(a,b)}=a||g||_{s}+b||g||_{w}\). The statement (i) implies
hence
proving (ii). The remaining part of the statement is a direct consequence of Lemma 10.
\(\square \)
We are ready to prove the main statement of this section.
Proof of Theorem 6
We need to estimate \(||\mathcal {L}_{\delta }^{n}(\nu )-\mu _{\delta }||_{s}\) . Let us denote by \(\nu _{n}\) the sequence of probability measures where \( \nu _{1}=\nu \) and \(\nu _{n}=L_{\delta ,\nu _{n-1}}\nu _{n-1}\). The sequence \(\mathcal {L}_{\delta }^{n}(\nu )\) can be seen as a sequential composition
where using the same notations as in (18)
We remark that by the assumptions, \(||L_{\delta ,\nu _{i}}||_{B_{s}\rightarrow B_{s}}\) are uniformly bounded. Let us estimate this by
Since our operators satisfy (Con1),...,(Con3) and \(\nu -\mu _{\delta }\in V\) we can estimate
using Proposition 9.Footnote 4
Let \(n_{1},\) \(\delta _{1},\rho _{1}\) and \(||~||_{(a,b)}\) the parameters and the norm found applying Proposition 9 (see in particular (23)) to (28). Let us consider \(\delta \le \delta _{1}\). We remark that the norm \(||~||_{(a,b)}\) also depends on \(\delta \).
To simplify notations let us define a general constant that will be used in the estimates. Let
and
By the assumptions (15), (16) we have that \( M_{1}<\infty \). To find \(\overline{\delta }\le \delta _{1}\) satisfying our statement we are going to impose a further condition to the parameter \( \delta \) which is again satisfied for \(\delta \) small enough. Let us state this condition: let us define for all \(n\ge 0,\) by induction the following sequence
Let
Now let us fix \(\overline{\delta }\ge 0\) such that
We now see why this condition is sufficient for our statement to hold. We have indeed
We recall that by (Con2)
Suppose inductively that
(where \(C_{n}\ge 1\) as defined in (29)) then
and
and by (32)
putting the two estimates together
Now we find a coarse estimate for \(||\nu _{n_{1}}-\mu _{\delta }||_{w},||\nu _{n_{1}-1}-\mu _{\delta }||_{w},...,||\nu _{1}-\mu _{\delta }||_{w}\) which will be sufficient for our purposes. Recalling that \(\nu _{n}=L_{\delta ,\nu _{n-1}}\nu _{n-1}\) we have
then
and
and then
Finally we have an estimate for \(||L_{\delta ,\nu _{n}}...L_{\delta ,\nu _{1}}\mu _{\delta }-L_{\delta ,\mu }^{n}(\mu _{\delta })||_{(a,b)}:\)
Now the main estimates are ready. Let us apply Proposition 9 to (28). We get
with \(\rho _{1}<1\) and then
where \(M_{2}\) is defined as in (30). But by (31)
Taking \(\delta \le \overline{\delta }\) we hence get that for all \(i\ge 1\)
proving the statement. \(\square \)
Remark 11
We remark that if in the previous proof instead of considering (27) we considered the estimate
we would have a much easier estimate for the summand
but estimating \(||L(n)(\nu )-L_{\delta ,\mu _{\delta }}^{n}(\nu )||_{s}\) by our assumptions (Con1), ..., (Con3) would involve a term of the kind \(||\nu ||_{ss}\), which would result in a weaker final statement.
5 Statistical Stability and Linear Response for Nonlinear Perturbations
The concept of Linear Response intends to quantify the response of the statistical properties of the system when it is submitted to a certain infinitesimal perturbation. This will be measured in some sense by the derivative of the invariant measure of the system with respect to the perturbation. Let \((\mathcal {L}_{\delta })_{\delta \ge 0}\) be a one parameter family of transfer operators associated with a family of perturbations of an initial operator \(\mathcal {L}_{0}\), with strength \( \delta ,\) and let us suppose that \(\mu _{\delta }\) is the unique invariant probability measure of the operator \(\ \mathcal {L}_{\delta }\) in a certain space \(B_{ss}\). The linear response of the invariant measure of \(\mathcal {L }_{0}\) under the given perturbation is defined by the limit
The topology where this convergence takes place may depend on the system and on the kind of perturbation applied. The linear response to the perturbation hence represents the first order term of the response of a system to a perturbation and when it holds, a linear response formula can be written: \( \mu _{\delta }=\mu _{0}+\dot{\mu }\delta +o(\delta )\), which is valid in some weaker or stronger sense.
We remark that given an observable function \(c:X\rightarrow \mathbb {R}\) if the convergence in (39) is strong enough with respect to the regularity of c we get
showing how the linear response of the invariant measure controls the behavior of observable averages. For instance the convergence in (40) hold when \(c\in L^{\infty }\) and the convergence of the linear response is in \(L^{1}\).
Linear response results in the context of deterministic dynamics have been obtained first in the case of uniformly hyperbolic systems in [39]. Nowadays linear response results are known for many other kinds of systems outside the uniformly hyperbolic case and also in the random case (see [3] for a survey mostly related to deterministic systems and the introduction of [15] for an overview of the mathematical results in the random case).
In the case of coupled hyperbolic map lattices with short range interaction, results on the smooth dependence of the SRB measure were obtained in [24, 25]. In the case of all-to-all coupled maps with mean field interaction and hence in the context of the present paper, linear response results were shown in [41]. Still in the context of all-to-all coupled maps, the works [45, 46] show numerical evidence of the fact that it is possible for a network of coupled maps to exhibit linear response, even if its units do not.
The interest of the study of the self consistent transfer operators in a weak coupling regime motivates the study of the response to nonlinear perturbations of linear operators. In this section we prove some stability and linear response results for the invariant measures of a family \(\mathcal { L}_{\delta }\) of such operators in the limit \(\delta \rightarrow 0\) in the case where the limit operator \(\mathcal {L}_{0}\) is linear. We remark that in [40] an abstract result is proved which can be also applied to the linear response of fixed points of nonlinear operators under suitable perturbations.
Standing assumptions 3. In this section we consider the following general setting similar to the one considered in [15] (see also [16, 27]) for families of linear operators and independent of the standing assumptions from the previous sections. Let X be a compact metric space. In the following we consider three normed vector subspaces of SM(X), the spaces \((B_{ss},\Vert ~\Vert _{ss})\subseteq (B_{s},\Vert ~\Vert _{s})\subseteq (B_{w},\Vert ~\Vert _{w})\subseteq SM(X)\) with norms satisfying
We remark that, a priori, some of these spaces can be taken equal. Their actual choice depends on the type of system and perturbation under study. Again, we will assume that the linear form \(\mu \rightarrow \mu (X)\) is continuous on \(B_{i}\), for \(i\in \{ss,s,w\}\). Since we will mainly consider positive, integral preserving operators acting on these spaces, the following closed invariant spaces \(V_{ss}\subseteq V_{s}\subseteq V_{w}\) of zero average measures defined as:
where \(i\in \{ss,s,w\}\), will play an important role (we recall that \(V_{s}\) was already considered in (Con3)).
Let us consider a family of functions \(\mathcal {L}_{\delta }:B_{i}\rightarrow B_{i}\), with \(\delta \in \left[ 0,\overline{\delta } \right) \). \(\mathcal {L}_{\delta }\) will be called a family of “nonlinear” Markov operators if:
-
each \(\mathcal {L}_{\delta }\) preserves positive measures,
-
for all \(\mu \in SM(X)\) it holds \([\mathcal {L}_{\delta }(\mu )](X)=\mu (X).\)
The following is a “statistical stability” statement for a suitable family of such operators, showing sufficient conditions under which the invariant probability measures of these operators are stable under small perturbations of the operators.
Theorem 12
Let \(\mathcal {L}_{\delta }:B_{i}\rightarrow B_{i}\) with \(\delta \in \left[ 0,\overline{\delta }\right) \) be a family of “nonlinear” Markov operators. Suppose that \(\mathcal {L}_{0}:B_{s}\rightarrow B_{s}\) is linear and bounded. Suppose that for all \(\delta \in \left[ 0,\overline{ \delta }\right) \) there is a probability measure \(h_{\delta }\in B_{ss}\) such that \(\mathcal {L}_{\delta }h_{\delta }=h_{\delta }\). Suppose furthermore that:
-
(SS1)
(regularity bounds) there is \(M\ge 0\) such that for all \( \delta \in \left[ 0,\overline{\delta }\right) \)
$$\begin{aligned} \Vert h_{\delta }\Vert _{ss}\le M. \end{aligned}$$ -
(SS2)
(convergence to equilibrium for the unperturbed operator) There is a sequence \(a_{n}\ge 0\) with \(a_{n}\rightarrow 0\) such that for all \( g\in V_{ss}\)
$$\begin{aligned} \Vert \mathcal {L}_{0}^{n}g\Vert _{s}\le a_{n}||g||_{ss}. \end{aligned}$$ -
(SS3)
(small perturbation) Let \(B_{2M}=\{x\in B_{ss},||x||_{ss}\le 2M\}\). There is \(K\ge 0\) such that and \(\mathcal {L}_{0}-\mathcal {L}_{\delta }:B_{2M}\rightarrow B_{s}\) is \(K\delta \)-Lipschitz.
Then
$$\begin{aligned} \lim _{\delta \rightarrow 0}\Vert h_{\delta }-h_{0}\Vert _{s}=0. \end{aligned}$$
Remark 13
The convergence to equilibrium assumption in (SS2) is required only for the unperturbed operator \(\mathcal {L}_{0}\), which is a linear operator. We also remark that under this assumption \(h_{0}\) is the unique invariant probability measure of \(\mathcal {L}_{0}\) in \(B_{ss}\).
Proof
Let us estimate \(\Vert h_{\delta }-h_{0}\Vert _{s}\) exploiting \(\mathcal {L} _{\delta }h_{\delta }=h_{\delta }\) in the following way:
Since \(h_{\delta },h_{0}\) are probability measures, \(h_{\delta }-h_{0}\in V_{ss}\) and by (SS1), \(\Vert h_{\delta }-h_{0}\Vert _{ss}\le 2M,\) then because of the assumption (SS2) we have
with \(Q(n)=2a_{n}M\rightarrow 0\) (not depending on \(\delta \)). This implies
To estimate \(\Vert \mathcal {L}_{\delta }^{n}h_{\delta }-\mathcal {L} _{0}^{n}h_{\delta }\Vert _{s}\) we rewrite the sum \(\mathcal {L}_{0}^{n}- \mathcal {L}_{\delta }^{n}\) telescopically so that
(note that only the linearity of \(\mathcal {L}_{0}\) is used here). The assumption that \(\Vert h_{\delta }\Vert _{ss}\le M,\) together with the small perturbation assumption (SS3) implies that \(\Vert (\mathcal {L} _{\delta }-\mathcal {L}_{0})h_{\delta }\Vert _{s}\le \delta KM\) as \(\delta \rightarrow 0.\) Thus
where \(M_{2}(n)=\max _{i\le N}(1,||\mathcal {L}_{0}||_{B_{s}\rightarrow B_{s}}^{i}).\) Choosing first n big enough to let Q(n) be close to 0 and then \(\delta \) small enough we can make \(nM_{2}(n)[\delta KM]\) as small as wanted, proving the statement. \(\square \)
We now show a general result about the linear response of fixed points of Markov operators under suitable nonlinear perturbations, the result will be applied to self-consistent transfer operators in the following sections.
Theorem 14
(Linear Response). Let \(\mathcal {L}_{\delta }:B_{s}\rightarrow B_{s}\) \( \mathcal {L}_{\delta }:B_{ss}\rightarrow B_{ss}\) with \(\delta \in \left[ 0, \overline{\delta }\right) \) be a family of nonlinear Markov operators. Suppose that \(\mathcal {L}_{0}\) is linear and bounded \(:B_{i}\rightarrow B_{i} \) for \(i\in \{w,s,ss\}\). Suppose that the family satisfy (SS1), (SS2), (SS3). Suppose furthermore that the family \(\mathcal {L}_{\delta }\) satisfy
-
(LR1)
(resolvent of the unperturbed operator) \((Id-\mathcal {L} _{0})^{-1}:=\sum _{i=0}^{\infty }\mathcal {L}_{0}^{i}\) is a bounded operator \( V_{w}\rightarrow V_{w}\).
-
(LR2)
(small perturbation and derivative operator) Let \(\overline{B} _{2M}=\{x\in B_{s},||x||_{s}\le 2M\}\). There is \(K\ge 0\) such that \( \mathcal {L}_{0}-\mathcal {L}_{\delta }:\overline{B}_{2M}\rightarrow B_{w}\) is \(K\delta \)-Lipschitz. Furthermore, there is \(\mathcal {\dot{L}}{h_{0}\in V_{w} }\) such that
$$\begin{aligned} \underset{\delta \rightarrow 0}{\lim }\left\| \frac{(\mathcal {L}_{\delta }-\mathcal {L}_{0})}{\delta }h_{0}-\mathcal {\dot{L}}h_{0}\right\| _{w}=0. \end{aligned}$$(42)
Then we have the following Linear Response formula
Remark 15
The assumption (LR1) on the existence of the resolvent is asked only for the unperturbed transfer operator, which is linear. This allows a large class of perturbations. In many systems this assumption will result from the presence of a spectral gap (compactness or quasi-compactness of \(\mathcal {L} _{0}\) acting on \(B_{w}\)).
Proof of Theorem 14
By Theorem 12 we have
Let us now consider \((Id-\mathcal {L}_{0})^{-1}\) as a continuous linear operator \(V_{w}\rightarrow V_{w}\). Remark that since \(\mathcal {\dot{L}} h_{0}\in V_{w},\) the resolvent can be computed at \(\mathcal {\dot{L}}h_{0}\). By using that \(h_{0}\) and \(h_{\delta }\) are fixed points of their respective operators we obtain that
Since the operators preserve probability measures, \((\mathcal {L}_{\delta }- \mathcal {L}_{0})h_{\delta }\in V_{w}\). By applying the resolvent to both sides
we obtain that the left hand side is equal to \(\frac{1}{\delta }(h_{\delta }-h_{0})\). Moreover, with respect to the right hand side we observe that, applying assumption (LR2) eventually, as \(\delta \rightarrow 0\)
which goes to zero thanks to Theorem 12. Thus considering the limit \( \delta \rightarrow 0\) we are left with
converging in the \(\Vert \cdot \Vert _{w}\) norm, which proves our claim. \(\square \)
In Sects. 3 and 4 we considered nonlinear self-consistent transfer operators of the type
for \(\mu \in A\subseteq P_{w}\). These functions are positive and integral preserving. In many cases these functions can be extended to nonlinear Markov operators \(B_{i}\rightarrow B_{i}\) for \(i\in \{w,s,ss\}\) and the above statistical stability theorems can be applied, as it will be shown in the next sections.
6 Mean Field Coupled Continuous Maps
We show the flexibility of Theorem 3 proving the existence of an invariant probability measure in the general case of continuous maps interacting by a Lipschitz coupling function h. In the following we denote by \(||~||_{Lip}\) the Lipschitz norm, defined by
for \(g:\mathbb {S}^{1}\rightarrow \mathbb {R}\).
Proposition 16
Let us consider a system of mean field coupled maps as described in Sect. 2 with a map \(T_{0}\in C^{0}(\mathbb {S}^{1}\rightarrow \mathbb {S}^{1})\), \(h\in Lip(\mathbb {S}^{1}\times \mathbb {S}^{1}\rightarrow \mathbb {R})\) and \(\delta \ge 0\), then there is \(\mu \in PM(\mathbb {S} ^{1}) \) such that
Proof
Let us consider the space of signed Borel measures \(SM(\mathbb {S}^{1})\). We consider two different norms on this space. \(||~||_{w},\) \(||~||_{s}\) defined by
and \(||\mu ||_{s}=\mu ^{+}(\mathbb {S}^{1})+\mu ^{-}(\mathbb {S}^{1})\) where \( \mu ^{\pm }\) are the positive and negative parts of \(\mu \) (the total variation norm). We apply Theorem 3 with \((SM(\mathbb {S} ^{1}),||~||_{w})\), \((SM(\mathbb {S}^{1}),||~||_{s})\) as a weak and strong space. We remark that by Prokhorov’s theorem, \(P_{w}\) is complete when considered with the \(||~||_{w}\) norm.
Now let us define a projection \(\pi _{n}\) as requested by Theorem 3. Let us consider \(n\in \mathbb {N}\) and divide \(\mathbb {S}^{1}\) into n equal intervals \(I_{1},...,I_{n},\) with \(I_{i}=[x_{i},x_{i+1})\). Let us consider a partition of unity \(\{\phi _{1},...,\phi _{n}\}\) made of continuous piecewise linear functions \(\phi _{i}\) which are affine on each interval of the partition, such that \(\phi _{i}(x_{i+1})=1\) and they are supported on \(I_{i \ {mod}(n)}\cup I_{i+1\ {mod}(n)}\) (hat functions). Let us consider the projection \(\pi _{n}:SM(\mathbb {S}^{1})\rightarrow SM( \mathbb {S}^{1})\) defined by
we have that this projection is linear, preserves probability measures, and \( ||\pi _{n}(\mu )||_{s}\le ||\mu ||_{s},\) \(||\pi _{n}(\mu )||_{w}\le ||\mu ||_{w}\) (the first inequality is straightforward, for the second see [21, Proposition 9.4] Proposition 9.4Footnote 5). Since, by the definition of \(\pi _{n}\), for each interval \(I_{n} \), the part of the measure \(\mu \) which is contained in \(I_{n}\) is transported to the endpoints of the interval \(\{x_{i},x_{i+1}\}\) and hence at a distance \(\le \frac{1}{n}\) we get (see [21, Proposition 9.4], proof of Proposition 9.5 for the details)
Each invariant probability measure \(\mu \) for each \(L_{\delta ,\mu }\) is such that \(||\mu ||_{s}\le 1\). The same can be said for the finite dimensional reduced operator \(\pi _{n}L_{\delta ,\pi _{n}\mu }\pi _{n},\) hence Exi1, Exi1.b are satisfied.
To verify Exi2 we have to verify that
we remark that since h is K Lipschitz, for all \(x\in \mathbb {S}^{1}\)
Hence
leading to 46.
We can then apply Theorem 3 leading to the existence of an invariant probability measure for \(\mathcal {L}_{\delta }\). \(\square \)
Remark 17
For simplicity the statement is proved for maps on \(\mathbb {S}^{1}\). It seems that the statement can be generalized with the same idea to maps on compact metric spaces for which there is a sequence of Lipschitz partitions of unity, which can be used to define suitable projections \(\pi _{n}\) on combinations of delta measures placed on some sequences of \(\epsilon -nets\) covering the space.
Remark 18
In the introduction we described this statement as a kind of Krilov-Bogoliubov theorem for mean field coupled maps. This similarity is restricted to the fact that we get a general statement about invariant measures and continuous maps. Our statement allows to find a fixed probability measure for the self-consistent transfer operator \(\mathcal {L} _{\delta }\) associated to the coupled system, and not an invariant measure for a continuous map on a compact metric space.
We remark that finding such a fixed probability measure for the self-consistent transfer operator \(\mathcal {L}_{\delta }\) associated to the system (which is a measure on \(\mathbb {S}^{1}\)) is not equivalent to the problem of finding invariant measures for the global system \((\mathcal {X}, \mathcal {T})\) associated to a network of coupled maps as defined in Sect. 2. These are measures on \((\mathbb {S}^{1})^{M}\) which could be equipped with the product \(\sigma -\)algebra. In this case the system \(( \mathcal {X},\mathcal {T})\) can also have invariant measures which are product of different measures on \(\mathbb {S}^{1}.\) For a trivial example let us think about the uncoupled system \((\mathbb {S}^{1},T,\delta ,h)\) where T is the doubling map and \(\delta =0\). In this case, an invariant measure is given by the product of the Lebesgue measure on some set of coordinates and the delta measure placed in 0 (which is a fixed point for T) in all the other coordinates.
7 Coupled Expanding Circle Maps
In this section we consider self-consistent operators modeling a network of all to all coupled expanding maps, we will prove the existence of an absolutely continuous invariant measure and exponential convergence to equilibrium for this kind of systems. Similar results appeared in [33] where the rigorous study of maps coupled by mean field interaction was started and in [7, 41] in a more general setting. We will also consider the zero-coupling limit and the related linear response. We show that the transfer operators in this limit satisfy the assumptions of our general theorems considering as a strong and weak spaces suitable Sobolev spaces \(W^{k,1}(\mathbb {S}^{1})\) of measures having a density whose k-th derivative is in \(L^{1}(\mathbb {S}^{1}).\)
Let \(k>1\) and \(T_{0}\in C^{k}(\mathbb {S}^{1},\mathbb {S}^{1})\) be a nonsingular mapFootnote 6 of the circle. Let us denote the transfer operator associated with \(T_{0}\) by \( L_{T_{0}}.\) We recall that the transfer operator associated with a map can be defined on signed measures by the pushforward of the map, however when the map is nonsingular, this operator preserves measures having a density with respect to the Lebesgue measure, \(L^{1}(\mathbb {S}^{1},\mathbb {R})\) and then with a small abuse of notation, identifying a measure \(\mu \) with its density \(h_{\mu }=\frac{d\mu }{dm}\) with respect to the Lebesgue measure m, the same operator can be also considered as \(L_{T_{0}}:L^{1}(\mathbb {S}^{1}, \mathbb {R})\rightarrow L^{1}(\mathbb {S}^{1},\mathbb {R})\). In this case, given any density \(\phi \in L^{1}(\mathbb {S}^{1},\mathbb {R})\) the action of the operator on the density can then be described by the explicit formula
Given \(h\in C^{k}(\mathbb {S}^{1}\times \mathbb {S}^{1},\mathbb {R}),\) \(\delta \ge 0\) and (a probability density) \(\psi \in L^{1}(\mathbb {S}^{1},\mathbb {R} )\), coherently with Sect. 2, we define \(\Phi _{\delta ,\psi }: \mathbb {S}^{1}\rightarrow \mathbb {S}^{1}\) as
We will always consider \(\delta \) small enough such that \(\Phi _{\delta ,\psi }\) is a diffeomorphism. Denote by \(Q_{\delta ,\psi }\) the transfer operator associated with \(\Phi _{\delta ,\psi },\)defined as
for any \(\phi \in L^{1}(S^{1},\mathbb {R})\).
We will consider expanding maps \(T_{0}:\mathbb {S}^{1}\rightarrow \mathbb {S} ^{1}\) satisfying the following assumptions:
-
(1)
\(T_{0}\in C^{6},\)
-
02
there is \(\alpha <1\) such that \(\forall x\in \mathbb {S}^{1}\), \( |T_{0}^{\prime }(x)|\ge \alpha ^{-1}>1\).
Definition 19
A set \(A_{M,L}\) of expanding maps is called a uniform family with parameters \(M\ge 0\) and \(L>1\) if it satisfies uniformly the expansiveness and regularity condition: \(\forall T\in A_{M,L}\)
It is well known that the transfer operator associated with a smooth expanding map has spectral gap and it is quasicompact when acting on suitable Sobolev spaces (see e.g. [27]). In the following we recall some particularly important related estimates we will use in this paper. We start by recalling the fact that such transfer operators satisfy some one step Lasota Yorke inequalities over these Sobolev spaces (see [15], Lemma 29 and its proof). This will be useful when applying the results of Sect. 4.
Lemma 20
Let \(A_{M,L}\) be a uniform family of expanding maps, the transfer operators \(L_{T}\) associated with a map \(T\in A_{M,L}\) satisfy a uniform Lasota-Yorke inequality on \(W^{k,1}(\mathbb {S}^{1})\): let \(\alpha :=L^{-1}<1\). For all \(1\le k\le 5\) there are, \(A_{k},~B_{k}\ge 0\) such that for all \(n\ge 0,\) \(T\in A_{M,L}\)
From this result, it is classically deduced that the transfer operator \( L_{T} \) of a \(C^{6}\) expanding map T is quasi-compact on each \( W^{k,1}(\mathbb {S}^{1}),\) with \(1\le k\le 5\). Furthermore, by the topological transitivity of expanding maps, 1 is the only eigenvalue on the unit circle and this implies the following result. (see [15] Proposition 30).
Proposition 21
For all \(T\in A_{M,L}\), there are \(C\ge 0\) and \(\rho \in (0,1)\) such that for all
with \(1\le k\le 5\) and \(n\ge 0\) it holds
In particular, the resolvent \(R(1,L):=(Id-L_{T})^{-1}=\sum _{i=0}^{\infty }L_{T}^{i}\) is a well-defined and bounded operator on \(V_{k}\).
Now we recall some estimates relative to small perturbations of expanding maps and their associated transfer operators. These will be useful to apply our general framework to self-consistent transfer operators representing a family of coupled expanding maps. The estimates will be useful to check that the assumptions of our general theorems are satisfied. We will again identify absolutely continuous measures with their densities and consider the spaces \(W^{3,1}(\mathbb {S}^{1})\),..., \(L^{1}(\mathbb {S}^{1})\) as strongest, strong and weak space.
Proposition 22
If \(L_{0}\) and \(L_{1}\) are transfer operators associated with expanding maps \(T_{0}\) and \(T_{1},\) then there is a \(C\in \mathbb {R}\) such that \(\forall k\in \{1,2,3\},~\forall f\in W^{k,1}\):
Proof
In the case \(k=1\) the proof of this statement can be found for example in [16], Proposition 26. When \(k=2\) we have to prove that
we have the well known formula (see [16] Equation 3) valid for \(\ i\in \{0,1\}\)
By (52) we have
Considering each summand and applying the statement for the case \(k=1\) we get
for some constant \(K_{1}\ge 0\). Similarly
for some constant \(K_{2}\ge 0\). Proving the statement. We remark that \( \left\| \frac{T_{0}^{\prime \prime }}{(T_{0}^{^{\prime }})^{2}} \right\| _{C^{1}}\) involves the third derivative of \(T_{0}.\)
When \(k=3\) we have to prove that
taking a further derivative in (52) for a transfer operator \( L_{1} \) we get
where
and
and the proof can be concluded as before. \(\square \)
Now we can prove that the self-consistent transfer operator associated with a family of coupled expanding maps has a regular invariant measure. We remark that since expanding maps are continuous, the mere existence for an invariant measure for these systems can be obtained by Proposition 16. In the following result we prove the existence in of such measure in a space of measures having a smooth density. Let us consider the expanding map \( T_{0} \) and denote with \(L_{T_{0}}\) its transfer operator, consider \( \delta \ge 0\) and a coupling function \(\ h\in C^{6}(\mathbb {S}^{1}\times \mathbb {S}^{1}\rightarrow \mathbb {R})\), consider the extended system \(( \mathbb {S}^{1},T_{0},\delta ,h)\) in which these maps are coupled by h as explained in Sect. 2 and the associated self-consistent transfer operator \(\mathcal {L}_{\delta }:L^{1}(\mathbb {S}^{1},\mathbb {R} )\rightarrow L^{1}(\mathbb {S}^{1},\mathbb {R})\)
as defined at (5). We show that this transfer operator has under suitable assumptions a fixed probability density in \(W^{5,1}\) which is unique when \(\delta \) is small enough.
Proposition 23
(Existence and uniqueness of the invariant measure). Let \(T_{0}\), h, \(\delta \) and \(\mathcal {L}_{\delta }\) as above. Suppose \(\delta \) is such that the set \(\underset{\phi \in P_{w}}{ \cup }\{\Phi _{\delta ,\phi }\circ T_{0}\}\subseteq A_{M,L}\) is contained in a uniform family of expanding maps with parameters M, L (see Definition 19). Then there is at least one probability density \(f_{\delta }\in W^{5,1}\) such that
For every such invariant measure, \(||f_{\delta }||_{W^{3,1}}\le C(M,L)\) (the \(W^{5,1}\) norm is bonded by a constant only depending on M and L).
Furthermore we have the uniqueness in the weak coupling regime. There is \( \overline{\delta }\) such that for each \(\delta \le \overline{\delta \text { }}\), \(\mathcal {L}_{\delta }\) has unique invariant measure in \(L^{1}\).
Before the proof of this proposition we need to collect some further preliminary result.
First we prove a one-step Lasota-Yorke inequality for the bounded variation norm for expanding maps. This result is surely known to the experts. We prove it for completeness.
Proposition 24
Let T be an expanding map of the circle. Let \(\phi \) a bounded variation density. Then
Proof
Let us suppose T of degree n and let us consider \(y_{1},...,y_{k}\in \mathbb {S}^{1}\). Suppose \(I_{i}=[y_{i},y_{i+1}]\) (where the indices are considered modulo k). Suppose \(T^{-1}(I_{i})=\cup _{1\le j\le n}J_{j,i}\) and denote \(J_{j,i}=[l_{j,i},r_{j,i}]\) (the left and right endpoints). Given a function \(\phi :\mathbb {S}^{1}\rightarrow \mathbb {R}\), let us denote by
We estimate \(Var(L_{T}[\phi ])\). We have \(Var(L_{T}[\phi ])\le \sum _{i=1}^{k}v(L[\phi ],I_{i})\).
We have that
The second summand can be bounded by remarking that by Lagrange theorem there is \(\xi _{j,i}\in J_{j,i}\) such that
Then
Finally we have
We remark that when the subdivision \(J_{j,i}\) is fine enough \( \sum _{i=1}^{k}\sum _{j=1}^{n}|\phi (r_{j,i})||r_{j,i}-l_{j,i}|\le 2\int _{ \mathbb {S}^{1}}\phi ~dm\) and \(\sum _{i=1}^{k}\sum _{j=1}^{n}v(\phi ,J_{j,i})\le Var(\phi )\). This leads directly to the result. \(\square \)
The following Lemma is about the nowadays well known statistical stability of expanding maps (see e.g. [16] Sects. 4 and 7.4. for more details).
Lemma 25
Given a uniform set of expanding maps \(A_{M,L}\), there is \( K\ge 1\) such that it holds
for all \(T_{1},T_{2}\in A_{M,L}\) having \(f_{1},f_{2}\in W^{5,1}\) as absolutely continuous invariant densities.
Now we estimate how the transfer operator \(Q_{\delta ,\psi }\) changes when changing \(\psi \). This will allow to apply Lemma 25 in the proof of Proposition 4.
Lemma 26
If \(T_{0},h\in C^{k}\) there are \(K_{1}\) \(\ge 1\) such that for all \(\psi ,\phi \in L^{1}\)
Proof
We have that \(\Phi _{\delta ,\psi }(x)=x+\pi (\delta \int _{\mathbb {S} ^{1}}h(x,y)\psi (y)dy)\) and \(\Phi _{\delta ,\phi }(x)=x+\pi (\delta \int _{ \mathbb {S}^{1}}h(x,y)\phi (y)dy)\), hence when \(\delta \) and \(||\psi -\phi ||_{L^{1}}\) are small enough
Considering the derivative with respect to x we get \(\Phi _{\delta ,\psi }^{\prime }(x)=1+\pi (\delta \int _{\mathbb {S}^{1}}\frac{\partial h(x,y)}{ \partial x}\psi (y)dy)\) and similarly for \(\Phi _{\delta ,\phi }(x)\). We have then
and
similarly, we get the same estimate for the further derivatives, proving the statement. \(\square \)
Now we are ready for the proof of Proposition 23.
Proof of Proposition 23
Now we consider the first part of the statement and the existence of an invariant measure in the stronger coupling case. The existence in \(L^{1}\) of a fixed probability measure for \(\mathcal {L}_{\delta }\) in this case follows from Theorem 3, applying it with \(B_{s}=BV[\mathbb {S} ^{1}]\) and \(B_{w}=L^{1}[\mathbb {S}^{1}]\) to the family of operators \( L_{\delta ,\mu }=Q_{\delta ,\mu }\circ L_{T_{0}}\). We now verify that the required assumptions hold.
The maps \(\Phi _{\delta ,\mu }\circ T_{0}\) involved in the system are a uniform family of expanding maps. By Proposition 24 the operators \( L_{\delta ,\mu }\) satisfy a common Lasota Yorke inequality on \(BV[\mathbb {S} ^{1}]\) and \(L^{1}[\mathbb {S}^{1}]\) and this gives a family of invariant measures for the operators \(L_{\delta ,\mu }\) which is uniformly bounded in in \(BV[\mathbb {S}^{1}]\) hence (Exi1) is verified in this case.
We now verify (Exi2) for the BV norm. Let \(f\in BV\), consider \( f_{\epsilon }\in W^{1,1}\) with \(||f_{\epsilon }||_{W^{1,1}}\le ||f||_{BV}+\epsilon \) and \(||f_{\epsilon }-f||_{L^{1}}\le \epsilon .\)
and since \(\epsilon \) is arbitrary, also (Exi2) is verified in this case.
Let \(\mathcal {P}_{n}\) be the partition subdividing the circle into n equal intervals. We can consider \(\pi _{n}:L^{1}(\mathbb {S}^{1})\rightarrow L^{1}( \mathbb {S}^{1})\) to be the Ulam discretization defined as \(\pi _{n}(f)= \mathbf {E}(f|\mathcal {P}_{n})\), where the conditional expectation is made using the Lebesgue measure, projecting to piecewise constant functions.
For the Ulam projection it is known that \(||\pi _{n}f-f||_{L^{1}}\le \frac{K }{n}||f||_{BV}\), \(||\pi _{n}||_{L^{1}\rightarrow L^{1}}\le 1\), \(||\pi _{n}||_{BV\rightarrow BV}\le 1\) (see [19] or the proof of [28, Lemma 4.1] e.g.) and then the discretized operators \(\pi _{n}L_{\delta ,\mu }\pi _{n}\) satisfy a uniform Lasota Yorke inequality on BV and \(L^{1}\) (see e.g. [16], Section 9.3). By this the assumption Exi1.b is satisfied. We can then apply Theorem 3, and get the existence of an invariant probability density f in BV. Since \(T_{0},h\) \(\in C^{6}\) and \(L_{\delta ,f}f=f\) we get that \(f\in W^{5,1}\) and its norm can be uniformly estimated by the uniform Lasota Yorke inequality on \(W^{5,1}\) and \(W^{4,1}\) and then on \(W^{4,1}\) and \(W^{3,1}\) and so on, satisfied uniformly by all the transfer operators related to the family of maps \( A_{M,L}.\)
For the second part of the statement (the weak coupling case) we apply Theorem 4 with \(B_{s}=W^{1,1}[\mathbb {S}^{1}]\) and \( B_{w}=L^{1}[\mathbb {S}^{1}].\)
By Lemmas 26 and 20 when \(\delta \) is small enough all the operators in the family \(L_{\delta ,\mu }\) with \(\mu \in P_{w}\) are the transfer operators associated with a uniform family of expanding maps and satisfy a uniform Lasota Yorke inequality on \(W^{1,1}\) and \(L^{1},\) by this each one of these operators has a unique invariant probability measure in \(W^{1,1}\) with uniformly bounded norm and (Exi1) is verified.
By Lemma 26 and Proposition 22 we get
verifying (Exi2) in this case.
By Lemmas 25, and 26 also (Exi3) is verified. Then we can apply Theorem 4 to get the existence and uniqueness for small \(\delta \). \(\square \)
The following statement is an estimate for the speed of convergence to equilibrium of mean field coupled expanding maps (see [33], Theorem 4 or [41] Theorem 1.1 for similar statements).
Proposition 27
(Exponential convergence to equilibrium). Let \(\mathcal {L}_{\delta }\) be the family of self-consistent transfer operators arising from \(T_{0}\in C^{6}\) and \(h\in C^{6}\) as above. Let \(f_{\delta }\in W^{1,1}\) be an invariant probability density of \( \mathcal {L}_{\delta }.\) Then there exists \(\overline{\delta }>0\) and \( C,\gamma \ge 0\) such that for all \(0<\delta <\overline{\delta }\), and each probability density \(\nu \in W^{1,1}\) we have
Proof
The proof is an application of Theorem 6, considering \( B_{ss}=W^{2,1},\) \(B_{s}=W^{1,1},\) \(B_{w}=L^{1}\). Let \(L_{\delta f}\) be the family of transfer operators associated with this system.
By the Lasota Yorke inequalities (Lemma 20) we have that the operators \(L_{\delta ,\mu }:W^{2,1}\rightarrow W^{2,1},~L_{\delta ,\mu }:W^{1,1}\rightarrow W^{1,1},\) \(L_{\delta ,\mu }:L^{1}\rightarrow L^{1}\) with \(\mu \in P_{w}\) are bounded uniformly for \(\delta \) small enough. By Lemma 20 they satisfy (Con1). Furthermore by Lemma 26 and Proposition 22 they satisfy (Con2).
By Proposition 23 the invariant measures \(f_{\delta }\) satisfy \(\lim _{\delta \rightarrow 0}||f_{\delta }||_{W^{2,1}}<+\infty .\) Since the circle expanding map \(T_{0}\) has convergence to equilibrium then (Con3) is satisfied. We can then apply Theorem 6 directly implying the statement. \(\square \)
To get some useful formula for the linear response for expanding maps coupled in a mean field regime, let us now consider small perturbations of expanding maps \(T:\mathbb {S}^{1}\rightarrow \mathbb {S}^{1}\) by left composition with a family of diffeomorphisms \((D_{\delta })_{\delta \in [-\epsilon ,\epsilon ]}\). More precisely, let \(D_{\delta }:\mathbb {S}^{1}\rightarrow \mathbb {S}^{1}\) be a diffeomorphism, with
and \(S\in C^{6}(\mathbb {S}^{1},\mathbb {R})\). In this setting let us define the perturbed transfer operators as
(remark that here \(L_{0}=L_{T}\) ). These kinds of perturbations are of the type induced by a mean field coupling, they satisfy the “small perturbation” and “existence of a derivative operator” assumptions of our general theorems like (Con2) or (LR2) of Theorem 14. We have indeed (see [15, Proposition 35, 36]):
Proposition 28
Let \((D_{\delta })_{\delta \in [0, \overline{\delta }]}\) be as in (57), and \(T:\mathbb {S} ^{1}\rightarrow \mathbb {S}^{1}\) be a \(C^{6}\) uniformly expanding map. Let us define \(\dot{L}:W^{4,1}(\mathbb {S}^{1})\rightarrow W^{3,1}(\mathbb {S}^{1})\) by
Then one has that for all \(1\le k\le 4\) and \(f\in W^{k,1}\)
We have now all the ingredients to prove a result regarding the Linear Response of the coupled system in the small coupling regime.
Proposition 29
(Linear Response for coupled expanding maps (zero coupling limit)). Consider the family of self-consistent transfer operators \(\mathcal {L}_{\delta }\) associated with a \(C^{6}\) expanding map T and a coupling driven by the function \(\ h\), with \(h\in C^{6}\). Let \(h_{0}\) be the unique invariant probability measure in \(L^{1}\) for \(\mathcal {L}_{0}\) and \(h_{\delta }\) some invariant probability measure for \(\mathcal {L} _{\delta }\). Then for \(\delta \rightarrow 0\) we have the following Linear Response formula
Proof
The proof is a direct application of Theorem 14 to our case with \(B_{ss}=W^{3,1}(\mathbb {S}^{1})\subset B_{s}=W^{2,1}(\mathbb {S} ^{1})\subset B_{w}=W^{1,1}(\mathbb {S}^{1}).\) Let us we see why the assumptions needed to apply the theorem are satisfied. We recall that the transfer operators \(\mathcal {L}_{\delta }:W^{3,1}(\mathbb {S}^{1})\rightarrow W^{3,1}(\mathbb {S}^{1})\) involved are defined by
The assumption (SS1) (regularity bounds), is implied by Proposition 23. The assumption (SS2) (convergence to equilibrium for the unperturbed operator), is well known to be verified, as it stands for the unperturbed transfer operator \(\mathcal {L}_{0}\) which is the transfer operator associated with a smooth expanding map. The assumption (LR1) regarding the existence of the resolvent of the unperturbed operator on the weak space \(W^{1,1}\) follows from Proposition 21.
As \(\mathcal {L}_{\delta }\) is a small perturbation of \(\mathcal {L}_{0}\) given by the composition of the transfer operator \(Q_{\delta ,\phi }\) associated with a diffeomorphism near to the identity, the assumption (SS3) and the first part of (LR2) (small perturbation) follows from Proposition 28, Proposition 22 and Lemma 26 as before. Let us prove indeed that there is \(K\ge 0\) such that and \( \mathcal {L}_{0}-\mathcal {L}_{\delta }\) is \(K\delta \)-Lipschitz when considered as a function \(\overline{B}_{2M}\rightarrow B_{w}\) and \( B_{2M}\rightarrow B_{s}\). In the first case we have to prove that for \(\phi _{1},\phi _{2}\in W^{2,1}\)
Developing the formula we get
and
by applying Lemma 26 with \(\psi =0\) and \(\phi =\phi _{1}\) and Proposition 22. The other term can be estimated as
using Proposition 22 and Lemma 26 and proving the Lipschitz assumption in the \(\ \overline{B}_{2M}\rightarrow B_{w}\) case. The case \(B_{2M}\rightarrow B_{s}\) is similar.
The assumption (LR2) on the derivative operator follows from Proposition 28. Let us apply it and find an expression for \( \mathcal {\dot{L}}{h_{0}}\) in our case. In this case the perturbing operator to be considered is \(Q_{\delta ,h_{0}}\) associated with the diffeomorphism \( \Phi _{\delta ,h_{0}}.\) With the notation (57) we have \(D_{\delta }=\Phi _{\delta ,h_{0}}=Id+\delta S\) with
and then
Applying Theorem 14, we then get
as in our case \(W^{1,1}\) is the weak space Substituting (62) in (63) we get (60). \(\square \)
Remark 30
From (40) we see that this response result with convergence in the quite strong topology \(W^{1,1}\) gives information on the behavior of a large class of observables, for example we can consider observables in \(L^{\infty }\) or \(L^{1}\) or even distributions in the dual of \(W^{1,1}\).
8 Maps with Additive Noise on \(\mathbb {S}^{1}\)
We illustrate the flexibility of our approach with an application to systems of coupled random maps. For simplicity we will consider a class of random dynamical systems on the unit circle \(\mathbb {S}^{1}\). Informally speaking, a random dynamics on \(\mathbb {S}^{1}\) is defined by the iteration of maps chosen randomly in the family \(T_{\omega }:\mathbb {S}^{1}\rightarrow \mathbb {S}^{1}\), \(\omega \in \Omega \) according to a certain probability distribution p defined on \(\Omega \). In our case we will model this random choice as independent and identically distributed at each time.
Let \(T_{0}\):\(~\mathbb {S}^{1}\rightarrow \mathbb {S}^{1}\) a continuous and piecewise \(C^{1},\) nonsingular mapFootnote 7. We consider a random dynamical system, corresponding to the stochastic process \((X_{n})_{n\in \mathbb {N}}\) defined by
where \((\Omega _{n})_{n\in \mathbb {N}}\) are i.i.d random variables distributed according to some smooth kernel \(\rho .\) We will call \(T_{0}\) the deterministic part of the system and \(\rho \) the noise kernel of the system.
Remark 31
We remark that the maps considered here are quite general. We do not require expansiveness or hyperbolicity, allowing many examples of random maps coming as models of natural phenomena (see e.g. [9, 20, 36]).
We will consider the annealed transfer operators associated with these systems (see [47], Sect. 5 for more details about transfer operators associated with this kind of systems or [15]). Let \(SM( \mathbb {S}^{1})\) be the space of signed Borel measures in \(\mathbb {S}^{1}\). The annealed transfer operator \(L:SM(\mathbb {S}^{1})\rightarrow SM(\mathbb {S} ^{1})\) associated with the random system is defined by
where \(L_{T_{\omega }}(\mu ):SM(\mathbb {S}^{1})\rightarrow SM(\mathbb {S} ^{1}) \) is the transfer operator associated with \(T_{\omega }\), hence taking the average of the pushforward maps with respect to p. For some class of random dynamical systems L is defined as an operator \(:L^{1}(\mathbb {S} ^{1})\rightarrow L^{1}(\mathbb {S}^{1})\) and sometime this operator is a kernel operator: let \(k\in L^{\infty }(\mathbb {S}^{1}\times \mathbb {S} ^{1})\) (the kernel), consider the operator L defined in the following way: for \(f\in L^{1}(\mathbb {S}^{1})\)
This kind of operators naturally appear when the random dynamics is defined by the action of a deterministic map and some additive noise Since the effect of the additive noise is to perturb the deterministic map by a translation, the annealed transfer operator will be an average of translations, i.e. a convolution. The well known regularization properties of convolutions then imply that the annealed transfer operator associated with a system with additive noise is a regularizing one.
Let us consider a probability density \(\rho :\) \(\mathbb {R}\rightarrow \mathbb {R}\) representing how the noise is distributed. For simplicity we will suppose \(\rho \) being such that \(\rho (x)=\rho (-x)\) for all \(x\in \mathbb {R}\) and being a Schwartz function, hence \(\rho \in C^{k}\) for all \( k\ge 1\). The periodization \(\tilde{\rho }:\mathbb {S}^{1}\rightarrow \mathbb {R}\) of such a function is defined as
which clearly converge for a rapidly decreasing function as \(\rho \).
Definition 32
Let \(f\in L^{1}(\mathbb {S}^{1})\) and \(\rho \) as before. We define the convolution \(\rho *f\) by
To a system with additive noise as defined in (64) we then associate the annealed transfer operator \(L:L^{1}\rightarrow L^{1}\) defined by
for all \(\phi \in L^{1},\) where \(L_{T_{0}}\) is the transfer operator associated with the deterministic map \(T_{0}\).
We now define the self-consistent transfer operator associated with an infinite collection of interacting random maps in a mean field coupling. Like in the deterministic case let us consider \(h\in C^{k}(\mathbb {S} ^{1}\times \mathbb {S}^{1},\mathbb {R}),\) \(\delta \ge 0\), for some \(k\ge 1\) and a probability density \(\psi \in L^{1}\). Define \(\Phi _{\delta ,\psi }: \mathbb {S}^{1}\rightarrow \mathbb {S}^{1}\) again as
Denote by \(Q_{\delta ,\psi }\) the transfer operator associated with \(\Phi _{\delta ,\psi },\) as in (47). We consider the following family of operators depending on a probability density \(\phi \in L^{1}\) and \(\delta \ge 0\) defined as
Finally we define the nonlinear self-consistent transfer operator associated with this system of coupled random maps by
This represents the idea that a certain initial condition is first moved by the deterministic part of the dynamics represented by the map \(T_{0}\) and by the mean field perturbation \(\Phi _{\delta ,\phi }\), then a further (external and independent of the dynamics) random perturbation is applied by the noise. In the remaining part of the section we will apply our general theory to this kind of operators.
The following proposition contains some of the regularization properties for the convolution we need (see [15] Proposition 15 for the proof and details).
Proposition 33
Let \(f\in L^{1}\) and \(\rho \) be as before. The convolution \(\rho *f\) has the following properties:
-
(1)
For all \(k\ge 1\), \(\rho *f:\mathbb {S}^{1}\rightarrow \mathbb {R}\) is \(C^{k}\), and \((\rho *f)^{(i)}=\rho ^{(i)}*f\) for any \(i\le k\).
-
(2)
One has the following regularization inequality:
$$\begin{aligned} \Vert \rho *f\Vert _{C^{k}}\le \Vert \rho \Vert _{C^{k}}\Vert f\Vert _{L^{1}}. \end{aligned}$$(71)
These regularization properties together with the Ascoli Arzela theory imply that a linear operator \(L_{0}:L^{1}\rightarrow L^{1}\) of the kind
is a compact operator. If we suppose that the system satisfy a convergence to equilibrium assumption, this will allow to obtain the spectral gap and the existence of the resolvent operators, required to apply Theorem 14.
Proposition 34
Let \(L_{0}\) be the annealed transfer operator associated with a map \(T_{0}\) with additive noise distributed with a kernel \(\rho \) as in (72). Consider \(m\ge 1\) and suppose that for all \(g\in C^{m}\) such that \(\int g~dm=0\)
Then for all \(k\ge 1,\) \((Id-L_{0})^{-1}:=\sum _{i=0}^{\infty }L_{0}^{i}\) is a bounded operator \(C^{k}\rightarrow C^{k}\).
Proof
(73) and (71) impliy that \(\lim _{n\rightarrow \infty }\Vert L_{0}^{n}g\Vert _{C^{k}}=0\) for all \(g\in L^{1}\) such that \(\int g~dm=0\) and then some iterate of the transfer operator is a uniform contraction on the space of \(C^{k}\) densities with zero average. By this the operator has a spectral gap, implying the existence of the resolvent operator (see for the details [15], section IV). \(\square \)
By [15, proposition 18 and 19] and their simple proof the lemma below directly follows
Lemma 35
Let us consider transfer operators \(L_{0},\) \(L_{1}\) associated with dynamical systems with additive noise having noise kernel \( \rho \), deterministic part given by continuous maps \(T_{0}\) and \(T_{1}\) and \( k\ge 0.\) Then there is \(C\ge 0\) such that for all such \(T_{0},\) \(T_{1}\) and \(f\in L^{1}\)
We state a result analogous to Proposition 23 in the case of systems with additive noise. The application to this case is simpler due to the regularizing effect of the noise.
Proposition 36
Suppose \(T_{0}\) is \(~\mathbb {S}^{1}\rightarrow \mathbb {S}^{1}\) continuous, nonsingular and piecewise \(C^{1}.\) Suppose \(h\in C^{1}\), let \(\mathcal {L}_{\delta }\) be the self-consistent family of operators associated with this coupled system as defined in (70), then for all \(\delta \ge 0\) there is \(f_{\delta }\in C^{\infty }\) such that for all \(k\ge 1\)
and
Let us suppose that the (linear) operator \(\mathcal {L}_{0}\) has convergence to equilibrium when considered as acting on the spaces \(C^{1}\) and \(L^{1}\) (see (73)) then there is \(\overline{\delta }>0\) such that for all \(\delta \in [0,\overline{\delta }],\)\(f_{\delta }\) is unique.
Proof
We sketch the proof, whose arguments are similar to the ones of Proposition 23. We will obtain the statement applying Theorems 3 and 4 to the family of operators
as defined in (69). First we will apply Theorem with \(B_{s}=BV\) and \(B_{w}=L^{1}\). We remark that given \(k\ge 1,\) (71) implies a Lasota Yorke inequality which is uniformly satisfied by these operators, indeed
This implies that the transfer operators in the family are uniformly bounded as operators \(L^{1}\rightarrow C^{k}\) and hence each invariant probability measure \(f_{\delta ,\phi }\) of \(L_{\delta ,\phi }\) is such that \(||f_{\delta ,\phi }||_{BV}\le ||f_{\delta ,\phi }||_{C^{k}}\le ||\rho ||_{C^{k}}\) and then the family of operators satisfy (Exi1).
The assumption (Exi2) (or (12)) is provided similarly as a consequence of the Lemma 26 and Lemma 35.
In order to apply Theorem 3 we consider a suitable projection \(\pi _{n}\). As in the proof of Proposition 23, let \(\mathcal { P}_{n}\) be the partition subdividing the circle into n equal intervals. Consider \(\pi _{n}\) defined as in the proof of Proposition 23 by \(\pi _{n}(f)=\mathbf {E}(f|\mathcal {P}_{n})\), where the conditional expectation is made using the Lebesgue measure, projecting to piecewise constant functions. Again, the discretized operators satisfy a uniform Lasota Yorke inequality on BV and \(L^{1}\), indeed
and Exi1.b is satisfied. We can then apply Theorem 3, and get the existence of an invariant probability density f in BV. Since \( \rho \) \(\in C^{k}\) and \(L_{\delta ,f}f=f\) we get that \(f\in C^{k}\) for all \( k\ge 1\), also proving (74).
Now we apply Theorem 4 to get the uniqueness. In this case we consider \(B_{s}=C^{1}\) and \(B_{w}=L^{1}\). We first have to prove that for \( \delta \) small enough each operator \(L_{\delta ,\phi }\) with \(\phi \in P_{w}\) ha a unique invariant probability measure in \(P_{w}.\) Since \(L_{0}\) has convergence to equilibrium, is regularizing and \(C^{1}\) is compactly immersed in \(L^{1}\) it is standard to find that this operator has a unique invariant probability measure. From the convergence to equilibrium, the small perturbation assumption (Exi2) we verified above and the regularization property (71) we get that there is \(\gamma \ge 0\) such that \(L_{\delta ,\phi }\) has convergence to equilibrium for all \(\delta \le \gamma \) and \(\phi \in P_{w}\). Indeed let us consider \(f\in V_{s}\) and suppose that by convergence to equilibrium n is such that \( ||L_{0}^{n}f||_{L^{1}}\le \frac{1}{2||\rho ||_{C^{1}}}||f||_{C^{1}}\) then
This implies that \(L_{0}^{n+1}\) is a contraction of \(V_{s}\). Now let us consider \(\phi \in P_{w},\) \(\gamma \le \frac{1}{4||\rho ||_{C^{1}}K(C+nB)}\) and \(\delta \le \gamma .\) By a computation similar to the proof of Lemma 8 (remark that \(Q=1\) in the case \(B_{w}=L^{1}\) and by (75), \(\lambda =0\)) we can get
and then \(||L_{\delta ,\phi }^{n}g||_{L^{1}}\le \frac{3}{4||\rho ||_{C^{1}}} ||g||_{C^{1}}\), thus repeating the same reasoning as before \(L_{\delta ,\phi }^{n+1}\) also is a contraction of \(V_{s}\). Hence we have that when \(\delta \) is small enough each \(L_{\delta ,\phi }\) has convergence to equilibrium. It follow that \(L_{\delta ,\phi }\) also has spectral gap on \(C^{1}\) and on \( L^{1}\) Indeed for all \(f\in V_{L^{1}}:=\{f\in L^{1},\int f=0\}\) we get \( ||L_{\delta ,\phi }f||_{C^{1}}\le ||\rho ||_{C^{1}}||f||_{L^{1}}\) and if we have if n is such that \(||L_{\delta ,\phi }^{n}f||_{L^{1}}\le \frac{3}{ 4||\rho ||_{C^{1}}}||f||_{C^{1}}\) then again
Thus each \(L_{\delta ,\phi }\) has a unique invariant probability measure \( f_{\phi }\in P_{w}\). Furthermore, the resolvent of \(L_{\delta ,\phi }\) is defined on \(V_{L^{1}}\)and its norm uniformly bounded for every \(\phi \in P_{w}\).
Now we can prove that (Exi3) holds. Let us consider probability measures \( \phi _{1}\) and \(\phi _{2}\in P_{w}\) and the operators \(L_{\delta ,\phi _{1}}\) \(L_{\delta ,\phi _{2}}\) we have seen that when \(\delta \le \gamma \) these operators have unique fixed probability densities \(f_{\phi _{1}},f_{\phi _{2}}\). We want to prove that
We hence apply a construction similar to the proof of Theorem to the family of operators \(\hat{L}_{\epsilon }:L^{1}\rightarrow L^{1}\) defined by
Consider
We have that
By the fact that \((Id-L_{\delta ,\phi _{2}})^{-1}\) is well defined and continuous on \(V_{L^{1}}\) remarked before and by the fact that \(||f_{\phi _{1}}||_{C^{1}}\le ||\rho ||_{C^{1}}\) and (Exi2) we get
and then (Exi3) is verified. Applying Theorem 4 we then get the uniqueness for \(\delta \) small enough. \(\square \)
Proposition 37
(Exponential convergence to equilibrium). Let \(\mathcal {L}_{\delta }\) be the family of self-consistent transfer operators arising from a map \(T_{0}\), a kernel \(\rho \) as above, and \(h\in C^{k}\) with \(k\ge 1\). Suppose the uncoupled system \(\mathcal {L} _{0}\) has convergence to equilibrium. Let \(f_{\delta }\) be an invariant probability measure of \(\mathcal {L}_{\delta }.\) Then there exists \(\overline{ \delta }>0\) and \(C,\gamma \ge 0\) such that for all \(0<\delta <\overline{ \delta }\) and each probability density \(\nu \in C^{k}\) we have
Proof
Again the proof is a direct application of Theorem 6 to \(\mathcal {L }_{\delta }\) considering the spaces \(B_{ss}=C^{k+1},B_{s}=C^{k}\) and \( B_{w}=L^{1}\). The assumption (Con1) for this kind of systems is already verified in (75). The assumption (Con2) is as a direct consequence of Lemmas 26 and 35. The assumption (Con3) is required as an assumption in this statement. \(\square \)
Let us now consider a linear response result for the invariant measure of \( \mathcal {L}_{\delta }\) when \(\delta \rightarrow 0\) in the case of coupled maps with additive noise.
Proposition 38
(Linear Response for coupled maps with additive noise). Let \(\mathcal {L}_{\delta }\) be the family of self-consistent transfer operators arising from a map \(T_{0}\), a kernel \( \rho \) and h as above. Suppose the uncoupled initial transfer operator \( \mathcal {L}_{0}\) has convergence to equilibrium in the sense of (73). Let \(f_{0}\in C^{k}\) be the unique invariant probability density of \(L_{0}\) and \(f_{\delta }\in C^{k}\) be the invariant probability density of \(L_{\delta }\) (unique when \(\delta \) is small enough). Then we have the following Linear Response formula
Before the proof, we recall some preliminary result on the response of systems with additive noise. We now consider small perturbations of our random maps with additive noise by composition with a map \(D_{\delta }\), which is when \(\delta \) is small, a diffeomorphism near to the identity. Consider a map \(S\in C^{2}(\mathbb {S}^{1},\mathbb {R})\) and the map \( D_{\delta }:\mathbb {S}^{1}\rightarrow \mathbb {S}^{1}\) defined by \(D_{\delta }=Id+\delta S\). Let us consider then the perturbation of \(T_{0}\) by composition with \(D_{\delta }\) defined by \(T_{\delta }=T_{0}\circ D_{\delta }.\) Starting from this family of maps and a kernel \(\rho \) we can consider a family of dynamical systems with additive noise as in (64 ). Since \(L_{T_{\delta }}=L_{D_{\delta }}\circ L_{T_{0}}\), to this system we associate the annealed transfer operator defined by
Now, in order to apply our general theorems it will be useful to consider the derivative operator \(\dot{L}\) for the family of operators \((L_{D_{\delta }\circ T_{0}})_{\delta \in [0,\overline{\delta }]}\). In this direction, the following result ( [15, Theorem 24]) gives some useful estimates.
Proposition 39
Let \((L_{\delta })_{\delta \in [0, \overline{\delta }]}\) be the family of transfer operators as described in (80). For all \(k\ge 2\)
where \(\dot{L}:C^{k}(\mathbb {S}^{1})\rightarrow C^{k-1}(\mathbb {S}^{1})\) is defined by:
Proof of Proposition 38
Similar to the proof of Proposition 29, the proof is a direct application of Theorem 14. We apply Theorem 14 to the family of operators \(\mathcal {L}_{\delta }(\phi )=\rho *[Q_{\delta ,\phi }(L_{T_{0}}(\phi ))]\) considering the spaces \( B_{ss}=C^{k+2}(\mathbb {S}^{1})\subseteq B_{s}=C^{k+1}(\mathbb {S}^{1})\subset B_{w}=C^{k}(\mathbb {S}^{1}).\) Let us now verify that the assumptions needed to apply the theorem are satisfied. The assumption (SS1) (regularity bounds), is implied by Proposition 36.
The assumption (SS2)(convergence to equilibrium for the unperturbed operator), is supposed to hold. The assumption (SS3) and the first part of the assumption (LR2) (small perturbation) follows from Lemma 26 and 35. Indeed we have to prove that there is \(K\ge 0\) such that \(\mathcal {L}_{0}-\mathcal {L}_{\delta }\) is \(K\delta \)-Lipschitz when considered as a function \(\overline{B}_{2M}\rightarrow B_{w}\) and \( B_{2M}\rightarrow B_{s}\). In the first case we have to prove that for \(\phi _{1},\phi _{2}\in \{\phi \in C^{k+1},||\phi ||_{C^{k+1}}\le 2M\}\)
We have
and
applying Lemma 26 with \(\psi =0\) and \(\phi =\phi _{1}\) and Lemma 35.
Furthermore
In the second case we have to prove that for \(\phi _{1},\phi _{2}\in \{\phi \in C^{k+2},||\phi ||_{C^{k+2}}\le 2M\}\)
which can be proved similarly as before.
The assumption (LR1) (resolvent of the unperturbed operator) follows from Proposition 34. The second part of assumption (LR2) (derivative operator) follows from Proposition 39 in a way similar to what is done in the proof of Proposition 29. Applying Theorem 14, we then get
We can now let the formula be more explicit by finding an expression for \( \mathcal {\dot{L}}.\) In our case
and then
\(\square \)
Remark 40
The convergence to equilibrium assumption (73) required in Proposition 37 and Proposition 38 for the uncoupled transfer operator \(\mathcal {L}_{0}\) is easy to be verified in many examples of systems whose deterministic part has some kind of topological mixing and the noise is distributed by a smooth kernel or it has large support in some sense, see [29, Corollary 5.7.1], [22, Lemma 41] or [1, Remarks 2.3 and 6.4]. In more complicated situations it can be also verified by computer aided estimates ([20]).
Remark 41
We remark that another meaningful definition for the transfer operator associated with a family of random maps coupled in by their mean field could be the following
In this case one applies the coupling directly to the annealed transfer operator of the random maps. Here for small \(\delta \) the application of our theory seems to be possible by estimates similar to the ones shown in this section and in Sect. 7. Indeed the transfer operator realizing the coupling \(Q_{\delta ,\phi }\) is applied after the convolution. Considering \(\phi \in L^{1}\), by (71) we get that \((\rho *L_{T_{0}}(\phi ))\) is regularized to the regularity of the kernel \(\rho \). If h is smooth enough and \(\delta \) small enough, this regularity is preserved by the application of \(Q_{\delta ,\phi }\) leading to the verification of regularity properties like Exi1, Exi1.b, Con1 and SS1.
The verification of small perturbation properties like Exi2, Con2, SS3 and LR2 for the family of transfer operators associated with (82) \(L_{\delta ,\phi }=Q_{\delta ,\phi }(\rho *L_{T_{0}})\) relies on the estimation of the distance of \(Q_{\delta ,\phi _{1}}\) from \(Q_{\delta ,\phi _{2}}\) on a mixed norm which can be done in a way similar to the use of Lemmas 22 and Lemma 26 as done in Sect. 7 . The form of the derivative operator \(\dot{L}\) is probably similar to the one given at Proposition 28.
9 Self-Consistent Operators not Coming from Coupled Map Networks
In this section we consider a class of self-consistent transfer operators not coming from networks of coupled maps, giving other examples of application of our general theory. The systems considered are inspired to some examples studied in [5, 44], where we have a map whose slope depends on the average of a certain observable during the iterates. We add noise to simplify the functional analytic properties of the system. Let us consider again a family of random maps on [0, 1] depending on a probability measure \(\mu \) and on a parameter \(\delta \ge 0.\)
Let us consider the classical tent map \(T:[0,1]\rightarrow [0,1]\), defined by \(T(x)=\min (2x,2-2x)\), the family of maps \(T_{\delta ,\mu }:[0,1]\rightarrow [0,1]\) we consider as a self-consistent perturbation of the tent map are defined by
Then adding a noise-like perturbation to the map \(T_{\delta ,\mu }\) we consider the process \((X_{n})_{n\in \mathbb {N}}\) defined on [0, 1] by
where \((\Omega _{n})_{n\in \mathbb {N}}\) are i.i.d random variables distributed according to a kernel \(\rho \in Lip(\mathbb {R}),\) supported on \( [-1,1]\) with Lipschitz constant L and where \(\hat{+}\) is the “boundary reflecting” sum, defined by \(a\hat{+}b:=\pi (a+b)\) , and \(\pi :\mathbb {R}\rightarrow [0,1]\) is the piecewise linear map \( \pi (x)=\min _{i\in \mathbb {Z}}|x-2i|\). This is a model of a system on [0, 1] with reflecting boundary conditions. When the noise sends a point outside the space [0, 1] the projection \(\pi \) is applied to let the image of the map again in [0, 1]. Let us denote as \(L_{\pi }\) the transfer operator \(L_{\pi }:L^{1}(\mathbb {R})\rightarrow L^{1}([0,1])\) associated with the map \(\pi .\) Let \(b\in \mathbb {R}\) and \(g\in Lip(\mathbb {R})\) consider the translation operator \(\tau _{b}\) defined by \((\tau _{b}~g)(y):=g(y+b)\).
The annealed transfer operator associated with the random dynamical system (83) is a Markov operator and is given by the following kernel operator (for details see [1], Section 6):
where
and \(x,y\in [0,1]\). Since the perturbation induced on the system with additive noise by increasing the parameter \(\delta \) is not coming from the composition with a diffeomorphism we cannot use the estimates from the previous sections directly. We hence take a slightly different point of view on systems with additive noise, and related basic estimates which were developed in [1].
In this case we will consider \(B_{w}=L^{2}[0,1].\) Let \(P_{w}\) be the set of measures having a probability density in \(L^{2}\). The nonlinear self-consistent operator we consider in this case hence is given by \( \mathcal {L}_{\delta }:P_{w}\rightarrow P_{w}\) defined as
for all \(\mu \in P_{w}.\) We remark that since \(\rho \in Lip(\mathbb {R})\) and it is supported on \([-1,1]\) the kernel of this operator is bounded: \( k_{\delta ,\mu }\in L^{\infty }([0,1]^{2})\). Let us recall some classical and useful facts about kernel operators.
-
If \(k_{\delta ,\mu }\in L^{\infty }([0,1]^{2})\), then
$$\begin{aligned} ||L_{\delta ,\mu }f||_{\infty }\le ||k_{\delta ,\mu }||_{L^{\infty }([0,1]^{2})}||f||_{1} \end{aligned}$$(87)and the operator \(L_{\delta ,\mu }:L^{1}\rightarrow L^{\infty }\) is bounded. Furthermore, \(\Vert L_{\delta ,\mu }\Vert _{L^{p}\rightarrow L^{\infty }}\le \Vert k_{\delta ,\mu }\Vert _{L^{\infty }([0,1]^{2})}\) for \(1\le p\le \infty \).
-
The operator \(L_{\delta ,\mu }:L^{2}\rightarrow L^{2}\) is compact and
$$\begin{aligned} ||L_{\delta ,\mu }f||_{2}\le ||k_{\delta ,\mu }||_{L^{2}([0,1]^{2})}||f||_{2} \end{aligned}$$(88)
It is also well known that these Markov operators have invariant probability densities in \(L^{2}\) (see e.g. [1, Theorem 2.2]). Since \(k_{\delta ,\mu }\in L^{\infty }([0,1]^{2}),\) by (87) we also have that any invariant probability density \(f_{\delta ,\mu }\) for this operator satisfies
In [1, Section 6] the following estimates are proved for such kernel operators coming from maps with additive noise and reflecting boundaries conditions (see Proposition 6.2):
Proposition 42
Assume that \(k_{\delta ,\mu }\) is the kernel associated to the transfer operator of a system with additive noise and reflecting boundaries composed by a map \(T_{\delta ,\mu }\) and a noise kernel \(\rho \) (see (85)). Let us fix \(\delta ,\) suppose that the family of interval maps \(\{T_{\epsilon }\}_{\epsilon \in [0,\overline{ \epsilon })}\) satisfies
where \(\dot{T},~T_{\epsilon }\in L^{2}\) and \(\Vert T_{\epsilon }\Vert _{2}=o(\epsilon )\). Consider the transfer operator \(L_{0}\) associated with the unperturbed system with map \(T_{0}\) and kernel \(\rho \). Let \( L_{\epsilon }\) be the transfer operator associated with the system driven by \(T_{\epsilon }\) and kernel \(\rho \). Then there are \(\overline{\epsilon } ,K\ge 0\) such that for \(\epsilon \in [0,\overline{\epsilon })\)
and \(\forall f_{0}\in L^{2}\)
with convergence in \(L^{2}.\)
The inequality (91) shows that the perturbations we are interested in applying to the transfer operators associated with this kind of systems are small perturbations in the \(L^{2}\rightarrow L^{2}\) topology. We will then consider the transfer operators associated with this kind of systems as operators acting on \(L^{2}[0,1]\) and in this subsection we will apply our general statements with the choice \(B_{ss}=B_{s}=B_{w}=L^{2}[0,1].\) We now can apply Theorem 4 and prove
Proposition 43
Let \(\mathcal {L}_{\delta }\) be the self-consistent transfer operator associated to \(T_{\delta ,\mu }\) and \(\rho \) as defined in (86). There are \(M,\overline{\delta }\ge 0\) such that for all \( \delta \in [0,\overline{\delta }]\) there is a unique \(f_{\delta }\in P_{w}\) with \(||f_{\delta }||_{L^{2}}\le M\) such that
Before the proof of Proposition 43 we need a couple of preliminary results
Proposition 44
There is \(C\ge 0\) such that for all \(\mu _{1},\) \(\mu _{2}\in P_{w}\subseteq L^{2}\),
Proof
The proof follows by (88), estimating the difference of the associated kernels. Let us first consider \(||L_{\delta ,\mu _{2}}-L_{\delta ,\mu _{1}}||_{L^{2}\rightarrow L^{2}}\). We have
We first estimate the distance between the two deterministic parts of the dynamics. For all \(y\in [0,1]\) we get
Now let us suppose that \(\rho \) is \(L-\)Lipschitz. Since \(\rho \) is supported in \([-1,1]\) we get that \(\tau _{-T_{\delta ,\mu }(y)}\rho (x)\) is supported in \([-2,1]\) for each \(\mu \). By this \(L_{\pi }(\tau _{-T_{\delta ,\mu }(y)}\rho (x))\) is the sum of at most three non zero contributions for each \( x\in [0,1],\) hence
proving the statement. The estimate for \(||L_{0,\mu _{1}}-L_{\delta ,\mu _{1}}||_{L^{2}\rightarrow L^{2}}\) is similar. We have
and the statement is obtained as before. \(\square \)
Proposition 45
Let us consider a self-consistent operator \(\mathcal {L}_{\delta }\) as defined at beginning of Sect. 9. Consider \( V_{L^{2}}:=\{v\in L^{2},\) \(\int vdm=0\}.\) Suppose that there is n such that for each \(v\in V_{L^{2}}\), \(||\mathcal {L}_{0}^{n}(v)||_{L^{2}}\le \frac{1}{2}||v||_{L^{2}}\). Then there are \(K,\overline{\delta }\ge 0\) such that for every \(\delta \in [0,\overline{\delta }),\) and probability measures \(\mu _{1},\mu _{2}\in L^{2}\) satisfying \(||\mu _{i}||_{L^{2}}\le ||\rho ||_{\infty }\) for all \(i\in \{1,2\}\) it holds that \(L_{\delta ,\mu _{i}}\) has a unique invariant probability measure with density in \(L^{2}\) which we denote by \(f_{\mu _{i}}.\) Furthermore, with these notations
Proof
We sketch the proof, which is similar to part of the proof of Proposition 36. Since \(||L_{0}^{n}(v)||_{L^{2}}\le \frac{1}{2} ||v||_{L^{2}},\) by Proposition 44 for \(\delta \) small enough we have \(||L_{\delta ,\mu _{1}}^{n}(v)||_{L^{2}}\le \frac{3}{4}||v||_{L^{2}}\) for all \(\mu _{1}\) with \(||\mu _{1}||_{L^{2}}\le ||\rho ||_{\infty }\) and \( v\in V_{L^{2}}\), impliying the uniqueness of the invariant probability density in \(L^{2}\). By this we can also define the resolvent for each such operator \(L_{\delta ,\mu _{1}}\) on \(V_{L^{2}}\) with a uniform bound on its \( L^{2}\) norm. Since
We have that
Since \(||(Id-L_{\delta ,\mu _{2}})^{-1}||_{L^{2}\rightarrow L^{2}}\) is uniformly bounded and \(||f_{\mu _{1}}||_{L^{2}}\le ||f_{\mu _{1}}||_{L^{\infty }}\le ||\rho ||_{\infty }\), applying Proposition 44 we get the statement. \(\square \)
Proof of Proposition 43
We apply Theorem 4 with \(B_{s}=B_{w}=L^{2}[0,1].\) The assumption (Exi1) is provided by (89), (Exi2) is provided by Proposition 44, (91) and (Exi3) is provided by Proposition 45. The unique fixed point we find is in \(L^{2}\) and since the kernels we consider in the construction are uniformly bounded in \( L^{\infty }\) the \(\ L^{2}\) norm of the fixed point is uniformly bounded as \( \delta \) varies. \(\square \)
Now we can prove the linear response formula for these self-consistent operators in the small nonlinear perturbation regime.
Proposition 46
(Linear response). Consider the family of self-consistent transfer operators \(\mathcal {L}_{\delta }:L^{2}\rightarrow L^{2}\) as described before with \(\delta \in (0,\overline{\delta })\) as found in Proposition 43 and with invariant probability measures \(f_{\delta }\). We have the following Linear Response formula
where \(a=\int tdf_{0}(t)\) and the limit is converging in \(L^{2}.\)
Proof
The proof is an application of Theorem 14 where the spaces considered in this case are \(B_{ss}=B_{s}=B_{w}=L^{2}\). The assumption (SS1) (regularity bounds), is implied by Proposition 43. Let us remark that the unperturbed system is a noisy tent map, hence it has convergence to equilibrium (by [1, Remarks 6.4]) and the assumption (SS2) is satisfied. To verify assumption (SS3) (small perturbation) we need to verify that, considering \(B_{2M}=\{x\in L^{2},||x||\le 2M\}\). There is \(K\ge 0\) such that and \(\mathcal {L}_{0}-\mathcal {L}_{\delta }:B_{2M}\rightarrow L^{2}\) is \(K\delta \)-Lipschitz. We have to verify that for all \(\mu _{1},\mu _{2}\in B_{2M}\)
Recalling that by Proposition 44 we have \(L_{0,\mu _{1}}=L_{0,\mu _{2}}:=L_{0},\) we have
Now by Proposition 44
and
proving the statement. Now we can apply Theorem 12 and deduce that \( f_{\delta }\rightarrow f_{0}\) in \(L^{2}.\) The assumption (LR1) on the existence of the resolvent is equivalent to (SS2) since we consider only one space \(L^{2}\) and for the same reason the first part of (LR2)is equivalent to (SS3). We now only need to compute the derivative operator. When the self-consistent operator is considered, as \(\delta \) increases, the effect of the perturbation on the system is only on the map defining the deterministic part of the dynamics. We then use (92), from Proposition 42. We remark that this perturbation on the deterministic part of the dynamics depends on the invariant measure \( f_{\delta }\) of the system as \(\delta \) changes, however we will see that since \(f_{\delta }\rightarrow f_{0}\) in \(L^{2}\) this also give rise to a family of maps with additive noise of the type
as in (90). Indeed let us compute \(\dot{T}\) in this case. Considering that \(T_{\delta ,f_{\delta }}(x)=\frac{T(x)}{1+\delta \int xdf_{\delta }}\) we get
Since \(f_{\delta }\rightarrow f_{0}\) in \(L^{2}\) hence
and we have the expression for \(\dot{L}f_{0}\) from (92). Applying Theorem 14 then, we then get
where \(a=\int tdf_{0}(t).\) \(\square \)
10 Coupling Different Maps
In this section we show how one can use a self-consistent transfer operator approach as a model for the behavior of networks of coupled maps of different types. We will see that our general theoretical framework naturally includes this case. For simplicity we will consider only two types of maps, also for simplicity we will consider coupled expanding maps on the circle. Let us consider two different \(C^{6}\) expanding maps of the circle \( (T_{1},S^{1}),\) \((T_{2},S^{1}).\) Given two probability densities \(\psi _{1},\psi _{2}\in L^{1}(\mathbb {S}^{1},\mathbb {R})\) representing the distribution of probability of the states in the two systems, two coupling functions \(h_{1},h_{2}\in C^{6}(\mathbb {S}^{1}\times \mathbb {S}^{1},\mathbb {R})\) and \(\delta \in [0,\epsilon _{0}]\) representing the way in which these distributions perturb the dynamics (which can be different for the two different systems). Let us define \(\Phi _{\delta ,\psi _{1},\psi _{2}}:\mathbb {S}^{1}\rightarrow \mathbb {S}^{1}\) with \(i\in \{1,2\}\) as
(here for simplicity we suppose that the diffeomorphism perturbing the two different maps is the same though with different contributions for the two different maps, but one can consider different ways to define \(\Phi _{\delta ,\psi _{i}}\) for each map) the maps will hence be perturbed by the combined action of the two densities \(\psi _{1}\) and \(\psi _{2}\).
Again we assume \(\epsilon _{0}\) is so small that \(\Phi _{\delta ,\psi _{1},\psi _{2}}\) is a diffeomorphism for all \(\delta \in [0,\epsilon _{0}]\) and \(\Phi _{\delta ,\psi _{1},\psi _{2}}^{\prime }>0.\) Denote by \(Q_{\delta ,\psi _{1},\psi _{2}}\) the transfer operator associated with \(\Phi _{\delta ,\psi _{1},\psi _{2}},\) defined as
for any \(\phi \in L^{1}(S^{1},\mathbb {R}).\) Now we consider the action of the two maps by considering a global system \((S^{1}\times S^{1},F_{\delta ,\psi _{1},\psi _{2}})\) with
Finally let us consider the space of functions \(B_{1}:=\{(f_{1},f_{2})\in L^{1}(\mathbb {S}^{1})\times L^{1}(\mathbb {S}^{1})\}\) with the norm \( ||(f_{1},f_{2})||_{B_{1}}=||f_{1}||_{L^{1}}+||f_{2}||_{L^{1}}\) (this is also called the direct sum \(L^{1}(\mathbb {S}^{1})\oplus L^{1}(\mathbb {S}^{1})\)), the space \(P_{1}\) of probability elements in \(B_{1},\) \(P_{1}=\) \( \{(f_{1},f_{2})\in B_{1}~s.t.\forall i\in \{1,2\},~f_{i}\ge 0,\int f_{i}dm=1\}\) and the stronger spaces \(B_{2}:=\{(f_{1},f_{2})\in W^{1,1}( \mathbb {S}^{1})\times W^{1,1}(\mathbb {S}^{1})\}\) with the norm \( ||(f_{1},f_{2})||_{B_{1}}=||f_{1}||_{W^{1,1}}+||f_{2}||_{W^{1,1}}\) and \( B_{3}:=\{(f_{1},f_{2})\in W^{2,1}(\mathbb {S}^{1})\times W^{2,1}(\mathbb {S} ^{1})\}\) with the norm \( ||(f_{1},f_{2})||_{B_{1}}=||f_{1}||_{W^{2,1}}+||f_{2}||_{W^{2,1}}\) (again direct sums of Sobolev spaces). These sets can be trivially endowed with a structure of normed vector space. Coherently with the previous sections we define a family of transfer operators \(L_{\delta ,\phi _{1},\phi _{2}}:B_{w}\rightarrow B_{w}\) depending on elements of the weaker space \( (\phi _{1},\phi _{2})\in P_{1}\) as
By this we can define the self-consistent transfer operator \(\mathcal {L} _{\delta }:B_{w}\rightarrow B_{w}\) associated with this system as
We remark that \(B_{1}\) can be identified with a closed subset of \(L^{1}( \mathbb {S}^{1}\times \mathbb {S}^{1})\) by \((f_{1},f_{2})\rightarrow f\) where f is defined by \(f(x,y)=f_{1}(x)f_{2}(y)\) and \(\mathcal {L}_{\delta }\) preserves this subspace.
We now prove the existence and uniqueness of the invariant measure for this kind of self-consistent operators for small \(\delta \), applying our general statement, Theorem 4.
Proposition 47
Let \(T_{1},T_{2}\) be two \(C^{6}\) expanding maps and let \(h_{1},h_{2}\in C^{6}(\mathbb {S}^{1}\times \mathbb {S}^{1},\mathbb {R}).\) Let us consider a globally coupled system as defined above. There is some \(\overline{\delta }\) such that for all \(\delta \in [0,\overline{\delta }]\) there is a unique \((f_{1,\delta },f_{2,\delta })\in B_{2}\) such that
Furthermore there is \(M\ge 0\) such that for all \(\delta \in [0, \overline{\delta }]\)
Proof
The proof follows by the application of Theorem 4 with \( B_{w}=B_{1}\) and \(B_{s}=B_{2}\). We verify the needed assumptions; the assumption (Exi1) is trivial, indeed given \(\mu =(\phi _{1},\phi _{2})\in B_{1}\) for any \(\delta \) small enough the invariant measure of \(L_{\delta ,\phi _{1},\phi _{2}}\), which is a system which is the product of two expanding maps, is trivially in \(B_{2}\) and if we let \((\phi _{1},\phi _{2})\) range in \(P_{1}\), the \(B_{2}\) norm of the associated invariant measure is uniformly bounded.
The assumption (Exi2) can be easily deduced by Proposition 22 as done in the case of system made by coupling identical maps obtaining that there is some \(K_{1}\ge 0\) such that
for \(\delta \) ranging in some neighborhood of the origin and \((\phi _{1},\phi _{2}),\) \((\phi _{3},\phi _{4})\in P_{1}\). Again, applying Lemma 25, like done in Proposition 23 we verify (Exi3) for this product system. Then Theorem 4 can be applied, giving the statement. \(\square \)
It seems that it is possible to extend all the results we proved for coupled expanding maps to this kind of systems, with the same ideas and estimates (but longer formulas and computations, as we have two coordinates). This work however would be quite long and outside of the scope of this paper.
During the revisions of the present paper, the preprint [42] was published. In this work a formalization of a system of coupled maps of different types and its related self-consistent transfer operators similar to the one shown in this section was used to study the synchronization of interacting clusters of globally coupled maps.
11 The Optimal Coupling
In this section we study the problem of finding an optimal small coupling functions \(\delta \dot{h}\) in order to maximize the average of a given observable. This is an optimal control problem in which the goal is to change the statistical properties of the system in an certain direction, in some optimal way. In this case we consider an initial uncoupled system and introduce a small perturbation by a coupling function \(\delta \dot{h}\) and we look for the response of the system to this small perturbation like in Theorem 14. We suppose the direction of perturbation \(\dot{h}\) can vary in some (infinite dimensional) set P, and in this set we look for an optimal one. In the context of extended systems this kind of problems were also defined as “management of the statistical properties of the complex system” ([37]). In some sense this is an inverse problem related to the linear response, in which the goal is to find the optimal perturbation giving a certain kind of response. Related problems in which the focus is more on the realization of a given fixed response have also been called “linear request” problems (see [17, 30]).
The problem of finding an optimal infinitesimal perturbation, in order to maximize the average of a given observable and other statistical properties of dynamics was investigated in the case of finite Markov chains in [2] and for a class of random dynamical systems whose transfer operators are Hilbert Schmidt operators in [1].
In this section we start the investigation of these kind of problems in the case of self-consistent transfer operators. We obtain existence and uniqueness of the optimal solution under assumptions similar to the ones used in [1]. We will focus on the question of finding the best coupling in order to optimize the behavior of a given observable. Let us explain more precisely but still a bit informally the kind of problem we are going to consider: given a certain system, we consider a set P of allowed infinitesimal perturbations we can put in the system. It is natural to think of the set of allowed perturbations P as a convex set because if two different perturbations of the system are possible, then their convex combination (applying the two perturbations with different intensities) should also be possible. We will also consider P as a subset of some Hilbert space \(\mathcal {H}\) (as it is useful for optimization purposes). Let \(\mu _{\dot{h},\delta }\) be the invariant probability measure of the system after applying a perturbation in the direction \(\dot{h}\in P\) with intensity \(\delta \) (we will formalize later what we mean by direction and intensity in our case). Let the response to this perturbation be denoted as
Let us consider \(c:[0,1]\rightarrow \mathbb {R}\). We are interested in the rate of increasing of the expectation of c
and the element \(\dot{h}\in P\) for which this is maximized, thus we are interested in finding \(\dot{h}_{opt}\) such that
By (39) and (40), under the suitable assumptions, this turns out to be equivalent to finding \(\dot{h}_{opt}\) such that
This is hence the maximization of a certain linear function on the set P.
11.1 Some reminders on optimization of a linear function on a convex set
The optimal perturbation problem we mean to consider is related to the maximization of a continuous linear function on the set of allowed infinitesimal perturbations P. The existence and uniqueness of an optimal perturbation hence depends on the properties of the convex bounded set P. We now recall some general results, adapted for our purposes, on optimizing a linear continuous function on a convex set. Let \(\mathcal {J}: \mathcal {H}\rightarrow {\mathbb {R}}\) be a continuous linear function, where \( \mathcal {H}\) is a separable Hilbert space and \(P\subset \mathcal {H}\).
The abstract problem we consider then is to find \(\dot{h}_{opt}\in P\) such that
The following propositions summarizes some efficient criteria for the existence and uniqueness of the solution of such problem (see [1], Section 4 for more details and the proofs).
Proposition 48
(Existence of the optimal solution). Let P be bounded, convex, and closed in \(\mathcal {H}\). Then, Problem (99) has at least one solution.
Uniqueness of the optimal solution will be provided by strict convexity of P.
Definition 49
We say that a convex closed set \(A\subseteq \mathcal {H}\) is strictly convex if for all pair \(x,y\in A\) and for all \(0<\gamma <1\), the points \(\gamma x+(1-\gamma )y\in \mathrm {int}(A)\), where the relative interiorFootnote 8 is meant.
Proposition 50
(Uniqueness of the optimal solution). Suppose P is closed, bounded, and strictly convex subset of \(\mathcal {H}\), and that P contains the zero vector in its relative interior. If \(\mathcal {J}\) is not uniformly vanishing on P then the optimal solution to (99) is unique.
We remark that in the case \(\mathcal {J}\) is uniformly vanishing, all the elements of P are solutions of the problem (98).
11.2 Optimizing the response of the expectation of an observable
Let \(c\in L^{1}\) be a given observable. We consider the problem of finding an infinitesimal perturbation that maximizes the expectation of c. As motivated before, we want to solve the problem stated in (98). Suppose that P is a closed, bounded, convex subset of \(\mathcal {H}\) containing the zero perturbation, and that \(\mathcal { J}\) is not uniformly vanishing on P. Let us consider the function \( \mathcal {J}(\dot{h})=\int c~dR(\dot{h}).\) When this function is continuous as a map from \((P,\Vert \cdot \Vert _{\mathcal {H}})\) to \(\mathbb {R}\), we may immediately apply Proposition 48 to obtain that there exists a solution to the problem considered in (98). If, in addition, P is strictly convex and \(\mathcal {J}\) is nonvanishing, then by Proposition 50 the solution to (98) is unique.
In the following subsections we hence apply these remarks to find the existence and uniqueness of the optimal coupling in the case of coupled expanding map and maps with additive noise.
11.2.1 The optimal coupling for expanding maps
We consider self-consistent transfer operators coming from a system of coupled maps as in Sect. 7, where \(\mathcal {L}_{0}\) is the uncoupled operator and \(\mathcal {L}_{\delta }\) is the self-consistent operator with coupling driven by a function \(\dot{h}:\mathbb {S}^{1}\times \mathbb {S}^{1}\rightarrow \mathbb {R}\) and with strength \(\delta .\) We proved in Proposition 29 (see (60)) that the response of the invariant measure of the system as \(\delta \) increases is given by
Given some observable \(c\in L^{1}\) and some convex set of allowed perturbations P we now apply the previous results to the problem of finding the optimal coupling \(\dot{h}_{opt}\in P\) solving the problem (98) for this response function \(R(\dot{h})\). From Remark 30 (see also (40)) we know that the rate of change of the average of c can be estimated by the linear response when the convergence of the linear response is in \(W^{1,1}\).
We remark that to apply the general results of Sect. 11.1 we need P being a subset of a Hilbert space. Since to apply Proposition 29 we need \(\dot{h}\in C^{6}\) we consider a Hilbert space of perturbations which is included in \(C^{6}.\) A simple choice is \(W^{7,2}\). We hence consider a system with coupled expanding maps, the Hilbert space \( W^{7,2}\) and a convex set \(P\subseteq W^{7,2}(S^{1}\times S^{1}).\)
Proposition 51
Under the above assumptions, supposing that P is a closed bounded convex set in \(W^{7,2},\) Problem (98) has a solution in P. If furthermore P is strictly convex either the optimal solution is unique or every \(\dot{h}\in P\) is the optimal solution.
Proof
The result directly follows applying Propositions 48 and 50. In order to apply the propositions we have to check that \(\dot{ h}\rightarrow \int c~dR(\dot{h})\) is continuous on P. Since
we have
Now the result follow by a direct application of Propositions and 50. \(\square \)
11.2.2 The optimal coupling for systems with additive noise
Now we consider the optimal coupling in order to maximize the average of one observable c in the case of the coupled maps with additive noise as described in Sect. 8. Since Proposition 38 gives a convergence of the linear response in the strong space \(C^{k}\), by Remark 30 we know that we can consider very general observables. For simplicity we will consider \(c\in L^{1}\) but in fact we could consider even weaker spaces as distribution spaces (the dual of \(C^{k}\)). For simplicity we also take \(P\subseteq W^{1,2}\) to let (79) make sense. The response formula in this case is
We will hence consider the problem (98) with this response function. Similarly to the expanding maps case we get the following statement.
Proposition 52
Under the above assumptions, supposing that P is a closed bounded convex set in \(W^{1,2},\) Problem (98) has a solution in P. If furthermore P is strictly convex either the solution is unique or every \( \dot{h}\in P\) is the optimal solution.
Proof
The result again directly follows applying Propositions 48 and 50. In order to apply the propositions we check that \(\dot{ h}\rightarrow \int c~dR(\dot{h})\) is continuous on P. Since in this case
we have
establishing the continuity of \(\dot{h}\rightarrow \int c~dR(\dot{h})\). \(\square \)
Notes
We could also consider in a similar way interacting systems of different types, where instead of a single measure representing the distribution of the states of the systems in a certain phase space we will have a a vector of measures representing the states of systems of different type (see Sect. 10 for more details).
The set M can be finite or infinite. In the case \(M=M_{n}:=\{1,\ldots ,n\}\) is finite we consider a finite set of interacting systems. In this case a natural choice is to set p as the uniform distribution \(p_{n}\) giving to each system the same weight \(\frac{1}{ n}\). We remark that in this case (3) becomes
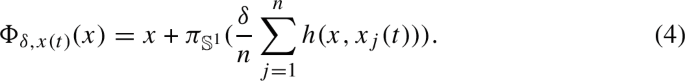
One approach to the definition of the dynamics of a system made of infinitely many globally interacting maps is to start by the case of n interacting maps and then considering the limit for \(n\rightarrow \infty \). The perturbation \(\Phi _{\delta ,x(t)}\) induced by the interaction between the systems is defined as a suitable limit of 4. This might raise some technical problem in selecting states and the assumptions for which the limit converge. With our approach we might also consider an infinite space of interacting systems as a limit of a finite interacting family. In this case it is sufficient to see (M, p) as a suitable limit of \( (M_{n},p_{n})\).
We recall that since \(\mu \rightarrow \mu (X)\) is continuous, \(V_{s}\) is closed. Furthermore \(\forall \mu \in P_{w},\) \(L_{\delta ,\mu }(V_{s})\subseteq V_{s}.\)
The proof is quite technical. We are going to explain its idea informally to help the reader to understand the motivation of various estimates: by Proposition 9 we get that \(||L(n)(\nu )-L(n)(\mu _{\delta })||_{s}\) decreases exponentially in n. The remaining term \(||L(n)(\mu _{\delta })-L_{\delta ,\mu }^{n}(\mu _{\delta })||s\) is small when \(\delta \) is small and \(\nu _{1},...,\nu _{n}\) are close to \(\mu _{\delta }\) because the operators involved in the composition L(n) are all near to \( L_{\delta ,\mu _{\delta }}.\)The idea is to use the balanced norm \(||~||_{(a,b)}\) to estimate \(||~||_{s}\) , and exploit the fact that after \(n_{1}\) iterates \(||L(n_{1})(\nu )-L(n_{1})(\mu _{\delta })||_{(a,b)}\) is contracted by a certain factor \( \rho _{1}<1\).If we prove that \(\delta \) can be made small enough so that \(||L(n_{1})(\mu _{\delta })-L_{\delta ,\mu _{\delta }}^{n_{1}}(\mu _{\delta })||_{(a,b)}\) is not relevant, then we have that also \(||L(n_{1})(\nu )-\mathcal {L} _{\delta }^{n_{1}}(\mu _{\delta })||_{(a,b)}\) is contracted. Hence continuing the iteration we have an exponential decrease of this norm, which implies exponential decrease of the \(||~||_{s}\) norm.
The idea of the proof is the following. We consider \(\mu \) with \(||\mu ||_{W}\le 1\) and prove \(||\pi _{n}\mu ||_{W}\le 1.\) For this we first remark that by the way the discretization is constructed, for each function \( \tilde{g}\) such that \(||\tilde{g}||_{Lip}\le 1\) and \(\tilde{g}\) is affine on each interval \(I_{n}\) we have \(\int \tilde{g}d\mu =\int \tilde{g}d\pi _{n}\mu \le 1.\) Then consider a generic Lipschitz function g with \( ||g||_{Lip}\le 1\) and note that there is a function \(\tilde{g}\) affine on each interval \(I_{n}\) such that \(||\tilde{g}||_{Lip}\le 1\) and \(\int \tilde{g}d\pi _{n}\mu =\int gd\pi _{n}\mu \) and then \(\int gd\pi _{n}\mu \le 1\).
A nonsingular map T is a map such that for any Lebesgue measurable set A we have \(m(A)=0\iff m(T^{-1}(A))=0\), where m is the Lebesgue measure. If T is nonsingular its associated pushforward map induces a function \(L^{1}( \mathbb {S}^{1},\mathbb {R})\rightarrow L^{1}(\mathbb {S}^{1},\mathbb {R})\).
We mean that \(\mathbb {S}^{1}\) can be partitioned in a finite set of intevrals where T is \(C^{1}\) and that the associated pushforward map \( T_{*}\) sends a measure which is absolutely continuous with respect to the Lebesgue measure to another measure which is absolutely continuous with respect to the Lebesgue measure.
The relative interior of a closed convex set C is the interior of C relative to the closed affine hull of C.
References
Antown, F., Froyland, G., Galatolo, S.: Optimal linear response for Markov Hilbert-Schmidt integral operators and stochastic dynamical systems. arXiv:2101.09411
Antown, F., Dragicevic, D., Froyland, G.: Optimal linear responses for Markov chains andstochastically perturbed dynamical systems. J. Stat. Phys. 170(6), 1051–1087 (2018)
Baladi, V.: Linear response, or else. ICM Proc. Seoul III, 525–545 (2014)
Bardet, J.B., Keller, G., Zweimüller, R.: Stochastically stable globally coupled maps with bistable thermodynamic limit. Commun. Math. Phys. 292(1), 237–270 (2009)
Blank, M.L.: Ergodic averaging with and without invariant measures. Nonlinearity 30(12), 4649 (2017)
Blank, M.L.: Self-consistent mappings and systems of interacting particles. Doklady Math. 83, 49–52 (2011)
Balint, P., Keller, G., Selley, F.M., Toth, I.P.: Synchronization versus stability of the invariant distribution for a class of globally coupled maps. Nonlinearity 31(8), 3770 (2018)
Chazottes, J.-R., Fernandez, B.: Dynamics of Coupled Map Lattices and of Related Spatially Extended Systems, Vol. 671. Springer Science & Business Media (2005)
Chihara, T., Sato, Y., Nisoli, I., Galatolo, S.: Existence of multiple noise-induced transitions in a Lasota-Mackey map. Chaos 32, 013117 (2022). https://doi.org/10.1063/5.0070198
Conway, J.: A course in functional analysis, Vol. 96. Springer Science & Business Media (2013)
Conze, J. P., Raugi, A.: Limit theorems for sequential expanding dynamical systems on , Ergodic theory and related fields, Contemp. Math., Vol. 430, AMS, Providence, RI, pp. 89–121 (2007)
Dietert, H., Fernandez, B.: The mathematics of asymptotic stability in the Kuramoto model. Proc. R. Soc. A 474(2220), 20180467 (2018)
Fernandez, B.: Breaking of ergodicity in expanding systems of globally coupled piecewise affine circle maps. J. Stat. Phys. 154(4), 999–1029 (2014)
Florenzano, M.: General Equilibrium Analysis: Existence and Optimality Properties of Equilibria. Springer, ISBN 9781402075124, (2003)
Galatolo, S., Sedro, J.: Quadratic response of random and deterministic dynamical systems. Chaos 30, 023113 (2020). https://doi.org/10.1063/1.5122658
Galatolo, S.: Statistical properties of dynamics. Introduction to the functional analytic approach. arXiv:1510.02615
Galatolo, S., Pollicott, M.: Controlling the statistical properties of expanding maps. Nonlinearity 30(7), 2737 (2017)
Galatolo, S., Nisoli, I., Saussol, B.: An elementary way to rigorously estimate convergence to equilibrium and escape rates. J. Comput. Dyn. 2(1), 51–64 (2015). https://doi.org/10.3934/jcd.2015.2.51
Galatolo, S., Nisoli, I.: An elementary approach to rigorous approximation of invariant measures. SIAM J. Appl. Dyn. Syst. 13(2), 958–985 (2014)
Galatolo, S., Monge, M., Nisoli, I.: Existence of noise induced order, a computer aided proof. Nonlinearity 33(9), 4237–4276 (2020)
Galatolo, S., Monge, M., Nisoli, I.: Rigorous approximation of stationary measures and convergence to equilibrium for iterated function systems. J. Phys. A: Math. Theor. 49, 274001 (2016)
Galatolo, S., Giulietti, P.: A linear response for dynamical systems with additive noise. Nonlinearity 32(6), 2269–2301 (2019)
Golse, F.: On the dynamics of large particle systems in the mean-field limit. In Muntean, A., Rademacher, J., Zagaris, A. (eds.), Macroscopicand Large Scale Phenomena: Coarse Graining, Mean Field Limits and Ergodicity. Lecture Notes Application Mathematics and Mechanics, Vol. 3, pp. 1–144. Springer (2016).
Jiang, M., de la Llave, R.: Smooth dependence of thermodynamic limits of SRB-measures. Commun. Math. Phys. 211(2), 303–333 (2000)
Jiang, M., de la Llave, R.: Linear response function for coupled hyperbolic attractors. Commun. Math. Phys. 261(2), 379–404 (2006)
Jiang, M., Pesin, Y.B.: Equilibrium measures for coupled map lattices: existence, uniqueness and finite-dimensional approximations. Commun. Math. Phys. 193(3), 675–711 (1998)
Liverani, C.: Invariant measures and their properties. A functional analytic point of view. Dynamical Systems. Part II: Topological Geometrical and Ergodic Properties of Dynamics. Centro di Ricerca Matematica “Ennio De Giorgi”: Proceedings. Published by the Scuola Normale Superiore in Pisa (2004)
Liverani, C.: Rigorous numerical investigation of the statistical properties of piecewise expanding maps: A feasibility study. Nonlinearity 14, 463–490 (2001)
Lasota, A., Mackey, M.: Probabilistic Properties of Deterministic Systems. Cambridge University Press (1985)
Kloeckner, B.: The linear request problem. Proc. Am. Math. Soc. 146(7), 2953–2962 (2018)
Kaneko, K.: Globally coupled chaos violates the law of large numbers but not the central limit theorem. Phys. Rev. Lett. 65(12), 1391 (1990)
Kolmogorov, A., Fomin, S.: Elements of the Theory of Functions and Functional Analysis. Volume 2: Measure. The Lebesgue Integral. Hilbert Space. Graylock (1961)
Keller, G.: An ergodic theoretic approach to mean field coupled maps. In: Fractal Geometry and Stochastics II, pp. 183–208. Springer (2000)
Keller, G., Liverani, C.: A spectral gap for a one-dimensional lattice of coupled piecewise expanding interval maps. In: Dynamics of Coupled Map Lattices and of Related Spatially Extended Systems, pp 115–151. Springer (2005)
Keller, G., Liverani, C.: Stability of the spectrum for transfer operators. Annali della Scuola Normale Superiore di Pisa 4(1), 141–152 (1999)
Marangio, L., Sedro, J., Galatolo, S., Di Garbo, A., Ghil, M.: Differentiability and non-monotonicity of the rotation number Arnold maps with noise. J. Stat. Phys. 179, 1594–1624 (2020)
MacKay, R.: Management of complex dynamical systems. Nonlinearity 31(2), R52 (2018)
Ott, W., Stenlund, M., Young, L.-S.: Memory loss for time-dependent dynamical systems. Math. Res. Lett. 16(2), 463–475 (2009)
Ruelle, D.: Differentiation of SRB states. Commun. Math. Phys. 187, 227–241 (1997)
Sedro, J.: A regularity result for fixed points, with applications to linear response. Nonlinearity 31, 1417 (2018)
Sélley, F.M., Tanzi, M.: Linear response for a family of self-consistent transfer operators. Commun. Math. Phys. 382(3), 1601–1624 (2021)
Sélley, F.M., Tanzi, M.: Synchronization for networks of globally coupled maps in the thermodynamic limit. arXiv:2110.05618
Sélley, F.M.: Asymptotic Properties of Mean Field Coupled Maps. PhD thesis (2019)
Sélley, F.M.: A self-consistent dynamical system with multiple absolutely continuous invariant measures. J. Comput. Dyn. 8(1), 932 (2021)
Wormell, C., Gottwald, G.: On the validity of linear response theory in high-dimensional deterministic dynamical systems. J. Stat. Phys. 172(6), 1479–1498 (2018)
Wormell, C.L., Gottwald, G.A.: Linear response for macroscopic observables in high-dimensional systems. Chaos: Interdiscip. J. Nonlinear Sci 29(11), 113127 (2019)
Viana, M.: Lectures on Lyapunov Exponents. Cambridge Studies in Advanced Mathematics 145, Cambridge University Press (2014)
Acknowledgements
S.G. is partially supported by the research project PRIN 2017S35EHN_004 “Regular and stochastic behavior in dynamical systems” of the Italian Ministry of Education and Research. The author whish to thank F. Sélley, S. Vaienti, M. Tanzi and C. Liverani for fruitful discussions during the preparation of the work. The author whish also to thank the anonymous reviewers for their patience and the help in revising this long text.
Funding
Open access funding provided by Università di Pisa within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by C. Liverani.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Galatolo, S. Self-Consistent Transfer Operators: Invariant Measures, Convergence to Equilibrium, Linear Response and Control of the Statistical Properties. Commun. Math. Phys. 395, 715–772 (2022). https://doi.org/10.1007/s00220-022-04444-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-022-04444-4