Continuum Limit of Random Matrix Products in Statistical Mechanics of Disordered Systems

Abstract

We consider a particular weak disorder limit (continuum limit) of matrix products that arise in the analysis of disordered statistical mechanics systems, with a particular focus on random transfer matrices. The limit system is a diffusion model for which the leading Lyapunov exponent can be expressed explicitly in terms of modified Bessel functions, a formula that appears in the physical literature on these disordered systems. We provide an analysis of the diffusion system as well as of the link with the matrix products. We then apply the results to the framework considered by Derrida and Hilhorst (J Phys A 16:2641–2654, 1983), which deals in particular with the strong interaction limit for disordered Ising model in one dimension and that identifies a singular behavior of the Lyapunov exponent (of the transfer matrix), and to the two dimensional Ising model with columnar disorder (McCoy–Wu model). We show that the continuum limit sharply captures the Derrida and Hilhorst singularity. Moreover we revisit the analysis by McCoy and Wu (Phys Rev 176:631–643, 1968) and remark that it can be interpreted in terms of the continuum limit approximation. We provide a mathematical analysis of the continuum approximation of the free energy of the McCoy–Wu model, clarifying the prediction (by McCoy and Wu) that, in this approximation, the free energy of the two dimensional Ising model with columnar disorder is $C^\infty$ but not analytic at the critical temperature.

Appendix A: The McCoy–Wu Model

In [30], McCoy and Wu examined a two-dimensional Ising model with bond disorder of a particular type (subsequently known as the McCoy–Wu model): the couplings between sites in neighboring columns have a constant strength $E_1$, while the couplings between neighboring sites in the same column take a random value $E_2(n)$ which is fixed within each row but varies independently—keeping the same distribution—between different rows (Fig. 1). They showed that in the thermodynamic limit the free energy per site of this model is given (up to the subtraction of an analytic function of $\beta$) by

$$\begin{aligned} \textsc {f}_{{\text {MW}}}(\beta )\, :=\, \frac{1}{4\pi }\int _{-\pi }^\pi {\mathcal {L}} ^{{\text {MW}}}_{\beta }(\theta ) \,\text {d}\theta \,, \end{aligned}$$

(A.1)

where ${\mathcal {L}} ^{{\text {MW}}}_{\beta }(\theta )$ is the Lyapunov exponent of the random matrix

$$\begin{aligned} M_\beta (\theta ) :=\begin{pmatrix} 1 &{}\quad \frac{a}{a^2+b^2} \\ \frac{a}{a^2+b^2} \lambda &{}\quad \frac{\lambda }{a^2+b^2} \end{pmatrix}, \end{aligned}$$

(A.2)

with

$$\begin{aligned} a(\theta )\, =\, -2z_1 \frac{\sin (\theta )}{\left| 1+z_1 \exp (i\theta ) \right| ^2}\ \ \text { and } \ \ b(\theta )\, =\, \frac{1-z_1^2}{\left| 1+z_1 \exp (i\theta ) \right| ^2}, \end{aligned}$$

(A.3)

where

$$\begin{aligned} z_1\, =\, \tanh \left( \beta E_1\right) , \ \ z_2(n)\, =\, \tanh \left( \beta E_2(n)\right) \ \ \text { and } \ \ \lambda =\lambda (n)= z_2^2(n). \end{aligned}$$

(A.4)

In [40] a different version of the model has been considered: vertical bounds are random in the horizontal direction and randomness is repeated in each line. This model, that allows frustration, is richer, but the features that are novel with respect to the McCoy–Wu model cannot be appreciated in the weak disorder limit: our analysis applies to [40] as well, but we will not develop this issue here.

Fig. 1

The McCoy–Wu disordered version of the two dimensional Ising model: the disordered interactions are in the vertical direction and they are distributed in an IID fashion within one column. This disorder is just copied to all the other columns and the horizontal interactions are non random. The disorder enters the free energy formula via independent copies of the random variable $\lambda = \tanh ^2 \left( \beta E_2\right)$

To avoid trivialities we assume that $E_1\ne 0$ as well as that $E_2$ is a non degenerate random variable: it is immediately clear that the sign of $E_2$ does not matter and just a little thought reveals that the sign of $E_1$ is irrelevant too. Therefore we assume that $E_1\in (0, \infty )$ and that $E_2$ is a random variable taking values in $(0, \infty )$. It is helpful (mostly to simplify the presentation) to assume that $E_2$ takes values in $[E_2^{-}, E_2^+]$, with $0<E_2^-<E_2^+< \infty$.

Moreover one directly sees that $a(\cdot )$ is odd and $b(\cdot )$ is even, which yields that ${\mathcal {L}} ^{{\text {MW}}}_{\beta }(\cdot )$ is even: in fact $D_\pm M_\beta (\theta ) D_\pm = M_\beta (-\theta )$, with $D_\pm$ the diagonal matrix with $(+1,-1)$ on the diagonal. Therefore:

$$\begin{aligned} \textsc {f}_{{\text {MW}}}(\beta )\, :=\, \frac{1}{2\pi }\int _{0}^\pi {\mathcal {L}} ^{{\text {MW}}}_{\beta } (\theta ) \,\text {d}\theta . \end{aligned}$$

(A.5)

McCoy and Wu claim that for every $\upsilon \in (0, \pi )$—our focus is on $\upsilon$ small—the function

$$\begin{aligned} \beta \mapsto \frac{1}{2\pi }\int _{\upsilon }^\pi {\mathcal {L}} ^{{\text {MW}}}_{\beta }(\theta ) \,\text {d}\theta \end{aligned}$$

(A.6)

is real analytic on $(0, \infty )$. This can be proven by applying the main result in [36] (see also [13]). We sketch the argument here by considering separately the case $\theta$ bounded away from 0 and $\pi$ and the case of $\theta$ near $\pi$: with $\delta >0$ small

• For $\theta \in [\delta , \pi -\delta ]$ the matrix $M_\beta (\theta )$ (with positive entries) maps the closure of the cone Q—here Q is first quadrant without the axes, that is the set of vectors with positive entries—to $Q\cup \{0\}$. More precisely, by the hypothesis we have made on the support of Z, for every $\delta \in (0, \pi /2)$ and every $\varrho \in (0,1)$ the closure of Q is mapped into a cone whose closure is a subset of $Q\cup \{0\}$ and this subset is the same for every choice of $\theta \in [\delta , \pi -\delta ]$ and every $\beta \in [\varrho ,1/\varrho ]$. This uniform cone property implies the real analyticity of $\beta \mapsto {\mathcal {L}} ^{{\text {MW}}}_{\beta }(\theta )$ with a convergence radius that is bounded away from zero uniformly in $\theta \in [\delta , \pi -\delta ]$ and $\beta \in [\varrho ,1/\varrho ]$.

• For $\theta \in [\pi -\delta ,\pi ]$ we argue by observing first that

  $$\begin{aligned} a(\pi ) = 0, \quad b(\pi ) = \frac{1-z_1^2}{(1-z_1)^2} = \frac{1+ \tanh \beta E_1}{1 - \tanh \beta E_1} = e^{2 \beta E_1}, \end{aligned}$$

  (A.7)

  so

  $$\begin{aligned} M_\beta (\pi ) \,=\,\begin{pmatrix} 1 &{}\quad 0 \\ 0 &{}\quad e^{-4 \beta E_1} \tanh ^2 \beta E_2 \end{pmatrix}. \end{aligned}$$

  (A.8)

  Since $e^{-4 \beta E_1} \tanh ^2 \beta E_2<1$ the action of $M_\beta (\pi )$ contracts uniformly any cone of the form $\{(x,y): \, y \ge \vert x\vert \}$, in the sense there exists $\varrho >0$ such that $M_\beta (\pi )$ sends $\{(x,y): \, y \ge \vert x\vert \}$ into $\{(x,y): \, y \ge (1+ \varrho ) \vert x\vert \}$, uniformly in $\beta >0$ and $E_2$. Elementary arguments show that this result is only slightly perturbed if we consider $\theta \in [\pi -\delta ,\pi ]$ with $\delta$ sufficiently small. This uniform cone property implies the real analyticity of $\beta \mapsto {\mathcal {L}} ^{{\text {MW}}}_{\beta }(\theta )$ with a convergence radius that is bounded away from zero uniformly in $\theta \in [\pi -\delta ,\pi ]$ and $\beta >0$.

Therefore the true issue is the regularity (or lack of it) of

$$\begin{aligned} \beta \mapsto \frac{1}{2\pi }\int _{0}^\upsilon {\mathcal {L}} ^{{\text {MW}}}_{\beta }(\theta ) \,\text {d}\theta \,, \end{aligned}$$

(A.9)

for a $\upsilon >0$ that can be chosen as small as one wishes. At this point McCoy and Wu claim that the only non analytic point of the map in (A.9) can be at $\beta _c$ defined by

$$\begin{aligned} 2 \beta _c E_1 + {\mathbb {E}}\left[ \log \tanh \beta _c E_2 \right] \, =\, 0. \end{aligned}$$

(A.10)

To see that this is the only possible candidate, McCoy and Wu point out that

$$\begin{aligned} a(0) = 0, \quad b(0) = \frac{1-z_1^2}{(1+z_1)^2} =\frac{1- \tanh \beta E_1}{1 + \tanh \beta E_2} = e^{-2 \beta E_1}, \end{aligned}$$

(A.11)

so

$$\begin{aligned} M_\beta (0) =\begin{pmatrix} 1 &{} \quad 0 \\ 0 &{} \quad e^{4 \beta E_1} \tanh ^2 \beta E_2 \end{pmatrix}, \end{aligned}$$

(A.12)

and so

$$\begin{aligned} {\mathcal {L}} ^{MW}_\beta (0) = \max \left( 0, 4 \beta E_1 + 2 {\mathbb {E}}\left[ \log \tanh \beta E_2 \right] \right) \end{aligned}$$

(A.13)

for $\beta$ real. This admits an analytic extension in a neighborhood of any positive $\beta$ except for $\beta _c$.

This is of course far from being close to a proof, since one has to control the integral over $\theta \in (0, \upsilon )$ and not the value in zero. But McCoy and Wu perform also a more subtle analysis that can be understood precisely via the diffusion limit of matrix products that is at the center of our analysis. To explain this let us make a further manipulation to match more sharply our framework.

In fact, as it stands, $M_\beta (\theta )$, cf. (A.2), is not of the form (1.1). But by noting that

$$\begin{aligned} \frac{1}{a^2(\theta )+b^2(\theta )} = \frac{(1+z_1)^4}{(1-z_1^2)^2} +O(\theta ^2) = \left( \frac{1+z_1}{1-z_1} \right) ^2+ O(\theta ^2) =e^{4 \beta E_1}+ O(\theta ^2), \end{aligned}$$

(A.14)

and

$$\begin{aligned} \frac{a}{a^2(\theta )+b^2(\theta )} = -2 \left( \frac{1+z_1}{1-z_1} \right) ^2 \theta + O(\theta ^2) = -2 e^{4 \beta E_1}+ O(\theta ^2), \end{aligned}$$

(A.15)

if we let

$$\begin{aligned} \widetilde{\varepsilon } := \frac{2 z_1}{(1-z_1)^2} \theta , \end{aligned}$$

(A.16)

we see that to leading order as $\theta \searrow 0$

$$\begin{aligned} \begin{pmatrix} 1 &{} \quad -\widetilde{\varepsilon } \\ -\widetilde{\varepsilon } \lambda &{}\quad e^{4 \beta E_1} \lambda \end{pmatrix} \end{aligned}$$

(A.17)

is $M_\beta (\theta )$. The matrix in (A.17) is of the form (1.1) up to a conjugation and a change of variables: in fact

$$\begin{aligned} \begin{pmatrix} 1&{}\quad \varepsilon \\ \varepsilon Z &{}\quad Z \end{pmatrix} \,:=\, \begin{pmatrix} 1&{}\quad \widetilde{\varepsilon } e^{-2 \beta E_1}\\ \widetilde{\varepsilon } e^{-2 \beta E_1} \lambda &{}\quad e^{4 \beta E_1} \lambda \end{pmatrix} \, =\, \begin{pmatrix} 1 &{}\quad 0 \\ 0 &{}\quad - e^{2 \beta E_1} \end{pmatrix} \begin{pmatrix} 1 &{}\quad -\widetilde{\varepsilon } \\ - \widetilde{\varepsilon } \lambda &{}\quad e^{4 \beta E_1} \lambda \end{pmatrix} \begin{pmatrix} 1 &{}\quad 0 \\ 0 &{}\quad - e^{-2 \beta E_1} \end{pmatrix}, \end{aligned}$$

(A.18)

and we observe—recall (A.16)—that $\varepsilon = c_\beta \theta$, with $c_\beta = 2 \sinh (2\beta E_1)$.

Remark A.1

It is important to remark at this stage that the inverse temperature $\beta$ and our fundamental parameter $\alpha$—we recall that $\alpha$ is the unique non zero real solution to ${\mathbb {E}}Z^\alpha =1$ ($Z=e^{4\beta E_1} \tanh ^2(\beta E_2)$ depends on $\beta$!) when such a solution exists and otherwise $\alpha =0$—should be seen as an analytic change of variable: this is treated in detail in Lemma A.2. In particular $\alpha (\beta _c)=0$ and therefore $\alpha (\beta )= (\beta -\beta _c) \alpha ' (\beta _c)+ O((\beta -\beta _c)^2)$, but the constant$\alpha ' (\beta _c)$ depends of the law of Z (with $\beta =\beta _c$) and this expansion should be done more carefully when the disorder is weak because, as we will see, $\alpha ' (\beta _c)$ becomes large in this limit: this is treated in (A.21)–(A.29).

What McCoy and Wu do at this point is

• making a specific choice of $Z=Z^\Delta =Z^\Delta _\beta$ that satisfies the hypotheses of Theorem 6.1 (say, with $\sigma =1$ for simplicity); this actually implements two choices:

  • 1. the first is evident and it is the fact that disorder can be made weak by making $\Delta$ small;

  • 2. the second is that $\beta -\beta _c$ is chosen small and, precisely, of the order of $\Delta$. As we will explain, if we set $y=(\beta -\beta _c)/ \Delta$ and we keep $y\in {\mathbb {R}}$ fixed, then $\alpha (\beta ) \sim -C_{\beta _c} y$, and the constant $C_{\beta _c}>0$ will be given explicit in the specific case that we are going to develop, see (A.29).

• they choose also $\upsilon \propto \Delta$: let us fix in an arbitrary fashion $\upsilon = \Delta$.

In physical terms these choices correspond to focusing on the critical window in the limit of weak disorder. Cutting the integral at $\theta = \Delta$ is harmless (as we have discussed before), but of course only as far as $\Delta$ is kept fixed.

McCoy and Wu are in the end just dealing (recall (A.18)) with the Lyapunov exponent $\widehat{{\mathcal {L}} }_{\Delta , \beta _c + y\Delta } (c_{\beta _c}x \Delta )$ of the matrix (we perform the change of variable $\theta =x \Delta$)

$$\begin{aligned} \begin{pmatrix} 1 &{}\quad c_{\beta _c} x \Delta \\ c_{\beta _c} x \Delta Z_{\beta _c + y\Delta }^\Delta &{}\quad Z_{\beta _c + y\Delta }^\Delta \end{pmatrix}. \end{aligned}$$

(A.19)

But Theorem 6.1 (see also Theorem 1.6) tells us that $\widehat{{\mathcal {L}} }_{\Delta , \beta _c + y\Delta } (c_{\beta _c }x)$ is asymptotically equivalent for $\Delta$ small to $\Delta {\mathcal {L}} _{1, C_{\beta _c}\alpha }( c_{\beta _c}x)$ so that

$$\begin{aligned} \int _{0}^\Delta {\mathcal {L}} ^{{\text {MW}}}_{\beta _c + y \Delta }(\theta ) \,\text {d}\theta \, \sim \, \Delta \int _{0}^1 \widehat{{\mathcal {L}} }_{\Delta , \beta _c + y\Delta } (c_{\beta _c }x)\,\text {d}x\, \sim \, \Delta ^2 \int _{0}^1 {\mathcal {L}} _{1,C_{\beta _c}\alpha } (c_{\beta _c}x)\,\text {d}x \end{aligned}$$

(A.20)

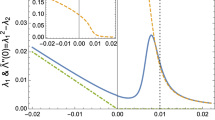
and we remind the reader that ${\mathcal {L}} _{1,C_{\beta _c}\alpha }( c_{\beta _c}x)$ has the explicit expression (1.6). Therefore, up to two inessential constants we arrived at (1.28). We did not fully justify the equivalences in (A.20), but this is not really the main problem: the main unresolved mathematical issue is that what we are after is proving that, for a fixed (possibly extremely small) value of $\Delta$, the leftmost term in (A.20) is a $C^\infty$ function of y at 0 and that the same expression is not analytic at zero. McCoy and Wu instead argue (and we prove in Theorem 1.7) that $\alpha \mapsto \int _{0}^1 {\mathcal {L}} _{1,C_{\beta _c}\alpha }( c_{\beta _c}x)\,\text {d}x$ has these properties: but this second statement does not imply the first.

We now complement our discussion with the analysis of the specific distribution chosen for the disorder law in [29, 30]. We also discuss more in detail the change of variable $\alpha (\beta )$.

1.1 Analysis of the Distribution Chosen by McCoy and Wu [29, 30]

McCoy and Wu consider the disordered variable $\lambda =\tanh ^2( \beta E_2)$ that depends on a parameter that they call $\mathtt {N}$ and it is large: in fact

$$\begin{aligned} \Delta \, =\, \mathtt {N}^{-2}. \end{aligned}$$

(A.21)

The density of $\lambda$ is supported on $(0, \lambda _0)$ and equal to $\mathtt {N}\lambda _0^{-\mathtt {N}}y^{\mathtt {N}-1}$ for $y\in (0, \lambda _0)$. Necessarily $\lambda _0=\lambda _0(\beta )= \tanh ^2(\beta E_2^*)$, with $E_2^*$ the maximum value that the random variable $E_2$ can reach. The density of $Z= Z_\mathtt {N}$ (recall that Z is defined in (A.18)) is therefore

$$\begin{aligned} \mathtt {N}\lambda _1^{-\mathtt {N}}y^{\mathtt {N}-1} \mathbf {1}_{(0, \lambda _1)}(y)\ \ \ \ \text { with } \ \lambda _1(\beta )\, =\, e^{4\beta E_1}\lambda _0(\beta ). \end{aligned}$$

(A.22)

Note that for every $\nu \in (-\mathtt {N}, \infty )$

$$\begin{aligned} {\mathbb {E}}\left[ \left( Z_\mathtt {N}\right) ^\nu \right] \, =\, \frac{\lambda _1(\beta )^\nu }{1+ \frac{\nu }{\mathtt {N}}}, \end{aligned}$$

(A.23)

and we want to solve for $\alpha =\alpha (\beta )\ne 0$ the equation

$$\begin{aligned} {{\mathbb {E}}\left[ \left( Z_\mathtt {N}\right) ^\alpha \right] \, -1} \, =\, \frac{\lambda _1(\beta )^\alpha - 1- \frac{\alpha }{\mathtt {N}}}{1+ \frac{\alpha }{\mathtt {N}}}\, =\, 0. \end{aligned}$$

(A.24)

On one hand we compute

$$\begin{aligned}&\log (\lambda _1(\beta ))\, \nonumber \\&\quad =\log \tanh ^2 (\beta _c E_2^*) - {\mathbb {E}}\left[ \log \tanh ^2 (\beta _c E_2)\right] \nonumber \\&\qquad + 4 (\beta -\beta _c)+ \log \tanh ^2 (\beta E_2^*) -\log \tanh ^2 (\beta _c E_2^*), \end{aligned}$$

(A.25)

and a straightforward computation yields

$$\begin{aligned} {\mathbb {E}}\left[ \log \tanh ^2 (\beta E_2)\right] \, =\, \log \tanh ^2 (\beta E_2^*) - \frac{1}{\mathtt {N}}, \end{aligned}$$

(A.26)

so for $\beta$ close $\beta _c$ we have

$$\begin{aligned} \log \lambda _1(\beta )\, =\, \frac{1}{\mathtt {N}}+ (\beta -\beta _c) \left( 4E_1 + \frac{1}{\sinh (2 \beta _c E_2^*)}\right) +O\left( ( \beta - \beta _c)^2\right) . \end{aligned}$$

(A.27)

On the other hand from (A.24) we see that if $\alpha$ is fixed (so we look at $\beta$ as a function of $\alpha$) we have

$$\begin{aligned} \log \lambda _1(\beta ) \,=\, \frac{\log \left( 1+ \frac{\alpha }{\mathtt {N}}\right) }{\alpha }{\mathop {=}\limits ^{\mathtt {N}\rightarrow \infty }}\, \frac{1}{\mathtt {N}}- \frac{\alpha }{2\mathtt {N}^2}+ O\left( \frac{1}{\mathtt {N}^3}\right) . \end{aligned}$$

(A.28)

By comparing (A.27) and (A.28) we see that if $(\beta -\beta _c) \mathtt {N}^2=O(1)$ then

$$\begin{aligned} \alpha (\beta ) \, =\, -(\beta -\beta _c) {\mathtt {N}^2} \left( 8E_1 + \frac{2}{\sinh (2 \beta _c E_2^*)}\right) + O\left( \mathtt {N}^{-1}\right) . \end{aligned}$$

(A.29)

1.2 On the Relation Between $\beta$ and $\alpha$

Here are the details of the important map that relates $\beta$ and $\alpha$:

Lemma A.2

Assume that the support of the random variable $E_2$ is bounded away from zero, so $Z= \exp (4 \beta E_2) \tanh ^2(\beta E_2)$ is supported on a compact subinterval of $(0, \infty )$. Assume also that $E_2$ is not constant. Then the equation

$$\begin{aligned} \frac{{\mathbb {E}}\left[ Z^\alpha \right] -1}{\alpha }\, =\, 0, \end{aligned}$$

(A.30)

has a unique real solution $\alpha$ for every $\beta >0$. This defines a map $\beta \mapsto \alpha (\beta )$ from $(0, \infty )$ to ${\mathbb {R}}$. This map is decreasing, hence it is a bijection, and it is real analytic.

Proof

Let $f: {\mathbb {R}}\times (0,\infty ) \rightarrow {\mathbb {R}}$ be the function defined by $f(\alpha , \beta ):=\frac{{\mathbb {E}}\left[ Z^\alpha \right] -1}{\alpha }$, for $\alpha \in {\mathbb {R}}{{\setminus }} \{0\}$ for $\alpha \ne 0$, and $f(0, \beta ):= {\mathbb {E}}[\log Z]$. It is straightforward to see, using the support properties of $E_2$, that f is real analytic on its entire domain. Then we observe that, for fixed $\alpha$, $Z^\alpha$ is an increasing function of $\beta$ and, by the support properties, this implies that $\partial _\beta f(\alpha , \beta )>0$ for every $\beta >0$ and $\alpha \in {\mathbb {R}}$. On the other hand if we set $g_\beta (\alpha )= {\mathbb {E}}\left[ Z^\alpha \right] -1$ we have that $\partial _\alpha f(\alpha , \beta )=( \alpha g'_\beta (\alpha )- g_\beta (\alpha )) / \alpha ^2$. But $g_\beta (\cdot )$ is (strictly) convex and $g_\beta (0)=0$: so $\alpha g'_\beta (\alpha )- g_\beta (\alpha )>0$ for $\alpha \ne 0$ and therefore $\partial _\alpha f(\alpha , \beta )>0$ for $\alpha \ne 0$. For $\alpha =0$ it suffices to perform a Taylor expansion of $g_\beta (\alpha )$ at $\alpha =0$ to see that $\partial _\alpha f(\alpha , \beta )\vert _{\alpha =0}= g^{\prime \prime }_\beta (0)/2>0$. The proof is completed by applying the Implicit Function Theorem for real analytic functions [26]. $\quad \square$