Abstract
Lattice Boltzmann schemes rely on the enlargement of the size of the target problem in order to solve PDEs in a highly parallelizable and efficient kinetic-like fashion, split into a collision and a stream phase. This structure, despite the well-known advantages from a computational standpoint, is not suitable to construct a rigorous notion of consistency with respect to the target equations and to provide a precise notion of stability. In order to alleviate these shortages and introduce a rigorous framework, we demonstrate that any lattice Boltzmann scheme can be rewritten as a corresponding multi-step Finite Difference scheme on the conserved variables. This is achieved by devising a suitable formalism based on operators, commutative algebra and polynomials. Therefore, the notion of consistency of the corresponding Finite Difference scheme allows to invoke the Lax-Richtmyer theorem in the case of linear lattice Boltzmann schemes. Moreover, we show that the frequently-used von Neumann-like stability analysis for lattice Boltzmann schemes entirely corresponds to the von Neumann stability analysis of their Finite Difference counterpart. More generally, the usual tools for the analysis of Finite Difference schemes are now readily available to study lattice Boltzmann schemes. Their relevance is verified by means of numerical illustrations.




Similar content being viewed by others
Notes
It is customary to call \(\text {D}_{d}\text {Q}_{q}\) a scheme in a \(d\)-dimensional space using \(q\) discrete velocities.
Matrix with zero entries on the diagonal.
We shall consistently use the notation \(\llbracket a, b \rrbracket {:}{=}\{a, a + 1, \dots , b\}\) for \(a, b \in {\mathbb {Z}}\) and \(a < b\).
In the whole work, the indeterminate of any polynomial shall be denoted by \(X\).
The function could take values in any ring, see [15].
Which interestingly corresponds to the discrete convolution product.
Since \({\mathbb {R}}\) is commutative, this is also an algebra over \({\mathbb {R}}\). It also an Hopf algebra over \({\mathbb {R}}\), since \({\mathbb {R}}\) is a field and can also be viewed as a free module where the scalars belong to \({\mathbb {R}}\) and the basis are the elements of the group \({\mathcal {T}}^{d}_{\Delta x}\).
Sometimes, we shall indulge to the notation
 .
.This is not always the case in literature but shall be used consistently in this paper. We put them at the beginning for the sake of presentation.
In this formulation, we do not account for the presence of source terms, since they do not play any role in the linear stability analysis.
This question is not harmless since for instance the \(\text {D}_{1}\text {Q}_{2}\) scheme rewrites as a leap-frog scheme [9] if the relaxation parameter is equal to two (see Appendix B). This very Finite Difference scheme can suffer from linear growth of the solution due to this issue, see Chapter 4 of [6].
The logarithmic term is rarely observed in simulations.
The same procedure is used to find the minimal polynomial, since we do not have a definition like Definition 4.
The principle is the same than the one linking the characteristic and the minimal polynomial through divisibility.
References
Chapman, S., Cowling, T.G., Burnett, D.: The Mathematical Theory of Non-uniform Gases: an Account of the Kinetic Theory of Viscosity. Thermal Conduction and Diffusion in Gases, Cambridge University Press, UK (1990)
Dubois, F.: Equivalent partial differential equations of a lattice Boltzmann scheme. Comput. Math. Appl. 55(7), 1441–1449 (2008)
Dubois, F.: Nonlinear fourth order Taylor expansion of lattice Boltzmann schemes. Asymptotic Analysis (Preprint), 1–41 (2019)
Benzi, R., Succi, S., Vergassola, M.: The lattice Boltzmann equation: theory and applications. Phys. Rep. 222(3), 145–197 (1992)
Sterling, J.D., Chen, S.: Stability analysis of lattice Boltzmann methods. J. Comput. Phys. 123(1), 196–206 (1996)
Strikwerda, J.C.: Finite Difference Schemes and Partial Differential Equations. SIAM, United States (2004)
Gustafsson, B., Kreiss, H.-O., Oliger, J.: Time-Dependent Problems and Difference Methods, vol. 123. John Wiley & Sons, US (2013)
Suga, S.: An accurate multi-level finite difference scheme for 1D diffusion equations derived from the lattice Boltzmann method. J. Stat. Phys. 140(3), 494–503 (2010)
Dellacherie, S.: Construction and analysis of lattice Boltzmann methods applied to a 1D convection-diffusion equation. Acta Appl. Math. 131(1), 69–140 (2014)
Ginzburg, I.: Une variation sur les propriétés magiques de modèles de Boltzmann pour l’écoulement microscopique et macroscopique. Thèse d’Habilitation à diriger des recherches Spécialité Sciences pour l’ingénieur (2009)
D’Humières, D., Ginzburg, I.: Viscosity independent numerical errors for Lattice Boltzmann models: From recurrence equations to “magic” collision numbers. Comput. Math. Appl. 58(5), 823–840 (2009)
Fučík, R., Straka, R.: Equivalent finite difference and partial differential equations for the lattice Boltzmann method. Comput. Math. Appl. 90, 96–103 (2021)
Bellotti, T.: Rigorous derivation of the macroscopic equations for the lattice Boltzmann method via the corresponding Finite Difference scheme. arXiv preprint arXiv:2205.02505 (2022)
Cull, P., Flahive, M., Robson, R.: Matrix Difference Equations, pp. 179–216. Springer, New York, NY (2005). https://doi.org/10.1007/0-387-27645-9_7
Milies, C.P., Sehgal, S.K., Sehgal, S.: An Introduction to Group Rings, vol. 1. Springer Science & Business Media, Berlin (2002)
Milne-Thomson, L.M.: The Calculus of Finite Differences. MacMillan and Co., United States (1933)
Miller, K.S.: An Introduction to the Calculus of Finite Differences and Difference Equations. Dover Publications, United States (1960)
Dummit, D.S., Foote, R.M.: Abstract Algebra, vol. 3. Wiley Hoboken, United States (2004)
Brewer, J.W., Bunce, J.W., Van Vleck, F.S.: Linear Systems over Commutative Rings. CRC Press, United States (1986)
Hou, S.-H.: Classroom Note: A Simple Proof of the Leverrier-Faddeev Characteristic Polynomial Algorithm. SIAM Rev. 40(3), 706–709 (1998)
D’Humières, D.: Generalized Lattice-Boltzmann Equations, pp. 450–458. American Institute of Aeronautics and Astronautics Inc, United States (1992). https://doi.org/10.2514/5.9781600866319.0450.0458
Graille, B.: Approximation of mono-dimensional hyperbolic systems: A lattice Boltzmann scheme as a relaxation method. J. Comput. Phys. 266, 74–88 (2014)
Farag, G., Zhao, S., Chiavassa, G., Boivin, P.: Consistency study of Lattice-Boltzmann schemes macroscopic limit. Phys. Fluids 33(3), 037101 (2021)
Dubois, F., Graille, B., Rao, S.R.: A notion of non-negativity preserving relaxation for a mono-dimensional three velocities scheme with relative velocity. J. Comput. Sci. 47, 101181 (2020)
Rota, G.-C., Kahaner, D., Odlyzko, A.: On the foundations of combinatorial theory. VIII. Finite operator calculus. J. Math. Anal. Appl. 42(3), 684–760 (1973)
Bellotti, T., Gouarin, L., Graille, B., Massot, M.: Multiresolution-based mesh adaptation and error control for lattice Boltzmann methods with applications to hyperbolic conservation laws. arXiv preprint arXiv:2102.12163 (2021)
Junk, M., Yang, Z.: \(L^2\) convergence of the lattice Boltzmann method for one dimensional convection-diffusion-reaction equations. Commun. Comput. Phy. 17(5), 1225–1245 (2015)
Van Leemput, P., Rheinländer, M., Junk, M.: Smooth initialization of lattice Boltzmann schemes. Comput. Math. Appl. 58(5), 867–882 (2009)
Rheinländer, M.K.: Analysis of lattice-Boltzmann methods: asymptotic and numeric investigation of a singularly perturbed system. PhD thesis (2007)
Coreixas, C., Chopard, B., Latt, J.: Comprehensive comparison of collision models in the lattice Boltzmann framework: Theoretical investigations. Phys. Rev. E 100(3), 033305 (2019)
Bouchut, F.: Nonlinear Stability of Finite Volume Methods for Hyperbolic Conservation Laws: And Well-Balanced Schemes for Sources. Springer Science & Business Media, Berlin (2004)
Junk, M., Yong, W.-A.: Weighted \(L^2\)-Stability of the Lattice Boltzmann Method. SIAM J. Numer. Anal. 47(3), 1651–1665 (2009)
Caetano, F., Dubois, F., Graille, B.: A result of convergence for a mono-dimensional two-velocities lattice Boltzmann scheme. arXiv preprint arXiv:1905.12393 (2019)
Ding, J., Zhou, A.: Eigenvalues of rank-one updated matrices with some applications. Appl. Math. Lett. 20(12), 1223–1226 (2007)
Junk, M., Rheinlander, M.: Regular and multiscale expansions of a lattice Boltzmann method. Prog. Comput. Fluid Dynamics Inter. J. 8(1–4), 25–37 (2008)
Simonis, S., Frank, M., Krause, M.J.: On relaxation systems and their relation to discrete velocity Boltzmann models for scalar advection-diffusion equations. Phil. Trans. R. Soc. A 378(2175), 20190400 (2020)
Miller, J.J.: On the location of zeros of certain classes of polynomials with applications to numerical analysis. IMA J. Appl. Math. 8(3), 397–406 (1971)
Lax, P.D., Richtmyer, R.D.: Survey of the stability of linear finite difference equations. Commun. Pure Appl. Math. 9(2), 267–293 (1956)
Dubois, F.: Simulation of strong nonlinear waves with vectorial lattice Boltzmann schemes. Int. J. Mod. Phys. C 25(12), 1441014 (2014)
Bellotti, T., Gouarin, L., Graille, B., Massot, M.: Multidimensional fully adaptive lattice Boltzmann methods with error control based on multiresolution analysis. arXiv preprint arXiv:2103.02903 (2021)
Dubois, F., Lallemand, P.: Towards higher order lattice Boltzmann schemes. J. Stat. Mech: Theory Exp. 2009(06), 06006 (2009)
Acknowledgements
The authors thank the three anonymous referees for the comments and suggestions allowing for a significant improvement of the manuscript. The authors deeply thank L. Gouarin for the help in the implementation of the symbolic computations needed to check the provided examples. T. Bellotti friendly thanks his fellow PhD candidates C. Houpert, Y. Le Calvez, A. Louvet, M. Piquerez and D. Stantejsky for the useful discussions on algebra. This author is supported by a PhD funding (year 2019) from Ecole polytechnique.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: A different reduction strategy: mathematical framework
According to the discussion presented in Sect. 5.3 through an example and again in the case \(N= 1\), we define the polynomial annihilating all the first row of the matrix \(\varvec{A}\), except the very first element.
Definition 8
We call \(\nu _{\varvec{A}} \in {\mathcal {D}}^{d}_{\Delta x}[X]\) “minimal polynomial annihilating most of the first row” (MPAMFR) of \(\varvec{A}\) the monic polynomial of minimal degree under the form
with \((\psi _{k})_{k= 0}^{k= \text {deg}(\nu _{\varvec{A}})} \subset {\mathcal {D}}^{d}_{\Delta x}\) such that for every \(j\in \llbracket 2, q \rrbracket \)
By seeing the coefficients of this unknown polynomial as the unknowns of a linear system, the problem of finding \(\nu _{\varvec{A}}\) can be rewritten in terms of matrices.Footnote 13 Let \(K \in \llbracket 1, \text {deg}(\mu _{\varvec{A}}) \rrbracket \) and construct the matrix of variable size
Therefore, we want to find the smallest \(K \in \llbracket 1, \text {deg}(\mu _{\varvec{A}}) \rrbracket \) such that \(\varvec{V}_{K} (\psi _1, \dots , \psi _{K-1})^{\intercal } = \varvec{r}_K\) On the other hand, it should be observed that the zero order coefficient \(\psi _0\) remains free. This underdetermination comes from the fact that we do not request that \(\nu _{\varvec{A}}\) annihilates the whole first row.
Proposition 14
Let \(N= 1\), then the lattice Boltzmann scheme (6) corresponds to a multi-step explicit Finite Difference scheme on the conserved moment \(m_1\) under the form
where \((\psi _{k})_{k= 1}^{k= \text {deg}(\nu _{\varvec{A}})} \subset {\mathcal {D}}^{d}_{\Delta x}\) are the coefficients of \(\nu _{\varvec{A}} = \sum _{k= 0}^{k= \text {deg}(\nu _{\varvec{A}})} \psi _{k} X^{k}\).
Proof
By the choice of polynomial, we have that
Restarting from the proof of Proposition 4, we have
therefore
Performing the usual change of indices yields the result. \(\square \)
Looking at Eq. (A2), we see that we do not need the value of \(\psi _0\) to reduce the scheme, neither to reduce \(\varvec{A}\) nor to deal with the equilibria through \(\varvec{B}\). Changing time indices and putting everything on the left hand side
where we have defined
This generates a polynomial, which is indeed \(\nu _{\varvec{A}}\) but with a precise choice of \(\psi _0\). We will soon give a precise characterization of this particular polynomial.
Definition 9
We call \({\tilde{\nu }}_{\varvec{A}} \in {\mathcal {D}}^{d}_{\Delta x}[X]\) “minimal polynomial annihilating the first row” (MPAFR) of \(\varvec{A}\) the monic polynomial of minimal degree under the form
such that for every \(j\in \llbracket 1, q \rrbracket \)
Compared to Definition 8, we are just asking the property to hold also for the very first element of the first row, namely for \(j= 1\). This polynomial is \(\nu _{\varvec{A}}\) for a particular choice of \(\psi _0\). It has been deduced from the reduction of the lattice Boltzmann scheme.
Lemma 15
The polynomial of degree \(\text {deg}(\nu _{\varvec{A}})\) given by
where \((\psi _{k})_{k= 1}^{k= \text {deg}(\nu _{\varvec{A}})} \subset {\mathcal {D}}^{d}_{\Delta x}\) are the coefficients of a MPAMFR \(\nu _{\varvec{A}}\) of \(\varvec{A}\) being \(\nu _{\varvec{A}} = \sum _{k= 0}^{k= \text {deg}(\nu _{\varvec{A}})} \psi _{k} X^{k}\), is the MPAFR \({\tilde{\nu }}_{\varvec{A}}\) of \(\varvec{A}\).
Proof
We are only left to check Eq. (A4) for \(j= 1\). \(\square \)
So in order to reduce the lattice Boltzmann scheme to a Finite Difference scheme using the new strategy, considering a MPAMFR or the MPAFR is exactly the same thing. Moreover, the MPAFR (but not the more general MPAMFR) can be linked to the minimal/characteristic polynomial.Footnote 14
Lemma 16
Let \(\mu _{\varvec{A}} \in {\mathcal {D}}^{d}_{\Delta x}[X]\) be the minimal polynomial of \(\varvec{A}\), then \({\tilde{\nu }}_{\varvec{A}}\) exists and divides the minimal polynomial \(\mu _{\varvec{A}}\). Moreover \(\text {deg}({\tilde{\nu }}_{\varvec{A}}) = \text {deg}(\nu _{\varvec{A}}) \le \text {deg}(\mu _{\varvec{A}})\).
Proof
The proof goes like the standard one of Lemma 7. Consider \(\mu _{\varvec{A}} = X^{\text {deg}(\mu _{\varvec{A}})} + \omega _{\text {deg}(\mu _{\varvec{A}})-1}X^{\text {deg}(\mu _{\varvec{A}})-1} + \dots + \omega _1 X+ \omega _0\). Consider the Euclidian division between \(\mu _{\varvec{A}}\) and \({\tilde{\nu }}_{\varvec{A}}\): there exist \(Q, R \in {\mathcal {D}}^{d}_{\Delta x}[X]\) such that
with either \(0< \text {deg}(R) < \text {deg}({\tilde{\nu }}_{\varvec{A}})\) or \(\text {deg}(R) =0\) (constant reminder polynomial). Let us indeed write
Suppose that \(R \not \equiv 0\), then we have for every \(j\in \llbracket 1, q \rrbracket \)
thus
with \(0<\text {deg}(R) < \text {deg}({\tilde{\nu }}_{\varvec{A}})\), which contradicts the minimality of \({\tilde{\nu }}_{\varvec{A}}\). Thus necessarily \(\text {deg}(R) = 0\) so the polynomial is constant, but to have the previous property, the constant must be zero, thus \(R \equiv 0\). \(\square \)
Appendix B: Additional examples
In this Section, we gather more examples concerning the application of our theory to lattice Boltzmann schemes which can be found in the literature.
1.1 B. 1 \(\text {D}_{1}\text {Q}_{2}\) with one conservation law
Consider the scheme by [9, 22] taking \(d= 1\), \(q= 2\) and \(N= 1\) with \(c_1 = 1\) and \(c_2 = -1\) and
We recall that \(m_2^{\text {eq}}: {\mathbb {R}}\rightarrow {\mathbb {R}}\) is a given function of \(m_1\). The scheme can be used to simulate a non-linear scalar conservation law such as Eq. (7) using an acoustic scaling and a non-linear diffusion equation with a parabolic scaling, namely when \(\lambda \propto 1/\Delta x\). However, the scheme is not rich enough to simulate more complex equations. As already pointed out in the introduction, the Finite Difference equivalent of this scheme has already been studied by [9] in the case where the equilibria are linear functions. It can be easily seen, even by hand since dealing with a \(2\times 2\) matrix, that

The minimal polynomial coincides with the characteristic polynomial. This can be seen, as usual, by trying to consider \(\alpha _0\) and \(\alpha _1\) such that
The only way of annihilating the first entry is to take \(\alpha _0 = \alpha _1 = 0\), which is trivial. Thus the minimal polynomial is of degree two and then coincides with the characteristic polynomial. The equivalent Finite Difference scheme is
This scheme is a linear combination of the Lax-Friedrichs scheme (for \(s_2 = 1\)) with weight \(2 - s_2\) and the leap-frog scheme (for \(s_2 = 2\)) with weight \(-(1-s_2)\). It is a \(\theta \)-scheme between them with \(\theta = 2 - s_2\) as long as \(s_2 \in [1, 2]\).
1.2 B. 2 \(\text {D}_{1}\text {Q}_{3}\) MRT for one conservation law
Consider the \(\text {D}_{1}\text {Q}_{3}\) MRT scheme by [12], which reads with our notations \(d= 1\), \(q= 3\) and \(N= 1\) with \(c_1 = 0\), \(c_2 = 1\) and \(c_3 = -1\) and
and \(m_2^{\text {eq}}, m_3^{\text {eq}}: {\mathbb {R}}\rightarrow {\mathbb {R}}\) being given functions of \(m_1\). The characteristic polynomial, corresponding to the minimal polynomial is

Then the corresponding Finite Difference scheme is
This coincides with the one found by [12]. The SRT version comes by considering \(s_2 = s_3\), thus having
coinciding with the one found by [12] and by [8].
1.3 B. 3 \(\text {D}_{2}\text {Q}_{4}\) for one conservation law
Consider \(d= 2\), \(q= 4\) and \(N= 1\) with \(\varvec{c}_1 = (1, 0)^{\intercal }\), \(\varvec{c}_2 = (0, 1)^{\intercal }\), \(\varvec{c}_3 = (-1, 0)^{\intercal }\) and \(\varvec{c}_4 = (0, -1)^{\intercal }\) and
We have decided to set \(s_3 = s_2\) not to favor one particular direction between x and y and \(s_4 = 1\) to keep the scheme simpler. Moreover, we take \(m_4^{\text {eq}} \equiv 0\) for simplicity and \(m_2^{\text {eq}}, m_3^{\text {eq}} : {\mathbb {R}}\rightarrow {\mathbb {R}}\) are given functions of \(m_1\). This can be used, for example, coupled with other schemes of the same nature (building what we call a “vectorial scheme” [39]) to easily simulate systems of non-linear conservation laws for \(d= 2\), see [40], under acoustic scaling. After some computation, the characteristic polynomial of \(\varvec{A}\) reads

where we have introduced the short-hands \({\mathsf {A}}_{\text {a}}{:}{=}({\mathsf {x}}+ \overline{{\mathsf {x}}} + {\mathsf {y}}+ \overline{{\mathsf {y}}})/4 \in {\mathcal {D}}^{d}_{\Delta x}\) and \({\mathsf {A}}_{\text {d}}{:}{=}({\mathsf {x}}{\mathsf {y}}+ {\mathsf {x}}\overline{{\mathsf {y}}} + \overline{{\mathsf {x}}} {\mathsf {y}}+ \overline{{\mathsf {x}}} \overline{{\mathsf {y}}})/4 \in {\mathcal {D}}^{d}_{\Delta x}\), yielding respectively the average between neighbors along the axis and along the diagonals. One can check as usual that it coincides with the minimal polynomial. The equivalent Finite Difference scheme is
It is interesting to observe how the scheme computes the first-order derivatives in space of \(m_2^{\text {eq}}\) and \(m_3^{\text {eq}}\) at time \(t^{n- 1}\).
1.4 B. 4 \(\text {D}_{2}\text {Q}_{5}\) for one conservation law
In this example, we consider the scheme taken from [41]. Let \(d= 2\), \(q= 5\) and \(N= 1\) with \(\varvec{c}_1 = (0, 0)^{\intercal }\), \(\varvec{c}_2 = (1, 0)^{\intercal }\), \(\varvec{c}_3 = (0, 1)^{\intercal }\), \(\varvec{c}_4 = (-1, 0)^{\intercal }\) and \(\varvec{c}_5 = (0, -1)^{\intercal }\) and
with \(s_2, s_3, s_4, s_5 \in ]0, 2]\). One does not favor the x direction compared to the y direction, see [41], thus we set \(s_2 = s_3\). Moreover, the assumptions on the moments at equilibrium are \(m_2^{\text {eq}} \equiv m_3^{\text {eq}} \equiv m_5^{\text {eq}} \equiv 0\). The only one which does not vanish is \(m_4^{\text {eq}} : {\mathbb {R}}\rightarrow {\mathbb {R}}\). The scheme can be used to solve thermic problems. Then, the characteristic polynomial of \(\varvec{A}\) is given by

where the coefficients are given by
and finally
Therefore, the corresponding Finite Difference scheme on the conserved variable \(m_1\) reads
where the operators applied on the equilibrium \(m_4^{\text {eq}}\) are given by
and finally
This example shows that for large lattice Boltzmann schemes, the corresponding Finite Difference scheme can be rather complicated and not simple to analyze, especially for large \(Q\).
Rights and permissions
About this article
Cite this article
Bellotti, T., Graille, B. & Massot, M. Finite Difference formulation of any lattice Boltzmann scheme. Numer. Math. 152, 1–40 (2022). https://doi.org/10.1007/s00211-022-01302-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-022-01302-2



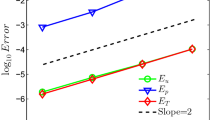
 .
.