Skip to main content

Advertisement

SpringerLink
Log in

Hierarchical error estimates for the energy functional in obstacle problems

  • Published:
Numerische Mathematik Aims and scope Submit manuscript

Abstract

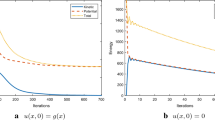
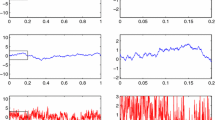
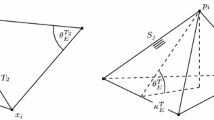
We present a hierarchical a posteriori error analysis for the minimum value of the energy functional in symmetric obstacle problems. The main result is that the error in the energy minimum is, up to oscillation terms, equivalent to an appropriate hierarchical estimator. The proof does not invoke any saturation assumption. We even show that small oscillation implies a related saturation assumption. In addition, we prove efficiency and reliability of an a posteriori estimate of the discretization error and thereby cast some light on the theoretical understanding of previous hierarchical estimators. Finally, we illustrate our theoretical results by numerical computations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ainsworth M., Oden J.T.: A posteriori error estimation in finite element analysis. Wiley, New York (2000)

    MATH  Google Scholar 

  2. Bank R.E., Smith R.K.: A posteriori error estimates based on hierarchical bases. SIAM J. Numer. Anal. 30, 921–935 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  3. Bartels S., Carstensen C.: Averaging techniques yield reliable a posteriori finite element error control for obstacle problems. Numer. Math. 99(2), 225–249 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  4. Bornemann F.A., Erdmann B., Kornhuber R.: A posteriori error estimates for elliptic problems in two and three space dimensions. SIAM J. Numer. Anal. 33, 1188–1204 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  5. Braess D.: A posteriori error estimators for obstacle problems—another look. Numer. Math. 101, 415–421 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  6. Braess D., Hoppe R.H.W., Schöberl J.: A posteriori estimator for obstacle problems by the hypercircle method. Comp. Vis. Sci. 11, 351–362 (2008)

    Article  Google Scholar 

  7. Brezzi F., Caffarelli L.A.: Convergence of the discrete free boundaries for finite element approximations. RAIRO Numer. Anal. 17, 385–395 (1983)

    MathSciNet  Google Scholar 

  8. Brezzi F., Hager W.W., Raviart P.A.: Error estimates for the finite element solution of variational inequalities I. Numer. Math. 28, 431–443 (1977)

    Article  MathSciNet  MATH  Google Scholar 

  9. Deuflhard P., Leinen P., Yserentant H.: Concepts of an adaptive hierarchical finite element code. IMPACT Comput. Sci. Eng. 1, 3–35 (1989)

    Article  MATH  Google Scholar 

  10. Dörfler W., Nochetto R.H.: Small data oscillation implies the saturation assumption. Numer. Math. 91, 1–12 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  11. Fierro, F., Veeser, A.: A posteriori error estimators for regularized total variation of characteristic functions. SIAM J. Numer. Anal. 41(6), 2032–2055 (2003, electronic)

    Google Scholar 

  12. Hoppe R.H.W., Kornhuber R.: Adaptive multilevel-methods for obstacle problems. SIAM J. Numer. Anal. 31(2), 301–323 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  13. Kornhuber R.: A posteriori error estimates for elliptic variational inequalities. Comp. Math. Appl. 31, 49–60 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  14. Kornhuber R.: Adaptive monotone multigrid methods for nonlinear variational problems. Teubner, Stuttgart (1997)

    MATH  Google Scholar 

  15. Kornhuber R., Zou Q.: Efficient and reliable hierarchical error estimates for the discretization error of elliptic obstacle problems. Preprint 519, DFG Research Center Matheon. Math. Comp. 80, 69–88 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  16. Nochetto R.H., Siebert K.G., Veeser A.: Pointwise a posteriori error control for elliptic obstacle problems. Numer. Math. 95, 631–658 (2003)

    Article  MathSciNet  Google Scholar 

  17. Sander, O.: Multidimensional coupling in a human knee model. PhD thesis, FU Berlin (2008)

  18. Siebert K.G., Veeser A.: A unilaterally constrained quadratic minimization with adaptive finite elements. SIAM J. Optim. 18, 260–289 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  19. Veeser A.: Efficient and reliable a posteriori error estimators for elliptic obstacle problems. SIAM J. Numer. Anal. 39(1), 146–167 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  20. Veeser A.: Convergent adaptive finite elements for the nonlinear Laplacian. Numer. Math. 92(4), 743–770 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  21. Veeser, A., Verfürth, R.: Poincaré constants of finite element stars. Report Dp. di Mathematica, U Milano and Fak. Mathematik, U Bochum (2010)

  22. Verfürth R.: A review of a posteriori error estimation and adaptive mesh—refinement techniques. Wiley-Teubner, New York (1996)

    MATH  Google Scholar 

  23. Zienkiewicz O.C., De S.R. Gago J.P., Kelly D.W.: The hierarchical concept in finite element analysis. Comp. Str. 16, 53–65 (1983)

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Freie Universität Berlin, Berlin, Germany

    Qingsong Zou, Andreas Veeser, Ralf Kornhuber & Carsten Gräser

Authors
  1. Qingsong Zou
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Andreas Veeser
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ralf Kornhuber
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Carsten Gräser
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ralf Kornhuber.

Additional information

The first author is partially supported by NSFC under the grant 10601070 and by an Alexander von Humboldt fellowship hosted by Freie Universität Berlin.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zou, Q., Veeser, A., Kornhuber, R. et al. Hierarchical error estimates for the energy functional in obstacle problems. Numer. Math. 117, 653–677 (2011). https://doi.org/10.1007/s00211-011-0364-5

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00211-011-0364-5

Keywords

Search

Navigation