Abstract.
The aim of this paper is to discuss the question of existence and multiplicity of strong local minimizers for a relatively large class of functionals  :
:  from a purely topological point of view. The basic assumptions on
from a purely topological point of view. The basic assumptions on  are sequential lower semicontinuity with respect to W1,p-weak convergence and W1,p-weak coercivity, and the target is a multiplicity bound on the number of such minimizers in terms of convenient topological invariants of the manifolds
are sequential lower semicontinuity with respect to W1,p-weak convergence and W1,p-weak coercivity, and the target is a multiplicity bound on the number of such minimizers in terms of convenient topological invariants of the manifolds  and
and  .
.
In the first part of the paper, we focus on the case where  is non-contractible and proceed by establishing a link between the latter problem and the question of enumeration of homotopy classes of continuous maps from various skeleta of
is non-contractible and proceed by establishing a link between the latter problem and the question of enumeration of homotopy classes of continuous maps from various skeleta of  into
into  . As this in turn can be tackled by the so-called obstruction method, it is evident that our results in this direction are of a cohomological nature.
. As this in turn can be tackled by the so-called obstruction method, it is evident that our results in this direction are of a cohomological nature.
The second part is devoted to the case where  =ℝN and
=ℝN and  is a bounded smooth domain. In particular we consider integrals
is a bounded smooth domain. In particular we consider integrals

where the above assumptions on  can be verified when the integrand F is quasiconvex and pointwise p-coercive with respect to the gradient argument. We introduce and exploit the notion of a topologically non-trivial domain and under this establish the first existence and multiplicity result for strong local minimizers of
can be verified when the integrand F is quasiconvex and pointwise p-coercive with respect to the gradient argument. We introduce and exploit the notion of a topologically non-trivial domain and under this establish the first existence and multiplicity result for strong local minimizers of  that in turn settles a longstanding open problem in the multi-dimensional calculus of variations as described in [6].
that in turn settles a longstanding open problem in the multi-dimensional calculus of variations as described in [6].
Similar content being viewed by others
References
Acerbi, E., Fusco, N.: Semicontinuity problems in the calculus of variations. Arch. Ration. Mech. Anal. 86, 125–145 (1984)
Ball, J.M.: Convexity conditions and existence theorems in nonlinear elasticity. Arch. Ration. Mech. Anal. 63, 337–403 (1977)
Ball, J.M.: Constitutive inequalities and existence theorems in nonlinear elastostatics. In: Nonlinear analysis and mechanics: Heriot-Watt Symposium 1, (Ed. Knops, R.J.), Pitman, London, 1977
Ball, J.M.: Global invertibility of Sobolev functions and the interpenetration of matter. Proc. Roy. Soc. Edin. A 88, 315–328 (1981)
Ball, J.M., Currie, J.C., Olver, P.J.: Null Lagrangians, weak continuity and variational problems of arbitrary order. J. Funct. Anal. 41, 135–174 (1981)
Ball, J.M.: Some open problems in elasticity. In: Geometry, mechanics and dynamics, Springer, New York, 3–59 (2002)
Bethuel, F., Zheng, X.: Density of smooth functions between two manifolds in Sobolev spaces. J. Funct. Anal. 80, 60–75 (1988)
Bethuel, F.: The approximation problem for Sobolev maps between two manifolds. Acta Math. 160, 153–206 (1991)
Birman, J.S.: Braids, links and mapping class groups. Annals of Mathematics studies 82, Princeton University Press, 1975
Bredon, G.E.: Topology and Geometry. Graduate Texts in Mathematics 139, Springer-Verlag, 1993
Brezis, H., Li, Y.Y.: Topology and Sobolev spaces. J. Funct. Anal. 183, 321–369 (2001)
Brezis, H., Li, Y.Y., Mironescu, P., Nirenberg, L.: Degree and Sobolev spaces. Topol. Methods Nonlinear Anal. 13, 181–190 (1991)
Brezis, H., Nirenberg, L.: Degree theory and BMO, Parts I & II: Compact manifolds without boundaries & Compact manifolds with boundaries. Selecta Math. 1 & 2, 197–263 & 309–368 (1995) & (1996)
Casson, A.J., Bleiler, S.A.: Automorphisms of surfaces after Nielsen and Thurston. LMSST 9, Cambridge University Press, 1988
Chang, K.C.: Infinite dimensional Morse theory and multiple solution problems. Progress in Nonlinear Differential Equations and their Applications 6, Bikhäuser, 1991
Dacorogna, B.: Direct methods in the calculus of variations. Applied Mathematical Sciences 78, Springer-Verlag, 1988
Dacorogna, B., Fonseca, I., Maly, J., Trivisa, K.: Manifold constrained variational problems. Calc. Var. & PDEs. 9, 185–206 (1999)
Dal Maso, G.: Introduction to Γ-convergence. Progress in Nonlinear Differential Equations and their Applications 8, Bikhäuser, 1992
De Giorgi, E.: Convergence problems for functionals and operators. In: Proc. Int. meeting on recent methods in nonlinear analysis, (Eds. De Giorgi, E. et. al.), 223–244 (1979)
Dieudonné, J.: A history of Algebraic and Differential Topology 1900–1960. Birkhäuser, 1989
Dugundji, J.: Topology. Allyn and Bacon Series in Advanced Mathematics, 1966
Duzaar, F., Kuwert, E.: Minimization of conformally invariant energies in homotopy classes. Calc. Var. & PDEs 6, 285–313 (1998)
Eells, J., Lemaire, L.: Two reports on harmonic maps, Bull. Lond. Math. Soc. 10 & 20, 1–68 & 385–524 (1978) & (1988)
Eells, J., Wood, J.C.: Restrictions on harmonic maps of surfaces. Topology 15, 263–266 (1976)
Eilenberg, S.: Cohomology and continuous mappings, Ann. of Math. 40, 231–251 (1940)
Evans, L.C., Gariepy, R.: Some remarks concerning quasiconvexity and strong convergence. Proc. Roy. Soc. Edin. A 106, 53–61 (1987)
Federer, H.: A study of function spaces by spectral sequences. Trans. Amer. Math. Soc. 82, 340–361 (1956)
Federer, H.: Geometric measure theory. Graduate Texts in Mathematics 153, Springer-Verlag, 1969.
Giaquinta, M., Modica, G., Souček, J.: The gap phenomenon for variational integrals in Sobolev spaces. Proc. Roy. Soc. Edin. A 120, 93–98 (1992)
Giaquinta, M., Modica, G., Souček, J.: Cartesian currents in the calculus of variations, Vols. I & II, A series of Modern Surveys in Mathematics 38, Springer, 1997
Gottlieb, D.H.: A certain subgroup of the fundamental group. Amer. J. Math. 87, 840–856 (1965)
Griffiths, H.B.: The fundamental group of a surface, and a theorem of Shreier. Acta Math. 110, 1–17 (1963)
Graves, L.M.: The Weierstrass condition for multiple integral variational problems. Duke Math. J. 5, 656–660 (1939)
Hajlasz, P.: Approximation of Sobolev mappings. Nonlinear Analysis TMA 22, 1579–1591 (1994)
Hansen, V.L.: The homotopy problem for the components in the space of maps on the n-sphere. Quart. J. Math. Oxford 25, 313–321 (1974)
Hansen, V.L.: Spaces of maps into Eilenberg-MacLane spaces. Can. J. Math. 33, 782–785 (1981)
Hansen, V.L.: The homotopy groups of a space of maps between oriented closed surfaces. Bull. Lond. Math. Soc. 15, 360–364 (1983)
Hang, F., Lin, F.H.: Topology of Sobolev mappings. Math. Res. Lett. 8, 321–330 (2001)
Hopf, H.: Abbildungsklassen n-dimensionaler Mannigfaltigkeiten. Math. Ann. 96, 209–224 (1927)
Hu, S.T.: Concerning the homotopy groups of the components of the mapping space
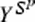 Indag. Math. 8, 623–629 (1946)
Indag. Math. 8, 623–629 (1946)Hu, S.T.: Homotopy theory. Academic Press, New York, 1959
Hurewicz, W.: Beiträge zur topologie der deformationen. Verh. Nedel. Akad. Wetensch. 38 & 39, 112–119, 521–528 & 117–126, 215–224 (1935) & (1936)
Hurewicz, W.: Collected works of Witold Hurewicz. (Ed. Kuperberg, K.), American Mathematical Society, 1995
Hüsseinov, F.: Weierstrass condition for the general basic variational problem. Proc. Roy. Soc. Edin. A 125, 801–806 (1995)
John, F.: Uniqueness of nonlinear equilibrium for prescribed boundary displacement and sufficiently small strains. Comm. Pure Appl. Math. 25, 617–634 (1972)
Kinderlehrer, D., Pedregal, P.: Characterization of Young measures generated by gradients. Arch. Ration. Mech. Anal. 115, 329–365 (1991)
Kinderlehrer, D., Pedregal, P.: Gradient Young measures generated by sequences in Sobolev spaces. J. Geom. Anal. 4, 59–90 (1994)
Kneser, H.: Die Deformationssätze der einfach zusammenhängenden Flächen. Math. Z. 25, 362–372 (1926)
Koh, S.S.: Note on the properties of the components of the mapping spaces
 Proc. Amer. Math. Soc. 11, 896–904 (1960)
Proc. Amer. Math. Soc. 11, 896–904 (1960)Knops, R., Stuart, C.: Quasiconvexity and uniqueness of equilibrium solutions in non-linear elasticity. Arch. Rational Mech. Anal. 86, 233–249 (1984)
Kohn, R.V., Sternberg, P.: Local minimisers and singular perturbations. Proc. Roy. Soc. Edin. A 111, 69–84 (1989)
Kristensen, J., Taheri, A.: Partial regularity of strong local minimizers in the multi-dimensional calculus of variations. Max-Planck-Institute MIS (Leipzig) Preprint-Nr. 59, 2001
Lemaire, L.: Applications harmoniques des surfaces Riemanniennes. J. Diff. Geom. 13, 51–87 (1978)
Lusternik, L., Schnirelman, L.: Méthodes topologiques dans les problémes variationelles. Actualities Sci. Ind. 188, 1934
Manfredi, J.: Weakly monotone functions. J. Geom. Anal. 4, 393–402 (1994)
Meyers, N.G.: Quasiconvexity and lower semicontinuity of multiple integrals of any order. Trans. Amer. Math. Soc. 119, 225–249 (1965)
Milnor, J.: Morse theory. Annals of Mathematics studies, 51, Princeton University Press, 1963
Morrey, C.B.: The problem of Plateau on a Riemannian manifold. Ann. of Math. 49, 807–851 (1948)
Morrey, C.B.: Multiple integrals in the calculus of variations. Graduate Texts in Mathematics 130, Springer-Verlag, 1966
Müller, S., Tang, Q., Yan, B.S.: On a new class of elastic deformations not allowing for cavitation. Ann. Inst. Henri Poincaré, Analyse non linéaire 11, 217–243 (1994)
Müller, S., Spector, S.J.: An existence theory for nonlinear elasticity that allows for cavitation. Arch. Rational Mech. Anal. 131, 1–66 (1995)
Müller, S., Spector, S.J., Tang, Q.: Invertibility and a topological property of Sobolev maps. SIAM J. Math. Anal. 27, 959–976 (1996)
Olum, P.: Obstructions to extensions and homotopies. Ann. of Math. 52, 1–50 (1950)
Olum, P.: Mappings to manifolds and the notion of degree. Ann. of Math. 58, 458–480 (1953)
Palais, R.S.: Morse theory on Hilbert manifolds. Topology. 2, 299–340 (1963)
Palais, R.S.: Lusternik Schnirelman theory on Banach manifolds. Topology. 5, 115–132 (1966)
Palais, R.S.: Homotopy theory of infinite dimensional manifolds. Topology. 5, 1–16 (1966)
Palais, R.S.: Foundations of global non-linear analysis. Benjamin, New York, 1968
Palais, R.S., Smale, S.: A generalized Morse theory. Bull. Amer. Math. Soc. 70, 165–171 (1964)
Post, K., Sivaloganathan, J.: On homotopy conditions and the existence of multiple equilibria in finite elasticity. Proc. Roy. Soc. Edin. A 127, 595–614 (1997)
Rubinstein, J., Sternberg, P.: Homotopy classification of minimizers of the Ginzburg-Landau energy and the existence of permanent currents. Comm. Math. Phys. 179, 257–263 (1996)
Sacks, J., Uhlenbeck, K.: The existence of minimal immersions of 2-spheres. Ann. of Math. 113, 1–24 (1981)
Smale, S.: Diffeomorphisms of the 2-sphere. Proc. Amer. Math. Soc. 10, 621–626 (1959)
Šverák, V.: Regularity properties of deformations with finite energy. Arch. Rational Mech. Anal. 100, 105–127 (1988)
Schoen, R., Uhlenbeck, K.: Boundary regularity and the Dirichlet problem for harmonic maps. J. Diff. Geom. 18, 253–268 (1983)
Schwartz, J.T.: Nonlinear functional analysis. Gordon and Breach Science Publishers, 1969
Scott, P.: The geometries of 3-manifolds. Bull. Lond. Math. Soc. 15, 401–487 (1983)
Taheri, A.: Sufficiency theorems for local minimizers of the multiple integrals of the calculus of variations. Proc. Roy. Soc. Edin. A 131, 155–184 (2001)
Taheri, A.: Strong versus weak local minimizers for the perturbed Dirichlet functional. Calc. Var. & PDEs 15, 215–235 (2002)
Taheri, A.: On critical points of functionals with polyconvex integrands. J. Convex Anal. 9, 55–72 (2002)
Taheri, A.: Quasiconvexity and uniqueness of stationary points in the multi-dimensional calculus of variations. To appear in Proc. Amer. Math. Soc. 2003
Taheri, A.: On Artin’s braid group and polyconvexity in the calculus of variations. To appear in J. Lond. Math. Soc. 2003
Uhlenbeck, K.: Morse theory on Banach Manifolds. J. Funct. Anal. 10, 430–445 (1972)
Uhlenbeck, K.: Morse theory by perturbation methods with applications to harmonic maps. Trans. Amer. Math. Soc. 267, 569–583 (1981)
Vodopyanov, S.K., Gol’dshtein, V.M.: Quasiconformal mappings and spaces of functions with generalized first derivatives. Siberian Math. J. 17, 515–531 (1977)
White, B.: Infima of energy functionals in homotopy classes of mappings. J. Diff. Geom. 23, 127–142 (1986)
White, B.: Homotopy classes in Sobolev spaces and the existence of energy minimizing maps. Acta Math. 160, 1–17 (1988)
Whitehead, G.W.: On products in homotopy groups. Ann. of Math. 47, 460–475 (1946)
Whitehead, G.W., Elements of homotopy theory, Graduate Texts in Mathematics 61, Springer, 1978.
Whitehead, J.H.C.: On certain theorems of G.W. Whitehead. Ann. of Math. 58, 418–428 (1953)
Whitney, H.: The maps of an n-complex into an n-sphere. Duke Math. J. 3, 51–55 (1937)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by C.A. Stuart
Rights and permissions
About this article
Cite this article
Taheri, A. Local Minimizers and Quasiconvexity – the Impact of Topology. Arch. Rational Mech. Anal. 176, 363–414 (2005). https://doi.org/10.1007/s00205-005-0356-7
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00205-005-0356-7



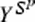 Indag. Math. 8, 623–629 (1946)
Indag. Math. 8, 623–629 (1946) Proc. Amer. Math. Soc. 11, 896–904 (1960)
Proc. Amer. Math. Soc. 11, 896–904 (1960)