Subgame-perfect $\epsilon$-equilibria in perfect information games with sigma-discrete discontinuities

Abstract

Multi-player perfect information games are known to admit a subgame-perfect $\epsilon$-equilibrium, for every $\epsilon >0$, under the condition that every player’s payoff function is bounded and continuous on the whole set of plays. In this paper, we address the question on which subsets of plays the condition of payoff continuity can be dropped without losing existence. Our main result is that if payoff continuity only fails on a sigma-discrete set (a countable union of discrete sets) of plays, then a subgame-perfect $\epsilon$-equilibrium, for every $\epsilon >0$, still exists. For a partial converse, given any subset of plays that is not sigma-discrete, we construct a game in which the payoff functions are continuous outside this set but the game admits no subgame-perfect $\epsilon$-equilibrium for small $\epsilon >0$.

1 Introduction

We consider multi-player perfect information games, without chance moves, which have arbitrary action spaces and infinite duration. As a consequence of Flesch et al. (2010) and Purves and Sudderth (2011), these games admit a subgame-perfect $\epsilon$-equilibrium, $\epsilon$-SPE for brevity, for every $\epsilon >0$, provided that every player’s payoff function is bounded and continuous on the whole set of plays. Here, continuity is meant with respect to the product topology on the set of plays, with the set of actions given its discrete topology.

The question naturally arises what happens in games in which continuity of the payoffs is not satisfied everywhere, but only on a subset of plays. More precisely, on which subsets of plays discontinuity can be allowed without loosing that an $\epsilon$-SPE exists for every $\epsilon >0$. We show that discontinuities can be allowed on a sigma-discrete set of plays, i.e., on a countable union of discrete sets. In the special case, when the action space is countable, a set of plays is sigma-discrete if and only if it is countable.

Our main findings are as follows:

• [1] If the set of discontinuities is sigma-discrete, then an $\epsilon$-SPE exists for every $\epsilon >0$.

• [2] Given a set of plays that is not sigma-discrete, there exists a game in which the payoff functions are continuous outside of the given set, and the game admits no subgame-perfect $\epsilon$-equilibrium for small $\epsilon > 0$. This is achieved by embedding a game given in Flesch et al. (2014), which has no $\epsilon$-SPE for small $\epsilon >0$.

The structure of the paper is follows. In Sect. 2, we define the model. Then, in Sect. 3, we present the main results and discuss the main ideas of the proof. Sections 4 and 5 contain the proofs, and Sect. 6 provides some concluding remarks.

2 The model and preliminaries

The game Let $N = \{1,\ldots , n\}$ denote the set of players and let $A$ be an arbitrary non-empty set. Let ${\mathbb {N}} = \{0,1,2,\ldots \}$. We denote by $H$ the set of all finite sequences of elements of $A$, including the empty sequence ø, and we denote by $P = A^{\mathbb {N}}$ the set of all infinite sequences of elements of $A$. The elements of $A$ are called actions, the elements of $H$ are called histories, and the elements of $P$ are called plays. There is a function $\iota : H \rightarrow N$ which assigns an active player to each history. Further, each player $i\in N$ is given a so-called payoff function $u_{i} : P \rightarrow {\mathbb {R}}$.

The game is played as follows: At period 0, player $\iota$(ø) chooses an action $a_{0}$. In general, suppose that up to period $t \in {\mathbb {N}}$ of the game, the sequence $h = (a_{0},\ldots , a_{t})$ of actions has been chosen. Then, at period $t+1$, player $\iota (h)$ chooses an action $a_{t + 1}$. The chosen action is observed by all players. Continuing this way, the players generate a play $p = (a_{0}, a_{1},\ldots )$, and finally, each player $i\in N$ receives payoff $u_{i}(p)$.

We remark that this setup encompasses all games of finite duration. Another important special case is the situation when the players receive instantaneous payoffs at every period of the game and then aggregate them into one payoff, for example, by taking the discounted sum.

The topological structure We endow the set $A$ with the discrete topology and $P=A^{{\mathbb {N}}}$ with the product topology ${\mathcal {T}}$. A basis for $(P,{\mathcal {T}})$ is formed by the cylinder sets $P(h)= \{p \in P: h \prec p\}$ for $h \in H$, where for a history $h \in H$ and a play $p \in P$ we write $h \prec p$ if $h$ is the initial segment of $p$. In this topology, a sequence of plays $(p_n)_{n\in {\mathbb {N}}}$ converges to a play $p$ precisely when for every $k\in {\mathbb {N}}$ there exists an $N_k\in {\mathbb {N}}$ such that for every $n\ge N_k$, the first $k$ coordinates of $p_n$ coincide with those of $p$. Note that $(P,{\mathcal {T}})$ is completely metrizable¹, and moreover, it is separable (and hence Polish) if and only if $A$ is countable².

A function $f : P \rightarrow {\mathbb {R}}$ is said to be continuous at a play $p\in P$ if, for every sequence of plays $(p_n)_{n\in {\mathbb {N}}}$ converging to $p$, we have $\lim _{n\rightarrow \infty } f(p_n) = f(p)$. Thus, $f$ is continuous at $p$ precisely when for every $\delta >0$ there is a history $h\prec p$ such that $|f(p)-f(q)|\le \delta$ for every $q \in P(h)$. Intuitively, continuity at $p$ means that, after following $p$ for a large number of periods, further actions have little effect on the value of $f$. The function $f$ is said to be discontinuous at a play $p$ if it is not continuous at $p$. Further, $f$ is said to be continuous if it is continuous at each play in $P$.

Subgames For the concatenation of histories and actions, we use the following notations. For a history $h=(a_0,\ldots ,a_t) \in H$ and finite sequence of actions $(b_0,\ldots ,b_m)$ in $A$, let $(h,b_1,\ldots ,b_m)=(a_0,\ldots ,a_t,b_1,\ldots ,b_m)$, whereas for an infinite sequence of actions $(b_0,b_1,\ldots )$ in $A$, let $(h,b_0,b_1,\ldots )=(a_0,\ldots ,a_t,b_0,b_1,\ldots )$.

Consider a history $h = (a_{0}, \ldots , a_{t})$ for some $t\in {\mathbb {N}}$. The subgame $G(h)$ corresponding to $h$ is played as follows: First, player $\iota (h)$ chooses an action $a_{t+1}$. In general, suppose that the sequence of actions $(a_{t+1},\ldots ,a_{t+m})$ is chosen. Then, player $\iota (h,a_{t+1},\ldots ,a_{t+m})$ chooses an action $a_{t +m+ 1}$. Continuing this way, the players generate a play $p = (h,a_{t+1}, a_{t+2}, \ldots )$ in $P(h)$, and finally, each player $i\in N$ receives payoff $u_{i}(p)$.

Strategies A strategy for player $i$ is a function $\sigma _{i} : \iota ^{-1}(i) \rightarrow \Delta _c(A)$, where $\iota ^{-1}(i)$ is the set of histories where player $i$ moves and where $\Delta _c(A)$ is the set of probability measures on $A$ with a countable support. The interpretation is that if a history $h\in \iota ^{-1}(i)$ arises, then $\sigma _i$ prescribes player $i$ to choose an action according to $\sigma _i(h)$. A strategy is called pure, if it always places probability one on one action. A strategy profile is a tuple $(\sigma _{1}, \ldots , \sigma _{n})$ where $\sigma _{i}$ is a strategy for player $i$. Given a strategy profile $\sigma = (\sigma _{1}, \ldots , \sigma _{n})$ and a strategy $\eta _{i}$ for player $i$, we write $\sigma /\eta _{i}$ to denote the strategy profile obtained from $\sigma$ by replacing $\sigma _{i}$ with $\eta _{i}$.

Every strategy profile $\sigma$ induces a probability measure $\mu _{\sigma }$ on the Borel sets of $P$. Similarly, by considering the subgame for a history $h\in H$, every strategy profile $\sigma$ induces a probability measure $\mu _{\sigma ,h}$ on the Borel sets of $P$, such that $\mu _{\sigma ,h}(P(h))=1$. We denote the expected payoff for player $i\in N$ in the beginning of the game by $u_i(\sigma )$ and in the subgame starting at $h$ by $u_i(\sigma ,h)$.

Subgame-perfect $\epsilon$-equilibrium Let $\epsilon \ge 0$ be an error term. A strategy profile $\sigma$ is called an $\epsilon$-equilibrium if no player can gain more than $\epsilon$ by a unilateral deviation, i.e., if for each player $i \in N$ and for each strategy $\sigma _{i}^{\prime }$ of player $i$, it holds that

$$\begin{aligned} u_{i}(\sigma ) \ge u_{i}(\sigma /\sigma _{i}^{\prime }) - \epsilon . \end{aligned}$$

A stronger concept arises if we require that the strategy profile induces an $\epsilon$-equilibrium in every subgame. A strategy profile $\sigma$ is called a subgame-perfect $\epsilon$-equilibrium, $\epsilon$-SPE for brevity, if for each history $h \in H$, each player $i \in N$, and each strategy $\sigma _{i}^{\prime }$ of player $i$, it holds that

$$\begin{aligned} u_{i}(\sigma ,h) \ge u_{i}(\sigma /\sigma _{i}^{\prime }, h) - \epsilon . \end{aligned}$$

A 0-equilibrium is simply called an equilibrium, and a 0-SPE is simply called an SPE.

Existence of $\epsilon$-SPE An $\epsilon$-SPE exists for every $\epsilon >0$ provided that each player’s payoff function is bounded and continuous. This follows from more general results in Flesch et al. (2010) and Purves and Sudderth (2011). Carmona (2005) shows that for every $\epsilon >0$, an $\epsilon$-SPE exists under the assumption that the payoff functions are bounded and continuous at infinity. Continuity at infinity implies continuity but not vice versa.³ Flesch et al. (2014) describe a game in which every player’s payoff function is bounded and Borel measurable, yet the game admits no $\epsilon$-SPE for small $\epsilon >0$.

Sigma-discrete and perfect sets Let $X$ be a topological space. Consider a subset $D \subseteq X$. A point $x\in D$ is called an isolated point of $D$ if $x$ has an open neighborhood that contains no point of $D\setminus \{x\}$. The set $D$ is discrete if every point of $D$ is isolated, and it is sigma-discrete if it is a countable union of discrete sets. If $X$ is completely metrizable and separable (i.e., Polish), then $D$ is sigma-discrete if and only if it is countable.

A non-empty subset of $X$ is said to be perfect if it is closed and has no isolated points. By Koumoullis (1984), if $X$ is completely metrizable, then a non-empty Borel subset $D$ of $X$ is sigma-discrete if and only if $D$ does not contain a perfect subset of $X$. Since the set of plays $P$ is completely metrizable, these results apply to Borel subsets of $P$.

3 Main results

In this section, we present our main results.

Theorem 1

Consider a perfect information game with bounded payoff functions. Suppose that for every player $i$ the payoff function $u_{i}$ is continuous outside a sigma-discrete subset of $P$. Then, for every $\epsilon >0$, the game admits an $\epsilon$-SPE.

In Appendix 7.3, we prove that the payoff functions satisfying the condition of theorem 1 are Borel measurable. Let $D_{i}$ denote the set of plays $p$ such that $u_{i}$ is not continuous at $p$, and let $D = \cup _{i \in N}D_{i}$. Under the hypothesis of theorem 1, the set $D_{i}$ is sigma-discrete for each $i \in N$. Since the set of players $N$ is finite, this is obviously equivalent to the requirement that the set $D$ be sigma-discrete.

If $D$ is a countable set, it is sigma-discrete. Moreover, if the set of actions $A$ is countable, then $D$ is sigma-discrete if and only if it is countable. The set of eventually constant plays is an example of a sigma-discrete set that is not discrete. Another such example is the set of eventually periodic plays.

The proof of theorem 1 is carried out in three steps. As a first step, we discretize the payoffs in the following sense: We show that there exist payoff functions $\bar{u}_{1},\ldots ,\bar{u}_{n}$ such that each $\bar{u}_{i}$ has finite range and is $\epsilon$-close to $u_{i}$, and the set of discontinuity points $\bar{D}_{i}$ of $\bar{u}_{i}$ is contained in $D_{i}$. This approach has the advantage that for each play $p$ that is a continuity point of each function $\bar{u}_{i}$ there exists a history $h \prec p$ such that each $\bar{u}_{i}$ is constant on the set $P(h)$. Obviously, the subgame starting at history $h$ has a $\delta$-SPE for every $\delta > 0$. In contrast, the existence of such a history in the game with the original payoff functions is not trivial to establish. It is for that reason that working with discretized payoffs is crucial for our method.

As a second step, we prove theorem 1 for the so-called stopping games with finite payoff range. Finally, we show theorem 1 along the following lines. We define $H^{*}$ as the set of histories $h \in H$ such that the subgame $G(h)$ has an $\epsilon$-SPE for each $\epsilon > 0$. We prove that $H^{*} = H$ by contradiction: assuming that $H^* \ne H$ we show that there is a history $h \in H \setminus H^{*}$ such that $G(h)$ can be reduced to a stopping game and thus shown to have an $\epsilon$-SPE for each $\epsilon > 0$.

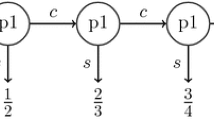
Theorem 1 cannot be strengthened to conclude that there is a pure $\epsilon$-SPE, a counterexample is readily provided by Solan and Vieille (2003). The game is a two-player stopping game in which the two players move alternatingly, and each player can either stop the game or continue:

The game admits no pure $\epsilon$-SPE for $\epsilon < 1$, but does admit an $\epsilon$-SPE in randomized strategies: Player 1 always stops with probability 1, while player 2 always stops with probability $\epsilon$. The main idea is that randomization by player 2 makes it impossible for player 1 to ever reach the only point of discontinuity in the game, the play $(c,c,c,\ldots )$. This conveys much of the intuition for how randomized strategies will be used in the proof of theorem 1.

We also prove a partial converse to theorem 1. Recall that the game is specified by the set of players, the set of actions, the assignment of the active players to histories, and the payoff functions.

Theorem 2

Let $A$ be any set of actions, and let $D$ be a subset of $P = A^{{\mathbb {N}}}$ that is not sigma-discrete. Then, there exists a two-player game with action set $A$ and with payoff functions that are continuous outside of $D$, such that the game admits no $\epsilon$-SPE for small $\epsilon >0$.

The proof makes use of a game in Flesch et al. (2014) that admits no $\epsilon$-SPE for small $\epsilon >0$. We embed this game into $D$ and define the payoffs elsewhere in such a way that the large game admits no $\epsilon$-SPE for small $\epsilon >0$ either.

The question that motivates the paper is for what kind of subsets of plays the condition of payoff continuity can be dropped without losing the existence of $\epsilon$-SPE. As shown above, the answer is sigma-discrete subsets of plays. Surprisingly, the answer is not strongly related to the topological notion of denseness, as illustrated by the following two examples.

Take $D$ to be the set of eventually constant plays. Then, $D$ is dense. However, $D$ is sigma-discrete, and hence, theorem 1 implies that any game with payoffs continuous outside of $D$ has an $\epsilon$-SPE for each $\epsilon > 0$. Conversely, let the action set be $A = \{0,1,2\}$, and $D$ be the set $\{1,2\}^{{\mathbb {N}}}$. Then, $D$ is nowhere dense. It is also perfect and thus is not sigma-discrete. Hence, theorem 2 implies that there is a game with payoff functions that are continuous outside of $D$ which has no $\epsilon$-SPE for small $\epsilon > 0$.

4 The proof of theorem 1

4.1 A reduction to a finite range of payoffs

In this section, we argue that it suffices to prove theorem 1 for games with payoff functions having finite range.

Lemma 3

Let $f : P \rightarrow [-r,r]$ be a Borel measurable function and let $\epsilon > 0$. Then, there exists a Borel measurable function $\bar{f} : P \rightarrow [-r,r]$ such that [1] $\bar{f}$ has finite range, [2] for every $p \in P, |\bar{f}(p) - f(p)| < \epsilon$, and [3] if $f$ is continuous at a play $p \in P$, then so is $\bar{f}$.

The proof of lemma 3 can be found in the Appendix.

We say that $\bar{f}$ is an $\epsilon$-discretization of the function $f$.

Now let $G$ be a game with the payoff functions $u_{1}, \ldots , u_{n}$ satisfying the assumptions of theorem 1. Fix an $\epsilon >0$, and let $\bar{u}_{1}, \ldots , \bar{u}_{n}$ be $\epsilon$-discretizations of the respective payoff functions. Then, the set of discontinuity points of the function $\bar{u}_{i}$ is contained in the set of the discontinuity points of the function $u_{i}$ and is therefore sigma-discrete. Moreover, any $\epsilon$-SPE of the game with the payoff functions $\bar{u}_{1}, \ldots , \bar{u}_{n}$ is a 2$\epsilon$-SPE of the game with the payoff functions $u_{1}, \ldots , u_{n}$.

This shows that it is sufficient to prove theorem 1 for games with payoff functions having finite range. In view of this result, we henceforth restrict our attention to games with a finite range of payoffs.

4.2 Stopping games with a finite range of payoffs

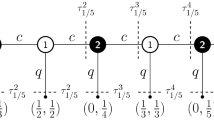
A game $G$ is said to be a stopping game if the action space is $A = \{s, c\}$, where $s$ stands for “stop”, $c$ stands for “continue”, and if for each $t \in {\mathbb {N}}$ and each player $i$, the payoff function $u_{i}$ is constant on the set $P(c^{t},s)$. Here, we write $(c^{t},s)$ to denote the history where action $c$ has been played successively $t$ times followed by the action $s$. So, in a stopping game, the payoffs are fixed once the active player decides to play action “stop”.

For each $t \in {\mathbb {N}}$ and each player $i$, let $\iota ^{t} = \iota (c^{t})$, and let $r_{i}^{t}$ denote player $i$’s constant payoff on $P(c^{t},s)$ and let $r_{i}^{\infty }$ denote $u_{i}(c^{\infty })$. A stopping game can be represented as follows:

Lemma 4

A stopping game with a finite range of payoffs admits an $\epsilon$-SPE for each $\epsilon > 0$.

This result follows from a more general theorem in Mashiah-Yaakovi (2014). For the sake of completeness, we give a direct proof of the lemma, see the Appendix.

4.3 Games with a finite range of payoffs

In this section, we prove theorem 1 for games with a finite range of payoffs. Let $G$ be a game satisfying the conditions of theorem 1 such that moreover the payoff functions $u_{1}, \ldots , u_{n}$ all have finite range. Let $D_{i}$ denote the set of plays $p$ such that $u_{i}$ is not continuous at $p$, and let $D = \cup _{i \in N}D_{i}$. Then, for each $p \in P \setminus D$, there exists a history $h \prec p$ such that each $u_{i}$ is constant on the set $P(h)$. Consider

$$\begin{aligned} H^{*} = \{h \in H: \text {for each }\epsilon > 0\text { the game }G(h)\text { has an }\epsilon \text {-SPE}\}. \end{aligned}$$

The following lemma is straightforward.

Lemma 5

Let $h \in H$. Then, $h \in H^{*}$ if and only if for each $a \in A, (h,a) \in H^{*}$.

Define the set

$$\begin{aligned} Q = \{q \in P:\text {for each }h \prec q\text { it holds that }h \notin H^{*}\}. \end{aligned}$$

Lemma 6

The set $Q$ has the following properties:

• [1] $Q$ is closed,

• [2] $Q \subseteq D$,

• [3] $H^{*} = \{h \in H: P(h) \cap Q = \emptyset \}$,

• [4] $Q$ is empty if and only if $H^{*} = H$.

Proof

• [1] To prove that $Q$ is closed we show that the complement of $Q$ is open. Thus, take $p \in P \setminus Q$. Then, there is an $h \prec p$ such that $h \in H^{*}$, and hence, $P(h) \subseteq P \setminus Q$.

• [2] To prove that $Q \subseteq D$ take a $p \in P \setminus D$. Since this is a continuity point of $u_{1}, \ldots , u_{n}$, and since each payoff function has finite range, there is an $h \prec p$ such that for every $i \in N$ the function $u_{i}$ is constant on $P(h)$. But then $h \in H^{*}$ as any strategy profile is an SPE of $G(h)$. Hence, $p \in P \setminus Q$.

• [3] The inclusion $H^{*} \subseteq \{h \in H: P(h) \cap Q = \emptyset \}$ is trivial. We prove the converse. Thus, take $h \in H$ such that $P(h) \cap Q = \emptyset$. Suppose that $h \in H \setminus H^{*}$. We recursively define a sequence $h_{0} \prec h_{1} \prec \cdots$ of elements of $H \setminus H^{*}$, as follows: Let $h_{0} = h$. Suppose we have defined $h_{k} \in H \setminus H^{*}$. By lemma , there is an action $a_{k} \in A$ such that $(h_{k},a_{k})\in H \setminus H^{*}$. Let $h_{k+1} = (h_{k},a_{k})$. Define $p = (h, a_{0},a_{1},\ldots )$. Then, $p \in P(h) \cap Q$, which is a contradiction.

• [4] It follows immediately from [3]. $\square$

To prove theorem 1, we need to show that $H = H^{*}$. Suppose not. Then, $Q$ is non-empty. If $Q$ has no isolated points, by the above lemma, it is a perfect set contained in $D$, contradicting the assumption of theorem 1. Therefore, $Q$ has an isolated point, say $p \in Q$. Choose an $h \in H$ such that $P(h) \cap Q = \{p\}$. We argue that $h \in H^{*}$, thus obtaining a contradiction to the item [3] of the lemma above.

Thus, take an $\epsilon > 0$. We show that $G(h)$ has an $\epsilon$-SPE.

For this purpose, we argue that $G(h)$ can be reduced to a stopping game. First, we rename the actions so that $p = (c,c,c,\ldots )$. Hence, $h = c^{k}$ for some $k \in {\mathbb {N}}$. Take an $m \ge k$, and consider the history $c^{m}$. If $A$ is a singleton, there is nothing to prove. So we assume that $A$ contains at least two actions. For each $a \ne c, P(c^{m},a)$ does not contain $p$ and is contained in $P(h)$. As $P(h) \cap Q = \{p\}$, we have $P(c^{m},a) \cap Q =\emptyset$. Therefore, by item [3] of the previous lemma, $(c^{m},a) \in H^{*}$. This allows us to replace the subgame $G(c^{m},a)$ by a payoff on some $\tfrac{1}{2}$ $\epsilon$-SPE of $G(c^{m},a)$, denoted $(w_{1}^{m}(a),\ldots ,w_{n}^{m}(a))$. Choose an action $a^{m} \in A \setminus \{c\}$ so as to maximize $w_{i}^{m}(a)$ for the player $i$ active at the history $c^{m}$. We can rename the actions so that $a^{m} = s$ for each $m \ge k$.

We thus obtain a game $G^{\prime }(h)$ where there are two distinguished actions, $s$ and $c$. Playing any action other than $c$ terminates the game (in the sense that subsequent actions do not affect the payoffs). Should a player choose to terminate the game, action $s$ yields the highest payoff. It is clear that all actions other than $c$ and $s$ can be safely ignored, so that $G^{\prime }(h)$ becomes a stopping game.

By lemma 4, the game $G^{\prime }(h)$ has an $\tfrac{1}{2}$ $\epsilon$-SPE. It is clear that the combination of the $\tfrac{1}{2}$ $\epsilon$-SPE in $G^{\prime }(h)$ with the chosen $\tfrac{1}{2}$ $\epsilon$-SPE in the subgames $G(c^{m},a)$, for $m \ge k$ and $a \in A \setminus \{c\}$, constitutes an $\epsilon$-SPE of $G(h)$.

5 Proof of theorem 2

In this section, we prove theorem 2. The proof makes use of the following game in Flesch et al. (2014) that does not admit an $\epsilon$-SPE for small $\epsilon >0$: There are two players, and the set of actions is $A = \{1, 2\}$. Player 1 starts the game. The active player decides who the next active player is by choosing the corresponding action. The payoffs are $(-1,2)$ if player 2 is active only finitely many times, $(-2,1)$ if player 1 is active only finitely many times, and $(0,0)$ if both players are active infinitely many times. In this game, the payoff functions are Borel, but discontinuous at every play. Flesch et al. (2014) prove that this game admits no $\epsilon$-SPE for $\epsilon \in (0,0.1]$.

Proof of theorem 2 Let $A$ be any set of actions, and let $D$ be a subset of $P = A^{{\mathbb {N}}}$ that is not sigma-discrete. We construct a two-player game $G$, with action set A and with payoff functions that are continuous outside of D, such that the game admits no $\epsilon$-SPE for small $\epsilon >0$.

Step 1: Construction of the game $G$. Since $D$ is not sigma-discrete, it contains a perfect subset $P^{*}$ of the set of plays $P$. We first construct a subset $D^*$ of $P^*$, on which we can define a game that is strategically equivalent with the game in Flesch et al. (2014).

Let $S$ denote the set of finite sequences of elements of $\{1,2\}$. Define a function $\varphi : S \rightarrow H$ recursively on the length of the sequence $s$. Let $\varphi$(ø) = ø. Suppose $\varphi (s)$ has been defined so that $P(\varphi (s)) \cap P^{*} \ne \emptyset$. The set $P(\varphi (s)) \cap P^{*}$ contains at least two distinct plays, say $p$ and $p^{\prime }$. Let $h$ be the longest common prefix of $p$ and $p^{\prime }$, and let $a$ and $a^{\prime }$ be the unique actions such that $(h,a) \prec p$ and $(h, a^{\prime }) \prec p^{\prime }$. Define $\varphi (s,1) = (h,a)$ and $\varphi (s,2) = (h,a^{\prime })$.

Now define the function $f : \{1,2\}^{{\mathbb {N}}} \rightarrow P^*$ by letting $f(x)$ be the unique play that extends the history $\varphi (x_{0},\ldots ,x_{m})$ for each $m \in {\mathbb {N}}$. Let $D^{*}$ be the image of $f$.⁴ Thus, $D^*\subseteq P^*\subseteq D\subset P$.

Let $H^*$ denote the set of histories that are consistent with $D^*$, i.e., there is a play $p\in D^*$ such that $h\prec p$. At every $h\in H^*$, let $A^*(h)$ denote the set of actions that keep play consistent with $D^*$, i.e., $A^*(h)=\{a\in A: (h,a)\in H^*\}$.

By construction, for every $h\in H^*$, it holds that

• $A^*(h)$ is either a singleton or it contains exactly two actions,

• there exists a history $\overline{h}\in H^*$ such that $\overline{h}\succeq h$ and $A^*(\overline{h})$ contains exactly two actions.

Define the game $G$ as follows: The set of players is $\{1, 2\}$. The function $\iota : H \rightarrow \{1,2\}$ is defined recursively as follows. Let $\iota$(ø)$\, =\, 1$. Suppose that $\iota (h)$ has been defined for $h \in H$. If $h \in H^{*}$ and $A^{*}(h)$ is the singleton $\{a\}$, let $\iota (h,a) = \iota (h)$. In this case, we rename the action $a$ into $\iota (h)$. If $h \in H^{*}$ and $A^{*}(h)$ consist of two actions $a$ and $a^{\prime }$, take the unique $s \in S$ such that $\varphi (s,1) = (h,a)$ and $\varphi (s,2) = (h,a^{\prime })$. Let $\iota (h,a) = 1$ and $\iota (h,a^{\prime }) = 2$. In this case, rename $a$ into $1$ and $a^{\prime }$ into $2$. If $h \in H \setminus H^{*}$, then $\iota (h,a)$ can be arbitrary, say equal to $1$, for each $a \in A$.

The payoffs on $D^{*}$ are defined exactly as in the game of Flesch et al. (2014). It remains to define the payoffs on the complement of $D^{*}$. Take a play $p \in P \setminus D^{*}$ and let $h$ be the shortest prefix of $p$ at which the active player, say player $i$, chooses an action $a$ such that $(h,a) \notin H^*$. In that case, regardless of future play, we define the payoff for player $i$ to be $-10$, and for the other player to be $5$.⁵ Notice that the payoffs are continuous outside of $D^*$, and hence, outside of $D$ as well.

Thus, the game $G$ proceeds just as the game in Flesch et al. (2014), unless an active player chooses an action outside of $A^{*}(h)$, in which that player is punished and the other player is rewarded.

Step 2: Proving that $G$ has no $\epsilon$-SPE for small $\epsilon >0$. We let $H_{i}^{*}$ be the set of histories in $H^{*}$ where player $i$ is active. Let $S_1$ denote the set of plays with the payoff $(-1,2)$; $S_2$ the set with the payoff $(-2,1)$; $Q_1$ the set with the payoff $(-10,5); Q_2$ denote the set of plays with the payoff $(5,-10)$, and $R$ the set with the payoff $(0,0)$.

Let $\sigma =(\sigma _1,\sigma _2)$ be an $\epsilon$-SPE where $\epsilon \in (0,\tfrac{1}{7})$. We first argue that

$$\begin{aligned} \mu _{\sigma ,h}(Q_{1}) \le \frac{\epsilon }{9},\quad \mu _{\sigma ,h}(Q_{2}) \le \frac{\epsilon }{9}\quad \text { for each }h \in H^{*}. \end{aligned}$$

(5.1)

To prove the first inequality, consider the following strategy $\tau _{1}$ for player 1: Follow $\sigma _{1}$ unless the outcome of the lottery $\sigma _{1}(h)$ at a history $h \in H_{1}^{*}$ is an action outside of $A^{*}(h)$. If that happens, play action $1$ for the rest of the game. Recall playing an action outside $A^{*}(h)$ gives player 1 a payoff of $-10$, whereas playing $1$ forever gives $-1$. Then, for each $h \in H^{*}$

$$\begin{aligned} \epsilon \ge u_{1}((\tau _{1},\sigma _{2}), h) - u_{1}((\sigma _{1},\sigma _{2}), h) \ge 9\cdot \mu _{\sigma ,h}(Q_{1}), \end{aligned}$$

from which the first inequality follows. The proof of the second inequality is similar.

The rest of the proof follows very closely the analysis in Flesch et al. (2014).

We argue that

$$\begin{aligned} \mu _{\sigma ,h}(R) = 0\quad \text { for each }h \in H^{*}. \end{aligned}$$

(5.2)

Otherwise by Lévy’s zero-one law, there is a history $h \in H^{*}$ where $\mu _{\sigma ,h}(R) \ge \frac{19}{20}$, which implies that $u_{2}(\sigma ,h) \le 10\cdot \frac{1}{20} < 1 - \epsilon$. This is impossible since at $h$ player 2 can guarantee a payoff of $1$ by always playing action 2 whenever it is his turn.

At any history $h \in H_{1}^{*}$, player 1 can guarantee a payoff of $-1$ by always playing action $1$, hence

$$\begin{aligned} u_{1}(\sigma ,h) \ge -1-\epsilon \quad \text { for each }h \in H_{1}^{*}. \end{aligned}$$

(5.3)

Now

$$\begin{aligned} u_1(\sigma ,h) = \;\mu _{\sigma ,h}(S_1)\cdot (-1)+\mu _{\sigma ,h}(S_2)\cdot (-2)+\mu _{\sigma ,h}(Q_1)\cdot (-10)+\mu _{\sigma ,h}(Q_2)\cdot 5. \end{aligned}$$

Combining this with (5.1), (5.2), and (5.3), we obtain $\mu _{\sigma ,h}(S_{1}) \ge 1 - 2\epsilon$ for every $h \in H_{1}^{*}$. This last inequality together with (5.1) give $u_2(\sigma ,h) \ge 2-6\epsilon$ for each $h \in H_{1}^{*}$. It is then easy to conclude that $u_2(\sigma ,h) \ge 2-7\epsilon$ for each $h \in H^{*}$. Since $u_2(\sigma ,h) \le \mu _{\sigma ,h}(S_{2}) + 10(1 - \mu _{\sigma ,h}(S_{2}))$, we obtain

$$\begin{aligned} \mu _{\sigma ,h}(S_{2}) \le \frac{8 + 7\epsilon }{9} < 1\quad \text { for each }h \in H^{*}. \end{aligned}$$

Therefore, applying Lévy’s zero-one law yields $\mu _{\sigma ,h}(S_{2}) = 0$ for each $h \in H^{*}$. Then, for each $h \in H^{*}$, we have $u_{1}(\sigma ,h) \le -\mu _{\sigma ,h}(S_{1}) + 10\mu _{\sigma ,h}(Q_{2}) \le -1+4\epsilon < -\epsilon$. On the other hand, player 1 can guarantee a payoff of $0$ at any history in $H^{*}$ by playing action $2$ whenever it is available. We arrive at a contradiction. $\square$

6 Concluding remarks

An interesting direction for future research is extending the results of this paper to the case where the set of players is infinite. Consider a game with infinitely many players.

First suppose that the payoff functions are all continuous. If the set of actions is finite, the existence of a pure SPE follows by the truncation approach of Fudenberg and Levine (1983). When the set of actions is infinite, an SPE need not exist, but one could follow the approach in Flesch and Predtetchinski (2015) to obtain existence of a pure $\epsilon$-SPE, for all $\epsilon >0$.

Much more challenging is the case where the continuity of payoff functions is only assumed outside of a sigma-discrete set. In this case, the question remains open whether an $\epsilon$-SPE exists for all $\epsilon >0$. We conjecture that the existence can be established at least in the special case when, on every play, infinitely many players are active. The intuition is that we can require a player who appears for the first time to randomize and place probability at least $\delta$ on at least two actions, where $\delta$ is a small positive number. This way the set of discontinuities can be avoided almost surely. A similar idea appeared in Cingiz et al. (2015).

Appendix

1.1 Proof of lemma 3

Let $E$ denote the set of histories $h\in H$ such that

$$\begin{aligned} \sup _{p,q\in P(h)}|f(p)-f(q)|\le \frac{\epsilon }{2}. \end{aligned}$$

We also let

$$\begin{aligned} P_{E} = \bigcup _{h \in E}P(h). \end{aligned}$$

Notice that $P_{E}$ is an open set. For each $p \in P_{E}$, let $h(p)$ be the minimal history such that $h \prec p$ and $h \in E$. Now fix an element $a \in A$ arbitrarily and define the function $\ell : P \rightarrow P$ as follows:

$$\begin{aligned} \ell (p) = {\left\{ \begin{array}{ll}(h(p),a,a,\ldots )&{}\quad \text {if }p \in P_{E}\\ p&{}\quad \text {otherwise.}\end{array}\right. } \end{aligned}$$

We argue that $\ell$ is a continuous function. Let $p_{k}$ be a sequence of plays converging to a play $p \in P$. We must show that $\ell (p_{k})$ converges to $\ell (p)$.

Suppose first that $p \in P_{E}$. Then, for $k$ large enough, we have $h(p) \prec p_{k}$, hence $p_{k} \in P_{E}$ with $h(p_{k}) = h(p)$, and so $\ell (p_{k}) = \ell (p)$.

Suppose now that $p \notin P_{E}$. Then, $\ell (p) = p$. We have to show that for each $h \prec p$, there is a $K \in {\mathbb {N}}$ such that $h \prec \ell (p_{k})$ for all $k \ge K$. Thus, take any $h \prec p$. There exists a $K \in {\mathbb {N}}$ such that $h \prec p_{k}$ for all $k \ge K$. Take any $k \ge K$. If $p_{k} \notin P_{E}$ then $\ell (p_{k}) = p_{k}$, and hence $h \prec \ell (p_{k})$, as desired. Suppose $p_{k} \in P_{E}$. Since $p_{k}$ extends both histories $h$ and $h(p_{k})$, we have either $h \preceq h(p_{k})$ or $h(p_{k}) \prec h$. But if $h(p_{k}) \prec h$ then $h(p_{k}) \prec p$, implying that $p \in P_{E}$, contrary to our supposition. Hence $h \preceq h(p_{k})$, which yields $h \prec \ell (p_{k})$, as desired. Thus, we have shown that $\ell (p_{k})$ indeed converges to $\ell (p)$.

Without loss of generality assume that $r$ is a multiple of $\tfrac{\epsilon }{2}$. Let $U$ be the set consisting of points $x \in [-r,r]$ that are multiples of $\tfrac{\epsilon }{2}$. Let $g : [-r,r] \rightarrow U$ be given by $g(x) = \min \{y \in U:x \le y\}$. Notice that $g$ is Borel and that $|g(x) - x| < \tfrac{\epsilon }{2}$ for every $x\in [-r,r]$.

Define the function $\bar{f}$ by letting $\bar{f}(p) = g(f(\ell (p)))$. It is Borel since $g$ and $f$ are Borel and $\ell$ is continuous. Moreover, $\bar{f}$ has finite range since $g$ does, so property [1] of the lemma is satisfied.

To check property [2], take a $p \in P$. If $p \notin P_{E}$, then

$$\begin{aligned} |\bar{f}(p) - f(p)| = |g(f(p)) - f(p)| < \tfrac{\epsilon }{2}. \end{aligned}$$

If $p \in P_{E}$, then

$$\begin{aligned} |\bar{f}(p) - f(p)| \le |g(f(\ell (p))) - f(\ell (p))| + |f(\ell (p)) - f(p)| < \tfrac{\epsilon }{2} + \tfrac{\epsilon }{2} = \epsilon . \end{aligned}$$

To check property [3], suppose that $f$ is continuous at a play $p\in P$. Then, $p \in P_{E}$ and so $p\in P(h(p))$. Since $\ell$ is constant on the whole set $P(h(p))$, so is $\bar{f}$. Thus, $\bar{f}$ is continuous on $P(h(p))$, and in particular at $p$. $\square$

1.2 Proof of lemma 4

The proof is by the induction on the number of players. Obviously, every 1-player stopping game with finite range of payoffs has an SPE, which is an $\epsilon$-SPE for each $\epsilon > 0$. So suppose that we have proven theorem 1 for all stopping games with finite range of payoffs with at most $n - 1$ players. Consider a stopping game $G$ with $n$ players with finite range of payoffs.

Given a $k \in {\mathbb {N}}$, we consider a “truncated” game $G_{k}$ where at time $k$ player $\iota ^{k}$ is forced to stop.⁶ By using backward induction, we can find a pure SPE $\sigma _{k}$ in the game $G_{k}$ with an additional property: for each $t < k$, whenever player $\iota ^{t}$ at history $c^{t}$ is indifferent between taking action $c$ and action $s$, the strategy profile $\sigma _{k}$ assigns action $s$. That is, $\sigma _{k}(c^{t}) = s$ if $u_{\iota ^{t}}(\sigma _{k},c^{t + 1}) = r_{\iota ^{t}}^{t}$.

We identify the strategy profile $\sigma _{k}$ with a point of $\{c,s\}^{{\mathbb {N}}}$. By taking a subsequence if necessary, we can assume that the sequence $\sigma _{k}$ converges to a strategy profile $\sigma$. We consider the following three cases:

• [1] There is no player $i \in N$ for which the set $\{t \in {\mathbb {N}}: \sigma _{i}(c^{t}) = s\}$ is infinite.

• [2] There exist at least two players $i \in N$ for which the set $\{t \in {\mathbb {N}}: \sigma _{i}(c^{t}) = s\}$ is infinite.

• [3] There exists exactly one player $i \in N$ for which the set $\{t \in {\mathbb {N}}: \sigma _{i}(c^{t}) = s\}$ is infinite.

We prove that case 1 is impossible, and that in case 2, the strategy profile $\sigma$ is an SPE. In case 3, we modify $\sigma$ to construct an $\epsilon$-SPE.

Case 1: We show that this case cannot occur. Let $T\in {\mathbb {N}}$ be so large that $\sigma (c^{t}) = s$ for every $t\ge T$. By replacing the game $G$ with the subgame starting with history $c^{T}$, we may assume that in fact $\sigma (c^{t}) = c$ for all $t \in {\mathbb {N}}$.

Let $\ell _{k}$ denote the first time that, under the strategy profile $\sigma _{k}$, action $s$ is taken. That is $\ell _{k} = \min \{t \in {\mathbb {N}}: \sigma _{k}(c^{t}) = s\}$. Notice that $\ell _{k} \le k$, since at history $c^{k}$, player $\iota ^{k}$ plays $s$ by the definition of $G_{k}$. We argue that the sequence $\{\ell _{k}\}$ is bounded.

Given a player $i \in N$, consider the set $R_{i} = \{r_{i}^{t}: t \in {\mathbb {N}},\iota ^{t} = i\}$ and for each $k \in {\mathbb {N}}$ let $R_{i}^{k} = \{r_{i}^{t}: t \in {\mathbb {N}},\iota ^{t} = i, t \le k\}$. The sets $R_{i}$ and $R_{i}^{k}$ are finite. Clearly $R_{i}^{0} \subseteq R_{i}^{1} \subseteq \cdots$ is an increasing sequence of sets with the limit $R_{i}$, so there exists a $k_{i}$ such that $R_{i}^{k_{i}} = R_{i}$. Now let $K = \max \{k_{1},\ldots ,k_{n}\}$. We argue that $\ell _{k} \le K$ for each $k \ge K$. Suppose on the contrary that $\ell _{k} > K$ for some $k \ge K$. Let $i = \iota ^{\ell _{k}}$. By the choice of $K$, there exists a $t \le K$ such that $r_{i}^{t} = r_{i}^{\ell _{k}}$. Since, under the strategy profile $\sigma _{k}$, no player stops before period $\ell _{k}$, at history $c^{t}$ player $i$ is indifferent between taking action $s$ and action $c$. Hence, our requirement on the strategy profile $\sigma _{k}$ implies that $\sigma _{k}(c^{t}) = s$. But this contradicts the definition of $\ell _{k}$.

Thus, we have shown that the sequence $\{\ell _{k}\}$ is bounded. By taking a subsequence if necessary, we may then assume that it converges, say to an $l \in {\mathbb {N}}$. However, then $\sigma (c^{l}) = s$, contradicting our assumption that $\sigma (c^{t}) = c$ for all $t \in {\mathbb {N}}$.

Case 2: We prove that $\sigma$ is an SPE.

Take a $t \in {\mathbb {N}}$. Let $m > t$ be the minimal number such that $\sigma (c^{m}) = s$ and $\iota ^{m} \ne \iota ^{t}$. Notice that such an $m$ exists by the condition defining case 2. Let $k \in {\mathbb {N}}$ be so large that $\sigma _{k}$ coincides with $\sigma$ on histories $c^{0},\ldots ,c^{m}$. Then, for any strategy $\eta _{\iota ^{t}}$ of player $\iota ^{t}$, we have $u_{\iota ^{t}}(\sigma _{k}/\eta _{\iota ^{t}},c^{t}) = u_{\iota ^{t}}(\sigma /\eta _{\iota ^{t}},c^{t})$. Since $\eta _{\iota ^{t}}$ is not a profitable deviation from $\sigma _{k}$, it is not a profitable deviation from $\sigma$.

Case 3: Let $i$ be the only player such that the set $S = \{t \in {\mathbb {N}}: \sigma _{i}(c^{t}) = s\}$ is infinite. One can show exactly as in case 2 that no player $j \ne i$ has a profitable deviation from the strategy profile $\sigma$.

Let $t_{0} < t_{1} < t_2\ldots$ be the increasing enumeration of the elements of $S$. It is easy to see that for each $m$

$$\begin{aligned} r_{i}^{t_{m}} = \max \{r_{i}^{\ell }:\ell \ge t_{m},\iota ^{\ell } = i\}. \end{aligned}$$

(7.1)

In particular, $r_{i}^{t_{0}} \ge r_{i}^{t_{1}} \ge \cdots$ is a non-increasing sequence. Define $\alpha$ to be the limit of this sequence. Define also

$$\begin{aligned} \beta = \max _{T \in {\mathbb {N}}}\min \{r_{i}^{t}:t \ge T,\iota ^{t} \ne i\}. \end{aligned}$$

Intuitively, $\beta$ is the minimal payoff in far subgames to player $i$ that he receives when other players decide to play action $s$. This payoff $\beta$ will serve as a threat payoff against player $i$. We distinguish the following three cases:

• [3.1] $\alpha \ge r_{i}^{\infty }$,

• [3.2] $\alpha < r_{i}^{\infty }$ and $\alpha < \beta$,

• [3.3] $\alpha < r_{i}^{\infty }$ and $\beta \le \alpha$.

Case 3.1: In this case, the strategy profile $\sigma$ is an SPE of the game $G$. Indeed, the fact that player $i$ has no profitable deviations from $\sigma$ follows since $r_{i}^{t_{0}} \ge r_{i}^{t_{1}} \ge \cdots \ge r_{i}^{\infty }$. Since, as noticed above, other players have no profitable deviations, $\sigma$ is an SPE.

Case 3.2: Choose an $m,\ell \in {\mathbb {N}}$ so large that $r_{i}^{t_{m}} = \alpha$ and $\min \{r_{i}^{t}:t \ge \ell ,\iota ^{t} \ne i\} = \beta$. Let $k = \max \{t_{m},\ell \}$. We argue that the subgame $G(c^k)$, that starts at history $c^{k}$, has an $\epsilon$-SPE. Then, due to backward induction, $G$ admits an $\epsilon$-SPE as well.

Notice that, in $G(c^{k})$, player $i$ has no incentive to ever stop. Indeed, stopping the game yields player $i$ a payoff of at most $\alpha$. If another player stops the game, player $i$’s payoff is at least $\beta$. And if no one stops, player $i$’s payoff is $r_{i}^{\infty }$.

Let $\eta _{i}$ be the strategy for player $i$ in $G(c^{k})$ that requires player $i$ to always continue. Fixing player $i$’s strategy to $\eta _{i}$ yields a new stopping game where the player set is $N \setminus \{i\}$. In view of our inductive hypothesis, this game has an $\epsilon$-SPE $\eta _{-i}$. It is now not difficult to see that $\eta = (\eta _{i},\eta _{-i})$ is an $\epsilon$-SPE in the game $G(c^{k})$.

Case 3.3: We construct an $\epsilon$-SPE of $G$.

Since $\beta \le \alpha$, there are infinitely many periods $t \in {\mathbb {N}}$ such that $\iota ^{t} \ne i$ and $r_{i}^{t} \le \alpha$. Consequently, we can construct an infinite increasing sequence $t_{0}^{\prime },t_{1}^{\prime },\ldots$ such that

• [A] for each $\ell \in {\mathbb {N}}$, we have $\iota ^{t_{\ell }^{\prime }} \ne i$ and $r_{i}^{t_{\ell }^{\prime }} \le \alpha$, and

• [B] for each $m \in {\mathbb {N}}$, there is at most one $\ell \in {\mathbb {N}}$ such that $t_{m} < t_{\ell }^{\prime } < t_{m + 1}$.

Let $M$ the maximum of $|r_{j}^{t}|$ over all $j \in N$ and $t \in {\mathbb {N}} \cup \{\infty \}$. If $M < \frac{\epsilon }{2}$, then any strategy is an $\epsilon$-SPE of $G$, so there is nothing to prove. Suppose that $M \ge \frac{\epsilon }{2}$ and let $\delta = \tfrac{\epsilon }{2M}$. Define the strategy profile $\eta$ by letting

$$\begin{aligned} \eta (t) = {\left\{ \begin{array}{ll}\delta s + (1 - \delta )c &{}\quad \text {if }t \in \{t_{0}^{\prime },t_{1}^{\prime },\ldots \}\\ \sigma (t)&{}\quad \text { otherwise.}\end{array}\right. } \end{aligned}$$

In particular, $\eta _{i} = \sigma _{i}$. We argue that $\eta$ is an $\epsilon$-SPE.

Consider a player $j \ne i$. Take a $t \in {\mathbb {N}}$ with $\iota ^{t} = j$. We show that for each strategy $\eta _{j}^{\prime }$ of player $j$, it holds that

$$\begin{aligned} |u_{j}(\eta /\eta _{j}^{\prime },t) - u_{j}(\sigma /\eta _{j}^{\prime },t)| \le \epsilon . \end{aligned}$$

(7.2)

It suffices to verify (7.2) for all pure strategies $\eta _{j}^{\prime }$ of player $j$. Thus, let $m$ be the minimal natural number such that $t < t_{m}$. By property [B], there is at most one $\ell$ for which $t \le t_{\ell }^{\prime } < t_{m}$. Consider now the play of the game starting at period $t$:

• If under the strategy profile $\sigma /\eta _{j}^{\prime }$ player $j$ stops the game at or before period $t_{\ell }^{\prime }$, the same occurs under $\eta /\eta _{j}^{\prime }$.

• If under the strategy profile $\sigma /\eta _{j}^{\prime }$ player $j$ stops the game at period $s > t_{\ell }^{\prime }$ (in which case $s < t_{m}$), then under $\eta /\eta _{j}^{\prime }$ the game stops at period $t_{\ell }^{\prime }$ with probability $\delta$ and at period $s$ with probability $1 - \delta$.

• Suppose that under the strategy profile $\sigma /\eta _{j}^{\prime }$ player $i$ stops the game at time $t_{m}$. If $\iota ^{t_{\ell }^{\prime }} = j$, then under $\eta /\eta _{j}^{\prime }$ the game stops at $t_{m}$ with probability 1. If $\iota ^{t_{\ell }^{\prime }} \ne j$, then the game stops at with $t_{\ell }^{\prime }$ with probability $\delta$ and stops at $t_{m}$ with probability $1 - \delta$.

In all three cases, the difference in the payoff to player $j$ is at most $\epsilon$.

Since for player $j$ no deviation from the strategy profile $\sigma$ is profitable, no deviation from the strategy profile $\eta$ increases player $j$’s payoff by more than $\epsilon$.

Consider player $i$. Take a $t \in {\mathbb {N}}$ with $\iota ^{t} = i$. Let $m$ be the least natural number with $t \le t_{m}$. It is not difficult to see that the payoff to player $i$ on the strategy profile $\eta$ is at least $r_{i}^{t_{m}} - \epsilon$.

Now let $\eta _{i}^{\prime }$ be a pure strategy for player $i$. Under the strategy profile $\eta /\eta _{i}^{\prime }$ with probability $1$ one of the following outcomes prevails: Either the game stops at some period in the set $\{t_{0}^{\prime }, t_{1}^{\prime }, \ldots \}$, or the game is stopped by player $i$ at a period $t^{\prime \prime } \ge t$. In the first case, the payoff to player $i$ is bounded above by $\alpha$ by property [A] above. Notice that $\alpha \le r_{i}^{t_{m}}$. In the second case, the payoff is $r_{i}^{t^{\prime \prime }}$. Notice that $r_{i}^{t^{\prime \prime }} \le r_{i}^{t_{m}}$ by (7.1). We conclude that under the strategy profile $\eta /\eta _{i}^{\prime }$ the payoff to player $i$ is at most $r_{i}^{t_{m}}$. Hence, the deviation to $\eta _{i}^{\prime }$ improves player $i$’s payoff by at most $\epsilon$.

This concludes the proof of theorem 1 for stopping games with finite payoff range. We remark that the method to solve case 3.3 is exactly the one that is needed to find an $\epsilon$-SPE in the above-mentioned game by Solan and Vieille.

1.3 sigma-discrete subsets of $P$ are Borel

Lemma 7

A sigma-discrete subset of $P$ is Borel. Furthermore, every function $f : P \rightarrow {\mathbb {R}}$ that is continuous outside a sigma-discrete subset of $P$ is Borel measurable.

Proof

Step 1: Let $Q\subset P$ be a discrete set of plays. We argue that $Q$ is a $G_\delta$-subset of $P$, i.e., a $\Pi ^0_2$-set of $P$. For every $q\in Q$, let

$$\begin{aligned} m(q)=\inf _{q'\in Q\setminus \{q\}}d(q,q'), \end{aligned}$$

where $d$ is the metric on $P$. Because $Q$ is discrete, $m(q)>0$. Now for every $n\in {\mathbb {N}}$, consider the set

$$\begin{aligned} U_n=\bigcup \limits _{q\in Q}B\left( q,\frac{1}{2^{n}}m(q)\right) , \end{aligned}$$

where $B(q,\varepsilon )$ denotes the open ball around a play $q$ of radius $\varepsilon$. Notice that the sequence $U_n$ is non-increasing.

We show that $U_1$ is a disjoint union. Take a $p\in P$ and suppose that there are two different $q_1,q_2\in Q$ such that $p\in B(q_1,\frac{1}{2}m(q_1))$ and $p\in B(q_2,\frac{1}{2}m(q_2))$. Assume that $m(q_1)\ge m(q_2)$. Then,

$$\begin{aligned} d(q_1,q_2)\le d(q_1,p)+d(p,q_2)<\frac{1}{2}m(q_1)+\frac{1}{2}m(q_2)\le m(q_1), \end{aligned}$$

which is in contradiction with the choice of $m(q_1)$.

It follows that

$$\begin{aligned} Q=\bigcap _{n\in {\mathbb {N}}} U_n. \end{aligned}$$

Indeed, the inclusion $\subseteq$ is trivial. To see the other inclusion $\supseteq$, take a $p\in \cap _{n\in {\mathbb {N}}} U_n$. Suppose by way of contradiction that $p\not \in Q$. Then, $p\in U_1\setminus Q$. Since $U_1$ is a disjoint union, there is a unique $q\in Q$ such that $p\in B(q,\frac{1}{2}m(q))$. Because $d(p,q)>0$, we conclude that $p\notin B(q,\frac{1}{2^n}m(q))$ for large $n$, and hence, $p\not \in U_n$ for large $n$. This is a contradiction with the choice of $p$.

Since each $U_n$ is open, $Q$ is a $G_\delta$-set of $P$, as desired.

Step 2: Let $Q\subset P$ be a sigma-discrete set of plays. Then, $Q$ is a countable union of $G_\delta$-sets of $P$, and hence, $Q$ is a Borel subset of $P$, in particular it is a $\Sigma ^0_3$-set of $P$.

Step 3: Let $f : P \rightarrow {\mathbb {R}}$ be continuous outside a sigma-discrete subset $D\subset P$. We argue that $f$ is Borel. Take a Borel set $X$ of ${\mathbb {R}}$. Let $f_C$ and $f_D$ denote the restriction of $f$ to the domain $P\setminus D$ and, respectively, to the domain $D$.

Since $f_C$ is continuous with respect to the relative topology on $P\setminus D$, the set $f_C^{-1}(X)$ is a Borel subset of $P\setminus D$. As $P\setminus D$ is a Borel subset of $P$ by step 2, $f_C^{-1}(X)$ is a Borel subset of $P$. Further, since any subset of $D$ is sigma-discrete, by step 2 $f_D^{-1}(X)$ is a Borel subset of $P$. Hence,

$$\begin{aligned} f^{-1}(X)=f_C^{-1}(X)\cup f_D^{-1}(X) \end{aligned}$$

is a Borel subset of $P$, as desired. $\square$