Assessing differences in household needs: a comparison of approaches for the estimation of equivalence scales using German expenditure data

Abstract

Equivalence scales are routinely applied to adjust the income of households of different sizes and compositions. Because of their practical importance for the measurement of inequality and poverty, a large number of methods for the estimation of equivalence scales have been proposed. Until now, however, no comprehensive comparison of current methods has been conducted. In this paper, we employ German household expenditure data to estimate equivalence scales using several parametric, semiparametric, and nonparametric approaches. Using a single dataset, we find that some approaches yield more plausible results than others while implausible scales are mostly based on linear Engel curves. The results we consider plausible are close to the modified OECD scale, and to the square root scale for larger households.

1 Introduction

Equivalence scales are used to make the incomes of households of different sizes and compositions comparable. They provide the basis for calculating inequality and poverty measures (e.g., Buhmann et al. 1988; Szelky et al. 2004). It has, however, been pointed out that these measures are sensitive to the specific equivalence scale used, and there has so far been no consensus on which equivalence scale should be applied (e.g., Lewbel 1989b; Blundell and Lewbel 1991).

A well-known example of an equivalence scale is the so-called modified OECD scale (Hagenaars et al. 1994). The household of an adult living alone is used as a reference and is assigned a value of one. Adding individuals aged 14 and older to the household increases this value by 0.5 per person, and adding children below age 14 increases it by 0.3 per child. Thus, for instance, a household of two adults with one child has an equivalence scale value of 1.8. Dividing the income of such households by 1.8 yields equivalence income, which is standardized relative to the reference household and can be directly compared across household types. Another commonly applied equivalence scale is the square root scale, which has been in use at least as long as the modified OECD scale (e.g., Atkinson et al. 1995) and has been applied by the OECD in some of their more recent publications (e.g., OECD 2008). In this approach, incomes are divided by the square root of the household size. Because they are easy to apply, the modified OECD scale and the square root scale are widely used in applied research.

Apart from these so-called expert scales, a broad range of empirical methods have been proposed for estimating equivalence scales (Phipps and Garner 1994; Muellbauer and van de Ven 2004). Comparisons of those methods are surprisingly scarce in the literature. Existing studies have focused on subjective approaches (Bellemare et al. 2002; Schwarze 2003) or have covered expenditure-based approaches that are mostly no longer in use (e.g., Nicholson 1976; Lancaster and Ray 1998).

In this paper, we conduct a direct comparison of several different methods for the estimation of equivalence scales using the same dataset, the German Sample Survey of Income and Expenditure (Einkommens- und Verbrauchsstrichprobe; EVS). We focus on approaches that use expenditure data to estimate a single equivalence scale value per household type that does not vary by household income. Using the classic approach of Engel (1895) as a starting point, we cover the modern methodological developments in the field. These include extensions of the Linear Expenditure System (Lluch 1973; Howe et al. 1979), which have often been applied to German expenditure data; the quadratic extension (QAI) (Banks et al. 1997) of the influential Almost Ideal Demand System (AI) (Deaton and Muellbauer 1980a), which is now the standard approach for modeling household demand; semiparametric approaches (Pendakur 1999; Stengos et al. 2006); and nonparametric approaches based on the counterfactual framework (Szulc 2009; Dudel 2015). These methods roughly span a continuum in terms of model complexity, data requirements, and the restrictiveness of the underlying assumptions.

To compare the different approaches for estimating equivalence scales, we apply several parametric, semiparametric, and nonparametric tests that enable us to assess the underlying identifying assumptions of the approaches. We also apply a set of theoretically and empirically grounded criteria that allow us to judge the plausibility of the equivalence scale estimates. These two sets of criteria (identification assumptions; plausibility criteria) can be consistently applied to all methods. To demonstrate the practical relevance of our research, we complement the analysis by using the resulting equivalence scales to calculate indices of inequality and poverty.

We find that a set of approaches lead to results that can be deemed more plausible than the results of other approaches, even though all of these approaches violate at least one of the plausibility criteria. The more plausible estimates are based on demand systems or newer semi- and nonparametric approaches. It appears that equivalence scales based on the more plausible estimates are also similar to the modified OECD scale, at least for households with fewer than two children. For larger families, they are closer to the square root scale.

Our paper contributes to the literature in several ways. To the best of our knowledge, we are conducting the first comparison of methods for the estimation of expenditure-based equivalence scales that covers more recent methodological developments from the literature and that uses recent data. Our comparison study is motivated by the observation that existing overviews of equivalence scales tend to obscure the differences between the methods applied because the countries, the datasets, and the time periods used in conjunction with these methods vary. For instance, equivalence scale estimates for several different countries are often shown next to each other (e.g., Buhmann et al. 1988). While some countries have similar scales (Phipps and Garner 1994; Burkhauser et al. 1996), this is not always the case, and discrepancies are possible (Lancaster et al. 1999). Similar issues might arise for equivalence scales based on different datasets because, for example, of differences in the variables used or in the preparation of the data (Dudel et al. 2017); for equivalence scales estimated for different points in time because, for example, the prices may have changed (Pendakur 2002). In our analysis, we try to avoid these issues. Our findings show that while equivalence scales differ considerably, a subset of the approaches in our application leads to more plausible equivalence scales and to consistent results with respect to inequality and poverty measurements.

The remainder of this paper is structured as follows. In Sect. 2, we introduce the basic assumptions of equivalence scales, as well as criteria for the assessment of equivalence scales. The approaches we apply to estimate equivalence scales, along with their underlying assumptions, are explained in Sect. 3. The dataset we use and the subset selection process are described in Sect. 4. In Sect. 5, we present results for the tests of the assumptions of the different approaches and for equivalence estimates. We also compare our estimates with results from earlier literature. Section 6 concludes.

2 Equivalence scales

2.1 Preliminaries and basic definition of equivalence scales

Let $\mathbf {z}=(z_1, \ldots ,z_k)$ denote a vector of k household characteristics, such as household size, number of children, or age of household members. All households can choose between m goods with prices captured in a vector $\mathbf {p}=(p_1, \ldots ,p_m)$. Household demand is given by the demand function $D(p,y,z)=\mathbf {q}=(q_1, \ldots ,q_m)$, where $q_i$ is the demand for good i and y is household income. Household utility is given by $U(\mathbf {q},z)$. The expenditure function can be defined by $E(u,\mathbf {p},\mathbf {z})=\min _q[\mathbf {p}'\mathbf {q}|U(\mathbf {q},z)=u]$.¹ Using these preliminaries, household equivalence scales are defined as

$$\begin{aligned} S(u,\mathbf {p},\mathbf {z}_h,\mathbf {z}_r) = \frac{E(u,\mathbf {p},\mathbf {z}_h)}{E(u,\mathbf {p},\mathbf {z}_r)}, \end{aligned}$$

(1)

where $\mathbf {z}_h$ and $\mathbf {z}_r$ are the household characteristics of two different households h and r. Thus, an equivalence scale is a function that returns the ratio of the expenditures of two households of different compositions with the same level of utility and facing the same prices. The reference household $\mathbf {z}_r$ is usually fixed as the household of a single adult, but any other household type could also be chosen. Throughout our analysis, we will often assume the former type, and will then write $S(u,\mathbf {p},\mathbf {z}_h)$, thus dropping $\mathbf {z}_r$.

2.2 Assessing equivalence scales: identification, income independence, and Engel curves

Equivalence scales as defined by Eq. (1) are not identified if ordinal utility is assumed (Pollak and Wales 1979; Lewbel 1989a; Blundell and Lewbel 1991; Pollak 1991). This is because equivalence scales require interpersonal comparisons of utility that are not possible under the assumption of ordinal utility. Any approach for estimating equivalence scales has to deal with this issue of identification. Three main approaches for obtaining equivalence scales are used in the literature. The first approach is based on experts’ more or less heuristic assessments of equivalence scales (see Fisher 2007, for a review). The second approach is based on individuals’ subjective evaluations of utility drawn from income (see Schröder 2004, for a review). This approach has, for example, been applied to survey data on income satisfaction (e.g., Schwarze 2003; Biewen and Juhasz 2017; Borah et al. 2019) and to customized survey data that directly relate specific income levels to specific welfare levels (Koulovatianos et al. 2005). The third main approach is based on consumption and expenditure data; this approach will be the focus of our study.

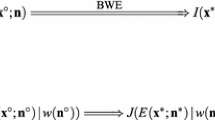
In expenditure-based approaches, a common solution to the identification problem is to employ (indirect) utility functions of a certain structure. For instance, if we assume that equivalence scales do not depend on the welfare level—i.e., $S(u,\mathbf {p},\mathbf {z}_h)=S(\mathbf {p},\mathbf {z}_h)$—they can be identified (e.g., Blundell and Lewbel 1991). This assumption is called, or is related to, independence of base (Lewbel 1989b) and equivalence scale exactness (Blackorby and Donaldson 1993) (IB/ESE). For practical purposes, this assumption often—but not always—implies that equivalence scales do not depend on the income levels (or expenditure levels) of the households under consideration. More specifically, equivalence scales are considered income-independent if the same value is applied to all households of a certain type.²

In practice, the independence of base is connected to assumptions about the functional form of Engel curves. Depending on the approach used for estimating equivalence scales, assumptions of varying levels of generality are applied. These assumptions can be tested empirically, which allows us to judge whether the corresponding approaches yield trustworthy estimates. In Sect. 3, we will discuss approaches that require (1) linear or quadratic Engel curves, which are only shifted by a constant for different household types; (2) arbitrarily shaped Engel curves, but which are only shifted by a constant for different household types, and thus have the same shape for all household types; (3) and arbitrarily shaped Engel curves with no restrictions across household types, which also implies that unlike for the first and second types of Engel curves, income independence does not hold.

2.3 Assessing equivalence scales: plausibility

In addition to applying the identification assumptions discussed above, we assess approaches for equivalence scale estimation by the resulting scale values; i.e., the values $S(u,\mathbf {p},\mathbf {z}_h)$ attain for different values of $\mathbf {z}_h$. In the literature, several criteria have been discussed based on economic theory and empirical regularities. While some of these criteria can be seen as properties that equivalence scales have to exhibit to be deemed plausible, other criteria are more debatable. None of the approaches we apply leads to estimates that satisfy any of the criteria by design, and all of the approaches could lead to estimates that violate one or several of the criteria.

To describe the criteria formally, we assume that the equivalence scales only depend on household size n, such that they can be written as $S(u,\mathbf {p},n)$ or, alternatively, that equivalence scales depend on the number of adults $n_a$ and the number of children $n_c$, $S(u,\mathbf {p},n_a,n_c)$. Using this notation, we discuss the following criteria:

$$\begin{aligned} S(u,\mathbf {p},n+1)> & {} S(u,\mathbf {p},n), \end{aligned}$$

(2)

$$\begin{aligned} S(u,\mathbf {p},n+1)\le & {} S(u,\mathbf {p},n) + 1, \end{aligned}$$

(3)

$$\begin{aligned} S(u,\mathbf {p},n+i+1) - S(u,\mathbf {p},n+i)\le & {} S(u,\mathbf {p},n+i) - S(u,\mathbf {p},n+i-1),\end{aligned}$$

(4)

$$\begin{aligned} S(u,\mathbf {p},n_a+1,n_c)> & {} S(u,\mathbf {p},n_a,n_c+1), \end{aligned}$$

(5)

The criterion stated in Eq. (2) has been referred to as the “household size effect” (Stengos et al. 2006) and indicates that equivalence scales have to be strictly increasing functions of household size. Using the household of a single person as a reference with $n=1$ thus implies that for $n>1$, the equivalence scale has to be larger than one. The assumption underlying this criterion is that every additional household member generates costs; i.e., $E(u,\mathbf {p},n+1)>E(u,\mathbf {p},n)$. As this criterion is generally accepted in the literature, many studies have used it to evaluate the plausibility of equivalence scales (e.g., Deaton and Muellbauer 1986; Wilke 2006; Stengos et al. 2006).

Criterion (3) states that the effect of the household size must be no more than one, due to economies of scale. Larger values would indicate, for example, that a couple needs more than two singles. This is unlikely, because of economies of scale in consumption. Two adults can reduce their costs when, for example, they cook together; children often share rooms (see Deaton and Muellbauer 1980b, for more examples). These observations also motivate criterion (4), which states that the scale increase diminishes with household size or at least remains constant. In other words, every additional household member adds less—or at least does not add more—to the scale than the previous one. There might be some constellations in which (4) does not hold. For example, a couple might have enough space in their current home for a first child, but if having a second child compels them to move into a larger dwelling. Therefore, adding the second child would be more expensive than adding the first, which demonstrates that there could be exceptions to criterion (4).

The fourth criterion in Eq. (5) states that an additional adult adds more to the equivalence scale than a child. This is based on the assumption that children generate lower costs than adults, because, for instance, they consume less food. The extent to which this criterion holds might depend on the age threshold used to distinguish between adults and children.

3 Expenditure-based methods for the estimation of equivalence scales

3.1 Engel’s approach

The idea of using household expenditures to assess household welfare is usually attributed to Engel (1895) and is based on the observation that the share of household expenditures spent on food depends on household type, and declines as income rises. Assuming that two households achieve the same level of welfare if the shares of their expenditures allocated to food are equal, the equivalence scales can be identified by comparing the incomes of different types of households that allocate the same share of their expenditures to food.

This approach can be implemented as follows (Deaton and Muellbauer 1986). Letting $w_f$ denote the share of expenditures on food, the following regression equation, as proposed by Working (1943), can be estimated based on demand data (also see Leser 1963):

$$\begin{aligned} w_f = \alpha + \beta _x \log (x/n) + \beta _a n_a + \beta _c n_c + \gamma '\mathbf {z}, \end{aligned}$$

(6)

where x is total expenditure, x/n is per capita expenditure, $n_a$ and $n_c$ denote the number of adults and children in the household, respectively; $\mathbf {z}$ captures socio-demographic variables other than household type. Now let us consider two households that allocate the same share of their expenditures to food as given by Eq. (6), but that are of different types. Equating expenditure shares and solving for the ratio of incomes $x_h$ and $x_r$ that the households need to achieve the share spent on food gives

$$\begin{aligned} S = \frac{x_h}{x_r} = \left( \frac{n_h}{n_r} \right) \exp \left( \frac{\beta _{a}}{\beta _{x}} (n_{a,h}-n_{a,r}) + \frac{\beta _{c}}{\beta _{x}} (n_{c,h}-n_{c,r})\right) , \end{aligned}$$

(7)

where $n_r$ is the size of the reference household, and $n_{a,r}$ and $n_{c,r}$ capture the number of adults and children in the reference household. $n_h$, $n_{a,h}$, and $n_{c,h}$ are defined in a similar way for the comparison household.

This approach assumes that equivalence scales do not depend on income or expenditure levels. Moreover, prices are usually not included, even though it would be possible to do so. Thus, this approach has low data requirements and is easy to apply. Engel curves, as defined by (6), are linear. While linear Engel curves are not necessary for applying this approach (Leser 1963), empirical applications typically use linear Engel curves.

One popular variant of the Engel approach was suggested by Rothbarth (1943). His idea was to assess the utility of adults by considering goods that are exclusively consumed by adults, such as tobacco, alcohol, and adult clothes. Compared to a couple without children, a couple with children needs to be compensated to the extent that the household resets its expenditures on those adult goods to the level of the reference household (Lancaster and Ray 1998).

3.2 Linear expenditure system and extensions

The Linear Expenditure System (LES) proposed by Stone (1954) is the earliest full expenditure system, meaning that it is based not on a single equation, but on a system of equations, each of which covers expenditures for one of the m goods. It also takes into account price changes, which makes it possible to impose and test restrictions of economic utility theory.³

Starting from a Stone-Geary utility function, the following set of m expenditure functions can be derived:

$$\begin{aligned} x_i= & {} p_ia_i + b_i \left( x - \sum _{j=1}^m p_ja_j \right) \end{aligned}$$

(8)

with x denoting total expenditures and $x_i=p_iq_i$, i.e., expenditure on good i; $p_ia_i$ being interpreted as the minimum expenditure on good i; and $b_i$ being the marginal budget share of good i, with the restriction that $\sum b_i = 1$.

This set of equations can be estimated separately for each household type (for an estimation of the LES, see, e.g., Deaton 1975). Given these parameter estimates, a pragmatic way to calculate the equivalence scales is based on a comparison of the minimum expenditures by household type (e.g., Kohn and Missong 2003), while $p_i$ is set to one.

$$\begin{aligned} S&= \frac{\sum _{i=1}^m a_i^h }{\sum _{i=1}^m a_i ^r }, \end{aligned}$$

(9)

where $a_i^r$ is the reference household’s minimum expenditure on good i facing prices p for good i; $a_i^h$ is the comparison household’s minimum expenditure on good i facing prices p for good i. The LES has inspired several extensions, of which we cover two variants: the Extended Linear Expenditure System (ELES; Lluch 1973) and the Quadratic Expenditure System (QES; Howe et al. 1979). Essentially, the ELES expands the LES by introducing saving, which is treated as an additional commodity. In contrast to the linear Engel curves of the LES, the QES assumes a quadratic relationship between expenditure and (marginal) total expenditure. For both variants, the equivalence scale can be calculated in the same way as in the basic LES.

In terms of data demands, the LES and its extensions fall somewhere in the middle: expenditure data are needed for several expenditure categories, whereas data on prices can be included, but are not needed, as $p_i$ can be set to one. Equivalence scales based on linear expenditure systems are income-independent, although the QES uses quadratic Engel curves instead of linear curves.

3.3 Almost ideal demand system and extensions

The AI system arose from the search for a model that provides a good fit for empirical demand data, while having properties deemed desirable for demand systems.⁴ Starting from the price-independent generalized logarithmic (PIGLOG) class of preferences, the expenditure share for good i, $w_i$ can be derived to equal:

$$\begin{aligned} w_i&= \alpha _i + \sum _{j=1}^m \gamma _{ij} \log p_j + \beta _i \log \left( \frac{x}{P}\right) , \end{aligned}$$

(10)

with

$$\begin{aligned} \log P&= \alpha _0 + \sum _{i=1}^m \alpha _i \log p_i + \frac{1}{2} \sum _{i=1}^m\sum _{j=1}^m\gamma _{ij} \log p_i \log p_j. \end{aligned}$$

with $\gamma _{ij}$ capturing the effect of the price of good j on the share of expenditures on good i, $\beta _i$ being the marginal effect of log income, and $\alpha _i$ being a parameter. P is a price deflator for income. As P makes the model nonlinear, in empirical applications linear approximations are often used (see, e.g., Barnett and Seck 2008). Here, we will use the (nonlinear) translog price index, as proposed by Deaton and Muellbauer (1980a).

To estimate equivalence scales, some parameters have to be added to the AI demand system. We follow a general approach suggested by Ray (1983) for introducing equivalence scales in demand systems. If we want to compare the reference household to one other household type only, this approach is implemented by using:

$$\begin{aligned} w_i&= \alpha _i + \sum _j \gamma _{ij} \log p_j + \beta _i^* \log \left( \frac{x}{SP}\right) , \end{aligned}$$

(11)

where

$$\begin{aligned} S&= 1 + \rho d_h\\ \beta _i^*&= \beta _i + \eta _i d_h \end{aligned}$$

while assuming that the comparison household needs more resources than the reference household. S denotes the equivalence scale value. $d_h$ is a dummy for the respective household comparison type while $\rho$ captures the needs of the comparison households relative to the needs of the reference household. $\eta _i$ plus $\beta _i$ gives the income elasticity for the comparison household. Given P, the parameters can be found using nonlinear, seemingly unrelated regressions (Greene 2012).

The AI demand system essentially assumes that the relationship between log income and expenditure shares is linear. But for some commodities, this relationship has been found to be nonlinear. To account for the nonlinearity, and to provide a better fit for the demand data, Banks et al. (1997) introduced the Quadratic AI demand system. The QAI demand system essentially includes an additional quadratic term of (deflated) log income. Equivalence scales are estimated by expanding the approach of Ray (1983) to cover this term.

While the AI and the QAI demand systems are rather flexible models that can fit many patterns of household demand, they also require data on prices. Thus, unlike in Engel’s approach, at least two cross sections of demand data are required in these systems. Equivalence scale exactness is also required.

3.4 Semiparametric approaches

The approaches presented so far all rely on the assumption that the relationship between log (deflated) income and expenditure or expenditure shares is linear or quadratic. While this assumption might be appropriate for some commodities, it might not hold for others (Banks et al. 1997). In an effort to address this problem, Pendakur (1999) developed a semiparametric approach to estimating equivalence scales that avoids strong assumptions regarding the relationship between income and expenditure shares by estimating nonlinear Engel curves. Writing the expenditure share for food, $w_f$, as a function of income y, prices p, and household type $d_h$, the approach assumes that

$$\begin{aligned} w_f(p,\log (y),d_h=0) = w_f(p, \log (y) + \phi ,d_h=1) + \mu (p). \end{aligned}$$

(12)

Here, the relationship between log income and the expenditure share for food as captured by $w_f(p,\log (y),d_h)$ can be of any functional form. It is, however, assumed that this functional form is equal across household types (“shape invariance”) and is only shifted vertically by price elasticity, $\mu (p)$, and horizontally by the log equivalence scale $\phi$. Equivalence scales can be calculated as

$$\begin{aligned} S=\exp (\phi ). \end{aligned}$$

(13)

Estimation proceeds by using nonparametric methods to estimate the shape of $w_f(p,\log (y),d_h=0)$ and of $w_f(p,\log (y),d_h=1)$. In a second step, assuming constant prices, the log equivalence scale $\phi$ is found via a grid search, whereby the difference between the two sides of Eq. (12) is minimized (Pendakur 1999). Stengos et al. (2006) proposed a variant of this method, which we also include in the set of methods we apply. They modified the second step of the approach, penalizing high or low values of $\phi$. This yields more plausible estimates than the original method of Pendakur (1999), particularly for comparisons in which the income distributions of the reference and the comparison household types overlap slightly, as the loss function used by Pendakur (1999) is deficient in this case.

While the semiparametric approach is flexible regarding the functional form of Engel curves, it requires the independence of base assumption (Pendakur 1999). The data requirements are relatively low, as a single cross section of data suffices. In principle, the share of expenditures on food can be replaced with the share of expenditures on other commodities. For instance, it would be possible to implement the ideas of Rothbarth (1943) in a semiparametric way (see Sect. 3.1). A drawback of the semiparametric approach is that including covariates in the first estimation step is not straightforward. Moreover, the approach relies to some extent on the selection of homogenous subsets of households.

3.5 Counterfactual approaches

The counterfactual approach rephrases equivalence scales in the potential outcomes framework (e.g., Holland 1986). Let us assume that in theory, every household can be considered to belong to the reference household type (e.g., single-adult household) and the comparison household type (e.g., couple with one child). $y^0(u)$ is the income needed to achieve utility u when the household is of the reference type, and $y^1(u)$ is the income needed to achieve utility u when the household is of the comparison type.

Assuming that a household achieves utility level $u^0$ when it is of the reference type, equivalence scales are given by $\mathrm {E}[y^1(u^0)/y^0(u^0)]$ (Szulc 2009; Dudel 2015). Note that this definition differs from the common definition of average treatment effects, where a difference is used instead of a ratio. Because of the ratio, $\mathrm {E}[y^1(u^0)/y^0(u^0)]$ is not point-identified using standard assumptions.

More specifically, either $y^0(u)$ or $y^1(u)$ is observed; never both. That is, at any point in time, some households are observed as being of the reference type, but not of the comparison type, and vice versa. Still, under some assumptions, the marginal distributions of $y^0(u)$ or $y^1(u)$ can be estimated (e.g., Imbens 2006). However, this strategy is not sufficient for estimating equivalence scales. Based on these expectations and after applying some simple algebra, the identification problem becomes clearer in (14).

$$\begin{aligned} \mathrm {E}\left[ \frac{y^1(u^0)}{y^0(u^0)} \right] =\frac{\mathrm {E}\left[ y^1(u^0)\right] }{\mathrm {E}\left[ y^0(u^0)\right] }-\frac{1}{\mathrm {E}\left[ y^0(u^0)\right] }\mathrm {Cov}\left[ \frac{y^1(u^0)}{y^0(u^0)},y^0(u^0)\right] . \end{aligned}$$

(14)

The covariance term on the right-hand side requires the joint distribution of $y^0(u)$ and $y^1(u)$, which is not point-identified (Abbring and Heckman 2007). Szulc (2009) avoided this problem by estimating the geometric mean of $y^1(u^0)/y^0(u^0)$ instead of (14), while Dudel (2015) has proposed the use of lower and upper bounds on (14). That is, the equivalence scales are not point-identified. For the comparison of, say, childless couples and couples with one child, the equivalence scales do not take on one specific value S, but can only be shown to be in an interval $[S^-,S^+]$. Here, we adopt this partially identified approach, as well as the approach of Szulc (2009). In the partially identified approach, estimation proceeds using a nonparametric method suggested by Fan et al. (2017). The approach of Szulc (2009) follows Abadie and Imbens (2006) and applies the Mahalanobis distance for the pair-matching of households.

In contrast to previous approaches, this identification strategy does not rely on the assumption that equivalence scales are independent of the welfare level. Furthermore, it does not rely on any specific Engel curve shape. While the partially identified approach requires few assumptions, it does not allow us to produce any point estimates. Moreover, the interval estimates generated using this approach might not be informative if they are too wide. The method proposed by Szulc (2009) avoids this issue by estimating the geometric mean, but the geometric mean will always be lower than arithmetic mean, and an increase in the variance of $y^1(u^0)/y^0(u^0)$ will push the geometric mean further away from the arithmetic mean (Cartwright and Field 1978), leading to potentially biased estimates.

Table 1 Empirical approaches to estimate equivalence scales and their underlying assumption and properties

3.6 Testing linearity of Engel curves, shape invariance, and income independence

Most of the methods described above rely on one of three assumptions (See Table 1). These are, ordered by increasing generality: linearity of Engel curves, shape invariance, and income independence. Linearity of Engel curves implies shape invariance and income independence; shape invariance implies income independence. On the other hand, income independence does not imply linearity or shape invariance. That is, both linearity and shape invariance are sufficient, but not necessary, for income independence.⁵ In the literature, several tests have been proposed to assess these assumptions.

To test whether Engel curves are linear, we use two approaches. First, as suggested by Lancaster and Ray (1998), we include a quadratic term for log income in the Engel approach; i.e., a quadratic term $\beta _{x2} \log (x)^2$ is added to Eq. (6). If this term is statistically significant, then linearity of Engel curves can be rejected. Second, in a similar vein, we check the statistical significance of the coefficients of the quadratic income terms in the QAI demand system (Banks et al. 1997). In line with the previous literature, we call those coefficients $\lambda$-parameter. For each expenditure category, there is one such coefficient; in our case, there are 12 coefficients.

For testing shape invariance, we apply three approaches. First, we add a new term to the main equation of the Engel approach, interacting household type and log income, as proposed by Pendakur (1999). If the coefficient is significant, then the regression line for the comparison household is not only shifted relative to the reference household, but is rotated, and shape invariance can be rejected. Second, we calculate a correlation between the reference Engel curve and the shifted Engel curve. Hacing values close to one can be regarded as a necessary, but not a sufficient condition of shape invariance (Stengos et al. 2006). Third, we use simulations to calculate the probability that the empirical goodness-of-fit of the semiparametric approach is observed given shape invariance. If this probability is below the conventional thresholds, shape invariance is rejected. For details on the implementation, see Pendakur (1999). Here, we use the loss function proposed by Stengos et al. (2006).

In addition to these parametric and semiparametric tests, we apply two nonparametric approaches. The first approach allows us to check both linearity of Engel curves and shape invariance and relies on the visual inspection of nonparametrically estimated Engel curves (Banks et al. 1997). The second method is based on the nonparametric, partially identified approach. A confidence interval on the bounds of the covariance term on the right-hand side of Eq. (14), $\mathrm {Cov}\left[ y^1(u^0)/y^0(u^0),y^0(u^0)\right]$, is estimated. If this confidence interval does not include zero, which is the value of the covariance that implies income independence, then income independence can be rejected.

All of the tests described above are applied for each household type; e.g., couples without children or couples with one child. Thus, it is possible that an assumption might be rejected for one household type, but not for other types.

4 Data and implementation

4.1 Data and sample selection

We applied the methods described in the previous section to data of the German Sample Survey of Income and Expenditure (Einkommens- und Verbrauchsstichprobe; EVS). The EVS is a quinquennial survey conducted by the German Federal Statistical Office that covers about $0.2\%$ of households in Germany. We used data from the years 2003, 2008, and 2013. The three cross sections of the EVS contain nearly 130,000 households in total. For each household, detailed information on the household’s income, expenditures, and savings is collected for one quarter of the year.

To reduce the heterogeneity of the sample and to ease the interpretation of the equivalence scale estimates, we selected a certain subset of households. We dropped about 34,000 households in which at least one of the adults was over age 65. Pensioners are not of major interest when calculating equivalence scales for children, as it may be expected that in most cases, their children have left the household. Based on a similar reasoning, we excluded another 14,000 households in which the children were over age 18. Next, we restricted the set of households to those residing in Western Germany, as there are large economic differences between Eastern and Western Germany (Brenke and Zimmermann 2009). This reduced the sample by another 12,000 observations.

For some household types, there were not enough observations to produce precisely estimated equivalence scales. This led us to exclude a few hundred families with more than three children and about 3000 single-parent families.⁶ We also excluded about 20,000 households that were dependent on welfare benefits, because otherwise our equivalence scales might be influenced by the equivalence scales implied by the welfare benefits received by different household types. In Germany, for example, welfare benefit levels are partly set using equivalence scales. A couple is assumed to need 1.8 times as much income as a single adult, and the welfare benefits the couple receives are set accordingly. Including low-income households then runs the risk of replicating this equivalence scale, which was created by policy-makers based not on differences in the behavior of households, but on assumptions made by politicians. For the same reason, we dropped about 300 households with a net income below the approximated welfare benefit level (excluding housing costs).⁷

Finally, we have tried to make the incomes and the expenditures of different households as comparable as possible. For example, when a family’s housing is paid for by an employer, the household’s income is not comparable to that of a household paying rent. Thus, we dropped 1200 cases in which an employer was covering these costs. Furthermore, in line with a common practice in the literature (e.g., Donaldson and Pendakur 2004), we removed 600 households that reported extreme income values and 6800 households that reported extreme expenditure values. These values were considered extreme if they exceeded the sample median plus two and a half standard deviations (Banks et al. 1997). Spending above this threshold is usually attributable to highly irregular expenses (e.g., buying a car, a health shock), which can have large effects on demand system estimates. Levels of extreme spending were not highly correlated across the 12 categories, and most outliers only counted as outliers for one of the categories. Households with zero expenditures on food were also dismissed (10 households). The final sample consisted of about 32000 households (about 11,000 households in the EVS 2013). The descriptive statistics are reported in Tables 2 and 3.

Table 2 Descriptive statistics

Table 3 Expenditure categories

4.2 Main variables

Expenditure information in the EVS is collected based on a German equivalent of the United Nations’ Classification of Individual Consumption According to Purpose (COICOP). Total expenditures are broken down into 12 commodity groups: (1) food and non-alcoholic beverages; (2) alcoholic beverages and tobacco; (3) clothing and footwear; (4) housing, water, electricity, and heating; (5) furniture, household equipment, and routine household maintenance; (6) health; (7) transportation; (8) communication; (9) recreation and culture; (10) education; (11) restaurants and hotels; and (12) miscellaneous goods and services. While these expenditure categories are, in turn, based on more detailed expenditure information, for our estimation, we used only these 12 categories.

Price information for each of the 12 expenditure categories was provided by the German Federal Statistical Office. Monthly prices were aggregated into quarterly prices by calculating the average. We thus included annual price variation between the years 2003, 2008, and 2013, as well as seasonal variation within these years.⁸

The socio-demographic variables we used included the number of adults and the number of children under age 18 in each household. The household type was assigned based on these two variables. We distinguished between households made up of a single adult (A), a childless couple (AA), a couple with one child (AAC), a couple with two children (AACC), and a couple with three children (AACCC) (see Table 2 for the sample composition with respect to the household type). Single-adult households were used as the reference household type for all equivalence scales.

Additional control variables were dummy variables indicating whether both partners in a couple were full-time employed; as well as variables capturing the quarter of the year (spring, summer, autumn, winter), the age and the level of education (1 = no education, 2 = vocational training, 3 = foreman, 4 = college, 5 = university degree) of the household head, the type of region (ranging from one for rural areas to seven for densely populated areas in cities), and a dummy variable for homeownership. We included full-time employment of both partners as a dummy, because these couples likely differed from other couples in the time they had available for home production, and, thus, in their expenditures. Including the quarter of the year allowed us to control for seasonal spending (e.g., vacations); including the type of region allowed us to indirectly capture price differences affecting behavior, like higher rents in cities; including homeownership enabled us to determine whether households had rent expenditures, which could represent a sizable proportion of household expenditures; and age and education allowed us to control for further heterogeneity in household spending.

4.3 Implementation

In this section, we briefly provide some details concerning the implementation of the approaches (see Sect. 3 for the theoretical concept of the approaches, or, for further details, see the studies that introduced the methods shown in Table 6).

First, to ease the comparison between the methods, we used total expenditures instead of income in all of the approaches but the ELES. While in the single parametric, the semiparamteric, and the counterfactual approaches, it was feasible to use either income or total expenditures, the ELES was explicitly designed to use income. Second, all of the single-equation models were estimated without price information and were based on the 2013 EVS sample. The demand systems, on the other hand, included price information for 2003, 2008, and 2013. Third, for the approach of Rothbarth (1943), we used alcohol as the adult good. In order to obtain reasonable results, we excluded families with zero expenditures on these commodities (García and Labeaga 1996). As a large number of the families in our sample had zero expenditures (about 2400), this sample restriction was applied only to this approach. Fourth, for the semiparametric approaches, we sought to find the values of $\phi$ and $\mu$ that minimize Eq. (12) by inserting start intervals that increase with household size—that is, 0.9 and 2.0 for AA, 0.9 and 2.2 for AAC, 0.9 and 2.5 for AACC, and 0.9 and 3.5 for AACCC for $\phi$—and used increments of 0.01.

The ability of the applied approaches to consider control variables was limited in some cases. For example, as the estimation of the Engel curves in the semiparametric approach was pursued nonparametrically, it did not allow for the consideration of control variables. In some of the other approaches, the control variables were not used in a conventional way. For example, in the matching approach by Szulc (2009) the control variables were used as matching variables. Moreover, in the nonparamteric approach by Dudel (2015) nonparamateric densities were calculated conditional on the control variables.

Depending on the specific approach applied, estimation was carried out using OLS as implemented in base R; nonlinear, seemingly unrelated regression as implemented in the R package nlsur (Garbuszus 2017); nonparametric kernel methods as implemented in the R package np (Hayfield and Racine 2008); and pair-matching as implemented in the R package Matching (Sekhon 2011).

To make standard errors between methods as comparable as possible, we calculated bootstrapped standard errors for every approach. However, for the QAI demand system and the QES, bootstrapping was computationally out of reach. For the QAI demand system, we used analytic standard errors (Ray 1983).⁹ For the rest of the approaches, we applied the resampling bootstrap and used 500 replications. The confidence intervals were based on percentiles of the bootstrap replications. Constructing confidence intervals for the nonparametric bounds by Dudel (2015) was not straightforward. Our general aim was to construct an interval that covered the complete identification region with a fixed probability ($95\%$). Further details are provided in the supplementary materials.

5 Results

5.1 Testing identifying assumptions: Linearity, shape invariance, income independence

Before we present the equivalence scale estimates, we discuss the results of the econometric tests regarding the identifying assumptions of the different approaches: namely, linearity of Engel curves, shape invariance, and income independence (see also Sect. 3.6).

The results for the linearity of Engel curves depended on the test, the commodity, and the household type used; but, overall, they indicate that linearity can be rejected. Estimating Engel’s approach as in Eq. (6) with an additional quadratic term of log per capita income gives a p value of 0.065 for the resulting coefficient. It is therefore significant at the 10$\%$-level. The results for Rothbarth’s approach are similar ($p=0.062$). Table 4 shows the $\lambda$-parameters of the QAI demand system. Most coefficients are highly statistically significant, except housing, health, and expenditures on education. In Fig. 1, nonparametric regression estimates of log income on the share of expenditures allocated to food are displayed, stratified by household type (see the supplementary materials for the other commodity groups). For the food share, the curves are mostly approximately linear, except at lower income levels, which likely explains the results for the QAI demand system. Visually inspecting the rest of the commodity groups, we notice that most cases are well fitted by a quadratic specification, while in a few cases, a nonparametric regression is needed (for example, clothing in families with three children; see Figure 5 in the supplementary materials); but those cases appear to be exceptions.

Table 4 $\lambda$-parameters of the QAI demand system

Fig. 1

Nonparametric estimation of Engel curves across household types. Data: German Sample Survey of Income and Expenditure 2013

Turning to shape invariance, the results mostly indicate that shape invariance seems to hold. Judging from the results shown in Fig. 1, Engel curves for the food expenditure share are approximately shape invariant. The exception might be families with three children. The parametric test of shape invariance confirms this, as in the comparison between singles and families with three children (Column AACCC in Table 5), the interaction term is significant at the 5$\%$ level. By contrast, the results of the semiparametric tests of shape invariance generally do not reject shape invariance (See Table 5). With the loss function of Pendakur (1999), the correlation coefficients are larger than they are with the loss function suggested by Stengos et al. (2006). Neither is low enough to lead us to reject shape invariance.

Table 5 Parametric and semiparametric tests of shape invariance and income independence

The outcomes of the nonparametric test, displayed in the last row of Table 5, indicate that income independence likely does not hold, even though shape variance is not rejected. This means that the different tests do not give a consistent picture. In the literature, tests of shape invariance have also led to mixed results, depending on the type of test, the expenditure category, and the household type (see Banks et al. 1997; Stengos et al. 2006; Pendakur 1999). On the other hand, the rejection of income independence is consistent with earlier findings (Koulovatianos et al. 2005; Biewen and Juhasz 2017). A potential explanation for this finding is that income independence only holds for middle and high incomes; while at low income levels, equivalence scales are income-dependent, as suggested by Fig. 1. Irrespective of why this might be the case, the results presented here make it hard to judge the approaches exclusively by their assumption; except for the approaches that assume linearity of Engel curves. It thus appears that the plausibility criteria laid out in Sect. 2 and applied below are crucial when attempting to decide between the nonlinear methods.

Table 6 Income-independent equivalence scales

5.2 Equivalence scale estimates

Equivalence scale estimates for all methods are presented in Table 6. More specifically, using the household of a single adult (A) as the reference, estimates are shown for childless couples (AA), couples with one child (AAC), couples with two children (AACC), and couples with three children (AACCC). Below the point estimates and in brackets, we show 95$\%$-confidence intervals based on bootstrapping (see Sect. 4.3). Unless it is otherwise stated, it may be assumed that we rely on these intervals when discussing similarities between the methods. In addition, we calculated the equivalence scale elasticity, which is defined through $S = h^\alpha$, where S is the equivalence scale value, h is household size, and $\alpha$ is elasticity (Buhmann et al. 1988). Generally, $\alpha$ lies between zero and one, with a value of zero implying that additional household members do not generate any additional costs, and a value of one implying that there are no economies of scale. Scale elasticity might hide some more subtle differences between equivalence scales, but it allows for a simple comparison across methods. Here, we discuss these more nuanced differences, while also presenting a broad overview based on elasticities. The last rows of Table 6 display the expert scales often used by researchers: namely, the modified OECD scale and the square root scale. In the last column, we show which plausibility criteria—as discussed in Sect. 2.3—the respective equivalence scale point estimates violate. The modified OECD scale and the square root scale do not violate any of these criteria. For additional comparisons, Table 7 shows examples of equivalence scale estimates based on older waves of the EVS taken from the literature. For the methods that have not yet been applied to the EVS, Table 8 shows equivalence scales for different countries and datasets.

Table 7 Equivalence scales estimated with the German Sample Survey of Income and Expenditure (EVS)

Table 8 Equivalence scales based on expenditure data for other datasets and countries

Compared to the other approaches we applied , the single-equation approach by Engel yields the highest scale values. The economies of scale are small for the second adult (A to AA) and are nonexistent for children. The equivalence scale elasticity is around 0.94, which is close to the estimate reported by Merz and Faik (1995) based on an older version of the EVS (see Table 7). A possible explanation for these high scale values was provided by Deaton and Muellbauer (1986), who argued that using expenditures on food, as Engel’s approach does, overestimates the costs of raising children. The reasoning is that most expenditures related to children will be expenditures on food; thus, even if after the birth of a child the consumption of the parents remains the same, the share of the household’s expenditures on food will increase. Thus, keeping the relative expenditures on food constant, as Engel’s approach does, will lead to overcompensation. In addition, the results of this approach are questionable, given that the linearity of Engel curves is rejected, and it is not consistent with most of the plausibility criteria.

For the Rothbarth approach, which replaces the food share in Engel’s approach with expenditures on an adult good, we use the household of two adults without a child as a reference. This approach is not suitable for estimating the equivalence scale value of a childless couple relative to that of the household of a single adult. The Rothbarth approach results in scale values that are considerably lower than those of the Engel approach, and its scale elasticity is rather small, especially compared to that of all of the other approaches. For instance, according to the Rothbarth estimates, a couple with one child needs roughly $30\%$ more income to be as well-off as a childless couple; while according to the Engel approach, the estimated additional income needed is around $50\%$ (calculated as 2.66 divided by 1.72). This observation is in line with Deaton and Muellbauer (1986), who argued that the Rothbarth approach underestimates the costs of having children and should therefore lead to lower equivalence scale values. Deaton and Muellbauer (1986) also reported findings based on the Rothbarth approach that are close to our estimates, although they based their analysis on data for Sri Lanka. However, as in the Engel approach, linearity of Engel curves is a questionable assumption. Moreover, the Rothbarth approach is also not consistent with two plausibility criteria, as it leads to equivalence scale values that are not strictly increasing with household size; the increases in the scale values by household size are not decreasing.¹⁰

The ELES yields a scale value for couples without children (AA) that is roughly similar to the value reported by the Engel approach. However, for larger households, the scale values of the ELES are lower than those of the Engel approach and are closer to the square root scale. The results are very similar to the findings of Faik (2011) based on the EVS 2003. For families with more than one child, our scale values are slightly higher. Compared to the scale values of the ELES, the QES has higher values for smaller households, but lower values for larger households. The equivalence scale elasticity is very similar in both cases, and between the elasticity of the square root scale and the modified OECD scale. In the QES, no confidence intervals are reported, as the estimation procedure did not converge for many of the bootstrap samples, and the inference conditional on convergence could be biased. Apart from this, using the QES might seem more appropriate than using the ELES, as it does not rely on linearity of Engel curves. On the other hand, the QES violates the “household size effect” criterion in Eq. (2), as couples with two children have a lower scale value than couples with one child. That is also the case for the QES estimated by Kohn and Missong (2003) with an older version of the EVS. As this criterion is generally considered essential for equivalence scales, the QES estimates can be seen as implausible.

The AI demand system leads to comparatively low equivalence scale values, and it has a rather low elasticity of 0.2, which indicates that additional household members add very little to the equivalence scales. As is the case for other methods that require linearity of Engel curves, the AI demand system might not lead to reliable estimates because one of its key identifying assumptions is violated. Thus, using the QAI demand system should be more appropriate. Apart from the scale value for couples without children, the estimates of the QAI demand system are between the square root scale and the modified OECD scale, and the confidence intervals of its scale values include the values of both of these expert scales. Correspondingly, its equivalence scale elasticity is also between the elasticities of the expert scales. While the QAI demand system has not been estimated with German data before, estimates for other countries are available (see Table 8). Our results fall somewhere in the middle; the estimates reported by Michelini (2001) are generally higher, while Balli and Tiezzi (2010) and Blacklow et al. (2010) reported lower estimates. Like the estimates provided by Balli and Tiezzi (2010), our results violate the plausibility criterion stating that the increase of scale values with household size should become smaller with increasing household size. However, for our estimates as well as for the estimates of Balli and Tiezzi (2010), this violation occurs for households with several children, for which there might be exceptions to this criterion, as we argued in Sect. 2.3.

Looking at the semiparametric methods, we can see that the approach by Pendakur (1999) leads to scale values that are rather spread out. For instance, the scale value of 1.2 for couples without children is low, while the scale value of 2.4 for a couple with one child is rather high. While shape invariance cannot be rejected, the estimates violate all four plausibility criteria. This might be due to the deficient loss function. While modifying the loss function according to Stengos et al. (2006) leads to more plausible results, it is still the case that not all criteria are satisfied; e.g., the scale values are not strictly increasing with household size. Compared with the estimates reported by Stengos et al. (2006) for Canada, our estimates are relatively low and are closer to the results of Wilke (2006) using the EVS of 1998. Equivalence scales reported by Wilke (2006) do not violate the household size effect (See Table 7). A possible explanation for this finding, is that in contrast to Pendakur (1999), Stengos et al. (2006), and our application; he used a model based on multiple expenditure categories.

Although it relies on a very different identification strategy, the approach by Szulc (2009) leads to estimates that are close to those of the QAI demand system. For most household types, the confidence intervals for the point estimates of the two methods overlap, and the scale elasticities are also very close. The latter is also the case when compared to the square root scale and the modified OECD scale. Compared to Szulc (2009), who calculated equivalence scales for Poland, we observe that the scale value for couples without children is similar (A to AA), while the scales for the other comparisons are lower. Of the four plausibility criteria, one is violated: the scale value increases by 0.22 for the second child, but by 0.26 for the third child. But as we argued previously this might be realistic. Moreover, this approach does not require linearity of Engel curves, shape invariance, or income independence. The identification bounds provided by the completely nonparametric approach of Dudel (2015) are generally lower than the estimates of the matching method. However, they do not strictly increase with household size (AACC to AACCC), even though the confidence intervals overlap.

To summarize, the approaches that assume linearity of Engel curves (Engel, Rothbarth, ELES, AI) and the semiparametric approach by Pendakur (1999) and its variant (Stengos et al. 2006) are either based on identifying assumptions that can be rejected or they contradict one or several of the plausibility criteria. The matching approach by Szulc (2009) and the QAI demand system (Banks et al. 1997) violate only criterion (4) for which exceptions seem realistic, especially for households with several children. The nonparametric approach by Dudel (2015) might violate criterion (2) and, thus, criterion (4), although this violation is not statistically significant based on a comparison of confidence intervals.

These finding indicate that, overall, there is no approach that does not violate at least one of the plausibility criteria. The approaches that are shown to have fewer or less serious violations are either based on the counterfactual framework and do not require strong identifying assumptions (matching, nonparametric) or make use of all expenditure categories and thus more data than most methods, combined with a flexible specification (QAI demand system). At the same time, applying the QAI demand system to different institutional contexts (Germany, Italy, Australia, New Zealand) can also lead to different results (Table 8). Studies using the same dataset and methods, but for different periods, have found roughly similar equivalence scales elasticities, compared to our results (Table 7). Finally, when using the more plausible equivalence scales to calculate common inequality and poverty indicators, we find that the resulting measures are very similar to each other (see supplementary materials).

6 Conclusion

In this paper, we compared 10 different empirical approaches for the estimation of equivalence scales, covering parametric, semiparametric, and fully nonparametric methods. Applying these approaches to German expenditure data from the Sample Survey of Income and Expenditure (waves 2003, 2008, 2013), we found that only a subset of methods produce plausible equivalence scales. These plausible equivalence scales are, however, similar to each other when applying them in the calculation of inequality and poverty indices. Our findings regarding income independence are somewhat mixed, but indicate that income-independent scales might be appropriate for many questions, especially when studying all income levels. If, on the other hand, the focus is on low or high incomes, then income-independent scales might not be a good choice.

While we covered several very different approaches, our conclusions are restricted to a limited set of methods only; many methods have been proposed in the literature that we were not able to include here. For example, the approach suggested by Pendakur and Sperlich (2010) was not applied, as it requires long time series of price variation. While the EVS dates back to 1962, there have been a number of structural breaks in the collection of the expenditure data that would complicate the analysis. Moreover, specifications other than the Working-Leser specification have been proposed, some of which make the resulting equivalence scales income-dependent (Donaldson and Pendakur 2004). Another potential restriction of our findings is their validity for other contexts; while our findings are promising, we cannot be certain that applying the methods to other countries and datasets would produce consistent sets of equivalence scales.

For researchers applying single exact equivalence scales, using the modified OECD scale can be seen as a reasonable choice if an income-independent scale is desired, at least for Germany. Our results further suggest that the square root scale should be used in estimates for large families.