Skip to main content
SpringerLink
Log in

Optimization design method of machine tool static geometric accuracy using tolerance modeling

  • ORIGINAL ARTICLE
  • Published:
The International Journal of Advanced Manufacturing Technology Aims and scope Submit manuscript

Abstract

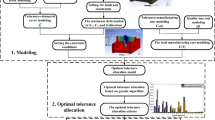
Existing precision design methods cannot directly guide the tolerance design. Therefore, in this study, an optimization design method of machine tool static geometric accuracy based on tolerance modeling is proposed. In this methodology, the mapping relationship between the geometric error of machine tools and tolerance design is established using the small displacement torsor to represent the tolerance information and the Monte Carlo simulation method is used to establish the response model of the torsor parameters and the tolerance variation bandwidths. An assembly accuracy model is then established by combining a machine tool topology analysis and the forming mechanism of the joint surface error. To calculate the tolerances of the component joint surface, a tolerance response model related to the component joint surface tolerance and torsor parameters is developed. Finally, according to the state function of assembly accuracy reliability, a function response model of the assembly accuracy, reliability, and tolerance is developed. Combining the assembly’s processing cost model with the accuracy, reliability, and tolerance principles, a tolerance optimization model of the static geometric accuracy of a CNC machine tool, a linear axis motion guide, is constructed as a case study. Using a simulated annealing genetic algorithm to solve the tolerance optimization model, the tolerance optimization value is obtained, thereby verifying the effectiveness of the proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Data availability

All data generated or analyzed during this paper are included in this published article.

Code availability

Not applicable.

References

  1. Corrado A, Polini W (2017) Assembly design in aeronautic field: From assembly jigs to tolerance analysis. Proc Inst Mech Eng B J Eng Manuf 231:2652–2663

    Article  Google Scholar 

  2. Wu H, Zheng H, Li X, Rong M, Fan J, Meng X (2020) Robust design method for optimizing the static accuracy of a vertical machining center. Int J Adv Manuf Technol 109(7/8):2009-2022. https://doi.org/10.1007/s00170-020-05596-0

  3. Dorndorf UKVS (1994) Optimal budgeting of quasistatic machine tool errors. J Eng  Industry 16:42–53. https://doi.org/10.1115/1.2901808

  4. Krishna AG, Rao KM (2006) Simultaneous optimal selection of design and manufacturing tolerances with different stack-up conditions using scatter search. Int J Adv Manuf Technol 30:328–333

    Article  Google Scholar 

  5. Singh PK, Jain PK, Jain SC (2003) Simultaneous optimal selection of design and manufacturing tolerances with different stack-up conditions using genetic algorithms. Int J Prod Res 41(11):2411–2429

  6. Huang MF, Zhong YR, Xu ZG (2005) Concurrent process tolerance design based on minimum product manufacturing cost and quality loss. Int J Adv Manuf Technol 25:714–722

    Article  Google Scholar 

  7. Jin SZCYK (2010) Tolerance design optimization on cost–quality trade-off using the Shapley value method. J Manuf Syst 29:142–150

    Article  Google Scholar 

  8. Yu ZM, Liu ZJ, Ai YD, Xiong M (2013) Geometric Error Model and Precision Distribution Based on Reliability Theory for Large CNC Gantry Guideway Grinder. Chin J Mech Eng 49:142–151. https://doi.org/10.3901/JME.2013.17.142

    Article  Google Scholar 

  9. Cheng Q, Zhao H, Zhang G, Gu P, Cai L (2014) An analytical approach for crucial geometric errors identification of multi-axis machine tool based on global sensitivity analysis. Int J Adv Manuf Technol 75:107–121

    Article  Google Scholar 

  10. Cai L, Zhang Z, Qiang C, Liu Z, Gu P, Yin Q (2016) An approach to optimize the machining accuracy retainability of multi-axis NC machine tool based on robust design. Precis Eng 43:370–386

    Article  Google Scholar 

  11. Zhang Z, Liu Z, Cai L, Cheng Q, Qi Y (2017) An accuracy design approach for a multi-axis NC machine tool based on reliability theory. Int J Adv Manuf Technol 91:1547–1566

    Article  Google Scholar 

  12. Zhang Z, Liu Z, Cheng Q, Qi Y, Cai L (2017) An approach of comprehensive error modeling and accuracy allocation for the improvement of reliability and optimization of cost of a multi-axis NC machine tool. Int J Adv Manuf Technol 89:561–579

    Article  Google Scholar 

  13. Cheng Q, Zhang Z, Zhang G, Gu P, Cai L (2015) Geometric accuracy allocation for multi-axis CNC machine tools based on sensitivity analysis and reliability theory. Proceedings of the Institution of Mechanical Engineers, Part C. J Mech Eng Sci 229:1134–1149

    Article  Google Scholar 

  14. Wu H, Zheng H, Li X, Wang W, Xiang X, Meng X (2020) A geometric accuracy analysis and tolerance robust design approach for a vertical machining center based on the reliability theory. Measurement  https://doi.org/10.1016/j.measurement.2020.107809

  15. Shi Y, Zhang D, Nie Y, Zhang H, Zhao X (2016) A new top-down design method for the stiffness of precision machine tools. Int J Adv Manuf Technol 83:1887–1904

    Article  Google Scholar 

  16. Wu H, Zheng H, Wang W, Xiang X, Rong M (2020) A method for tracing key geometric errors of vertical machining center based on global sensitivity analysis. Int J Adv Manuf Technol 106(9/10):3943–3956. https://doi.org/10.1007/s00170-019-04876-8

  17. Peng H, Lu W (2018) Modeling of Geometric Variations Within Three-Dimensional Tolerance Zones. J Harbin Inst Technol (New Ser) 25:41–49

    Google Scholar 

  18. Bourdet PD (1984) Tolerancing of component dimensions in CAD. Elsevier 16(1):25–32

  19. Ghie W, Laperriere L, Desrochers A (2003) A unified jacobian-torsor model for analysis in computer aided tolerancing: Recent Advances in Integrated Design and Manufacturing in Mechanical Engineering Clermont-Ferrand 2002:63–72

  20. Li H, Zhu H, Li P, He F (2014) Tolerance analysis of mechanical assemblies based on small displacement torsor and deviation propagation theories. Int J Adv Manuf Technol 72:89–99

    Article  Google Scholar 

  21. Marziale M, Polini W (2011) A review of two models for tolerance analysis of an assembly: Jacobian and torsor. Int J Comput Integ M 24(1/3):74–86. https://doi.org/10.1080/0951192X.2010.531286

  22. Peng Heping,Wang Bin (2018) A statistical approach for three-dimensional tolerance redesign of mechanical assemblies. P I Mech Eng 232(12):2132–2144. https://doi.org/10.1177/0954406217716956

  23. Mu XK, Sun QC, Sun KP, Sun W (2018) 3D Tolerance Modeling and Accuracy Analysis of Flexible Body Based on Load Action. J Mech Eng 54:39–48

    Article  Google Scholar 

  24. Yu ZM (2014) Research on Design Method of Precision Chain of CNC Machine Tool. PHD Thesis, Hunan University

  25. Liu H, Yang R, Wang P, Chen J, Xiang H, Chen G (2020) Measurement point selection and compensation of geometric error of NC machine tools. Int J Adv Manuf Technol 108:3537–3546

  26. Fu G, Liu J, Rao Y, Gao H, Lu C, Deng X (2020) Geometric error compensation of five-axis ball-end milling based on tool orientation optimization and tool path smoothing. Int J Adv Manuf Technol 108(5-6)

  27. Ding S, Song Z, Wu W, Guo E, Huang X, Song A (2020) Geometric error modeling and compensation of horizontal CNC turning center for TI worm turning. Int J Mech Sci 167. https://doi.org/10.1016/j.ijmecsci.2019.105266

  28. Jiang WW (2017) Application of tolerance backstepping design with performance targets in engine precision manufacturing. China Standarization 2:199–201. https://doi.org/10.3969/j.issn.1002-5944.2017.01.171

  29. Aguilar JJ, Velazquez J, Aguado S, Santolaria J, Samper D (2016) Improving a real milling machine accuracy through an indirect measurement of its geometric errors. J Manuf Syst 40:26–36

    Article  Google Scholar 

  30. Fu G, Fu J, Shen H, Xu Y, Jin YA (2015) Product-of-exponential formulas for precision enhancement of five-axis machine tools via geometric error modeling and compensation. Int J Adv Manuf Technol 81:289–305

    Article  Google Scholar 

Download references

Funding

The authors wish to thank the major technological innovation projects in Chengdu (2019-YF08-00162-GX), which supported the research presented in this paper.

Author information

Authors and Affiliations

  1. School of Electronic Information and Electrical Engineering, Chengdu University, No. 2025 Chengluo Avenue, Chengdu, 610106, Sichuan, China

    Haorong Wu & Yongxin Zhao

  2. School of Mechanical Engineering, Chengdu University, Chengdu, 610106, Sichuan, China

    Xiaoxiao Li & Fuchun Sun

  3. School of Mechatronic Engineering, Southwest Petroleum University, Chengdu, 610500, Sichuan, China

    Hualin Zheng

Authors
  1. Haorong Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiaoxiao Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Fuchun Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hualin Zheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Yongxin Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Haorong Wu: Conceptualization, Methodology, Software, Investigation, Writing—original draft, Writing—review & editing. Xiaoxiao Li: Validation, Formal analysis, Visualization. Fuchun Sun: Validation, Formal analysis, Visualization, Software. Hualin Zheng: Validation, Formal analysis, Visualization. Yongxin Zhao: Formal analysis.

Corresponding author

Correspondence to Haorong Wu.

Ethics declarations

Ethics approval

Not applicable.

Consent to participate

Not applicable.

Consent for publication

Not applicable.

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wu, H., Li, X., Sun, F. et al. Optimization design method of machine tool static geometric accuracy using tolerance modeling. Int J Adv Manuf Technol 118, 1793–1809 (2022). https://doi.org/10.1007/s00170-021-07992-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00170-021-07992-6

Keywords

Search

Navigation