Skip to main content
SpringerLink
Log in

Discrete structures equivalent to nonlinear Dirichlet and wave equations

  • Original Article
  • Published:
Continuum Mechanics and Thermodynamics Aims and scope Submit manuscript

An Erratum to this article was published on 16 April 2016

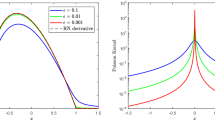
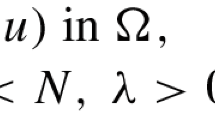Abstract

The Amann–Conley–Zehnder (ACZ) reduction is a global Lyapunov–Schmidt reduction for PDEs based on spectral decomposition. ACZ has been applied in conjunction to diverse topological methods, to derive existence and multiplicity results for Hamiltonian systems, for elliptic boundary value problems, and for nonlinear wave equations. Recently, the ACZ reduction has been translated numerically for semilinear Dirichlet problems and for modeling molecular dynamics, showing competitive performances with standard techniques. In this paper, we apply ACZ to a class of nonlinear wave equations in \({\mathbb{T}^n}\), attaining to the definition of a finite lattice of harmonic oscillators weakly nonlinearly coupled exactly equivalent to the continuum model. This result can be thought as a thermodynamic limit arrested at a small but finite scale without residuals. Reduced dimensional models reveal the macroscopic scaled features of the continuum, which could be interpreted as collective variables.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Amann H.: Multiple positive fixed points of asymptotically linear maps. J. Funct. Anal. 17, 174–213 (1974)

    Article  MATH  MathSciNet  Google Scholar 

  2. Amann H.: Saddle points and multiple solutions of differential equations. Math. Z. 169, 933–944 (1979)

    Article  MathSciNet  Google Scholar 

  3. Amann H., Zehnder E.: Nontrivial solutions for a class of nonresonance problems and applications to nonlinear differential equations. Ann. Sc. Norm. Super. Pisa CC. Sci. IV(7), 539–603 (1980)

    MathSciNet  Google Scholar 

  4. Amann H., Zehnder E.: Periodic solutions of asymptotically linear Hamiltonian systems. Manuscr. Math. 32, 149–189 (1980)

    Article  MATH  MathSciNet  Google Scholar 

  5. Amann H., Zehnder E.: Multiple periodic solutions for a class of nonlinear autonomous wave equations. Houston J. Math. 7, 147–174 (1981)

    MATH  MathSciNet  Google Scholar 

  6. Ambrosetti A.: Critical points and nonlinear variational problems. Mém. Soc. Math. France (N.S.) 49, 1–139 (1992)

    MathSciNet  Google Scholar 

  7. Antman S.S.: The equations for large vibrations of strings. Am. Math. Mon. 87(5), 359–370 (1980)

    Article  MATH  MathSciNet  Google Scholar 

  8. Bambusi D., Paleari S.: Families of periodic solutions of resonant PDEs. J. Nonlinear Sci. 11, 69–87 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  9. Berti M., Bolle P.: Periodic solutions of nonlinear wave equations with general nonlinearities. Commun. Math. Phys. 243(2), 315–328 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  10. Berti M., Bolle P.: Multiplicity of Periodic solutions of nonlinear wave equations. Nonlinear Anal. 56(7), 1011–1046 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  11. Berti, M., Bolle, P.: Sobolev periodic solutions of nonlinear wave equations in higher spatial dimensions. Arch. Rational Mech. Anal. (2009). doi:10.1007/s00205-008-0211-8

  12. Berkovits J., Leinfelder H., Mustonen V.: Existence and multiplicity results for wave equations with time-independent nonlinearity. Topol. Methods Nonlinear Anal. 22(2), 273–295 (2003)

    MATH  MathSciNet  Google Scholar 

  13. Bobbo A.: Magistral Thesis in Mathematics. University of Padova, Padova (2006)

    Google Scholar 

  14. Boldrighini C., De Masi A., Pellegrinotti A., Presutti E.: Collective phenomena in interacting particle systems. Stoch. Process. Appl. 25(1), 137–152 (1987)

    Article  MATH  MathSciNet  Google Scholar 

  15. Born M., Von Kármán T.: Vibrations in space-gratings (molecular frequencies). Physik. Z. 13, 297–309 (1912)

    Google Scholar 

  16. Bourgain J.: Construction of periodic solutions of nonlinear wave equations in higher dimension. Geom. Funct. Anal. 5(4), 629–639 (1995)

    Article  MATH  MathSciNet  Google Scholar 

  17. Braun O.M., Kivshar Y.S.: The Frenkel–Kontorova model. Theor. Math. Phys. XVIII, 472 (2004)

    MathSciNet  Google Scholar 

  18. Cardin F.: Global finite generating functions for field theory. Class. Quantum Integrability Banach Cent. Publ. 59, 133–142 (2003)

    Article  MathSciNet  Google Scholar 

  19. Cardin F., Lovison A., Putti M.: A numerical implementation of an exact reduction for nonlinear Dirichlet problems. Int. J. Numer. Methods Eng. 69(9), 1804–1818 (2007)

    Article  MathSciNet  Google Scholar 

  20. Cardin F., Tebaldi C.: Finite reductions for dissipative systems and viscous fluid-dynamic models on T2. J. Math. Anal. Appl. 345, 213–222 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  21. Conley, C.: Isolated invariant sets and the Morse index. CBMS Regional Conference Series in Mathematics, vol 38 (1978)

  22. Conley C., Zehnder E.: The Birkhoff–Lewis fixed point theorem and a conjecture of V.I.Arnol’d. Invent. Math. 73, 33–49 (1983)

    Article  MATH  MathSciNet  Google Scholar 

  23. Coron J.M.: Résolution de l’équation Au + Bu = f où A est linéaire autoadjoint et B déduit d’un potential convexe. C. R. Acad. Sci. Paris Sér. A-B 288, A805–808 (1979)

    MathSciNet  Google Scholar 

  24. Canino A., Degiovanni M.: A variational approach to a class of singular semilinear elliptic equations. J. Convex Anal. 11(1), 147–162 (2004)

    MATH  MathSciNet  Google Scholar 

  25. DeLa Llave R.: Variational methods for quasi-periodic solutions of partial differential equations. World Sci. Monogr. Ser. Math. 6, 214–228 (2000)

    Article  MathSciNet  Google Scholar 

  26. Di Carlo, A.: Private communication (2008)

  27. Evans, L.C.: Partial Differential Equations. Graduate Studies in Mathematics, vol. 19 (1998)

  28. Foias C., Prodi G.: Sur le comportement global des solutions non-stationnaires des équations de Navier–Stokes en dimension 2. Rend. Sem. Mat. Univ. Padova 39, 1–34 (1967)

    MATH  MathSciNet  Google Scholar 

  29. Foias C., Sell G.R., Temam R.: Variétés inertielles des équations différentielles dissipatives. C. R. Acad. Sci. I 301, 139 (1985)

    MATH  MathSciNet  Google Scholar 

  30. Frenkel J., Kontorova T.: J. Phys. USSR 1, 137 (1939)

    MathSciNet  Google Scholar 

  31. Henry D.: Geometric Theory of Semilinear Parabolic Equations. Springer, Berlin (1981)

    MATH  Google Scholar 

  32. Korteweg D.J., de Vries F.: On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Philos. Mag. 39, 422–443 (1895)

    Google Scholar 

  33. Mancini G.: Periodic solutions of some semilinear autonomous wave equations. Boll. Un. Mat. Ital. (5) 15(B), 649–672 (1978)

    MATH  MathSciNet  Google Scholar 

  34. Maragliano L., Fischer A., Vanden-Eijnden E., Ciccotti G.: String method in collective variables: minimum free energy paths and isocommittor surfaces. J. Chem. Phys. 125(2), 024106 (2006)

    Article  Google Scholar 

  35. Marcello L., Magrone P., Zhou H.S.: A Dirichlet problem with asymptotically linear and changing sign nonlinearity. Rev. Mat. Complut. 16(2), 465–481 (2003)

    MATH  MathSciNet  Google Scholar 

  36. Mikhaĭlov V.: Équations aux dérivées partielles. Mir, Moscow (1980)

    Google Scholar 

  37. Nirenberg L.: Variational and topological methods in nonlinear problems. Bull. Am. Math. Soc. (N.S.) 3(4), 267–302 (1981)

    Article  MathSciNet  Google Scholar 

  38. Ponno A.: Soliton theory and the Fermi–Pasta–Ulam problem in the thermodynamic limit. Europhys. Lett. 64(5), 606–612 (2003)

    Article  MathSciNet  Google Scholar 

  39. Rabinowitz P.: Free vibrations for a semilinear wave equation. Comm. Pure Appl. Math. 31(1), 31–68 (1967)

    MathSciNet  Google Scholar 

  40. Robinson J.C.: A concise proof of the “geometric” construction of inertial manifolds. Phys. Lett. A 200, 415–417 (1995)

    Article  MATH  MathSciNet  Google Scholar 

  41. Rybicki S.: Periodic solutions of vibrating strings. Degree theory approach. Ann. Math. Pura Appl. 179(1), 197–214 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  42. Temam R.: Infinite dimensional dynamical systems in mechanics and physics. Springer, Berlin (1988)

    MATH  Google Scholar 

  43. Turco A., Passerone D., Cardin F.: Tonelli principle: finite reduction and fixed energy molecular dynamics trajectories. Multiscale Model. Simul. 7(3), 1171–1191 (2009)

    Article  MathSciNet  Google Scholar 

  44. Vainberg M.M.: Variational Methods for the Study of Nonlinear Operators. Holden-Day, San Francisco (1964)

    MATH  Google Scholar 

  45. Viterbo C.: Recent progress in periodic orbits of autonomous Hamiltonian systems and applications to symplectic geometry. Lect. Notes Pure Appl. Math. 121, 227–250 (1990)

    MathSciNet  Google Scholar 

  46. Volterra V.: Leç cons sur les Fonctions de Ligne. Gauthier-Villars, Paris (1913)

    Google Scholar 

  47. Wang Z.Q.: Multiple periodic solutions for a class of nonlinear nonautonomous wave equations. Acta Math. Sinica N. S. 5(3), 197–213 (1989)

    Article  MATH  MathSciNet  Google Scholar 

  48. Yukhnovskiĭ I.R.: Phase transitions of the second order. Collective variables method. World Scientific, Singapore (1987)

    MATH  Google Scholar 

  49. Zabusky N.J., Kruskal M.D.: Interaction of solitons in a collisionless plasma and the recurrence of initial states. Phys. Rev. Let. 15, 240–243 (1965)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Dipartimento di Matematica Pura ed Applicata, Università degli Studi di Padova, Via Trieste, 63, 35121, Padua, Italy

    Alberto Lovison, Franco Cardin & Alessia Bobbo

Authors
  1. Alberto Lovison
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Franco Cardin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Alessia Bobbo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Alberto Lovison.

Additional information

Communicated by S. Luckhaus.

An erratum to this article is available at http://dx.doi.org/10.1007/s00161-016-0498-x.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Lovison, A., Cardin, F. & Bobbo, A. Discrete structures equivalent to nonlinear Dirichlet and wave equations. Continuum Mech. Thermodyn. 21, 27–40 (2009). https://doi.org/10.1007/s00161-009-0097-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00161-009-0097-1

Keywords

PACS

Search

Navigation