Towards closed-walled designs in topology optimization using selective penalization

Abstract

3D topology optimization using a density approach with penalization usually produces truss-like, open-walled structures. The coarser the mesh, the smaller the volume fraction, and the faster the penalization is increased, the more pronounced this effect tends to be. However, closed-walled designs are often more efficient and have other beneficial properties. For instance, closed walls can contribute to achieving self-supporting designs for additive manufacturing that potentially require fewer sacrificial support structures than truss-like designs. This paper presents a two-step optimization procedure for generating closed-walled designs using coarse meshes. The first step takes the usual Eulerian approach of performing a SIMP-based topology optimization on a fixed mesh. To keep thin geometrical features, like walls with a thickness below element size, penalization is switched off deliberately where the formation of such features is detected. Adopting a Lagrangian description, intermediate densities still present in the optimized design are subsequently eliminated in a second step by shrinking each element according to its density. By analogy with volumetric thermal contraction, this is accomplished by solving a fictitious thermo-elastic problem where the temperature has been replaced by a density expression. The outcome is a morphed mesh with a somewhat smoothed surface and a volume close to the specified material volume limit. This body-fitted representation of the design considerably simplifies the final conversion into a manufacturable CAD-type geometry. The two-step optimization procedure is applied to a cantilever, a torsion rod, and a disk reinforcement benchmark problem. Optimized designs are closed-walled and show very good agreement to those found for much finer meshes. Problem-specific stiffness improvements over truss-like designs between $6\%$ and almost $30\%$ were achieved and confirmed the findings previously reported by other authors.

1 Introduction

Under simplifying assumptions, almost any complex lightweight structure can be decomposed into idealized structural elements which greatly facilitate both analysis and design. Line elements like rods are used to resist uniaxial stress whereas surface elements like plates can resist biaxial stress. Volume elements are suitable for triaxial stress. Their usage is usually limited to join line and surface elements as well as to carry applied concentrated loads, but they may also be required due to local design domain restrictions and multiple load cases.

A prototypical example may be given by a thin-walled beam of isotropic material. It consists of upper and lower horizontal flanges subjected to tension and compression and a single web in between which, in an idealized setting, carries the external shear loads only. The flanges are realized by rods effective in carrying axial loads, but there are two possible variants for the web: it can be either a diagonal network of line elements or a surface element. The former variant resists external shear loads like a truss consisting of straight members oriented along the principal directions. These members undergo mainly axial deformation. The number of web openings may be large, depending on the granularity of the truss. By contrast, the latter variant is essentially the closed surface web of a usual I-beam resisting the external shear force by simple shear deformation.

The above observations may be generalized to other macroscopic structures as well. Adopting the terminology by Sigmund et al. (2016), open-walled refers to a structure with line elements, thus constituting a truss. By closed-walled we mean a structure which partly consists of surface elements under biaxial stress.

Topology optimization for three-dimensional structural problems is often associated with open-walled structures and they are sometimes even perceived as more efficient than their closed-walled counterparts. In fact, however, open-walled designs are clearly non-optimal solutions to the common small deformation minimum compliance problem. Inherently mesh-dependent topology optimization schemes like SIMP often fail to predict designs exhibiting closed walls and converge to open-walled truss-like designs instead. As it has been shown by Sigmund (1999) in the context of bone microstructure, the character of the optimized topology is significantly affected by the length scale imposed by either filtering or the mesh resolution itself, whichever is greater. A smaller minimum length scale allows to represent finer details driving the solution more towards closed-walled designs. Increasing the material volume fraction limit can have a similar effect but obviously leads to a different physical optimization problem as well. As truss-like designs may be local minima (Sigmund 1999), using an appropriate continuation method can also be helpful to favor efficient closed-walled designs.

The added value of closed walls may not be limited to a potentially superior structural efficiency. In several applications, they also serve some secondary purpose. For instance, the closed surfaces of a gear housing act as a mechanical support structure while containing the lubricant and providing protection against dust. Furthermore, they serve as a safety guard to cover rotating equipment, but also provide a mechanical barrier against any other environmental impacts like minor pressure loads, splash water, vapor, radiation, or sparks as well as insulation against heat, cold, airborne sound, and fire.

In some cases, reducing the number of holes of a design can lower its manufacturing effort significantly. This is particularly true for sheet-metal forming processes such as deep drawing and again motivates designs with closed surfaces (Dienemann et al. 2017). More recently, reducing sacrificial support structures in additive manufacturing has emerged as an interesting new application for closed-walled designs. A well-chosen part orientation provided, closed-walled designs are sometimes largely self-supporting and, thus, require less post-processing effort than similar truss designs of the same weight. This situation is illustrated in Fig. 1 showing two different variants of a topology optimized lifting beam. The optimization problem is essentially a three-dimensional version of the popular MBB-beam benchmark problem (Rozvany 1998). The part orientation with respect to the build platform of the laser additive manufacturing machine was chosen with the aim of minimizing support area for the truss design and was adopted also for the closed-walled variant for easier comparison. It is recognizable that the necessary amount of sacrificial support structures is much lower for the closed-walled variant leading to a better cost effectiveness of the finished part. Moreover, support removal will probably be more difficult for the open-walled design due to its higher geometrical complexity. It should be noted that manufacturing is usually feasible if the overhang angle of a down-skin is kept slightly above the critical angle, but surface quality is likely to be poor, nonetheless.

Fig. 1

Metal additive manufacturing of a lifting beam using laser powder bed fusion: the truss-like design (right) is the result of a classical SIMP-based topology optimization, whereas the closed-walled design (left) has been found using the selective penalization approach presented in this paper. Both variants have the same part weight. A critical overhang angle of $40^\circ$ was assumed to determine the necessary amount of support structures shown in blue. (Color figure online)

Different approaches can be taken to resolve the difficulties of density-based topology optimization related to closed surfaces. Ensuring an adequate mesh resolution is the most straightforward approach to recover optimized designs which are closed-walled on a macroscopic scale, see the systematic study conducted by Sigmund et al. (2016). In their work on topology optimization of an entire wing’s inner structure, Aage et al. (2017) found that discrete, closed-walled spars, ribs and a variable thickness skin evolved to form a load-carrying structure with high torsional and bending stiffness, a so-called wing box. In contrast, in the more lightly loaded areas fore and aft of the wing box open-walled structures in the form of a thin truss infill are still dominant providing shear stiffness to the outer aerodynamic shell, which was prescribed during the optimization. Similar results were reported by Liu et al. (2019) and Villanueva and Maute (2014).

The downside of capturing thin walls by global mesh refinement is that the required number of design variables grows tremendously fast, especially for problems with low volume fractions. Hence, many of these attempts fall into the category of being large scale in nature. From an industrial perspective, where the goal often is to get a first conceptual design within a reasonably short period of time, the computational cost of this approach is often prohibitively high. The drawbacks of global mesh refinement can be partly circumvented by adaptive re-meshing of the non-void regions, see, e.g., the work by Zhou et al. (2022) on thin-walled designs.

Another path is to work with an alternative design description. The resulting topology can be a subset of an initially populated closed-walled grid structure found by sizing or removal of walls, or it is created by shaping and connecting only a few geometric base features more freely to form a global structure. The former is essentially a ground structure approach and has been used among others for topology design of extrusion profiles for vehicular crashworthiness (Duddeck et al. 2016). An approach of the latter type based on moving morphable components (MMC) has been applied to cross section design for thin-walled beams by Guo et al. (2021), again in an essentially two-dimensional setting. Another recent MMC-based paper by Jiang et al. (2022) investigates the optimization of thin-walled ribs that stiffen a given planar or curved base shell. A number of assumptions are made on the admissible designs including a constant height of the ribs and their orientation being always perpendicular to the base shell. A reduction to an essentially planar optimization problem is accomplished by an appropriate mapping from the 3D space to a 2D parameter space. Among other examples, the authors demonstrate an application to the core design of sandwich panels. For two different loading conditions, tailored cellular structures made up of closed vertical walls were found.

In general, explicit schemes like the MMC (Guo et al. 2014) have a number of properties which are particularly useful for closed-walled designs. These include, first and foremost, a much greater shape control allowing for optimizing the placement, orientation, wall thickness or curvature of closed-walled features directly. Moreover, the numbers of design variables and degrees of freedom are much lower compared to density-based topology optimization which usually requires very fine meshes (Jiang et al. 2023). Nevertheless, the achievable geometrical complexity of the final design is limited by the number and the initial geometry of the components and the ability of the optimization framework to deform and rearrange these building blocks to form a more complex structure (Li et al. 2023). A limited geometrical complexity may even be favorable for conventional manufacturing. However, optimality of closed-walled designs can, with some exceptions, only be achieved with varying thickness. Moreover, closed-walled designs are not necessarily entirely thin-walled, but may also exhibit fairly compact members. An efficient explicit topology optimization scheme that is able to represent such a range of structural details, that can be applied to true 3D optimization problems without simplifying assumptions and which does not require any previous knowledge to choose a reasonable set of components still appears to be missing.

A combination of a large scale solid-element-based approach with shell elements as an alternative design description has been proposed by Träff et al. (2021). Another promising approach which has the potential to generate efficient closed-walled designs is the so-called de-homogenization concept, see for instance the work by Groen et al. (2020) and Groen et al. (2021). The key idea is to perform a multi-scale homogenization-based topology optimization on a coarse grid assuming microstructural material. A single-scale interpretation on a much finer mesh is obtained by a projection method in a subsequent post-processing step.

Nevertheless, probably the most common way to address the issue of open-walled designs still is a load-carrying truss structure where the openings between the outmost members are closed with flat plates or curved shells in a post-processing step to achieve a closed surface design. The truss is optimized to satisfy stiffness requirements while the sheets are added manually by the designer using a reasonably small, uniform thickness. Although this approach most likely leads to the least optimal results, it is based on state-of-the-art software and does not require particularly fine meshes. As computational time is low but weight reductions can still be considerable compared to conventional designs, this approach is often taken in industrial practice, see, e.g., the case study on the AM redesign of a gear housing by Barreiro et al. (2019).

This paper presents a low-cost two-step optimization procedure with the aim of obtaining efficient, closed-walled and discrete 0–1 designs of isotropic material in 3D without the need for fine meshes. In the first step, a SIMP-based topology optimization is performed. However, penalization is switched off locally where potential thin features consisting of only a single layer of elements start to evolve during the optimization. A simple and inexpensive method is used to detect these regions at the beginning of every design iteration. As penalization is still applied elsewhere, large spatially extended and voluminous regions with intermediate densities are effectively suppressed. Switching the penalization is realized by replacing the exponent of the power law, which is a single number for the classical SIMP, by a bi-valued scalar field.

Customization of the penalization exponent in general is an established concept in density-based topology optimization. Continuation methods are frequently used to achieve a slow transition from a convex to a non-convex optimization problem by gradually increasing the penalization exponent (Allaire and Kohn 1993, Allaire and Francfort 1993). A combination of a continuation method on the penalization exponent with mesh adaptivity has been presented by Gupta et al. (2016). In their work on topology optimization with constant wall thickness and deep drawing constraints, Dienemann et al. (2017) used an unpenalized solution as an initial guess for a subsequent optimization with penalization to avoid convergence to poor designs. A more specific penalization exponent may also be chosen to represent a material that can be interpreted in physical terms (Bendsøe and Sigmund 1999). Application to multi-material topology optimization using a piecewise-defined SIMP interpolation scheme has been demonstrated by Zuo and Saitou (2017). The above-mentioned examples have in common that the penalization exponent is still homogeneous with respect to the design domain.

Unlike classical SIMP with homogeneous penalization, the selective penalization approach presented here leads to designs that are not yet fully discrete. Instead, the results are partly true 0–1 designs but may also exhibit regions with intermediate densities representing thin features that cannot be approximated economically by a single closed layer of solid elements. The usefulness of such a design is that a meaningful interpretation of the intermediate densities in the thin regions can be gained from looking upon them as a variable thickness of a shell-like feature. This perception is inspired by the 2.5D design problem of variable thickness sheets (Rossow and Taylor 1973) and in some sense may be seen as an embedding of the latter into the 3D space. The resizing of the wall thicknesses is done in a post-processing step.

For this purpose, a subdomain is extracted from the entire design domain based on a threshold criterion on the density field from the topology optimization with selective penalization. This body-fitted domain is further processed to remove remaining intermediate densities by a shrinking deformation where the local volumetric contraction is proportional to the density. As usual, deformation is formulated with respect to a Lagrangian frame of reference. We assume a linear elastic, isotropic material with a Poisson’s ratio close to the incompressibility limit. Moreover, we assume small deformations and a superposition of inelastic, prescribed shrinkage strains and elastic strains. Note that in the post-treatment of the de-homogenization concept (Pantz and Trabelsi 2008) multi-scale information on the layer normals and layer widths of the composite can be used to reconstruct the final design. By contrast, in the isotropic case discussed here, there is no information available other than the scalar density.

The shrinking contraction itself, as well as the elastic response of the material, is modeled as purely isotropic. This implies that we do not explicitly specify the out-of-plane direction of shell-like features along which we want the shrinking to occur. Instead, we connect every point of the subdomain to an elastic foundation. As it will be shown later, this leads to the desired effect of sizing of the local wall thickness proportional to its density value. A beneficial side-effect is the smoothing of the shape of the deformed body. The outcome is a morphed mesh serving as a body-fitted representation of an optimized, entirely solid design with a material volume close to the specified limit. The post-processing step is completed by manual or semi-automatic conversion of the morphed mesh into a manufacturable CAD-type geometry.

The rest of the paper is organized as follows: Sect. 2 covers the topology optimization step of the proposed procedure. We present the selective penalization scheme, explain the way we detect potentially thin features and provide the discretized form of the optimization problem. We introduce the post-processing step in the following Sect. 3, discuss its goal, and explain in detail the mechanical modeling of the shrinking process. The entire procedure is summarized in a flow chart given in Sect. 4. Three example problems were solved to benchmark the optimization procedure. A discussion of the numerical results and a comparison with both analytical and numerical solutions reported in the literature are provided in Sect. 5. A brief summary and comments on future work can be found in the last Sect. 6.

2 Topology optimization with selective penalization

2.1 Material interpolation scheme

We propose an extension of the original SIMP interpolation scheme (Bendsøe 1989) allowing to locally switch between a material with ($p>1$) or without penalization ($p=1$). This selective penalization behavior is achieved by redefining the penalty exponent of the power law as a spatially varying, bi-valued field

$$\begin{aligned} p(\varvec{x})={\left\{ \begin{array}{ll} 1\quad \text {if } g(\varvec{x})> g_c,\\ \hat{p}\quad \text {else}. \end{array}\right. } \end{aligned}$$

(1)

Here $g(\varvec{x})$ denotes a scalar measure which, if exceeding some critical value $g_c$, shall be seen as an indicator of a thin feature and causes the penalization to be switched off. In the remaining part of the design domain, the penalization exponent takes the value $\hat{p}$ which is either kept constant throughout the design optimization or it is gradually increased from 1 to a certain $\hat{p}_{max}$ using a continuation method. With this modification, the stiffness properties of the material at some point $\varvec{x}$ become a function of the density and the penalty exponent field:

$$\begin{aligned} \mathbbm {C}(\varvec{x})=\rho (\varvec{x})^{p(\varvec{x})}\mathbbm {C}_0, \end{aligned}$$

(2)

where $\mathbbm {C}_0$ denotes the linear elastic, isotropic stiffness tensor of the solid material. In our implementation, the penalty exponent field is re-evaluated and adjusted at the beginning of each design iteration.

The purpose and also the physical interpretation of the fictitious material defined by Eq. (2) is twofold. In the penalized case, it is used as a tool to steer the design toward almost discrete solutions. To this end, values of $\hat{p}\ge 3$ are deemed necessary by experience (Bendsøe and Sigmund 2004) and will also be used in this work. Thus, it is not regarded as a material in the narrower sense although for such large values of the penalization exponent an isotropic composite with the same constitutive properties could in fact be realized. Such a 3D material is not available for the unpenalized case as a linear interpolation of the stiffness tensor between void and solid material, also referred to as Voigt upper bound, will violate the Hashin-Shtrikman upper bound for isotropic composites (Bendsøe and Sigmund 1999). Instead, to justify the use of a linear interpolation scheme, we adopt the physical interpretation of an intermediate density as a sizing parameter of a variable-thickness-sheet-like feature.

2.2 Thin feature detection

The identification of thin features from the current density field plays a central role in the proposed optimization procedure as it directly controls the selective penalization behavior of the penalty exponent in Eq. (1). Hence, choosing a suitable measure $g(\varvec{x})$ together with a threshold $g_c$ is essential. The main challenge is that the method has to prove useful not only for largely discrete designs with sharp transitions between material and void, but should also behave reasonably well for blurry designs from early iterations or as a result of checkerboard control or mesh-independency filtering. The formulation used in this work is based on a comparison of the density at some fixed point $\varvec{x}$ to the average density of all neighboring points $\tilde{\varvec{x}}$ found within a maximum distance $r_{min}$ from that point. Hence, the measure is obtained by applying a linear filter to the density field as follows:

$$\begin{aligned} g(\varvec{x})= \frac{\rho (\varvec{x})\int _{\Omega }H_{\varvec{x}}(\tilde{\varvec{x}})~\textrm{d}\tilde{V}}{ \int _{\Omega }H_{\varvec{x}}(\tilde{\varvec{x}})\rho (\tilde{\varvec{x}})~\textrm{d}\tilde{V}}, \end{aligned}$$

(3)

where $\Omega$ denotes the entire design domain and $H_{\varvec{x}}(\tilde{\varvec{x}})$ is a uniform kernel function with finite support defined as:

$$\begin{aligned} H_{\varvec{x}}(\tilde{\varvec{x}})={\left\{ \begin{array}{ll} 1\quad \text {for } \Vert \tilde{\varvec{x}}-\varvec{x}\Vert \le r_{min}, \\ 0\quad \text {else}. \end{array}\right. } \end{aligned}$$

(4)

For a point $\varvec{x}$ on a thin-walled feature, the ratio $g(\varvec{x})$ will usually be greater than one, provided $r_{min}$ is large enough with respect to the local wall thickness to capture points with lower density along one or both sides of the wall-like feature. In contrast, the ratio will be close to one if the density is almost homogeneous within the neighborhood, irrespective of whether it belongs to a large void region, a thick solid member or an intermediate density region, e.g., due to a homogeneous distribution of material being used as a starting guess. Ratios significantly smaller than one will occur in transition zones where $\varvec{x}$ itself has low density but is located close to a feature with higher densities.

The working principle of the proposed thin feature detection is illustrated for a fixed density field in Fig. 2. Comparing the cross sectional plots of $g(\varvec{x})$ and $\rho (\varvec{x})$ confirms, that the closed-walled web of the cantilever beam is indeed correctly recognized as a thin feature, whereas, in contrast, in the center of the more compact, filled cross sections of upper and lower flanges, the measure stays below the critical value, as expected. Moreover, the regions where $g>g_c$ holds, are not fragmented, which is key to achieving a firm connection of thin features with intermediate density, like the web, to solid features, such as the flanges. If this were not the case, the desired closed-walled features would likely break up during optimization and the design would converge to a truss-like structure instead.

From the above considerations, one can derive bounds on the threshold for thin feature detection $g_c$ in Eq. (1). As a necessary requirement, $g_c>1$ needs to be satisfied to penalize void regions with constant density $\rho =\rho _{min}$, which cover most of $\Omega$ in a typical setting, see for instance Fig. 2. However, choosing a value larger but still almost equal to one has the disadvantages of being too conservative in the sense that too many regions are erroneously considered as thin features. For instance, the flanges in Fig. 2 would remain unpenalized also in their centers if only a single neighboring element with lower density existed. On the contrary, if $g_c$ is chosen too large, some thin features are no longer detected with the transition zones between thin and thick regions being particularly affected. Although keeping these gaps filled with material is necessary to preserve a closed-walled structure, this can be too costly due to the reactivated penalization. Thus, the optimizer will introduce holes which initiate a transformation away from a closed-walled and toward an open-walled structure, as explained earlier.

From Fig. 2, one might even try to establish a useful upper bound on $g_c$ based on the argument, that the thin-walled web shall still be unpenalized, which is true as long as $g_c<1.35$. However, insights from such a simplified sensitivity analysis have very little practical importance, since demonstrating that a certain threshold is compatible with a given final solution does not necessarily imply that starting from an initial guess the iterative optimization procedure will actually converge to that desired solution. Instead we found a practically useful threshold of 1.05 from numerical experiments where we tested different optimization problems with varying material volume fraction limits.

Fig. 2

Extraction of thin features from the density field of the cantilever beam studied in Sect. 5.1: optimized topology of the cantilever beam and positioning of the slice plane (left), corresponding density field $\rho (\varvec{x})$ (middle left), feature detection measure $g(\varvec{x})$ with continuous (middle right) and bi-valued color scale (right). To compute $g(\varvec{x})$, a filter radius $r_{min}$ equal to 1.2 times the element size was used, as indicated by the yellow circle. The sensitivity filtering applied throughout the optimization and using the same filter radius, was switched off before final convergence. The threshold for thin feature detection $g_c$ was set to 1.05. (Color figure online)

One may note that not only thin walls are detected. In fact, the entire contour line of the beam cross section in Fig. 2, or more generally the boundary of its 3D topology, satisfies the proposed threshold criterion. If the contours are drawn by elements of a coarse FE-mesh, like the bicolored plot on the right in Fig. 2, the thin web can be seen as just a special case where both right and left contour lines of the section have become locally congruent.

The false detection of thin features, other than the desired closed walls, could also include bars or even isolated particles. However, we found that these potential issues apparently have no visible adverse effect on the optimization results in practice. This conclusion is also supported by the numerical results presented in Sect. 5 and may be due to two reasons: First, even if the formation of certain undesired thin features with intermediate density is not penalized, such a formation will not necessarily happen, though. For instance, the optimizer will still prefer a more efficient, closed wall over a planar truss consisting of thin bars. The same argument applies to the boundary of thick features. As it can be seen from Fig. 2, intermediate densities are not penalized in the outer region of the flanges, but in this section, the optimized design exhibits a sharp 0–1 transition nonetheless. The second reason is, that any remaining intermediate density will still be post-processed in the subsequent mesh morphing step. Fortunately, this works equally well also for such false features, which rather resemble a thin coating to an otherwise thick feature.

2.3 Optimization problem and finite element discretization

The selective penalization approach is applied within the classical setting of a minimum compliance design of a structure subject to a constraint on the available material volume, see the textbook by Bendsøe and Sigmund (2004) for a detailed derivation of the continuous problem statement. We follow the common solution approach based on a geometrically linear finite element method with first order elements for the displacements $\varvec{u}(\varvec{x})$ and a discontinuous, element-wise constant interpolation of the density $\rho (\varvec{x})$, the feature detection measure $g(\varvec{x})$ and the penalization exponent $p(\varvec{x})$. For the purpose of determining the support of the kernel function given by Eq. (4) that is associated with a certain element, we follow the convention that any neighboring element is fully taken into account if the distance between their centers is smaller than the specified filter radius $r_{min}$. For a design domain $\Omega$ discretized by N elements, the optimization problem takes the form

$$\begin{aligned} \begin{aligned}&\min _{\varvec{\rho }}~l\\ \text {s.t.: }&\varvec{K}\varvec{d}=\varvec{f},\\&\rho _{min}\le \rho _e \le 1, \qquad e=1,\dots ,N,\\&\varvec{v}^T\varvec{\rho }\le V_{max}, \end{aligned} \end{aligned}$$

(5)

where $\varvec{K}$ is the global stiffness matrix, $\varvec{d}$ is the nodal displacement vector, $\varvec{f}$ is the nodal force vector, $\varvec{\rho }$ is the vector of element densities, $V_{max}$ is the material volume limit and $\varvec{v}$ is the vector of element volumes satisfying $\sum _{e=1}^Nv_e=\text {Vol}(\Omega )$. The compliance computes as $l=\varvec{f}^T\varvec{d}$. The global stiffness matrix is assembled from element-wise contributions as follows:

$$\begin{aligned} \varvec{K}(\varvec{\rho },\varvec{p})=\sum ^{N_e}_{e=1} \rho _e^{p_e}\varvec{k}_e, \end{aligned}$$

(6)

where $\varvec{k}_e$ denotes the element stiffness matrix of the e-th element assuming solid material. The element penalty exponents $\varvec{p}$ will be updated at the beginning of every iteration. Nevertheless, they shall be treated as fixed parameters rather than physical variables which makes the derivation of the sensitivities of the objective function as easy as for the classical SIMP. Using the adjoint method results in the expression:

$$\begin{aligned} \frac{\partial l}{\partial \rho _e} =-p_e\rho _e^{p_e-1}\varvec{d}^T\varvec{k}_e\varvec{d}. \end{aligned}$$

(7)

3 Mesh morphing

A typical outcome of the topology optimization step with selective penalization is a closed-walled design, which, to a varying degree, exhibits flat or curved shell-like regions with intermediate densities. While this is an expected and even desired behavior, additional post-processing is required to finally get a useful and manufacturable 0–1 design. As a first step, a roughly body-fitted, undeformed representation of the design $\mathcal {B}_0$ is determined as the subset of the design domain $\Omega$ which has a density above a specified threshold $\rho _{_\mathcal {B}}$. To provide a reasonable approximation of the anticipated final topology, a comparatively low threshold is chosen such that void regions are removed but thin-walled features are still safely captured.

The goal of the post-processing procedure is to transform the design $\mathcal {B}_0$ into a deformed configuration $\mathcal {B}$ such that the local change in volume leads to an overall deformed volume $\text {Vol}(\mathcal {B})$ equal to the target material volume $V_{max}$. The modeling is similar to a thermo-elasticity problem, with the exception that the driving force for the inelastic strains is not a temperature deviation from a certain reference temperature. Instead, the shrinkage strains are governed by the density deviation from the solid limit ($\rho =1$) as follows:

$$\begin{aligned} \varvec{\varepsilon }_s= (\root 3 \of {\rho }-1)\varvec{1}, \end{aligned}$$

(8)

where $\varvec{1}$ denotes the second-order identity tensor. The local change in volume induced by the isotropic shrinking is proportional to the density, as it can be confirmed by computing the Jacobian determinant $\det (\varvec{\varepsilon }_s+\varvec{1})=\rho$. The body has isotropic, linear elastic material properties with Young’s modulus of the solid material $E_0$, Poisson’s ratio $\nu _s$ and proportional stiffness, which corresponds to the classical SIMP with $p=1$. For the reason explained below, we support the entire body on an elastic foundation, which is stress-free in the undeformed configuration $\mathcal {B}_0$. Hence, the elastic foundation exerts a force to every point on $\mathcal {B}$ that brings it back toward its reference position on $\mathcal {B}_0$. This is realized by adding a body force per unit material volume of the form

$$\begin{aligned} \varvec{b}= -k\rho \varvec{u}, \end{aligned}$$

(9)

where k is the elastic foundation stiffness and the negative sign accounts for the nature of a restoring force. Introducing the set of kinematically admissible displacements U and the virtual displacements $\varvec{w}$, the principle of virtual work for the shrinkage problem can be written as

$$\begin{aligned} a(\varvec{u},\varvec{w})=l(\varvec{w}),\quad \forall \varvec{w} \in U, \end{aligned}$$

(10)

with the bilinear form

$$\begin{aligned} a(\varvec{u},\varvec{w})=\int _{\mathcal {B}_0} \varvec{\varepsilon }(\varvec{u}):\mathbbm {C}:\varvec{\varepsilon }(\varvec{w})~\textrm{d}V + \int _{\mathcal {B}_0} k\rho \varvec{u} \varvec{w}~\textrm{d}V \end{aligned}$$

(11)

and the load linear form

$$\begin{aligned} l(\varvec{w})=\int _{\mathcal {B}_0} (\root 3 \of {\rho }-1)\varvec{1} :\mathbbm {C}:\varvec{\varepsilon }(\varvec{w})~\textrm{d}V. \end{aligned}$$

(12)

Equation (10) can optionally be supplemented by Dirichlet boundary conditions, for instance to avoid deformation of supports, interfaces, or surfaces subject to external loads. The shrinkage problem is solved by the same finite element method as used before during the topology optimization step. The discretized form of Eq. (10) is given by the linear system

$$\begin{aligned} \varvec{K}_s \varvec{d} = \varvec{f}_s, \end{aligned}$$

(13)

where the stiffness matrix $\varvec{K}_s$ and the nodal force vector $\varvec{f}_s$ follow from the discretization of the bilinear form (11) and linear form (12), respectively. The solution to the shrinkage problem is given by a solid design which occupies the shrunk configuration $\mathcal {B}$. The result will be exported as a morphed surface mesh realized by a movement of the mesh vertices equal to the nodal displacements found from Eq. (13). The morphed mesh later serves as a reference shape and guides the rebuilding of a smooth CAD geometry.

The effect of the elastic foundation is a mechanical resistance to any deformation or motion. Here we take advantage of the fact, that the influence on the global deformation is sensitive to the shape of the structure itself. More specifically, a structural feature whose thickness is very small when compared with other dimensions, like plates or shells, will shrink primarily in thickness-direction. This is even more pronounced for almost incompressible materials, where the volumetric change due to the inelastic shrinkage strains will lead to a thickness reduction by the same factor. This behavior is visualized in Fig. 3 for a simple wall structure with a density field decreasing linearly in vertical direction. In the case of a vanishing elastic foundation stiffness, the measured wall thickness in the deformed configuration is very close to the cubic root of the density which suggests isotropic shrinking. In contrast, in the case of a properly chosen elastic foundation stiffness, the deformation occurs mainly in the out-of-plane direction of the wall whereas the formerly large in-plane-deformations are minimized. Thus, a resizing of the wall thickness proportional to the density is achieved whereas the overall shape is largely retained.

It needs to be considered that for a constant k, the influence of the elastic foundation grows with the square of the size of the design $\mathcal {B}_0$. For instance, to ensure that solutions to the shrinkage problem in Fig. 3 will still be comparable if the discretized wall structure is scaled equally in all three dimensions by a certain factor, the elastic foundation stiffness k needs to be scaled inversely proportional to the square of that factor. Nevertheless, this does not answer the question how the elastic foundation stiffness k can be determined for an entirely new problem. One possibility is to choose k proportional to the reciprocal of the squared element size h. This is motivated by the fact that shrinking deformation does only affect intermediate density elements, which typically occur in the form of walls or shells consisting of a few layers of elements at the most. Thus, one may use the element size h to characterize those features of the design. For the three numerical examples presented in Sect. 5, reasonable values for k could be found in the range of $1/h^2$ to $10/h^2$.

Fig. 3

Shrinking deformation procedure applied to a wall clamped at its bottom face: undeformed configuration with intermediate densities (left), deformed configurations without elastic foundation (middle) and with an elastic foundation stiffness $k=10$ (right). The material volumes of the three configurations are almost identical with a difference less than 1%. The gray color of the two deformed walls indicates solid material and the hidden blocks in the top-left part have been cut off for better visualization. We have chosen a nearly incompressible material ($\nu =0.47$, $E_0=1$) to ensure that the elastic part of the deformation is isochoric. (Color figure online)

One may argue that the arising deformations will obviously not be small, which raises the question whether the use of a linear strain tensor $\varvec{\varepsilon }$ and superposition of the inelastic and elastic strain contributions are actually too severe simplifications. However, recall that the shrinking deformation is used only as a tool for post-processing which is merely inspired by a physical process. Thus, the quality of the morphed mesh should rather be evaluated based on how well it supports an either manual or automatic derivation of a manufacturable CAD geometry and how accurately the latter resembles the original optimization results in terms of global shape, material volume and mechanical performance. Also, switching to a geometrically non-linear framework may lead to further complications. While the significantly increased computational effort will still be small compared to the topology optimization step, convergence issues due to nearly incompressible material properties and undesired deformation phenomena like buckling become even more of a concern.

4 Two-step optimization procedure

A flowchart of the entire two-step optimization procedure is shown in Fig. 4. After initialization, a topology optimization is performed, this step is made up of the green and blue iteration loops. During the green iteration loop, the selective penalization scheme is applied and checkerboard control is established by the common sensitivity filtering techniques (Bendsøe and Sigmund 2004). We use the same filter radius $r_{min}$ for the kernel functions of the sensitivity filtering and feature detection. Optionally, a continuation scheme can be used to gradually increase penalization. The green loop is repeated until the relative objective change becomes smaller than a given tolerance $\hat{\epsilon }$ and, if applicable, the continuation scheme has finished. Afterward, the algorithm proceeds with the blue iteration loop while the penalty exponents $\varvec{p}$ are frozen and the sensitivity filtering as well as the selective penalization update scheme are deactivated. The reason for deactivating the sensitivity filtering is the removal of the blurry transition zones at the boundaries caused by the filter. If the design has already converged sufficiently close to a (local) optimum we found that switching off the filter can be done safely leading to crisp boundaries without causing the structure to break up. For thin and closed-walled structures the additional reduction of compliance is considerable and amounts to roughly $10\%$ for the numerical examples presented in Sect. 5. Thus, without deactivation of the filtering in the blue iteration loop a fair comparison of the topology optimization results with analytical solutions or values found from analysis of smooth CAD geometries is hardly possible.

The stopping criterion is based on the relative objective change as well, but the tolerance $\epsilon$ can be chosen smaller compared to the green loop. The topology optimization step is followed by a post-processing step which is indicated by the red flowline. The post-processing comprises three tasks: Extraction of the subdomain $\mathcal {B}_0$, computation of the morphed mesh $\mathcal {B}$ by solving the shrinkage problem and finally the derivation of a CAD-type geometry.

For all numerical examples discussed in this paper, we used the software Inspire by Altair Engineering Inc. to wrap the morphed mesh with smooth free-form surfaces represented by non-uniform rational basis splines. Based on the morphed mesh $\mathcal {B}$ the tool generated a reasonable initial CAD geometry almost automatically. Manual fine tuning of the surfaces was necessary to a limited extend to achieve a global volume within a few percent of the specified limit as well as to correct some surfaces that were not properly aligned with the morphed mesh.

Fig. 4

Flowchart of the two-step optimization procedure

5 Numerical examples

In the following Sects. 5.1, 5.2, and 5.3, the two-step optimization procedure is applied to three different 3D optimal design problems.

In general, efficiency improvements gained through transition from truss to closed-walled structures are greater in the case of shear or torsional loads as compared to pure bending or uniaxial tension. Two such examples, which will serve as benchmark problems for our two-step optimization procedure, are a torsion rod and the web of an I-beam section. Several numerical and analytical solutions to both problems as well as an in-depth discussion in the context of closed-walled designs can be found in Sigmund et al. (2016).

To compute the design updates, we use the method of moving asymptotes (MMA) by Svanberg (1987) with $\texttt{asyinit}=0.1$, $\texttt{asyincr}=1.1$ and default parameters otherwise. The major part of the finite element analysis is carried out using the FEniCS library (Alnæs et al. 2015) and its successor FEniCSx. We use a progressive continuation method on the penalization parameter $\hat{p}$. Before computing the shrunk configuration $\mathcal {B}$ as part of the post-processing step, we fix any node which either belongs to a solid element, a loaded face or a support. Apart from problem-specific geometries, boundary conditions and loads, we use the same set of parameters for all three benchmark problems, see Table 1. One may note that the density threshold for mesh morphing $\rho _{_\mathcal {B}}=0.05$ is one order of magnitude smaller than the value 0.5, which is a commonly used cutoff in a classical post-treatment strategy.

Table 1 Parameters and material properties for the three numerical examples in Sects. 5.1, 5.2, and 5.3

5.1 Cantilever beam

The first numerical example is a standard cantilever beam optimization problem. The problem set-up is visualized in Fig. 5 and the corresponding values of the parameters can be read from Table 2. To establish a baseline result, we first solved the topology optimization problem using a classical SIMP-based approach. This can be achieved within the procedure of Fig. 4, e.g., by setting the feature detection measure $\varvec{g}$ equal to the zero vector. The result is, not unexpectedly, an open-walled truss-like structure and shown in Fig. 6a. The design is discrete and intermediate densities are practically non-existent.

Fig. 5

Problem set-up of the cantilever beam example: the box-shaped design domain $\Omega$ has a fixed support at $x=0$. A uniformly distributed shear load with a resultant force F acts on the dashed rectangular face at $x=A$

Table 2 Cantilever beam example: problem-specific parameters, dimensions, and loads

The same topology optimization problem was solved again, now using the selective penalization approach. The optimized design is depicted in Fig. 6b and displays some notable characteristics. Most obviously, the cantilever beam exhibits a closed-walled web consisting of a single layer of non-void elements that is surrounded by curved, solid flanges. The density of these elements varies along the height of the beam, which, as shown in the following, corresponds to an optimized and non-uniform web thickness. While the truss design exhibits a right-angled triangular opening between the pinned supports, this area is filled in with a thin sheet connecting the web to the supported back side in the case of the closed-walled design. The entire surface of the closed-walled design is more than 40% larger compared to the truss design.

Fig. 6

Optimization results for the cantilever beam example: topology obtained using classical SIMP a, topology obtained using selective penalization before b and after mesh morphing c, rebuilt CAD geometry d, selected cross sections of the morphed mesh e and cross sections of the rebuilt CAD geometry with black contour lines approximating the morphed mesh drawn in magenta f

The result from the topology optimization step with selective penalization was further altered to give physical meaning to intermediate densities. Nodes lying on the supported back side of the design domain ($x=0$) or on the loaded rectangular face at $x=A$ were fixed during this post-processing step. The outcome is the body-fitted, morphed mesh shown in Fig. 6c. There is no visible deformation or motion of the solid elements along the flanges and also the overall shape remains largely unchanged. However, the web consisting of a single layer of intermediate density elements has been transformed into a variable-thickness-sheet-like feature. This is illustrated in Fig. 6e in more detail. There is a smooth transition from the thin web, with an effective web thickness smaller than the element size, to the much thicker flanges. The four measured wall thicknesses of the morphed mesh are compared to the product of the density and the undeformed element size $\rho h$, which in a way can be seen as the target value. Table 3 reveals that the agreement is in fact quite close for the two greater wall thicknesses $t_2$ and $t_3$, whereas the deviations are larger for the two smaller wall thicknesses $t_1$ and $t_4$.

Table 3 Cantilever beam example: density compared to wall thickness of the morphed mesh at the four different positions shown in Fig. 6e

Finally, the morphed mesh was reverse engineered into a solid CAD model based on smooth free-form surfaces, see Fig. 6d. The overall goal was to create a geometry of the same volume which is smooth but still gives a reasonable approximation to the original shape including all relevant details. As it can be seen from Fig. 6f, this task may be achieved by simple surface fitting if the morphed mesh is sufficiently smooth due to the shrinking of low density regions. Thus, redesigning the already near-net shaped web is fairly straightforward whereas the rough surfaces of the flanges need some more interpretation.

Table 4 lists the material volume and the compliance for the different results. For the sake of completeness, we included the corresponding values for the planar Michell frame solution, being aware that the essentially 2.5D Michell solution has a pinned support, a point load and zero Poisson’s ratio, which deviates from the assumptions made in this work. We do not provide compliance values for two intermediate results, namely the undeformed mesh $\mathcal {B}_0$ and the morphed mesh $\mathcal {B}$. In the former case, the only difference to the classical SIMP result is a $1\%$ loss of material volume due to the removal of low density and, in this particular example almost exclusively, void $(\rho =\rho _{min})$ elements whose contribution to stiffness is negligible. In the latter case, obtaining a useful estimate of the compliance is not straightforward because of the strong distortions of the morphed mesh which make a direct reanalysis impracticable. Since the morphed mesh itself is too coarse to be used for re-meshing and a smooth, geometrical representation of the domain $\mathcal {B}$ is not available before the final CAD geometry has been created, we skip the computation of the compliance at this point.

Table 4 Cantilever beam example: Material volumes and compliance results

Comparing the normalized compliances reveals that the selective penalization result is approximately $10\%$ more efficient than the classical SIMP design and still about $5\%$ more efficient than the Michell frame solution. These relative improvements are largely comparable to those achieved through conventional mesh refinement by Sigmund et al. (2016). Transformation of the selective penalization result into a solid CAD geometry comes along with an additional reduction of the normalized compliance by more than $1\%$. This further improvement can be attributed to the smoothing of the surfaces. Moreover, it indicates that the use of proportional stiffness in unpenalized regions, which is a key ingredient of the proposed selective penalization approach, seems to give a reasonable and not too optimistic estimation of the stiffness of such wall-like, thin features.

The material volume of the rebuilt CAD geometry matches the target value $V_{max}$ within a reasonable tolerance. As the reverse engineering is an at least partly manual task, this difference can obviously be further cut down to arbitrarily small values. Nevertheless, the quality of the global correlation between the CAD geometry and the optimization result always remains somewhat subjective.

Note that the normalized compliance of our classical SIMP solution is $0.8\%$ below the value found by Sigmund et al. (2016). The reason for this marginal difference is that we do not impose mirror symmetry about the center plane defined by $z=B/2$. Dropping the symmetry requirement allows for a slightly more economical material placement since the thicknesses of wall-like features parallel to the symmetry plane no longer need to be an even multiple of the element size h. However, due to the particular spatial discretization with an even number of elements in z-direction, a web centered at $z=B/2$ with a thickness equal to the element size h cannot be realized. This explains why the selective penalization approach does not lead to a cantilever beam with a perfectly flat web, see the longitudinal section in Fig. 6e resembling more a gentle wavy line.

The evolution of the compliance and the material volume during the topology optimization step can be studied in Fig. 7. The stepwise nature of the compliance graph is caused by the continuation scheme and the deactivation of the sensitivity filtering at iteration $i=553$. Apart from that, one observes a stable and reasonably fast convergence. Some minor fluctuations appear between $i=100$ and $i=200$ which correlate with similar variations of the material volume. Except for the first two iterations, the material volume does not fall below $98\%$ of its target value $V_{max}$. We draw the conclusion that the overall convergence history is not considerably worse than that of a classical SIMP optimization. Nor did we notice that the selective penalization approach distinctly increases the known tendency of too aggressive penalization schemes to promote convergence towards bad local minima.

Fig. 7

Cantilever beam example: evolution of the normalized compliance and material volume during topology optimization. The stopping criteria of the design iteration loops with and without sensitivity filtering are met after 553 and 618 iterations, respectively. The penalization exponent is progressively increased from 1 to $\hat{p}_{max}$

Nevertheless, we observed small oscillations of the objective which still remained after the final design had clearly been reached. This is mainly due to the selective penalization scheme and, to a much lesser degree, due to the sensitivity filtering. This is actually not surprising, since updating the penalization exponents $\varvec{p}$ happens abruptly and changes the optimization problem to be solved. Potential variations of $\varvec{p}$ are not captured by the sensitivities, cf. Sect. 2.3, making it difficult for the MMA to construct an accurate convex approximation. That is why we work with an only moderate tolerance $\hat{\epsilon }$ within the green loop, see Fig. 4. Since filtering is switched off and the penalization exponent field is fixed within the blue loop, the corresponding tolerance $\epsilon$ has been chosen two orders of magnitude smaller, but could be reduced even further.

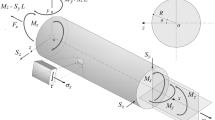
5.2 Torsion rod

In the second example we study the optimization of a structure within a cylindrical design domain for a single torsional load case. The problem set-up is shown in Fig. 8 and the corresponding values can be found in Table 5. The solid annulus is assigned a large Young’s modulus $E_a$ to mimic a rigid body which is connected to but not part of the design domain $\Omega$. The design domain is discretized with $1.7\cdot 10^4$ linear hexahedron elements.

Fig. 8

Problem set-up of the torsion rod example: the cylindrical design domain $\Omega$ has a fixed support at $z=0$ and is connected to the yellow-colored, solid annulus at $z=L$. The annulus is almost rigid and subject to a torsional moment T. (Color figure online)

Table 5 Torsion rod example: problem-specific parameters, dimensions, material properties and loads

The optimized designs are portrayed in Fig. 9. The results confirm expectations that the available material needs to be placed as far from the axis of the cylinder as possible in order to maximize torsional stiffness. The classical SIMP solution (Fig. 9a) is an open-walled tube consisting of helically coiled strips with a winding angle of $\pm 45^\circ$. By contrast, the selective penalization result (Fig. 9b) is a closed-walled tube made up of a single layer of elements with a constant, intermediate density. As highlighted in Fig. 9c, application of the post-processing gives a solid wall thickness $t_1=0.0358$ which is very close to the target value $\rho h=0.0355$.

Fig. 9

Optimization results for the torsion rod example: topology obtained using classical SIMP a, topology obtained using selective penalization before b and after mesh morphing c, rebuilt CAD geometry d. The optimized closed-walled design consists of a single layer of elements

The material volumes and the compliances are summarized in Table 6. The analytical solution of a thin-walled circular tube has the lowest compliance, which is given by the approximation

$$\begin{aligned} l=\frac{T^2L(1+\nu )}{E_0\pi tR_m^3}, \end{aligned}$$

(14)

where $t=R(1-\sqrt{1-\frac{V_{max}}{\text {Vol}(\Omega )}})$ is the wall thickness and $R_m=R-t/2$ is the mean radius. The largest compliance belongs to the Michell frame solution emphasizing the inferiority of Michell-like truss microstructures toward closed shell designs under simple shear. The classical SIMP design resembles a macroscopic Michell-like frame structure with members oriented along the principal directions. These members, in turn, are thin shell-like strips effective in resisting shear. Consequently, the compliance is smaller compared to the Michell frame solution though still significantly larger compared to the thin-walled circular tube. Application of the selective penalization approach reduces the compliance by roughly $30\%$ compared to the classical SIMP design. Interestingly, the same value has been found before by Sigmund et al. (2016) performing a SIMP-based topology optimization but with a hundred times more cubic elements.

Table 6 Torsion rod example: material volume $\int \rho \textrm{d}V$ and compliance results

As discussed earlier, the selective penalization result consists of a single layer of elements with intermediate density. This constitutes a mean radius of $R-h/2$, which is $1.5\%$ below the mean radius of the solid analytical solution which has the same outer diameter R but a smaller wall thickness. Moreover, one finds from Eq. (14) that the compliance is inversely proportional to the product $E t R_m^3$, thus it is rather sensitive to such variations of the mean radius. Other less relevant contributing factors are the unwanted amount of material remaining in the inner of the tube due to the non-zero lower bound $\rho _{min}$ as well as the slightly lower material volume, due to the inexact discretization of the cylindrical design domain.

Finally, one observes a good agreement of the CAD geometry and the selective penalization result with an only $0.7\%$ lower material volume accompanied by a small increase in compliance of $1.1\%$. Note that due to the elastic foundation, reduction of the wall thickness by shrinking is symmetric with respect to the mid-surface defined by the element centers. Thus, the mean radius will remain largely unchanged after mesh morphing and no further improvement of the compliance is achieved by the CAD design, as opposed to the cantilever beam example in the previous Sect. 5.1.

The design iteration history is depicted in Fig. 10 indicating a fast and smooth convergence behavior. A sudden drop of the material volume can be seen at $i=233$ which is due to the deactivation of the sensitivity filtering. The target value $V_{max}$ is recovered already in the next iteration.

Fig. 10

Torsion rod example: evolution of the normalized compliance and material volume during topology optimization. The stopping criteria of the design iteration loops with and without sensitivity filtering are met after 233 and 279 iterations, respectively. The penalization exponent is progressively increased from 1 to $\hat{p}_{max}$

5.3 Disk reinforcement

In a third example we address a solid disk loaded in normal direction at its center. We seek an optimized reinforcement design within a cylindrical design domain underneath the disk. The problem set-up is given in Fig. 11 and the corresponding parameters can be found in Table 7. The aim of this numerical example is twofold: On the one hand, the selective penalization approach shall be tested under varying material volume fraction limits. On the other hand, it shall serve as a benchmark problem to demonstrate the ability of the selective penalization approach to also generate more complex designs like closed cellular structures with multiple thin walls.

In Fig. 12, the optimized topology for a material volume fraction limit of 0.2 is shown from the outside. The disk is supported by a bowl-shaped closed shell which is flattened at the bottom due to the finite height of the cylindrical design domain. The internal features are made visible in Fig. 13b and comprise essentially two types of structural elements: First, an arrangement of twenty closed-walled ribs radiating from the center. The ribs carry the shear loads and connect the bowl-shaped shell to the disk, which are subjection to tension and compression, respectively. Second, a solid cylindrical region below the loaded face at the center which introduces the external loads into the ribs. The results obtained using selective penalization in Fig. 13b make extensive use of intermediate densities to represent the ribs. Even the four crossed ribs which are slightly more pronounced, most probably because they are aligned with the Cartesian grid, have a density clearly below one. This explains why the inner structure of the design obtained for the same optimization problem using classical SIMP, which is shown in Fig. 13a, is no longer entirely closed-walled. Instead, it has four solid crossed ribs dividing the structure into four segments and each segment is stiffened by two additional compact diagonal bars. The result of the mesh morphing is visualized in Fig. 13c and the rebuilt CAD geometry is shown in Fig. 13d and e.

A quantitative evaluation of the four designs can be carried out with the values provided in Table 8. For a fair comparison, we computed the scaled compliance $l\int \rho dV$ as suggested by Sigmund (2022), since the material volume is not exactly conserved during the post-processing of the two-step optimization procedure. Note that the material volume fraction limit refers exclusively to the design domain whereas the material volumes listed in Table 8 include both the reinforcement structure within the design domain as well as the solid disk itself. Three conclusions can be drawn: First, although the designs obtained using classical SIMP and selective penalization both feature a closed bowl-shaped shell, the latter still has a $6\%$ smaller scaled compliance due to its more efficient cellular core design made of thin closed-walled ribs. Second, the mesh morphing step yields a deformed mesh volume with a satisfactory deviation of about $4\%$ from the material volume of the undeformed mesh. However, the agreement is not as close as for the two less complex numerical examples presented in the preceding Sects. 5.1 and 5.2. Third, the efficiency of the CAD geometry expressed by its scaled compliance matches the efficiency predicted by the topology optimization with selective penalization.

To further investigate the behavior of the selective penalization approach, we solved the disk reinforcement problem for a series of different material volume fraction limits and again contrasted the results with SIMP-based designs, see Fig. 14. It can be seen that as the volume fraction decreases, the disk reinforcement changes into an open-walled truss for the SIMP case. This is in contrast to the designs obtained using selective penalization which do not lose their closed-walled topology even though the number of ribs becomes smaller. Thus, increasing or decreasing the volume fraction mainly leads to a resizing of the wall thicknesses.

The corresponding material volumes and scaled compliances are provided in Table 9. Pairwise comparison for every material volume fraction limit confirms, that the efficiency improvements gained through the use of the selective penalization approach are indeed most significant in the low volume regime and amount to almost $30\%$ for $f=0.05$.

One might assume that the scaled compliance of the designs obtained using selective penalization should be more or less constant as suggested by the invariance of the closed-walled topology shown in Fig. 9. However, this is not the case due to the prescribed solid disk. The smaller the material volume fraction limit, the larger is the relative share of the material volume spent on the disk. This leads to a structural response being increasingly dominated by the disk subject to bending which is clearly non-optimal. As stated earlier, note that the material volume fraction limit is defined with respect to the design domain only while the material volume also covers the disk.

Fig. 11

Problem set-up of the disk reinforcement example: the cylindrical design domain $\Omega$ is connected to the yellow-colored, solid disk which is fixed along its upper edge. A uniformly distributed normal load with a resultant force F acts on the dashed circular face on the upper side of the disk. (Color figure online)

Fig. 12

Disk reinforcement example: outer view of the optimized design for a material volume fraction limit of 0.2 obtained from the selective penalization approach prior to mesh morphing

Table 7 Disk reinforcement example: problem-specific parameters, dimensions and loads

Table 8 Disk reinforcement example: material volume $\int \rho \textrm{d}V$ and scaled compliance $l\int \rho \textrm{d}V$ for a material volume fraction limit of 0.2

Fig. 13

Optimization results for the disk reinforcement example with a material volume fraction limit of 0.2: topology obtained using classical SIMP a, topology obtained using selective penalization before b and after mesh morphing c, normal view d and half section view e of the rebuilt CAD geometry. To reveal the inner structure of the designs, the figure shows section cuts using a clipping plane at $z/H=0.95$ to hide the solid disk

Fig. 14

Optimization results for the disk reinforcement example: comparison of the optimized topologies obtained using either the classical SIMP method (top row) or the selective penalization approach prior to mesh morphing (bottom row). The columns correspond to four different volume fractions $f=0.05$, $f= 0.1$, $f= 0.15$ and $f=0.2$ (from left to right). To reveal the inner structure of the designs, the figure shows section cuts using a clipping plane at $z/H=0.95$ to hide the solid disk

Table 9 Disk reinforcement example: compliance results for different material volume fraction limits using the classical SIMP method and the selective penalization approach

6 Conclusion

Closed-walled designs can be more efficient, multifunctional and even easier to manufacture, but fairly fine meshes are usually required to obtain them from density-based topology optimization with penalization. This paper introduced a two-step optimization procedure which makes the generation of 3D closed-walled designs feasible on coarse meshes and in particular for small material volume fractions. In a first step, a topology optimization is performed where the penalization of an intermediate element density hinges on the morphology in a neighborhood of the element. Elements belonging to thin features, like planar sheets or curved shells, are assigned proportional stiffness, whereas a sufficiently large penalization exponent is still applied everywhere else. The topology optimization result will be a combination of thick solid features and thin-walled intermediate density features typically consisting of a single layer of elements. In a second post-processing step, this intermediate result is transformed into a purely solid design. Taking a Lagrangian approach, we shrink each element volume to its material volume. This is achieved by solving a modified linear elasticity problem with imposed inelastic shrinkage strains. The resulting morphed mesh serves as a reference shape for the creation of a CAD-type geometry, which is the final result of the two-step optimization procedure.

We have tested the procedure on three compliance minimization benchmark problems, a cantilever beam, a torsion rod and a disk reinforcement structure. In the cantilever beam example, the thin-walled intermediate density region was limited to the web, whereas the flanges were still solid. Compared against truss-like designs, we found stiffness improvements of about $10\%$. A closed-walled design was also obtained for the torsion rod example, consisting entirely of a thin-walled intermediate density shell and leading to a reduction in compliance of almost $30\%$. Values found for the geometrically more complex results of the disk reinforcement example were in the same range as well. Moreover, it could be shown that the topologies of the closed-walled designs obtained from the selective penalization approach are not sensitive to variations of the material volume fraction limit. As shown in the literature, similar efficiency improvements could have been achieved by mesh refinement. However, at least halving the element size would be necessary in the cantilever beam example leading to higher computational cost. For all three examples, smooth CAD geometries were created through reverse engineering of the morphed meshes. Compliances found by finite element analysis showed a close agreement to the values predicted by the topology optimization.

The promising results motivate a number of new directions for future work. In view of the fact that closed-walled designs exhibit larger surfaces compared to their truss-like counterparts, it should be investigated how this affects manufacturability of real structures. For instance, from an additive manufacturing perspective, the orientation of large, wall-like features with respect to the build direction is of crucial importance. With the aim of reducing, though not eliminating, sacrificial support structures, it might be beneficial to locally revert back to a truss-like morphology where the slope of an overhang is below some critical angle.

Given that usually closed-walled designs are also thin-walled, they are likely more susceptible to buckling. Though this is an aspect of thin-walled structures in general and not specifically related to the design method used, it would certainly be interesting to see if and how this issue could be addressed within the proposed optimization procedure, e.g., by penalization of the proportional stiffness of thin features to account for the cost of additional stiffeners.

Another worthwhile topic to explore is the applicability of the procedure to more challenging problems with other objectives, more constraints, and complex shaped design domains including several fixed solid regions.