Layout optimization of simplified trusses using mixed integer linear programming with runtime generation of constraints

Abstract

Traditional truss layout optimization employing the ground structure method will often generate layouts that are too complex to fabricate in practice. To address this, mixed integer linear programming can be used to enforce buildability constraints, leading to simplified truss forms. Limits on the number of joints in the structure and/or the minimum angle between connected members can be imposed, with the joints arising from crossover of pairs of members accounted for. However, in layout optimization, the number of constraints arising from ‘crossover joints’ increases rapidly with problem size, along with computational expense. To address this, crossover constraints are here dynamically generated and added at runtime only as required (so-called lazy constraints); speedups of more than 20 times are observed whilst ensuring that there is no loss of solution quality. Also, results from the layout optimization step are shown to provide a suitable starting point for a non-linear geometry optimization step, enabling results to be obtained that are in agreement with literature solutions. It is also shown that symmetric problems may not have symmetric optimal solutions, and that multiple distinct and equally optimal solutions may be found.

1 Introduction

Reducing the volume of material consumed in construction projects is a challenge of increasing importance. The theory of minimum volume structures is well established (Michell 1904) and can provide benchmark values to help evaluate the structural efficiency of proposed designs. However, for practical usage, the truss-like continua generated by classical methods are often challenging or impossible to construct in practice. Whilst novel construction methods may allow more complex designs to be realized in the future, more immediate benefits may arise through the use of optimization methods capable of generating less complex solutions.

Numerical topology and layout optimization methods allow structurally efficient forms to be identified. These methods can be divided into continuum-based approaches and discrete truss/frame-based methods. Perhaps the best known of the continuum-based approaches is the SIMP method (Bendsøe and Sigmund 1999). This uses penalization to drive the solution to a distinct structural form. A number of extensions to the SIMP method have been suggested to control the complexity of the forms identified. For example, minimum length scale (Zhou et al. 2015) and maximum perimeter length (Park et al. 2018) constraints have been proposed. However, the quantities involved are not intuitive when considered in the context of a typical structural engineering design problem. More generally, interpreting solutions from a continuum topology optimization in a structural engineering context will often be challenging, and is likely to necessitate considerable manual post-processing effort. Furthermore, the fraction of the available design space occupied by structural members in a typical building or bridge structure will generally be very small, such that very high numerical resolutions are required to achieve accurate results (see, e.g. Aage et al. 2017).

Here, attention is therefore focussed on methods that directly represent the structure as a frame or truss composed of a series of discrete members. The most well-known numerical method of this type is the ground structure layout optimization method (Dorn et al. 1964), in which an optimal set of members is chosen from a dense initial ground structure. The commonly used plastic design formulation gives rise to a problem that can be solved using linear programming, allowing problems involving large numbers of potential members to be solved rapidly.

One potential method for limiting the complexity of a truss structure was suggested by Parkes (1975). This involves adding a volume penalty to represent the material required in the connections joining each member in the structure, known as a joint cost. The penalty is linearly related to the member volume, allowing this method to readily be integrated with numerical ground structure based layout optimization methods, whilst retaining computational efficiency. However, as this method penalizes short members, rather than the number of members, its efficacy is problem dependent.

Another, similar concept was presented by Prager (1977); however, here the cost of a joint was assumed to be constant. With Prager’s approach minimum volume trusses with fixed numbers of joints are first found, with the ranges of costs for which they are optimal later established. The minimum volume trusses are based on use of a mesh-wise constant strain field, furnishing a set of geometrical rules for the joints. Mazurek et al. (2011) identify the same rules by direct optimization of joint positions for simple structures, building on the principles of graphical statics. These rules imply that the angles between members at every unsupported joint should be identical. Prager (1978) extends these rules to the case where σ_T≠σ_C, where σ_T and σ_C are respectively the limiting stress in tension and compression. Each of the aforementioned authors applies their approach to three-force problems, such as the classical Michell cantilever problem (where two of the three forces are support reactions).

Of these approaches, only the linear joint cost method is applicable to multiple load-case problems. When multiple load-cases are present, the optimal solutions for elastic and plastic design problems diverge. The plastic problem gives rise to the simplest numerical formulation and, since it is accepted by many structural design codes, is considered here.

Optimality criteria for multiple load-case plastic design problems were first given by Prager and Shield (1967). For scenarios with two load-cases, it is possible to use the superposition principle derived by Nagtegaal and Prager (1973) to split the problem into two single load-case problems that can then be superimposed. The superposition principle was later extended to problems with more than two load-cases by Rozvany and Hill (1978), although this has a restricted range of applicability. However, numerical results for various problems demonstrate the ‘overlapping’ nature of many of the optimal layouts identified. In such cases, manually identifying the layout of a discretized structure becomes challenging.

Various means of characterizing the complexity of a given structure are possible. However, whatever the chosen complexity measure, it generally results in a non-smooth problem that can be challenging to solve numerically. Conceptually, the simplest measures of complexity are the numbers of joints or members in a given structure. Additionally, significant attention has been devoted to limiting the numbers of different cross sections present in a given solution.

Kanno and Fujita (2018) limit the number of joints in solutions whilst minimizing the compliance of the structure, considering both a heuristic method and a mathematical programming formulation including integer variables. However, although the resulting mixed integer second-order cone programming (MISOCP) problem could solve problems with up to 1500 potential members reasonably quickly (in a time of 112 s), conditions were not imposed to prevent intersecting or overlapping members. Therefore, many of their results contain members that cross, which would likely be interpreted as additional joints by practitioners, therefore limiting the usefulness of the results obtained.

A similar approach based on plastic design principles with volume minimization was used by Park (2013), resulting in a mixed integer linear programming (MILP) problem. Here, complexity was reduced by imposing limits on the numbers of members in the solution; he also used a similar approach to identify tensegrity forms.

Tensegrity forms were also identified by Kanno (2013), using another MILP formulation considering both compliance and stress constraints, as well as a number of practical considerations. This formulation prevents the inclusion of intersecting members by including constraints for every intersecting pair of potential members in the ground structure. As the problems considered are limited in size (with ground structures containing up to 18 nodes and 99 potential members), the number of potential intersection points is small (≤ 32). Nonetheless, the problems took up to 67,000 s to solve, and the number of intersection points and the time required would rapidly increase at higher resolutions.

The great majority of work on truss-based optimization methods with discrete constraints has focused on restricting the cross sections of each member to be chosen from a given list of catalogue sections. A comprehensive review of methods for approaching this problem can be found in Stolpe (2016), covering both deterministic (e.g., integer programming) and meta-heuristic methods. In this, it is observed that complex formulations generally restrict the size of problems, such that these fall within the realm of ‘size optimization’ rather than true layout or topology optimization. Identification of global optima (deterministic methods) generally has a high computational cost; for example when Achtziger and Stolpe (2007) identified the global optimum for a problem with 131 potential members and 6 possible cross sections, the associated computational time was 488,592 s.

Heuristic methods are simple to implement and are therefore popular with many researchers (e.g. Ahrari et al. 2015; Mortazavi and Toǧan 2016; Gonçalves et al. 2015). However, the number of independent design variables is then usually limited (≪ 100). Therefore, these methods generally employ very low-resolution and/or restricted ground structures, often tailored to individual problems.

The moving morphable components (MMC) method, developed by Guo et al. (2014), combines a continuum level-set model and explicit description of geometry. Although this does not obviate the need to employ high resolutions, this does allow complexity to be controlled in intuitive ways. For example, Hoang and Jang (2017) limit the thickness of members, and Zhang et al. (2017) limit the number of ‘effective components’ (≈ number of members). However, the problem is highly non-linear and prone to identification of local optima; there are also issues treating problems with low-volume fractions.

Identification of local optima is also an issue for ground structure–based methods involving continuous non-linear approximations, such as those of Asadpoure et al. (2015) and Torii et al. (2016), which are usually non-convex. Leng and Duan (2012) use a continuum approximation based on the Heaviside function to prevent intersecting bars; however, only problems with up to 68 potential members are considered, and there is no indication of the associated computational cost.

Ohsaki and Katoh (2005) also include a constraint on member intersection, as well as nodal stability and stress constraints. They use non-linear programming (NLP) and MILP in combination to provide both upper and lower bounds on solutions; problems solved have a maximum of 72 bars, and the ground structure is such that very few members can intersect. Times of up to 3000 s are reported.

Ohsaki (2016) also considers the truss topology optimization problem with discrete cross sections, and additionally considers the problem of combined topology and geometry optimization of trusses, i.e. where the nodal locations are also included as design variables. In this, it is noted that these problems may be both non-convex and non-smooth, and therefore solving them is very difficult. A number of other means of addressing this are also possible, such as the implicit programming approach of Achtziger (2007), and the post-processing rationalization method used by He and Gilbert (2015).

MILP formulations have also been used to incorporate a range of other constraints, including buckling (Groenwold and Stander 1997; Mela 2014), stress constraints (Kanno and Guo 2010), and the requirements of real-world design codes (Van Mellaert et al. 2018). Complex real-world and design code constraints have also been studied using meta-heuristic methods (e.g. Koumousis and Georgiou 1994; Villar et al. 2016; Huang and Xie 2007). However, for both MILP and metaheuristic methods, the additional complexity that these constraints cause limits their applicability to size optimization or very low-resolution layout optimization (up to around 200 potential member) problems.

Most numerical approaches in the literature that consider buildability constraints can therefore be seen to fall into one of the following categories: (i) those that present topology optimization problem formulations of such complexity that only trivial scenarios can be solved, and (ii) those that present solution algorithms that produce structures with no guarantee or measure of optimality. The methodology presented in this paper seeks to extend the scale of truss layout optimization problems with basic buildability constraints that are solvable, so as to provide a potentially useful conceptual design tool for practitioners. To this end, an MILP formulation is used to find a globally optimal solution for a ground structure of finite resolution. The main contribution of this paper is to substantially increase the speed by which problems can be solved, and hence also the scale of problems solvable. This is achieved through the runtime generation of some constraints (so-called lazy constraints), as part of a two-stage design process. The MILP problem forms the first stage, followed by an optional second non-linear geometry optimization refinement stage. Application of the developed procedure to a range of problems allows observations to be drawn on the nature of the structures identified as optimal under the imposed buildability constraint, with results compared with analytical solutions in the case of one of the problems considered.

The paper is organized as follows: Section 2 describes the layout optimization formulations that will be employed in the present study; Section 3 describes the non-linear geometry optimization stage; Section 4 describes application of the methods described to a range of numerical example problems; conclusions from the study are then drawn in Section 5.

2 Truss layout optimization formulations

2.1 Linear programming formulation

The well-known plastic layout optimization formulation for volume minimization of trusses subject to stress constraints (Dorn et al. 1964) is used herein; the process involves setting up a ground structure (Fig. 1) and solving the following linear programming problem:

$$ \begin{array}{@{}rcl@{}} \text{minimize } V &=& \mathbf{l}^{T}\mathbf{a} \end{array} $$

(1a)

$$ \begin{array}{@{}rcl@{}} \text{subject to } (\mathbf{Bq}_{k} &=& \mathbf{f}_{k} )_{\forall k} \end{array} $$

(1b)

$$ \begin{array}{@{}rcl@{}} (\sigma_{T}\mathbf{a} -\mathbf{q}_{k} &\geq& 0 )_{\forall k} \end{array} $$

(1c)

$$ \begin{array}{@{}rcl@{}} (\sigma_{C}\mathbf{a} +\mathbf{q}_{k} &\geq& 0 )_{\forall k} \end{array} $$

(1d)

$$ \begin{array}{@{}rcl@{}} \mathbf{a} &\geq& 0 \end{array} $$

(1e)

where V is the total volume of all members, l is a vector of all potential member lengths, and a is a vector of all potential member areas. B is a suitable 2n × m equilibrium matrix (for planar problems), where n is the number of nodes and m the number of potential truss members in the ground structure. q_k is the vector of member internal forces, and f_k is the externally applied loading, in load-case k. σ_T and σ_C are the limiting stresses in tension and compression. Note that in this formulation, buckling of members may be considered only in a highly simplified manner, by reducing σ_C.

Fig. 1

Truss layout optimization: a problem specification (applied load(s), supports and design domain); b discretization with nodes; c ground structure without overlapping members; d unique optimal solution associated with (c); e ground structure including overlapping members (as used herein); f alternative optimal solution obtainable only when using (e)

Note that when limitations on structural complexity are imposed (see Section 2.2), it is useful to include overlapping members in the ground structure. For example, considering the problem shown in Fig. 1, if it is required that the solution contains no more than four joints (or members), it is evident that the structure shown in Fig. 1d is not feasible, whereas the structure shown in Fig. 1f is feasible, where these structures were generated respectively without and with overlapping members in the ground structure. In the former case, this would result in an alternative, suboptimal, solution being generated. Thus, overlapping members are included in the ground structures of all problems considered herein.

2.2 MILP formulations

2.2.1 Addition of discrete flag variables

The previous formulation can be extended using mixed integer linear programming (MILP) to provide a flexible method capable of imposing a wide range of constraints, including constraints designed to increase the practicality and buildability of a truss structure. In this formulation, a new set of binary variables are added that represent, e.g., the existence of a given potential member or joint. In the case of member flag variables, these are set based on cross section area:

$$ \begin{array}{@{}rcl@{}} M\mathbf{w} - \mathbf{a} &\geq& 0 \end{array} $$

(2a)

$$ \begin{array}{@{}rcl@{}} w_{i} &\in& \{0,1\} \qquad {i}{= 1, 2, ..., m} \end{array} $$

(2b)

where w = [w₁,w₂,...,w_m]^T is the vector of flag variables for each potential member in the ground structure. M is a large number, which becomes effectively an upper bound on cross section area and must therefore be larger than any required cross section in the final solution. However, if M is too large, numerical issues can arise; here, M was pragmatically chosen to be 20 times the maximum magnitude of any point load divided by the minimum limiting stress.

To provide flag variables to represent the existence of a joint, the sum of the areas of all members linked to a given node is used:

$$ \begin{array}{@{}rcl@{}} \hat{M}v_{j} - {\sum\limits_{i\in J_{j}}} a_{i} &\geq& 0 \qquad {j} {= 1, 2, ..., n} \end{array} $$

(3a)

$$ \begin{array}{@{}rcl@{}} v_{j} &\in& \{0,1\} \qquad {j} {= 1, 2, ..., n} \end{array} $$

(3b)

where J_j is the set of member indices for all members connected to node j. v = [v₁,v₂,...,v_n]^T is another vector of flag variables, where here v_j is the flag variable indicating the involvement of node j. $\hat {M}$ is another sufficiently large number. In this case, $\hat {M}$ should be bigger than the total area of members connected to any node; here, $\hat {M}$ was pragmatically taken to be 4 times M.

The modelling of (3a) is similar to that found in the literature (e.g. Kanno and Fujita 2018) when only the number of nodes are limited. However in light of the presence of integer flags for member existence in the present formulation, an equivalent formulation whereby v and w are linked is possible. This was found to produce inferior performance compared to (3a) (for more details, see Appendix A).

These flag variables can then be used to form constraints to increase the practicality of the forms produced.

2.2.2 Limits on the number of joints, including ‘crossover joints’

Due to the much lower number of nodes compared to potential members (∝ n instead of ∝ n²), imposing a limit on the number of nodes is comparatively computationally efficient. The simplest method to limit the number of joints to some given value η is to add the following constraint

$$ {\sum\limits^{n}_{j=1}} v_{j} \leq \eta $$

(4)

and constraints (3a) to the problem given in (1e).

However, this formulation may produce a structure which contains members that intersect each other partway between their ends. These ‘crossover joints’ will appear to be additional joints from the point of view of the designer, but will by default not be counted as such in the formulation.

To prevent this, constraints can be added for each pair of intersecting members, preventing both of them from being present in the solution at the same time:

$$ \begin{array}{@{}rcl@{}} {\sum\limits^{n}_{j=1}} v_{j} &\leq& \eta \end{array} $$

(5a)

$$ \begin{array}{@{}rcl@{}} (w_{h} + w_{i} &\leq& 1)_{\forall \{h,i\} \in X} \end{array} $$

(5b)

where X is a set containing unordered pairs of indices, {h,i}, for each pair of intersecting elements.

However, the size of X increases at a very high rate (∝ n⁴), meaning that the full form of this problem will be extremely computationally expensive to formulate and solve. Fortunately, since only a small subset of these constraints are likely to be used, these can instead be generated on-the-fly, during the running of the solver. Most commercial solvers, including CPLEX (IBM Corp 2015) and Gurobi (2018), are capable of implementing these so-called lazy constraints by allowing user-defined code (often referred to as a callback function) to be called at intervals during a single run of the solver. As any intermediate solution which violates one or more potential constraints will be eliminated, this methodology does not alter the final solution, which remains identical to the solution of the full MILP problem containing all constraints from the beginning.

Lazy constraints have previously been used when solving the travelling salesman and related problems (Dantzig et al. 1954), where they have been shown to provide significant advantages in terms of computational efficiency. More recently, Haunert and Wolff (2010) have applied them to the simplification of building outlines for maps. Here it is shown that, when applied to truss structures, the use of lazy constraints enables true topology optimization problems to be solved, i.e., layout optimization problems utilizing fully connected, non-problem specific, ground structures to identify optimal topologies under various different constraints.

The problem is initially provided to the solver without the constraints of (5b) (see Appendix B for the full problem statement). In the initial problem, all member flags in w can be assumed to be equal to 1 without violating any of the initial constraints. This can be used as a partial warm start, although the speed advantage in explicitly doing so was found to be modest. When a feasible solution is found, the set of members with non-zero areas are identified and each pair from this set (of which there are several orders of magnitude fewer than all pairs of potential members) is checked to see if a crossover joint is produced. If a crossover is found, then an appropriate constraint of the form of (5b) is added to the problem, and remains present in the active problem until the final solution is found.

Note also that for multiple load-case problems, optimal solutions are often made up of multiple, almost independent, forms overlain on top of each other. Therefore, it is preferable to allow crossovers in the solutions, and to take account of them when computing the total number of joints. i.e. (5b) becomes:

$$ \begin{array}{@{}rcl@{}} {\sum\limits^{n}_{j=1}} v_{j} + {\sum\limits^{b}_{g=1}} \bar{v}_{g} &\leq& \eta \end{array} $$

(6a)

$$ \begin{array}{@{}rcl@{}} (w_{h} + w_{i} - \bar{v} &\leq& 1 )_{\forall h,i \in X} \end{array} $$

(6b)

where $\bar {\mathbf {v}} = [\bar {v}_{1}, \bar {v}_{2}, ..., \bar {v}_{b}]^{T}$ is a vector of flag variables representing the existence of each possible crossover between members of the ground structure. The length of $\bar {\mathbf {v}}$, denoted by b, will be approximately proportional to n⁴, although it will also depend on the exact positions of the ground structure nodes.

The constraints of (6b) describe the case where two lines overlap. A similar constraint could be derived for a point where three or more lines intersect. However, identifying these points becomes reliant on the tolerances used in the calculations, and such cases are unlikely to occur in practical situations. As such, this extension will not be considered further in this paper. Note that the general case of three members intersecting at three points (i.e. forming a triangle) is handled correctly by the constraints of (6b).

When the constraints of (6b) are implemented using lazy constraints, the size of $\bar {\mathbf {v}}$ can be greatly reduced. $\bar {\mathbf {v}}$ becomes a pool of variables, which are assigned to crossovers as required. The pool size should be chosen to be larger than the number of lazy constraints expected to be added, but small enough to not require excessive memory. For the problems shown here, a pool size of 100 was found to be sufficient. In this case, the variables in $\bar {\mathbf {v}}$ can be set to zero without affecting the optimality of the problem as initially provided; this affects the problem in a similar manner to the variables in w.

Initial tests suggested that it was more advantageous to check and impose these lazy constraints each time a feasible integer solution was identified, rather than each time a continuous relaxation was solved. This also reduced the number of times the check was performed, and meant a smaller pool of constraints could be used. This approach was therefore adopted here. As the solution is not changed by the proposed method, these heuristics impact only the speed with which the solution is obtained, and not the solution itself.

The procedure used to dynamically generate these constraints is shown in Fig. 2 and Algorithm 1. The process to instead forbid crossovers is similar, except that all references to $\bar {\mathbf {v}}$ are removed, and the newly added lazy constraint is instead w_p + w_q ≤ 1.

Fig. 2

Procedure for runtime constraint generation. Problem shown involves imposing a limit on the number of joints, including ‘crossover joints’. The steps in the shaded region are performed within the callback function which is called by the MILP solver (e.g. Gurobi)

In the procedure, once a constraint has been added to the current reduced problem, it will not be removed. This ensures that the solution obtained by successively adding dynamically generated constraints will converge to the globally optimal solution for the original full problem (i.e. the problem that includes all constraints from the outset). This will occur when the solution for the current reduced problem, comprising only a subset of all possible constraints, is also found to be feasible for the original full problem. For continuous linear optimization problems, a similar principle underpins the cutting plane method (Kelley 1960) and analogous column generation method (Dantzig and Wolfe 1960), which has been successfully used by Gilbert and Tyas (2003) to develop a computationally efficient ‘member adding’ procedure for large-scale truss layout optimization problems.

Finally, note that the optional geometry optimization post-processing step (see Section 3) is not shown in Fig. 2 and Algorithm 1, and is performed following a successful termination of the solver.

2.2.3 Imposing symmetry

For a given problem with symmetrical design domain, loads and supports, it is known (Stolpe 2010) that truss optimization with discrete cross sections may have an optimal solution that is not symmetrical; it will be shown that this is also the case when the MILP problem formulation proposed here is used to impose limits on the number of joints in the structure.

However, it is useful to consider how a requirement for a symmetrical solution can be imposed as an additional constraint, since symmetry will often be preferred for reasons of standardization or aesthetics. It also allows problem size to be significantly reduced, as only half of the design domain needs to be explicitly modelled. To impose a symmetry condition, each symmetrical pair of members is assigned only a single area variable. Additionally, only one integer flag is added to each symmetrical pair of members or nodes. Members that cross the defined line of symmetry, or ‘mirror plane’, are not included, as they can be approximately modelled using nodes that lie on the mirror plane, as shown in Fig. 3. Thus, the number of potential members (and therefore variables) will be reduced to approximately a quarter of the initial number.

Fig. 3

Approximation of members crossing a mirror plane in part of a layout optimization solution: a members crossing the mirror plane (shown as a dash-dotted line) permitted, noting that the crossover joint will be counted due to (6b); b members crossing the mirror plane not permitted, with a node on the mirror plane used to approximate (a); c geometry optimization used improve (b), with the node on the mirror plane in this case moving to the same location as in (a)

To achieve this, some modifications to the constraints are needed. A node which lies on the mirror plane and which is connected only to members which are perpendicular to the mirror plane will not appear to be a joint in the final design. Therefore, for nodes lying on the mirror plane, (3a) is replaced by

$$ \hat{M}v_{j} - {\sum\limits_{i\in J^{\prime}_{j}}} a_{i} \geq 0 \qquad \qquad j = 1, 2, ..., n $$

(7)

where $J^{\prime }_{j}$ is the set of member indices for members connected to node j, but not including those members which are perpendicular to the mirror plane.

The constraint on the total number of joints must also be modified such that joints that are formed by crossovers or nodes lying remote from the mirror plane are counted twice in the computations.

2.2.4 Limits on the angle between members

A feature that can make Michell structures difficult to manufacture is the presence of small angles between adjacent members, especially in fan-type regions. To prevent this, integer constraints can be added in the layout optimization stage as follows:

$$ (w_{h} + w_{i} \leq 1)_{\forall \{h,i\} \in D} $$

(8)

where D = {{h₁,i₁},{h₂,i₂},...} is the set containing unordered pairs of indices for all pairs of members that form an angle that is smaller than μ, the minimum permitted joint angle. Note that this angle may be formed either at a node which is common to both members or at a point where the members intersect, partway along one or both of their lengths.

Again, the full formulation is very time consuming to compute as the number of these constraints is approximately proportional to n⁴. These constraints are therefore also implemented as lazy constraints. The procedure is similar to that outlined in Fig. 2; however, references to $\bar {\mathbf {v}}$ are removed, and the check on each pair of members, p & q, is to identify if they form an angle (either at a crossover point or at an end node) which is outside the permitted range.

3 Geometry optimization post-processing step

Once the integer programming stage has been completed, the resulting structure can be further refined by the use of the geometry optimization post-processing rationalization method developed by He and Gilbert (2015). This adds the nodal positions of the structure as design variables, resulting in a non-linear and non-convex problem. This stage is optional as the structure generated by solving the MILP problem will satisfy all the specified design constraints. However it is attractive as it further reduces the volume and may allow results which match analytically derived solutions from the literature to be obtained.

As the geometry optimization problem is non-convex, it is not generally possible to solve this to a guaranteed globally optimal solution; thus this method relies on the starting point provided by the topology optimization being sufficiently close to the optimal point. A finding of this study is that the solution of the MILP problem can successfully be used as the starting point for geometry optimization.

During the geometry optimization stage, it will be important to ensure that the solutions continue to be feasible with respect to the practical constraints imposed in the previous sections. The remainder of this section will outline the required modifications to the algorithm proposed by He and Gilbert (2015). Note that the original buildability constraints, involving integer variables, need not be included at this stage, as the overall topology is generally not significantly changed. Instead the buildability constraints are reformulated as constraints on the nodal positions, leading to a non-linear but continuous problem.

When a limited number of joints are permitted, no additional constraints will be required in the geometry optimization (GO) stage. This is because the number of joints in the problem generally remain constant, or will reduce due to joint merging, or due to all connected members at a joint vanishing.

The only possible means by which new joints can appear is if the topology is changed by a member passing over another joint, as shown in Fig. 4. However, this situation can easily be avoided by converting the topology between the MILP and GO stages such that all ‘crossover joints’ become standard joints.

Fig. 4

Detail of a layout, showing the importance of converting ‘crossover joints’ to standard joints between the MILP and geometry optimization post-processing stages when imposing a limit on the total number of joints: a before geometry optimization, containing 3 joints in this region; b after geometry optimization, now containing 4 joints in this region (due to a ‘crossover’ joint not first being converted to a standard joint)

When a limit on the angle between members has been imposed, this must be converted to a continuous constraint on the joint coordinates. This will be in the form:

$$ \frac{\overrightarrow{\text{CA}}\cdot\overrightarrow{\text{CB}}}{|\overrightarrow{\text{CA}}| |\overrightarrow{\text{CB}}|} \leq \cos(\mu) $$

(9)

where C is the joint common to two members, A and B are the other joints of each member, and μ is the imposed minimum angle. Note that this requires point C to be a standard joint; therefore, ‘crossover joints’ must again be converted to standard joints before the geometry optimization stage.

In some cases where a minimum angle is imposed, additional parameters may be required for the geometry optimized results to be meaningful. For example, when a branch-type form (as shown in Fig. 5a) is identified as the optimal solution of the integer programming problem, the branch joint tends to move towards the ‘root’ joint, as in Fig. 5b. The joint merging phase will then combine the two joints, and there then may be pairs of members which violate the angle constraint (Fig. 5c). If the permitted movement radius of the joints is sufficiently large, the feasibility restoration phase of the non-linear solver is likely to be able to find a new feasible solution using the new topology (Fig. 5d).

Fig. 5

Detail of area containing branched members during the geometry optimization post-processing step: a initial branched member topology; b joints moving closer together, though as the bottom and middle member do not meet, the angle between them is not checked; c joints are merged, but the bottom and middle members now have an angle constraint, which is violated; d the feasibility restoration phase finds a point at which all constraints are satisfied, but the geometry is now quite different to the MILP starting point

This new form may now be notably different from the initial starting point, and therefore potentially inefficient. However, simply eliminating the joint merging step would result in a final design where two joints were infinitesimally close together. A minimum member length constraint can be added to prevent this, i.e.

$$ |\overrightarrow{\text{AB}}| \geq l_{\min} $$

(10)

where A and B are the end points of the member, and $l_{\min \limits }$ is the minimum permitted length. This constraint is only explicitly required in the geometry optimization stage, since during layout optimization, short members can simply be omitted from the ground structure. Here, length limits have generally been added only in the geometry optimization stage, with $l_{\min \limits }$ being set at or below the nodal spacing of the original ground structure.

Within the examples of this paper, it has been observed that the geometry optimization procedure did not need to make use of several considerations of He and Gilbert (2015), due to the simplified nature of the starting structures. For example, new crossover joints were added only at the initialization of geometry optimization. Also, the joint merging procedure was triggered only in cases with branching type structures. From this, it can be seen that the structures produced by geometry optimization are generally topologically very similar to the solutions obtained at the end of the initial MILP stage.

4 Numerical examples

All numerical example problems were run on an Intel Core i7-6700HQ CPU @ 2.60 GHz, with 16GB of RAM. Gurobi 7.0.1 (2018) was used to solve the MILP problems, with 4 physical cores available for use. All problems mentioned were solved to a 0.01% optimality gap (the default value when using Gurobi). For practical usage, this level of accuracy may not be required, and a higher value can be used to reduce computation time. All other Gurobi parameters were set to their default value. The computational times reported are wall clock times, and include the time taken to set up the problem.

4.1 Simple cantilever

The first example involves the setup shown in Fig. 6. This consists of two load-cases denoted as P₁ and P₂. These each contain a single point load, which are each applied at a given angle 𝜃 to the global coordinate axes at point (d,0), and have magnitude, Q.

Fig. 6

Simple cantilever: details of applied load cases, a load case P₁, and b load case P₂

Derivations of the minimum volume structures, both unconstrained and with a maximum of 3 joints, can be found in Appendix C. The optimal member sizes and support locations are shown in Fig. 7.

Fig. 7

Simple cantilever: theoretical results, a volumes of optimal structures with unlimited complexity (light grey) and maximum 3 joints (dark grey) for values of 𝜃 between 0 and $\frac {\pi }{2}$; b locations of support points for optimal structures with unrestricted complexity (light grey) and maximum 3 joints (dark grey), with line width proportional to the area of the member which connects there (forms e and h shown for context); c–f forms of optimal structures with unlimited complexity for $\theta = \frac {\pi }{4}, \theta _{2}, \frac {3\pi }{8}, \frac {\pi }{2}$; g–j forms of optimal structures with only 3 joints for $\theta = \frac {\pi }{4}, \theta _{2}, \frac {3\pi }{8}, \frac {\pi }{2}$

It can be seen that even for this very simple problem, the behaviour is quite complex and unintuitive. The rationalized structures are not closely linked to the equivalent un-rationalized form, which may make such structures difficult to obtain by intuitive or mathematical post processing. The volume penalty caused by imposing the three joint limit is at most 20.3%.

Table 1 shows the difference between the theoretical and numerical results for this example. The MILP results were found with nodes permitted only along the support, at 0.02d spacing over − 1.5d ≤ y ≤ 1.5d (i.e. 152 nodes, including the loaded node). As none of the members in the ground structure crossed, crossover constraints were not required. Geometry optimization (GO) was also performed to further refine the results.

Table 1 Simple cantilever: comparison of theoretical and numerical methods for problem with 3 joints

The numerical and analytical volumes can be observed to be in close agreement. At 𝜃 = 𝜃₂ a discontinuity occurs, where two distinct results are equally optimal (see Appendix C.2.3). Here, the MILP solver identifies one of these solutions. Then, use of the interior point method for the GO stage perturbs this solution, resulting in identification of the alternative solution.

When a limit on the angle between members is imposed, solutions may be more complex in form, involving members that do not simply directly connect the loaded point and a point on the support. Therefore, numerical solutions for joint angle limits have been calculated using a 5×13 grid of nodes, and a fully connected ground structure (m = 2080).

Figure 8 shows results for the problem with angle $\theta = \frac {3\pi }{8}$ radians, i.e. as shown in Fig. 7e and i. The scenario is subjected to limits on the minimum angles between members of 35^∘ and 45^∘. The unusual topologies identified demonstrate the difficulty in trying to identify optimal solutions for this problem analytically or manually.

Fig. 8

Simple cantilever: numerical results for problem with specified minimum angles between members (load inclination $\theta =\frac {3\pi }{8}$ radians)

The problem was solved firstly by imposing all angle constraints from the outset (‘basic formulation’), and then by implementing the angle limit (i.e. Eq. (8)) using lazy constraints. Both implementations produced identical final results; however, it can be seen that the use of lazy constraints reduced the time required by approximately a factor of 20.

Figure 8 also shows the result of applying geometry optimization post-processing. Despite the different topologies identified in the MILP stage, similar topologies are found after geometry optimization. Additionally, it can be observed that the volumes after geometry optimization are both lower than the three-joint form shown in Fig. 7i, demonstrating that the more complex topology is beneficial, albeit only by 3.6% and 2.8% respectively. This suggests that, although the geometry optimization process is non-convex and therefore cannot be proven to identify a global optimum, the starting points provided by the MILP formulation appear to be sufficient to provide good results.

4.2 Michell cantilever

4.2.1 Problem specification

The proposed methods are now applied to a classical Michell cantilever problem, as shown in Fig. 9. The theoretical minimum volume can be found using equations derived by Chan (1960) to be V_T = 39.43Qd. Discretized versions of this problem have been studied by Prager (1977) and Achtziger and Stolpe (2007). In both cases, the topology of the optimal structures was manually inferred from the continuum form; however, their observations are useful for comparative purposes.

Fig. 9

Michell cantilever: problem specification (fully connected ground structure used)

A fully connected ground structure of 99 nodes is used here; this contains 4851 potential members. The solution to the standard layout optimization problem at this resolution has a volume of 40.45Qd, an increase of 2.6% over V_T, although this reduces to + 0.8% after GO is applied, and the resulting solution has 20 joints (Table 2).

Table 2 Michell cantilever: results with limits imposed on the total number of joints

4.2.2 Limiting the number of joints

To set up the problem with all crossover constraints from the beginning requires checking 11,763,675 pairs of members, of which 2,795,779 produce a constraint. (Simply performing these checks was found to take nearly 20 minutes with the C++ code used here.)

Alternatively, using lazy constraints, the problem can be set up almost instantly, producing an initial problem with 14,553 variables and 14,844 constraints. The problem was first solved using lazy constraints to prevent crossovers but without limiting the number of joints. This produced a structure with 12 joints, and required 240 lazy constraints, around 0.01% of the full number.

The problem was then solved with limits imposed on the maximum numbers of joints, η, from 3 to 11. The results can be seen in Table 2 and Figs. 10 and 11, with further details available in Online Resource 1. Note that the longest time taken to solve any of these problems was under 5 minutes, around a quarter of the time needed just to formulate the full problem.

Fig. 10

Michell cantilever: Results after MILP (top) and GO (bottom) stages. The volume difference between MILP and GO solutions is 1%, 1.4% and 1.6% respectively

Fig. 11

Michell cantilever: results with limits imposed on the total number of joints. (Volume shown as percentage above theoretical minimum volume, V_T = 39.43Qd. Forms shown after MILP and GO. An example cost function is also shown where each joint has a constant cost, equal to an increase in volume 0.7% of V_T.)

It may be observed that the forms for 3, 6 or 11 joints agree with those found by Prager (1977)¹. Also the unsymmetrical 8 joint solution is somewhat similar to the unsymmetrical solution presented by Mazurek et al. (2011, fig 22).

4.2.3 Other related problems

Prager extended his results to postulate a solution to the related problem of minimizing total cost, comprising a material cost and a fixed cost per joint. It is possible to reformulate the integer programming problem to consider this directly, by changing the objective function to be of the form

$$ \text{minimize } \mathbf{l}^{T}\mathbf{a} + c_{j}\mathbf{v} $$

(11)

where c_j is the normalized cost of a joint.

However, (11) may alternatively be expressed in the form of an equation, plotted as a straight line on Fig. 11. The example objective function shown on Fig. 11 is a line of constant cost when the joint cost, c_j, is equal to the cost of a volume increase of 0.7% of the minimum volume, V_T. In this case, the solutions with 6 and 8 joints are equally optimal. However, the 7-joint solution has a higher cost; it is therefore not optimal for any objective function in the form of (11).

Prager’s solution to this problem over a range of values for c_j consisted of only the 3, 6 and 11 joint solutions. From Fig. 11, this can now be extended to add solutions with 4, 5 and 8 joints. The ranges of joint cost c_j for which each solution is optimal is shown in the final column of Table 2.

Limiting the number of members in a solution is another concern for ensuring practicality. As this is a single load-case problem, and due to the Simplex solver used to solve the LP sub-problems of the MILP problem, the optimal structures identified are all likely to be statically determinate, meaning that the number of joints is directly linked to the number of members (number of members = 2η − 4). Therefore, this method can also be used as a proxy for limiting the number of members.

4.2.4 Limiting the angles between members

Solutions for the same Michell truss problem, but with imposed minimum angle limits, from 15^∘ to 45^∘ are shown in Table 3 and Fig. 12, with further details provided in Online Resource 2. It can be seen that the topologies shown in Fig. 12 are symmetrical, and several are distinct from those shown in Fig. 11.

Table 3 Michell cantilever example: results with limited joint angle (Volume shown as percentage above theoretical minimum volume.)

Fig. 12

Michell cantilever: results with limited joint angle. (Volume given as percentage above theoretical minimum volume. Forms shown after MILP and GO. For branched forms, results both with and without a length limit are shown)

In the layout optimization stage, only a limited number of member angles are available; therefore, the structures identified do not have a minimum angle that exactly corresponds to the limit. Generally, once the geometry optimization post-processing step has been applied, the angle limits become active, although this is not always the case (e.g. in the case of the 20^∘ limit). In some cases, such as the 40^∘ and 45^∘ solutions, the same initial result is identified for multiple angle limits, and the solutions only diverge in the geometry optimization stage.

Most results in Fig. 12 are shown after geometry optimization with no length limit imposed. However, for the limit of 30^∘, a branching form similar to that shown in Fig. 5 was identified. During the geometry optimization stage for this result, the merging of the ‘root’ and ‘branch’ joint occurred, leading to a significant change in topology. The solution reduces in volume as the distance between the branching joints approaches zero, but then increases again in order to ensure compliance with the new angle constraint.

A length limit was therefore imposed to produce more meaningful results. For practical purposes, this is likely to be defined by the same manufacturing process that dictates the minimum angle between members; here $l_{\min \limits }$ will be set at or below the length of the shortest member in the ground structure (0.5d). When $l_{\min \limits } =0.5d$, the new volume was only slightly smaller (+ 2.51% vs. + 2.55%). However, for small values of $l_{\min \limits }$, the volume reduced to + 1.9%; this is shown as a dotted line in Fig. 12. Both the results with no length limit and with $l_{\min \limits } = 0.5d$ are illustrated in Fig. 12.

By comparing the results in Tables 2 and 3, it can be seen that the angle limits require a greater number of lazy constraints to be added, leading to correspondingly longer execution times. This is likely to be due to the fact that, when a limit on the number of joint is imposed, the initial constraints significantly reduce the number of feasible integer topologies before any lazy constraints are required. However, the maximum number of lazy constraints added in Table 3 was at most 0.3% of the total number possible (for the 45^∘ limit), showing that the advantage of using lazy constraints is still very significant.

4.3 Spanning example

A more complex, two load-case problem is now considered. This consists of two point loads which are applied separately, and transmitted to a pair of pinned supports; the problem specification is shown in Fig. 13.

Fig. 13

Spanning example: problem specification, after Sokół and Rozvany (2013) (The two point loads are applied separately. Grey shading shows the area modelled when the symmetry condition is imposed.)

This is a symmetrical problem, and therefore the minimum volume structure is also symmetrical when no discrete buildability constraints are imposed. The minimum volume solution, V_T, is given by Sokół and Rozvany (2013) as $3.44363\frac {Qd}{\sigma }$. The design domain is discretized using a grid of 90 nodes. The layout and geometry optimization solution for this resolution had a volume 1.2% greater than the theoretical optimal value.

The problem was first solved without imposing a requirement for a symmetrical solution. Solutions with maximum numbers of joints, η, ranging from 5 to 9 were found. Solutions with odd numbers of joints were found to be symmetrical, and were equal to the corresponding results shown in Fig. 15 and Table 4. However, the solutions with 6 and 8 joints were asymmetric, as shown in Fig. 14. Note that the 8 joint example approximately consists of one-half from each of the topologies with 7 and 9 joints.

Table 4 Spanning example: results with symmetry condition imposed and limits on numbers of joints (Bold values highlight when the two methods produce different results)

Fig. 14

Spanning example: results after MILP and GO showing asymmetric optimal solutions

Due to these findings, and the general preference in practice for symmetrical designs, the model was modified to explicitly impose a symmetry condition about the centre line, using (7) and the method outlined in Section 2.2.3. Solutions were again sought for 6 and 8 joints; however, the optimal solutions were found to be identical to the solutions for 5 and 7 joints respectively. This demonstrates that the lack of a symmetrical optimal solution, a characteristic previously noted in the solutions of truss optimization problems with discrete cross sections, is also a characteristic of the problem with continuous cross sections when limits are imposed on the numbers of joints.

Results for various numbers of joints are given in Table 4 and Fig. 15, with further details provided in Online Resource 3. The constraints (5b) (to prevent ‘crossover joints’) and (6b) (to include ‘crossover joints’ in the total number of joints to be limited) have both been tested. When ‘crossover joints’ are not permitted, only structures with up to 17 joints can be identified; results in the range 17 < η < 45 can only be identified by allowing ‘crossover joints’ and explicitly including them in the total limit.

Fig. 15

Spanning example: results with limited numbers of joints (Volume shown as percentage above theoretical minimum volume. Forms shown are after MILP and GO, with symmetrical solutions required. Results preventing crossover joints are shown only where they differ from the result of counting the crossover joints)

The problem of including the ‘crossover joints’ is a more relaxed version of the problem where ‘crossover joints’ are prevented. Therefore, solutions from the MILP problems that take account of crossovers must be at least as good as solutions found when these are prevented. However, the geometry optimization stage is non-linear, and therefore local optima may result, depending on the initial point provided. It can be seen that for the 15 and 17 joint solutions, local optima have been identified; both methods appear to be susceptible to this. However, the volume difference is less than 0.2%, demonstrating that at this point, multiple solutions of similar volume and complexity are available, any one of which would likely be suitable for practical application. Many commercial solvers (e.g. IBM Corp 2015; Gurobi Optimization LLC 2018) provide the ability to record a pool of nearly optimal solutions, which may be of use in addressing this issue.

As a multiple load-case problem, the solutions identified are generally not statically determinate, and therefore there is not a direct relationship between number of members and number of joints. However, Fig. 16 shows that there is still a very strong correlation between the number of members and the number of joints. Therefore, for practical purposes, this method is still likely to produce useful results when structures with few members are desired.

Fig. 16

Spanning example: number of joints and members in solutions where the number of joints has been limited, also showing best fit line. (R² = 0.997)

4.4 Commentary

The numerical examples described here have demonstrated the applicability of the method to single and multiple load case problems in 2D. The method described could also be immediately applied to 3D problems, if crossovers are considered to occur at points where the centrelines of two members intersect exactly, or to within some predefined tolerance. Some modification of the approach described would be necessary in order to prevent the outer faces of members intersecting, taking into account the chosen member cross section form. As is generally the case with layout optimization methods, a greater number of nodes would be required to fill a 3D domain to a similar density compared to a 2D domain, increasing the computational requirements.

The method has proved effective at identifying simple truss structures. However, from a practical point of view, the simplest structure may not be a truss. For example, in the case of the spanning example considered in Section 4.3, a single beam along the base of the domain would generally be considered to provide a simpler, albeit less efficient, solution. When bending is involved the chosen cross-section form needs to be taken into account, and the associated numerical formulation is somewhat more complex. However, many of the principles described herein are still applicable in this case.

5 Conclusions

It was found that the use of dynamically generated lazy constraints can significantly reduce the computational time required to solve layout optimization problems with discrete buildability constraints. Specifically, the use of lazy constraints permitted ‘crossover joints’ to be dealt with in a computationally efficient manner. Improvements in speed of over a factor of 20 were observed for relatively small problems; this difference is likely to increase further as problem size increases. This allows the proposed method to be used for problem sizes that would be intractable using the standard formulation.

Rationalized structures with limited numbers of joints or limited angles between adjacent members have been identified for a range of problems, including those with multiple load-cases, using a two-stage process incorporating a layout optimization stage and a geometry optimization stage. Using this process, results were found to agree with analytically derived results from the literature, suggesting that the proposed separation of topology and geometry/shape optimization is effective, and that MILP solutions are suitable starting points for a non-linear optimization stage.

The rationalized structures were often found to have a volume within a few percent of the corresponding minimum volume Michell structure, whilst being far more feasible to construct. A number of interesting features of these solutions have been observed:

• Symmetrical problems do not always have symmetrical optimal solutions when limits on the numbers of joints are imposed. Therefore, the decision to use symmetry to reduce the computational expense of a problem should be made with care.

• Multiple optimal or near optimal solutions are possible. Many numerical methods, such as geometry optimization, will identify only one of these, although there may be many that would be acceptable for practical use.

• When the angle between adjacent members is limited, ‘branching’ type structures may occur. This may then require the addition of a minimum length constraint to produce practical results.

• When the number of joints is limited, it was found that the number of members in the solution was strongly linked to the number of joints. This may provide a computationally efficient proxy problem.

Appendices

Appendix A: Comparison of problem formulations

Several equivalent formulations are possible to ensure that the flag variables v accurately represent the existence of each node. The method that is used within this paper links the value of v_j to the sum of the members connected to node j using (3a), reproduced here:

$$ \hat{M}v_{j} - {\textstyle\sum}_{i\in J_{j}} a_{i} \geq 0 \qquad j = 1, 2, ..., n $$

(12)

This formulation will be referred to as formulation $\mathcal {A}$.

An alternative formulation,z which may be considered to be more standard in the general integer programming community, is to link the value of v_j to the flag variables of the members connected to node j:

$$ N v_{j} - {\textstyle\sum}_{i\in J_{j}} w_{i} \geq 0 \qquad j = 1, 2, ..., n $$

(13)

In this formulation, the arbitrary large number, $\hat {M}$, is replaced by N, the maximum number of members which will be permitted to connect to any node. This formulation will be referred to as formulation $\mathcal {W}$.

For both $\mathcal {A}$ and $\mathcal {W}$, the remainder of the formulation is as described in Section 2.2. The two formulations produce identical solutions; however, the computational requirements may differ.

To investigate this, both formulations have been used to test the Michell cantilever problem with a limit imposed on the number of joints. Full results using form $\mathcal {A}$ are given in Table 2. A comparison of the speed of the two formulations is given in Table 5.

Table 5 Speed comparison between formulations for defining the node flag variables, v

It can be seen that formulation $\mathcal {A}$ takes roughly half the time to solve the problems compared to formulation $\mathcal {W}$. This is as expected if the characteristics of the two formulations prior to the addition of any lazy constraints is considered. Formulation $\mathcal {A}$ initially begins with all the member flags, w, unconstrained; i.e., they may all be set equal to 1 without making any potential solution infeasible. It only becomes necessary to begin to branch on any variable w_i once the member i is part of an added crossover constraint.

In contrast, formulation $\mathcal {W}$ couples all integer variables from the outset, leading to a much more challenging initial problem. This outweighs the potential benefits of eliminating $\hat {M}$.

Formulation $\mathcal {A}$ has therefore been used to generate all results contained in the main body of the present paper.

Note that the findings in this section apply only to problems where the number of joints is limited, as limiting the angle between members does not require the presence of node flags, v_j.

Appendix B: Full problem statements

For clarity, full problem statements for the problems solved in this paper are given here. Symbols are as defined in the main body of the paper, and are also summarized in Table 6. Firstly, the problem to restrict the number of joints in a solution, whilst preventing crossover nodes, is given by:

$$ \begin{array}{@{}rcl@{}} \text{minimize } V &=& \mathbf{l}^{T}\mathbf{a} \end{array} $$

(14a)

$$ \begin{array}{@{}rcl@{}} \text{subject to } (\mathbf{Bq}_{k} &=& \mathbf{f}_{k} )_{\forall k} \end{array} $$

(14b)

$$ \begin{array}{@{}rcl@{}} (\sigma_{T}\mathbf{a} -\mathbf{q}_{k} &\geq& 0 )_{\forall k} \end{array} $$

(14c)

$$ \begin{array}{@{}rcl@{}} (\sigma_{C}\mathbf{a} +\mathbf{q}_{k} &\geq& 0 )_{\forall k} \end{array} $$

(14d)

$$ \begin{array}{@{}rcl@{}} M\mathbf{w} - \mathbf{a} &\geq& 0 \end{array} $$

(14e)

$$ \begin{array}{@{}rcl@{}} \hat{M}v_{j} - \sum\limits_{i\in J_{j}} a_{i} &\geq& 0 \qquad j = 1, 2, ..., n \end{array} $$

(14f)

$$ \begin{array}{@{}rcl@{}} \sum\limits^{n}_{j=1} v_{j} &\leq& \eta \end{array} $$

(14g)

$$ \begin{array}{@{}rcl@{}} (w_{h} + w_{i} &\leq& 1)_{\forall \{h,i\} \in X} \end{array} $$

(14h)

$$ \begin{array}{@{}rcl@{}} \mathbf{a} &\geq& 0 \end{array} $$

(14i)

$$ \begin{array}{@{}rcl@{}} w_{i} &\in& \{0,1\} \qquad i= 1, 2, ..., m \end{array} $$

(14j)

$$ \begin{array}{@{}rcl@{}} v_{j} &\in& \{0,1\} \qquad j = 1, 2, ..., n \end{array} $$

(14k)

Table 6 Symbols used in problem statements

The problem initially supplied to the solver is as above but excluding the constraints of (14h), which are generated as required during the running of the solver.

The problem to count ‘crossover joints’ as contributing to the limiting number of joints is fully stated as:

$$ \begin{array}{@{}rcl@{}} \text{minimize } V &=& \mathbf{l}^{T}\mathbf{a} \end{array} $$

(15a)

$$ \begin{array}{@{}rcl@{}} \text{subject to } (\mathbf{Bq}_{k} &=& \mathbf{f}_{k} )_{\forall k} \end{array} $$

(15b)

$$ \begin{array}{@{}rcl@{}} (\sigma_{T}\mathbf{a} -\mathbf{q}_{k} &\geq &0 )_{\forall k} \end{array} $$

(15c)

$$ \begin{array}{@{}rcl@{}} (\sigma_{C}\mathbf{a} +\mathbf{q}_{k} &\geq &0 )_{\forall k} \end{array} $$

(15d)

$$ \begin{array}{@{}rcl@{}} M\mathbf{w} - \mathbf{a} &\geq& 0 \end{array} $$

(15e)

$$ \begin{array}{@{}rcl@{}} \hat{M}v_{j} - \sum\limits_{i\in J_{j}} a_{i} &\geq &0 \qquad j = 1, 2, ..., n \end{array} $$

(15f)

$$ \begin{array}{@{}rcl@{}} \sum\limits^{n}_{j=1} v_{j} + \sum\limits^{b}_{g=1} \bar{v}_{g} &\leq& \eta \end{array} $$

(15g)

$$ \begin{array}{@{}rcl@{}} (w_{h} + w_{i} - \bar{v} &\leq& 1 )_{\forall h,i \in X} \end{array} $$

(15h)

$$ \begin{array}{@{}rcl@{}} \mathbf{a} &\geq& 0 \end{array} $$

(15i)

$$ \begin{array}{@{}rcl@{}} w_{i} &\in& \{0,1\} \qquad i= 1, 2, ..., m \end{array} $$

(15j)

$$ \begin{array}{@{}rcl@{}} v_{j} &\in& \{0,1\} \qquad j = 1, 2, ..., n \end{array} $$

(15k)

$$ \begin{array}{@{}rcl@{}} \bar{v}_{g} &\in& \{0,1\} \qquad j = 1, 2, ..., b \end{array} $$

(15l)

When implemented using lazy constraints, the constraints of (15h) are omitted from the initially provided problem, and generated generated as required during the running of the solver. In addition, b may be reduced to a value less than the total number of potential crossover points.

The problem of eliminating small angles between members can be stated as:

$$ \begin{array}{@{}rcl@{}} \text{minimize } V &=& \mathbf{l}^{T}\mathbf{a} \end{array} $$

(16a)

$$ \begin{array}{@{}rcl@{}} \text{subject to } (\mathbf{Bq}_{k} &=& \mathbf{f}_{k} )_{\forall k} \end{array} $$

(16b)

$$ \begin{array}{@{}rcl@{}} (\sigma_{T}\mathbf{a} -\mathbf{q}_{k} &\geq& 0 )_{\forall k} \end{array} $$

(16c)

$$ \begin{array}{@{}rcl@{}} (\sigma_{C}\mathbf{a} +\mathbf{q}_{k} &\geq& 0 )_{\forall k} \end{array} $$

(16d)

$$ \begin{array}{@{}rcl@{}} M\mathbf{w} - \mathbf{a} &\geq& 0 \end{array} $$

(16e)

$$ \begin{array}{@{}rcl@{}} (w_{h} + w_{i} &\leq& 1)_{\forall \{h,i\} \in D} \end{array} $$

(16f)

$$ \begin{array}{@{}rcl@{}} \mathbf{a} &\geq& 0 \end{array} $$

(16g)

$$ \begin{array}{@{}rcl@{}} w_{i} &\in& \{0,1\} \qquad i= 1, 2, ..., m \end{array} $$

(16h)

When implemented using lazy constraints, the problem is initially provided to the solver omitting constraints (16f), which are generated as required during the running of the solver.

Appendix C: Derivation of global solutions for simple cantilever problem

1.1 C.1 Minimum volume solution

To provide a global solution for validation, a simple problem is considered. This consists of 2 load-cases denoted as P₁ and P₂. These each contain a single point load, which are both applied at the point with coordinates (d, 0), and with the same magnitude, Q. The two loads are applied orthogonally, and the load in P₁ is at an angle of 𝜃 to the horizontal (Fig. 17a, b), cases where $0\leq \theta \leq \frac {\pi }{2}$ will be considered. Two special cases of this, with 𝜃 = 0 and $\theta = \frac {\pi }{4}$, were studied by Rozvany et al. (2014).

First the component load-cases are calculated; the sum component load-case²$\mathbf {P}^{*}_{1} = (\mathbf {P}_{2} + \mathbf {P}_{1})/\sqrt {2}$ contains a point load of magnitude Q and inclined at an angle of $\theta -\frac {\pi }{4}$ (Fig. 17c). The difference component $\mathbf {P}^{*}_{2} = (\mathbf {P}_{2} - \mathbf {P}_{1})/\sqrt {2}$ is also of magnitude Q and inclined at an angle of $\theta - \frac {3\pi }{4}$ (Fig. 17d).

The solution for $\mathbf {P}^{*}_{1}$ consists of a single member inclined at the same angle as the force (Fig. 17e), i.e. connecting to the support at $y = -d\tan (\theta -\frac {\pi }{4})$. The member has an internal force of − Q. The length of the member is $\frac {d}{\cos \limits (\theta -\frac {\pi }{4})}$. Therefore, the component volume is

$$ V^{*}_{1} = \frac{Qd}{\sigma\cos(\theta-\frac{\pi}{4})} $$

(17)

Fig. 17

Simple cantilever: problem specification and component load-cases, a–b, imposed load-cases; c–d, component load-cases; e–f component solutions with unlimited complexity; g–h final optimal solution with unlimited complexity; i–j component solutions with only 2 members. k–l final solution with only 2 members

For $\mathbf {P}^{*}_{2}$, the external load is again of magnitude Q and its direction varies by $\frac {\pi }{4}$ either side of vertical, the solution to this was given my Rozvany et al. (1995). This consists of 2 symmetrical, orthogonal members, which connect to the support at heights y = ±d (Fig. 17f). The length of each member is $d\sqrt {2}$. The internal force in the top member is $Q\sin \limits \theta$ and in the bottom member is $Q\cos \limits \theta$. Therefore, the volume in this component is

$$ V^{*}_{2} = \frac{Qd}{\sigma}\sqrt{2}\cos\theta + \sqrt{2}\sin\theta $$

(18)

By the superposition principle, these two component solutions are combined to give the optimal design (Fig. 17g–h). The total volume is given by:

$$ V = \frac{V^{*}_{1} + V^{*}_{2}}{\sqrt{2}} =\frac{Qd}{\sigma}\left( \frac{1}{\sqrt{2}\cos(\theta-\frac{\pi}{4})} + \cos\theta + \sin\theta\right) $$

(19)

As there are no co-incident members, the final member areas are given by dividing the component areas by $\sqrt {2}$.

Fig. 18

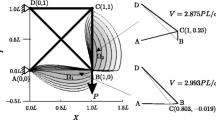
Simple cantilever: volume of two member truss with for 0 ≤ y_A ≤ 2d and 0 ≤ y_B ≤ 2d for various force inclinations, 𝜃. (The solid region shows where ${q_{1}^{A}}<0, {q_{1}^{B}}<0, {q_{2}^{A}}<0$ and ${q_{2}^{B}}>0$, the blue cross shows the globally minimum volume/design to resist each set of forces)

1.2 C.2 Limited complexity solution

1.2.1 C.2.1 Internal member forces

It is now required to find the minimum volume solution for the same problem, but with the additional constraint that only 3 joints are permitted. This permits only a single topology; two members reaching from the point of application of the forces to the support line. Therefore, all potential solutions to this problem can be enumerated using 2 degrees of freedom, the vertical locations of the two support points, which will be denoted y_A and y_B (Fig. 17i-j).

The two component load-cases are identical to the previous section. The lengths of the members are given by $l_{A} = \sqrt {{y_{A}^{2}}+d}$ and $l_{B} = \sqrt {{y_{B}^{2}}+d}$ respectively.

The member forces are found from equilibrium equations at the loaded point. In $\mathbf {P}^{*}_{1}$ the member forces in members A and B are

$$ {q^{A}_{1}} = Q\frac{(\sin(\frac{\pi}{4}+\theta)y_{B}-\cos(\frac{\pi}{4}+\theta)d)\sqrt{{y_{A}^{2}}+1}}{d(y_{A}-y_{B})} $$

(20)

$$ {q^{B}_{1}} = Q\frac{(-\sin(\frac{\pi}{4}+\theta)y_{A}+\cos(\frac{\pi}{4}+\theta)d)\sqrt{{y_{B}^{2}}+1}}{d(y_{A}-y_{B})} $$

(21)

In $\mathbf {P}^{*}_{2}$, the member forces are

$$ {q^{A}_{2}} = -Q\frac{(-\cos(\frac{\pi}{4}+\theta)y_{B}-\sin(\frac{\pi}{4}+\theta)d)\sqrt{{y_{A}^{2}}+1}}{d(y_{A}-y_{B})} $$

(22)

$$ {q^{B}_{2}} = -Q\frac{(\cos(\frac{\pi}{4}+\theta)y_{A}+\sin(\frac{\pi}{4}+\theta)d)\sqrt{{y_{B}^{2}}+1}}{d(y_{A}-y_{B})} $$

(23)

The superposition principle is again used to find the overall design (Fig. 17k, l), and define the total volume as:

$$ V = \frac{V^{*}_{1} + V^{*}_{2}}{\sqrt{2}} = \frac{(|{q^{A}_{1}} l_{A}| + |{q^{B}_{1}} l_{B}|) + (|{q^{A}_{2}} l_{A}| + |{q^{B}_{2}} l_{B}|)}{\sigma\sqrt{2}} $$

(24)

By inspection of the graph for all values of $0\leq \theta \leq \frac {\pi }{2}$ (see examples in Fig. 18), it can be seen that the minimum volume solution falls within or on the border of the region where the member forces in $\mathbf {P}^{*}_{1}$ are in the same direction, and the member forces in $\mathbf {P}^{*}_{2}$ are in opposing directions. Based on this, the expression for V is re-written without using the absolute value operator, for the purposes of this derivation using the sign convention that tensile stresses are negative.

$$ V = \frac{-{q^{A}_{1}} l_{A} - {q^{B}_{1}} l_{B} - {q^{A}_{2}} l_{A} + {q^{B}_{2}} l_{B}}{\sqrt{2}} $$

(25)

Additionally, the cusps of the plots in Fig. 18 must be considered; these define the limits of the region within which (25) is valid. They are given by:

$$ \begin{array}{@{}rcl@{}} {q_{1}^{A}} &\leq& 0 \qquad\qquad {q_{2}^{A}} \leq 0 \end{array} $$

(26)

$$ \begin{array}{@{}rcl@{}} {q_{1}^{B}} &\leq& 0 \qquad\qquad {q_{2}^{B}} \geq 0 \end{array} $$

(27)

For a given value of 𝜃, these equations each define a vertical plane. Equations (26) are planes with constant y_B, and (27) are planes with constant y_A.

1.2.2 C.2.2 Optimal values in each region

The equations which describe the optimal solution vary depending upon the value of 𝜃. Three regions are possible, and each of these are considered separately.

When 𝜃 > 𝜃₂ (where 𝜃₂ is a critical value, approximately equal to 0.9), the minimal value is found on the cusp of the volume function defined by ${q_{1}^{A}} = 0$. The optimal point lies on the minima of the cusp line, i.e. where the partial derivative $V_{y_{A}} = 0$. In this region, the optimal values of y_A and y_B, and the optimal volume V are given by:

$$ \begin{array}{@{}rcl@{}} y_{A} &=& \frac{1}{\tan(\frac{\pi}{4}+\theta)} + \frac{\sqrt{2}}{\sin(\frac{\pi}{4}+\theta)} \end{array} $$

(28a)

$$ \begin{array}{@{}rcl@{}} y_{B} &=& \frac{-1}{\tan(\frac{\pi}{4}+\theta)} \end{array} $$

(28b)

$$ \begin{array}{@{}rcl@{}} V &=& \frac{\sqrt{2} \left( \sin (\theta+\frac{\pi}{4}) +2\sqrt{2} +3\cos(\theta+\frac{\pi}{4} ) \right) }{ 2 \sin^{2} (\theta+\frac{\pi}{4}) } \end{array} $$

(28c)

Similarly, for values of 𝜃 ≤ 𝜃₁ (where 𝜃₁ ≈ 0.65), the minimal value is found on the intersection of $V_{y_{B}} = 0$ and ${q_{1}^{B}} = 0$. This gives

$$ \begin{array}{@{}rcl@{}} y_{A} &=& \frac{1}{\tan(\frac{\pi}{4}+\theta)} \end{array} $$

(29a)

$$ \begin{array}{@{}rcl@{}} y_{B} &=& \frac{-1}{\tan(\frac{\pi}{4}+\theta)} + \frac{\sqrt{2}}{\sin(\frac{\pi}{4}+\theta)} \end{array} $$

(29b)

$$ \begin{array}{@{}rcl@{}} V &=& \frac{\sqrt{2} \left( \sin (\theta+\frac{\pi}{4}) +2\sqrt{2} -3\cos(\theta+\frac{\pi}{4} ) \right) }{ 2 \sin^{2} (\theta+\frac{\pi}{4}) } \end{array} $$

(29c)

In the inner region, where 𝜃₁ ≤ 𝜃 ≤ 𝜃₂, the minimum volume structure is found at the local minima of (25), i.e. where $V_{y_{A}} = 0$ and $V_{y_{B}} = 0$. In this region, values for pairs of y_A and y_B are given by the equation:

$$ \begin{array}{lllllll} 0=& & & & & {y_{B}^{4}} \\ & & &-2{y_{A}^{2}}{y_{B}^{3}} &+2y_{A}{y_{B}^{3}} & \\ & &-2{y_{A}^{3}}{y_{B}^{2}}& &+4y_{A}{y_{B}^{2}} & \\ & &+2{y_{A}^{3}}y_{B} &+4{y_{A}^{2}}y_{B} &+4y_{A}y_{B} &-2y_{B} \\ &+{y_{A}^{4}}& & &-2y_{A} & -2 \end{array} $$

(30)

To calculate the corresponding value of 𝜃 for such a pair, the values of y_A and y_B are simply substituted into either $V_{y_{A}} = 0$ or $V_{y_{B}} = 0$. For this region, it is quite difficult to begin with a value of 𝜃 and calculate the optimal values of y_A and y_B.

1.2.3 C.2.3 Boundaries between regions

The final task is to establish the boundary values, 𝜃₁ and 𝜃₂ between the outer and inner regions. To do this, some points of interest must first be defined. The point C is defined as the minimum volume point lying on the cusp ${q_{1}^{A}}=0$, this is the point given by the (28c), and is the optimal value when 𝜃 ≥ 𝜃₂.

Next, the stationary points of (25) are considered, these lie on the line defined by (30). There are at most 2 stationary points in the region in which this function is valid. To characterize these, the discriminant of this function, ${\Delta } = V_{y_{A}y_{A}} V_{y_{B}y_{B}} - (V_{y_{A}y_{B}})^{2}$ is calculated. The stationary point at which Δ > 0 is defined as point M, this is a local minima, and additionally represents the optimal value in the central region (𝜃₁ ≤ 𝜃 ≤ 𝜃₂). The stationary point where Δ < 0 is defined as S, this is a saddle point of the function. The critical value 𝜃₂ is the point at which the optimal value switches from point C to point M.

Table 7 gives values of y_A,y_B and V for these three points at notable values of 𝜃. Additionally it provides illustrations of the topography of the volume function in the vicinity of C, M and P; these illustrations show the approximate profile the volume function at the bottom of a ‘valley’ which runs roughly parallel to the plane y_A + y_B = 1. This valley may also be observed in the plots in Fig. 18, particularly when $\theta =\frac {\pi }{4}$

Table 7 Simple cantilever: behaviour of volume function in vicinity of optimal values for force inclinations in the vicinity of θ₂. (Point M is a local minimum, point S is a saddle point, and point C is the minimum value along the cusp at line ${q_{1}^{A}} =0$. Values in boldface are the optimal points for that problem, note that when θ = 0.90068 two equally optimal solutions exist)

When 𝜃 < 0.900110, the point S is outside of the valid region for (25). Point S enters the valid region when the relations from (28c) are substituted into (30), giving 𝜃 = 0.900110. Here, points S and C are co-incident and have a volume which is 0.005% greater than the optimal value at M.

At the point where $V_{y_{A}} = 0$, $V_{y_{B}} = 0$ and Δ = 0, a single degenerate stationary point is formed as points S and M become co-incident. This occurs when 𝜃 = 0.900874, and the volume at points S and M is 0.0008% higher than the volume at C. Therefore the value 𝜃₂, at which points M and C are equally optimal must lie in the region 0.900110 ≤ 𝜃₂ ≤ 0.900874.

The value of 𝜃₂ is found at the point where $V_{y_{A}} = 0$, $V_{y_{B}}=0$ and the right-hand side of (28c) is equal to the right-hand side of (25) (where the values of y_A and y_B refer to the point M). From this, it is found that 𝜃₂ = 0.9006836427. By a similar logic, 𝜃₁ = 0.6701126839.

It has been shown that within the the region 0.900110 ≤ 𝜃 ≤ 0.900874, the range of volumes is small (< 0.005%) over a wide range of possible values for y_A and y_B (of up to 0.1d). This may cause problems for numerical methods if accuracy levels are not set high enough. Additionally, when 𝜃 = 𝜃₁ or 𝜃₂, two distinct solutions are equally optimal.