Abstract
This paper presents an approach to design composite panels via multiple stacking sequence tables (SST) such that the continuity constraints between adjacent regions are maintained. Traditional SST methods determine all the stacking sequences with only one SST, but this simplification limits the design option space. To increase the design freedom, this research utilizes multiple SSTs to blend the stacking sequences of a laminated structure. In the design process of the proposed approach, the monotonicity property of predicted laminate thicknesses is employed to determine the number of SSTs, and an SST rebuilding method is developed to satisfy the blending constraints. In the implementation of the simulated annealing algorithm for solving the optimal design problem, an SST difference code is introduced to represent feasible solutions, and a particular neighborhood structure is proposed to sufficiently explore the solutions in design space. Finally, the 18-region benchmark problem is chosen to validate the efficiency and accuracy of the proposed method. The results reveal that, compared with other existing methods, the proposed method can generate manufacturable solutions with lower weights under the symmetry and balance constraints.































Similar content being viewed by others
References
Bakis CE, Bank LC, Brown VL, Cosenza E, Davalos JF, Lesko JJ et al (2002) Fiber-reinforced polymer composites for construction: state-of-the-art review. J Compos Constr 6:73–87. https://doi.org/10.1061/(ASCE)1090-0268(2002)6:2(73)
Liu Y, Zwingmann B, Schlaich M (2015) Carbon fiber reinforced polymer for cable structures: a review. Polymers 7(10):2078–2099. https://doi.org/10.3390/polym7101501
Patel KA, Chaudhary S, Nagpal AK (2016) An element incorporating cracking for reinforced concrete skeletal structures at service load. Adv Struct Eng 20:1257–1276. https://doi.org/10.1177/1369433216673642
Haftka RT, Walsh JL (1992) Stacking-sequence optimization for buckling of laminated plates by integer programming. AIAA J 30(3):814–819
Kassapoglou C (2010) Design and analysis of composite structures: with applications to aerospace structures. John Wiley and Sons, Ltd, West Sussex. https://doi.org/10.1002/9781118536933
Gibson RF (1994) Principles of composite material mechanics. 4rd. CRC Press, Boca Raton
Bushnell D (1985) Computerized buckling analysis of shells. Kluwer Academic Publishers, London. https://doi.org/10.1007/978-94-009-5063-4
Massard TN (1984) Computer sizing of composite laminates for strength. J Reinf Plast Comp 3:300–345. https://doi.org/10.1177/073168448400300405
Martin PMJW (2007) Optimum design of anisotropic sandwich panels with thin faces. Eng Optimiz 11:3–12. https://doi.org/10.1080/03052158708941031
Huang C, Kröplin B (1995) On the optimization of composite laminated plates. Eng Comput 12:403–414. https://doi.org/10.1108/02644409510799712
Song SR, Hwang W, Park HC, Han KS (1995) Optimum stacking sequence of composite laminates for maximum strength. Mech Compos Mater 31:290–300
Mohite PM, Upadhyay CS (2015) Adaptive finite element based shape optimization in laminated composite plates. ComputStruct 153:19–35. https://doi.org/10.1016/j.compstruc.2015.02.020
Akbulut M, Sonmez FO (2011) Design optimization of laminated composites using a new variant of simulated annealing. Comput Struct 89:1712–1724. https://doi.org/10.1016/j.compstruc.2011.04.007
Jiang C, Han X, Liu GP (2008) Uncertain optimization of composite laminated plates using a nonlinear interval number programming method. Comput Struct 86:1696–1703. https://doi.org/10.1016/j.compstruc.2008.02.009
Omkar SN, Mudigere D, Naik GN, Gopalakrishnan S (2008) Vector evaluated particle swarm optimization (VEPSO) for multi-objective design optimization of composite structures. Comput Struct 86:1–14. https://doi.org/10.1016/j.compstruc.2007.06.004
Graesser DL, Zabinsky ZB, Tuttle ME, Kim GI (1991) Designing laminated composites using random search techniques. Compos Struct 18:311–325
Xu Y, Zhu J, Wu Z et al (2018) A review on the design of laminated composite structures: constant and variable stiffness design and topology optimization. Adv Compos Hybrid Mater. https://doi.org/10.1007/s42114-018-0032-7
Ghiasi H, Fayazbakhsh K, Pasini D, Lessard L (2010) Optimum stacking sequence design of composite materials. Part II: variable stiffness design. Compos Struct 93:1–13
Soremekun G, Gürdal Z, Kassapoglou C, Toni D (2002) Stacking sequence blending of multiple composite laminates using genetic algorithms. Compos Struct 56:53–62. https://doi.org/10.1016/S0263-8223(01)00185-4
Adams DB, Watson LT, Gürdal Z (2003) Optimization and blending of composite laminates using genetic algorithms with migration. Mech Adv Mater Struc 10:183–203. https://doi.org/10.1080/15376490306741
He K, Hoa SV, Ganesan R (2000) The study of tapered laminated composite structures: a review. Compos Sci Technol 60:2643–2657. https://doi.org/10.1016/S0266-3538(00)00138-X
Liu B, Haftka RT (2001) Composite wing structural design optimization with continuity constraints. In: 42nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Material Conference, Seattle. https://doi.org/10.2514/6.2001-1205
Kennedy GJ, Martins JRRA (2013) A laminate parameterization technique for discrete ply-angle problems with manufacturing constraints. Struct Multi discip Optim 48:379–393. https://doi.org/10.1007/s00158-013-0906-9
Kristinsdottir BP, Zabinsky ZB, Tuttle ME, Neogi S (2001) Optimal design of large composite panels with varying loads. Compos Struct 51:93–102. https://doi.org/10.1016/S0263-8223(00)00128-8
Adams DB, Watson LT, Gürdal Z, Anderson-Cook CM (2004) Genetic algorithm optimization and blending of composite laminates by locally reducing laminate thickness. Adv Eng Softw 35:35–43. https://doi.org/10.1016/j.advengsoft.2003.09.001
Irisarri FX, Lasseigne A, Leroy FH, Le Riche R (2014) Optimal design of laminated composite structures with ply drops using stacking sequence tables. Compos Struct 107:559–569. https://doi.org/10.1016/j.compstruct.2013.08.030
Yang J, Song B, Zhong X, Jin P (2016) Optimal design of blended composite laminate structures using ply drop sequence. Compos Struct 135:30–37. https://doi.org/10.1016/j.compstruct.2015.08.101
Zein S, Madhavan V, Dumas D, Ravier L, Yague I (2016) From stacking sequences to ply layouts: An algorithm to design manufacturable composite structures. Compos Struct 141:32–38. https://doi.org/10.1016/j.compstruct.2016.01.027
Zein S, Colson B, Grihon S (2011) A primal-dual backtracking optimization method for blended composite structures. Struct Multi discip Optim 45:669–680. https://doi.org/10.1007/s00158-011-0716-x
Zein S, Basso P, Grihon S (2014) A constraint satisfaction programming approach for computing manufacturable stacking sequences. Comput Struct 136:56–63. https://doi.org/10.1016/j.compstruc.2014.01.016
Zein S, Bruyneel M (2015) A bilevel integer programming method for blended composite structures. Adv Eng Softw 79:1–12. https://doi.org/10.1016/j.advengsoft.2014.08.008
Irisarri F-X, Peeters DMJ, Abdalla MM (2016) Optimisation of ply drop order in variable stiffness laminates. Compos Struct 152:791–799. https://doi.org/10.1016/j.compstruct.2016.05.076
Jing Z, Sun Q, Silberschmidt VV (2016a) A framework for design and optimization of tapered composite structures. Part I: from individual panel to global blending structure. Compos Struct 154:106–128. https://doi.org/10.1016/j.compstruct.2016.05.095
Tsuzuki MSG, Martins TC (2014) Simulated annealing : strategies, potential uses and advantages. Nova Science Publishers, Incorporated, New York
An H, Chen S, Huang H (2015) Improved genetic algorithm with two-level approximation method for laminate stacking sequence optimization by considering engineering requirements. Math Probl Eng 2015:1–13. https://doi.org/10.1155/2015/595484
Seresta O, Abdalla M, Gurdal Z (2009) A genetic algorithm based blending scheme for design of multiple composite laminates. In: 50th AIAA/ASME/ASCE/AHS/ASC structures, structural dynamics and materials conference, Palm Springs, California. https://doi.org/10.2514/6.2009-2699
Liu D, Toroporov VV, Querin OM, Barton DC (2011) Bilevel optimization of blended composite wing panels. J Aircraft 48:107–118. https://doi.org/10.2514/1.c000261
Liu D, Toropov VV (2013) A lamination parameter-based strategy for solving an integer-continuous problem arising in composite optimization. Comput Struct 128:170–174. https://doi.org/10.1016/j.compstruc.2013.06.003
Hao P, Yuan X, Liu H, Wang B, Liu C, Yang D et al (2017) Isogeometric buckling analysis of composite variable-stiffness panels. Compos Struct 165:192–208. https://doi.org/10.1016/j.compstruct.2017.01.016
Fan H-T, Wang H, Chen X-H (2016) An optimization method for composite structures with ply-drops. Compos Struct 136:650–661. https://doi.org/10.1016/j.compstruct.2015.11.003
Ijsselmuiden ST, Abdalla MM, Seresta O, Gürdal Z (2009) Multi-step blended stacking sequence design of panel assemblies with buckling constraints. Compos Part B-eng 40:329–336. https://doi.org/10.1016/j.compositesb.2008.12.002
Park CH, Lee WI, Han WS, Vautrin A (2008) Improved genetic algorithm for multidisciplinary optimization of composite laminates. Comput Struct 86:1894–1903. https://doi.org/10.1016/j.compstruc.2008.03.001
Jing Z, Sun Q, Silberschmidt VV (2016b) Sequential permutation table method for optimization of stacking sequence in composite laminates. Compos Struct 141:240–252. https://doi.org/10.1016/j.compstruct.2016.01.052
Acknowledgments
The authors would like to thank Mr. Kuan Fan for his support in programming work. In addition, we thank the anonymous reviewers for their comments and suggestions, which are valuable for improving the manuscript.
Funding
This project is supported by the National Natural Science Foundation of China (Grant Nos. 51775202 and 51475186).
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible Editor: Ji-Hong Zhu
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1. Calculation of buckling load factor
In this work, buckling of symmetrical and balanced laminates, simply supported on boundaries, under normal compressions (Fx,Fy) is analyzed. The formulation of buckling load factor λcb is as follows:
Here, m and n are the numbers of half wavelengths along x and y directions respectively, a and b are the length and width of region respectively, and D11, D12, D66, and D22 are bending stiffness obtained by classical lamination theory. The same formulation is used in (Soremekun et al. 2002; Adams et al. 2004; Irisarri et al. 2014; Yang et al. 2016; Jing et al. 2016a; Seresta et al. 2009; Fan et al. 2016; Ijsselmuiden et al. 2009; Park et al. 2008).
Appendix 2. Laminate thickness prediction
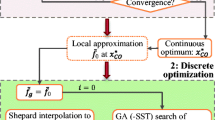
According to Eq. (4), λcb is a linear function of bending stiffness parameters, and reaches an extreme value with the same ply orientation at all stacking positions (Jing et al. 2016b). The multi-panel sequential permutation table (MSPT) method was developed in (Jing et al. 2016a, b) to predict the minimum thickness without considering the blending requirement. The algorithm for obtaining the minimum-thickness distribution with MSPT is summarized in Algorithm A1.

Rights and permissions
About this article
Cite this article
Zeng, J., Huang, Z., Chen, Y. et al. A simulated annealing approach for optimizing composite structures blended with multiple stacking sequence tables. Struct Multidisc Optim 60, 537–563 (2019). https://doi.org/10.1007/s00158-019-02223-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00158-019-02223-9