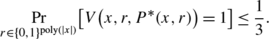Enhancements of Trapdoor Permutations

Abstract

We take a closer look at several enhancements of the notion of trapdoor permutations. Specifically, we consider the notions of enhanced trapdoor permutation (Goldreich, Foundation of Cryptography: Basic Applications, 2004) and doubly enhanced trapdoor permutation (Goldreich, Computational Complexity: A Conceptual Perspective, 2011) as well as intermediate notions (Rothblum, A Taxonomy of Enhanced Trapdoor Permutations, 2010). These enhancements arose in the study of Oblivious Transfer and NIZK, but they address natural concerns that may arise also in other applications of trapdoor permutations. We clarify why these enhancements are needed in such applications, and show that they actually suffice for these needs.

1 Introduction

This article surveys and studies two enhancements of the notion of trapdoor permutations (TDP). Our exposition clarifies how these enhancements of TDP emerge in two central applications, and shows that these enhancements actually suffice for the corresponding applications. As is often the case when studying known definitions, we find it useful to start with a review of the historical roots of the various definitions.

1.1 A historical perspective

The notion of trapdoor permutations was formulated by Yao [25] as a sufficient condition for the construction of secure public-key encryption schemes (put forward by Diffie and Hellman [7] and rigorously defined by Goldwasser and Micali [19]). Indeed, building on the ideas of [6, 19], Yao [25] showed that any collection of trapdoor permutations can be used to construct a secure public-key encryption scheme. The abstract notion of trapdoor permutations was inspired by the RSA and Rabin collections (cf. [22, 23], resp.), which still serve as the archetypical examples (see Appendix B).

Loosely speaking, the notion of trapdoor permutations (TDP) refers to a collection of permutations that are easy to sample and have domains that are easy to sample from (when given the description of the permutation). The main requirements are that these permutations are easy to evaluate, easy to invert when given a suitable trapdoor, but hard to invert when only given the description of the permutation (but not the trapdoor).

The minimal requirements regarding the sampleability of permutations and their domains were glossed over when constructing secure public-key encryption schemes (both in [19, 25] and [5] (cf. [14, Sect. 5.3.4])). Consequently, in later years, researchers have tended to think of TDP in terms of an idealized case in which sampling permutations as well as elements in their domains is trivial (i.e., the sampling algorithms just output their random coin tosses).¹ This tendency seems to be the source of the flaws that followed.

Specifically, trapdoor permutations were suggested as a basis for the construction of Oblivious Transfer (OT) protocols [8] and general Non-Interactive Zero-Knowledge proof (NIZK) systems [9]. In both cases, an idealized TDP suffices for these constructions, and this promoted a false belief that a general TDP would also do. (We note that the difference between idealized TDP and general TDP is crucial, because no candidate for an idealized TDP is known, whereas a general TDP can be constructed based, say, on factoring.)

The first difficulty was discovered by Bellare and Yung [2], who observed that the soundness of the NIZK construction of [9] relies on the hypothesis that the set of permutations in the collection is easily recognizable (which is trivial in the idealized case). Since this hypothesis does not hold in the known candidate TDPs,² Bellare and Yung relaxed the hypothesis to requiring that membership in the aforementioned set (or actually just being almost 1-1) can be demonstrated by a special-purpose NIZK, and showed that the relaxed hypothesis can be met for all known candidates [2]. Interestingly, their presentation avoids the problem of sampling in the domains of the various permutations, by postulating that these domains consist of all strings of a specific length (which, in turn, can be easily determined by the description of the permutation). We note that all known candidates can be converted to such a form. Still, there is a difference between the latter form (of trivially sampleable domains) and the general case, and the rest of our discussion refers to that difference.

The difference between TDP with trivially sampleable domains and general TDP was first observed by Goldreich [12], when producing a detailed proof of the secure multi-party computation result of [18], which relies on the construction of OT. Specifically, he discovered that the construction of OT outlined in [8, 18], which works when the TDP has trivially sampleable domains, may not be secure when a general TDP is employed, but is secure when using an enhanced notion of a TDP. This enhancement requires that the permutation is hard to invert also when one is given the coins that were used to sample the domain element (rather than merely the domain element itself).

We note that the enhanced notion of hardness-to-invert collapses to the original notion (of hardness-to-invert) in the case that the domain-sampling algorithm is trivial (i.e., the permutation’s domain consists of all strings of a specific length). More generally, this enhancement is insignificant whenever it is easy to invert the domain-sampling algorithm (i.e., given an element in the domain, to sample (uniformly) random coins that cause the domain-sampling algorithm to produce the given element). We also mention that, for the purpose of constructing OT, the enhancement may be avoided if the permutation’s domain is dense (by using a more complex OT construction; cf. [21]).

Turning back to the main thread, we mention that while Goldreich [14, Appendix C.4.1] claimed that the aforementioned enhancement of TDP suffices for constructing general NIZK, Jon Katz raised doubts regarding this claim. These justified doubts led Goldreich [16] to propose the notion of doubly enhanced TDP, and show that this notion does suffice for constructing general NIZK.

Subsequent work by Rothblum [24] showed that the security of a natural extension of the OT protocol of [8, 18] to 1-out-of-k OT for k≥3 also requires the second enhancement (however, a more cumbersome construction may be based solely on the first enhancement). Rothblum [24] also uncovered a taxonomy of notions of TDP, residing between enhanced TDP and doubly enhanced TDP. These intermediate notions will be further discussed in Sect. 6.

To summarize the historical account, we note that the general formulation of TDP was envisioned as the most general and/or minimal formulation of a collection of functions that allows for the construction of secure public-key encryption schemes. This application determined the main requirements (i.e., easy to evaluate, easy to invert when given a suitable trapdoor, but hard to invert when not given the trapdoor), whereas the sampling conditions were stated in the most general form possible (i.e., merely requiring easy sampling of permutations and domain elements). However, the general (and innocent-looking) formulation of the sampling conditions turned out to be a problem when seeking to construct OT and general NIZK based on TDP.

Before proceeding to the next subsection, in which we review these difficulties, we note that these problems are not just intellectual but also affect some of the popular TDP candidates. While we shall offer an abstract presentation (considering general TDP), some readers may find it useful to consider these issues in the context of the RSA or Rabin collections (discussed in Appendix B).

1.2 The Difficulties

The following presentation does not preserve the chronological order (which was followed in Sect. 1.1). Also, we shall only sketch the nature of the difficulties that arise and the way in which they are addressed by the enhancements. Corresponding detailed descriptions appear in later sections.

We shall refer to a collection of the permutations of the form f _α :D _α →D _α , where α is the index (or description) of the permutation f _α , and to two sampling algorithms: (1) an index-sampling algorithm I ₁ that, on input coins s, outputs an index α=I ₁(s); and (2) a domain-sampling algorithm S that, on input an index α and coins r∈{0,1}^|α|, outputs an element in the corresponding domain (i.e., S(α,r)∈D _α ).³ Indeed, the index of the permutation is associated with its description, and the hardness-to-invert condition refers to inverting f _α on y, when α and y are selected by the foregoing sampling algorithms (i.e., α←I ₁(s) and y←S(α,r), where s and r are selected uniformly in {0,1}ⁿ). The idealized case, mentioned in Sect. 1.1, refers to the case that all strings are valid indices and D _α ={0,1}^|α| for every α.

The first difficulty refers to the construction of OT based on TDP. The security of the standard construction of [8] (as well as other applications) relies on the hypothesis that a party knowing α=I ₁(s) and r (which are chosen as above), is unable to invert f _α on S(α,r). Note that this would follow from the hardness-to-invert condition if given (α and) y one can efficiently find a random r such that y=S(α,r). However, there is no reason to assume that such a “reverse-sampling” is feasible in general. Instead, one may define enhanced TDP as TDP that satisfy this enhanced hardness-to-invert condition, and note that the popular candidates for TDP actually yield enhanced TDP. Using any such enhanced TDP allows one to construct an OT protocol.

The second difficulty refers to the soundness of a general NIZK based on TDP. In this setting the prover is supposed to select a random permutation (in the TDP collection) and send its description to the verifier, and the soundness of the proof system relies on the hypothesis that the description sent (i.e., α) indeed refers to an almost 1-1 function (i.e., f _α is almost 1-1). In general, as observed in [2], this hypothesis needs to be tested (by the verifier), and a natural way of doing so is by asking the prover to provide the inverses of the function (i.e., of f _α ) on a sequence of randomly selected domain elements. If we use a general TDP, then the prover is asked to provide the inverses of f _α on S(α,r ₁),…,S(α,r _m ), when given r ₁,…,r _m that are randomly distributed (and are part of the common random string).

The latter proposal brings us to a third difficulty, which refers to the question of whether providing the value of $f_{\alpha}^{-1}(S(\alpha,r))$ for a random r is zero-knowledge. The answer would have been positive if (given α) it were feasible to generate random samples of the form (x,r) such that S(α,r)=f _α (x), since in this case $x=f_{\alpha}^{-1}(S(\alpha,r))$. But, again, this condition may not hold in general, and postulating that it does hold is the content of another enhancement.⁴

The construction of general NIZK based on TDP uses the two aforementioned enhancements: The first enhancement is used in order to argue that, when seeing α and r, the (unrevealed) value of $f_{\alpha}^{-1}(S(\alpha,r))$ remains secret. The second enhancement is used in order to argue that revealing $f_{\alpha}^{-1}(S(\alpha,r))$ for a random r is actually zero-knowledge (w.r.t. a fixed α).

We note that the two difficulties that give rise to the two enhancements of TDP are natural ones, and are likely to arise also in other (sophisticated) applications of TDP. One such application that we show is the construction of public-key encryption (from trapdoor permutations) with the property that ciphertexts can be sampled obliviously from the plaintext.

We also note that the source of both difficulties is that, in general, obtaining an element of D _α may not be computationally equivalent to obtaining the coins that are used to produce this element. This computational equivalence holds only in the special case in which there exists an efficient reversed domain sampler (i.e., a probabilistic polynomial-time algorithm that on input (α,y) outputs a string that is uniformly distributed in {r:S(α,r)=y}). (We mention that adequate implementations and/or variants of the popular candidate collections of trapdoor permutations (e.g., the RSA and Rabin collections) do have efficient reversed domain samplers.)

1.3 The Current Article

This article provides a revised account of the findings in [16, 24]. The focus of the current article is on the notion of TDP and its enhancements. In contrast, the focus of Goldreich [16] is on the application to general NIZK, whereas the starting point of Rothblum [24] is the two enhancements mentioned in Sects. 1.1 and 1.2. In particular, we explore the entire range between general TDP and doubly enhanced TDP, while Rothblum [24] focuses on the range between enhanced TDP and doubly enhanced TDP. We also present an additional application of the aforementioned enhancements in the context of public-key encryption. While we describe both the difficulties and the corresponding security notions with respect to TDP, one may consider the affect on general collections of one-to-one trapdoor functions (of which TDP are a special case). In fact, enhanced versions of trapdoor functions suffice for the three main applications considered in this article: public-key encryption, oblivious transfer and non-interactive zero-knowledge proofs for $\mathcal {NP}$. For more details on TDF and their enhancements see Sect. 7.

We note that [16, 24] did not appeared in a refereed publication before, and the current article should be viewed as a combined journal version of these two works. We view the current article as a hybrid of a survey and a research article, and hope that it will help to clarify the confusion around the various notions of enhanced TDP.

Organization

In Sect. 2 we recall the definition of TDP and present its two aforementioned enhancements. These enhancements were motivated in Sect. 1.2, and these motivations will be detailed in the subsequent sections. In particular, Sect. 3 details how the first enhancement arises out of the construction of 1-out-of-2 OT, whereas Sect. 4 details how the second enhancement arises out of the construction of 1-out-of-3 OT and general NIZK systems. In Sect. 5 we discuss an application of the two enhancements to oblivious sampling of ciphertexts in public-key encryption. In Sect. 6, we consider some intermediate notions of TDP that arise naturally in the foregoing applications. In Sect. 7 we consider the effect of enhancements on general collections of one-to-one trapdoor functions and even more generally on any collection of one-way functions. Appendix B discusses the RSA and Rabin collections, showing that (natural versions of) both collections satisfy both the enhancements.

Notation

We denote by A(x) the output distribution of algorithm A on input x and by A(x;r) the deterministic output of algorithm A on input x and the random string r.

2 Definitions

Collections of finite functions arise naturally in cryptography, and collections of trapdoor permutations are indeed a prime example. For example, the standard presentation of the “RSA function” refers to a collection of permutations, indexed by pairs (N,e), where N is a product of two large primes and e is relatively prime to the order of $Z_{N}^{*}$, and the permutation index by (N,e) has domain Z _N (or $Z_{N}^{*}$). This description presumes that permutations in the collection are easy to select (at random), and uniformly sampling their domain is also easy. Indeed, in general, when talking about a collection of functions, we wish the collection to be “usable” in the sense that (1) it is easy to select function at random in the collection, and (2) it is easy to uniformly sample an element in the domain of a given function. These two conditions appear in the standard definition of a collection of trapdoor permutations, reproduced next.

Standard Trapdoor Permutations

Recall that a collection of trapdoor permutations, as defined in [13, Def. 2.4.5], is a collection of finite permutations, denoted {f _α :D _α →D _α }, accompanied by four probabilistic polynomial-time algorithms, denoted I,S,F and B (for index, sample, forward and backward), such that the following (syntactic) conditions hold:

• 1. On input 1ⁿ, algorithm I selects at random an n-bit long index α (not necessarily uniformly) of a permutation f _α , along with a corresponding trapdoor τ;

• 2. On input α, algorithm S samples the domain of f _α , returning an almost uniformly distributed element in it;

• 3. For any x in the domain of f _α , given α and x, algorithm F returns f _α (x) (i.e., F(α,x)=f _α (x));

• 4. For any y in the range of f _α if (α,τ) is a possible output of I(1ⁿ), then, given τ and y, algorithm B returns $f_{\alpha}^{-1}(y)$ (i.e., $B(\tau,y)=f_{\alpha}^{-1}(y)$).

The standard hardness condition (as in [13, Def. 2.4.5]) refers to the difficulty of inverting f _α on a uniformly distributed element of its range, when given only the range-element and the index α. That is, letting I ₁(1ⁿ) denote the first element in the output of I(1ⁿ) (i.e., the index), it is required that, for every probabilistic polynomial-time algorithm A (resp., every non-uniform family of polynomial-size circuits A={A _n } _n ), we have

$$ \operatorname* {Pr}_{\substack{\alpha\gets I_1(1^n)\\x\gets S(\alpha)}} \bigl[A \bigl(\alpha ,f_{\alpha}(x) \bigr)=x \bigr] = \mu(n), $$

(1)

where μ denotes a generic negligible function. Namely, A (resp., A _n ) fails to invert f _α on f _α (x), where α and x are selected by I and S as above. An equivalent way of writing (1) is

$$ \operatorname* {Pr}_{\substack{\alpha\gets I_1(1^n)\\r\gets R_n}} \bigl[A \bigl(\alpha,S( \alpha;r) \bigr)=f_{\alpha}^{-1} \bigl(S(\alpha;r) \bigr) \bigr] = \mu(n), $$

(2)

where R _n denotes the distribution of the coins of S on n-bit long inputs. That is, A fails to invert f _α on S(α;r), where α and r are selected as above.

We note that the idealized cased mentioned in the introduction refers to the special case in which (1) I ₁(1ⁿ) is uniformly distributed in {0,1}ⁿ, and (2) D _α ={0,1}^|α|. Recall that Condition (1) seems unrealistic, and avoiding it was the contents of [2]. Our focus, instead, is on avoiding (or relaxing) Condition (2). Furthermore, we focus on the case that the domain sampler S cannot be efficiently inverted.

Before proceeding, recall that any collection of trapdoor permutations can be easily modified to have a hard-core predicate [6, 17], denoted h. Loosely speaking, such a predicate h is easy to compute, but given α←I ₁(1ⁿ) and x←S(α), it is infeasible to guess the value of $h(\alpha,f_{\alpha}^{-1}(x))$ non-negligibly better than by a coin toss.

Enhanced Trapdoor Permutations

Although the foregoing definition suffices for some applications⁵, in other cases (further discussed in Sects. 3 and 4) we will need an enhanced hardness condition. Specifically, we will require that it is hard to invert f _α on a random input x (in the domain of f _α ) even when given the coins used by S in the generation of x. (Note that, given these coins (and the index α), the resulting domain element x is easily determined, and so we may omit it from the input given to the potential inverter.)

Definition 2.1

(Enhanced Trapdoor Permutations [14, Def. C.1.1])

Let {f _α :D _α →D _α } be a collection of trapdoor permutations. We say that this collection is enhanced (and call it an enhanced collection of trapdoor permutations) if, for every probabilistic polynomial-time algorithm A, we have

$$ \operatorname* {Pr}_{\substack{\alpha\gets I_1(1^n)\\r\gets R_n}} \bigl[A( \alpha,r)=f_{\alpha}^{-1} \bigl(S(\alpha;r) \bigr) \bigr] = \mu(n), $$

(3)

where R _n and μ are as above. The non-uniform version is defined analogously.

Definition 2.1 requires that it is infeasible to invert f _α on S(α;r), when given α and r, which are selected as above (i.e., α←I ₁(1ⁿ) and r←R _n ). Note that any trapdoor permutation in which D _α ={0,1}^|α| satisfies Definition 2.1 (because, without loss of generality, the sampling algorithm S may satisfy S(α;r)=r). This implies that modified versions of the RSA and Rabin collections satisfy Definition 2.1. (More natural versions of both collections can also be shown to satisfy Definition 2.1. For further discussion see Appendix B.)

We note that Definition 2.1 is satisfied by any collection of trapdoor permutations that has a reversed domain sampler (i.e., a probabilistic polynomial-time algorithm that on input (α,y) outputs a string that is uniformly distributed in {r:S(α;r)=y}). Indeed, the existence of a reversed domain sampler eliminates the difference between being given (α,r) and being given (α,S(α;r)).

Any collection of enhanced trapdoor permutations can also be augmented by a hard-core predicate (or rather by an enhanced hard-core predicate). Loosely speaking, such a predicate h is easy to compute, but given α←I ₁(1ⁿ) and r←R _n , it is infeasible to guess the value of $h(\alpha,f_{\alpha}^{-1}(S(\alpha;r)))$ non-negligibly better than by a coin toss. Before presenting the actual definition, we stress that the proof of [17] extends to the current setting (cf. [13, Sect. 2.5.2] or better [15, Thm. 7.8]).

Definition 2.2

(Enhanced Hard-Core Predicate)

Let {f _α :D _α →D _α } be a collection of enhanced trapdoor permutations. We say that h:{0,1}^∗×{0,1}^∗→{0,1} is an enhanced hard-core predicate of {f _α } if h is polynomial-time computable and for every probabilistic polynomial-time algorithm A,

$$ \operatorname* {Pr}_{\substack{\alpha\gets I_1(1^n)\\r\gets R_n}} \bigl[A(\alpha,r)=h \bigl( \alpha,f_{\alpha}^{-1} \bigl(S(\alpha;r) \bigr) \bigr) \bigr] $$

(4)

where R _n and μ are as above. The non-uniform version is defined analogously.

For simplicity, for both standard and enhanced hard-core predicates, we usually drop the index from the input of h and write h(x) where we actually mean h(α,x). (This can be done without loss of generality, since the hard-core predicate of [17] does not use the index α.)

Doubly Enhanced Trapdoor Permutations

Although collections of enhanced trapdoor permutations suffice for the construction of Oblivious Transfer (see Sect. 3), it seems that they do not suffice for constructing a general NIZK proof system (see Sect. 4). Thus, we further enhance Definition 2.1 so to provide for such an implementation. Specifically, we will require that, given α, it is feasible to generate a random pair (x,r) such that r is uniformly distributed in {0,1}^poly(|α|) and x is a preimage of S(α;r) under f _α ; that is, we should generate a random x∈D _α along with coins that fit the generation of f _α (x) (rather than coins that fit the generation of x). The relation between the various notions of trapdoor permutations (TDP) is schematically depicted in Fig. 1. An example of a factoring-based enhanced TDP that is not doubly enhanced is provided in Appendix C.

Fig. 1.

The different enhancements of TDP. Mappings that are infeasible to affect are marked by ↛, and mappings that are easy to affect are marked by →.

Definition 2.3

(Doubly Enhanced Trapdoor Permutations)

Let {f _α :D _α →D _α } be an enhanced collection of trapdoor permutations (as in Def. 2.1). We say that this collection is doubly enhanced (and call it a doubly enhanced collection of trapdoor permutations) if there exists a probabilistic polynomial-time algorithm that on input α outputs a pair (x,r) such that r is distributed identically to R _|α| and f _α (x)=S(α;r).

We note that Definition 2.3 is satisfied by any collection of trapdoor permutations that has a reversed domain sampler. Indeed, the existence of a reversed domain sampler eliminates the difference between producing random pairs (x,r) such that f _α (x)=S(α;r) and producing random pairs of the form (x,S(α;r)) such that f _α (x)=S(α;r) (i.e., random pairs (x,y) such that f _α (x)=y).

A useful relaxation of Definition 2.3 allows r to be distributed almost-identically (rather than identically) to R _|α|, where by almost-identical distributions we mean that the corresponding variation distance is negligible (i.e., the distributions are statistically close). Needless to say, in this case the definition of a reversed domain sampler should be relaxed accordingly.

We stress that suitable implementations of the popular candidate collections of trapdoor permutations (e.g., the RSA and Rabin collections) do satisfy the foregoing doubly enhanced condition (see Appendix B). In fact, any collection of trapdoor permutations that has dense and easily recognizable domains satisfies this condition, where D _α ⊆{0,1}^|α| is dense if |D _α |≥2^|α|/poly(|α|). The reason is that having such domains offer a very simple domain sampler, which can be inverted efficiently: The sampler merely generates a sequence of |α|-bit long strings and outputs the first string in D _α , whereas the reversed domain sampler just generates such a sequence and replaces the first string in D _α by the element given to it.

Again, any collection of doubly enhanced trapdoor permutations can also be augmented by a hard-core predicate (or rather by a doubly enhanced hard-core predicate). That is, such a predicate is required to satisfy the conditions of Definition 2.2 with respect to a collection {f _α :D _α →D _α } that is doubly enhanced (rather than just enhanced).

3 Enhanced TDP and 1-out-of-2 OT

Oblivious transfer (OT) is an interactive protocol between two parties, a sender and a receiver. In the 1-out-of-2 version, introduced by Even et al. [8], the sender gets as input two bits σ ₀ and σ ₁ and the receiver gets a single bit i. The parties exchange messages and at the end of the protocol the receiver should learn the bit σ _i but gain no knowledge regarding σ _1−i and the sender should gain no knowledge of i. Oblivious transfer turned out to be a central cryptographic tool, especially in the context of secure multi-party computation [18].

In this section we present the standard OT protocol based on TDP, which originates in [8, 18] and is hereafter referred to as the EGL protocol. We highlight the difficulty the arises when the protocol is implemented with general TDP, and show that under the strengthened notion of enhanced TDP the protocol is actually secure.

Semi-honest OT

We consider OT in the semi-honest model, where both parties follow the protocol but may try to learn additional information based on their view of the interaction. Recall that (using any one-way function) Goldreich et al. [18] showed a compiler that transforms protocols secure in the semi-honest model into protocols that are secure against malicious adversaries (which may deviate arbitrarily from the specified protocol). Informally an OT protocol should satisfy the following requirements (w.r.t. the sender input (σ ₀,σ ₁)∈{0,1}² and the receiver input i∈{0,1}):

• 1. Correctness—At end of the protocol the receiver outputs σ _i (and the sender outputs nothing).

• 2. Receiver privacy—the sender does not learn the selection bit i (i.e., the view of the sender can be simulated based on σ ₀,σ ₁).

• 3. Sender privacy—the receiver does not learn the bit σ _1−i (i.e., the view of the receiver can be simulated based on i and σ _i ).

A precise definition of OT is provided in Appendix A.

3.1 The EGL Protocol

The EGL protocol uses a TDP {f _α :D _α →D _α } _α with a hard-core predicate h. We denote the algorithms associated with the TDP by I (index/trapdoor sampler), S (domain sampler), F (forward evaluation) and B (backward evaluation). The protocol is depicted in Fig. 2.

Fig. 2.

The EGL protocol for 1-out-of-2 oblivious transfer.

Even when implemented with general TDP (or in fact any collection of permutations), it is not hard to verify that correctness holds. That is, at the end of the protocol, the receiver outputs σ _i . Also, the receiver’s privacy holds, since the sender just sees two uniformly distributed elements y ₀,y ₁∈D _α , and therefore the selection bit i is perfectly hidden (here we use the fact that f _α is a permutation).

It is tempting to argue that the sender’s privacy also holds. The misleading intuition is that the receiver does not know the preimage $x_{1-i}=f^{-1}_{\alpha}(z_{1-i})$ and therefore the bit σ _1−i is computationally hidden by the “mask” h(x _1−i ). The reason this argument fails is that the receiver may be able to efficiently compute the preimage of z _1−i under $f^{-1}_{\alpha}$ by using the random coins that it has used to generate z _1−i . A general TDP does not guarantee that given an index α and random coins that are used to sample z _1−i ∈D _α it is infeasible to obtain $f^{-1}_{\alpha}(z_{1-i})$ or just guess $h(f^{-1}_{\alpha}(z_{1-i}))$ with non-negligible advantage. Indeed, as we shall see next, such guarantees are provided by enhanced TDPs.

3.2 Security of the EGL Protocol Based on ETDP

The source of trouble (as discussed right above) is that the random coins of the sampling algorithm may reveal the preimage of the sampled element. To overcome this difficulty we use a stronger assumption about the TDP: We assume that it is actually an enhanced TDP (Definition 2.1). Recall that the enhancement means that even given the random coins of the domain sampler it is hard to invert a sampled element. If the EGL protocol is implemented with enhanced TDP, then intuitively the additional information that the receiver has regarding the sampled elements no longer helps and the protocol is secure. Thus, we obtain the following.

Claim 3.1

If {f _α } is an enhanced TDP and h is its enhanced hard-core predicate, then the EGL protocol securely implements 1-out-of-2 OT in the semi-honest model.

Proof

We first detail the correctness and receiver’s privacy, which were sketched above. Correctness follows by the following syntactic equalities:

To show that sender and receiver privacy hold, we show simulators that based on the local input and output of the corresponding party simulate the party’s view.

We first show that the receiver’s privacy holds. Consider the following (simple) simulation of the sender’s view. On input (σ ₀,σ ₁), the simulator selects a random string s and uses it to sample an index α of a permutation. The simulator also selects two elements y ₀,y ₁←S(α) in the permutation’s domain and outputs ((σ ₀,σ ₁,1ⁿ),s,(y ₀,y ₁)), where the first part is the sender’s input, the second part its random string, and the third part is the message that it receives. Because α is a permutation, and since S samples almost uniformly in the domain, the simulated view is statistically close to the actual view of the sender in the protocol execution, and therefore the receiver enjoys statistical privacy.⁶

We now turn to the sender’s privacy. Recall that the simulator gets i and σ _i and needs to simulate the receiver’s view in the protocol execution. The simulator proceeds as follows:

Simulator(i,σ _i ,1ⁿ)

• 1. Select a random index α of a permutation.

• 2. Select two random strings r ₁ and r ₂ for the domain sampler S and set z _j =S(α;r _j ) for j∈{0,1}. Set y _i =f _α (z _i ) and y _1−i =z _1−i .

• 3. Set c _i =σ _i ⊕h(z _i ) and select a bit c _1−i ∈{0,1} uniformly at random.

• 4. Output (i,(r ₁,r ₂),(α,(c ₁,c ₂))), where the first part simulates the receiver’s input, the second part its random string, and the third part simulates the two messages that it receives.

We claim that the output of the simulator is computationally indistinguishable from the actual view of the receiver. To see this observe that, except for c _1−i , the output of the simulator is distributed identically to the view of the receiver. Thus, an adversary that distinguishes between the simulation and the actual execution view, also distinguishes between c _1−i (which is distributed uniformly and independent of anything else) and $h(f_{\alpha}^{-1}(S(\alpha;r_{1-i})))$, when given random α and r _1−i , which contradicts the hypothesis that h is an enhanced hard-core predicate.⁷ □

4 Doubly Enhanced TDP, 1-out-of-3 OT, and NIZK

In the previous section we showed that the presumptions that a randomly sampled element and the random coins used to sample it are computationally equivalent is false (i.e., it may be infeasible to retrieve the coins from the sampled element), and that this fact may lead to the insecurity of cryptographic protocols that rely on this (false) presumption. While enhanced TDP do bring us closer to idealized TDP (in which random coins and sampled elements are computationally equivalent), in this section we demonstrate that a significant gap exists also between the enhanced and the idealized notions of TDP.

The gap that we refer to is related to the fact that many applications of TDP use the property that for a given permutation α it is easy to generate a random pair (x,y) such that y=f _α (x). This can obviously be done by just sampling x at random (in the domain) and applying the permutation to obtain y (as f _α (x)). However, in some applications a variant of this property is needed; namely, the ability to generate a random pair (x,r) such that r is the random string used to sample y=f _α (x). For idealized TDP this is easy since we can sample (x,y) and use r=y, but for general TDP obtaining r from y (s.t. y=S(α;r)) may be infeasible.⁸ (We mention that the ability to generate such random pairs may be used in the proof of security of a given protocol and not in the protocol execution.)

Next we show two protocols that use enhanced TDP for which the infeasibility of generating such pairs may lead to security problems. These problems (in both protocols) can be resolved by using an additional enhancement of TDP referred to as doubly enhanced TDP. Recall that doubly enhanced TDP (which were defined specifically for this purpose—see Definition 2.3) are enhanced TDP for which, in addition to the “standard” enhancement, it is feasible to generate pairs (x,r) as above.

4.1 1-out-of-3 OT

As a first example we consider the natural extension of the EGL protocol to 1-out-of-k OT, for any k≥3. For simplicity we consider the 1-out-of-3 case in which the sender gets as input three bits σ ₁,σ ₂,σ ₃ and the receiver gets an index i∈{1,2,3}. As before, the receiver should learn σ _i but gain no knowledge on σ _j for j≠i, and the sender should gain no knowledge on i. The protocol for the case k≡3 is depicted in Fig. 3.

Fig. 3.

The EGL protocol for 1-out-of-3 oblivious transfer.

At first glance, it seems that the protocol is secure when using enhanced TDP (for similar reasons as in the 1-out-of-2 case). Nevertheless, we show that there is a subtle issue that makes it insecure. Before proceeding, we note that there are other ways to extend the EGL protocol to 1-out-of-k while preserving security (e.g., a simple generic transformation from 1-out-of-2 OT to 1-out-of-k, for any k≥2).⁹ Hence 1-out-of-k OT can be constructed based on enhanced TDP, it is only that a specific natural way of doing it (i.e., Fig. 3) is insecure. That is, we show the insecurity of the foregoing (natural) construction (of Fig. 3) in order to demonstrate that enhanced TDP cannot be treated as an idealized TDP.

The Problem with the 1-out-of-3 EGL Protocol

For sake of concreteness, consider the case i=1 (i.e., the receiver wants to receive the bit σ ₁). As in the case of 1-out-of-2 OT, correctness and the receiver’s privacy follow from the fact that {f _α } _α is a collection of permutations. Intuitively it seems that the sender’s privacy should also hold. Indeed, since {f _α } _α is an enhanced TDP the receiver does not know x ₂ nor x ₃ and therefore can learn neither σ ₂ nor σ ₃ (since each is “masked” by a pseudorandom bit). However, privacy requires not only that the individual bits be pseudorandom, but also that they be pseudorandom together. But the fact that h(x ₂) and h(x ₃) are each pseudorandom does not imply that (h(x ₂),h(x ₃)) is pseudorandom. For example, perhaps the adversary can learn h(x ₂)⊕h(x ₃), and thus break the security of the 1-out-of-3 EGL protocol (by obtaining the value of σ ₂⊕σ ₃). We note that it may be tempting to try to prove this joint pseudorandomness using a hybrid argument. The problem with such an argument is that generating the necessary hybrid involves the generation of (say) r ₂ together with h(x ₂) which may not be feasible if the TDP is not doubly enhanced.

This gap in the security proof can actually be used to form an attack. Specifically we refer to the existence of an enhanced TDP (based on a standard intractability assumption) with an enhanced hard-core predicate for which given α,r ₁,r ₂ it is easy to compute the exclusive-or of the hard-core bits of the preimages (i.e., $h(f^{-1}_{\alpha}(S(\alpha;r_{1}))) \oplus h(f^{-1}_{\alpha}(S(\alpha;r_{2})))$). When the extended EGL protocol is invoked with such an enhanced TDP the receiver can actually learn σ ₂⊕σ ₃ thereby breaking (semi-honest) security. An enhanced TDP with the above property is presented in Appendix C.

We stress that the difference between the cases of k=2 and k≥3 (for the extended EGL protocol) is that in the former we only referred to the (enhanced) hardness of a single bit, whereas in the latter we need to refer to the simultaneous (enhanced) hardness of two or more bits. That is, the protocol uses k bits, but one is revealed, and so it refers to the security of the remaining k−1 bits. While a single hard-core bit of an enhanced TDP is certainly pseudorandom (which suffices for the k=2), two or more hard-core bits may not be simultaneously pseudorandom (which fails the case of k≥3).

Doubly Enhanced TDP Resolve the Problem

The essence of the problem in the 1-out-of-k EGL protocol is that in this setting (where the adversary sees random strings and not just sampled elements) hard-core bits are not necessarily pseudorandom. Recall that the standard way to prove that many hard-core bits are (simultaneously) pseudorandom is via a hybrid argument. For the hybrid argument to go through in this setting, we need the ability to generate intermediate hybrids, which boils down to generating random pairs (h(x),r) such that $x = f^{-1}_{\alpha}(S(\alpha;r))$. For enhanced TDP we have no guarantee that such pairs can be efficiently generated; furthermore, as mentioned above, there exist enhanced TDP for which it is infeasible to generate such pairs. On the other hand, hard-core bits of doubly enhanced trapdoor permutations are pseudorandom in this setting (i.e., also when the adversary sees the randomness used to sample the images). This is the case since the second enhancement guarantees the feasibility of generating random pairs (x,r) such that f _α (x)=S(α;r), and this allows to employ a hybrid argument in order to prove the following claim.

Claim 4.1

Suppose that {f _α } is a doubly enhanced TDP and h is its enhanced hard-core predicate. Then, for every polynomial m=m(n), the sequences (α,r ₁,…,r _m ,h(x ₁),…,h(x _m )) and (α,r ₁,…,r _m ,b ₁,…,b _m ) are computationally indistinguishable, where the r _i ’s are independently drawn from R _n , each x _i is such that f _α (x _i )=S(α;r _i ), and the b _i ’s are independent uniformly distributed bits.

By setting k=m+1, it follows that, for every polynomial k, if the TDP is doubly enhanced, then the EGL protocol (of Fig. 3) securely implements 1-out-of-k OT in the semi-honest model.

Proof

For m=1, the claim follows by the definition of enhanced hard-core predicate (i.e., Definition 2.2). For m>1, we use a hybrid argument. Given α and (r,z), where r←R _n and z∈{0,1}, we select uniformly i∈[m], generate i−1 pairs (r ₁,x ₁),…,(r _i−1,x _i−1) such that f _α (x _j )=S(α;r _j ) for every j∈[i−1], compute b _j =h(x _j ) for every j∈[i−1], select b _i+1,…,b _m uniformly in {0,1} (and r _i+1,…,r _m from R _n ), and produce the sequence

$$(\alpha,r_1,\ldots,r_{i-1},r,r_{i+1}, \ldots,r_{m}, b_1,\ldots,b_{i-1},z,b_{i+1}, \ldots,b_{m}). $$

Now, the indistinguishability of neighboring hybrids follows from the hypothesis that h is an enhanced hard-core predicate, whereas the extreme hybrids correspond to the desired conclusion. □

4.2 Non-interactive Zero-Knowledge Proofs

As a second example, we consider a construction of non-interactive zero-knowledge proofs for any $\mathcal {NP}$ language. Recall that zero-knowledge proofs allow a prover to convince a verifier that a given statement is valid without disclosing any additional information other than the validity of the statement [20]. Non-interactive zero-knowledge proof systems (NIZK), introduced by Blum, Feldman, and Micali [4], are zero-knowledge proofs in which there is no actual interaction; that is, a single message is sent from the prover to the verifier, which either accepts or rejects. Instead of bi-directional interaction, a setup assumption is used; specifically, the existence of a (uniformly distributed)¹⁰ common random string (CRS), to which both parties have (read-only) access. For a definition of NIZK proofs see Appendix A.

Assuming the existence of one-way permutations, Feige, Lapidot, and Shamir [9] constructed NIZK proof systems for any $\mathcal {NP}$ language. They also offer an efficient implementation of the prescribed prover, by using an idealized TDP. We refer to this construction as the FLS protocol, and consider what happens when it is implemented when using a general TDP (and the two enhancements of this notion).

There are two gaps when trying to replace idealized TDP in the FLS protocol with general TDP. The first gap (discovered by Bellare and Yung [2]) is that the soundness of the FLS construction relies on the feasibility of recognizing permutations in the collection. We start by elaborating on this gap, while noting that the solution will lead to the second gap.

Proving that a Function is 1-1

In the FLS protocol the prover provides the verifier an index α of a permutation in the collection, and the soundness is based on the assumption that α does indeed describe a permutation. This assumption always holds in the case of idealized TDP (where any index describes a permutation), but for all popular candidate TDPs it is unknown how to efficiently check whether a given string describes a valid permutation (cf. [2]). Therefore, when the FLS protocol is implemented with general TDP, a cheating prover may provide a string that does not correspond to any permutation (but rather describes a many-to-one function, which in turn may be used to violate the soundness condition). Bellare and Yung suggested to resolve this problem by augmenting the main NIZK, with a (non-interactive zero-knowledge) proof that the given index α does indeed describe a function that is practically a permutation. This is done by presenting sufficiently many domain elements (described as part of the common random string) and expecting the prover to provide the inverses of these elements (where the validity of these preimages can be checked by applying the function f _α in the forward direction). Soundness follows from the fact that if the function is not (almost) 1-1, then, with high probability, a cheating prover will not be able to supply preimages for random domain elements. Unfortunately, it turns out that this protocol is not necessarily zero-knowledge when using general (or singly enhanced) TDP, but it is zero-knowledge in case the domain of f _α equals {0,1}^|α|.

The reason that the foregoing protocol may not be zero-knowledge is the essence of the second aforementioned gap, and we shall discuss this gap now, while first detailing the foregoing proof system. In this proof system, both parties are given an index α (which allegedly describes a permutation in the collection), and the prover is also given a corresponding trapdoor. Both parties have access to a common random string that is partitioned into ℓ strings, denoted r ₁,…,r _ℓ , each of length that fits the number of coins used by S(α). The prover uses the random strings to obtain ℓ elements, y ₁,…,y _ℓ such that y _i =S(α;r _i ), inverts them (using the trapdoor) to obtain x ₁,…,x _ℓ such that $x_{i} = f^{-1}_{\alpha}(y_{i})$, and sends x ₁,…,x _ℓ to the verifier. The verifier computes by itself y _i =S(α;r _i ) and verifies that y _i =f _α (x _i ), for all i∈{1,…,ℓ}. Although this may convince the verifier that f _α is almost 1-1 (i.e., if n/ℓ fraction of D _α has no preimage under f _α , then the verifier will reject with overwhelming high probability), but it may not be zero-knowledge in general. The point is that the verifier obtains a random pair (x,r) such that f _α (x)=S(α;r) (actually it gets many such pairs), and it is not clear that the verifier could have generated such a pair (let alone many such pairs) by itself. This concern remains valid if the collection is an enhanced TDP, but it disappears by the assumption that the collection is doubly enhanced (which indeed is tailored for such applications).

General NIZK

We mention that the difficulty encountered in the foregoing protocol (for proving that a function is 1-1) also presents itself in the basic FLS protocol. Specifically, the FLS verifier sees random pairs of the form (x,r) such that f _α (x)=S(α;r) also in the basic FLS protocol (i.e., before its augmentation by [2]). Again, as above (and as in the case of the EGL OT protocol for k≥3), the difficulty is resolved by using doubly enhanced TDP. In such a case, by definition, the ability to efficiently generate random (x,r) such that f _α (x)=S(α;r) is guaranteed, and the zero-knowledge property of the protocol follows.

5 Obliviously Sampling Ciphertexts

In this section we consider the standard construction of public-key encryption based on trapdoor permutations [19, 25]. The construction is indeed secure given any TDP (i.e., no enhancement is necessary).¹¹ Still, there are natural properties that are guaranteed for the encryption scheme only when using a TDP that is either enhanced or doubly enhanced. Specifically, we refer to the ability to generate ciphertexts obliviously of the plaintext. We focus on public-key schemes for which this property means that, given the encryption-key, it is feasible to sample an encryption of a random message such that even the sampler itself does not know the message (assuming that it does not have the decryption-key). In contrast, the trivial sampler that chooses a random message and encrypts it is inherently non-oblivious.

We use the standard definition of a public-key encryption scheme, except that we allow a restriction of the message space. Recall that such a scheme is described in terms of three algorithms (i.e., key-generation, encryption and decryption). For sake of simplicity, we assume that the message space consists of all strings of length ℓ(n), where n is the security parameter and ℓ is a polynomially bounded function. Typical cases are ℓ≡1 (i.e., bit encryption) and ℓ(n)=n.

Definition 5.1

(Oblivious Ciphertext Sampleability)

We say that a public-key encryption scheme (G,E,D) is an oblivious ciphertext sampleable (OCS) scheme if there exists a probabilistic polynomial-time algorithm O (called the oblivious ciphertext sampling algorithm) such that the following holds:

• 1. For any encryption-key e the output of O(e) is distributed identically to a random encryption of a random message; that is O(e) is distributed identically to E _e (U) where U is distributed uniformly in the message space. ¹²

• 2. Given the encryption-key e and the random coins of the sampler r, the value D _d (O(e;r)) is pseudorandom; that is, (e,r,D _d (O(e;r))) and (e,r,U) are computationally indistinguishable, when e,r and U are random.

Note that the essence of the obliviousness condition is captured in the second item, which asserts that the plaintext looks random even when the coins used to produce the ciphertext are known. We mention that OCS encryption schemes were considered by Gertner et al. [10],¹³ who showed that they can be used to construct a 3-round OT protocol.

5.1 On Constructing Public-Key OCS Schemes

As a concrete example of an OCS scheme consider the standard construction of public-key bit encryption from TDP. Recall that in this construction the encryption-key is an index α of a TDP, the decryption-key is the corresponding trapdoor τ, and the message space is {0,1}. Using the encryption-key α, the bit σ∈{0,1} is encrypted by selecting a random domain element x←S(α), and outputting (f _α (x),h(x)⊕σ), where h is a hard-core predicate of the TDP. The ciphertext (y,b) is decrypted via the decryption-key τ by outputting $h(f^{-1}_{\alpha}(y)) \oplus b$ (where f _α is inverted using τ).

At first glance, it seems that, in this scheme, it is easy to sample ciphertexts obliviously of the plaintexts, since an encryption of a random message is uniformly distributed in D _α ×{0,1}. Specifically, consider the algorithm O(α) that outputs (y,b) such that y←S(α) and b is a random bit. While the sampler O clearly outputs the right distribution (and so satisfies the first item of Definition 5.1), it is not necessarily oblivious (i.e., it does not necessarily satisfy the second item). The random coins of O include the random coins that are used to produce the sample y∈D _α , and therefore, as shown in Sect. 3, when using a general TDP, it may be possible (using these random coins) to invert f _α on y, and so retrieve the plaintext. Hence the suggested sampling algorithm may not satisfy the conditions of Definition 5.1.

To resolve this issue we yet again use enhanced TDP (and assume that h is an enhanced hard-core predicate). Indeed, if the TDP is enhanced, then the foregoing O is an oblivious ciphertext sampler (i.e., it satisfies the conditions of Definition 5.1).¹⁴

5.2 Sampling Multiple Ciphertexts Obliviously

Consider extending the notion of obliviously sampling a single ciphertext to sampling multiple ciphertexts obliviously. Informally a k-OCS public-key encryption scheme is one in which it is feasible given the encryption-key e to sample from the joint distribution E _e (m ₁)×…×E _e (m _k ) such that m ₁,…,m _k are (1) uniformly distributed in the message space and (2) pseudorandom even given the random coins of the sampler (although they are information-theoretically determined).

Intuitively, it may seem that any regular OCS scheme (i.e., a 1-OCS scheme) directly yields a k-OCS scheme, by merely invoking the oblivious sampling algorithm k times. Clearly, these k samples will be distributed correctly, but these samples may not be pseudorandom given the random coins of the sampler. That is, while each individual message m _i is guaranteed to be pseudorandom, the joint distribution (m ₁,…,m _k ) is not necessarily pseudorandom. To see this we return to the construction of public-key bit encryption based on enhanced TDP discussed above. Even for k=2 the suggested sampler is not necessarily oblivious. This follows from reasons similar to those discussed in Sect. 4 and the difficulty can be resolved similarly by using a doubly enhanced TDP. Details follow.

Consider the standard TDP-based encryption scheme and the corresponding oblivious sampler O (outlined in Sect. 5.1). Let O ² denote the direct product of O; that is, O ²(α) selects two random elements y ₁,y ₂∈D _α and two random bits b ₀,b ₁∈{0,1} and outputs ((y ₁,b ₁),(y ₂,b ₂)). The output of O ² is indeed distributed identically to a pair of encryptions of independent random bits. However, the random string used by O ² is (r ₁,b ₁,r ₂,b ₂) where r ₁ and r ₂ are the random strings that respectively sample y ₁ and y ₂ (i.e., y _i =S(α;r _i )). In Sect. 4 we showed that for an enhanced TDP, given α,r ₁ and r ₂, it may be feasible to compute h(x ₁)⊕h(x ₂) where $x_{i}=f^{-1}_{\alpha}(y_{i})$. Since the two plaintext bits (corresponding to ciphertexts (y ₁,b ₁) and y ₂,b ₂) are, respectively, “masked” by h(x ₁) and h(x ₂), the random string used by O ² may reveal whether the two plaintexts are equal or not.

As mentioned above, the difficulty can be resolved by using a doubly enhanced TDP. When using a doubly enhanced TDP, for any polynomial k=k(n), the sampler that outputs (y ₁,b ₁),…,(y _k ,b _k ), where y ₁,…,y _k are random domain elements and b ₁,…,b _k are random bits, is a k-oblivious sampler for the TDP-based public-key encryption scheme. This fact follows from Claim 4.1, which states that even given the random strings r ₁,…,r _k , which are used to sample y ₁,…,y _k , respectively, the bits h(x ₁),…,h(x _k ), where $x_{j} = f^{-1}_{\alpha}(y_{j})$, are pseudorandom. Thus, given r ₁,…,r _k , the k plaintext bits that correspond to the k ciphertexts (y ₁,b ₁),…,(y _k ,b _k ), are also pseudorandom since they are, respectively, “masked” by the pseudorandom bits h(x ₁),…,h(x _k ).

6 Intermediate Notions

So far we have mainly considered general TDP, enhanced TDP, doubly enhanced TDP and idealized TDP. In this section we present a few intermediate notions. We first consider the realm between doubly enhanced TDP and idealized TDP and then an intermediate notion between enhanced and doubly enhanced TDP.

6.1 Between Doubly Enhanced and Idealized TDP

Recall that idealized TDP are TDP which have domain {0,1}^|α| (and therefore have a trivial sampler) and for which the set of indices with respect to security parameter n are {0,1}ⁿ. The first relaxation that we discuss refers to dropping the latter requirement:

Definition 6.1

A TDP is called a full-domain TDP if for every index α←I ₁(1ⁿ) we have D _α ={0,1}^|α|.

This definition as well as the subsequent three definitions were mentioned in passing in Sect. 2. Assuming, for simplicity, that D _α ⊆{0,1}^|α|, we consider a relaxation of Definition 6.1 by allowing domains that are either dense and/or efficiently recognizable.

Definition 6.2

A TDP is dense if for every index α←I ₁(1ⁿ) we have $|D_{\alpha}| \geq\frac{2^{|\alpha|}}{\mathrm {poly}(\alpha)}$.

Definition 6.3

A TDP has an efficiently recognizable domain if it is possible to efficiently check, given an index α and a string x∈{0,1}^|α|, whether x∈D _α .

We note that given a TDP with dense and efficiently recognizable domain, one can construct a full-domain TDP. This is done in two steps: First, we construct a full-domain weak TDP (in the sense of weak one-way functions), and then we apply the transformation from weak one-way functions to strong one-way functions (see [13, Theorem 2.3.2]) to obtain a full-domain (strong) TDP.¹⁵ Lastly we recall an additional relaxation discussed in Sect. 2:

Definition 6.4

A TDP is said to have a reversed domain sampler if there exists a probabilistic polynomial-time algorithm that on input an index α and a domain element y∈D _α outputs a string that is uniformly distributed in {r:S(α;r)=y}.

As mentioned in Sect. 2, any TDP that has a reversed domain sampler is doubly enhanced. The first enhancement follows by using the reversed domain sampler to reduce the standard inverting task to the enhanced-inverting task (i.e., given (α,y), we invoke the enhanced-inverter on input (α,r) where r is random subject to S(α;r)=y). For the second enhancement, we can sample a random (x,r) such that f _α (x)=S(α;r) by selecting a random element x∈D _α , computing y=f _α (x), and using the reversed domain sampler to obtain r.

6.2 Between Enhanced and Doubly Enhanced TDP

In some of the protocols discussed above we used the doubly enhanced property to argue that many hard-core bits of a doubly enhanced TDP are pseudorandom in the enhanced settings. Although we have an example for an enhanced TDP whose enhanced hard-core bits are not pseudorandom it may be possible to transform any enhanced TDP to one whose hard-core bits are pseudorandom. The following theorem takes a step in this direction by showing that up to logarithmically many hard-core bits of a specific enhanced hard-core predicate are pseudorandom.

Theorem 6.5

Let {f _α :D _α →D _α } _α be an enhanced TDP where D _α ⊆{0,1}^|α| and let {g _α :D _α ×{0,1}^|α|→D _α ×{0,1}^|α|} _α be the enhanced TDP defined as g _α (x,s)=(f _α (x),s) where |x|=|s|=|α|. Then, for the GL enhanced hard-core predicate of {g _α } _α , defined as $h(x,s) \stackrel {\mathrm {def}}{=}\langle{x,s}\rangle = \sum_{i=1}^{n} x_{i}s_{i} \bmod2$, logarithmically many hard-core bits are pseudorandom. That is, for any k=O(log|α|) the following ensembles are computationally indistinguishable:

• {(h(x ₁,s ₁),…,h(x _k ,s _k )),((r ₁,s ₁),…,(r _k ,s _k ))} _α where each pair (r _i ,s _i ) is a uniform random string of the domain sampler of g and $x_{i} = f^{-1}_{\alpha}(S(\alpha;r_{i}))$.

• {(σ ₁,…,σ _k ),((r ₁,s ₁),…,(r _k ,s _k ))} _α where each pair (r _i ,s _i ) is a uniform random strings of the domain sampler of g and each σ _i is a uniformly random bit.

To prove Theorem 6.5 we show that given an index α of a permutation and k=O(logn) random strings (r ₁,s ₁),…,(r _k ,s _k ) of the domain sampler S _g (the sampling algorithm of {g _α } _α ), it is infeasible to approximate ⨁ _j∈U b _j , for any non-empty set U⊆[k] (where b _j =h(x _j ,s _j ) and $x_{j}=f_{\alpha}^{-1}(S(\alpha;r_{j}))$). The theorem follows by applying the computational XOR lemma for hard-core functions [13, Lem. 2.5.8]. (This XOR lemma asserts that if it is infeasible to approximate the parity of a random subset of logarithmically many hard-core bits, then these bits are pseudorandom.)

Proposition 6.6

Let k=k(n) be O(logn). For any probabilistic polynomial-time algorithm A and any non-empty set U⊆[k], we have

(5)

where $b_{j} \stackrel {\mathrm {def}}{=}h(x_{j},s_{j}) = \langle{x_{j},s_{j}}\rangle$ and $x_{j} \stackrel {\mathrm {def}}{=}f_{\alpha}^{-1}(S(\alpha;r_{j}))$ (and μ is a generic negligible function).

Proof

Assume toward a contradiction that this is not the case. That is, there exists a non-empty set U⊆[k] and an algorithm A that has a non-negligible advantage in approximating ⨁ _j∈U b _j based on α,U and (r ₁,s ₁),…,(r _k ,s _k ). Furthermore, such a set U can be found in probabilistic polynomial-time by experimenting with all possible sets (while generating random samples of I(1ⁿ)). Fixing such a set U={j ₁,…,j _k′}, we observe that ⨁ _j∈U b _j =⨁ _j∈U 〈x _j ,s _j 〉 equals $\langle{x_{j_{1}}\circ\dots\circ x_{j_{k'}},s_{j_{1}}\circ\dots\circ s_{j_{k'}}}\rangle$, which is the GL hard-core predicate of $g'_{\alpha}$ that is defined by the direct produce of k′ values of g _α (i.e., $g'_{\alpha}((x_{1},s_{1}),\dots,(x_{k},s_{k})) =(g_{\alpha}(x_{1},r_{1}),\dots,g_{\alpha}(x_{k},s_{k}))$). Thus, it suffices to note that $g'_{\alpha}$ is an enhanced trapdoor permutation,¹⁶ and the result of [17] (cf. [13, Sect. 2.5.2] or better [15, Thm. 7.8]) implies that the said predicate is indeed an enhanced hard-core. □

Corollary

Theorem 6.5 implies that, when using the GL hard-core predicate, the extended EGL protocol is secure for any logarithmically bounded k.

Further Notions

Theorem 6.5 refers to the pseudorandomness of the sequence h(x ₁,s ₁),…,h(x _k ,s _k ) relative to (α,(r ₁,s ₁),…,(r _k ,s _k )), where $x_{i} \stackrel {\mathrm {def}}{=}f_{\alpha}^{-1}(S(\alpha;r_{i}))$. Alternative notions that refer to the unpredictability of related sequences arise naturally. The interested reader is referred to [24] for a taxonomy of notions of TDP that lie between enhanced and doubly enhanced.

7 Enhancements of Trapdoor Functions and general One-Way Functions

Recall that a collection of one-way functions (OWF) is a collection of efficiently computable functions {f _α :D _α →R _α } _α that is hard to invert on the average (for a formal definition, see [13, Sect. 2.4.2]). Of course any collection of TDP is a collection of OWF with the additional properties that (1) indices can be sampled together with corresponding trapdoors, and (2) the functions are permutations.

In this section we consider the effect of the two enhancements when applied to any collection of one-way functions (OWF), rather than when applied to collections of TDP only. We note that to the best of our knowledge enhanced versions of general collections of OWF have not been considered before. In Sect. 7.1 we provide a general treatment. In Sect. 7.2 we consider the special case of one-to-one trapdoor functions and their enhancements as these can replace the use of TDP in the three main applications considered in this article: oblivious transfer, non-interactive zero-knowledge proofs for $\mathcal {NP}$, and public-key encryption.

7.1 A General Treatment

Recall that the first difficulty discussed above (in the context of TDP) refers to the possibility of sampling an element in the domain (of the permutation) without obtaining its preimage (under the permutation). When considering general collections of OWF (which may not be permutations), it is important to distinguish between sampling in the domain and sampling in the range (since the two might not coincide). We note that the first issue is actually concerned with sampling an element from the range; that is, the possibility of generating a sample y in the range of the function f _α without also obtaining the preimage $f_{\alpha}^{-1}(y)$ (which is an element in the domain).

Note that while a domain sampler is guaranteed by the definition of a collection of OWF, a range sampler is not explicitly required. Nevertheless, a trivial range sampler may be obtained by sampling an element in the domain and then applying the function. However, as seen in the case of TDP, the random coins of this specific range sampler totally reveal a corresponding preimage. Obtaining a range sampler that does not reveal a preimage does not seem obvious and therefore it is natural to define an enhanced collection of OWF (analogously to enhanced TDP):

Definition 7.1

(Enhanced Collection of OWF)

Let {f _α :D _α →R _α } be a collection of OWF, and let S _D be the domain sampler associated with it. We say that the collection is an enhanced if there exists an efficient range sampler S _R such that the output distribution of S _R (α) is statistically close to f _α (S _D (α)) and such that, for every probabilistic polynomial-time algorithm A, we have

$$ \operatorname* {Pr}_{\substack{\alpha\gets I_1(1^n)\\r \in_R \{0,1\}^{\mathrm {poly}(|\alpha|)}}} \bigl[ A(\alpha,r) \in f_{\alpha}^{-1} \bigl( S_R(\alpha;r) \bigr) \bigr] = \mu(n), $$

where μ refers to a generic negligible function.

The range sampler of an enhanced collection of OWF has the property that its random coins do not reveal a corresponding preimage. However, as is the case with enhanced TDP, it could potentially be useful to jointly sample a random string of the range sampler together with a corresponding preimage. Since there does not seem to be an obvious way to do so, we also define a doubly enhanced collection of OWF (analogously to doubly enhanced TDP):

Definition 7.2

(Doubly Enhanced Collection of OWF)

Let {f _α :D _α →R _α } _α be an enhanced collection of OWF (as in Definition 7.1) with domain sampler S _D and range sampler S _R . We say that this collection is doubly enhanced (and call it a doubly enhanced collection of OWF) if there exists a probabilistic polynomial-time algorithm that on input α outputs a pair (x,r) such that x is distributed identically to S _D (α) and r is distributed uniformly in {r′:S _R (α;r′)=f _α (x)}.

7.2 Enhancements of 1-1 TDF

A one-to-one trapdoor function (1-1 TDF) may be thought of as a relaxation of a TDP in which every function merely needs to be injective (and not necessarily a permutation). Note that the inversion process is still well defined since there is a unique preimage. More formally, a collection of 1-1 TDF is a collection {f _α :D _α →R _α } of one-way functions such that (1) all the functions in the collection are one-to-one and (2) the index-sampling algorithm I on input 1ⁿ outputs, in addition to an index α of a function, a corresponding trapdoor τ and there exists an efficient algorithm that on input τ and y∈R _α (where τ is the trapdoor corresponding to α) outputs $f^{-1}_{\alpha}(y)$. We note that 1-1 TDF can be used instead of TDP in the standard construction of public-key encryption (see Sect. 5).

Using the enhanced notions of one-wayness defined in Sect. 7.1 (for general collections of OWF), it is straightforward to define an enhanced 1-1 TDF. Specifically, a 1-1 TDF is said to be enhanced if it is an enhanced collection of OWF (in addition to being a 1-1 TDF). Similarly, a 1-1 TDF is doubly enhanced if it is additionally a doubly enhanced collection of OWF.

We find these enhanced 1-1 TDF particularly interesting because they can be used instead of (enhanced) TDP in the main applications discussed in this article. Specifically, examining the protocols for oblivious transfer (OT) (Sect. 3) and non-interactive zero-knowledge (NIZK) for $\mathcal {NP}$ (Sect. 4), we observe that the enhanced versions of TDPs used there may actually be replaced by the corresponding enhanced versions of 1-1 TDFs. Moreover, it seems as though permutations were originally used in these protocols because it was implicitly assumed that they (rather than functions) provide enhanced one-wayness: In a sense, the use of 1-1 TDFs rather than TDP better clarifies the issues at hand. Specifically, in the OT protocol we want to allow a party (which does not have the trapdoor) to sample an element in the range of the function without revealing the preimage (i.e., an enhanced TDF) and in the NIZK protocol we want to reveal random coins of the range sampler such that (1) the preimage is not revealed and (2) if needed then we can later reveal the preimage.

Appendices

Appendix A. Definitions of OT and NIZK

For sake of simplicity, we present a non-uniform formulation of all definitions; that is, the inputs to the protocols are quantified over all possibilities. Thus, constructing such protocols may require non-uniformly hard TDP. Uniform-complexity formulations can be derived by considering only polynomial-time sampleable inputs (cf. [11] or [14, Sect. 5.2.5]).

1.1 A.1 Oblivious Transfer

Here k=k(n) is a polynomially bounded function. A pair of probabilistic polynomial-time strategies (S,R) constitute a 1-out-of- k OT protocol (in the semi-honest model) if the following conditions hold.

• Correctness: For every σ ₁,…,σ _k ∈{0,1} and i∈{1,…,k}, when S(1ⁿ,σ ₁,…,σ _k ) interacts with R(1ⁿ,i) the receiver R outputs σ _i and the sender S outputs nothing.

• Receiver security: There exists a probabilistic polynomial-time simulator S ₁ such that the following two probability ensembles are computationally indistinguishable.

  • 1. $\{S_{1}(\sigma_{1},\dots,\sigma_{k},1^{n}) \}_{n\in \mathsf {N},\sigma_{1},\dots,\sigma_{k},i}$ and

  • 2. $\{\mathtt {view}_{1}(\sigma_{1},\dots,\sigma_{k},i,1^{n}) \}_{n \in \mathsf {N}, \sigma_{1},\dots,\sigma_{k},i}$, where view ₁ is a random variable that consists of the sender’s view in the interaction (i.e. its input, randomness and received messages).

• Sender security: There exists a probabilistic polynomial-time simulator S ₂ such that the following two probability ensembles are computationally indistinguishable.

  • 1. $\{S_{2}(i,1^{n},\sigma_{i})\}_{n \in \mathsf {N},\sigma_{1},\dots,\sigma_{k},i}$ and

  • 2. $\{\mathtt {view}_{2}(\sigma_{1},\dots,\sigma_{k},i,1^{n}) \}_{n \in \mathsf {N},\sigma_{1},\dots,\sigma_{k},i}$, where view ₂ is a random variable that consists of the receiver’s view in the interaction (i.e. its input, randomness and received messages).

1.2 A.2 Non-interactive Zero-Knowledge Proofs

A pair of probabilistic polynomial-time algorithms (P,V) constitute an (efficient-prover) non-interactive zero-knowledge proof for an $\mathcal {NP}$ language L with the witness relation R _L if the following conditions hold.

• Completeness: For every x∈L and every witness w such that (x,w)∈R _L ,

  

• Soundness: For every x∉L and every cheating strategy P ^∗,

  

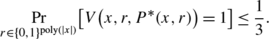
• Zero-Knowledge: There exists a probabilistic polynomial-time simulator M such that the following two probability ensembles are computationally indistinguishable.

  • 1. $\{M(x)\}_{x \in L,w\in R_{L}(x)}$, where R _L (x)={w:(x,w)∈R _L } and

  • 2. $\{(x,R_{|x|},P(x,w,R_{|x|}))\}_{x \in L, w\in R_{L}(x)}$, where R _n denotes a random variable uniformly distributed over poly(n).

Appendix B. On the RSA and Rabin Collections

In this appendix we show that suitable versions of the RSA and Rabin collections satisfy the two aforementioned enhancements (presented in Definitions 2.1 and 2.3, respectively). Establishing this claim is quite straightforward for the RSA collection, whereas for the Rabin collection some modifications (of the straightforward version) seem necessary. In order to establish this claim we will consider a variant of the Rabin collection in which the corresponding domains are dense and easy to recognize, and will show that having such domains suffices for establishing the claim.

2.1 B.1 The RSA Collection Satisfies Both Enhancements

We start our treatment by considering the RSA collection (as presented in [13, Sect. 2.4.3.1] and further discussed in [13, Sect. 2.4.3.2]). Note that in order to discuss the enhanced hardness condition (of Def. 2.1) it is necessary to specify the domain sampler, which is not entirely trivial (since sampling $Z_{N}^{*}$ (or even Z _N ) by using a sequence of unbiased coins is not that trivial).

A natural sampler for $Z_{N}^{*}$ (or Z _N ) generates random elements in the domain by using a regular mapping from a set of sufficiently long strings to $Z_{N}^{*}$ (or to Z _N ). Specifically, the sampler uses $\ell \stackrel {\mathrm {def}}{=}2{\lfloor \log_{2}N\rfloor }$ random bits, views them as an integer in i∈{0,1,…,2^ℓ−1}, and outputs imodN. This yields an almost uniform sample in Z _N , and an almost uniform sample in $Z_{N}^{*}$ can be obtained by discarding the few elements in $Z_{N}\setminus Z_{N}^{*}$.

The fact that the foregoing implementation of the RSA collection satisfies Definition 2.1 (as well as Definition 2.3) follows from the fact that it has an efficient reversed sample (which eliminates the potential gap between having a domain element and having a random sequence of coins that makes the domain-sample output this element). Specifically, given an element e∈Z _N , the reversed sampler outputs an almost uniformly distributed element of $\{i\!\in\!\{0,1,\ldots,2^{\ell}-1\}\!:i\equiv e\;(\textrm{mod}~N)\}$ by selecting uniformly j∈{0,1,…,⌊2^ℓ/N⌋−1} and outputting i←j⋅N+e.

2.2 B.2 Versions of the Rabin Collection that Satisfy Both Enhancements

In contrast to the case of the RSA, the Rabin Collection (as defined in [13, Sect. 2.4.3.3]), does not satisfy Definition 2.1 (because the coins of the sampling algorithm give away a modular square root of the domain element). Still, the Rabin Collection can be easily modify to yield a doubly enhanced collection of trapdoor permutations, provided that factoring is hard (in the same sense as assumed in [13, Sect. 2.4.3]).

The modification is based on modifying the domain of these permutations (following [1]). Specifically, rather than considering the permutation induced (by the modular squaring function) on the set Q _N of the quadratic residues modulo N, we consider the permutations induced on the set M _N , where M _N contains all integers in {1,…,N/2} that have Jacobi symbol modulo N that equals 1. Note that, as in case of Q _N , each quadratic residue has a unique square root in M _N (because exactly two square roots have Jacobi symbol that equals 1 and their sum equals N; indeed, as in case of Q _N , we use the fact that −1 has Jacobi symbol 1). However, unlike Q _N , membership in M _N can be determined in polynomial-time (when given N without its factorization). Lastly, note that squaring modulo N is a 1-1 mapping of M _N to Q _N . In order to obtain a permutation over M _N , we modify the function a little such that if the result of modular squaring is bigger than N/2, then we use its additive inverse (i.e., rather than outputting y>N/2, we output N−y).

Using the fact that M _N is dense (w.r.t. $\{0,1\}^{{\lfloor \log_{2}N\rfloor }+1}$) and easy to recognize, we may proceed in one of two ways, which are actually generic. Thus, let us assume that we are given an arbitrary collection of trapdoor permutations, denoted $\{f_{\alpha}:D_{\alpha}\to D_{\alpha}\}_{\alpha\in{ \overline{I}}}$, such that D _α ⊆{0,1}^|α| is dense (i.e., |D _α |>2^|α|/poly(|α|))¹⁷ and easy to recognize (i.e., there exists an efficient algorithm that given (α,x) decides whether or not x∈D _α ).

• 1. The most natural way to proceed is showing that the collection {f _α } itself is doubly enhanced. This is shown by presenting a rather straightforward domain sampler that satisfies the enhanced hardness condition (of Def. 2.1), and noting that this sampler has an efficient reversed sampler (which implies that Def. 2.3 is satisfied).

  The domain sampler that we have in mind repeatedly selects random (i.e., uniformly distributed) |α|-bit long strings and outputs the first such string that resides in D _α (and a special failure symbols if |α|⋅2^|α|/|D _α | attempts have failed). This sampler has an efficient reversed sampler that, given x∈D _α , generates a random sequence of |α|-bit long strings and replaces the first string that resides in D _α by the string x.

• 2. An alternative way of obtaining a doubly enhanced collection is to first define a (rather artificial) collection of weak trapdoor permutations, $\{f'_{\alpha}:\{0,1\}^{|\alpha|}\to \{0,1\}^{|\alpha|}\}_{\alpha \in{ \overline{I}}}$, such that $f'_{\alpha}(x)=f_{\alpha}(x)$ if x∈D _α and $f'_{\alpha}(x)=x$ otherwise. Using the amplification of a weak one-way property to a standard one-way property (as in [13, Sects. 2.3 and 2.6]), we are done.

Indeed, in the first alternative we amplified the trivial domain sampler that succeeds with noticeable probability, whereas in the second alternative we amplified the one-way property of the trivial extension of f _α to the domain {0,1}^|α|. Either way we obtain a doubly enhanced collection of trapdoor permutations, provided that {f _α } is an ordinary collection of trapdoor permutations.

We mention that the foregoing modifications of the Rabin collection follows the outline of the second modification that is presented in [14, Appendix C.1]. In contrast, as pointed out by Jonathan Katz, the first implementation (of an enhanced trapdoor permutation based on factoring) that is presented in [14, Appendix C.1] is not doubly enhanced.

Appendix C. An Enhanced TDP whose Hardcore Bits are not Pseudorandom

In this section we show that a variant of the factoring-based enhanced TDP (presented in Appendix B.2) has an enhanced hard-core predicate for which two or more samples are not pseudorandom. Note that since polynomially many samples of a doubly enhanced TDP are pseudorandom (see Claim 4.1), the following construction is an example of an enhanced TDP that is not doubly enhanced.¹⁸

Notation

For a Blum integer N, let J _N be the set of all elements in $Z_{N}^{*}$ that have Jacobi symbol +1 modulo N and let $M_{N} \stackrel {\mathrm {def}}{=}J_{N} \cap\{1,\dots,\lfloor\frac{N}{2} \rfloor \}$. For $x \in Z^{*}_{N}$, let QR _N (x) be 1 if x is quadratic residue (modulo N) and 0 otherwise.

Construction C.1

(A factoring-based enhanced TDP)

I(1ⁿ)::

Let N=PQ where P and Q are two uniformly selected primes such that 2ⁿ⁻¹≤P,Q≤2ⁿ and P≡Q≡3mod4. Select a random element y∈J _N and output (N,y) as the index and (P,Q) as the trapdoor.

Sampler S(N,y)::

Select, uniformly at random $r \in Z_{N}^{*}$, and let z=y⋅r ²modN. If $z \leq\lfloor\frac{N}{2} \rfloor$, output z and otherwise output N−z.

F((N,y),x)::

Set z=x ²modN. If $z \leq\lfloor \frac{N}{2} \rfloor$ output z and otherwise output N−z.

B((N,y),x)::

Given the factorization of N, it is possible to compute square roots modulo N and to invert this permutation (for details see [14, Sect. 2.4.4.2]).

Note that Construction C.1 is almost the same as the enhanced TDP of Appendix B.2, where the only difference is in how elements are sampled in the domain M _N (and the augmentation of the index that is used for that purpose). In particular, the evaluation and inversion algorithms remain the same, and therefore, as discussed in Appendix B.2, the function F _N is a permutation over M _N . Additionally, the sampling algorithm S(N,y) produces a uniformly distributed element in M _N , since S(N,y) induces a 4-to-1 mapping from its random strings to M _N .

We proceed to show an enhanced hard-core predicate for Construction C.1 (which implies, in particular, that the TDP is enhanced). Specifically, we show that the predicate $h_{N,y}(x) \stackrel {\mathrm {def}}{=}QR_{N}(F_{N,y}(x))$ (i.e., the predicate that equals 1 if the image of x under F _N,y is a quadratic residue and 0 otherwise) is an enhanced hard-core predicate.

Claim C.2

Assuming the quadratic residuosity assumption,¹⁹ the predicate h _N,y is an enhanced hard-core predicate of Construction C.1.

Proof

Given x, the predicate h _N,y is indeed easy to compute (i.e., if F _N,y (x)=x ²modN, then h _N,y (x)=1, otherwise it must be that F _N,y (x)=N−x ²modN which implies that h _N,y (x)=0). What remains to be shown is that given (N,y) and r, it is infeasible to predict QR _N (S(N,y;r)). The key point is that multiplication by r ² preserves quadratic residuosity whereas multiplication by −r ² complements it (i.e., y⋅r ² is a quadratic residue if and only if y is a quadratic residue and −y⋅r ² is a residue if and only if y is a non-residue). Thus, given N,y and r it is easy to check whether y and S(N,y;r) have the same QR _N value (i.e., compute QR _N (y)⊕QR _N (S(N,y;r))), by checking whether S multiplies y by r ² or by −r ². Thus, an adversary that computes QR(S(N,y;r)) can be used to compute QR _N (y). Details follow.

Consider an adversary A that on input (N,y) and r, breaks the hard-core predicate by outputting QR _N (S(N,y;r)) with probability $\frac{1}{2} + \epsilon$. We use A to construct an adversary A′ to the quadratic residuosity problem as follows. The adversary A′ is given N and y and needs to compute QR _N (y). To do so A′ selects uniformly at random $r \in Z^{*}_{N}$, computes b=QR _N (y)⊕QR _N (S(N,y;r)) and outputs A((N,y),r)⊕b. With probability $\frac{1}{2}+\epsilon$ the output of A′ equals QR _N (S(N,y;r))⊕(QR _N (y)⊕QR _N (S(N,y;r))) which in turn equals QR _N (y). □

Thus, based on the quadratic residuosity assumption, the predicate h _N,y is an enhanced hard-core predicate. However, we argue that the enhanced hard-core bits are not pseudorandom. Specifically, we show that, given the index (N,y) and two random strings r ₁ and r ₂, it is easy to check whether the hard-core bits of the preimages of the elements sampled by r ₁ and r ₂ are equal or not. To do so, first compute QR _N (y)⊕QR _N (S(N,y;r ₁)) and QR _N (y)⊕QR _N (S(N,y;r ₂)), by checking whether S multiplies y by $r_{i}^{2}$ or by $-r_{i}^{2}$ (as above). Then, compute the exclusive-or of these two values, which yields QR _N (S(N,y;r ₁))⊕QR _N (S(N,y;r ₂)) (i.e., the exclusive-or of the two hard-core bits).

Hence, the predicate h _N,y is an enhanced hard-core predicate but is not pseudorandom (in the enhanced setting) for even two samples.