Abstract
We prove two results on arithmetic quantum chaos for dihedral Maaß forms, both of which are manifestations of Berry’s random wave conjecture: Planck scale mass equidistribution and an asymptotic formula for the fourth moment. For level 1 forms, these results were previously known for Eisenstein series and conditionally on the generalised Lindelöf hypothesis for Hecke–Maaß eigenforms. A key aspect of the proofs is bounds for certain mixed moments of L-functions that imply hybrid subconvexity.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The random wave conjecture of Berry [Ber77] is the heuristic that the eigenfunctions of a classically ergodic system ought to evince Gaussian random behaviour, as though they were random waves, in the large eigenvalue limit. In this article, we study and resolve two manifestations of this conjecture for a particular subsequence of Laplacian eigenfunctions, dihedral Maaß forms, on the surface \(\Gamma _0(q) \backslash \mathbb {H}\).
1.1 The rate of equidistribution for quantum unique ergodicity.
Given a positive integer q and a Dirichlet character \(\chi \) modulo q, denote by \(L^2(\Gamma _0(q) \backslash \mathbb {H}, \chi )\) the space of measurable functions \(f : \mathbb {H}\rightarrow \mathbb {C}\) satisfying
and \(\langle f,f\rangle _q < \infty \), where \(\langle \cdot ,\cdot \rangle _q\) denotes the inner product
with \(d\mu (z) = y^{-2} \, dx \, dy\) on any fundamental domain of \(\Gamma _0(q) \backslash \mathbb {H}\).
Quantum unique ergodicity in configuration space for \(L^2(\Gamma _0(q) \backslash \mathbb {H}, \chi )\) is the statement that for any subsequence of Laplacian eigenfunctions \(g \in L^2(\Gamma _0(q) \backslash \mathbb {H}, \chi )\) normalised such that \(\langle g, g \rangle _q = 1\) with eigenvalue \(\lambda _g = 1/4 + t_g^2\) tending to infinity,
for every \(f \in C_b\left( \Gamma _0(q) \backslash \mathbb {H}\right) \), or equivalently for every indicator function \(f = 1_B\) of a continuity set \(B \subset \Gamma _0(q) \backslash \mathbb {H}\). This is known to be true (and in a stronger form, in the sense of quantum unique ergodicity on phase space), provided each eigenfunction g is a Hecke–Maaß eigenform, via the work of Lindenstrauss [Lin06] and Soundararajan [Sou10].
One may ask whether the rate of equidistribution for quantum unique ergodicity can be quantified in some way; Lindenstrauss’ proof is via ergodic methods and does not address this aspect. One method of quantification is to give explicit rates of decay as \(\lambda _g\) tends to infinity for the terms
for a fixed Hecke–Maaß eigenform f or incomplete Eisenstein series \(E_{\mathfrak {a}}(z,\psi )\); optimal decay rates for these integrals, namely \(O_{q,f,\varepsilon }(t_g^{-1/2 + \varepsilon })\) and \(O_{q,\psi ,\varepsilon }(t_g^{-1/2 + \varepsilon })\) respectively, follow from the generalised Lindelöf hypothesis [Wat08, Corollary 1]. Ghosh, Reznikov, and Sarnak have proposed other quantifications [GRS13, Conjecture A.1 and A.3].
Another quantification of the rate of equidistribution, closely related to the spherical cap discrepancy discussed in [LS95], is small scale mass equidistribution. Let \(B_R(w)\) denote the hyperbolic ball of radius R centred at \(w \in \Gamma _0(q) \backslash \mathbb {H}\) with volume \(4\pi \sinh ^2 (R/2)\). Two small scale refinements of quantum unique ergodicity were studied in [You16] and [Hum18] respectively, namely the investigation of the rates of decay in R, with regards to the growth of the spectral parameter \(t_g \in [0,\infty ) \cup i(0,1/2)\), for which either the asymptotic formula
or the bound
holds as \(t_g\) tends to infinity along any subsequence of \(g \in \mathcal {B}_0^{*}(q,\chi )\), the set of \(L^2\)-normalised newforms g of weight zero, level q, nebentypus \(\chi \), and Laplacian eigenvalue \(\lambda _g = 1/4 + t_g^2\).
Remark 1.4
One can interpret these two small scale equidistribution questions in terms of random variables, as in [GW17, Section 1.5] and [WY19, Section 1.3]. We define the random variable \(X_{g;R} : \Gamma _0(q) \backslash \mathbb {H}\rightarrow [0,\infty )\) by
which has expectation \(1/{{\,\mathrm{vol}\,}}(\Gamma _0(q) \backslash \mathbb {H})\). The asymptotic formula (1.2) is equivalent to the pointwise convergence of \(X_{g;R}\) to 1, while (1.3) is simply the convergence in probability of \(X_{g;R}\) to 1, a consequence of the bound \({{\,\mathrm{Var}\,}}(X_{g;R}) = o(1)\). One could ask for further refinements of these problems, such as asymptotic formulæ for this variance and a central limit theorem, as studied in [WY19] for toral Laplace eigenfunctions, though we do not pursue these problems.
For \(q = 1\), Young [You16, Proposition 1.5] has shown that (1.2) holds when \(R \gg t_g^{-\delta }\) with \(0< \delta < 1/3\) under the assumption of the generalised Lindelöf hypothesis, and that an analogous result with \(0< \delta < 1/9\) is true unconditionally for the Eisenstein series \(g(z) = E(z,1/2 + it_g)\) [You16, Theorem 1.4]. One expects that this is true for \(0< \delta < 1\), but the method of proof of [You16, Proposition 1.5] is hindered by an inability to detect cancellation involving a spectral sum of terms not necessarily all of the same sign; see [You16, p. 965].
This hindrance does not arise for (1.3), and so we are lead to the following conjecture on Planck scale mass equidistribution, which roughly states that quantum unique ergodicity holds for almost every shrinking ball whose radius is larger than the Planck scale \(\lambda _g^{-1/2}\).
Conjecture 1.5
Suppose that \(R \gg t_g^{-\delta }\) with \(0< \delta < 1\). Then (1.3) holds as \(t_g\) tends to infinity along any subsequence of newforms \(g \in \mathcal {B}_0^{*}(q,\chi )\).
Via Chebyshev’s inequality, the left-hand side of (1.3) is bounded by \(c^{-2} {{\,\mathrm{Var}\,}}(g;R)\), where
This reduces the problem to bounding this variance. For \(q = 1\), the first author showed that if \(R \gg t_g^{-\delta }\) with \(0< \delta < 1\), then \({{\,\mathrm{Var}\,}}(g;R) = o(1)\) under the assumption of the generalised Lindelöf hypothesis [Hum18, Proposition 5.1]; an analogous result is also proved unconditionally for g(z) equal to an Eisenstein series \(E(z,1/2 + it_g)\) [Hum18, Proposition 5.5]. The barrier \(R \asymp t_g^{-1}\) is the Planck scale, at which equidistribution need not hold [Hum18, Theorem 1.14]; as discussed in [HR92, Section 5.1], the topography of Maaß forms below this scale is “essentially sinusoidal” and so Maaß forms should not be expected to exhibit random behaviour, such as mass equidistribution, at such minuscule scales.
1.2 The fourth moment of a Maaß form.
Another manifestation of Berry’s conjecture is the Gaussian moments conjecture (see [Hum18, Conjecture 1.1]), which states that the (suitably normalised) n-th moment of a real-valued Maaß newform g restricted to a fixed compact subset K of \(\Gamma _0(q) \backslash \mathbb {H}\) should converge to the n-th moment of a real-valued Gaussian random variable with mean 0 and variance 1 as \(t_g\) tends to infinity. A similar conjecture may also be posed for complex-valued Maaß newforms, as well as for holomorphic newforms in the large weight limit; cf. [BKY13, Conjectures 1.2 and 1.3]. A closely related conjecture, namely essentially sharp upper bounds for \(L^p\)-norms of automorphic forms, has been posed by Sarnak [Sar03, Conjecture 4]. For \(n = 2\), the Gaussian moments conjecture is simply quantum unique ergodicity, and for small values of n, this is also conjectured to be true for noncompact K (but not for large n; cf. [Hum18, Section 1.1.2]).
The fourth moment is of particular interest, for, as first observed by Sarnak [Sar03, p. 461], it can be expressed as a spectral sum of L-functions. The conjecture takes the following form for \(K = \Gamma _0(q) \backslash \mathbb {H}\).
Conjecture 1.6
As \(t_g\) tends to infinity along a subsequence of real-valued newforms \(g \in \mathcal {B}_0^{*}(q,\chi )\),
This has been proven for \(q = 1\) conditionally under the generalised Lindelöf hypothesis by Buttcane and the second author [BuK17b, Theorem 1.1], but an unconditional proof currently seems well out of reach (cf. [Hum18, Remark 3.3] and Remark 1.24). Djanković and the second author have formulated [DK18a] and subsequently proven [DK18b, Theorem 1.1] a regularised version of this conjecture for Eisenstein series, improving upon earlier work of Spinu [Spi03, Theorem 1.1 (A)] that proves the upper bound \(O_{\varepsilon }(t_g^{\varepsilon })\) in this setting. Numerical investigations of this conjecture for the family of dihedral Maaß newforms have also been undertaken by Hejhal and Strömbergsson [HS01], and the upper bound \(O_{q,\varepsilon }(t_g^{\varepsilon })\) for dihedral forms has been proven by Luo [Luo14, Theorem] (cf. Remark 1.23). Furthermore, bounds for the fourth moment in the level aspect have also been investigated by many authors [Blo13, BuK15, Liu15, LMY13].
1.3 Results.
This paper gives the first unconditional resolutions of Conjectures 1.5 and 1.6 for a family of cusp forms. We prove these two conjectures in the particular case when \(q = D \equiv 1 \pmod {4}\) is a fixed positive squarefree fundamental discriminant, \(\chi = \chi _D\) is the primitive quadratic character modulo D, and \(t_g\) tends to infinity along any subsequence of dihedral Maaß newforms \(g = g_{\psi } \in \mathcal {B}_0^{*}(D,\chi _D)\).
Theorem 1.7
Let \(D \equiv 1 \pmod {4}\) be a positive squarefree fundamental discriminant and let \(\chi _D\) be the primitive quadratic character modulo D. Suppose that \(R \gg t_g^{-\delta }\) for some \(0< \delta < 1\). Then there exists \(\delta ' > 0\) dependent only on \(\delta \) such that
as the spectral parameter \(t_g\) tends to infinity along any subsequence of dihedral Maaß newforms \(g_{\psi } \in \mathcal {B}_0^{*}(D,\chi _D)\). Consequently,
tends to zero as \(t_g\) tends to infinity for any fixed \(c > 0\).
Theorem 1.9
Let \(D \equiv 1 \pmod {4}\) be a positive squarefree fundamental discriminant and let \(\chi _D\) be the primitive quadratic character modulo D. Then there exists an absolute constant \(\delta ' > 0\) such that
as \(t_g\) tends to infinity along any subsequence of dihedral Maaß newforms \(g_{\psi } \in \mathcal {B}_0^{*}(D,\chi _D)\).
Dihedral newforms form a particularly thin subsequence of Maaß forms; the number of dihedral Maaß newforms with spectral parameter less than T is asymptotic to \(c_{1,D} T\), whereas the number of Maaß newforms with spectral parameter less than T is asymptotic to \(c_{2,D} T^2\), where \(c_{1,D},c_{2,D} > 0\) are constants dependent only on D. We explain in Section 1.8 the properties of dihedral Maaß newforms, not shared by nondihedral forms, that are crucial to our proofs of Theorems 1.7 and 1.9.
Remark 1.11
Previous work [Blo13, BuK15, BuK17a, Liu15, LMY13, Luo14] on the fourth moment has been subject to the restriction that D be a prime. We weaken this restriction to D being squarefree. The additional complexity that arises is determining explicit expressions for the inner product of \(|g|^2\) with oldforms. Removing the squarefree restriction on D, while likely presently feasible, would undoubtedly involve significant extra work.
Remark 1.12
An examination of the proofs of Theorems 1.7 and 1.9 shows that the dependence on D in the error terms in (1.8) and (1.10) is polynomial.
1.4 Notation.
Throughout this article, we make use of the \(\varepsilon \)-convention: \(\varepsilon \) denotes an arbitrarily small positive constant whose value may change from occurrence to occurrence. Results are stated involving level D when only valid for positive squarefree \(D \equiv 1 \pmod {4}\) and are stated involving level q otherwise. The primitive quadratic character modulo D will always be denoted by \(\chi _D\). Since we regard D as being fixed, all implicit constants in Vinogradov \(\ll \) and big O notation may depend on D unless otherwise specified. We write \(\mathbb {N}_0 :=\mathbb {N}\cup \{0\}\) for the nonnegative integers. A dihedral Maaß newform will be written as \(g_{\psi } \in \mathcal {B}_0^{*}(D,\chi _D)\); this is associated to a Hecke Größencharakter \(\psi \) of \(\mathbb {Q}(\sqrt{D})\) as described in Appendix A.
1.5 Elements of the Proofs.
The proofs of Theorems 1.7 and 1.9, which we give in Section 2, follow by combining three key tools; the approach that we follow is that first pioneered by Sarnak [Sar03, p. 461] and Spinu [Spi03].
First, we spectrally expand the variance and the fourth moment, obtaining the following explicit formulæ.
Proposition 1.13
Let q be squarefree and let \(\chi \) be a primitive Dirichlet character modulo q. Then for a newform \(g \in \mathcal {B}_0^{*}(q,\chi )\), the variance \({{\,\mathrm{Var}\,}}(g;R)\) is equal to
where \(\mathcal {B}_0^{*}(\Gamma _0(q_1)) \ni f\) is an orthonormal basis of the space of newforms of weight zero, level \(q_1\), and principal nebentypus, normalised such that \(\langle f, f\rangle _q = 1\), \(E_{\infty }(z,s)\) denotes the Eisenstein series associated to the cusp at infinity of \(\Gamma _0(q) \backslash \mathbb {H}\), and
Similarly, the fourth moment \(\int _{\Gamma _0(q) \backslash \mathbb {H}} |g(z)|^4 \, d\mu (z)\) is equal to
The arithmetic functions \(\omega ,\nu ,\varphi \) are defined by \(\omega (n) :=\# \left\{ p \mid n\right\} \), \(\nu (n) :=n \prod _{p \mid n} (1 + p^{-1})\), and \(\varphi (n) :=n \prod _{p \mid n} (1 - p^{-1})\). We have written \(L_p(s,\pi )\) for the p-component of the Euler product of an L-function \(L(s,\pi )\), while
where \(\Lambda (s,\pi ) :=q(\pi )^{s/2} L_{\infty }(s,\pi ) L(s,\pi )\) denotes the completed L-function with conductor \(q(\pi )\) and archimedean component \(L_{\infty }(s,\pi )\).
Next, we obtain explicit expressions in terms of L-functions for the inner products \(|\langle |g|^2, f\rangle _q|^2\) and \(|\langle |g|^2, E_{\infty }(\cdot ,1/2 + it)\rangle |^2\); this is the Watson–Ichino formula.
Proposition 1.16
Let \(q = q_1 q_2\) be squarefree and let \(\chi \) be a primitive Dirichlet character modulo q. Then for \(g \in \mathcal {B}_0^{*}(q,\chi )\) and for \(f \in \mathcal {B}_0^{*}(\Gamma _0(q_1))\) of parity \(\epsilon _f \in \{1,-1\}\) normalised such that \(\langle g, g\rangle _q = \langle f, f\rangle _q = 1\),
Similarly,
Now we specialise to \(g = g_{\psi } \in \mathcal {B}_0^{*}(D,\chi _D)\). Observe that \({{\,\mathrm{ad}\,}}g_{\psi }\) is equal to the (noncuspidal) isobaric sum \(\chi _D \boxplus g_{\psi ^2}\), where \(g_{\psi ^2} \in \mathcal {B}_0^{*}(D,\chi _D)\) is the dihedral Maaß newform associated to the Hecke Größencharakter \(\psi ^2\) of \(\mathbb {Q}(\sqrt{D})\), and so
which can readily be seen by comparing Euler factors. Then the identity (1.17) holds with \(1 + \epsilon _f\) replaced by 2 as both sides vanish when f is odd: the right-hand side vanishes due to the fact that \(\Lambda (1/2,f \otimes \chi _D) = \Lambda (1/2,f) \Lambda (1/2,f \otimes g_{\psi ^2}) = 0\), for Lemma A.2 shows that the root number in both cases is \(-1\), while the left-hand side vanishes since one can make the change of variables \(z \mapsto -{\overline{z}}\) in the integral over \(\Gamma _0(D) \backslash \mathbb {H}\), which leaves \(|g_{\psi }(z)|^2\) unchanged but replaces f(z) with \(-f(z)\).
We have thereby reduced both problems to subconvex moment bounds. To this end, for a function \(h : \mathbb {R}\cup i(-1/2,1/2) \rightarrow \mathbb {C}\), we define the mixed moments
We prove the following bounds for these terms for various choices of function h.
Proposition 1.21
There exists some \(\alpha > 0\) and a constant \(\delta > 0\) such that the following hold:
- (1)
For \(h(t) = 1_{E \cup -E}(t)\) with \(E = [T,2T]\) and \(T \le t_g^{1 - \alpha }\),
$$\begin{aligned} \mathcal {M}^{\text{ Maa }\ss {}}(h) + \mathcal {M}^{\text{ Eis }}(h) \ll T t_g^{1 - \delta }. \end{aligned}$$ - (2)
For
$$\begin{aligned} h(t) = \frac{\pi H(t) 1_{E \cup -E}(t)}{8D^2 L(1,\chi _D)^2 L(1,g_{\psi ^2})^2} \end{aligned}$$with H(t) as in (2.3) and \(E = (t_g^{1 - \alpha }, 2t_g - t_g^{1 - \alpha })\),
$$\begin{aligned} \mathcal {M}^{\text{ Maa }\ss {}}(h) + \mathcal {M}^{\text{ Eis }}(h) = \frac{2}{{{\,\mathrm{vol}\,}}(\Gamma _0(D) \backslash \mathbb {H})} + O(t_g^{-\delta }). \end{aligned}$$ - (3)
For \(h(t) = 1_{E \cup -E}(t)\) with \(E = [T - U,T + U]\), where \(2t_g - t_g^{1 - \alpha } \le T \le 2t_g + t_g^{1 - \alpha }\) and \(\max \{|2t_g - T|,T^{1/3}\} \ll U \le T\),
$$\begin{aligned} \mathcal {M}^{\text{ Maa }\ss {}}(h) + \mathcal {M}^{\text{ Eis }}(h) \ll _{\varepsilon } (TU)^{1 + \varepsilon }. \end{aligned}$$ - (4)
For \(h(t) = 1_{E \cup -E}(t)\) with \(E = [T,2T]\) and \(T > 2t_g + t_g^{1 - \alpha }\),
$$\begin{aligned} \mathcal {M}^{\text{ Maa }\ss {}}(h) + \mathcal {M}^{\text{ Eis }}(h) \ll _{\varepsilon } T^{2 + \varepsilon }. \end{aligned}$$ - (5)
For \(h(t) = 1_{E \cup -E}(t)\) with \(E = i(0,1/2)\),
$$\begin{aligned} \mathcal {M}^{\text{ Maa }\ss {}}(h) \ll t_g^{1 - \delta }. \end{aligned}$$
As in [Hum18, Section 3.2], this covers the five ranges of the spectral expansion:
- (1)
the short initial range \([-t_g^{1 - \alpha },t_g^{1 - \alpha }]\),
- (2)
the bulk range \((-2t_g + t_g^{1 - \alpha }, -t_g^{1 - \alpha }) \cup (t_g^{1 - \alpha }, 2t_g - t_g^{1 - \alpha })\),
- (3)
the short transition range \([-2t_g - t_g^{\alpha }, -2t_g + t_g^{1 - \alpha }] \cup [2t_g - t_g^{1 - \alpha }, 2t_g + t_g^{1 - \alpha }]\),
- (4)
the tail range \((-\infty , -2t_g - t_g^{1 - \alpha }) \cup (2t_g + t_g^{1 - \alpha },\infty )\), and
- (5)
the exceptional range \(i(-1/2,1/2) \setminus \{0\}\).
Remark 1.22
For the purposes of proving Theorem 1.7, the exact identities in Propositions 1.13 and 1.16 as well as the asymptotic formula in Proposition 1.21 (2) are superfluous, for we could make do with upper bounds in each case in order to prove the desired upper bound for \({{\,\mathrm{Var}\,}}(g_{\psi };R)\). These identities, however, are necessary to prove the desired asymptotic formula for the fourth moment of \(g_{\psi }\) in Theorem 1.9.
Remark 1.23
The large sieve yields with relative ease the bounds \(O_{\varepsilon }((Tt_g)^{1 + \varepsilon })\) and \(O_{\varepsilon }(t_g^{\varepsilon })\) for Proposition 1.21 (1) and (2) respectively; dropping all but one term then only yields the convexity bound for the associated L-functions. These weaker bounds imply that the variance \({{\,\mathrm{Var}\,}}(g_{\psi };R)\) and the fourth moment of \(g_{\psi }\) are both \(O_{\varepsilon }(t_g^{\varepsilon })\), with the latter being a result of Luo [Luo14, Theorem] and the former falling just short of proving small scale mass equidistribution.
1.6 A sketch of the proofs and the structure of the paper.
We briefly sketch the main ideas behind the proofs of Propositions 1.13, 1.16, and 1.21.
The proof of Proposition 1.13, given in Section 3, uses the spectral decomposition of \(L^2(\Gamma _0(q) \backslash \mathbb {H})\) and Parseval’s identity to spectrally expand the variance and the fourth moment. We then require an orthonormal basis in terms of newforms and translates of oldforms together with an explicit description of the action of Atkin–Lehner operators on these Maaß forms in order to obtain (1.14) and (1.15).
Proposition 1.16 is an explicit form of the Watson–Ichino formula, which relates the integral of three \({{\,\mathrm{GL}\,}}_2\)-automorphic forms to a special value of a triple product L-function; we present this material in Section 4. To ensure that the identities (1.17) and (1.18) are correct not merely up to multiplication by an unspecified constant requires a careful translation of the adèlic identity [Ich08, Theorem 1.1] into the classical language of automorphic forms. Moreover, this identity involves local constants at ramified primes, and the precise set-up of our problem involves determining such local constants, which is undertaken in Section 5. This problem of the determination of local constants in the Watson–Ichino formula is of independent interest; see, for example, [Col18, Col19, Hu16, Hu17, Wat08].
The proof of Proposition 1.21 takes up the bulk of this paper, for it is rather involved and requires several different strategies to deal with various ranges. The many (predominantly) standard automorphic tools used in the course of the proof, such as the approximate functional equation, the Kuznetsov formula, and the large sieve, are relegated to Appendix A; we recommend that on first reading, the reader familiarise themself with these tools via a quick perusal of Appendix A before continuing on to the proof of Proposition 1.21 that begins in Section 6.
Proposition 1.21 (1), proven in Section 9, requires three different treatments for three different parts of the short initial range. We may use hybrid subconvex bounds for \(L(1/2,f \otimes g_{\psi ^2})\) and \(|L(1/2 + it,g_{\psi ^2})|^2\) due to Michel and Venkatesh [MV10] to treat the range \(T \le t_g^{\beta }\) for an absolute constant \(\beta > 0\). For \(t_g^{\beta } < T \le t_g^{1/2}\), we use subconvex bounds for \(L(1/2, f \otimes \chi _D)\) and \(|L(1/2 + it,\chi _D)|^2\) due to Young [You17] together with bounds proven in Section 6 for the first moment of \(L(1/2,f \otimes g_{\psi ^2})\) and of \(|L(1/2 + it,g_{\psi ^2})|^2\). This approach relies crucially on the nonnegativity of \(L(1/2,f \otimes g_{\psi ^2})\) (see, for example, the discussion on this point in [HT14, Section 1.1]). Bounds for the remaining range \(t_g^{1/2} < T \le t_g^{1 - \alpha }\) for Proposition 1.21 (1) are shown in Sections 7 and 8 to follow from the previous bounds for the range \(t_g^{\alpha } \ll T \ll t_g^{1/2}\). This is spectral reciprocity: via the triad of Kuznetsov, Voronoĭ, and Kloosterman summation formulæ (the latter being the Kuznetsov formula in the formulation that expresses sums of Kloosterman sums in terms of Fourier coefficients of automorphic forms), bounds of the form
with \(h(t) = 1_{E \cup -E}(t)\) for \(E = [T,2T]\) are essentially implied by the same bounds with \(E = [t_g/T,2t_g/T]\) together with analogous bounds for moments involving holomorphic cusp forms of even weight \(k \in [t_g/T,2t_g/T]\).
The proof of Proposition 1.21 (2) for the bulk range, appearing in Section 10, mimics that of the analogous result for Eisenstein series given in [DK18b]. As such, we give a laconic sketch of the proof, highlighting mainly the slight differences compared to the Eisenstein case.
Proposition 1.21 (3) is proven in Section 13 and relies upon the Cauchy–Schwarz inequality; the resulting short second moment of Rankin–Selberg L-functions is bounded via the large sieve, while a bound is also required for a short mixed moment of four L-functions. This latter bound is again a consequence of spectral reciprocity, akin to [Jut01, Theorem], and is detailed in Sections 11 and 12.
In Section 14, we show that Proposition 1.21 (4) is a simple consequence of the large sieve, while Proposition 1.21 (5) is shown in Section 15 to follow once more from hybrid subconvex bounds for \(L(1/2,f \otimes g_{\psi ^2})\) and \(|L(1/2 + it,g_{\psi ^2})|^2\) due to Michel and Venkatesh [MV10].
1.7 Further heuristics.
We give some very rough back-of-the-envelope type calculations to go along with the sketch above. Proposition 1.21 requires the evaluation of a mean value of L-functions looking essentially like
where we pretend that D equals 1, since it is anyway fixed. The goal is to extract the main term with an error term bounded by a negative power of \(t_g\). The expression remains unchanged if the summand is multiplied by the parity \(\epsilon _f = \pm 1\) of f, because \(L(1/2,f) = 0\) when \(\epsilon _f = -1\). Summing over \(t_f\) using the opposite-sign case of the Kuznetsov formula gives, in the dyadic range \( t_f\sim T\), an off-diagonal of the shape
where d(n) is the divisor function. Note that for the sake of argument, we use approximate functional equations, although our proof works with Dirichlet series in regions of absolute convergence and continues meromorphically at the last possible moment.
Consider the case \(t_g^{\alpha } \le T \le 2t_g - t_g^{1 - \alpha }\), which includes the short initial and bulk ranges, so that \(m \sim t_g^2\) and \(c \sim t_g\). Applying the Voronoĭ summation formula to both n and m returns a sum like
Note that \(c \sim (T/2t_g) \sqrt{mn}\), so applying the Kloosterman summation formula gives
This can be recast as essentially
The phenomenon of the same mean value of L-functions reappearing but with the range of summation now reciprocated to \(t_f < 2t_g/T\) is spectral reciprocity, as alluded to above.
When \(T \sim t_g\), the bulk range, we immediately get a satisfactory estimate by inserting subconvexity bounds. When \(T < t_g^{1 - \alpha }\), the short initial range, we are not done right away, but we at least reduce to the case \(T < t_g^{1/2}\). In this range, we must use a new approach. The idea is to bound, using nonnegativity of central values, \(L(1/2,f)^2\) by subconvexity bounds and then to estimate the first moment \(\sum _{t_f \sim T} L(1/2, f\otimes g_{\psi ^2})\). This is not an easy task because the sum over \(t_f\) is very short. We expand the first moment using approximate functional equations, apply the Kuznetsov formula, use the Voronoĭ summation formula, and then estimate; this turns out to be sufficient. Finally, it remains to consider the short transition range \(|t_f - 2t_g| \sim T\) with \(|T| < t_g^{1 - \alpha }\). Here the strategy is to apply the Cauchy–Schwarz inequality and consider \(\sum _{t_f} L(1/2,f)^4\) and \(\sum _{t_f} L(1/2, f\otimes g_{\psi ^2})^2\), the latter of which can be estimated sharply using the spectral large sieve, while the former can be bounded once again via spectral reciprocity.
1.8 Related results for the fourth moment and spectral reciprocity.
Bounds of the form \(O_{\varepsilon }(t_g^{\varepsilon })\) for the fourth moment of the truncation of an Eisenstein series \(E(z,1/2 + it_g)\) or for a dihedral Maaß form \(g = g_{\psi }\) have been proven by Spinu [Spi03] and Luo [Luo14] respectively; the proofs use the Cauchy–Schwarz inequality and the large sieve to bound moments of L-functions and rely on the factorisation of the L-functions appearing in the Watson–Ichino formula. In applying the large sieve to the bulk range, this approach loses the ability to obtain an asymptotic formula.
Sarnak and Watson [Sar03, Theorem 3(a)] noticed that via the \({{\,\mathrm{GL}\,}}_3\) Voronoĭ summation formula coupled with the convexity bound for \(L(1/2,f \otimes {{\,\mathrm{sym}\,}}^2 g)\), one could prove the bound \(O_{\varepsilon }(t_g^{\varepsilon })\) for the bulk range of the spectral expansion of the fourth moment of a Maaß cusp form (cf. [Hum18, Remark 3.3]). This approach was expanded upon by Buttcane and the second author [BuK17b], where an asymptotic for this bulk range was proven under the assumption of the generalised Lindelöf hypothesis. Asymptotics for a moment closely related to that appearing in Proposition 1.21 (2) are proven in [BuK17a]; the method is extremely similar to that used in [BuK17b]. Finally, asymptotics for the bulk range appearing in the spectral expansion of the regularised fourth moment of an Eisenstein series are proven in [DK18b] (and Proposition 1.21 (2) is proven via minor modifications of this proof). These results all follow via the triad of Kuznetsov, Voronoĭ, and Kloosterman summation formulæ, and are cases of spectral reciprocity: the moment of L-functions in the bulk range is shown to be equal to a main term together with a moment of L-functions that is essentially extremely short, namely involving forms f for which \(t_f \ll t_g^{\varepsilon }\).
This nonetheless leaves the issue of dealing with the short initial and transition ranges. Assuming the generalised Lindelöf hypothesis, it is readily seen that these are negligible. Spectral reciprocity in the short initial range is insufficient to prove this, since it merely replaces the problem of bounding the contribution from the range [T, 2T] with that of the range \([T/t_g,2T/t_g]\). Our key observation is that spectral reciprocity reduces the problem to the range \(T < t_g^{1/2}\), at which point we may employ a different strategy, namely subconvex bounds for \(L(1/2,f) L(1/2, f \otimes \chi _D)\) together with a bound for the first moment of \(L(1/2, f \otimes g_{\psi ^2})\). This approach, albeit in a somewhat disguised form, is behind the success of the unconditional proofs of the negligibility of the short initial and transition ranges for the regularised fourth moment of an Eisenstein series. These follow from the work of Jutila [Jut01] and Jutila and Motohashi [JM05]; see [Hum18, Lemmata 3.7 and 3.8].
1.9 Connections to subconvexity.
Quantifying the rate of equidistribution for quantum unique ergodicity in terms of bounds for (1.1) is, via the Watson–Ichino formula, equivalent to determining subconvex bounds for \(L(1/2,f \otimes {{\,\mathrm{ad}\,}}g)\) in the \(t_g\)-aspect. Such bounds are yet to be proven except in a select few cases, namely when g is dihedral or an Eisenstein series, where \(L(1/2, f \otimes {{\,\mathrm{ad}\,}}g)\) factorises as
Indeed, quantum unique ergodicity was already known for Eisenstein series [LS95] before the work of Lindenstrauss [Lin06] and Soundararajan [Sou10], and for dihedral Maaß forms [Blo05] with quantitative bounds for (1.1) shortly thereafter (see also [Sar01, LY02, LLY06a, LLY06b]). The proofs of Theorems 1.7 and 1.9, as well as their Eisenstein series counterparts [DK18b, Hum18], rely crucially on these factorisations, and the chief hindrance behind the lack of an unconditional proof of these theorems for an arbitrary Maaß cusp form is the lack of such a factorisation.
In proving Theorem 1.7, on the other hand, we require bounds for the moments given in Proposition 1.21, most notably in the range \(E = [T,2T]\) with \(T < t_g^{1 - \alpha }\). Dropping all but one term in this range implies the hybrid subconvex bounds
for these products of L-functions with analytic conductors \(\asymp (t_f t_g)^4\) and \(\asymp (|t| t_g)^4\) respectively. Such bounds for product L-functions were previously known, and at various points in the proof of Proposition 1.21 we make use of known subconvex bounds for individual L-functions in this product; what is noteworthy is that individual subconvex bounds are insufficient for proving Theorems 1.7 and 1.9, but rather bounds for moments that imply subconvexity are required.
Remark 1.24
This demonstrates the difficulty of proving Theorems 1.7 and 1.9 unconditionally for arbitrary Hecke–Maaß eigenforms g: as mentioned in [BuK17b, p. 1493], we would require a subconvex bound of the form \(L(1/2,f \otimes {{\,\mathrm{ad}\,}}g) \ll t_g^{1 - \delta }\) uniformly in \(t_f < t_g^{\delta '}\) for some \(\delta ' > 0\), a well-known open problem. On the other hand, Sarnak [Sar03, Conjecture 4] conjectures the weaker upper bound \(O_{\varepsilon }(t_g^{\varepsilon })\) for the fourth moment of an arbitrary Hecke–Maaß eigenform g, which would not require such a subconvex bound.
2 Proofs of Theorems 1.7 and 1.9
Proofs of Theorems 1.7 and 1.9 assuming Propositions 1.13, 1.16, and 1.21
From Propositions 1.13 and 1.16, \({{\,\mathrm{Var}\,}}(g_{\psi };R)\) is equal to the sum of
and
with
Via Stirling’s formula
for \(\left| \arg s\right| < \pi \) [GR07, 8.327.1],
for \(t \in \mathbb {R}\cup i(-1/2,1/2)\), where
It follows that
with
We recall the bound \(L(1, g_{\psi ^2}) \gg 1/\log t_g\), as well as [Hum18, Lemma 4.2], which states that as R tends to zero,
where \(J_{\nu }(z)\) denotes the Bessel function of the first kind. Moreover, \(h_R(t) \ll 1\) if \(R \ll 1\) and \(t \in i(0,1/2)\).
We bound \(\mathcal {M}^{\text{ Maa }\ss {}}(h) + \mathcal {M}^{\text{ Eis }}(h)\) by breaking this up into intervals for which we can apply Proposition 1.21 and using the bounds (2.5) and (2.6): for the short initial and tail ranges, we use dyadic intervals, while for the short transition range, we divide into intervals of the form \([T - U,T + U]\) with \(T = 2t_g \mp 3 \cdot 2^{-n - 1} t_g^{1 - \alpha }\) and \(U = 2^{-n - 1} t_g^{1 - \alpha }\) for positive integers \(n \le (\frac{2}{3} - \alpha ) \frac{\log t_g}{\log 2} - 1\), as well as the interval \([2t_g - t_g^{1/3},2t_g + t_g^{1/3}]\). The fact that \(R \gg t_g^{-\delta }\) with \(\delta < 1\) implies that \(h_R(t)\) has polynomial decay in t when t is in the bulk range; the proof of Theorem 1.7 is thereby complete.
Theorem 1.9 is proven much in the same way, as the fourth moment is equal to the sum of \(1/{{\,\mathrm{vol}\,}}(\Gamma _0(D) \backslash \mathbb {H})\), (2.1), and (2.2) with \(h_R(t)\) replaced by 1. We find that the short initial, short transition, tail, and exceptional ranges all contribute at most \(O(t_g^{-\delta '})\), while the bulk range contributes \(2/{{\,\mathrm{vol}\,}}(\Gamma _0(D) \backslash \mathbb {H}) + O(t_g^{-\delta '})\). \(\square \)
Remark 2.7
The method of proof also gives \({{\,\mathrm{Var}\,}}(g_{\psi };R) \sim 2/{{\,\mathrm{vol}\,}}(\Gamma _0(D) \backslash \mathbb {H})\) if \(R \ll t_g^{-\delta }\) with \(\delta > 1\), while a modification of Proposition 1.21 (2) implies that there exists an absolute constant \(\alpha > 0\) such that for \(t_g^{-1 - \alpha } \ll R \ll t_g^{-1 + \alpha }\),
where \({}_{p}{F}_q\) denotes the generalised hypergeometric function. This corrects an erroneous asymptotic formula in [Hum18, Remark 5.4].
3 The Spectral Expansion of \({{\,\mathrm{Var}\,}}(g;R)\) and the Fourth Moment
3.1 An orthonormal basis of Maaß cusp forms for squarefree levels.
The proof of Proposition 1.13, which we give in Section 3.4, invokes the spectral decomposition of \(L^2(\Gamma _0(q) \backslash \mathbb {H})\), which involves a spectral sum indexed by an orthonormal basis \(\mathcal {B}_0(\Gamma _0(q))\) of the space of Maaß cusp forms of weight zero, level q, and principal nebentypus. This space has the Atkin–Lehner decomposition
where \((\iota _{\ell } f)(z) :=f(\ell z)\), but this decomposition is not orthogonal for \(q > 1\). Nevertheless, an orthonormal basis can be formed using linear combinations of elements of this decomposition.
Lemma 3.1
([ILS00, Proposition 2.6]). An orthonormal basis of the space of Maaß cusp forms of weight zero, squarefree level q, and principal nebentypus is given by
where each newform \(f \in \mathcal {B}_0^{*}\left( \Gamma _0(q_1)\right) \) is normalised such that \(\langle f, f \rangle _q = 1\) and
Proof
In [ILS00, Proposition 2.6], this is proved with
Using the fact that \(\lambda _f(p)^2 = \lambda _f(p^2) + 1\) and
for \(p \not \mid q_1\), this simplifies to the desired identity. \(\square \)
We record here the following identities, which follow readily from the multiplicativity of the summands involved.
Lemma 3.2
Suppose that \(q_1,q_2\) are squarefree with \((q_1,q_2) = 1\). Then for a newform \(f \in \mathcal {B}_0^{*}(\Gamma _0(q_1))\) and \(\ell \mid q_2\), we have that
3.2 An orthonormal basis of Eisenstein series for squarefree levels.
A similar orthonormal basis exists for Eisenstein series. Instead of the usual orthonormal basis
we may form an orthonormal basis out of Eisenstein series newforms and oldforms: a basis of the space of Eisenstein series of weight zero, level q, and principal nebentypus is given by
Here
where E(z, s) is the usual Eisenstein series on \(\Gamma \backslash \mathbb {H}\), defined for \(\mathfrak {R}(s) > 1\) by
with \(\Gamma :={{\,\mathrm{SL}\,}}_2(\mathbb {Z})\) and \(\Gamma _{\infty } :=\{\gamma \in \Gamma : \gamma \infty = \infty \}\) the stabiliser of the cusp at infinity. For \(t \in \mathbb {R}\setminus \{0\}\), this has the Fourier expansion
with \(W_{\alpha ,\beta }\) the Whittaker function,
The Eisenstein series \(E(z,1/2 + it)\) is normalised such that its formal inner product with itself on \(\Gamma \backslash \mathbb {H}\) is 1 (in the sense of [Iwa02, Proposition 7.1]), and so the formal inner product of \(E_1(z,1/2 + it)\) with itself on \(\Gamma _0(q) \backslash \mathbb {H}\) is 1.
This basis is not orthogonal for \(q > 1\), but Young [You19] has shown that there exists an orthonormal basis derived from this basis just as for Maaß cusp forms, as in Lemma 3.1.
Lemma 3.3
([You19, Section 8.4]). An orthonormal basis of the space of Eisenstein series of weight 0, level q, and principal nebentypus is given by
where \(E_{\ell }(z,1/2 + it)\) is defined to be
As with Lemma 3.2, we have the following identities.
Lemma 3.4
For squarefree q and \(\ell \mid q\), we have that
3.3 Inner products with oldforms and Eisenstein series.
To deal with inner products involving oldforms and Eisenstein series, we use Atkin–Lehner operators. For squarefree q, write \(q = vw\), and denote by
the Atkin–Lehner operator on \(\Gamma _0(q)\) associated to w, where \(a,b,c,d \in \mathbb {Z}\) and \(\det W_w = adw - bcv = 1\). We denote by \(\mathcal {B}_{\text{ hol }}^{*}(q,\chi )\) the set of holomorphic newforms f of level q, nebentypus \(\chi \), and arbitrary even weight \(k_f \in 2\mathbb {N}\); again, we write \(\mathcal {B}_{\text{ hol }}^{*}(\Gamma _0(q))\) when \(\chi \) is the principal character.
Lemma 3.5
([AL78, Theorem 2.1]; see also [KMV02, Proposition A.1]). Let \(q = vw\) be squarefree and let \(\chi \) be a Dirichlet character of conductor \(q_{\chi }\) dividing q, so that we may write \(\chi = \chi _v \chi _w\). Then for \(g \in \mathcal {B}_0^{*}(q,\chi )\), \(g(W_w z)\) is equal to \(\eta _g(w) (g \otimes \overline{\chi _w})(z)\), where \(g \otimes \overline{\chi _w} \in \mathcal {B}_0^{*}(q, \chi _v \overline{\chi _w})\) with
In particular, \(|\eta _g(w)| = 1\). Moreover, the same result holds for \(g \in \mathcal {B}_{\text{ hol }}^{*}(q,\chi )\), so that \(g \otimes \overline{\chi _w} \in \mathcal {B}_{\text{ hol }}^{*}(q, \chi _v \overline{\chi _w})\).
We call \(\eta _g(w)\) the Atkin–Lehner pseudo-eigenvalue; note that it is independent of \(a,b,c,d \in \mathbb {Z}\) when either \(\chi \) is the principal character or \(a \equiv 1 \pmod {v}\) and \(b \equiv 1 \pmod {w}\), or equivalently \(d \equiv {\overline{w}} \pmod {v}\) and \(c \equiv {\overline{v}} \pmod {w}\).
Lemma 3.6
Let \(q = q_1 q_2\) be squarefree, let \(\chi \) be a Dirichlet character modulo q, and let \(g \in \mathcal {B}_0^{*}\left( q,\chi \right) \) and \(f \in \mathcal {B}_0^{*}\left( \Gamma _0(q_1)\right) \). Then for \(vw = q_2\), so that \(\chi = \chi _v \chi _w \chi _{q_1}\),
Proof
Since the Atkin–Lehner operators normalise \(\Gamma _0(q)\),
By Lemma 3.5, \(|g(W_w z)|^2 = |(g \otimes \overline{\chi _w})(z)|^2\), while
and so as f is invariant under the action of \(\Gamma _0(q_1)\),
So whenever v divides \(q_2\), \(\left\langle |g|^2, \iota _v f \right\rangle _q = \left\langle |g \otimes \overline{\chi _w}|^2, \iota _{q_2} f \right\rangle _q\). Taking \(v = 1\), \(w = q_2\), and replacing g with \(g \otimes \overline{\chi _v}\), which has nebentypus \(\overline{\chi _v} \chi _w \chi _{q_1}\), then shows that \(\left\langle |g \otimes \overline{\chi _v}|^2, f \right\rangle _q = \left\langle |g \otimes \overline{\chi _w}|^2, \iota _{q_2} f \right\rangle _q\). \(\square \)
We now prove an analogous result for Eisenstein series. In this case, we may use Eisenstein series indexed by cusps (though later we will find it advantageous to work with Eisenstein newforms and oldforms). As q is squarefree, a cusp \(\mathfrak {a}\) of \(\Gamma _0(q) \backslash \mathbb {H}\) has a representative of the form 1/v for some divisor v of q, and every cusp has a unique representative of this form; when \(\AA \sim \infty \), for example, we have that \(v = q\). We define the Eisenstein series
which converges absolutely for \(\mathfrak {R}(s) > 1\) and \(z \in \mathbb {H}\), where
is the stabiliser of the cusp \(\mathfrak {a}\), and the scaling matrix \(\sigma _{\mathfrak {a}} \in {{\,\mathrm{SL}\,}}_2(\mathbb {R})\) is such that
The Eisenstein series \(E_{\mathfrak {a}}(z,s)\) is independent of the choice of scaling matrix.
Writing \(q = vw\), we may choose \(\sigma _{\mathfrak {a}} = W_w\) with
the Atkin–Lehner operator on \(\Gamma _0(q)\) associated to w, where \(dw - bv = 1\).
Lemma 3.7
Let \(g \in \mathcal {B}_0^{*}(q,\chi )\) with q squarefree, and let \(\AA \sim 1/v\) be a cusp of \(\Gamma _0(q) \backslash \mathbb {H}\). Then
Proof
By unfolding, using Lemma 3.5, and folding, we find that
\(\square \)
Finally, we claim that twisting g leaves these inner products unchanged. Alas, we do not know a simple proof of this fact; as such, the proof is a consequence of calculations in Sections 4 and 5.
Lemma 3.8
For \(q = q_1 q_2\) squarefree and \(g \in \mathcal {B}_0^{*}(q,\chi )\) with \(\chi \) primitive, we have that
Furthermore, for \(f \in \mathcal {B}_0^{*}(\Gamma _0(q_1))\) and \(w \mid q_2\),
Proof
The former is a consequence of Corollary 4.9, while the latter follows upon combining Lemma 3.6 with Corollary 4.19. \(\square \)
3.4 Proof of Proposition 1.13.
Proof of Proposition 1.13
An application of Parseval’s identity, using the spectral decomposition of \(L^2(\Gamma _0(q) \backslash \mathbb {H})\) [IK04, Theorem 15.5], together with the fact that
for any Laplacian eigenfunction f [Hum18, Lemma 4.3], yields
see [Hum18, Proof of Proposition 5.2]. By Lemmata 3.1, 3.2, 3.6, and 3.8,
for any \(t \in [0,\infty ) \cup i(0,1/2)\). Similarly, Lemmata 3.7 and 3.8 imply that
for any \(t \in \mathbb {R}\). This gives the desired spectral expansion for \({{\,\mathrm{Var}\,}}(g;R)\), while the spectral expansion for the fourth moment of g follows similarly, noting that the constant term \(1/\sqrt{{{\,\mathrm{vol}\,}}(\Gamma _0(q) \backslash \mathbb {H})}\) in the spectral expansion gives rise to the term \(1/{{\,\mathrm{vol}\,}}(\Gamma _0(q) \backslash \mathbb {H})\) in (1.15). \(\square \)
4 The Watson–Ichino Formula
4.1 The Watson–Ichino formula for Eisenstein series.
We require explicit expressions in terms of L-functions for \(|\langle |g|^2,f \rangle _q|^2\) and \(|\langle |g|^2,E_{\infty }(\cdot ,1/2 + it) \rangle _q|^2\). This is the contents of the Watson–Ichino formula. In the latter case, this result is simply the Rankin–Selberg method, which far predates the work of Watson and Ichino; it can be proven by purely classical means via unfolding the Eisenstein series, as we shall now detail.
Recall that a Maaß newform \(g \in \mathcal {B}_0^{*}(q,\chi )\) has the Fourier expansion about the cusp at infinity of the form
where the Fourier coefficients \(\rho _g(n)\) satisfy \(\rho _g(n) = \epsilon _g \rho _g(-n)\), with the parity \(\epsilon _g\) of g equal to 1 if g is even and \(-1\) if g is odd. The Hecke eigenvalues \(\lambda _g(n)\) of g satisfy
Lemma 4.4
Let \(g \in \mathcal {B}_0^{*}(q_1,\chi )\) with \(q_1 q_2 = q\) and \(q_1 \equiv 0 \pmod {q_{\chi }}\), where \(q_{\chi }\) is the conductor of \(\chi \). We have that
Proof
Unfolding the integral and using Parseval’s identity and (4.3) yields
after the change of variables \(y \mapsto y/(4\pi |n|y)\). The result then follows via the Mellin–Barnes formula [GR07, 6.576.4]. \(\square \)
Lemma 4.6
Let q be squarefree, and let \(g \in \mathcal {B}_0^{*}(q_1,\chi )\) with \(q_1 q_2 = q\) and \(q_1 \equiv 0 \pmod {q_{\chi }}\). We have that
for \(\mathfrak {R}(s) > 1\) and that
Proof
We recall that
with
Using (4.1) and (4.2) together with the fact that
we obtain (4.7). Next, we take the residue of (4.5) at \({\overline{s}} = 1\), noting that \(E_{\infty }(z,s)\) has residue
at \(s = 1\) independently of \(z \in \Gamma _0(q) \backslash \mathbb {H}\). This yields the desired identity (4.8). \(\square \)
Corollary 4.9
Let q be squarefree, and let \(g \in \mathcal {B}_0^{*}(q_1,\chi )\) with \(q_1 q_2 = q\) and \(q_1 \equiv 0 \pmod {q_{\chi }}\), where g is normalised such that \(\langle g, g \rangle _q = 1\). We have that
for \(\mathfrak {R}(s) \ge 1/2\) with \(s \ne 1\), so that
Note that Corollary 4.9 remains valid when g is replaced by \(g \otimes \chi _v\) for \(v \mid q_{\chi }\), since the level is unchanged and \({{\,\mathrm{ad}\,}}(g \otimes \chi _v) = {{\,\mathrm{ad}\,}}g\).
Remark 4.11
One can also prove (4.10) adèlically; see, for example, [MV10, (4.21)].
4.2 The Adèlic Watson–Ichino formula for Maaß newforms.
Now we consider the inner product \(|\langle |g|^2, f\rangle _q|^2\). The Watson–Ichino formula is an adèlic statement: the integral over \(\Gamma _0(q) \backslash \mathbb {H}\) is replaced by an integral over \(\mathrm {Z}(\mathbb {A}_{\mathbb {Q}}) {{\,\mathrm{GL}\,}}_2(\mathbb {Q}) \backslash {{\,\mathrm{GL}\,}}_2(\mathbb {A}_{\mathbb {Q}})\), and g and f are replaced by functions on \({{\,\mathrm{GL}\,}}_2(\mathbb {Q}) \backslash {{\,\mathrm{GL}\,}}_2(\mathbb {A}_{\mathbb {Q}})\) that are square integrable modulo the centre \(\mathrm {Z}(\mathbb {A}_{\mathbb {Q}})\) and are elements of cuspidal automorphic representations of \({{\,\mathrm{GL}\,}}_2(\mathbb {A}_{\mathbb {Q}})\). In Section 4.3, we translate this adèlic statement into a statement in the classical language of automorphic forms.
Let F be a number field, and let \(\varphi _1 = \bigotimes _v \varphi _{1,v}\), \(\varphi _2 = \bigotimes _v \varphi _{2,v}\), \(\varphi _3 = \bigotimes _v \varphi _{3,v}\) be pure tensors in unitary cuspidal automorphic representations \(\pi _1 = \bigotimes _v \pi _{1,v}\), \(\pi _2 = \bigotimes _v \pi _{2,v}\), \(\pi _3 = \bigotimes _v \pi _{3,v}\) of \({{\,\mathrm{GL}\,}}_2(\mathbb {A}_F)\) with central characters \(\omega _{\pi _1}\), \(\omega _{\pi _2}\), \(\omega _{\pi _3}\) satisfying \(\omega _{\pi _1} \omega _{\pi _2} \omega _{\pi _3} = 1\), and let \({\widetilde{\varphi }}_1 = \bigotimes _v {\widetilde{\varphi }}_{1,v}\), \({\widetilde{\varphi }}_2 = \bigotimes _v {\widetilde{\varphi }}_{2,v}\), \({\widetilde{\varphi }}_3 = \bigotimes _v {\widetilde{\varphi }}_{3,v}\) be pure tensors in the contragredient representations \({\widetilde{\pi }}_1 = \bigotimes _v {\widetilde{\pi }}_{1,v}\), \({\widetilde{\pi }}_2 = \bigotimes _v {\widetilde{\pi }}_{2,v}\), \({\widetilde{\pi }}_3 = \bigotimes _v \pi _{3,v}\). Let
with dg the Tamagawa measure on \(\mathrm {Z}(\mathbb {A}_F) {{\,\mathrm{GL}\,}}_2(F) \backslash {{\,\mathrm{GL}\,}}_2(\mathbb {A}_F)\). For each place v of F with corresponding local field \(F_v\), we also let
The Haar measure \(dg_v\) on \(\mathrm {Z}(F_v) \backslash {{\,\mathrm{GL}\,}}_2(F_v)\) is normalised as follows:
For v nonarchimedean and \(x_v \in \mathrm {Z}(F_v) \backslash {{\,\mathrm{GL}\,}}_2(F_v)\), we may use the Iwasawa decomposition to write \(g_v = \left( {\begin{matrix} a_v &{} x_v \\ 0 &{} 1 \end{matrix}}\right) k_v\) with \(x_v \in F_v\), \(a_v \in F_v^{\times }\), and \(k_v \in {{\,\mathrm{GL}\,}}_2(\mathcal {O}_v)\). Then \(dg_v = dx_v \, |a_v|_v^{-1} \, d^{\times } a_v \, dk_v\). Here the additive Haar measure \(dx_v\) on \(F_v\) is normalised to give \(\mathcal {O}_v\) volume 1, the multiplicative Haar measure \(d^{\times } a_v = \zeta _v(1) |a_v|_v^{-1} \, da_v\) on \(F_v^{\times }\) is normalised to give \(\mathcal {O}_v^{\times } = {{\,\mathrm{GL}\,}}_1(\mathcal {O}_v)\) volume 1, and \(dk_v\) is the Haar probability measure on the compact group \({{\,\mathrm{GL}\,}}_2(\mathcal {O}_v)\).
For \(F_v \cong \mathbb {R}\) and \(x_v \in \mathrm {Z}(F_v) \backslash {{\,\mathrm{GL}\,}}_2(F_v)\), we may use the Iwasawa decomposition to write \(g_v = \left( {\begin{matrix} a_v &{} x_v \\ 0 &{} 1 \end{matrix}}\right) k_v\) with \(x_v \in \mathbb {R}\), \(a_v \in \mathbb {R}^{\times }\), and \(k_v = \left( {\begin{matrix} \cos \theta &{} \sin \theta \\ -\sin \theta &{} \cos \theta \end{matrix}}\right) \in {{\,\mathrm{SO}\,}}(2)\) with \(\theta \in [0,2\pi )\). Then \(dg_v = dx_v \, |a_v|_v^{-1} \, d^{\times } a_v \, dk_v\), where the additive Haar measure \(dx_v\) on \(\mathbb {R}\) is the usual Lebesgue measure normalised to give [0, 1] volume 1, the multiplicative Haar measure \(d^{\times } a_v\) on \(\mathbb {R}^{\times }\) is \(|a_v|_v^{-1} \, da_v\), and \(dk_v = (2\pi )^{-1} \, d\theta \) is the Haar probability measure on the compact group \({{\,\mathrm{SO}\,}}(2)\).
A similar definition can also be given for \(F_v \cong \mathbb {C}\), though we do not need this, since we will eventually take \(F = \mathbb {Q}\).
The Tamagawa measure dg on \(\mathrm {Z}(\mathbb {A}_F) {{\,\mathrm{GL}\,}}_2(F) \backslash {{\,\mathrm{GL}\,}}_2(\mathbb {A}_F)\) is such that
where
Here \(d_F\) denotes the discriminant of F, and we recall that the conductor of the Dedekind zeta function is \(|d_F|\), so that the completed Dedekind zeta function is \(\Lambda _F(s) = |d_F|^{s/2} \prod _v \zeta _v(s)\).
Theorem 4.14
([Ich08, Theorem 1.1]). The period integral \(I(\varphi \otimes {\widetilde{\varphi }}) / \langle \varphi , {\widetilde{\varphi }} \rangle \) is equal to
with \(I_v'(\varphi _v \otimes {\widetilde{\varphi }}_v)\) equal to 1 whenever \(\varphi _{1,v}\), \(\varphi _{2,v}\), \(\varphi _{3,v}\) and \({\widetilde{\varphi }}_{1,v}\), \({\widetilde{\varphi }}_{2,v}\), \({\widetilde{\varphi }}_{3,v}\) are spherical vectors at a nonarchimedean place v.
The quantity \(I_v'(\varphi _v \otimes {\widetilde{\varphi }}_v)\) is often called the local constant. When \(\varphi _1\), \(\varphi _2\), \(\varphi _3\) are pure tensors consisting of local newforms in the sense of Casselman (or in some cases translates of local newforms; see [Hu17] and [Col19, Section 2.1]), then these local constants depend only (but sensitively!) on the representations \(\pi _{1,v}\), \(\pi _{2,v}\), \(\pi _{3,v}\). The local constants have been explicitly determined for many different combinations of representations \(\pi _{1,v}\), \(\pi _{2,v}\), \(\pi _{3,v}\) of \({{\,\mathrm{GL}\,}}_2(F_v)\) (cf. [Col19, Sections 2.2 and 2.3]). We require several particular combinations of representations for our applications.
For \(F_v \cong \mathbb {R}\), let \(k(\pi _v) \in \mathbb {Z}\) denote the weight of \(\pi _v\) and let \(\epsilon _v \in \{1,i,-1,-i\}\) denote the local root number, so that \(\epsilon _v = (-1)^{m_v}\) for \(\pi _v\) a weight zero principal series representation \({{\,\mathrm{sgn}\,}}^{m_v} |\cdot |_v^{s_{1,v}} \boxplus {{\,\mathrm{sgn}\,}}^{m_v} |\cdot |_v^{s_{2,v}}\) with \(m_v \in \{0,1\}\).
Proposition 4.15
([Wat08, Theorem 3]). For \(F_v \cong \mathbb {R}\),
if \(k(\pi _{1,v}) = k(\pi _{2,v}) = k(\pi _{3,v}) = 0\).
Now let \(F_v\) be a nonarchimedean local field with uniformiser \(\varpi _v\) and cardinality \(q_v\) of the residue field. In Section 5, we prove the following.
Proposition 4.16
Let \(\pi _{1,v} = \omega _{1,v} \boxplus \omega _{1,v}'\) and \(\pi _{2,v} = {\widetilde{\pi }}_{1,v} = \omega _{1,v}'^{-1} \boxplus \omega _{1,v}^{-1}\) be principal series representations of \({{\,\mathrm{GL}\,}}_2(F_v)\) for which the characters \(\omega _{1,v}\), \(\omega _{1,v'}\) of \(F_v^{\times }\) have conductor exponents \(c(\omega _{1,v}) = 1\) and \(c(\omega _{1,v}') = 0\), and let \(\pi _{3,v} = \omega _{3,v} \mathrm {St}_v\) be a special representation with \(c(\omega _{3,v}) = 0\) and \(\omega _{3,v}^2 = 1\). Suppose that \(\pi _{1,v}\), \(\pi _{2,v}\), \(\pi _{3,v}\) are irreducible and unitarisable, so that \(\omega _{1,v}\), \(\omega _{1,v}'\), \(\omega _{3,v}\) are unitary. Then if \(\varphi _{1,v}\), \(\varphi _{2,v}\), \(\varphi _{3,v}\), \({\widetilde{\varphi }}_{1,v}\), \({\widetilde{\varphi }}_{2,v}\), \({\widetilde{\varphi }}_{3,v}\) are all local newforms,
Proposition 4.17
Let \(\pi _{1,v} = \omega _{1,v} \boxplus \omega _{1,v}'\), \(\pi _{2,v} = {\widetilde{\pi }}_{1,v} = \omega _{1,v}'^{-1} \boxplus \omega _{1,v}^{-1}\), and \(\pi _{3,v} = \omega _{3,v} \boxplus \omega _{3,v}^{-1}\) be principal series representations of \({{\,\mathrm{GL}\,}}_2(F_v)\) with \(c(\omega _{1,v}) = 1\) and \(c(\omega _{1,v}') = 0\), with \(c(\omega _{3,v}) = 0\). Suppose that \(\pi _{1,v}\), \(\pi _{2,v}\), \(\pi _{3,v}\) are irreducible and unitarisable, so that \(\omega _{1,v}\), \(\omega _{1,v}'\) are unitary while \(q^{-1/2}< |\omega _{3,v}(\varpi _v)| < q^{1/2}\). Then if \(\varphi _{1,v}\), \(\varphi _{2,v}\), \(\varphi _{3,v}\), \({\widetilde{\varphi }}_{1,v}\), \({\widetilde{\varphi }}_{2,v}\), \({\widetilde{\varphi }}_{3,v}\) are all local newforms,
This also holds if either or both \(\varphi _{3,v}\) and \({\widetilde{\varphi }}_{3,v}\) are translates of local newforms by \(\pi _{3,v} \left( {\begin{matrix}\varpi _v^{-1} &{} 0 \\ 0 &{} 1 \end{matrix}}\right) \) and \({\widetilde{\pi }}_{3,v} \left( {\begin{matrix}\varpi _v^{-1} &{} 0 \\ 0 &{} 1 \end{matrix}}\right) \) respectively.
Remark 4.18
The latter local constant has also been determined by Collins [Col19, Proposition 2.2.3]. Moreover, Collins [Col18, Section 5.2] has numerically verified both of these local constants, as well as the local constant in Remark 5.19.
4.3 The classical Watson–Ichino formula for Maaß newforms.
Now we restate the Watson–Ichino formula in the classical setting. For \(\ell \in \{1,2,3\}\), let \(f_{\ell } \in \mathcal {B}_0(q,\chi _{\ell })\) be a Hecke–Maaß eigenform of level q, nebentypus \(\chi _{\ell }\), and parity \(\epsilon _{f_{\ell }}\), and similarly let \({\widetilde{f}}_{\ell } \in \mathcal {B}_0(q,\overline{\chi _{\ell }})\) be a Hecke–Maaß eigenform such that \(f_{\ell }\) and \(\overline{{\widetilde{f}}}_{\ell }\) are both associated to the same newform. We assume additionally that \(\chi _1 \chi _2 \chi _3 = \chi _{0(q)}\), the principal character modulo q. Letting \(\varphi _1\), \(\varphi _2\), \(\varphi _3\) and \({\widetilde{\varphi }}_1\), \({\widetilde{\varphi }}_2\), \({\widetilde{\varphi }}_3\) denote the adèlic lifts of the Hecke–Maaß eigenforms \(f_1\), \(f_2\), \(f_3\) and \({\widetilde{f}}_1\), \({\widetilde{f}}_2\), \({\widetilde{f}}_3\), we have that
This adèlic-to-classical interpretation of the Watson–Ichino formula uses the fact that \(\Lambda (2) = \pi / 6\) and \({{\,\mathrm{vol}\,}}(\Gamma _0(q) \backslash \mathbb {H}) = \pi \nu (q) / 3\), as well as the identity
for \(f \in L^1(\Gamma _0(q) \backslash \mathbb {H})\) with corresponding adèlic lift \(\phi \in L^1(\mathrm {Z}(\mathbb {A}_{\mathbb {Q}}) {{\,\mathrm{GL}\,}}_2(\mathbb {Q}) \backslash {{\,\mathrm{GL}\,}}_2(\mathbb {A}_{\mathbb {Q}}))\); the factor 2 is present for this is the Tamagawa number of \(\mathrm {Z}(\mathbb {A}_{\mathbb {Q}}) {{\,\mathrm{GL}\,}}_2(\mathbb {Q}) \backslash {{\,\mathrm{GL}\,}}_2(\mathbb {A}_{\mathbb {Q}})\).
Corollary 4.19
For squarefree \(q = q_1 q_2\), \(g \in \mathcal {B}_0^{*}(q,\chi )\) with \(\chi \) primitive, \(f \in \mathcal {B}_0^{*}(q_1)\) normalised such that \(\langle g,g\rangle _q = \langle f,f\rangle _q = 1\), and \(w_1, w_2 \mid q_2\), we have that
Proof
We have the isobaric decomposition \(g \otimes {\overline{g}} = 1 \boxplus {{\,\mathrm{ad}\,}}g\), so that \(g \otimes {\overline{g}} \otimes f = f \boxplus f \otimes {{\,\mathrm{ad}\,}}g\), while \(f = {\overline{f}}\) implies that \({{\,\mathrm{ad}\,}}f = {{\,\mathrm{sym}\,}}^2 f\), and \({{\,\mathrm{ad}\,}}{\overline{g}} = {{\,\mathrm{ad}\,}}g\). Consequently, the conductor \(q(g \otimes {\overline{g}} \otimes f)\) also factorises as \(q(f) q(f \otimes {{\,\mathrm{ad}\,}}g)\). The conductors of f, \(f \otimes {{\,\mathrm{ad}\,}}g\), \({{\,\mathrm{ad}\,}}g\), and \({{\,\mathrm{sym}\,}}^2 f\) are \(q_1\), \(q^4 q_1\), \(q^2\), and \(q_1^2\) respectively (cf. Lemma A.2).
We denote by \(\pi _g\), \(\pi _{{\overline{g}}}\), \(\pi _f\) the cuspidal automorphic representations of \({{\,\mathrm{GL}\,}}_2(\mathbb {A}_{\mathbb {Q}})\) associated to g, \({\overline{g}}\), f respectively; note that \(\pi _{{\overline{g}}} = {\widetilde{\pi }}_g\). The Watson–Ichino formula gives
It remains to determine the local constants \(I_p'(\varphi _p \otimes {\widetilde{\varphi }}_p)\). We observe the following:
When \(p \mid q_1\), the local component \(\pi _{g,p}\) of g is a unitarisable ramified principal series representation \(\omega _{1,p} \boxplus \omega _{1,p}'\), where the unitary characters \(\omega _{1,p}, \omega _{1,p}'\) of \(\mathbb {Q}_p^{\times }\) have conductor exponents \(c(\omega _{1,p}) = 1\) and \(c(\omega _{1,p}') = 0\). The local component \(\pi _{f,p}\) of f is a special representation \(\omega _{3,p} \mathrm {St}\), where \(\omega _{3,p}\) is either the trivial character or the unramified quadratic character of \(\mathbb {Q}_p^{\times }\). Finally, \(\varphi _{1,p}\), \(\varphi _{2,p}\), \(\varphi _{3,p}\), \({\widetilde{\varphi }}_{1,p}\), \({\widetilde{\varphi }}_{2,p}\), \({\widetilde{\varphi }}_{3,p}\) are all local newforms.
When \(p \mid q_2\) but \(p \not \mid [w_1,w_2]\), the local component \(\pi _{g,p}\) of g is of the same form as for \(p \mid q_1\). The local component \(\pi _{f,p}\) of f is a unitarisable unramified principal series representation \(\omega _{3,p} \boxplus \omega _{3,p}^{-1}\), where \(c(\omega _{3,p}) = 0\) and \(p^{-1/2}< |\omega _{3,p}(p)| < p^{1/2}\). Once again, all local forms are newforms.
When \(p \mid (w_1,w_2)\), the setting is as above except both \(\varphi _{3,p}\) and \({\widetilde{\varphi }}_{3,p}\) are translates of local newforms by \(\pi _{3,p}\left( {\begin{matrix} p^{-1} &{} 0 \\ 0 &{} 1 \end{matrix}}\right) \) and \({\widetilde{\pi }}_{3,p}\left( {\begin{matrix} p^{-1} &{} 0 \\ 0 &{} 1 \end{matrix}}\right) \) respectively.
When \(p \mid w_1\) but \(p \not \mid w_2\), the setting is as above except only \(\varphi _{3,p}\) is the translate of the local newform.
Finally, when \(p \mid w_2\) but \(p \not \mid w_1\), the setting is as above except instead only \({\widetilde{\varphi }}_{3,p}\) is the translate of the local newform.
For the former case, we apply Proposition 4.16 with \(F_v = \mathbb {Q}_p\) and \(q_v = p\), while Proposition 4.17 is applied to the remaining cases. This gives the result. \(\square \)
4.4 Proof of Proposition 1.16.
Proof of Proposition 1.16
The identity (1.18) for \(|\langle |g|^2, E_{\infty }(\cdot ,1/2 + it)\rangle _q|^2\) follows from Corollary 4.9, while Corollary 4.19 gives the identity (1.17) for \(|\langle |g|^2, f\rangle _q|^2\). \(\square \)
Remark 4.20
It behoves us to mention that both [Luo14, Section 4] and [Liu15, Section 2] mistakenly apply identities of Watson [Wat08] that are only valid when all three automorphic forms \(f_1,f_2,f_3\) have principal nebentypen; the correct identities are given in Proposition 1.16 and rely on Propositions 4.16 and 4.17. Ultimately, this does not affect the validity of [Luo14, Theorem]. For [Liu15], there are two additional errata: the factorisations of \(L(s,f \otimes f \otimes g)\) in [Liu15, (2.3) and (2.4)] are interchanged (with the same issue also being present in [Sar01, p. 422]), for the isobaric decompositions \(f \otimes f = \chi _{-q} \boxplus {{\,\mathrm{sym}\,}}^2 f\) and \({{\,\mathrm{sym}\,}}^2 f = F \boxplus 1\) imply the correct factorisations
and finally the approximate functional equation for \(L(1/2,F \otimes g)\) given in [Liu15, Proof of Lemma 3.2] ought to involve a sum over \(n \le q^{3/2 + \varepsilon }\), not \(q^{1 + \varepsilon }\) (which is to say that the conductor of \(F \otimes g\) is \(q^3\), not \(q^2\); see Lemma A.2). The first of these two errata is readily rectified; the second, however, means that the exponent in [Liu15, Theorem 1.1] is subsequently weakened to \(-2/3 - \delta /3 + \varepsilon \) rather than \(-11/12 - \delta /3 + \varepsilon \).
5 Local Constants in the Watson–Ichino Formula
This section is devoted to the proofs of Propositions 4.16 and 4.17. Since every calculation is purely local, we drop the subscripts v. Let F be a nonarchimedean local field with ring of integers \(\mathcal {O}_F\), uniformiser \(\varpi \), and maximal ideal \(\mathfrak {p}= \varpi \mathcal {O}_F\). Let \(q = N(\mathfrak {p}) = \# \mathcal {O}_F / \mathfrak {p}= |\varpi |^{-1}\), where the norm \(|\cdot |\) is such that \(|x| = q^{-v(x)}\) for \(x \in \varpi ^{v(x)} \mathcal {O}_F^{\times }\). We set \(K :={{\,\mathrm{GL}\,}}_2(\mathcal {O}_F)\) and define the congruence subgroup
for any nonnegative integer m. We normalise the additive Haar measure da on F to give \(\mathcal {O}_F\) volume 1, while the multiplicative Haar measure \(d^{\times } a = \zeta _F(1) |a|^{-1} \, da\) on \(F^{\times }\) is normalised to give \(\mathcal {O}_F^{\times }\) volume 1, where \(\zeta _F(s) = (1 - q^{-s})^{-1}\).
5.1 Reduction to formulæ for Whittaker functions.
For \(\pi \) equal to a principal series representation \(\omega \boxplus \omega '\) or a special representation \(\omega \mathrm {St}\), and given a vector \(\varphi _{\pi }\) in the induced model of \(\pi \), we let
denote the corresponding element of the Whittaker model \(\mathcal {W}(\pi ,\psi )\), where \(w = \left( {\begin{matrix} 0 &{} -1 \\ 1 &{} 0 \end{matrix}}\right) \) and \(\psi \) is an unramified additive character of F; the normalisation of the Whittaker functional follows [MV10, Section 3.2.1].
For generic irreducible unitarisable representations \(\pi _1\), \(\pi _2\), \(\pi _3\) with \(\pi _1\) a principal series representation, and for \(\varphi _1\) in the induced model of \(\pi _1\), \(W_2 \in \mathcal {W}(\pi _2,\psi )\), and \(W_3 \in \mathcal {W}(\pi _3,\psi ^{-1})\), we define the local Rankin–Selberg integral \(\ell _{\mathrm {RS}}(\varphi _1, W_2, W_3)\) to be
(see [MV10, (3.28)]). The importance of this quantity is the following identity of Michel and Venkatesh.
Lemma 5.2
([MV10, Lemma 3.4.2]). For \(g,h \in {{\,\mathrm{GL}\,}}_2(F)\), \(\varphi = \varphi _{\pi _1} \otimes \varphi _{\pi _2} \otimes \pi _3(g) \cdot \varphi _{\pi _3}\), and \({\widetilde{\varphi }} = {\widetilde{\varphi }}_{\pi _1} \otimes {\widetilde{\varphi }}_{\pi _2} \otimes {\widetilde{\pi }}_3(h) \cdot {\widetilde{\varphi }}_{\pi _3}\) with \(\varphi _{\pi _1}\), \(\varphi _{\pi _2}\), \(\varphi _{\pi _3}\), \({\widetilde{\varphi }}_{\pi _1}\), \({\widetilde{\varphi }}_{\pi _2}\), \({\widetilde{\varphi }}_{\pi _3}\) newforms, we have the identity
whenever \(\pi _2\) is tempered.
Remark 5.3
[MV10, Lemma 3.4.2] only covers the case \(g = h\), but the proof generalises via the polarisation identity.
5.2 Formulæ for Whittaker functions.
Lemma 5.2 reduces the determination of local constants to evaluating integrals involving \(\varphi _{\pi _1}\), \(\varphi _{\pi _2}\), and \(W_{\pi _3}\). Thus we must determine the values of these functions at certain values of \(g \in {{\,\mathrm{GL}\,}}_2(F)\). We observe that both \(\varphi _{\pi }\) and \(W_{\pi }\) are right \(K_1(\mathfrak {p}^{c(\pi )})\)-invariant, where \(c(\pi )\) denotes the conductor exponent of \(\pi \); we will use this fact to limit ourselves to determining the values of these functions at \(g = \left( {\begin{matrix} a &{} 0 \\ 0 &{} 1 \end{matrix}}\right) \) and \(g = \left( {\begin{matrix} a &{} 0 \\ 0 &{} 1 \end{matrix}}\right) \left( {\begin{matrix} 1 &{} 0 \\ 1 &{} 1 \end{matrix}}\right) \).
We are interested in two cases, namely \(\pi _1 = \omega _1 \boxplus \omega _1'\), \(\pi _2 = \omega _1'^{-1} \boxplus \omega _1^{-1}\) with \(\omega _1\), \(\omega _1'\) both unitary, \(c(\omega _1) = 1\) and \(c(\omega _1') = 0\), so that \(c(\pi _1) = c(\pi _2) = 1\), and \(\pi _3\) either \(\omega _3 \mathrm {St}\) with \(\omega _3\) unitary and \(c(\omega _3) = 0\), so that \(c(\pi _3) = 1\), or \(\omega _3 \boxplus \omega _3^{-1}\) with \(q^{-1/2}< |\omega _3(\varpi )| < q^{1/2}\) and \(c(\omega _3) = 0\), so that \(c(\pi _3) = 0\). Moreover, we require that the product of the central characters of \(\pi _1\), \(\pi _2\), \(\pi _3\) be trivial: in the former case, as the central character of \(\pi _3\) is \(\omega _3^2\), this means that \(\omega _3^{-1} = \omega _3\), so that \(\omega _3\) is either the trivial character or the unramified quadratic character of \(F^{\times }\).
5.2.1 The case \(\pi _3 = \omega _3 \mathrm {St}\).
In this section, we deal with the first case, so that \(\pi _3 = \omega _3 \mathrm {St}\).
Lemma 5.4
([Sch02, Lemma 1.1.1]). We have that
Lemma 5.6
([Sch02, Proposition 2.1.2]). The newform for \(\pi _1\) in the induced model, normalised such that \(W_{\pi _1} \left( {\begin{matrix} 1 &{} 0 \\ 0 &{} 1 \end{matrix}}\right) = 1\), is given by
The newform for \(\pi _3\) is equal to
Note that the normalisation of these newforms differs slightly than the normalisation in [Sch02, Proposition 2.1.2]; it is such that \(W_{\pi _3}\left( {\begin{matrix} 1 &{} 0 \\ 0 &{} 1 \end{matrix}}\right) = 1\).
Lemma 5.9
([Sch02, §2.4]). For \(a \in F^{\times }\), we have that
Proof
Let
Then
and so upon combining (5.1) and (5.7),
Since \(|x| \le |a|\), \(|a + x \varpi | = |a|\), while \(\omega _1^{-1} \omega _1'(a + x \varpi ) = \omega _1^{-1} \omega _1'(a)\) as \(\omega _1^{-1} \omega _1'\) has conductor exponent 1. So
from which the desired identity for \(W_{\pi _1} \left( {\begin{matrix} a &{} 0 \\ 0 &{} 1 \end{matrix}}\right) \) follows via (5.5). The identity for \(W_{\pi _2} \left( {\begin{matrix} a &{} 0 \\ 0 &{} 1 \end{matrix}}\right) \) follows by taking complex conjugates. Finally, we insert (5.8) into (5.1) in order to see that \(W_{\pi _3} \left( {\begin{matrix} a &{} 0 \\ 0 &{} 1 \end{matrix}}\right) \) is equal to
The result then follows once again via (5.5). \(\square \)
Lemma 5.10
([Sch02, Lemma 1.1.1]). For any ramified character \(\omega \) of \(F^{\times }\) of conductor exponent \(c(\omega ) \ge 1\) and any \(s \in \mathbb {C}\), we have that
Here \(\epsilon (s,\omega ,\psi ) = \epsilon (1/2,\omega ,\psi ) q^{- c(\omega ) (s - 1/2)}\) and \(|\epsilon (1/2,\omega ,\psi )| = 1\).
Lemma 5.12
(Cf. [Hu17, Lemma 2.13]). We have that
Proof
Let
Then
Combining (5.1) and (5.7) yields
Upon making the change of variables \(x \mapsto x - a\) and using (5.11), the identity for \(W_{\pi _1}\) is derived. The identity for \(W_{\pi _2}\) follows by taking complex conjugates. Finally, combining (5.1) and (5.8) shows that
The result then follows via (5.5) after the change of variables \(x \mapsto x - a\). \(\square \)
5.2.2 The case \(\pi _3 = \omega _3 \boxplus \omega _3^{-1}\).
Finally, we deal with the case \(\pi _3 = \omega _3 \boxplus \omega _3^{-1}\).
Lemma 5.13
The newform in the induced model is
Again, the normalisation is such that \(W_{\pi _3}\left( {\begin{matrix} 1 &{} 0 \\ 0 &{} 1 \end{matrix}}\right) = 1\).
Lemma 5.15
([Sch02, §2.4]). We have that
Lemma 5.16
We have that
Proof
This follows from the fact that \(\pi _3\left( {\begin{matrix} \varpi ^{-1} &{} 0 \\ 0 &{} 1 \end{matrix}}\right) \cdot W_{\pi _3}\) is right \(K_1(\mathfrak {p})\)-invariant. \(\square \)
Lemma 5.17
We have that
Proof
For
we have that
From this and (5.14), \(\varphi _{\pi _3}\left( w \left( {\begin{matrix} 1 &{} x \\ 0 &{} 1 \end{matrix}}\right) g \left( {\begin{matrix} \varpi ^{-1} &{} 0 \\ 0 &{} 1 \end{matrix}}\right) \right) \) is equal to
Coupled with (5.1), \(\pi _3\left( {\begin{matrix} \varpi ^{-1} &{} 0 \\ 0 &{} 1 \end{matrix}}\right) \cdot W_{\pi _3}\left( \left( {\begin{matrix} a &{} 0 \\ 0 &{} 1 \end{matrix}}\right) \left( {\begin{matrix} 1 &{} 0 \\ 1 &{} 1 \end{matrix}}\right) \right) \) is thereby equal to
after making the change of variables \(x \mapsto x - a\), which gives the result via (5.5). \(\square \)
5.3 Proofs of Propositions 4.16 and 4.17.
To prove Propositions 4.16 and 4.17, we use Lemma 5.2 to reduce the problem to evaluating local Rankin–Selberg integrals. We then use the identities in Section 5.2 for values of \(\varphi _{\pi }\) and \(W_{\pi }\) together with the following lemma.
Lemma 5.18
([Hu16, Lemma 2.2]). Suppose that \(f : {{\,\mathrm{GL}\,}}_2(F) \rightarrow \mathbb {C}\) is right K-integrable and right \(K_1(\mathfrak {p}^m)\)-invariant for some \(m \in \mathbb {N}\). Then
Proof of Proposition 4.16
Lemmata 5.9, 5.12, and 5.18 imply that
The integral is readily seen to be equal to \(q \omega _3^{-1}(\varpi ) L(1,\omega _3)\) via the change of variables \(a \mapsto \varpi ^{-1} a\); Lemma 5.2 then gives the identity
Now
where
and Lemma 5.9 implies that
We conclude that
On the other hand, we have the isobaric decomposition
so that
Moreover,
so that
while \({{\,\mathrm{ad}\,}}\pi _3\) is the special representation of \({{\,\mathrm{GL}\,}}_3(F)\) associated to the trivial character, so that
So
and consequently, upon recalling (4.13),
\(\square \)
Remark 5.19
A similar calculation shows that \(I'(\varphi \otimes {\widetilde{\varphi }})\) is again equal to \(q^{-1} (1 + q^{-1})\) when \(\pi _1\), \(\pi _2\), \(\pi _3\) are all irreducible unitarisable principal series representations of conductor exponent one for which \(\omega _{\pi _1} \omega _{\pi _2} \omega _{\pi _3} = 1\).
Proof of Proposition 4.17
For \(\pi _3 = \omega _3 \boxplus \omega _3^{-1}\) with \(c(\omega _3) = c(\omega _3^{-1}) = 0\), the right K-invariance of \(W_{\pi _3}\) allow us to see that \(\ell _{\mathrm {RS}}(\varphi _{\pi _1}, W_{\pi _2}, W_{\pi _3})\) is equal to
via Lemmata 5.9, 5.12, 5.15, and 5.18. The integral simplifies to \(L(1/2, \omega _3) L(1/2, \omega _3^{-1})\). Similarly, the Rankin–Selberg integral \(\ell _{\mathrm {RS}}\left( \varphi _{\pi _1}, W_{\pi _2}, \pi _3\left( {\begin{matrix} \varpi ^{-1} &{} 0 \\ 0 &{} 1 \end{matrix}}\right) \cdot W_{\pi _3}\right) \) is equal to
additionally using Lemmata 5.16 and 5.17. After making the change of variables \(a \mapsto \varpi ^{-1}a\), we see that this is equal to \(\ell _{\mathrm {RS}}(\varphi _{\pi _1}, W_{\pi _2}, W_{\pi _3})\). So by Lemma 5.2,
As
(see, for example, [MV10, Section 3.4.1]), we find that
On the other hand,
so that
and so
\(\square \)
Remark 5.20
One can also prove Propositions 4.16 and 4.17 by the methods used in [Hu17]: in place of Lemma 5.2, we instead calculate \(I(\varphi \otimes {\widetilde{\varphi }})\) via the fact that
recalling (4.12), where \(\Phi _{\pi }\) denotes the normalised matrix coefficient
Since \(W_{\pi }\) is right \(K_1(\mathfrak {p})\)-invariant, Lemma 5.18 together with the Iwasawa decomposition imply that \(I(\varphi \otimes {\widetilde{\varphi }}) / \langle \varphi , {\widetilde{\varphi }} \rangle \) is equal to
where \(b = \left( {\begin{matrix} a &{} x \\ 0 &{} 1 \end{matrix}}\right) \) with \(a \in F^{\times }\), \(x \in F\), and \(db = |a|^{-1} \, d^{\times } a \, dx\). One can then use Lemmata 5.9 and 5.12 and the fact that \(W_{\pi }\left( \left( {\begin{matrix} 1 &{} x \\ 0 &{} 1 \end{matrix}}\right) g\right) = \psi (x) W_{\pi }(g)\) to show that
where \(\pi _1\), \(\pi _2\), \(\pi _3\) are as in Proposition 4.16. Inserting these identities into (5.21) and evaluating the resulting integrals thereby reproves Proposition 4.16; similar calculations yield Proposition 4.17.
6 The First Moment in the Short Initial Range
The main results of this section are bounds for the first moments
which will be required in the course of the proof of Proposition 1.21 (1).
Proposition 6.1
Fix \(\beta > 0\), and suppose that \(t_g^{\beta } \le T \le t_g^{1 - \beta }\).
- (1)
For \(h(t) = 1_{E \cup -E}(t)\) with \(E = [T,2T]\),
$$\begin{aligned} {\widetilde{\mathcal {M}}}^{\text{ Maa }\ss {}}(h) + {\widetilde{\mathcal {M}}}^{\text{ Eis }}(h) \ll _{\varepsilon } T^{2 + \varepsilon } + t_g^{1 + \varepsilon }. \end{aligned}$$ - (2)
For \(h^{\text{ hol }}(k) = 1_E(k)\) with \(E = [T,2T]\),
$$\begin{aligned} {\widetilde{\mathcal {M}}}^{\text{ hol }}(h^{\text{ hol }}) \ll _{\varepsilon } T^{2 + \varepsilon } + t_g^{1 + \varepsilon }. \end{aligned}$$
Were we to replace \(g_{\psi ^2}\) with an Eisenstein series \(E(z,1/2 + 2it_g)\), so that \(L(1/2,f \otimes g_{\psi ^2})\) would be replaced by \(|L(1/2 + 2it_g,f)|^2\), then we would immediately obtain the desired bound via the large sieve, Theorem A.32. Thus this result is of similar strength to the large sieve; in particular, dropping all but one term returns the convexity bounds for \(L(1/2,f \otimes g_{\psi ^2})\) and \(|L(1/2 + it,g_{\psi ^2})|^2\) for \(T \ll t_g^{1/2}\). However, we cannot proceed via the large sieve as in the Eisenstein case because we do not know how to bound \(L(1/2,f \otimes g_{\psi ^2})\) by the square of a Dirichlet polynomial of length \(t_g^2\), and if we were to instead first apply the Cauchy–Schwarz inequality and then use the large sieve, we would only obtain the bound \(O_{\varepsilon }(T^{2 + \varepsilon } + t_g^{2 + \varepsilon })\), which is insufficient for our requirements.
Our approach to prove Proposition 6.1 is to first use the approximate functional equation to write the L-functions involved as Dirichlet polynomials and then apply the Kuznetsov and Petersson formulæ in order to express \({\widetilde{\mathcal {M}}}^{\text{ Maa }\ss {}}(h) + {\widetilde{\mathcal {M}}}^{\text{ Eis }}(h)\) and \({\widetilde{\mathcal {M}}}^{\text{ hol }}(h^{\text{ hol }})\) in terms of a delta term, which is trivially bounded, and sums of Kloosterman sums. We then open up the Kloosterman sums and apply the Voronoĭ summation formula. The proof is completed via employing a stationary phase-type argument to the ensuing expression.
Remark 6.2
This strategy is used elsewhere to obtain results that are similar to Proposition 6.1. Holowinsky and Templier use this approach in order to prove [HT14, Theorem 5], which gives a hybrid level aspect bound for a first moment of Rankin–Selberg L-functions involving holomorphic forms of fixed weight; the moment involves a sum over holomorphic newforms f of level N, while \(g_{\psi }\) is of level M, and the bound for this moment is a hybrid bound in terms of N and M (with unspecified polynomial dependence on the weights of f and \(g_{\psi }\)). The first author and Radziwiłł have recently proven a hybrid bound [HR19, Proposition 2.28] akin to Proposition 6.1 where \(g_{\psi }\) is replaced by the Eisenstein newform \(E_{\chi ,1}(z) :=E_{\infty }(z,1/2,\chi _D)\) of level D and nebentypus \(\chi _D\); the bound for this moment is a hybrid bound in terms of T and D, and the method is also valid for cuspidal dihedral forms \(g_{\psi }\) (with unspecified polynomial dependence on the weight or spectral parameter of \(g_{\psi }\)).
In applying the approximate functional equation in order to prove Proposition 6.1, we immediately run into difficulties because the length of the approximate functional equation depends on the level, and the Kuznetsov and Petersson formulæ involve cusp forms of all levels dividing D. Since we are evaluating a first moment rather than a second moment, we cannot merely use positivity and oversum the Dirichlet polynomial coming from the approximate functional equation.
One possible approach to overcome this obstacle would be to use the Kuznetsov and Petersson formulæ for newforms; see [HT14, Lemma 5] and [You19, Section 10.2]. Instead, we work around this issue by using the Kuznetsov and Petersson formulæ associated to the pair of cusps \((\mathfrak {a},\mathfrak {b})\) with \(\mathfrak {a}\sim \infty \) and \(\mathfrak {b}\sim 1\). As shall be seen, this introduces the root number of \(f \otimes g_{\psi ^2}\) in such a way to give approximate functional equations of the correct length for each level dividing D.
We will give the proof of Proposition 6.1 (1), then describe the minor modifications needed for the proof of Proposition 6.1 (2). Via the positivity of \(L(1/2,f \otimes g_{\psi ^2})\), it suffices to prove the result with h replaced by
We remind the reader that from here onwards, we will make use of many standard automorphic tools that are detailed in Appendix A.
Lemma 6.4
The first moment \({\widetilde{\mathcal {M}}}^{\text{ Maa }\ss {}}(h_T) + {\widetilde{\mathcal {M}}}^{\text{ Eis }}(h_T)\) is equal to
where
Here \(d_{\text{ spec }}r\), S(m, n; c), \(\mathscr {K}^{\pm }\), and \(V_2^1\) are as in (A.15), (A.12), (A.13), and (A.7) respectively.
Proof
We take \(m = 1\) and \(h = V_2^1(n \ell ^2/D^{3/2},\cdot ) h_T\) in the Kuznetsov formula, Theorem A.10, using the explicit expressions in Lemma A.8, which we then multiply by \(\chi _D(\ell )/2\sqrt{n} \ell \) and sum over \(n,\ell \in \mathbb {N}\) and over both the same sign and opposite sign Kuznetsov formulæ. After making the change of variables \(n \mapsto w_2 n\), using the fact that \(\lambda _{g_{\psi ^2}}(w_2 n) = \lambda _{g_{\psi ^2}}(n)\) for all \(w_2 \mid D\) via Lemma A.1, and simplifying the resulting sum over \(v_2 w_2 = \ell \) using the multiplicativity of the summands, the spectral sum ends up as
We do the same with the Kuznetsov formula associated to the \((\infty ,1)\) pair of cusps, Theorem A.16, using the explicit expressions in Lemma A.9, obtaining
We add these two expressions together and use the approximate functional equation, Lemma A.5, with \(X = \sqrt{d_2}/w_2\). Recalling Lemma 3.2, this yields \({\widetilde{\mathcal {M}}}^{\text{ Maa }\ss {}}(h_T)\). Similarly, the sum of the Eisenstein terms is \({\widetilde{\mathcal {M}}}^{\text{ Eis }}(h_T)\). Upon noting that the delta term only arises when we take \(n = 1\) in the same sign Kuznetsov formula with the \((\infty ,\infty )\) pair of cusps, the desired identity follows. \(\square \)
Lemma 6.6
Both of the terms
are \(O_{\varepsilon }(t_g^{1 + \varepsilon })\).
Proof
The strategy is to apply the Voronoĭ summation formula, Lemma A.30, to the sum over n, and then to bound carefully the resulting dual sum using a stationary phase-type argument (although this will be masked by integration by parts). We only cover the proof for the first term, since the second term follows by the exact same argument save for a slightly different formulation of the Voronoĭ summation formula, which gives rise to Ramanujan sums in place of Gauss sums.
Dividing the n-sum and the r-integral in the definition of \(\mathscr {K}^{+}\), (A.13), into dyadic intervals, we consider the sum
for any \(N < t_g^{2 + \varepsilon }\), where W and h are smooth functions compactly supported on (1, 2). Here the function \(h_T\) has been absorbed into h. By Stirling’s formula (2.4), we have that
for \(j,k \in \mathbb {N}_0\), where we follow the \(\varepsilon \)-convention. To understand the transform \(\mathscr {K}^{+}\), we refer to [BuK17a, Lemma 3.7]. By [BuK17a, (3.61)], we must bound
by \(O_{\varepsilon }(t_g^{1 + \varepsilon })\). We make the substitutions \(r \mapsto rT\) and \(u \mapsto u/T\). Repeated integration by parts with respect to r, recalling (6.7) and using \((d/dr)^k(\tanh \pi r T)\ll _k\ e^{-T}\) for \(k\ge 1\), shows that we may restrict to \(|u| < T^{\varepsilon }\), up to a negligible error. After making this restriction, using \(\tanh (\pi r T)=1+O(e^{-T})\), and taking the Taylor expansion of \(\cosh (\pi u / T)\), we need to show
is \(O_{\varepsilon }(t_g^{1 + \varepsilon })\). Now we integrate by parts multiple times with respect to u, differentiating the exponential \(e(\frac{2\sqrt{n}}{c} (\frac{1}{2!} (\frac{\pi u}{T})^2 + \frac{1}{4!} (\frac{\pi u}{T})^4 + \cdots ))\) and integrating the exponential \(e(-ur)\). This shows that we may restrict the summation over c to \(c < \sqrt{N} / T^{2 - \varepsilon }\), because the contribution of the terms not satisfying this condition will be negligible. In particular, we may assume that \(N > T^{4 - \varepsilon }\), for otherwise the c-sum is empty. Also, the contribution of the endpoints \(u=\pm T^\varepsilon \) after integration by parts is negligible by repeated integration by parts with respect to r (the same argument which allowed us to truncate the u-integral in the first place). Thus we have shown that it suffices to prove that
is \(O_{\varepsilon }(t_g^{1 + \varepsilon })\) for any smooth function \(\Omega \) satisfying \(\Omega ^{(j)} \ll _j 1\) for \(j \in \mathbb {N}_0\) and any \(r \in (1,2)\).
We now open up the Kloosterman sum and apply the Voronoĭ summation formula, Lemma A.30. Via Mellin inversion, (6.8) is equal to
for any \(\sigma \ge 0\), where \(\mathcal {J}_{2t_g}^{\pm }\) is as in (A.14) with Mellin transform \(\widehat{\mathcal {J}_{2t_g}^{\pm }}\) given by (A.24) and (A.26). Repeated integration by parts in the x integral, integrating \(x^{-s}\) and differentiating the rest and recalling (6.7), shows that up to negligible error, we may restrict the s-integral to
Moving the line of integration in (6.9) far to the right and using the bounds in Corollary A.27 for the Mellin transform of \(\mathcal {J}_{2t_g}^{\pm }\), we may crudely restrict to \(n < t_g^{2 + \varepsilon }\). Upon fixing \(\sigma = 0\) in (6.9), so that the s-integral is on the line \(s = it\) and \(x^{-s} = e(-\frac{t\log x}{2\pi })\), and making the substitution \(x \mapsto x^2\), it suffices to prove that
is \(O_{\varepsilon }(t_g^{1 + \varepsilon })\), where we have used Lemma A.31 to reexpress the sum over d as a sum over \(a \mid (c/D,n \mp 1)\), and
We write \(\Xi = \Xi _1 + \Xi _2\), where \(\Xi _1\) is the same expression as \(\Xi \) but with the t-integral further restricted to
and \(\Xi _2\) is the same expression as \(\Xi \) but with the t-integral further restricted to
Thus \(\Xi _1\) keeps close to the stationary point of the x-integral in the definition of I(t), while \(\Xi _2\) keeps away.
We first bound \(\Xi _1\). Using the bound \(\widehat{\mathcal {J}_{2t_g}^{\pm }}(2(1 + it)) \ll _{\varepsilon } t_g^{1 + \varepsilon }\) in the range (6.10) from Corollary A.27 and the trivial bound \(I(t) \ll 1\), we get
upon making the change of variables \(n \mapsto an \pm 1\) and recalling that \(N < t_g^{2 + \varepsilon }\).
We now turn to bounding \(\Xi _2\). The difference here is that we will not trivially bound the integral I(t). Keeping in mind the restriction (6.11), we write
We integrate by parts k-times with respect to x, differentiating the product of terms on the first line above and integrating the product of terms on the second line. This leads to the bound
where the first term in the upper bound comes from the derivatives of \(\Omega (\frac{\sqrt{N} x}{cT^2})\), while the second term comes from the derivatives of \((\frac{2\sqrt{N}}{c} - \frac{t}{\pi x})^{-1}\). By (6.10) and (6.11), the second term in this upper bound is negligible. The first term is negligible unless
But the contribution to \(\Xi _2\) of t in this range is
which is trivially bounded, using the fact that \(\widehat{\mathcal {J}_{2t_g}^{\pm }}(2(1 + it)) \ll _{\varepsilon } t_g^{1 + \varepsilon }\), by
which is more than sufficient. \(\square \)
Lemma 6.12
Both of the terms
are \(O_{\varepsilon }(t_g^{1 + \varepsilon })\).
Proof
The strategy is the same: to apply the Voronoĭ summation formula to the sum over n, and then to bound trivially. This time, however, there will be no stationary phase analysis, so the proof is more straightforward. Again, we will only detail the proof of the bound for the first term.
Dividing as before the n-sum and the r-integral in the definition of \({\mathcal {K}}^-\) into dyadic intervals, we consider the sum
for any \(N < t_g^{2 + \varepsilon }\), where W and h are smooth functions compactly supported on (1, 2), with the function \(h_T\) having been absorbed into h. To understand the transform \(\mathscr {K}^{-}\), we refer to [BuK17a, Lemma 3.8]. By [BuK17a, (3.68)] and the fact that \(\tanh \pi r = 1 + O(e^{-2\pi |r|})\), we must bound
by \(O_{\varepsilon }(t_g^{1 + \varepsilon })\). We make the substitutions \(r \mapsto Tr\) and \(u \mapsto u/T\). Repeated integration by parts with respect to r shows that we may restrict to \(|u| < T^{\varepsilon }\), up to a negligible error. After making this restriction and taking the Taylor expansion of \(\sinh (\pi u / T)\), we need to prove that
is \(O_{\varepsilon }(t_g^{1 + \varepsilon })\). We integrate by parts multiple times with respect to u, differentiating the exponential \(e(-\frac{2\sqrt{n}}{c} (\frac{\pi u}{T} + \frac{1}{3!} (\frac{\pi u}{T})^3 + \cdots ))\) and integrating the exponential \(e(-ur)\). This shows that we may restrict the summation over c to \(c < \sqrt{N} / T^{1 - \varepsilon }\), because the contribution of the terms not satisfying this condition will be negligible. In particular, we may assume that \(N > T^{2 - \varepsilon }\), for otherwise the c-sum is empty. Thus we have shown that it suffices to prove that
is \(O_{\varepsilon }(t_g^{1 + \varepsilon })\) for any smooth function \(\Omega \) satisfying \(\Omega ^{(j)} \ll _j 1\) for \(j \in \mathbb {N}_0\) and any \(r \in (1,2)\).
We now open up the Kloosterman sum and apply the Voronoĭ summation formula, Lemma A.30. Via Mellin inversion, (6.13) is equal to
for any \(\sigma \ge 0\). We again use Lemma A.31 to write the Gauss sum over d as a sum over \(a \mid (c/D,n \pm 1)\). Repeated integration by parts in the x-integral shows that the s-integral may be restricted to
Moving the line of integration in (6.14) far to the right and using the bounds in Corollary A.27 for \(\widehat{\mathcal {J}_{2t_g}^{\pm }}\), we may once again restrict to \(n < t_g^{2 + \varepsilon }\). Upon fixing \(\sigma = 0\) in (6.14) and bounding the resulting integral trivially by \(\frac{\sqrt{N}}{cT} t_g^{1 + \varepsilon }\), since \(\widehat{\mathcal {J}_{2t_g}^{\pm }}(2(1 + it)) \ll _{\varepsilon } t_g^{1 + \varepsilon }\), we arrive at the bound
upon making the change of variables \(n \mapsto an \mp 1\) and recalling that \(N < t_g^{2 + \varepsilon }\). \(\square \)
Proof of Proposition 6.1 (1)
It is clear that the first term in (6.5) is \(O_{\varepsilon }(T^{2 + \varepsilon })\). Lemmata 6.6 and 6.12 then bound the second and third terms by \(O_{\varepsilon }(t_g^{1 + \varepsilon })\). \(\square \)
Proof of Proposition 6.1 (2)
A similar identity to (6.5) for \({\widetilde{\mathcal {M}}}^{\text{ hol }}(h^{\text{ hol }})\) may be obtained by using the Petersson formula, Theorems A.17 and A.19, instead of the Kuznetsov formula, namely
Here \(\mathscr {K}^{\text{ hol }}\) is as in (A.18) and
The first term in (6.15) is bounded by \(O_{\varepsilon }(T^{2 + \varepsilon })\). For the latter two terms, we use the methods of [Iwa97, Section 5.5] to understand \(\mathscr {K}^{\text{ hol }}\) in place of [BuK17a, Lemmata 3.7 and 3.8] to understand \(\mathscr {K}^{\pm }\): this gives terms of the form
and
as well as the counterparts involving sums over \(c \in \mathbb {N}\) with \((c,D) = 1\). The former term is then treated via the same methods as Lemma 6.6, while the latter is treated as in Lemma 6.12. \(\square \)
7 Spectral Reciprocity for the Short Initial Range
The main result of this section is an identity for
for a (suitably well-behaved) function \(\mathfrak {h}:=(h,h^{\text{ hol }}) : (\mathbb {R}\cup i(-1/2,1/2)) \times 2\mathbb {N}\rightarrow \mathbb {C}^2\), with \(\mathcal {M}^{\text{ Maa }\ss {}}(h)\) and \(\mathcal {M}^{\text{ Eis }}(h)\) as in (1.19) and (1.20), and
We will take \(\mathfrak {h}\) to be an admissible function in the sense of [BlK19b, Lemma 8b)], namely h(t) is even and holomorphic in the horizontal strip \(|\mathfrak {I}(t)| < 500\), in which it satisfies \(h(t) \ll (1 + |t|)^{-502}\) and has zeroes at \(\pm (n + 1/2) i\) for nonnegative integers \(n < 500\), while \(h^{\text{ hol }}(k) \equiv 0\). We will later make the choice
for some fixed large integer \(N \ge 500\) and \(T > 0\); suffice it to say, one may read the rest of this section with this test function in mind.
Proposition 7.1
For an admissible function \(\mathfrak {h}\), we have the identity
where
Here \(\mathscr {L}^{\pm }\) and \(\mathscr {L}^{\text{ hol }}\) are as in (A.21), \(\mathscr {N}\) and \(\mathscr {K}^{-}\) as in (A.13), and \(\mathcal {J}_r^{\pm }\) as in (A.14). The proof of Proposition 7.1, which we give at the end of this section, is via the triad of Kuznetsov, Voronoĭ, and Kloosterman summation formulæ. Following the work of Blomer, Li, and Miller [BLM19] and Blomer and the second author [BlK19a, BlK19b], we avoid using approximate functional equations but instead use Dirichlet series in regions of absolute convergence to obtain an identity akin to (7.2), and then extend this identity holomorphically to give the desired identity.
Remark 7.6
This approach obviates the need for complicated stationary phase estimates and any utilisation of the spectral decomposition of shifted convolution sums, which is the (rather technically demanding) approach taken by Jutila and Motohashi [JM05, Theorem 2] in obtaining the bound
which is used in [DK18b, Hum18] in the proofs of Theorems 1.7 and 1.9 for Eisenstein series. Indeed, the method of proof of spectral reciprocity in Proposition 7.1 could be used to give a simpler proof (and slightly stronger version) of [JM05, Theorem 2].
Remark 7.7
Structurally, Proposition 7.1 is proven in a similar way to [BuK17a, Theorem 1.1], where an asymptotic with a power savings is given for a moment of L-functions that closely resembles \(\mathcal {M}^{-}(\mathfrak {h})\); see in particular the sketch of proof in [BuK17a, Section 2], which highlights the process of Kuznetsov, Voronoĭ, and Kloosterman summation formulæ. The chief difference is the usage of Dirichlet series in regions of absolute convergence coupled with analytic continuation in place of approximate functional equations.
We define
for \(s_1,s_2 \in \mathbb {C}\), where
We additionally set
Lemma 7.8
For admissible \(\mathfrak {h}\) and \(5/4< \mathfrak {R}(s_1), \mathfrak {R}(s_2) < 3/2\), we have that
where
and
with
where \(-3< \sigma _1 < 2(1 - \max \{\mathfrak {R}(s_1),\mathfrak {R}(s_2)\})\).
The proof of this is similar to the proofs of analogous results in [BLM19, BlK19a, BlK19b]; as such, we will be terse at times in justifying various technical steps, especially governing the absolute convergence required for the valid shifting of contours and interchanging of orders of integration and summation, for the details may be found in the aforementioned references.
Proof
We multiply the opposite sign Kuznetsov formula, Theorem A.10, by
with \(\mathfrak {R}(s_1), \mathfrak {R}(s_2) > 1\) and sum over \(m,n \in \mathbb {N}\), with \(\lambda _{\chi _D,1}(m,0) = \sum _{ab = m} \chi _D(a)\) as in (A.3). Via Lemmata A.4 and A.8, the Maaß cusp form and the Eisenstein terms are
after making the change of variables \(m \mapsto v_1 m\) and \(n \mapsto v_2 n\), and noting that \(\lambda _{\chi _D,1}(vm,0) = \lambda _{\chi _D,1}(m,0)\) and \(\lambda _{g_{\psi ^2}}(vn) = \lambda _{g_{\psi ^2}}(n)\) whenever \(v \mid D\) via Lemma A.1. Since this is an application of the opposite sign Kuznetsov formula, there is no delta term. Finally, Mellin inversion together with Lemma A.28 give the identity
for \(-3< \sigma _0 < 3\). Using this, the Kloosterman term is seen to be
with the Voronoĭ L-series as in (A.29). This rearrangement is valid for \(2 - 2 \min \{\mathfrak {R}(s_1),\mathfrak {R}(s_2)\}< \sigma _0 < -1/2\), for then both Voronoĭ L-series converge absolutely, while the Weil bound ensures that the sum over c converges.
Assuming that \(\max \{\mathfrak {R}(s_1),\mathfrak {R}(s_2)\} < 3/2\), we may move the contour \(\mathfrak {R}(s) = \sigma _0\) to \(\mathfrak {R}(s) = \sigma _1\) such that \(-3< \sigma _1 < -2\max \{\mathfrak {R}(s_1),\mathfrak {R}(s_2)\}\); the Phragmén–Lindelöf convexity principle ensures that the ensuing integral converges. The only pole that we encounter along the way is at \(s = 2(1 - s_1)\), with the resulting residue being
via Lemma A.30. For \(\mathfrak {R}(s_2) > \mathfrak {R}(s_1)\), the Voronoĭ L-series \(L(1 - s_1 + s_2, g_{\psi ^2}, -{\overline{d}}/c)\) may be written as an absolutely convergent Dirichlet series, so that the sum over c and d is equal to
The sum over d is a Gauss sum, which may be reexpressed as a sum over \(a \mid (c/D, m)\) via Lemma A.31. By making the change of variables \(c \mapsto acD\) and \(m \mapsto am\), (7.13) becomes
Applying Möbius inversion to (4.1), we see that
Making the change of variables \(a \mapsto ab\) and \(m \mapsto bm\), (7.13) is rewritten as
recalling that \(g_{\psi ^2}\) being dihedral means that it is twist-invariant by \(\chi _D\). So the residue (7.12) is \(\mathcal {N}(s_1,s_2;\mathfrak {h}) / L(2s_1,\chi _D) L(2s_2,\chi _D)\), at least initially for \(\mathfrak {R}(s_2) > \mathfrak {R}(s_1)\), and this is also valid for \(5/4< \mathfrak {R}(s_1),\mathfrak {R}(s_2) < 3/2\), since it is holomorphic in this region.
Now we wish to reexpress (7.11), where \(\sigma _0\) has been replaced by \(\sigma _1\), with \(-3< \sigma _1 < -2 \max \{\mathfrak {R}(s_1),\mathfrak {R}(s_2)\}\). We apply the Voronoĭ summation formulæ, Lemma A.30, to both Voronoĭ L-series. The resulting Voronoĭ L-series are absolutely convergent Dirichlet series; opening these up and interchanging the order of summation and integration then leads to the expression
with \(\mathcal {O}_D\) as in (A.11) and \(H_{s_1,s_2,t_g}^{\pm }\) as in (7.10). As the Mellin transform of \(\mathscr {K}^{-} h\) defines a holomorphic function of s for \(-3< \mathfrak {R}(s) < 3\), while the Mellin transform of \(\mathcal {J}_r^{\pm }\) has simple poles at \(s = 2(\pm ir - n)\) with \(n \in \mathbb {N}_0\), the integrand is holomorphic in the strip \(-3< \mathfrak {R}(s) < 2(1 - \max \{\mathfrak {R}(s_1),\mathfrak {R}(s_2)\})\).
Finally, we apply Theorem A.20, the Kloosterman summation formula, in order to express this sum of Kloosterman sums in terms of Fourier coefficients of automorphic forms; the admissibility of \(\mathfrak {h}\) ensures that \(H_{s_1,s_2,t_g}^{\pm }\) satisfies the requisite conditions for this formula to be valid. We then interchange the order of summation and once again use Lemmas A.4 and A.8, making the change of variables \(m \mapsto v_1 m\) and \(n \mapsto v_2 n\). In this way, we arrive at
The proof is complete upon multiplying both sides by \(L(2s_1,\chi _D) L(2s_2,\chi _D)\). \(\square \)
Proof of Proposition 7.1
This follows the same method as [BLM19, Proof of Theorem 1], [BlK19b, Proof of Theorem 1], and [BlK19a, Proof of Theorem 2]: it is shown in [BlK19b, Section 10] that for \(1/2 \le \mathfrak {R}(s_1), \mathfrak {R}(s_2) \le 3/2\), \(\mathscr {T}_{s_1,s_2,t_g}^{\pm } \mathfrak {h}\) is weakly admissible in the sense of [BlK19b, (1.3)], which implies that \(\mathcal {N}(s_1,s_2;\mathfrak {h})\) and \(\mathcal {M}^{\pm } (s_2,s_1;\mathscr {T}_{s_1,s_2,t_g}^{\pm } \mathfrak {h})\) extend meromorphically to this region. Moreover, we have the identity \(\mathcal {M}^{\pm }(1/2,1/2;\mathfrak {h}) = \mathcal {M}^{\pm }(\mathfrak {h})\), since
via Lemmata 3.2 and 3.4, while \(\mathcal {M}^{\text{ Maa }\ss {},\pm }(1/2,1/2,h)\) is equal to \(\mathcal {M}^{\text{ Maa }\ss {}}(h)\) as \(L(1/2,f \otimes \chi _D) = L(1/2,f) L(1/2,f \otimes g_{\psi ^2}) = 0\) when \(\epsilon _f = -1\).
This process of meromorphic continuation is straightforward for the terms \(\mathcal {M}^{\text{ Maa }\ss {},-}(s_1,s_2;h)\), \(\mathcal {M}^{\text{ Maa }\ss {},\pm } (s_2,s_1;\mathscr {L}^{\pm } H_{s_1,s_2,t_g}^{\pm })\), \(\mathcal {M}^{\text{ hol }} (s_2,s_1;\mathscr {L}^{\text{ hol }} H_{s_1,s_2,t_g}^{+})\), and \(\mathcal {N}(s_1,s_2;\mathfrak {h})\), but for \(\mathcal {M}^{\text{ Eis }}(s_1,s_2;h)\) and \(\mathcal {M}^{\text{ Eis }} (s_2,s_1;\mathscr {L}^{\pm } H_{s_1,s_2,t_g}^{\pm })\), additional polar divisors arise via shifting the contour in the integration over t; see, for example, [BlK19b, Lemma 16] and [BlK19a, Lemma 3]. In this way, the additional terms
arise when \(\mathfrak {R}(s_1), \mathfrak {R}(s_2) < 1\). But these vanish when \(s_1 = s_2 = 1/2\) since \(\chi _D\) is even and so \(L(s,\chi _D)\) has a trivial zero at \(s = 0\). \(\square \)
8 Bounds for the Transform for the Short Initial Range
We take \(\mathfrak {h}= (h,0)\) in Proposition 7.1 to be
for some fixed large integer \(N \ge 500\) and \(T > 0\), which is positive on \(\mathbb {R}\cup i(-1/2,1/2)\) and bounded from below by a constant for \(t \in [-2T,-T] \cup [T,2T]\). We wish to determine the asymptotic behaviour of the functions \((\mathscr {L}^{\pm } H_{T,t_g}^{\pm })(t)\) and \((\mathscr {L}^{\text{ hol }} H_{T,t_g}^{+})(k)\) with uniformity in all variables T, \(t_g\), and t or k, where \(H_{t_g}^{\pm } = H_{T,t_g}^{\pm }\) is as in (7.4). Were we to consider \(t_g\) as being fixed, then such asymptotic behaviour has been studied by Blomer, Li, and Miller [BLM19, Lemma 3]. As we are interested in the behaviour of \(\mathscr {T}_{t_g}^{\pm } \mathfrak {h}\) as \(t_g\) tends to infinity, a little additional work is required.
Lemma 8.2
Define
For \(s = \sigma + i\tau \) with \(-N/2< \sigma < 1\), provided that additionally s is at least a bounded distance away from \(\{2(\pm it - n) : n \in \mathbb {N}_0\}\), and for \(t \in \mathbb {R}\cup i(-1/2,1/2)\) we have that
and for \(t \in \mathbb {R}\),
For \(s = \sigma + i\tau \) with \(-N/2< \sigma < 1\), provided that additionally s is at least a bounded distance away from \(\{2(\pm it - n) : n \in \mathbb {N}_0\}\), and for \(k \in 2\mathbb {N}\), we have that
and
Proof
From [BLM19, Lemma 4], we have the bound
for \(j \in \{0,\ldots ,N\}\), and consequently the Mellin transform of \(\mathscr {K}^{-} h_T\) is holomorphic in the strip \(-N/2< \mathfrak {R}(s) < N/2\), in which it satisfies the bounds
for \(s = \sigma + i\tau \). Next, we use Corollary A.27 to bound \(\widehat{\mathcal {J}_k^{\text{ hol }}}(s)\) and \(\widehat{\mathcal {J}_t^{\pm }}(s)\), as well as bound the residues at \(s = 1 - k - 2n\) and \(s = 2(\pm it - n)\) respectively, where \(n \in \mathbb {N}_0\). Finally, Stirling’s formula (2.4) shows that
for \(s = \sigma + i\tau \) with \(\sigma < 1\), and similarly
Combining these bounds yields the result. \(\square \)
Corollary 8.3
For fixed \(-N/2< \sigma < 1\), \(t_g^{1/2} \ll T \ll t_g\), \(t \in \mathbb {R}\cup i(-1/2,1/2)\), and \(k \in 2\mathbb {N}\), we have that
Proof
By Mellin inversion,
for any \(0< \sigma _1 < 1\). We break each of these integrals over \(s = \sigma _1 + i\tau \) into different ranges of \(\tau \) depending on the size of |t| or k relative to \(t_g\) and use the bounds for the integrands obtained in Lemma 8.2 to bound each portion of the integrals. In most regimes, we have exponential decay of the integrands due to the presence of \(e^{-\frac{\pi }{2} \Omega ^{\pm }(\tau ,t,t_g)}\) or \(e^{-\frac{\pi }{2} \Omega ^{\text{ hol }}(\tau ,k,t_g)}\); it is predominantly the regimes for which \(\Omega ^{\pm }(\tau ,t,t_g)\) or \(\Omega ^{\text{ hol }}(\tau ,k,t_g)\) are zero that have nonnegligible contributions.
For \((\mathscr {L}^{+} H_{T,t_g}^{+})(t)\), this is straightforward, noting that we can assume without loss of generality in this case that \(0< \sigma < 1\) with \(\sigma _1 = \sigma \); the dominant contribution comes from the section of the integral with \(2|t| \le |\tau | \le 4t_g\), as this is the regime for which \(\Omega ^+(\tau ,t,t_g)\) is equal to zero.
Similarly, for \((\mathscr {L}^{-} H_{T,t_g}^{-})(t)\), we may assume that \(0 \le \sigma < 1\) with \(\sigma _1 = \sigma \) for \(1 + |t| \le t_g T^{-1}\). For \(1 + |t| > t_g T^{-1}\), we may assume that \(-N/2 < \sigma \le 0\): we shift the contour from \(\mathfrak {R}(s) = \sigma _1\) to \(\mathfrak {R}(s) = \sigma \), picking up residues at the poles at \(s = 2(\pm it - n)\) for \(0 \le n < N/4\), with the dominant contribution in both cases being from the section of the integral with \(|\tau |\) bounded (the remaining regimes involve exponential decay from the presence of \(e^{-\frac{\pi }{2} \Omega ^{-}(\tau ,t,t_g)}\) unless \(4t_g \le |\tau | \le 2|t|\), in which case \((1 + |\tau |)^{-N - \sigma }\) contributes significant polynomial decay).
Finally, we may again assume without loss of generality for \((\mathscr {L}^{\text{ hol }} H_{T,t_g}^{+})(k)\) that \(0 \le \sigma < 1\) for \(k \le t_g T^{-1}\) and \(-N/2 < \sigma \le 0\) for \(k > t_g T^{-1}\), since we may shift the contour with impunity in this vertical strip; once again, the dominant contribution comes from the section of the integral with \(|\tau |\) bounded due to the polynomial decay of \((1 + |\tau |)^{-N - \sigma }\). \(\square \)
9 Proof of Proposition 1.21 (1): The Short Initial Range
Proof of Proposition 1.21 (1)
For \(T < t_g^{\delta /2(1 + A)}\), where \(\delta , A > 0\) are absolute constants arising from Theorem A.34, we use the subconvex bounds in Theorem A.34 to bound the terms \(L(1/2, f \otimes g_{\psi ^2})\) and \(|L(1/2 + it,g_{\psi ^2})|\) by \(O(T^A t_g^{1 - \delta })\), so that for \(h(t) = 1_{E \cup -E}(t)\) with \(E = [T,2T]\),
We then use the Cauchy–Schwarz inequality, the approximate functional equation, Lemma A.5, and the large sieve, Theorem A.32, to bound the remaining moments of \(L(1/2,f) L(1/2,f \otimes \chi _D)\) and of \(|\zeta (1/2 + it) L(1/2 + it,\chi _D)|^2\) by \(O_{\varepsilon }(T^{2 + \varepsilon })\), and so in this range,
For \(t_g^{\delta /2(1 + A)} \le T < t_g^{1/2}\), the subconvex bounds in Theorems A.33 and A.34 are used to bound the terms \(2^{\omega (d_1)} L(1/2,f) L(1/2,f \otimes \chi _D)\) and \(2^{\omega (D)} |\zeta (1/2 + it) L(1/2 + it, \chi _D)|^2\) by \(O_{\varepsilon }(T^{5/6 + \varepsilon })\), so that
with \(h_T\) as in (6.3). Proposition 6.1 (1) then bounds \({\widetilde{\mathcal {M}}}^{\text{ Maa }\ss {}}(h_T) + {\widetilde{\mathcal {M}}}^{\text{ Eis }}(h_T)\) by \(O_{\varepsilon }(t_g^{1 + \varepsilon })\). So in this range,
For \(t_g^{1/2} \le T \ll t_g^{1 - \alpha }\), Proposition 7.1 implies that
where \(\mathfrak {h}= (h_T,0)\) with \(h_T\) as in (8.1). Noting that \(\mathcal {N}(\mathfrak {h}) \ll _{\varepsilon } T^{2 + \varepsilon }\), Corollary 8.3 then shows that \(\mathcal {M}^{\pm } (\mathscr {T}_{t_g}^{\pm } \mathfrak {h})\) are both \(O(Tt_g^{1 - \delta })\) via the Cauchy–Schwarz inequality together with the approximate functional equation and the large sieve, except in a select few ranges, namely the range \(t_f \asymp t_g/T\) in the term \(\mathcal {M}^{\text{ Maa }\ss {},-}(\mathscr {L}^{-} H_{T,t_g}^{-})\), the range \(|t| \asymp t_g/T\) in \(\mathcal {M}^{\text{ Eis }}(\mathscr {L}^{-} H_{T,t_g}^{-})\), and the range \(k_f \asymp t_g/T\) in \(\mathcal {M}^{\text{ hol }}(\mathscr {L}^{\text{ hol }} H_{T,t_g}^{+})\). The former two terms are then treated as we have just done for \(T < t_g^{\delta /2(1 + A)}\) and for \(t_g^{\delta /2(1 + A)} \le T < t_g^{1/2}\), and the latter is treated via the same method, recalling that Proposition 6.1 (2) entails such bounds for holomorphic cusp forms. \(\square \)
Remark 9.1
For the treatment of the range \(t_g^{\delta /2(1 + A)} \le T < t_g^{1/2}\), we in fact have the bound \(O_{\varepsilon }(T^{2/3 + \varepsilon })\) for \(2^{\omega (d_1)} L(1/2,f) L(1/2,f \otimes \chi _D)\) and \(2^{\omega (D)} |\zeta (1/2 + it) L(1/2 + it, \chi _D)|^2\); see Remark 13.2. In the treatment of the range \(t_g^{1/2} \le T \ll t_g^{1 - \alpha }\), we use spectral reciprocity and subsequently require subconvex bounds for \(2^{\omega (d_1)} L(1/2,f) L(1/2,f \otimes \chi _D)\) with f a holomorphic newform of level \(d_1 \mid D\) and weight \(k_f \asymp t_g/T\). Here we do not know of such strong bounds if \(d_1 > 1\): while the bound \(L(1/2,f \otimes \chi _D) \ll _{\varepsilon } k_f^{1/3 + \varepsilon }\) is known [You17, Theorem 1.1], and of course \(L(1/2,f) \ll _{\varepsilon } k_f^{1/2 + \varepsilon }\) is merely the convexity bound, the bound \(L(1/2,f) \ll _{\varepsilon } k_f^{1/3 + \varepsilon }\) is only known for \(d_1 = 1\) [Pen01, Theorem 3.1.1], and a modification of the proof of this bound to allow \(d_1 > 1\) seems to be reasonably nontrivial.
10 Proof of Proposition 1.21 (2): The Bulk Range
The proof that we give of Proposition 1.21 (2) follows the approach of [DK18b], where an asymptotic formula is obtained for a similar expression pertaining instead to the regularised fourth moment of an Eisenstein series. As such, we shall be extremely brief, detailing only the minor ways in which our proof differs from that of [DK18b].
10.1 An application of the Kuznetsov formula.
Following [DK18b, Section 2.1], it suffices to obtain asymptotic formulæ for
analogously to [DK18b, (2.2)], where H(t) is as in (2.3) and \(W(t) = W_{\alpha }(t)\) is a certain weight function given in [BuK17b, Lemma 5.1] that localises h(t) to the range \([-2t_g + t_g^{1 - \alpha }, -t_g^{1 - \alpha }] \cup [t_g^{1 - \alpha },2t_g - t_g^{1 - \alpha }]\). We may artificially insert the parity \(\epsilon _f\) into the spectral sum \(\mathcal {M}^{\text{ Maa }\ss {}}(h)\) since \(L(1/2,f \otimes \chi _D) = L(1/2,f) L(1/2,f \otimes g_{\psi ^2}) = 0\) when \(\epsilon _f = -1\); this allows us to use the opposite sign Kuznetsov formula, which greatly simplifies future calculations.
Akin to the proof of Lemma 6.4, we make use of the Kuznetsov formula associated to the pair of cusps \((\mathfrak {a},\mathfrak {b})\) with \(\AA \sim \infty \) and \(\mathfrak {b}\sim 1\), which once again naturally introduces the root numbers of \(f \boxplus f \otimes \chi _D\) and of \(f \otimes g_{\psi ^2}\) in such a way to give approximate functional equations of the correct length for each level dividing D.
Lemma 10.2
With h as in (10.1), we have that
Here \(V_1^1\) and \(V_2^1\) are as in (A.6) and (A.7).
Proof
We use the opposite sign Kuznetsov formula associated to the \((\infty ,\infty )\) pair of cusps, Theorem A.10, with
noting that this requires Yoshida’s extension of the Kuznetsov formula [Yos97, Theorem], since H(t) has poles at \(t = \pm _1 2t_g \pm _2 i/2\). We subsequently multiply through by
and sum over \(n,m,k,\ell \in \mathbb {N}\). Via the explicit expression in Lemma A.8, the Maaß cusp form term is
after making the change of variables \(m \mapsto v_1 m\) and \(n \mapsto v_2 n\).
We do the same with the opposite sign Kuznetsov formula associated to the \((\infty ,1)\) pair of cusps, Theorem A.16, for which the resulting Maaß cusp form term is
via the explicit expression in Lemma A.9, after making the change of variables \(m \mapsto d_2 m/ w_1\), \(n \mapsto v_2 n\), and interchanging \(v_1\) and \(w_1\). We also do the same but with m and n interchanged.
We add twice the first expression to the second and the third. Using the approximate functional equations, Lemma A.5, with \(X = \sqrt{d_2}/v_1\) and \(X = \sqrt{d_2}/v_2\) respectively, and recalling Lemma 3.2, we obtain \(\mathcal {M}^{\text{ Maa }\ss {}}(h)\) with h as in (10.1) as well as an error term arising from using \(V_1^1\) in place of \(V_1^{-1}\) for the odd Maaß cusp forms, just as in [DK18b, (2.9)]. By [DK18b, (2.5)], the Cauchy–Schwarz inequality, and the large sieve, Theorem A.32, this error is \(O_{\varepsilon }(t_g^{-1 + \varepsilon })\).
The Eisenstein terms from these instances of the Kuznetsov formula give rise to \(\mathcal {M}^{\text{ Eis }}(h)\) plus an error term of size \(O_A(T^{-A})\) for any \(A > 0\). There are no delta terms as these are opposite sign Kuznetsov formulæ. Finally, the Kloosterman terms sum to the desired expression in (10.3). \(\square \)
Following [DK18b, Section 2.3], we insert a smooth compactly supported function \(U(r/2t_g)\) as in [DK18b, (2.13)] into the integrand of the right-hand side of (10.3), absorb W(r) into \(U(r/2t_g)\), replace H(r) with its leading order term via Stirling’s formula (2.4), and treat only the leading order terms \(V(nk^2/D^{3/2}r^2)\) and \(V(m\ell ^2/D^{3/2}(4t_g^2 - r^2))\) of \(V_1^1(nk^2/D^{3/2},r)\) and \(V_2^1(m\ell ^2/D^{3/2},r)\) respectively, with
as in [DK18b, (2.14)]. Defining
as in [DK18b, (2.16)], this shows that the integrals in (10.3) can be replaced with
respectively, as in [DK18b, (2.15)], at the cost of a negligible error. We are left with obtaining an asymptotic formula for
We open up both Kloosterman sums and use the Voronoĭ summation formula, Lemma A.30, for the sum over n. In both sums over c, the corresponding Voronoĭ L-series has a pole at \(s = 1\), which contributes a main term that we now calculate.
10.2 The main term.
Lemma 10.7
The pole at \(s = 1\) in the Voronoĭ L-series contributes a main term equal to
for (10.6) for some \(\delta > 0\).
Proof
For the first sum over c, the pole of the associated Voronoĭ L-series as in Lemma A.30 yields a residue equal to
Following [DK18b, Section 3], we make the change of variables \(x \mapsto cx^2/2\pi \sqrt{m}\), extend the function \(U(r/2t_g)\) in the definition (10.5) of Q(r) to the endpoints 0 and \(2t_g\) at the cost of a negligible error, make the change of variables \(x \mapsto 2t_g x\), and use the definition (10.4) of V as a Mellin transform, yielding an asymptotic expression of the form
where \(1/4< \sigma _1< \sigma _2 < 1/2\). We use Lemma A.31 to reexpress the sum over d, a Gauss sum, as a sum over \(a \mid (c/D,m)\); next, we make the change of variables \(c \mapsto acD\) and \(m \mapsto am\), then use (7.14) to separate \(\lambda _{g_{\psi ^2}}(am)\) as a sum over \(b \mid (a,m)\); finally, we make the change of variables \(a \mapsto ab\) and \(m \mapsto bm\), yielding
The sums over m, k, \(\ell \), c, a, and b in the second line simplify to
We shift the contour in the integral over \(s_2\) to the line \(\mathfrak {R}(s_2) = \sigma _1 - 1/2\); via the subconvex bounds in Theorem A.34, the resulting contour integral is bounded by a negative power of \(t_g\), so that the dominant contribution comes from the residue due to the simple pole at \(s_2 = 0\), namely
Now we do the same with the second sum over c. We open up the Kloosterman sum, make the change of variables \(d \mapsto -{\overline{Dd}}\), and use the Voronoĭ summation formula, Lemma A.30, for the sum over n; the pole of the Voronoĭ L-series at \(s = 1\) yields the term
We make the change of variables \(x \mapsto c\sqrt{D} x^2/2\pi \sqrt{m}\), extend the function \(U(r/2t_g)\) in the definition (10.5) of Q(r) to the endpoints 0 and \(2t_g\) at the cost of a negligible error, make the change of variables \(x \mapsto 2t_g x\), and use the definition (10.4) of V as a Mellin transform, yielding the asymptotic expression
The sum over d is a Ramanujan sum, \(\sum _{a \mid (m,c)} a \mu (c/a)\). We make the change of variables \(c \mapsto ac\) and \(m \mapsto am\), then use (7.14) and make the change of variables \(a \mapsto ab\) and \(m \mapsto bm\), leading to
The sums over m, k, \(\ell \), c, a, and b in the second line simplify to
Again, we shift the contour in the integral over \(s_2\) to the line \(\mathfrak {R}(s_2) = \sigma _1 - 1/2\), with a main term coming from the residue at \(s_2 = 0\) given by
We finish by adding together these two main contributions and observing that the resulting integrand is odd and hence equal to half its residue at \(s_1 = 0\), namely
\(\square \)
10.3 The Voronoĭ dual sums.
Having applied the Voronoĭ summation formula, Lemma A.30, to the sum over n in (10.6) and dealt with the terms arising from the pole of the Voronoĭ L-series, we now treat the terms arising from the Voronoĭ dual sums.
Lemma 10.8
The Voronoĭ dual sums are of size \(O(t_g^{-\delta })\) for some \(\delta > 0\).
Proof
There are two dual sums associated to the two sums over c in (10.6). We prove this bound only for the former dual sum; the proof for the latter follows with minor modifications. The dual sum to the first term can be expressed as a dyadic sum over \(N \le t_g^{2 + \varepsilon }\) times
where \(\Phi _1\) is a smooth function compactly supported on (1/2, 3/2) and
with \(\sigma > 0\). This identity for the dual sum is proven in the same way as in [DK18b, Section 4.1]: we insert a smooth partition of unity \(\Psi _1(n/N)\) to the sum over n in (10.6), then apply of the Voronoĭ summation formula, Lemma A.30, to the ensuing sum over n.
We proceed along the exact same lines as [DK18b, Section 4.1]; in this way, the problem is reduced to proving that the quantity
is \(O(t_g^{-\delta })\) for any \(n < t_g^{\varepsilon }\) and \(t_g^{2 - \varepsilon }< M < t_g^{2 + \varepsilon }\), as in [DK18b, (4.3)], with \(\Psi _2\) another smooth function supported on (1/2, 3/2) and \(Z(x) :=U(x)/4|x|\sqrt{1 - x^2}\).
Now we apply the Voronoĭ summation formula, Lemma A.30, to the sum over m, yielding
where for \(\sigma > 0\),
We continue to follow [DK18b, Section 4.2], by which the problem is reduced to showing that the quantity
is \(O(t_g^{-\delta })\), as in [DK18b, (4.6)], where \(\Phi \) and \(\Psi \) are smooth bump functions with \(\Psi \) supported on (1/2, 3/2) and \(B \le t_g^{2 + \varepsilon }\).
We spectrally expand the sums of Kloosterman sums via Kloosterman summation formulæ, Theorems A.20 and A.22, with \(H = \Phi \). From [BuK17b, Lemma 3.6], \((\mathscr {L}^{\pm } \Phi )(t) \ll t_g^{-A}\) and \((\mathscr {L}^{\text{ hol }} \Phi )(k) \ll t_g^{-A}\) for any \(A > 0\) unless \(|t| < t_g^{\varepsilon }\) and \(k < t_g^{\varepsilon }\), in which case we instead have the bound \(O_{\varepsilon }(t_g^{\varepsilon })\). Using the explicit expressions for the Maaß cusp form, Eisenstein, and holomorphic cusp form terms given in Lemmata A.8 and A.9, we have reduced the problem to showing that both
are \(O(t_g^{-\delta })\) for \(B < t_g^{2 + \varepsilon }\) for all f in either \(\mathcal {B}_0^{*}(\Gamma _0(d_1))\) with \(|t_f| < t_g^{\varepsilon }\) or in \(\mathcal {B}_{\text{ hol }}^{*}(\Gamma _0(d_1))\) with \(k_f < t_g^{\varepsilon }\), where \(d_1 \mid D\), and for \(|t| < t_g^{\varepsilon }\). By Mellin inversion, these two expressions are respectively equal to
for any \(\sigma > 1/2\). The rapid decay of \({\widehat{\Psi }}\) in vertical strips allows the integral to be restricted to \(|\mathfrak {I}(s)| < t_g^{\varepsilon }\) and shifted to \(\sigma = 0\), at which point the subconvex bounds in Theorem A.34 bound the numerators by \(O(t_g^{1 - \delta })\) for some \(\delta > 0\), which completes the proof. \(\square \)
Proof of Proposition 1.21 (2)
This follows directly upon combining Lemmata 10.2, 10.7, and 10.8. \(\square \)
Remark 10.9
Perhaps one can prove this result using analytic continuation, as in the proof of Proposition 7.1, instead of using approximate functional equations. We choose the latter path since the groundwork is laid out in [DK18b], and it avoids technical difficulties in the analytic continuation approach of ensuring a valid choice of test function h.
11 Spectral Reciprocity for the Short Transition Range
For \(\mathfrak {h}:=(h,h^{\text{ hol }}) : (\mathbb {R}\cup i(-1/2,1/2)) \times 2\mathbb {N}\rightarrow \mathbb {C}^2\), let
with
The main result of this section is the following identity.
Proposition 11.1
(Cf. Proposition 7.1). For admissible \(\mathfrak {h}\), we have that
where \(\mathscr {T}_0^{\pm }\) is as in (7.3) with \(t_g\) replaced by 0 and \({\mathop {\sim }\limits ^{\mathcal {G}}}(\mathfrak {h})\) is the holomorphic extension to \((s_1,s_2) = (1/2,1/2)\) of
with
Here \(\mathscr {T}_{s_1,s_2,0}^{\pm } \mathfrak {h}\) is as in (7.9) with \(t_g\) replaced by 0.
Similarly to Section 7, we define
for \(s_1,s_2 \in \mathbb {C}\). We additionally set
Lemma 11.2
(Cf. Lemma 7.8). For admissible \(\mathfrak {h}\) and \(5/4< \mathfrak {R}(s_1), \mathfrak {R}(s_2) < 3/2\) with \(s_1 \ne s_2\), we have that
Proof
This follows by the same method of proof as for Proposition 7.1 except that we replace \(\lambda _{g_{\psi ^2}}(n)\) with \(\lambda _{\chi _D,1}(n,0)\), so that \(t_g\) is replaced by 0. In place of a simple pole at \(s = 2(1 - s_1)\) with residue given by (7.12), there are two simple poles at \(s = 2(1 - s_1)\) and \(s = 2(1 - s_2)\). When \(\mathfrak {R}(s_2) > \mathfrak {R}(s_1)\), the former is given by
by Lemma A.30. Just as in the proof of Proposition 7.1, we open up the Voronoĭ L-series, reexpress the Gauss sum over d as a sum over \(a \mid (c/D,m)\) via Lemma A.31, make the change of variables \(c \mapsto acD\) and \(m \mapsto am\), apply (7.14), and then make the change of variables \(m \mapsto bm\) and \(a \mapsto ab\), which leads us to
While only initially valid for \(\mathfrak {R}(s_2) > \mathfrak {R}(s_1)\), this extends holomorphically in the region \(5/4< \mathfrak {R}(s_1), \mathfrak {R}(s_2) < 3/2\) with \(s_1 \ne s_2\). An identical calculation yields the residue at \(s = 2(1 - s_2)\). \(\square \)
Proof of Proposition 11.1
This follows the same method as [BLM19, Proof of Theorem 1], [BlK19b, Proof of Theorem 1], and [BlK19a, Proof of Theorem 2]. The holomorphic extensions of \(\mathcal {M}^{\text{ Eis }}(s_1,s_2;h)\) and \(\mathcal {M}^{\text{ Eis }} (s_2,s_1;\mathscr {L}^{\pm } H_{s_1,s_2,0}^{\pm })\) for \(\mathfrak {R}(s_1), \mathfrak {R}(s_2) < 1\) give rise to additional polar divisors arise via shifting the contour in the integration over t, namely \({\mathop {\sim }\limits ^{\mathcal {R}}}(s_1,s_2;\mathfrak {h})\) and \({\mathop {\sim }\limits ^{\mathcal {R}}}(s_2,s_1;\mathscr {T}_{s_1,s_2,0}^{\pm } \mathfrak {h})\). In this way, we obtain the identity
for \(\mathfrak {R}(s_1),\mathfrak {R}(s_2) \ge 1/2\) with \(s_1 \ne s_2\). It remains to note that since the terms \({\mathop {\sim }\limits ^{\mathcal {M}}}^{-}(s_1,s_2;\mathfrak {h})\) and \({\mathop {\sim }\limits ^{\mathcal {M}}}^{\pm }(s_2,s_1;\mathscr {T}_{s_1,s_2,0}^{\pm } \mathfrak {h})\) extend holomorphically to \((s_1,s_2) = (1/2,1/2)\), so must \({\mathop {\sim }\limits ^{\mathcal {G}}}(s_1,s_2;\mathfrak {h})\). \(\square \)
12 Bounds for the Transform for the Short Transition Range
We take \(\mathfrak {h}= (h,0)\) in Proposition 11.1 to be
for some fixed large integer \(N \ge 500\), \(T > 0\), and \(T^{1/3} \ll U \ll T\), so that \(h_{T,U}(t)\) is positive for \(t \in \mathbb {R}\cup i(-1/2,1/2)\) and bounded from below by a constant dependent only on N for \(t \in [-T - U, -T + U] \cup [T - U, T + U]\). The transform \(H_{T,U}^{\pm }\) as in (7.4) of \(h_{T,U}\) is
with \(-3< \sigma _1 < 1\), where \(\mathcal {G}_0^{\pm }(s)\) is as in (7.5). We once again wish to determine the asymptotic behaviour of the functions
with uniformity in all variables T, U, and t or k.
Lemma 12.2
(Cf. [BLM19, Lemma 4], [BlK19a, Lemma 1]). For \(j \in \mathbb {N}_0\) with \(j \le N\), we have that
Proof
The proof will follow via the same methods as [BLM19, Proof of Lemma 4] and [BlK19a, Proof of Lemma 1], which in turn are inspired by [BuK17a, Proof of Lemma 3.8], so we only sketch the details. We recall that
We will use the following, from [BLM19, (2.15), (A.1), (A.2), (A.3), (A.6)]:
We first deal with the range \(x \le 1\). We use (12.3) to split up into \(I_{2ir}(4\pi x)\) and \(I_{-2ir}(4\pi x)\), then shift the contour to \(\mathfrak {I}(r) = -N\) and \(\mathfrak {I}(r) = N\) respectively. We differentiate under the integral sign and then use (12.5) and (12.7), which shows that
which is certainly sufficient.
Next, we deal with the range \(1 \le x \le T^{13/12}\). We consider
The j-th derivative of the Fourier transform \(\check{h}_{\text{ spec }}(x)\) is
We integrate by parts \(A_1\) times:
By the Leibniz rule, we find that
for \(0 \le A_1 \le 4N\). Alternatively, we may shift the contour to \(\mathfrak {I}(r) = -{{\,\mathrm{sgn}\,}}(x)N\), which gives
Following [BLM19, Proof of Lemma 4], using (12.8) and (12.9) in place of [BLM19, (6.3) and (6.4)], we find that \(x^j (\mathscr {K}^{-} h_{T,U})^{(j)}(x)\) is equal to [BLM19, (6.12)], except for the three error terms in this equation being bounded by \(UT^{1 + \frac{5}{14}j - N}\), and the main term being a linear combination of terms of the form
where \(0 \le \alpha \le \frac{3}{7} (6N - 2j - 3)\), \(0 \le \beta \le \alpha /3\), \(0 \le n \le j \le N\), and \(n \le \gamma \le \frac{2}{21} (14N + 9j - 7)\). For \(|x - T| \ge U \log T\), this decays faster than any power of T. If \(|x - T| \le U^2/T\), then we have the bound O(T). Finally, for \(U^2/T \le |x - T| \le U \log T\), the bound
holds provided that \(U \gg T^{1/3}\).
Finally, for \(x \ge T^{13/12}\), we use (12.4) and (12.6) and split the integral at \(|r| = x/3\pi \), which is readily seen to give
as in [BLM19, Proof of Lemma 4], which is more than sufficient. \(\square \)
Corollary 12.10
For \(-N/2< \sigma < N/2\) and \(j \in \mathbb {N}_0\) with \(j \le N/2\),
Proof
We estimate the integral
by breaking this into the three ranges \((0,T - U\log T)\), \([T - U\log T, T + U\log T]\), and \((T + U\log T,\infty )\). We then estimate each of these ranges via integration by parts and Lemma 12.2; the main contribution comes from the middle range. \(\square \)
Lemma 12.11
(Cf. Lemma 8.2). Define
For \(s = \sigma + i\tau \) with \(-N/2< \sigma < 1\) and \(j \in \mathbb {N}_0\) with \(j \le N/2\), proved that additionally s is at least a bounded distance away from \(\{2(\pm it - n) : n \in \mathbb {N}_0\}\),
and
For \(s = \sigma + i\tau \) with \(-N/2< \sigma < 1\) and \(j \in \mathbb {N}_0\) with \(j \le N/2\), proved that additionally s is at least a bounded distance away from \(\{1 - k - 2n : n \in \mathbb {N}_0\}\),
and
Proof
This follows via the same method as the proof of Lemma 8.2, using Corollary 12.10 in place of [BLM19, Lemma 4]. \(\square \)
Corollary 12.12
(Cf. Corollary 8.3). For fixed \(j \in \mathbb {N}_0\) with \(j \le N/2\),
while for fixed \(-\min \{N/2,1 - k\}< \sigma < 1\),
Proof
By Mellin inversion,
where \(0< \sigma _1 < 1\). As in the proof of Corollary 8.3, we use Lemma 12.11 to bound these integrals. For \((\mathscr {L}^{\pm } H_{T,U}^{\pm })(t)\), we shift the contour from \(\mathfrak {R}(s) = \sigma _1\) to \(\mathfrak {R}(s) = \sigma \) with \(-2< \sigma < 0\), with the dominant contribution combing from the residues at the poles at \(s = \pm 2it\). We do the same with \((\mathscr {L}^{\text{ hol }} H_{T,U}^{+})(k)\) with \(-\min \{N/2,1 - k\}< \sigma < 1\); the dominant contribution of the ensuing integral comes from when \(|\tau |\) is small. \(\square \)
Lemma 12.13
We have that \({\mathop {\sim }\limits ^{\mathcal {G}}}(\mathfrak {h}) \ll _{\varepsilon } (TU)^{1 + \varepsilon }\).
Proof
Via Mellin inversion, we have that for \(1/2< \mathfrak {R}(s_1),\mathfrak {R}(s_2) < 1\) with \(s_1 \ne s_2\),
where \(4(1 - \mathfrak {R}(s_1) - \mathfrak {R}(s_2)) + 2\max \{\mathfrak {R}(s_1),\mathfrak {R}(s_2)\}< \sigma < 2(1 - \max \{\mathfrak {R}(s_1),\mathfrak {R}(s_2)\})\). We shift the contour to \(\mathfrak {R}(s) = \sigma _2\) with \(\sigma _2\) slightly to the left of \(4(1 - \mathfrak {R}(s_1) - \mathfrak {R}(s_2)) + 2\max \{\mathfrak {R}(s_1),\mathfrak {R}(s_2)\}\), picking up a residue at \(s = 4 - 4s_1 - 2s_2\) equal to
Similar calculations hold for the terms \((\mathscr {L}^{+} H_{s_1,s_2,0}^{+})(\pm i(s_2 - 1))\), \((\mathscr {L}^{-} H_{s_1,s_2,0}^{-})(\pm i(s_1 - 1))\), and \((\mathscr {L}^{-} H_{s_1,s_2,0}^{-})(\pm i(s_2 - 1))\).
Now we let \(s_1 = 1/2\) and consider the Laurent expansions about \(s_2 = 1/2\) of \({\mathop {\sim }\limits ^{\mathcal {N}}}(1/2,s_2;\mathfrak {h})\), \(-{\mathop {\sim }\limits ^{\mathcal {R}}}(1/2,s_2;\mathfrak {h})\), and \({\mathop {\sim }\limits ^{\mathcal {R}}}(1/2,s_2;\mathscr {T}_{1/2,s_2,0}^{\pm } \mathfrak {h})\). Since \({\mathop {\sim }\limits ^{\mathcal {G}}}(1/2,s_2;\mathfrak {h})\) is holomorphic at \(s_2 = 1/2\), the principal parts must sum to zero, and so it suffices to bound the constant term in each Laurent expansion. For \({\mathop {\sim }\limits ^{\mathcal {R}}}(1/2,s_2;\mathscr {T}_{1/2,s_2,0}^{\pm } \mathfrak {h})\), we use Corollary 12.10 to bound (12.14) with \(\sigma _1\) replaced by \(\sigma _2 \in (0,1)\). For the remaining terms, it is readily seen that the dominant contribution is bounded by a constant multiple dependent on D of
\(\square \)
13 Proof of Proposition 1.21 (3): The Short Transition Range
Proof of Proposition 1.21 (3)
Via the approximate functional equation, Lemma A.5, and the large sieve, Theorem A.32,
for \(1 + |2t_g - T| \ll U \le T \ll t_g\). Next, we claim that
for \(T^{1/3} \ll U \le T\). To see this, we use Proposition 11.1 with \(\mathfrak {h}= (h_{T,U},0)\), where \(h_{T,U}\) is as in (12.1). Lemma 12.13 shows that \({\mathop {\sim }\limits ^{\mathcal {G}}}(\mathfrak {h}) \ll _{\varepsilon } (TU)^{1 + \varepsilon }\). For \({\mathop {\sim }\limits ^{\mathcal {M}}}^{\pm } (\mathscr {T}_0^{\pm } \mathfrak {h})\), we break up each term into dyadic intervals and use Corollary 12.12 to bound \((\mathscr {L}^{\pm } H_{T,U}^{\pm })(t)\) and \((\mathscr {L}^{\text{ hol }} H_{T,U}^{+})(t)\) and the approximate functional equation and large sieve to bound each spectral sum of L-functions. The largest contributions come from \({\mathop {\sim }\limits ^{\mathcal {M}}}^{\text{ Maa }\ss {},-}(\mathscr {L}^{-} H_{T,U}^{-})\) when \(t_f \asymp T/U\) and \({\mathop {\sim }\limits ^{\mathcal {M}}}^{\text{ Eis }}(\mathscr {L}^{-} H_{T,U}^{-})\) when \(|t| \asymp T/U\), which give terms of size \(O_{\varepsilon }(T^{3/2 + \varepsilon } U^{-1/2 + \varepsilon })\). Since \(U \ge T^{1/3}\), this is \(O_{\varepsilon }((TU)^{1 + \varepsilon })\).
The result now follows from the Cauchy–Schwarz inequality. \(\square \)
Remark 13.2
Taking \(U = T^{1/3}\) and dropping all but one term in (13.1) implies that
for \(f \in \mathcal {B}_0^{*}(\Gamma _0(d_1))\) and \(t \in \mathbb {R}\), where we have additionally kept track of the D-dependence. This is a Weyl-strength subconvex bound in the \(t_f\)- and t-aspects and a convex bound in the D-aspect. For \(D = 1\), (13.1) and its corollary (13.3) are results of Jutila [Jut01, Theorem]; the proof is not wholly dissimilar, though it is perhaps slightly less direct, for it passes through the spectral decomposition of shifted convolution sums.
References
A. O. L. Atkin and Wen-Ch’ing Winnie Li. Twists of newforms and pseudo-eigenvalues of \(W\)-operators. Inventiones Mathematicae, (48)3 (1978), 221–243
M. V. Berry. Regular and irregular semiclassical wavefunctions. Journal of Physics A: Mathematical and General, (10)12 (1977), 2083–2091
V. Blomer. Rankin–Selberg \(L\)-functions on the critical line. manuscripta mathematica, (117)2 (2005), 111–133
Valentin Blomer. On the \(4\)-norm of an automorphic form. Journal of the European Mathematical Society, (15)5 (2013), 1825–1852
Valentin Blomer and Rizwanur Khan. Uniform subconvexity and symmetry breaking reciprocity. Journal of Functional Analysis, (276)7 (2019), 2315–2358
Valentin Blomer and Rizwanur Khan. Twisted moments of \(L\)-functions and spectral reciprocity. Duke Mathematical Journal, (168)6 (2019), 1109–1177
Valentin Blomer, Rizwanur Khan, and Matthew Young. Distribution of mass of holomorphic cusp forms. Duke Mathematical Journal, (162)14 (2013), 2609–2644
Valentin Blomer, Xiaoqing Li, and Stephen D. Miller. A spectral reciprocity formula and non-vanishing for \(L\)-functions on \(\text{ GL }(4) \times \text{ GL }(2)\). Journal of Number Theory Prime, (205) (2019), 1–43
Jack Buttcane and Rizwanur Khan. \(L^4\)-Norms of Hecke newforms of large level. Mathematische Annalen, (362)3–4 (2015), 699–715
Jack Buttcane and Rizwanur Khan. A mean value of a triple product of \(L\)-functions. Mathematische Zeitschrift, (285)1 (2017), 565–591
Jack Buttcane and Rizwanur Khan. On the fourth moment of Hecke Maass forms and the random wave conjecture. Compositio Mathematica, (153)7 (2017), 1479–1511
Dan J. Collins. Numerical computation of Petersson inner products and \(q\)-expansions. preprint (2018), 24 pages.
Dan J. Collins. Anticyclotomic \(p\)-adic \(L\)-functions and Ichino’s formula. To appear in Annales mathématiques du Québec, (2019), 63 pages.
Goran Djanković and Rizwanur Khan. A conjecture for the regularized fourth moment of Eisenstein series. Journal of Number Theory, (182) (2018), 236–257
Goran Djanković and Rizwanur Khan. On the random wave conjecture for Eisenstein series. To appear In: International Mathematics Research Notices, (2018), 23 pages.
Amit Ghosh, Andre Reznikov, and Peter Sarnak. Nodal domains of Maass forms I. Geometric and Functional Analysis, (23)5 (2013), 1515–1568
I. S. Gradshteyn and I. M. Ryzhik, Table of Integrals, Series, and Products, Seventh Edition. Editors Alan Jeffrey and Daniel Zwillinger. Academic Press, Burlington (2007).
Andrew Granville and Igor Wigman. Planck-scale mass equidistribution of toral laplace eigenfunctions. Communications in Mathematical Physics, (355)2 (2017), 767–802
Gergely Harcos and Philippe Michel. The subconvexity problem for Rankin–Selberg \(L\)-functions and equidistribution of Heegner points. II. Inventiones Mathematicae, (163)3 (2006), 581–655
Dennis A. Hejhal and Barry N. Rackner. On the topography of Maass waveforms for \(\text{ PSL }(2,{\mathbb{Z}})\). Experimental Mathematics, (1)4 (1992), 275–305
Dennis A. Hejhal and Andreas Strömbergsson. On quantum Chaos and Maass waveforms of CM-type. Foundations of Physics, (31)3 (2001), 519–533
Roman Holowinsky and Nicolas Templier. First moment of Rankin–Selberg central \(L\)-values and subconvexity in the level aspect. Ramanujan Journal, (33)1 (2014), 131–151
Yueke Hu. Cuspidal part of an Eisenstein series restricted to an index \(2\) subfield. Research in Number Theory, (2)33 (2016), 61 pages
Yueke Hu. Triple product formula and the subconvexity bound of triple product \(L\)-function in level aspect. American Journal of Mathematics, (139)1 (2017), 215–259
Peter Humphries. Equidistribution in shrinking sets and \(L^4\)-norm bounds for automorphic forms. Mathematische Annalen, (371)3–4 (2018), 1497–1543
Peter Humphries and Maksym Radziwiłł. Optimal small scale equidistribution of lattice points on the sphere, Heegner points, and closed geodesics. Preprint (2019), 43 pages.
Atsushi Ichino. Trilinear forms and the central values of triple product \(L\)-functions. Duke Mathematical Journal, (145)2 (2008), 281–307
Henryk Iwaniec. Topics in Classical Automorphic Forms. Graduate Studies in Mathematics, Vol. 17. American Mathematical Society, Providence (1997).
Henryk Iwaniec. Spectral Methods of Automorphic Forms, Second Edition. Graduate Studies in Mathematics, Vol. 53. American Mathematical Society, Providence (2002).
Henryk Iwaniec and Emmanuel Kowalski. Analytic Number Theory. American Mathematical Society Colloquium Publications, Vol. 53. American Mathematical Society, Providence (2004).
Henryk Iwaniec, Wenzhi Luo, and Peter Sarnak. Low lying zeros of families of \(L\)-functions. Publications Mathématiques de l’Institut des Hautes Études Scientifiques, (91)1 (2000), 55–131
Matti Jutila. The Fourth Moment of Central Values of Hecke Series. In Number Theory: Proceedings of the Turku Symposium on Number Theory in Memory of Kustaa Inkeri, editors Matti Jutila and Tauno Metsänkylä. Walter de Gruyter, Berlin (2001), pp. 167–177
Matti Jutila and Yoichi Motohashi. Uniform bound for Hecke \(L\)-functions. Acta Mathematica, (195)1 (2005), 61–115
E. Kowalski, P. Michel, and J. VanderKam. Rankin–Selberg \(L\)-functions in the level aspect. Duke Mathematical Journal, (114)1 (2002), 123–191
Jonathan Kim Chung Lam. A local large sieve inequality for cusp forms. Journal de Théorie des Nombres de Bordeaux, (26)3 (2014), 757–787
Yuk-Kam Lau, Jianya Liu, and Yangbo Ye. A NewBound \(k^{2/3 + \varepsilon }\) for Rankin–Selberg \(L\)-functions for Hecke congruence subgroups. International Mathematics Research Papers, (2006) (2006), 1–78
Yuk-Kam Lau, Jianya Liu, and Yangbo Ye. Subconvexity bounds for Rankin–Selberg \(L\)-functions for congruence subgroups. Journal of Number Theory, (121)2 (2006), 204–223
Yuk-Kam Lau and Kai-Man Tsang. A mean square formula for central values of twisted automorphic \(L\)-functions. Acta Arithmetica, (118)3 (2005), 232–262
Elon Lindenstrauss. Invariant measures and arithmetic quantum unique ergodicity. Annals of Mathematics, (163)1 (2006), 165–219
Jianya Liu and Yangbo Ye. Subconvexity for Rankin–Selberg \(L\)-functions of Maass forms. Geometric and Functional Analysis, (12)6 (2002), 1296–1323
Sheng-Chi Liu. \(L^4\)-norms of the holomorphic dihedral forms of large level. Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg, (85)1 (2015), 53–57
Sheng-Chi Liu, Riad Masri, and Matthew P. Young. Subconvexity and equidistribution of Heegner points in the level aspect. Compositio Mathematica, (149)7 (2013), 1150–1174
Wenzhi Luo. \(L^4\)-norms of the dihedral Maass forms. International Mathematics Research Notices, (2014)8 (2014), 2294–2304
Wenzhi Luo and Peter Sarnak. Quantum ergodicity of eigenfunctions on \(\text{ PSL }_2({\mathbb{Z}}) \backslash {\mathbb{H}}^2\). Publications Mathématiques de l’Institut des Hautes Études Scientifiques, (81) (1995), 207–237
Philippe Michel and Akshay Venkatesh. The subconvexity problem for \(\text{ GL }_2\). Publications Mathématiques de l’Institut des Hautes Études Scientifiques, (111) (2010), 171–271
Toshitsune Miyake. Modular Forms. Springer Monographs in Mathematics. Springer, Berlin (2006).
Yoichi Motohashi. Spectral Theory of the Riemann Zeta-Function. Cambridge Tracts in Mathematics, Vol. 127. Cambridge University Press, Cambridge (1997).
Zhuangzhuang Peng. Zeros and Central Values of Automorphic \(L\)-Functions. Ph.D. Thesis, Princeton University (2001).
Peter Sarnak. Estimates for Rankin–Selberg \(L\)-functions and quantum unique ergodicity. Journal of Functional Analysis, (184)2 (2001), 419–453
Peter Sarnak. Spectra of hyperbolic surfaces. Bulletin of the American Mathematical Society, (40)4 (2003), 441–478
Ralf Schmidt. Some remarks on local newforms for \(\text{ GL }(2)\). Journal of the Ramanujan Mathematical Society, (17) (2002), 115–147
Kannan Soundararajan. Quantum unique ergodicity for \(\text{ SL }_2({\mathbb{Z}}) \backslash {\mathbb{H}} \). Annals of Mathematics, (172)2 (2010), 1529–1538
Florin Spinu. The \(L^4\)Norm of the Eisenstein series. Ph.D. Thesis, Princeton University (2003).
Thomas C. Watson. Rankin triple products and quantum chaos, Ph.D. Thesis, Princeton University, 2002 (revised 2008).
Igor Wigman and Nadav Yesha. Central limit theorem for Planck scale mass equidistribution of toral Laplace eigenfunctions. Mathematika, (65)3 (2019), 643–676
Eiji Yoshida. Remarks on the Kuznetsov trace formula. In: Analytic Number Theory. editor Y. Motohashi, London Mathematical Society Lecture Note Series, Vol. 247. Cambridge University Press, Cambridge (1997), pp. 377–382.
Matthew P. Young. The quantum unique ergodicity conjecture for thin sets. Advances in Mathematics, (286) (2016), 958–1016
Matthew P. Young. Weyl-type hybrid subconvexity bounds for twisted \(L\)-functions and Heegner points on shrinking sets. Journal of the European Mathematical Society, (19)5 (2017), 1545–1576
Matthew P. Young. Explicit calculations with Eisenstein series. Journal of Number Theory, (199) (2019), 1–48
Acknowledgements
The first author would like to thank Paul Nelson for suggesting the usage of Lemma 5.2 in place of the method sketched in Remark 5.20, Dan Collins for many useful conversations about local constants in the Watson–Ichino formula, and above all Peter Sarnak for his encouragement on working on this problem. The authors would also like to thank Bingrong Huang and the anonymous referee for helpful suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The first author is supported by the European Research Council Grant Agreement 670239. The second author is supported by the Simons Foundation, award number 630985.
Automorphic Machinery
Automorphic Machinery
In this appendix, we detail the many tools that are used in the course of proving Proposition 1.21. These are the following: the explicit relation between dihedral Maaß newforms and Hecke Größencharaktere; several root number calculations; the approximate functional equation; explicit forms of the Kuznetsov, Petersson, Kloosterman, and Voronoĭ summation formulæ; details on Mellin transforms of certain functions arising in the aforementioned summation formulæ; the large sieve; and pre-existing subconvexity estimates for certain L-functions.
1.1 Dihedral Maaß newforms and Hecke Größencharaktere.
Let \(D \equiv 1 \pmod {4}\) be a positive squarefree fundamental discriminant of a real quadratic field \(K = \mathbb {Q}(\sqrt{D})\) with ring of integers \(\mathcal {O}_K\) and let \(\chi _D\) be the quadratic character modulo D associated to the extension \(K/\mathbb {Q}\) via class field theory. We record here the fact that the Gauss sum \(\tau (\chi _D)\) of \(\chi _D\) is equal to \(\sqrt{D}\).
The Hecke Größencharaktere \(\psi \) of conductor \(\mathcal {O}_K\) satisfy
for every principal ideal \((\alpha )\) of \(\mathcal {O}_K\), with \(\ell \in \mathbb {Z}\) and \(\kappa \in \{0,1\}\) subject to the restriction that \(\kappa = 0\) if \(\epsilon _K \sigma (\epsilon _K) = -1\), where \(\sigma \) denotes the nontrivial element of \({{\,\mathrm{Gal}\,}}(K/\mathbb {Q})\) and \(\epsilon _K > 0\) is the fundamental unit of K. Moreover, every Hecke Größencharakter is determined by \(\ell \), \(\kappa \), and a class group character, and such a Hecke Größencharakter does not factor through the norm map \(N_{K/\mathbb {Q}}\) if and only if either \(\ell \) is positive or the class group character associated to \(\psi \) is complex.
A dihedral Maaß newform \(g = g_{\psi }\) is the automorphic induction of a Hecke Größencharakter \(\psi \) of K for which \(\psi \) does not factor through the norm map \(N_{K/\mathbb {Q}}\). When \(\psi \) has conductor \(\mathcal {O}_K\), \(g_{\psi }\) is an element of \(\mathcal {B}_0^{*}(D,\chi _D)\) whose Fourier expansion about the cusp at infinity is given by
where
and \(N(\mathfrak {a}) :=\# \mathcal {O}_K / \mathfrak {a}\) denotes the absolute norm of a nonzero ideal \(\AA \subset \mathcal {O}_K\). Note that \(\rho _{g_{\psi }}(-n) = (-1)^{\kappa } \rho _{g_{\psi }}(n)\); that is, \((-1)^{\kappa }\) is the parity of \(g_{\psi }\). In particular, \(g_{\psi }\) is even if \(\psi \) is the square of another Hecke Größencharakter.
The Satake parameters \(\alpha _{g_{\psi }}(p),\beta _{g_{\psi }}(p)\) of \(g_{\psi }\) at a prime p are related to the Hecke eigenvalue \(\lambda _{g_{\psi }}(p)\) and nebentypus \(\chi _D(p)\) via
The relationship between the Satake parameters of \(g_{\psi }\) at a prime p and the values of the Hecke Größencharakter \(\psi \) on prime ideals \(\mathfrak {p}\mid p \mathcal {O}_K\) is as follows:
If \(\chi _D(p) = 1\), then p splits in K, so that \(p \mathcal {O}_K = \mathfrak {p}\sigma (\mathfrak {p})\), and its Satake parameters are \(\alpha _f(p) = \psi (\mathfrak {p})\) and \(\beta _f(p) = \psi (\sigma (\mathfrak {p})) = {\overline{\psi }}(\mathfrak {p})\).
If \(\chi _D(p) = -1\), then p is inert in K, so that \(p \mathcal {O}_K = \mathfrak {p}\), and \(\alpha _{g_{\psi }}(p) = -\beta _{g_{\psi }}(p) = 1\).
If \(\chi _D(p) = 0\), then p ramifies in K, so that \(p \mathcal {O}_K = \mathfrak {p}^2\), and \(\alpha _{g_{\psi }}(p) = \psi (\mathfrak {p})\) while \(\beta _{g_{\psi }}(p) = 0\).
In all cases, \(|\alpha _{g_{\psi }}(p)| = 1\). We record the following useful consequences.
Lemma A.1
The Hecke eigenvalues of a dihedral newform \(g_{\psi } \in \mathcal {B}_0^{*}(D,\chi _D)\) satisfy \(\lambda _{g_{\psi }}(p) \in [-2,2]\) and \(\lambda _{g_{\psi }}(n) \in \{\pm 1\}\) when \(n \mid D^{\infty }\); moreover, \(\lambda _{g_{\psi }}(n) = 1\) when \(n \mid D^{\infty }\) if \(g_{\psi }\) is even. We have that \(g_{\psi } \otimes \chi _D = \overline{g_{\psi }} = g_{\psi }\) and \(\lambda _{g_{\psi }}(n) \chi _D(n) = \delta _{(D,n),1} \lambda _{g_{\psi }}(n)\).
1.2 Root number calculations.
Since Proposition 1.21 involves moments of L-functions of level greater than 1, we must explicitly determine the root numbers and conductors of these L-functions in order to precisely utilise the approximate functional equation.
Recall that the Atkin–Lehner pseudo-eigenvalue \(\eta _f(w)\) of \(f \in \mathcal {B}_0^{*}(\Gamma _0(q))\) with \(w \mid q\) is independent of the choice of integer entries \(a,b,c,d \in \mathbb {Z}\) in the definition of the Atkin–Lehner operator \(W_w\) provided that \(\det W_w = 1\) (cf. Section 3.3).
Lemma A.2
(Cf. [HT14, Section 2.3]). Let f be either a member of \(\mathcal {B}_0^{*}(\Gamma _0(d_1))\) or \(\mathcal {B}_{\text{ hol }}^{*}(\Gamma _0(d_1))\) with \(d_1 d_2 = D\). Then the conductors and root numbers of f, \(f \otimes \chi _D\), and \(f \otimes g_{\psi ^2}\) are given by
Proof
This follows by a local argument studying the local components of \(\pi _f\), \(\pi _f \otimes \omega _D\), and \(\pi _f \otimes \pi _{g_{\psi ^2}}\), where \(\pi _f, \pi _{g_{\psi ^2}}\) are the cuspidal automorphic representations of \({{\,\mathrm{GL}\,}}_2(\mathbb {A}_{\mathbb {Q}})\) associated to the newforms \(f, g_{\psi ^2}\) and \(\omega _D\) is the Hecke character of \(\mathbb {Q}^{\times } \backslash \mathbb {A}_{\mathbb {Q}}^{\times }\) that is the idèlic lift of \(\chi _D\). We give only the proof for the root number and conductor of \(f \otimes g_{\psi ^2}\), for the other two cases are similar but simpler.
At the archimedean place, \(f \in \mathcal {B}_0^{*}(\Gamma _0(d_1))\) implies that \(\pi _{f,\infty }\) is a principal series representation \({{\,\mathrm{sgn}\,}}^{\kappa _f} |\cdot |^{it_f} \boxplus {{\,\mathrm{sgn}\,}}^{\kappa _f} |\cdot |^{-it_f}\) and \(\pi _{g_{\psi ^2},\infty } = |\cdot |^{2it_g} \boxplus |\cdot |^{-2it_g}\), where \(\kappa _f\) is zero if f is even and one if f is odd, and so
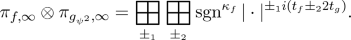
The local epsilon factor \(\epsilon (s,\pi _{f,\infty } \otimes \pi _{g_{\psi ^2},\infty },\psi _{\infty })\) is \(i^{4\kappa _f} = 1\). Similarly, \(f \in \mathcal {B}_{\text{ hol }}^{*}(\Gamma _0(d_1))\) implies that \(\pi _{f,\infty } = D_{k_f}\) where \(k_f \in 2\mathbb {N}\) is the weight of f and \(D_k\) is the discrete series representation of weight k. Then
$$\begin{aligned} \pi _{f,\infty } \otimes \pi _{g_{\psi ^2},\infty } = D_{k_f} \left| \det \right| ^{2it_g} \boxplus D_{k_f} \left| \det \right| ^{-2it_g}. \end{aligned}$$The local epsilon factor is \(i^{2k_f} = 1\).
At a prime \(p \mid d_1\), \(\pi _{f,p}\) is a special representation \(\omega _{f,p} \mathrm {St}_p\), where \(\omega _{f,p}\) is either trivial or the unramified quadratic character, and \(\pi _{g_{\psi ^2},p} = \omega _{g_{\psi ^2},p} \boxplus 1\), where \(\omega _{g_{\psi ^2},p}\) is the local component of \(\chi _D\) (and hence a ramified character of \(\mathbb {Q}_p^{\times }\) of conductor exponent \(c(\omega _{g_{\psi ^2},p}) = 1\)). It follows that
$$\begin{aligned} \pi _{f,p} \otimes \pi _{g_{\psi ^2},p} = \omega _{g_{\psi ^2},p} \omega _{f,p} \mathrm {St}_p \boxplus \omega _{f,p} \mathrm {St}_p, \end{aligned}$$and so the local conductor exponent \(c(\pi _{f,p} \otimes \pi _{g_{\psi ^2},p})\) is
$$\begin{aligned} c\left( \omega _{g_{\psi ^2},p} \omega _{f,p} \mathrm {St}_p\right) + c\left( \omega _{f,p} \mathrm {St}_p\right) = 2 + 1 = 3, \end{aligned}$$while the local epsilon factor \(\epsilon (s,\pi _{f,p} \otimes \pi _{g_{\psi ^2},p},\psi _p)\) is equal to
$$\begin{aligned} \epsilon \left( s,\omega _{g_{\psi ^2},p} \omega _{f,p} \mathrm {St}_p,\psi _p\right) \epsilon \left( s,\omega _{f,p} \mathrm {St}_p,\psi _p\right) = -\omega _{f,p}(p) \epsilon \left( \frac{1}{2},\omega _{g_{\psi ^2},p},\psi _p\right) ^2 p^{-3\left( s - \frac{1}{2}\right) }, \end{aligned}$$and \(\epsilon (1/2,\omega _{g_{\psi ^2},p},\psi _p)\) is \(\tau (\chi _p) p^{-1/2}\), where \(\chi _p\) is the quadratic character modulo p, while \(\omega _{f,p}(p)\) is \(\lambda _f(p) \sqrt{p}\).
At a prime \(p \mid d_2\), \(\pi _{f,p} = \omega _{f,p} \boxplus \omega _{f,p}^{-1}\), where both characters are unramified, and \(\pi _{g_{\psi ^2},p} = \omega _{g_{\psi ^2},p} \boxplus 1\), where \(\omega _{g_{\psi ^2},p}\) is the local component of \(\chi _D\). It follows that
$$\begin{aligned} \pi _{f,p} \otimes \pi _{g_{\psi ^2},p} = \omega _{g_{\psi ^2},p} \omega _{f,p} \boxplus \omega _{g_{\psi ^2},p} \omega _{f,p}^{-1} \boxplus \omega _{f,p} \boxplus \omega _{f,p}^{-1}, \end{aligned}$$and so the local conductor exponent \(c(\pi _{f,p} \otimes \pi _{g_{\psi ^2},p})\) is
$$\begin{aligned} c\left( \omega _{g_{\psi ^2},p} \omega _{f,p}\right) + c\left( \omega _{g_{\psi ^2},p} \omega _{f,p}^{-1}\right) + c\left( \omega _{f,p}\right) + c\left( \omega _{f,p}^{-1}\right) = 1 + 1 + 0 + 0 = 2, \end{aligned}$$while the local root number \(\epsilon (s,\pi _{f,p} \otimes \pi _{g_{\psi ^2},p},\psi _p)\) is equal to
$$\begin{aligned}&\epsilon \left( s,\omega _{g_{\psi ^2},p} \omega _{f,p}, \psi _p\right) \epsilon \left( s,\omega _{g_{\psi ^2},p} \omega _{f,p}^{-1}, \psi _p\right) \epsilon \left( s,\omega _{f,p}, \psi _p\right) \epsilon \left( s,\omega _{f,p}^{-1}, \psi _p\right) \\&\quad = \epsilon \left( \frac{1}{2},\omega _{g_{\psi ^2},p},\psi _p\right) ^2 p^{-2\left( s - \frac{1}{2}\right) }, \end{aligned}$$and again \(\epsilon (1/2,\omega _{g_{\psi ^2},p},\psi _p)\) is \(\tau (\chi _p) p^{-1/2}\).
At a prime \(p \not \mid D\), both \(\pi _{f,p}\) and \(\pi _{g_{\psi ^2},p}\) are spherical principal series representations, so that \(c(\pi _{f,p} \otimes \pi _{g_{\psi ^2},p}) = 0\) and \(\epsilon (s,\pi _{f,p} \otimes \pi _{g_{\psi ^2},p},\psi _p) = 1\).
With this, we see that
while the fact that
and D being 1 modulo 4 ensuring that it has an even number of prime divisors that are 3 modulo 4 implies that the root number \(\epsilon (f \otimes g_{\psi ^2}) = \epsilon (1/2,\pi _f \otimes \pi _{g_{\psi ^2}})\) is
As \(\tau (\chi _{0(d_1)}) = \mu (d_1)\) and \(\lambda _f(d_1) \sqrt{d_1} \in \{1,-1\}\), this is precisely \(\eta _f(d_1)\). \(\square \)
1.3 The approximate functional equation.
First, we recall some standard identities for writing Rankin–Selberg L-functions as Dirichlet series. Let \(\chi \) be an even primitive character modulo q with \(q > 1\), and denote by \(E_{\infty }(z,s,\chi )\) the Eisenstein series of weight 0, level q, and nebentypus \(\chi \) associated to the cusp at infinity, which is given by
for \(\mathfrak {R}(s) > 1\) and extends by meromorphic continuation to the entire complex plane. In particular, \(E_{\infty }(z,1/2 + it,\chi )\) is an Eisenstein series newform [You19] with Hecke eigenvalues
Lemma A.4
For f either in \(\mathcal {B}_0^{*}(\Gamma _0(d_1))\) or \(\mathcal {B}_{\text{ hol }}^{*}(\Gamma _0(d_1))\) with \(d_1 \mid D\) and \(t \in \mathbb {R}\), we have the identities
for \(\mathfrak {R}(s) > 1\).
Lemma A.5
Fix \(X > 0\). For \(f \in \mathcal {B}_0^{*}(\Gamma _0(d_1))\) and \(t \in \mathbb {R}\setminus \{0\}\), we have that
where for \(\Gamma _{\mathbb {R}}(s) :=\pi ^{-s/2} \Gamma (s/2)\),
and for \(x,\sigma > 0\), \(t \in \mathbb {R}\), and \(\epsilon \in \{1,-1\}\),
Finally,
for \(f \in \mathcal {B}_{\text{ hol }}^{*}(\Gamma _0(d_1))\), where
Proof
This follows from [IK04, Theorem 5.3] coupled with Lemmata A.2 and A.4.
\(\square \)
We briefly mention the fact that [IK04, Proposition 5.4] implies that the functions \(V(x,\cdot )\) appearing in Lemma A.5 are of rapid decay in x once x is much larger than the square root of the archimedean part of the analytic conductor of the associated L-function.
1.4 Explicit expressions for spectral sums.
For a function \(h : \mathbb {R}\cup i(-1/2,1/2)\) and \(m,n,q \in \mathbb {N}\), define
where \(\mathcal {B}_0(\Gamma _0(q))\) is an orthonormal basis of the space of Maaß cusp forms of weight zero, level q, and principal nebentypus, and the Fourier expansion of such a Maaß cusp form f with Laplacian eigenvalue \(\lambda _f = 1/4 + t_f^2\) about the cusp at infinity is
Similarly, for a sequence \(h^{\text{ hol }} : 2\mathbb {N}\rightarrow \mathbb {C}\), define
where \(\mathcal {B}_{\text{ hol }}(\Gamma _0(q)) \ni f\) is an orthonormal basis of holomorphic cusp forms of weight \(k_f \in 2\mathbb {N}\), level q, and principal nebentypus, and the Fourier expansion of such a holomorphic cusp form f about the cusp at infinity is
Lemma A.8
For squarefree q, \(\mathcal {A}_q^{\text{ Maa }\ss {}}(m,\pm n;h)\) is equal to
\(\mathcal {A}_q^{\text{ Eis }}(m,\pm n;h)\) is equal to
and \(\mathcal {A}_q^{\text{ hol }}(m,n; h^{\text{ hol }})\) is equal to
Proof
For \(\mathcal {A}_q^{\text{ Maa }\ss {}}(m,\pm n;h)\), we use the orthonormal basis in Lemma 3.1 and make use of (4.3), so that for \(f \in \mathcal {B}_0^{*}(\Gamma _0(q_1))\) and \(\ell \mid q_2\),
Lemma 4.6 gives an explicit expression for \(|\rho _f(1)|^2\), which gives the desired identity.
The orthonormal basis in Lemma 3.3 similarly gives the identity for \(\mathcal {A}_q^{\text{ Eis }}(m,\pm n;h)\).
Finally, an orthonormal basis of \(\mathcal {B}_{\text{ hol }}(\Gamma _0(q))\) is given by
via [ILS00, Proposition 2.6], where
with \(f \in \mathcal {B}_{\text{ hol }}^{*}(\Gamma _0(q_1))\) normalised such that \(\langle f, f \rangle _q = 1\), so that
Moreover, via the same method of proof of Lemma 4.6,
for \(f \in \mathcal {B}_{\text{ hol }}^{*}(\Gamma _0(q_1))\) with \(q_1 q_2 = q\). The result then follows. \(\square \)
The terms \(\mathcal {A}_q^{\text{ Maa }\ss {}}(m,\pm n;h)\), \(\mathcal {A}_q^{\text{ Eis }}(m,\pm n;h)\), and \(\mathcal {A}_q^{\text{ hol }}(m,n;h^{\text{ hol }})\) arise from the spectral expansion of the inner product of two Poincaré series associated to the pair of cusps \((\mathfrak {a},\mathfrak {b}) = (\infty ,\infty )\). We require similar identities for \(\mathfrak {b}\sim 1\), for which we choose the scaling matrix
where \(b,d \in \mathbb {Z}\) are such that \(dq - b = 1\). We define
Here \(\rho _f(\sigma _{\mathfrak {b}};m)\) denotes the m-Fourier coefficient of \(f(\sigma _{\mathfrak {b}} z)\) and \(\rho _{\mathfrak {a}}(\sigma _{\mathfrak {b}};m,t)\) denotes the m-th Fourier coefficient of \(E_{\mathfrak {a}}(\sigma _{\mathfrak {b}} z,1/2 + it)\).
Lemma A.9
For squarefree q, \(\mathcal {A}_q^{\text{ Maa }\ss {}}(\sigma _{\mathfrak {b}};m,\pm n;h)\) is equal to
\(\mathcal {A}_q^{\text{ Eis }}(\sigma _{\mathfrak {b}};m,\pm n;h)\) is equal to
and \(\mathcal {A}_q^{\text{ hol }}(\sigma _{\mathfrak {b}};m,n;h^{\text{ hol }})\) is equal to
Proof
If \(vw = q_2\) with \(q_1 q_2 = q\),
So if f is a member of \(\mathcal {B}_0^{*}(\Gamma _0(q_1))\) or \(\mathcal {B}_{\text{ hol }}^{*}(\Gamma _0(q_1))\),
by Lemma 3.6. The Fourier coefficients \(\rho _{\iota _v f}(\sigma _{\mathfrak {b}};n)\) of \((\iota _v f)(\sigma _{\mathfrak {b}} z)\) therefore satisfy
via (4.3). It follows that for \(\ell \mid q_2\),
Now the proof follows in the same way as the proof of Lemma A.8. \(\square \)
1.5 Spectral summation formulæ
1.5.1 The Kuznetsov formula.
The Kuznetsov formula is an identity between a spectral sum of Fourier coefficients of Maaß cusps forms and integral of Fourier coefficients of Eisenstein series and a delta term and weighted sum of Kloosterman sums.
Theorem A.10
([Iwa02, Theorem 9.3]). Let \(\delta > 0\), and let h be a function that is even, holomorphic in the horizontal strip \(|\mathfrak {I}(t)| \le 1/4 + \delta \), and satisfies \(h(t) \ll (1 + |t|)^{-2 - \delta }\). Then for \(m,n \in \mathbb {N}\),
where
Here
where \(K_{\nu }(z)\) denotes the modified Bessel function of the second kind.
This is the Kuznetsov formula associated to the pair of cusps \((\mathfrak {a},\mathfrak {b}) = (\infty ,\infty )\). We also require the Kuznetsov formula associated to the pair of cusps \((\mathfrak {a},\mathfrak {b}) = (\infty ,1)\).
Theorem A.16
([Iwa02, Theorem 9.3]). Let \(\delta > 0\), and let h be a function that is even, holomorphic in the horizontal strip \(|\mathfrak {I}(t)| \le 1/4 + \delta \), and satisfies \(h(t) \ll (1 + |t|)^{-2 - \delta }\). Then for \(m,n \in \mathbb {N}\) and \(q > 1\),
where for \({\overline{q}} \in \mathbb {Z}\) such that \({\overline{q}} q \equiv 1 \pmod {c}\),
The weakening of the requirement that h need only be holomorphic in the strip \(|\mathfrak {I}(t)| \le 1/4 + \delta \) instead of \(1/2 + \delta \) is due to Yoshida [Yos97, Theorem], where this is proven only in the case \(q = 1\); the proof generalises immediately to all cases of the Kuznetsov formula for which the Kloosterman sums appearing in the Kloosterman term satisfy the Weil bound.
1.5.2 The Petersson formula.
The Petersson formula is an identity between a sum of Fourier coefficients of holomorphic cusps forms and a delta term and weighted sum of Kloosterman sums.
Theorem A.17
([Iwa02, Theorem 9.6]). Let \(h^{\text{ hol }} : 2\mathbb {N}\rightarrow \mathbb {C}\) be a sequence satisfying \(h^{\text{ hol }}(k) \ll k^{-2 - \delta }\) for some \(\delta > 0\). Then for \(m,n \in \mathbb {N}\),
where
Here
We also require the Petersson formula associated to \((\mathfrak {a},\mathfrak {b}) = (\infty ,1)\).
Theorem A.19
([Iwa02, Theorem 9.6]). Let \(h^{\text{ hol }} : 2\mathbb {N}\rightarrow \mathbb {C}\) be a sequence satisfying \(h^{\text{ hol }}(k) \ll k^{-2 - \delta }\) for some \(\delta > 0\). Then for \(m,n \in \mathbb {N}\) and \(q > 1\),
where
1.5.3 The Kloosterman summation formula.
The Kloosterman summation formula (due to Kuznetsov and often referred to as the Kuznetsov formula, though differing from Theorem A.10) gives an expression in reverse to Theorems A.10 and A.17. Rather than expressing sums of Fourier coefficients of automorphic forms weighted by functions h or \(h^{\text{ hol }}\) in terms of a delta term and sums of Kloosterman sums weighted by transformed functions \(\mathscr {K}^{\pm } h\) and \(\mathscr {K}^{\text{ hol }} h^{\text{ hol }}\), it expresses sums of Kloosterman sums weighted by a function H in terms of sums of automorphic forms weighted by transformed functions \(\mathscr {L}^{\pm } H\) and \(\mathscr {L}^{\text{ hol }} H\). Notably, there is no delta term in the Kloosterman summation formula.
Theorem A.20
([IK04, Theorem 16.5]). For \(H \in C^3((0,\infty ))\) satisfying
for \(j \in \{0,1,2,3\}\) and \(m,n \ge 1\), we have that
where
Once more, we will require the Kloosterman summation formula associated to the pair of cusps \((\mathfrak {a},\mathfrak {b}) = (\infty ,1)\).
Theorem A.22
For \(H \in C^3((0,\infty ))\) satisfying
for \(j \in \{0,1,2,3\}\) and \(m,n \ge 1\), we have that
1.6 The Mellin transform.
We recall the following definitions and properties of the Mellin transform; see [BlK19b, Section 2.1]. Let \(W : [0,\infty ) \rightarrow \mathbb {C}\) be a J-times continuously differentiable function satisfying \(x^j W^{(j)}(x) \ll _{J,a,b} \min \{x^{-a},x^{-b}\}\) for some \(-\infty< a< b < \infty \) and \(j \in \{0,\ldots ,J\}\). The Mellin transform \({\widehat{W}}\) of W is
This is defined initially as an absolutely convergent integral for \(a< \mathfrak {R}(s) < b\) and satisfies \({\widehat{W}}(s) \ll _J (1 + |s|)^{-J}\) in this region. Similarly, the inverse Mellin transform of a holomorphic function \(\mathcal {W}:\{z \in \mathbb {C}: a< \mathfrak {R}(s) < b\} \rightarrow \mathbb {C}\) satisfying \(\mathcal {W}(s) \ll _r (1 + |s|)^{-r}\) for some \(r > 1\) is given by

where \(a< \sigma < b\). This is a J-times continuously differentiable function on \([0,\infty )\), where \(J = \lceil r \rceil - 1\), and satisfies  for \(j \in \{0,\ldots ,J\}\).
for \(j \in \{0,\ldots ,J\}\).
Lemma A.23
([BLM19, (A.7)], [BlK19b, (3.13)]). We have that
From Stirling’s formula (2.4), we obtain the following.
Corollary A.27
The functions \(\widehat{\mathcal {J}_r^{\pm }}(s)\) extend meromorphically to \(\mathbb {C}\) with simple poles at \(s = 2(\pm ir - n)\) for \(n \in \mathbb {N}_0\). For \(s = \sigma + i\tau \in \mathbb {C}\) in bounded vertical strips at least a bounded distance away from \(\{2(\pm ir - n) : n \in \mathbb {N}_0\}\) and \(r = u + iv\) in bounded horizontal strips,
Moreover,
For \(s = \sigma + i\tau \in \mathbb {C}\) in bounded vertical strips, at least a bounded distance away from \(\{1 - k - 2n : n \in \mathbb {N}_0\}\),
Moreover,
We require the following result on properties of \(\widehat{\mathscr {K}^{-} h}(s)\).
Lemma A.28
([Mot97, Section 3.3]). Suppose that h(r) is an even holomorphic function in the strip \(-3/2< \mathfrak {I}(r) < 3/2\) with zeroes at \(\pm i/2\) and satisfies \(h(r) \ll (1 + |r|)^{-4 - \delta }\) in this region for some \(\delta > 0\). Then the Mellin transform of \(\mathscr {K}^{-} h\) extends to a holomorphic function in the strip \(-3< \mathfrak {R}(s) < 1\).
Proof
Since h is even and recalling (A.25), we have that for \(0< \mathfrak {R}(s) < 1\),
Indeed, standard bounds for \(\mathcal {J}_r^{-}(x)\) (see, for example, [BLM19, (A.3)]) allow us to interchange the order of integration. For \(\mathfrak {R}(s) > -\sigma _0\), we may shift the contour to \(\mathfrak {I}(r) = -\sigma _0/2 - \varepsilon \); provided that the integral converges, we see that the integral extends holomorphically to \(-\sigma _0< \mathfrak {R}(s) < 1\). Corollary A.27 then implies that the integral over r converges provided that \(h(r) \ll (1 + |r|)^{-1 - \mathfrak {R}(s) - \delta }\) for some \(\delta > 0\).
This proves the analytic continuation of the integral to \(-3< \mathfrak {R}(s) < 1\). The Mellin transform of \(\mathscr {K}^{-} h\) may have a pole at \(s = 1\), however, due to the presence of the term \(\cos (\pi s/2)\). The integral in this case is
We move the contour back to \(\mathfrak {I}(r) = 0\). The resulting integral vanishes, while we pick up a residue at \(r = -i/2\) given by \(-\pi i h(i/2)\). By assumption, this vanishes, which completes the proof. \(\square \)
1.7 Voronoĭ summation formulæ.
For \(\mathfrak {R}(s) > 1\), \(c \in \mathbb {N}\), and \(d \in (\mathbb {Z}/c\mathbb {Z})^{\times }\), we define the Voronoĭ L-series
These functions are associated to the automorphic forms \(E_{\chi ,1}(z) :=E_{\infty }(z,1/2,\chi )\) and even \(g \in \mathcal {B}_0^{*}(q,\chi )\) respectively.
Lemma A.30
For \(c \equiv 0 \pmod {q}\) or \((c,q) = 1\), the Voronoĭ L-series \(L(s,E_{\chi ,1},d/c)\) extends to a meromorphic function on \(\mathbb {C}\) with a simple pole at \(s = 1\) with residue
while the Voronoĭ L-series L(s, g, d/c) extends to an entire function. We have the functional equations
if \(c \equiv 0 \pmod {q}\), while for \((c,q) = 1\),
Proof
For L(s, g, d/c), this follows from [KMV02, Appendix A.4] and [HM06, Section 2.4]. After Mellin inversion, the identities for \(L(s,E_{\chi ,1},d/c)\) are shown in [IK04, Theorems 4.13 and 4.14] and also [LT05, Theorem A]. \(\square \)
A useful tool to couple with the Voronoĭ summation formula is the following identity for Gauss sums.
Lemma A.31
([Miy06, Lemma 3.1.3]). Let \(\chi \) be a primitive Dirichlet character modulo q and \(c \equiv 0 \pmod {q}\). We have that
1.8 The large sieve.
Theorem A.32
([Lam14, Theorems 2.2 and 2.6]). For squarefree q, \(1 \ll U \ll T\), and \(N \ge 1\), each of the quantities
is bounded by a constant multiple depending on \(\varepsilon \) of
1.9 Subconvexity estimates.
We record the following subconvexity estimates.
Theorem A.33
([You17, Theorem 1.1]). Let \(\chi _q\) be the primitive quadratic Dirichlet character modulo q for squarefree odd q. Then for \(q_1 \mid q\),
Theorem A.34
([MV10, Theorems 1.1 and 1.2]; see also [Blo05, Theorem 1 and Remarks, p. 114], and cf. [LLY06a, Corollary 1.2 and Remark 1.3]). Let \(g \in \mathcal {B}_0^{*}(q,\chi )\) and \(t \in \mathbb {R}\). Then for \(q_1 \mid q\), there exist absolute constants \(A > 0\) and \(\delta > 0\) such that
Remark A.35
More explicit subconvex bounds are known for \(\zeta (1/2 + it)\), as well as for L(1/2, f) when \(q = 1\), but all we truly require are subconvex bounds
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Humphries, P., Khan, R. On the Random Wave Conjecture for Dihedral Maaß Forms. Geom. Funct. Anal. 30, 34–125 (2020). https://doi.org/10.1007/s00039-020-00526-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00039-020-00526-4