Introduction

The role of swimming organisms in enhancing turbulence and mixing in stratified water bodies is still uncertain. Experiments, observational studies, and numerical simulations have tried to determine whether biogenic turbulence may be an underrepresented source of energy in oceans and lakes, in particular when compared to other mechanisms, such as winds and tides (Dewar et al. 2006; Kunze et al. 2006; Gregg and Horne 2009; Katija 2012). Of particular relevance to lakes is the question of whether migrations of small zooplankton can elevate turbulence relative to the generally quiescent levels typically observed in the lake interior, the part below the surface and away from the bottom and shores. While migrations of smaller zooplankton in ocean environments have shown negligible increases compared to the higher background turbulence levels in the ocean (Rousseau et al. 2010; Dean et al. 2016), recent lab (Wilhelmus and Dabiri 2014; Houghton et al. 2018) and numerical (Wang and Ardekani 2015) studies indicate that aggregations of small zooplankton at sufficient concentrations can elevate turbulence and mixing through interactions between the swimmers.

Biologically-generated turbulence and mixing can be qualitatively described considering the turbulent kinetic energy (TKE) budget, which for steady state and spatially homogenous conditions, reads (Ivey and Imberger 1991):

$$m = b + \varepsilon,$$
(1)

where m is the production term of TKE, b the buoyancy flux which accounts for changes in the potential energy field, and \(\varepsilon\) is the rate at which energy is lost from the fluid due to water viscosity. Swimming organisms, by moving their appendages, can create hydrodynamic instabilities and energetic eddies (see Fig. 1a), usually comparable with the organism’s size, and supply TKE (m) to the fluid (Huntley and Zhou 2004). This additional energy m can either be converted into potential energy (b) to achieve mixing or be dissipated and lost as heat via \(\varepsilon\). This energy-conversion process from m to b is efficient and can lead to substantial mixing, as long as the size of the biologically-generated instabilities are sufficiently large and energy is constantly added to the fluid.

Equation 1 can also be re-arranged to explain mixing in terms of eddy diffusivity \(K_V\). Using the generalized flux Richardson number \(R_f = b/m\) and a flux-gradient relationship yields (Ivey and Imberger 1991):

$$K_V = \frac{R_f}{1-R_f}\frac{\varepsilon }{N^2} = \varGamma \frac{\varepsilon }{N^2},$$
(2)

where \(N=-\,[(g/ \rho ) \partial \rho / \partial z]^{1/2}\) is the buoyancy frequency depending on the gravitational acceleration g and the density \(\rho\). In Eq. 2, \(\varGamma\) describes the efficiency of the energy-conversion process, Osborn (1980) suggested that \(\varGamma\) reaches the maximum of 0.2 for shear-generated turbulence, however, the value for biomixing is currently unknown. Visser (2007) argued that \(\varGamma\) scales as \((l/L_{OZ})^{4/3}\) within the biosphere, where l is the scale of the biologically-generated overturn and \(L_{OZ}=(\varepsilon / N^3) ^{1/2}\) the Ozmidov length scale. For example, for krill, no important mixing can occur because \(\varGamma \approx 10^{-4}- 10^{-2}\) (Visser 2007; Rousseau et al. 2010; Kunze 2011). On the other hand, for a small freshwater zooplanktonic organism (\(l\approx\) 1 mm), \(\varGamma\) can range between \(10^{-3}\) and \(10^{-1}\) depending on the stratification and turbulence conditions (Visser 2007). Moreover, zooplankton aggregations can create larger hydrodynamics disturbances via collective or synchronized motions which may increase the effective value of l by a few orders of magnitude (Noss and Lorke 2014). For waters stratified by temperature, the vertical eddy diffusivity \(K_V\) can typically range between \(10^{-7}\) and \(10^{-3}\) m2 s−1. When \(K_V> D_T\), where \(D_T \approx 10^{-7}\) m2 s−1 is the molecular temperature diffusivity, turbulence can efficiently mix the water column. However, when \(K_V = D_T\), heat will spread slowly at the molecular level only.

The first observations of biogenic turbulence from migrators were made by Kunze et al. (2006), who measured enhanced turbulent dissipation rates (\(\varepsilon\)) between \(10^{-5}\) and \(10^{-4}\) W kg−1 during krill vertical migration in a Canadian inlet. Maximum diffusivities \(K_V\) reached \(10^{-2}\) m2 s−1, as large as those from winds and tides, but assuming \(\varGamma =0.2\). Dissipation rates agreed with those found in the model by Huntley and Zhou (2004) that suggests that biota can deliver a significant amount of mechanical energy regardless of the species. Later measurements by Rippeth et al. (2007), however, did not show such dramatic dissipation rates in a different coastal environment, suggesting that measurements may be limited to that particular coastal system. Numerical simulations by Dean et al. (2016) suggest that TKE enhancements observed by Kunze et al. (2006) are only possible with very high krill density above 10 org. L−1. Later measurements by Rousseau et al. (2010) concluded and supported the hypothesis that biologically-generated turbulence from krill vertical migration is an intermittent mechanism and no mixing can occur.

Other studies focused on small but more abundant zooplankton. Noss and Lorke (2014) performed a laboratory experiment in a stratified tank on the mixing induced by the vertical motion of Daphnia magna. For this species, they found that vertical mixing is not enhanced; the observed vertical eddy diffusivity was as low as \(10^{-9}\) m2 s−1, an order of magnitude smaller than the diffusivity of the stratifying agent. Despite Daphnia being able to generate turbulence as high as \(10^{-5}\) W kg−1 in their turbulent wake (Noss and Lorke 2012; Wickramarathna et al. 2014), no mixing occurred because \(\varGamma\) was too small (Eq. 2). However, the result may depend on the organisms’ concentration and how the migration was triggered in artificial laboratory conditions (Simoncelli et al. 2017). Experimental measurements in a stratified tank by Houghton et al. (2018) indicate instead that collective motions, arising from small zooplankton swimming at high concentration, can trigger fluid instabilities bigger than the size of the individual organism and lead to irreversible mixing. Very recent numerical simulations by Wang and Ardekani (2015), in the intermediate Reynolds number regime, show that millimeter-sized organisms swimming with collective motions, can enhance \(K_V\) up to \(10^{-6}\) m2 s−1 but at a high concentration of zooplankton. Heat and gas fluxes can still be affected by biomixing, as the molecular diffusivity of heat \(D_T \approx 10^{-7}\) m2 s−1 and gases \(D_G \approx 10^{-9}\) m2 s−1 are smaller than the enhanced \(K_V\). A simple model by Leshansky and Pismen (2010) reported instead a smaller diffusivity of \(10^{-7}\) m2 s−1, with no enhancement of heat diffusion.

Other studies in the ocean and lakes suggest instead that mixing by bacteria or micro-zooplankton is feasible under certain conditions. At very high concentrations, small organisms can enhance vertical mixing via creation of convective cells (Kils 1993; Sommer et al. 2017) rather than via turbulent wake formation from the moving appendages. This mechanism, however, does not seem to govern TKE energy production for high abundances of meso-zooplankton, such as Daphnia, where energy can be supplied via Kelvin–Helmholtz instabilities (Wilhelmus and Dabiri 2014).

A full review of previous studies of small zooplankton can be found in Simoncelli et al. (2017). To date, observational studies on zooplankton biomixing have been limited to oceanic species only and no field studies exist on the turbulence production and mixing due to small zooplankton in freshwaters. We present a field study of turbulence measurements during the vertical migration (DVM) of small zooplankton in the interior of a small lake, where the community is dominated by Daphnia spp. This genus frequently engages in a DVM at sunset, with many organisms crossing the thermocline, despite the density stratification. During the ascent phase, they may create interacting wake or jet structures (see Fig. 1a) and large scale motions, and add mechanical energy in the quiescent part of the lake, away from the boundaries, where the thermal stratification usually suppresses turbulence and vertical diffusion (Wüest and Lorke 2003). Temperature instabilities and turbulence were sampled before and during the DVM under calm conditions to isolate biologically-generated temperature perturbations from those originating from other processes such as the wind. Measurements can be used to infer the zooplankton contribution towards interior mixing and the likely ecological importance in lake ecosystems.

Fig. 1
figure 1

a A schematic of swimming Daphnia and their interacting turbulent wakes (continuous lines). The eddies show the turbulent instabilities created within the wake that can be a source of TKE. b The experimental setup. The dashed lines show the acoustic cone of the ADCP, while the gray trapezoids indicate segment sizes for acoustic and microstructure measurements

Full size image

Materials and methods

Study site

Measurements were carried out on three different days during the summer stratification period (21 July, 28 July and 18 August 2016) in Vobster Quay, a shallow man-made lake situated in Radstock, UK (Fig. 2). The lake, with an average depth of 15 m and maximum depth of 40 m, is wind-sheltered with a fetch of approximately 500 m. It was originally created by filling a decommissioned quarry, so has very steep sloping boundaries and a flat bottom, providing a very simple bathymetry ideal for this study. It is fed by rainfall and infiltration of cold groundwater on the northwest side during heavy rainfall events. The lake stratifies from early May until late August with a maximum surface temperature of 22 \(^{\circ }\)C and a bottom temperature between 9 and 12 \(^{\circ }\)C. Figure 3 shows the temperature profiles for the three sampling dates as well as the buoyancy frequency. The metalimnion usually extends from 5 to 17 m. The water had an average Secchi depth of 10 m over the summer. The lake was chosen because of its simple shape, small wind fetch, and the lack of topographic features or boundary effects which might affect mixing during the measurement campaign.

Fig. 2
figure 2

Geometry and bathymetry of Vobster Quay. “S” denotes the sampling station where microstructure and zooplankton measurements were taken. The locations of the thermistor chain (T chain) and ADCP are also shown

Full size image
Fig. 3
figure 3

Conditions before the DVM for the three different sampling dates: a average temperature profile from SCAMP data, and b buoyancy frequency. The red band shows the average depth range inhabited by zooplankton during the day, just below the depth of maximum buoyancy. (Color figure online)

Full size image

Zooplankton abundance

In order to gather data on crustacean zooplankton population density and vertical distribution, zooplankton samples were collected using a conical net (Hydro-Bios) mounted on a stainless-steel hoop with a cowl cone (mesh = 100 μm, diameter \(d=100\) mm, length approximately 50 cm). Samples were collected within consecutive strata of thickness \(h=3\) m, from the surface down to 24 m, in daytime. Three samples (\(n=3\)) were collected and pooled for each stratum. Samples were collected before the DVM at location S (Fig. 2) and were stored in a 70% ethanol solution to fix and preserve the organisms (Black and Dodson 2003). Sample collection from the entire water column took about 80 min. Zooplankton were enumerated by counting the organisms under a dissecting microscope and distinguishing four taxonomic groups: Daphnia spp., copepods, small Cladocera and copepod nauplii. Due to the high numbers of organisms present in each sample, enumeration of zooplankton was conducted on three replicate sub-samples of each sample. The concentration \(C_{g}\) of a group g was then estimated by dividing the abundance by the filtered water volume \(V= \pi /4 \cdot d^2 \cdot h/n\).

Acoustic measurements

A bottom-mounted 500-kHz acoustic-Doppler current profiler (ADCP, Nortek Signature 500) was also deployed at a depth of 25 m (Fig. 1b and ADCP in Fig. 2) to record the acoustic backscatter strength (BS) and velocities during the summer stratification. The device has four acoustic transducers slanted at 25\(^{\circ }\) to the vertical and one additional beam pointing vertically. The ADCP was set-up to measure with a ping frequency of 0.5 Hz for the vertical beam and 1 Hz for the others, with a vertical resolution of 0.5 m. Data approximately 1 m below the surface were removed due to surface reflection of the pings, while data 1 m above the sediment are not available due to the deployment configuration and the ADCP blanking distance. Velocity data are not reported here because the observed velocity range was too low to provide reliable information.

The strength of the returned signal or backscatter strength (BS) from the vertical beam can be used as a proxy to track the position of the zooplankton layer and the timing of the migrations potentially relevant for turbulence measurements (Noss and Lorke 2014; Record and de Young 2006). The BS however needs to be converted to the relative volume backscatter strength (VBS) to account for any transmission loss of the intensity signal. For this purpose, a simplified version of the sonar equation was applied to the vertical beam only (Huber et al. 2011; Noss and Lorke 2014):

$$VBS = BS - P_{DBW} - L_{DBM} + 2 \cdot \alpha \cdot R + 20 \,log_{10} \cdot R,$$
(3)

where \(P_{DBW}\) is the transmitted power sent in the ensonified water, \(L_{DBM}\) the log10 of the transmit pulse length P, R the slant acoustic range and \(\alpha\) the acoustic absorption coefficient. \(P_{DBW}\) was set to zero because the transmit power is not a function of the battery for short period measurements, while P was set to 0.5 m being close to the cell size (Nortek, pers. comm.). The sound absorption was estimated from the model by Francois et al. (1982) and using the temperature profiles from the thermistor chain. The result of the conversion process for the three datasets is reported in the “Electronic Supplementary Material” document, online resource 1.

Microstructure measurements

Profiles of temperature fluctuations were acquired at the same location “S” (Fig. 2) before and during the DVM with a Self-Contained Autonomous MicroProfiler (SCAMP, PME), a temperature microstructure profiler using two Thermometrics FP07 thermistors. The SCAMP was deployed in downwards mode to sink at 10 cm s−1 (Fig. 1b). Expecting very small currents in the lake interior, each SCAMP cast was separated by a distance of at least 5 m with a GPS, but always kept near the sampling location, to avoid sampling the wake generated from the device itself when recovered after a previous profile. Fifteen SCAMP profiles were acquired on the 21 July, 19 on 28 July and 19 on the 18 August, approximately every 5 min. Turbulence was also sampled before the DVM to characterize the background condition in absence of vertical migrators.

Each profile was split into segments of variable length, following the segmentation method by Chen et al. (2002). The method employs a wavelet-based test, sensitive to changes in spectral shape and magnitude, to ensure that each segment is statistically stationary. The dissipation of temperature variance \(\chi _{T}\) was computed for each segment by integrating the observed spectrum assuming isotropy (Thorpe. 2005). Dissipation rates of TKE \(\varepsilon\) were then estimated for each segment by fitting the data to the theoretical spectrum (Batchelor 1959). Bad fits, with invalid TKE dissipation rates, were rejected and removed using the statistical criteria proposed by Ruddick et al. (2000).

Mixing and length scales

The eddy diffusivity coefficient \(K_T\) was estimated for each segment using the model by Osborn and Cox (1972), assuming steady-state and spatial homogeneity in each segment. Each SCAMP segment was also analysed to compute characteristic length scales: the Thorpe scale \(L_{T}\), the maximum Thorpe displacement \(L_{Tmax}\) and the Ozmidov scale \(L_{OZ}\). The scales \(L_{T}\) and \(L_{Tmax}\) were calculated after denoising the temperature and pressure profiles using the procedure by Piera et al. (2002) based on wavelet analysis. The advantage of the method is that it removes small but spurious patches generated by instrumental noise. The scale \(L_{OZ}\) was instead calculated using the buoyancy frequency N following the procedure by Wain and Rehmann (2010) and using the dissipation rate \(\varepsilon\) estimated from the spectral analysis. Each segment was then considered as a valid patch if \(L_{Tmax} < L_P\) and \(\int {d_T(z)} < 0.05 \cdot L_P\), where \(L_P\) is the segment length (Piera et al. 2002).

Other measurements

A Secchi disk was employed to provide an estimation of the water transparency and compare it to the zooplankton daytime depth distribution. A thermistor chain (Fig. 2) was also deployed near the location “S” with 10 RBR thermistors (Solo T, RBR Ltd.) and 5 Hobo loggers (TidbiT v2, Onset Computer) sampling every 5 min.

Results and discussion

Zooplankton distribution

The zooplankton community was mainly composed of Daphnia spp. and copepods which accounted for about 70% of the total abundance in spring and summer. The average size (\(l_O\)) of both Daphnia and adult copepods was approximately 1 mm, with some organisms reaching 2 mm. The zooplankton maximum concentration in the lake usually varies with the season with highest values in late May. The profiles of Daphnia concentration (Fig. 4) show that this taxon exhibited a similar vertical distribution during the three sampling days, with low population densities near the surface and the lake bottom, and peaks in the metalimnion. On 21 July, Daphnids were mostly located in the 12–15 m layer at a concentration of 20 org. L−1 and were also abundant near the lake bottom, at concentrations of less than 15 org. L−1. Copepod nauplii were as abundant as Daphnia below 12 m, but were unlikely to generate turbulence because of their small body size (\(l_O \ll 1\) mm). On 28 July, Daphnia were more abundant between 9 m and 12 m with a maximum concentration of 23 org. L−1, which is the maximum observed in July from the zooplankton tows. Concentrations below 12 m decreased abruptly to approximately 5 org. L−1. The next most abundant group, the adult and copepodite stage of copepods, reached a maximum density of 10 org. L−1 in the 9–12 m layer. On 18 August, the zooplankton concentration reached the seasonal minimum, with a maximum of Daphnia spp. density of only 10 org. L−1 between 12 and 15 m.

Fig. 4
figure 4

Profiles of zooplankton concentration for Daphnia spp., copepods, small Cladocera and copepods nauplii collected before the DVM and SCAMP measurements

Full size image

ADCP calibration

Data from the zooplankton net tows (Fig. 4) offer only a snapshot of the situation during daytime, and before the DVM begins. To overcome this limitation, the measured ADCP echo intensity (see Online Resource 1 in the “Electronic supplementary material”) can be used as a proxy for the zooplankton abundance, where the highest values correspond to the highest abundance, while the lowest value corresponds to those parts of the water column free of zooplankton or with a negligible concentration. Several studies in the ocean and lakes (Fielding et al. 2004; Lorke et al. 2004; Rahkola-Sorsa et al. 2014; Record and de Young 2006; Huber et al. 2011) show that the concentration of different taxonomic groups can be related to the linear volume backscatter strength (\(VBS_{linear}=10^{VBS/10}\)) via a physical and acoustic-based model. This ADCP calibration allows us to (1) continuously estimate zooplankton concentration without resorting to multiple net tows; (2) use finer vertical resolution (0.5 m) than zooplankton tows (3 m); (3) provide an estimation of the concentration within the migrating layer during the DVM, as it is not possible to sample the water column with the net during the migration and obtain a concentration profile under reasonably stationary conditions because the concentration changes too quickly during the DVM; (4) understand which taxonomic groups explain and contribute the most to the acoustic signal and to its variation. It is possible to express \(VBS_{linear}\) as a function of the concentration \(C_g\) of a taxonomic group g through a multiple linear regression as:

$$VBS_{linear} = k_0 + \sum _{g=1}^{4}{k_g \cdot C_g},$$
(4)

where \(C_g\) is the abundance measured from net hauls and \(k_g\) is its calibration coefficient. In the equation above, \(VBS_{linear}\) can be computed by averaging the backscatter in each of the depth strata sampled for zooplankton at the time of the net tows. Deviations from the model relating \(VBS_{linear}\) and \(C_g\) may be due to omitted loss terms in Eq. 3, surface reflection of the acoustic signal or net avoidance reactions by zooplankton (Brinton 1967; Ianson et al. 2004). Despite the fact the zooplankton may be able to sense pressure variation when the net is approaching, the towing speed was controlled and kept very low to limit this artefact during sample collection. Finally the presence of the mouth-reducing cone helps reduce forward physical disturbances caused by the net itself (UNESCO 1968).

Table 1 Regression coefficient \(k_g\) and p values from multiple regression analysis between the zooplankton groups and the linear VBS using the data from the three sampling days
Full size table

Table 1 shows the coefficients \(k_g\) and p values from the multiple regression analysis to test the statistical significance of each taxonomic group against the VBS. Results show that Daphnia spp. make the most significant contribution to the VBS signal (\(p=0.0024\)). The abundances of the other taxa were poorly correlated with the VBS (\(p> 0.1\)), indicating that Daphnia are the major contributor to the observed acoustic strength. For this reasons it is possible to simplify the model by regressing \(VBS_{linear}\) with \(C_{Daphnia}\) only:

$$VBS_{linear} = k_0 + k_1 \cdot C_{Daphnia}.$$
(5)

From the analysis, \(k_0=7.144 \pm 4.481 \times 10^6\) and \(k_1=2.315 \pm 0.425 \times 10^6\) L org.−1; the coefficient of determination (\(R^2\)) only reduces to about 0.6 from 0.7 using the model described by Eq. 4, still indicating a good fit. The standard deviation of the regression is \(\pm \, 5\) ind. L−1. A comparison between the measured \(C_{Daphnia}\) and that estimated from Eq. 5 is reported in Fig. 5a (black dots). The significant correlation between the VBS and Daphnia concentrations is linked to the balloon-like shape of Daphnids that scatters back acoustic waves more effectively than the other species (Lorke et al. 2004; Rinke et al. 2007; Huber et al. 2011). Sound wave reflection does not depend on Daphnia’s orientation or on their acoustic cross-section area, as much as for the elongated copepods. The regression coefficients for copepod nauplii and small Cladocera have a negative sign, indicating the lack of statistical dependence with the VBS. Their effect upon VBS is negligible because of their small size. The target strength of scatterers in the water becomes negligible when \(2 \pi /\lambda \cdot a=1\), where \(\lambda\) is the acoustic wavelength and a the zooplankton radius. For a 500 kHz ADCP, this occurs when \(a \sim 0.44\) mm. Therefore zooplankton, whose size \(l_O < 2 a\) (i.e. copepod nauplii and small Cladocera), do not contribute to the VBS as much as Daphnia. This is also suggested by the coefficient of determination \(R^2\) not changing significantly after removing these taxonomic groups.

Equation 5 was also validated by using a validation dataset of \(C_{Daphnia}\) and \(VBS_{linear}\) measured in the lake on 30 June 2016 (see Fig. 5b). The empty dots in Fig. 5a show the comparison between the observed Daphnia concentrations and those estimated via Eq. 5 by using the \(VBS_{linear}\) acquired on that date. The good agreement between the observation and the estimation (\(R^2=0.75\), \(p= 6\times 10^{-10}\)) indicates that Eq. 5 can be reliably used to estimated \(C_{Daphnia}\), when \(VBS_{linear}\) is only available, also for higher Daphnia concentrations.

Fig. 5
figure 5

a Comparison between the observed Daphnia concentration and that estimated from Eq. 5 using the measured VBS. Black dots show the datasets collected on 21 July, 28 July and 18 August used to estimated \(k_0\) and \(k_1\) in Eq. 5. Empty dots show data from the validation dataset collected on 30 June 16 (see b). The dashed line is the 1:1 relationship. b Profiles of linear VBS (red line) and Daphnia concentration (black line) collected on the 30 June 2016

Full size image
Fig. 6
figure 6

Time series of Daphnia concentration (greyscale-bar) for the three different days. Blue line highlights the sunset time when the migration begins. (Color figure online)

Full size image

DVM pattern

By inverting Eq. 5, it is possible to plot a time series of Daphnia concentration (Fig. 6). The figure shows that the Daphnia layer occupies the metalimnion during the day and is scattered around a stationary depth but always below the depth of maximum buoyancy frequency (see red bands in Fig. 3). Patches of higher concentration can be identified in the time series as well, but they are usually short-lived, suggesting that organisms are swimming either vertically or horizontally outside the acoustic cone of the ADCP. Daphnia begin migrating towards the epilimnion at sunset (blue dashed lines in Fig. 6), reaching the surface layer in approximately one hour with a bulk velocity of 3.4, 3.0 and 4.3 mm s\(^{-1}\) on the three dates respectively. Secchi depths were 10 m on 21 July, between 7.5 and 8 m on 28 July, and 8 m for the last sampling date, indicating that Daphnia spp. resided in the region with low light conditions of the lake water column during daylight hours.

Figure 6 also shows that the DVM pattern adopted by Daphnia is light-driven (Iwasa 1982; Ringelberg 1999; Rinke and Petzoldt 2008) and migration took place in response to visual predation. However, Daphnia may change position in the water column during daytime as well. This happened on 28 July after 19:30 when the zooplankton layer at 10-m depth migrated downward before the beginning of the DVM at 21:00. The reasons for this unexpected behavior are currently unknown: local cloud cover or other weather conditions did not change during the measurements, but the presence of chemical substances released by predators, such as kairomones, may have affected the vertical distribution during the day (Cohen and Forward 2009).

Table 2 Mean and maximum Daphnia concentration (\(C_{Daphnia}\)) in the migrating layer estimated from the simplified regression model
Full size table

Table 2 shows a summary of the estimated mean and maximum concentration of Daphnia within the migrating layer during the DVM, based upon ADCP data and extrapolation from the simplified regression model (see Eq. 5). Concentrations were lowest on 18 August, with a few zooplankton patches reaching a maximum of 70 org. L−1. The maximum observed concentrations in the migrating layer were found on 28 July, with some small patches reaching almost 99 org. L−1. Moreover, data on the same day show a zooplankton band homogeneously distributed between 5 and 10 m which is not well captured by the zooplankton profile (Fig. 4b) because of the coarse 3-m resolution of the net tows. This layer starts descending at 19:20 (local time) and again at 20:20, finally merging with the main zooplankton layer few minutes after 20:30. After 20:30, Daphnia’s abundance declines in the 6–9 m strata and increases instead between 12 and 15 m, where average concentration peaks at \(70 \pm 5\) org. L−1. Before 21:00, at sunset, the whole band begins to migrate upwards.

Dissipation rates

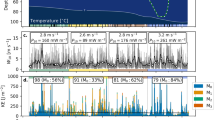
Figure 7 show the time series of the dissipation rates \(\varepsilon\) for the three datasets. The dissipation rates of thermal variance \(\chi _T\) can be found in Online resource 2 in the “Electronic Supplementary Material”. Data were overlapped to the estimated Daphnia concentration (greyscale background). The empty blocks in the panels, where data are not present, represent non-stationary turbulent segments for which spectral analysis was not performed. The panels of \(\varepsilon\) show additional empty regions corresponding to rejected fits of the Batchelor spectrum, where the dissipation rates were ignored. Forty-five spectral fits out of 537 were invalid on 21 July, 66 out of 727 on 28 July, and 56 out of 618 on 18 August 2016.

An important condition for turbulence measurements is related to the stationarity of the flow field generated by Daphnia. A single organism usually swims unsteadily, creating therefore an unsteady flow field in their wake (Kiorboe 2014). However, a hopping and sinking Daphnia generates a quasi-stationary flow (Gries et al. 1999) and stationarity may be satisfied during the DVM when Daphnia usually adopts a fast-swimming behaviour (Dodson et al. 1997).

The measurements showed the highest dissipations in the epilimnion, confined to 3 m in depth on 21 July, 6 m on 28 July, and 7 m on 18 August 2016. Below this depth, turbulence was suppressed by the vertical stratification and dissipation rates rarely exceeded \(\varepsilon = 10^{-8}\) W kg−1 and \(\chi _T = 10^{-6.5}\) K2 s−1. Because turbulent production is a patchy and intermittent process by nature, a turbulence burst of \(\chi _T\) or \(\varepsilon\), above the background level in a few patches within the migrating layer, is not proof of turbulent energy production by zooplankton. If zooplankton-generated turbulence occurred, we would expect to observe persistent turbulence dissipations in the migrating layer only. However, in our measurements, patches of enhanced \(\chi _T\) were present after sunset in all the three datasets and production of thermal anomalies took place outside the Daphnia migrating layer as well. Our measurements therefore suggest that the swimming zooplankton are not an efficient energy production mechanism in the lake.

Fig. 7
figure 7

Time series of dissipation rates \(\varepsilon\) of TKE (top color-bar) and Daphnia concentration (greyscale-bar) for the three different days. Blue line highlights the sunset time when the migration begins. Spaces with no colour highlight the parts of the water column with non-stationary turbulence segments and invalid fits of the Batchelor spectrum

Full size image

From the time series in Figs. 6 and 7, it is possible to extract and correlate the dissipation rates against the mean Daphnia concentration, measured in each turbulent segment within the migrating layer. The result is reported in Fig. 8 for \(\chi _T\) (green triangles) and \(\varepsilon\) (black dots) for all the three datasets. The lack of any correlation clearly demonstrates that turbulence was not intensified during the dusk ascent, even for concentrations as high as 60 org. L−1. A few patches showed increased bursts of \(\chi _T\) for concentrations above 40 org. L−1, however, data constantly approached the mean background dissipation level of \(\varepsilon \sim 10^{-9}\) W kg−1 (gray-shaded area) and \(\chi _T \sim 10^{-7.8}\) K2 s−1 (green-shaded area). Noss and Lorke (2012) measured \(\varepsilon \sim 10^{-6}\) W kg−1 near the body of a single swimming Daphnia, but this was not observed in our data in the vicinity of multiple swimming organisms. Dissipation rates of TKE were also below the prediction of Huntley and Zhou (2004)’s model with \(\varepsilon \sim 10^{-5}\) W kg−1. Finally, according to acoustic measurements, Daphnia concentration peaked at 99 org. L−1 on 28 July (see Table 2). However, denser patches of zooplankton are usually very small and are short-lived in a turbulent patch. After averaging the concentration in each SCAMP segment, the maximum concentration reduced to 60 org. L−1 (Fig. 8). This concentration may have been too low to enhance dissipations as there was likely no superposition of the organisms’ volume of influence.

Fig. 8
figure 8

Dissipation rates \(\varepsilon\) (black dots) and \(\chi _T\) (green triangles) as a function of Daphnia concentration in the turbulent patches during the DVM for the three different datasets. The gray and green areas show the mean background dissipation level for \(\varepsilon\) and \(\chi _T\) respectively

Full size image

Mixing

Mixing \(K_T\) from the Osborn and Cox model (see Online resource 3 in the “Electronic Supplementary Material”) did not increase below the epilimnion, consistently approaching the molecular heat diffusivity (\(D_T = 10^{-7}\) m2 s−1). Limited patches in the metalimnion with higher mixing up to \(K_T = 10^{-6}\) m2 s−1 were short-lived. The assumption of stationary and homogenous turbulent conditions may not be applicable to the case of biomixing.

Fig. 9
figure 9

Thorpe length scale \(L_T\) as a function of the Ozmidov scale \(L_{OZ}\) in the turbulent patches inside the migrating layer (filled dots) and outside (empty dots) after sunset. The dashed line is the 1:1 relationship

Full size image

The analysis of the overturning length scales (see Fig. 9) shows that the scales inside the migrating layer (filled dots) were characterised by \(L_{T}\) constantly below \(L_{OZ}\). Overturns outside the layer (empty dots) were instead scattered around \(L_{T} \sim L_{OZ}\). The same difference was observed by Gregg and Horne (2009), but over a wider range for pelagic nekton. The fluctuations were also above the size of a single Daphnia (\(l_O=1\) mm). However, no significant and persistent differences in the displacements were generally observed between the situation outside and inside the migrating layer. This further suggests the hypothesis that no important fluctuations were generated by the migrating Daphnia and that no potential energy was created.

Fig. 10
figure 10

Eddy diffusivity coefficient \(K_V\) as a function of Daphnia spp. concentration from different studies in the literature. The green dot represents data from this study. The error bar shows the observed minimum and maximum concentration and the dot its mean. (Color figure online)

Full size image

Available estimations of the eddy diffusivity coefficient provide different values of \(K_V\), depending on the concentration of the swimming Daphnia aggregation (see Fig. 10). Laboratory experiment by Noss and Lorke (2014) provided \(K_V = 10^{-9}\) m2 s−1 with 4 org. L−1. Numerical simulations by Wang and Ardekani (2015) suggest instead that biomixing by zooplankton is a likely mechanism. \(K_V\) can be enhanced up to \(10^{-5}\) m2 s−1, but only using unrealistic concentrations of Daphnia. The observed mean concentration within the turbulent patches in our data varied instead between 4 and 60 org. L−1. These values were above the concentration employed by Noss and Lorke (2014) and three orders of magnitude smaller than those used in numerical estimations. In our study we estimated \(K_V = K_T= 10^{-7}\) m2 s−1, therefore vertically-swimming zooplankton did not affect the vertical thermal stratification in the lake.

In biomixing studies there are two zooplankton concentrations of interest: the background or daytime concentration \(C_b\) before the DVM and the concentration \(C_{DVM}\) in the migrating layer during the DVM. Other field studies report \(C_b\) values for Daphnia similar to those measured in Vobster Quay (Hembre and Megard. 2003; Rinke et al. 2007). However, it is not certain how \(C_{DVM}\) increases with respect to \(C_b\) in other lakes, because its value depends on the presence of other migrating species, predators and light conditions (Ringelberg 2010; Simoncelli et al. 2017). The experiment by Houghton et al. (2018) showed that A. salina (\(l_O=5\)–8 mm), swimming in tank-averaged concentration \(C_b> 46\) org. L−1, can generate irreversible mixing. Taking into account the smaller size of Daphnia (\(l_O=1\) mm) compared to A. salina, their smaller volume of influence and the maximum daytime concentration of \(C_b=23\) org. L−1 from our study, this suggests that at least double this concentration is needed for smaller zooplankton to enhance mixing in lakes. Unfortunately, we cannot draw any comparison for \(C_{DVM}\) we observed in Vobster Quay (maximum of 60 org. L−1), because in their experiment this concentration was not measured. Since zooplankton abundance is a lake and time-dependent factor, this does not rule out the possibility that collective action and synchronised movements of larger zooplankton and/or higher abundances may produce significant instabilities in other lakes.

Finally, other field methods besides turbulent microstructure profiling may provide insight into potential in situ mixing by migrating organisms. Acoustic methods for turbulence measurements, such as acoustic-Doppler velocimeters, need to be used with care, as the signal will be dominated by the swimmers as opposed to passive particles in the water. Submersible particle image velocimetry or tracer injections can instead help to directly assess if irreversible mixing is generated by small zooplankton in sufficient concentration.

Conclusions

In this study we measured in situ dissipation rates of temperature variance and estimated dissipation rates of TKE and eddy diffusivity in the metalimnion of a small lake during the diurnal vertical migration of a small zooplankton species to verify whether migrating zooplankton can trigger hydrodynamic instabilities and enhance vertical mixing in the lake interior. We did not observe important and persistent turbulent enhancements with respect to the background levels during the DVM of the zooplankton layer. No correlations between concentration and dissipation rates were observed. No biomixing was detected even though the estimated Daphnia abundances of almost 60 org. L−1 were fifteen times larger than those used in the laboratory experiment by Noss and Lorke (2014). This suggests that migrating Daphnia do not affect mixing at these concentrations. However, there might still be a concentration threshold over which synchronised movements of Daphnia may become relevant.