1 Introduction

To understand the mechanical properties of a fault, such as its strength and stability against a slip, investigations of the stress state around the fault are vitally important. For example, Zoback et al. (1987) estimated the stress state around the San Andreas fault, central California, and found that the orientation of the maximum horizontal compression (SHmax) is nearly normal to the fault. Sato et al. (2003) and Yamamoto and Yabe (2001) measured in situ stress near the Nojima fault, central Japan, on which the 1995 Southern Hyogo Prefecture Earthquake (M7.3) occurred. They showed that the shear stress acting on the fault was very small. These results suggest that some faults in the Earth’s crust are weak. On the other hand, Scholz (2000) claimed that the fault-normal compression in central California is a result of active folding in this area. He found that the SHmax direction in southern California has an angle of 30°–60° to the San Andreas fault, implying that the fault is strong. Yamashita et al. (2004) showed that the small shear stress on the Nojima fault was a result of the stress change associated with the coseismic slip. By correcting for the coseismic stress change, they found that the average ratio of the shear stress to the effective normal stress on the Nojima fault was ~ 0.6 before the earthquake. However, their estimate is strongly dependent on their assumptions regarding the pore pressure. Further, Yabe et al. (2008) detected localized stress perturbations close to both sides of the Chelungpu fault, central Taiwan, on which the 1999 Chi-Chi earthquake (Mw7.6) occurred. Thus, despite its importance, the issue of fault strength remains unresolved. Stress measurements around a fault are important, not only to determine the strength of the fault, but also to evaluate the likelihood of earthquake occurrence on the fault (e.g. Yabe & Omura, 2011; Yabe et al., 2010).

In deep gold mines in South Africa, a thin, tabular ore body (locally known as a “reef”) is excavated at depths larger than 3 km. Stresses around the mined-out stope are disturbed by several tens of MPa within a few hundred meters ahead of the stope (Chamber of Mines Research Organization, 1988). Nonlocal stress redistribution induced by relatively large-scale mining may cause relatively large earthquakes of up to M ~ 3 (strong enough to damage nearby mine workings) on preexisting weak planes or discontinuities, such as faults or dike contacts (Gay et al., 1984; Gibowicz & Kijko, 1994; Ziegler et al., 2015). The induced earthquakes occur within a few hundred meters of tunnels or stopes to which mine workers commute every day. Therefore, deep mines provide good opportunities to directly observe source faults of seismic events (e.g. Gay & Ortlepp, 1979; Heesakkers et al., 2011a, b; Mngadi et al., 2019). Further, it is possible to deploy an observation network very close to or within the source regions of the induced earthquakes (e.g. Ogasawara et al., 2002a, b; Reches et al., 2006). The closeness between the observation network and the seismic sources offers opportunities to record less distorted seismic signals (e.g. Yamada et al., 2005, 2007), and to reach the source fault itself with a short drill hole (e.g. Yabe et al., 2013).

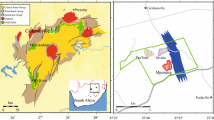
A local seismic network (~ 40 m span) consisting of eight acoustic emission (AE) sensors and two strain meters was installed along a tunnel at 3.3 km depth in Mponeng mine (Fig. 1), which is located ~ 70 km west of Johannesburg, in June 2006 by the JAGUARS (Japanese-German Underground Acoustic Emission Research in South Africa) project (Nakatani et al., 2008). The tunnel was ~ 90 m below a gold reef that was planned to be mined in 2006–2007 and passed through a 30-m-thick gabbroic dike, called the Pink and Green dike or, simply, the PG dike. Because the dike does not contain gold, it was left unmined as a dip pillar. The overburden weight above the stope concentrated on the PG dike in the JAGUARS site.

Fig. 1
figure 1

a Map view and b NNW–SSE and c WSW–ENE cross-sections of the studied area. Areas mined-out by 2007 and dikes are shaded light and dark gray, respectively. Red line shows the trace of the Y-hole. Red solid circle is drilling site of the Y-hole. Dots represent hypocenters of aftershocks. The dots are colored according to the occurrence time of aftershocks. Rectangle surrounding concentrated aftershocks in b represents an approximate rupture area of the mainshock. Black line segments are underground structures developed for mining. Only tunnels at 3.3 km depth are shown

Full size image

On 27 December 2007, ~ 6 months after the deployment of the JAGUARS network, an Mw2.2 earthquake (mainshock) occurred in the JAGUARS site. The hypocenter of the mainshock was located in the PG dike and ~ 30 m above the JAGUARS network (Naoi et al., 2011; Yabe et al., 2009). Its foreshock and aftershock activity was investigated in detail by Yabe et al. (2009, 2015) and Naoi et al. (2011).

Hofmann et al. (2012) used a homogeneous boundary element model (BEM) to investigate whether this event was induced by stress transfer due to nearby mining. Ziegler et al. (2015) developed a more realistic three-dimensional finite element model (FEM) to evaluate the Coulomb failure stress changes (ΔCFS) on the mainshock fault associated with mining excavation. Both concluded that the Mw2.2 earthquake was induced by mining activity. They also showed that the mainshock fault was the optimally oriented plane under the stress state produced by mining. Since no stress measurement had been carried out in Mponeng mine, Hofmann et al. (2012) and Ziegler et al. (2015) adopted the far-field stress state in Tau Tona mine (neighboring Mponeng mine) estimated by Lucier et al. (2009) as the initial stress state of the models. Therefore, more direct investigation of the stress state in the source area was essential to validate their findings.

Yabe et al. (2013) drilled a 90-m-long hole (Y-hole, hereafter) with an inclination of 22° penetrating the source region of the mainshock ~ 1.5 years after its occurrence. The Y-hole intersected the source fault of the mainshock at ~ 8 m south of the hypocenter. The aftershock distribution along the Y-hole showed a concentration at ~ 70 m from the borehole collar (Fig. 2), suggesting that the borehole intersected the source fault there. The borehole core samples were recovered from the Y-hole, except for a 10-m section in the hanging wall on the source fault. Core disking (CD) and borehole breakout (BO) were found to occur intermittently. Yabe et al. (2013) were able to constrain the principal stress state around the source fault based on the occurrence criteria for CD (Kaga et al., 2003; Li & Schmitt, 1998; Matsuki et al., 2004) and BO (Barton et al., 1988; Zoback et al., 1985). The slip direction of the mainshock was also used as a constraint. The calculated principal directions were roughly consistent with the focal mechanism solution of the mainshock. However, estimation errors of the principal directions were large. Only the upper and the lower limit of the principal stress magnitudes could be estimated.

Fig. 2
figure 2

A summary of statuses of the Y-hole and core modified from Yabe et al. (2013). a Black, gray, and red bars represent number of aftershocks in a 1-m-long cylinder along the Y-hole with radius of 5 m, 2 m, and 1 m, respectively. Background color shows rock type (orange, quartzite; light-blue, the PG dike; yellow, calcite vein). b Recovered core length. c Distribution of disking and indication of disking. d Status of borehole wall based on video image

Full size image

In the present study, we seek further constraints on the stress states. We apply Deformation Rate Analysis (DRA; Yamamoto, 2009; Yamamoto et al., 1990) and Diametrical Core Deformation Analysis (DCDA; Funato & Ito, 2017) techniques to the core samples. We then combine the DRA and DCDA measurements with the CD and BO occurrence criteria and the slip direction of the mainshock to determine the principal stress state in the source region more precisely.

2 Data and Methods

2.1 Overview of the Mainshock

Since the mainshock occurred during the end-of-year shutdown, more than 20,000 micro-earthquakes down to M ~ −4.4 (Kwiatek et al., 2010) were detected under low-noise environment by the JAGUARS network within the 150 h following the mainshock (Naoi et al., 2011). More than 13,000 of them formed a distinct planar cluster (~ 100 m × 80 m) on which the mainshock hypocenter lay. The aftershock plane has a strike subparallel to that of the PG dike and dip of ~ 60° to the northeast, cutting the dike diagonally (Fig. 1). Naoi et al. (2011) determined the CMT solution of the mainshock from seismic waveforms recorded by an ordinary seismic network operated by the mine. The mainshock had a normal fault mechanism, which is typical for mining-induced earthquakes in deep mines in South Africa. Because one of the nodal planes of the CMT solution coincided with the aftershock plane, the aftershock plane is thought to delineate the mainshock rupture plane.

Ogasawara et al. (2014) monitored the strain accumulation in the PG dike and in the host rock to the east of the dike from March 2007 using Ishii strain meters. The strain accumulation for ~ 9 months to the occurrence of the mainshock showed subvertical contraction and subhorizontal NE–SW extension in both the dike and the host rock. The amounts of the strain accumulation in the dike and the host rock were almost the same. This means that an increase in the subvertical compression associated with nearby mining was larger in the dike than in the host rock, because Young’s modulus of the dike is larger than that of the host rock (Table 1).

Table 1 Mechanical properties of rock samples in individual sections (Yabe et al., 2013)
Full size table

Based on the spatial and temporal evolution of the foreshock activity, Yabe et al. (2015) deduced the following mainshock nucleation process. The foreshocks concentrated in three clusters, which were interpreted to represent potential nucleation patches. Subsequent numerical modeling of the stress perturbation due to mining showed that two of the clusters were in a high shear stress zone on the mainshock fault (Hofmann et al., 2012). The foreshock activity in one of the nucleation patches in the high stress zone started to accelerate ~ 7 days before the occurrence of the mainshock, suggesting that this nucleation patch had reached a critical state. However, probably due to strength heterogeneity on the fault, the dynamic expansion of the critical patch was suppressed, although it continued to expand quasi-statically along the high stress zone. When the two nucleation patches in the high stress zone coalesced, the mainshock was finally initiated.

2.2 Stress Measurement Techniques

2.2.1 Diametrical Core Deformation Analysis (DCDA)

The DCDA method was proposed by Funato and Ito (2017). This technique measures the azimuthal variation in the diameter of a borehole core to estimate the differential stress in the plane normal to the borehole. The authors assumed that the borehole core expands elastically in response to stress relief when it is cut from rock mass by boring. The azimuthal variation in the diameter of the expanding core can be expressed by

$$d(\theta ) = \frac{{d_{{\rm max}} + d_{{\rm min}} }}{2} + \frac{{d_{{\rm max}} - d_{{\rm min}} }}{2}{\text{cos}}2(\theta - \alpha )$$
(1)

where \(d(\theta )\) is the core diameter at an azimuth \(\theta\), \(d_{{\rm max}}\) and \(d_{{\rm min}}\) are the maximum and the minimum diameter of borehole core, respectively, and \(\alpha\) is the azimuth of \(d_{{\rm max}}\). The maximum and the minimum diameter of the core sample can be related to the differential stress in the plane normal to the borehole by

$$\sigma_{x} - \sigma_{y} = \frac{{d_{{\rm max}} - d_{\rm min} }}{{d_{0} }}\frac{E}{1 + \nu } \approx \frac{{d_{{\rm max}} - d_{{\rm min}} }}{{d_{\rm min} }}\frac{E}{1 + \nu }$$
(2)

where \(\sigma_{x}\) and \(\sigma_{y}\) are the maximum and the minimum stress magnitudes, respectively, in the plane normal to the borehole. E and \({\nu }\) are Young’s modulus and Poisson’s ratio, respectively. d0 represents the diameter of the borehole core before it expands in response to the stress relief. Since it is difficult to know d0 in most cases, Funato and Ito (2017) assumed that \(d_{{\rm min}} - d_{0} \ll d_{0}\) and that \(\frac{{d_{{\rm max}} - d_{{\rm min}} }}{{d_{0} }}\) could be replaced by \(\frac{{d_{{\rm max}} - d_{{\rm min}} }}{{d_{{\rm min}} }}\).

Since borehole cores used in this study were not oriented, we measured the diameter of each borehole core every 2° from an arbitrary reference orientation along four or more profile lines separated by ~ 2 cm. The azimuthal variation in diameter can be disturbed for various reasons, such as dents on the core surface, inhomogeneous elasticity at a vein, and grooving during drilling. Therefore, consistency among phases of the azimuthal variations along profile lines on individual borehole cores was examined by the naked eye. If the out-of-phase variation was obtained along only one profile line, and other profile lines provided consistent diameter variations, data along the out-of-phase profile line were excluded from calculation of the average azimuthal variation. If the out-of-phase variations were found along two or more profile lines on a borehole core, the borehole core was not used for the DCDA.

The average azimuthal variation in each borehole core was calculated from the consistent azimuthal variations in its diameter. When a diameter on a profile line at an azimuth deviated by more than twice the standard deviation from the average diameter at the azimuth, the datum was regarded as an outlier. The average variation was then recalculated by excluding the outliers. The theoretical curve [Eq. (2)] was fitted to thus-obtained average azimuthal variation in core diameter to estimate \(d_{{\rm max}}\) and \(d_{{\rm min}}\).

2.2.2 Deformation Rate Analysis (DRA)

The DRA method was proposed by Yamamoto et al. (1990) and Yamamoto (2009) to recover the stress memory of a rock from hysteresis of the stress–strain curve under cyclic uniaxial loading. The hysteresis is evaluated by the strain difference function \(\Delta \varepsilon_{i, j} (\sigma )\) defined by

$$\Delta \varepsilon_{i, j} (\sigma ) = \varepsilon_{j} (\sigma ) - \varepsilon_{i} (\sigma ) ,\quad j > i,$$
(3)

where \(\sigma\) is the applied axial stress and \(\varepsilon_{i} (\sigma )\) is the axial strain for the i-th loading. The stress memory is revealed by the bending of this function. In this study, five cyclic loading–unloading tests were conducted to obtain the strain difference functions. Further detail of the DRA is described in previous studies (Hsieh & Dight, 2016; Sato et al., 2003; Wang et al., 2012; Yabe & Omura, 2011; Yabe et al., 2008, 2010; Yamamoto, 2009; Yamamoto et al., 1990;). Further, de Andrade Penido (2021) demonstrated an advantage of simultaneous application of DCDA and DRA.

2.2.3 Borehole Breakout (BO) and Core Disking (CD)

When a borehole is drilled in a rock mass under compressional stresses, the compressional stresses are enhanced on the borehole wall due to stress concentration, while a tensile stress is induced ahead of the borehole bottom. If the enhanced compression is larger than the uniaxial compression strength (UCS) of the rock mass, borehole breakout (BO) takes place on the borehole wall in the direction of the minimum compression in the plane normal to the borehole (\(\sigma_{y}\)). In the case where the magnitude of tensile stress ahead of the borehole end reaches the uniaxial tensile strength (UTS) of the rock mass, core disking (CD) occurs. Therefore, the occurrence of BO and CD provides clues to constrain stresses, if the UCS and the UTS are known.

The occurrence criterion of BO is given by Zoback et al. (1985) and Barton et al. (1988) as the following:

$${\text{UCS}} \le 3\sigma_{x} - \sigma_{y} - P$$
(4)

where P is pore pressure. Because water is drained from rock mass in gold mines in South Africa before mining operations commence, it is assumed that \(P = 0\) in this study. The occurrence of BO was visually determined by inspection of the borehole wall by an optical televiewer. Because of the low resolution of the televiewer (Fig. 3a), the orientation of BO could be measured with precision of ~ 10°.

Fig. 3
figure 3

An example screenshot of a BO at 69.8 m depth (distance from the hole collar) and b exfoliation at 79.5 m depth on the Y-hole wall. Because the borehole wall was covered by a black material, probably relating to a microorganism, they are not well seen on the screenshots. However, they are clearly recognized in the movie. White dashed line in a traces the borehole wall. c Indication of CD observed on cores recovered from 22–24 m depths of the Y-hole. d A close-up view of Y22 enclosed by a red box in c. White arrows point to indications of CD

Full size image

The occurrence criteria of CD are expressed by

$${\text{UTS}} = - A\sigma_{m} + B\sigma_{x} - D(\sigma_{x} - \sigma_{y} )$$
(5)
$$- \sigma_{y} + \frac{19}{{11}}\sigma_{z} \le \sigma_{x} \le 17\sigma_{y} - 7\sigma_{z}$$
(6)

where the coefficients A, B and D are functions of the disk thickness, \(\sigma_{z}\) is the normal stress parallel to the borehole and \(\sigma_{m}\) is the average of \(\sigma_{x} ,\; \sigma_{y}\) and \(\sigma_{z}\) (Kaga et al., 2003; Matsuki et al., 2004). In this study, the thicknesses of ~ 10 disks in each section of continuous occurrence of the CD were averaged to determine the coefficients A, B and D.

3 Results

Because the DCDA is a nondestructive and time-efficient technique, we used this technique as the first option to measure the differential stress in the plane normal to the Y-hole. When CD occurred, \(\sigma_{z}\) could be constrained from the occurrence criteria of CD. However, CD did not occur in the dike-footwall section, except at a calcite vein with a thickness of a few decimeters. We applied the DRA to borehole cores recovered from the dike-footwall section to evaluate \(\sigma_{z}\) in this section. The differential stress in the plane normal to the Y-hole in the dike-footwall section was also estimated by the DRA to confirm consistency between measurements by the DCDA and the DRA.

3.1 Borehole Breakout and Core Disking

BOs in the Y-hole and CDs of its cores were investigated by Yabe et al. (2013, Fig. 2). Their results are briefly summarized below.

The contact between the PG dike and the host rock was identified at a distance of 54.2 m from the Y-hole collar. Borehole cores were not recovered within a distance of 70–80 m (just after passing the fault). The UCS and the UTS were measured by uniaxial compression (test piece size was 14 mm in diameter and 36 mm in length) and Brazilian tests (42 or 27 mm in diameter and 21.5 or 16.5 mm in thickness), respectively. These strength values of the host rock, the dike-footwall and the dike-hanging wall, as well as their elastic moduli evaluated from the deformation during the UCS test, are summarized in Table 1 (see also Supplementary Information for data for each test piece). These values are used to constrain stresses based on the occurrence criteria of BO and CD.

Figure 4a shows the orientation of BOs and exfoliations with respect to the distance from the mainshock fault along the Y-hole. The orientation is measured counterclockwise from the horizontal by looking from the borehole collar. Exfoliation is revealed by continuous paired light damage or series of paired dents on the opposite sides of the borehole wall (Fig. 3b). Because the orientations of exfoliation are consistent with those of BO (Fig. 4a), we considered that the exfoliation is an initial stage of BO under a condition that the tangential stress concentration on the borehole wall is almost equal to the UCS of the rock mass. Therefore, the occurrence of the exfoliation may give tighter constraints on the stress magnitude than that of BO, because it can occur only when equality between both sides of Eq. (4) are satisfied. Further, the orientation of the exfoliation represents the orientation of \(\sigma_{y}\).

Fig. 4
figure 4

Spatial variation in a orientation of borehole breakout (solid circles) and exfoliation (open circles) on the borehole wall, b thickness of disking (solid squares) and interval between indications of disking (open squares), and c the differential stress in the plane normal to the Y-hole estimated by DCDA (solid diamonds), DRA (open diamonds) and Yabe et al. (2013; gray bars) with respect to the distance from the mainshock fault along the Y-hole. Black dashed lines represent location of the dike contact and the fault that divide the host rock, the dike-footwall, and the dike-hanging wall sections. Gray dashed line indicates location of calcite vein

Full size image

Along the Y-hole, BO and the exfoliation were found at several places over the host rock and the dike-hanging wall sections. In the dike-footwall section, BO and the exfoliation occurred at limited points near the fault and the contact. Except for proximity to the fault, the orientations of BO and the exfoliation are about −20° irrespective of the rock types. The orientation seems to rotate from 10° to −30° with an increase in the distance from the fault from −0.75 m (in the dike-footwall) to 3.4 m, (in the dike-hanging wall), probably reflecting such stress disturbance localized to the mainshock as reported by Yabe et al. (2008).

CD occurred on the borehole cores in the host rock section and in the dike-hanging wall section, while there was no CD in the dike-footwall section, except at the calcite veins. The average thickness of core disks in the dike-hanging wall section showed a systematic variation with distance from the fault (Fig. 4b). That is, it increases from 10.6 to 16.7 mm with an increase in the distance from the fault from 6 to 11.6 m. This suggests that the stresses rapidly decrease with an increase in the distance from the fault.

In the host rock section, it was observed that damages accumulate along evenly spaced annulus lines on the periphery of a core (Fig. 3c, d), while the core was not split. Li and Schmitt (1998) and Matsuki et al. (2004), for example, demonstrated that tensile stress around the borehole end induced by drilling is the largest at the periphery of the root of the core stub. The damage accumulation should represent nucleation of CD (tensile fracture along a plane normal to the borehole) or indication of CD under a condition that the tensile stress at the periphery of the root of the core stub is slightly less than the UTS. Therefore, the average separation of the damage accumulation lines is also plotted in Fig. 4b. Although they are within error ranges of each other, a tendency for the distance between damage accumulation lines to be greater than the thickness of CDs in the host rock is consistent with the abovementioned interpretation of the peripheral damage accumulation as the indication of CD.

3.2 Differential Stress Measured by Diametrical Core Deformation Analysis

Figure 5 shows examples of DCDA data in individual sections. DCDA was applied to 21 pieces of the borehole core, among which seven pieces were recovered from the host rock section and 13 pieces were from the dike-footwall section. Because the first 10 m of borehole cores in the dike-hanging wall section was severely damaged, only one piece could be measured by DCDA in this section. However, because nine pieces showed incoherent azimuthal variations in diameters, the \(d_{{\rm max}}\) and \(d_{{\rm min}}\) were obtained only from 12 pieces (four from the host rock, seven from the dike-footwall, one from the dike-hanging wall). When an anisotropy of rock mass from which a borehole core was recovered is significant, the differential stress estimation by DCDA is degraded. Figure 6 shows azimuthal variations in Young’s modulus and Poisson’s ratio in the plane normal to the Y-hole obtained from stress–strain curves during the UCS test. It should be noted that the azimuth is measured from an arbitrary reference, which may be different from the reference orientation of DCDA, since the Y-hole core is not oriented. When a sinusoidal function is fitted, the largest anisotropy of Young’s modulus and Poisson’s ratio is estimated to be 14% and 22%, respectively, in the dike-hanging wall. Our preliminary calculation (in preparation) indicates that an anisotropy of ~ 15% would cause ~ 10% error of the DCDA measurement. Further, variations in these elastic moduli at individual azimuths are similar to or larger than the magnitudes of anisotropy, implying that the estimated magnitudes of anisotropy are apparent. Therefore, we consider that an error of the differential stress estimated by DCDA is less than 10%.

Fig. 5
figure 5

Examples of azimuthal variations in the diameter of borehole cores recovered from a the host rock (41 m depth), b the dike-footwall (54 m depth) and c the dike-hanging wall (89 m depth) sections measured by DCDA. Thin light gray and thick dark gray curves show raw data and their average, respectively. Thick black dashed curve is the best-fitted sinusoidal function

Full size image
Fig. 6
figure 6

Azimuthal variation in Young’s modulus (black solid circles, left axis) and Poisson’s ratio (red solid diamonds, right axis) of borehole cores recovered from a the host rock (34 m depth), b the dike-footwall (64 m depth) and c the dike-hanging wall (82 m depth) sections. Black and red curves are the best-fitted sinusoidal function to Young’s modulus and Poisson’s ratio, respectively

Full size image

Spatial variation in the differential stress determined by DCDA is shown in Fig. 4c with respect to the distance from the mainshock fault along the Y-hole. The differential stresses are 20–30 MPa in the host rock section. It is also 20–30 MPa near the contact in the dike-footwall, while it increases to ~ 100 ± 30 MPa in the dike-footwall section away from the contact. Twin densities of the calcite in the dike-footwall were counted to evaluate the maximum differential stress to be ~ 95 MPa at a point close to the fault (Janssen, personal communication; Rybacki et al., 2013). This is consistent with the differential stress measured by DCDA. The differential stress in the dike-hanging wall section is reduced to ~ 80 MPa, though this is within the error of the differential stress in the dike-footwall.

3.3 Stresses Measured by Deformation Rate Analysis

Normal stresses parallel to the Y-hole axis (\(\sigma_{z}\)) and in four directions (every 45°) in the plane normal to the Y-hole were measured by DRA using core samples recovered from the dike-footwall section at 59 m (Y59) and 68 m (Y68) distances from the hole collar of the Y-hole. Figure 7 shows examples of the strain difference functions obtained from three specimens of Y59 parallel to the Y-hole. Clear bending at 50–70 MPa is commonly seen on these strain difference functions. Though less clear than these cases, other strain difference functions also bend at similar stresses. By taking average of the bending stresses among the strain difference functions, the magnitude of \(\sigma_{z}\) at Y59 was determined to be 61.3 ± 6.4 MPa.

Fig. 7
figure 7

Examples of the strain difference functions parallel to the axis of the Y-hole at a distance of 59 m from the borehole collar. Dashed lines are shown to emphasize the bending of the strain difference functions indicated by arrows. Text inserted to the upper-right of each strain difference function in the form of “Y59-aaa-bb-c i-j” means that the strain difference function was obtained from a borehole core recovered from a distance of 59 m along the Y-hole by taking the difference between the stress–strain curves of the i-th and j-th loading applied on the c-th subsample cut in the orientation of aaa from a reference direction and the plunge of bb from the plane normal to the borehole

Full size image

Figure 8 shows the strain difference functions obtained from specimens in the plane normal to the Y-hole at Y59. Azimuthal variations in normal stress in the plane normal to the Y-hole at Y59 and Y68 are plotted in Fig. 9. The magnitude of σz at Y59 is also shown in Fig. 9a. The azimuthal variation in normal stress can be expressed by \({\sigma } ( \theta ) = \sigma_{i} + 0.5\sigma_{d} {\text{cos}} ( {2 ( {\theta - \phi } )} )\), where \(\theta\) is azimuth from a reference direction and \(\phi\) is azimuth of the maximum compression. \(\sigma_{i} =0.5( \sigma_{x} + \sigma_{y})\) and \(\sigma_{d} = \sigma_{x} - \sigma_{y}\) are the isotropic and the differential stress, respectively. By fitting this function to the normal stresses determined by DRA, the isotropic and differential stresses at Y59 and Y68 are estimated to be 70–80 MPa and ~ 70 MPa, respectively. As shown in Fig. 4c, the differential stresses estimated by DRA and DCDA are consistent with each other, suggesting that the two techniques have similar reliability in the estimation of the differential stress.

Fig. 8
figure 8

Same as Fig. 7, but of subsamples in a 0°, b 45°, c 90° and d 135° from an arbitrary reference direction on the plane normal to the Y-hole

Full size image
Fig. 9
figure 9

Azimuthal variation in the normal stress in the plane normal to the Y-hole at depths of a 59 m and b 68 m. Open circles with error bar and a curve represent normal stresses determined for each subsample and the best-fitted sinusoidal function, respectively. Shaded area in a shows the magnitude of normal stress along the Y-hole at a depth of 59 m. Note that the reference orientation is arbitrary

Full size image

3.4 Retrieved Principal Stress State

The principal stress state in the source region of the mainshock was estimated by the following grid-search procedure; (1) a set of three magnitudes of the principal stress (\(\sigma_{1} \ge \sigma_{2} \ge \sigma_{3}\)) and three rotation angles of the principal direction (\(\phi_{1}\), \(\phi_{2}\), \(\phi_{3}\); see Fig. 10 for the definition) is given. The given principal magnitudes were in a range from 0 to 300 MPa, at 5 MPa intervals. Because of their symmetry, the given principal directions were in a range from 0° to 180°, at 5° intervals. (2) Magnitudes of \(\sigma_{x}\), \(\sigma_{y}\) and \(\sigma_{z}\) and orientation of \(\sigma_{y}\) under the stress state given in (1) are calculated. (3) It is tested if these stresses are consistent with DCDA (\(\sigma_{x} - \sigma_{y}\)) and DRA (\(\sigma_{z}\), \(\sigma_{x} + \sigma_{y}\)) measurements within errors. Further, it is also examined if these stresses satisfy the occurrence criteria of BO and/or CD within errors of the strength measurements. The orientation of σy is compared with that of BO on the Y-hole wall to confirm that they are consistent within the BO orientation error of 20°. The coseismic slip direction of the mainshock is also considered. That is, misfit between direction of the maximum shear stress resolved on the mainshock fault and the slip direction should not be larger than 45°. (4) If the given principal stress state satisfies all conditions tested in (3), a unity score is added to individual bins of the principal stress magnitudes and those of the principal directions. (5) The principal stress magnitudes and the principal directions with the largest score are regarded as the most robust estimation of the principal stress, because a higher score of a parameter means that its adaptability to the conditions tested in (3) is less affected by values of the other parameters.

Fig. 10
figure 10

Definition of the rotation angles in the grid-search procedure to estimate the principal stress state. E, N and U denote the east, the north and upward, respectively. E″-, N″- and U″-axes are supposed to be axes of the maximum, the intermediate, and the minimum principal stress, respectively

Full size image

Stress measurement methods and conditions to be satisfied to constrain the principal stress in individual sections along the Y-hole are listed in Table 2. Errors given in Table 2 are set to twice the standard deviation of individual measurements. As BO did not occur in the dike-footwall section, the stress concentration on borehole wall (\(3\sigma_{x} - \sigma_{y}\)) in this section is required to be less than UCS. Strictly speaking, at a point where CD occurred, DCDA or DRA measurements cannot be applied. Therefore, the conditions to reproduce DCDA and DRA measurements and those to satisfy the occurrence criteria of CD are not necessarily required to be satisfied at the same time. However, for simplicity, it was assumed that the stress state is uniform in each section along the Y-hole and that all conditions should be satisfied at the same time.

Table 2 Stress measurement techniques and conditions used to constrain the principal stress in individual sections
Full size table

Figure 11 shows the score distributions of individual parameters of the principal stress. Scores of all parameters in the host rock and the dike-hanging wall sections showed a single peak distribution. The most robust estimations could be uniquely determined in these sections. However, in the dike-footwall section, while the principal stress magnitudes and the third rotation angle (\(\phi_{3}\)) could be determined uniquely, scores of the first (\(\phi_{1}\)) and the second (\(\phi_{2}\)) rotations show two peaks. That is, \(\phi_{1}\) = 7.5° or 97.5°, and \(\phi_{2}\) = 27.5° or 112.5°. This may be because no information of \(\sigma_{y}\) orientation was obtained in this section. Four candidates of the principal axes are plotted on the lower hemisphere in Fig. 12. Background colors of this figure represent scores counted every 10° × 10° bins in azimuth and dip of the principal axis and normalized by its maximum for each axis. The normalized score of the maximum stress axis distributes in a broader region from (0, 30) to (270, 60) in azimuth (measured clockwise from north) and dip, while those of the intermediate and the minimum stress show a single peak at about (200, 0) and (100, 30), respectively. The combination of rotation angles with which the principal axes come close to the respective high score regions is (\(\phi_{1}\), \(\phi_{2}\), \(\phi_{3}\)) = (97.5°, 27.5°, 137.5°). Therefore, this combination of rotation angles is adopted as the robust estimation in the dike-footwall region.

Fig. 11
figure 11

Score distribution of the principal stress magnitudes and rotation angles of the principal axes that satisfy the constraint conditions in each section (Table 2) of a, b the host rock, c, d the dike-footwall and e, f the dike-hanging wall

Full size image
Fig. 12
figure 12

Comparison of the four candidates of the maximum (red symbols), the intermediate (green symbols), and the minimum (blue symbols) stress axes with distribution of the normalized scores projected to the lower hemisphere. N denotes the north. The numerals in parentheses on the right represent the rotation angles (\(\phi_{1}\), \(\phi_{2}\), \(\phi_{3}\)). Colors of small circles represent normalized score distribution of the individual principal axes by color scales at the bottom

Full size image

The principal stress state thus obtained in each section is shown in Fig. 13, in which those within a half-width of the score distribution are also plotted as a proxy of the estimation errors.

Fig. 13
figure 13

The principal stress state in individual sections determined by the grid-search procedure. Lower-hemisphere projections on top represent the principal axes with the highest scores (large circles) and those within a half-width of the score distribution (small circles) in individual sections. Red, green and blue symbols are for the maximum, the intermediate and the minimum principal stresses, respectively. N denotes the north. The mainshock fault plane and slip direction are shown by a black curve and a gray dot, respectively. Black plus sign represents the Y-hole direction. Thick horizontal bars in the lower panel show the principal stress magnitudes with the highest scores. The half width of the score distribution of the principal stress magnitude is shaded by the corresponding color

Full size image

The axes of \(\sigma_{1}\), \(\sigma_{2}\) and \(\sigma_{3}\) in the host rock section are well constrained to be about (318, 73), (119, 17) and (211, 5), respectively, in azimuth and dip. The \(\sigma_{3}\)-axis is almost parallel to the Y-hole. The most robust estimations of the principal stress magnitudes are \(\sigma_{1}\) = 102.5 MPa (98–110 MPa), \(\sigma_{2}\) = 87.5 MPa (75–96 MPa) and \(\sigma_{3}\) = 2.5 MPa (≤ 8 MPa). Here, the stress magnitude ranges in parentheses indicate the stress values where scores were larger than half the maximum score. For the minimum principal stress, since the largest score was at the lowest given magnitude (2.5 MPa), only its upper limit could be identified from score distribution.

The principal directions of \(\sigma_{1}\), \(\sigma_{2}\) and \(\sigma_{3}\) in the dike-footwall section are (353, 28), (240, 37) and (109, 41), respectively, being significantly different from those in the host rock and the dike-hanging wall sections. One of the most significant features is that dip of \(\sigma_{1}\)-axis is slightly smaller than those of \(\sigma_{2}\)- and \(\sigma_{3}\)-axes. This means that stress regime in this section is revers faulting, rather than the normal faulting regime that is typical in deep mines in South Africa. The principal stress magnitudes are \(\sigma_{1}\) = 97.5 MPa (93–109 MPa), \(\sigma_{2}\) = 52.5 MPa (20–66 MPa) and \(\sigma_{3}\) = 2.5 MPa (≤ 8 MPa).

The principal directions of \(\sigma_{1}\), \(\sigma_{2}\) and \(\sigma_{3}\) in the dike-hanging-wall section are (333, 58), (100, 21) and (200, 23), respectively. These are nearly identical to those in the host rock within error. However, the principal stress magnitudes are \(\sigma_{1}\) = 137.5 MPa (130–145 MPa), \(\sigma_{2}\) = 57.5 MPa (48–67 MPa) and \(\sigma_{3}\) = 2.5 MPa (≤ 17 MPa). That is, \(\sigma_{1}\) is ~ 30% larger and \(\sigma_{2}\) is ~ 30% smaller than those in the host rock.

4 Discussion

4.1 Relation to the Mw2.2 Earthquake

The P-, T- and B-axes of the CMT solution of the mainshock determined by Naoi et al. (2011) are projected on the lower hemisphere with the principal stress axes in the host rock section in Fig. 14a. P- and T-axes agree well with the maximum and the minimum stress axes, respectively, in this section. Since we used the slip direction on the fault calculated from the CMT solution to constrain the principal stress, this agreement could be artifact. To test this concern, we carried out the grid-search without the constraint condition of the slip direction. The obtained stress state is shown in Fig. 14b. While the error ranges of the principal stress axes become larger, both magnitudes and directions of the principal stress are almost unchanged. Therefore, the good agreement of P- and T-axes with \(\sigma_{1}\)- and \(\sigma_{2}\)-axes, respectively, is reliable. Shear stress along the slip direction of the mainshock relative to normal stress acting on the fault takes the largest scores in a range of 0.5–0.6, being consistent with a typical friction coefficient of dry rocks (Byerlee, 1978). This suggests that the mainshock occurred on the preferably oriented fault, as was pointed out by Ziegler et al. (2015). Further, it implies that our assumption that the fault was dry and \(P = 0\) in Eq. (4) was suitable.

Fig. 14
figure 14

The principal axes in the host rock section estimated a with and b without constraint of slip direction on the mainshock fault. Numerals in parentheses are magnitude of the maximum, the intermediate and the minimum stresses (\(\sigma_{1}\), \(\sigma_{2}\), \(\sigma_{3}\)) in MPa. Score distribution of \(\sigma_{1}\)-axis in the dike-footwall c with and d without constraint of slip direction. Black crosses in a and c show P-, T- and B-axes of the CMT solution obtained by Naoi et al. (2011). Black plus sign is the Y-hole direction

Full size image

Since BO did not occur in the dike-footwall section, the only constraint condition on the principal direction in this section is the slip direction of the mainshock. Figure 14c shows the score distribution of the \(\sigma_{1}\)-axis in this section obtained with the constraint of the slip direction. The high-score area is limited around the P-axis. When the constraint of the slip direction is omitted, the high-score area shows a zonal distribution (Fig. 14d). Therefore, the constraint of the slip direction plays an important role in constraining the principal direction in this section of the borehole where there is no information of stress orientation in the plane normal to the borehole.

4.2 Relation to Far-Field Stress State

Figure 15 compares the principal stress state in the host rock (quartzite) section determined in this study with those obtained by Lucier et al. (2009) and Ogasawara et al. (2013). Lucier et al. (2009) modeled the far-field stress state of Tau Tona mine (neighboring Mponeng mine) based on the distribution of borehole failures (BO and drilling induced tensile fracture) along multiple boreholes in quartzite. They concluded that the far-field stress state is a normal faulting regime as shown in Fig. 15b and that gradients of the principal stress magnitude are \(\sigma_{1}\) = 27 MPa/km, \(\sigma_{2}\) = 26 MPa/km and \(\sigma_{3}\) = 13 MPa/km. The principal stress magnitude in Fig. 15b is calculated from these gradients and depth of the JAGUARS site (3.3 km). Ogasawara et al. (2013) measured in situ stress at 3.4 km depth in Mponeng mine by a stress relief technique (Compact Conical-ended Borehole Overcoring, CCBO; Sugawara & Obara, 1999). As their measurement was carried out in quartzite at a site less affected by mining, their result can be proxy of the unaltered virgin stress state in this mine. The principal direction and magnitude of the virgin stress are shown in Fig. 15c. Considering estimation errors of ± 10–20°, the principal directions are consistent among these studies. However, the magnitudes of \(\sigma_{1}\) estimated in this study is ~ 10 MPa larger than those obtained by Lucier et al. (2009) and Ogasawara et al. (2013). On the other hand, the magnitude of \(\sigma_{3}\) estimated in this study is much smaller than that by Lucier et al. (2009) and Ogasawara et al. (2013). This is caused by the alteration of the stress state by mining and the earthquake, as discussed in the next section.

Fig. 15
figure 15

Comparison of the principal stress state in quartzite estimated a in this study with those obtained by b Lucier et al. (2009) and c Ogasawara et al. (2013). Red, green and blue circles denote the maximum, the intermediate and the minimum stress axes, respectively. Numerals in parentheses are magnitudes of the maximum, the intermediate and the minimum stresses (\(\sigma_{1}\), \(\sigma_{2}\), \(\sigma_{3}\)) in MPa. Thick black plus sign in a is the Y-hole direction. The mainshock fault and slip direction is drawn by a thin black curve and a gray dot in a

Full size image

4.3 Alteration of Stress State by Mining and Faulting

4.3.1 Stress Transfer by Mining

As stated earlier, Ogasawara et al. (2014) observed subvertical contraction and subhorizontal NE–SW extension in both of the host rock and the PG dike for 9 months before the mainshock. While the amplitudes of these deformations in the host rock and the dike were almost equal to each other, stress changes were estimated to be larger in the dike because of a larger Young’s modulus.

As the \(\sigma_{1}\)-axis of the virgin stress state is subvertical, it should be enhanced by the increase in subvertical compression by mining. Further, the NE–SW orientation of the extension induced by mining is nearly parallel to the \(\sigma_{3}\)-axis of the virgin stress state. Hence, the magnitude of \(\sigma_{3}\) should be reduced. Thus, the larger magnitudes of \(\sigma_{1}\) and smaller magnitudes of \(\sigma_{3}\) estimated in the host rock and the dike-hanging wall sections than those of the virgin stress may be caused by the mining induced stress transfer. However, since the estimated stress state in the dike-footwall significantly differs from the virgin stress state, a stress alteration mechanism in addition to the stress transfer by mining is needed.

The vertical stress (qv in MPa) in gold mines in South Africa is expressed by a standard stress model (Jager & Ryder, 1999);

$$q_{{\rm v}} = 0.027 h$$
(7)

where h is the depth from ground surface in meters. As the depth of the JAGUARS site is ~ 3300 m, the expected vertical stress is 89 MPa. The vertical stresses in the host rock, the dike-footwall and the dike-hanging wall sections estimated in this study are \(\sigma_{{\rm v}}\) = 100 MPa, 40 MPa and 106 MPa, respectively, and 81 MPa on average. As uncertainty of our estimation is several or a dozen MPa, the average vertical stress is consistent with the standard model. The spatial variation in the vertical stress is induced partly by the stress transfer by mining, as stated above. However, since the distance from the Y-hole to the nearest mining area was ~ 90 m and both sides of the PG dike were excavated, such a large difference as 66 MPa between the vertical stress in the dike-footwall and the dike-hanging wall sections within a short distance of ~ 20 m is unlikely attributable to the stress transfer by mining. This significant contrast of the vertical stresses should be a result of the stress redistribution by the mainshock.

4.3.2 Stress Redistribution by the Mainshock

The aftershock distribution on a cross-section normal to the fault strike at the intersection of Y-hole with the mainshock fault delineates a nonplanar geometry of the fault (Fig. 16). While the aftershocks shallower then the mainshock hypocenter align along a steeply (82°) dipping plane with a width of ~ 35 m, those deeper than the hypocenter align along a moderately (58°) dipping plane with a width of ~ 25 m. As the intersection of Y-hole with the fault coincides with this bending of the fault, the non-planarity of the fault should asymmetrically disturb the stress states in the hanging wall and the footwall.

Fig. 16
figure 16

Perturbation to the vertical stress induced by the mainshock with respective slips on the steeply dipping upper and the moderately dipping lower fault segment of a 10 mm and 10 mm, b 12 mm and 9 mm, and c 15 mm and 5 mm. A yellow star and black dots represent hypocenters of the mainshock and aftershocks, respectively Aftershocks within 5 m from the vertical plane on which the intersection of the Y-hole with the mainshock fault lays are plotted. The focal mechanism solution of the main shock projected on a vertical plane normal to the strike of the mainshock fault is shown in a. Green line is projection of the Y-hole trace. White lines along the aftershock distribution are assumed fault segments to calculate the stress change distribution shown by red-to-blue color scale. A paired-arrow attached to each segment indicates slip sense on the segment. Shaded area is the host rock (quartzite)

Full size image

The seismic moment (\(M_{0}\)) is related to the moment magnitude (\(M_{w}\)) by \(\log M_{0} = 1.5 M_{w} + 9.1\). The average slip (d) on a fault can be estimated from the seismic moment by \(M_{0} = \mu Sd\), where \(\mu\) and \(S\) are the rigidity and the fault area, respectively. Taking into account a fault length of 100 m estimated from the aftershock distribution (Fig. 1b) and the rigidity of ~ 34 GPa calculated from Young’s modulus and the Poisson ratio of the PG dike (Yabe et al., 2013, Table 1), the average slip of the mainshock is estimated as ~ 10 mm when the slip is uniform over the two fault segments of the steeply and the moderately dipping planes.

To evaluate the stress redistribution in close proximity to the fault, we need detailed information regarding the coseismic slip distribution on the fault. However, seismic waveforms recorded by the mine-wide network were not of sufficiently high frequency to resolve the slip distribution of such a small earthquake as Mw2.2. Waveforms recorded by the JAGUARS network were saturated. Therefore, we assume that the slip on each of the two fault segments is rather uniform with a rake of −90° (normal fault). Further, for simplicity, only vertical stress disturbance is evaluated.

Hofmann et al. (2012) numerically evaluated a distribution of shear stress increases on the mainshock fault due to mining to suggest that slip in the upper half of the fault was much larger than that in the lower half. Therefore, we assumed three models of slips on the upper and the lower fault segments to be (a) 10 mm and 10 mm, (b) 12 mm and 9 mm and (c) 15 mm and 5 mm, respectively. The slips on the segments in individual models were adjusted to increase their difference between the segments from (a) to (c), but to conserve the seismic moment. Stress disturbance by the mainshock has been evaluated using Coulomb 3.3 (Lin & Stein, 2004; Toda et al., 2005), in which deformation of rock mass associated with slips on faults is calculated using Green’s functions of Okada (1992).

As shown in Fig. 16, all three models predict a decrease in the vertical stress by several tens of MPa in a region that the Y-hole passes in the footwall. This agrees with our estimations of vertical stress as small as \(\sigma_{{\rm v}}\) = 40 MPa in the dike-footwall. In contrast, the extent of a region with an increase in the vertical stress by more than a few MPa in the hanging wall shows significant variation among models. That is, the region where the vertical stress is significantly increased becomes wider, as the difference between slips on the upper and the lower fault segment is larger. The observation that the continuous occurrence of BO is limited to 10 m from the fault (Fig. 2) suggests that the extent of the region of significantly increased vertical stress is 10 m. Among the three models tested, model (b) shows a good agreement with this observation. These comparisons of the model prediction on the disturbance of the vertical stress and the observations imply that the reduction in the vertical stress in the dike-footwall was mostly caused by the non-planarity of the fault, while the significant enhancement of the vertical stress in the dike-hanging wall requires a nonuniform slip on the nonplanar fault.

5 Conclusions

Borehole cores were recovered from a borehole intersecting the source fault of an Mw2.2 earthquake that occurred in a gabbroic dike at ~ 3.3 km depth in a deep mine in South Africa. They were analyzed to constrain the principal stress state in the source region of the Mw2.2 earthquake. The source region was divided into three sections along the borehole from the hole collar: the host rock of the dike, the footwall in the dike (dike-footwall) and the hanging wall in the dike (dike-hanging wall). The differential stress in the plane normal to the borehole in each segment was measured by the DCDA method. The isotropic component of the stress in the plane normal to the borehole and the normal stress along the borehole were determined by the DRA method. These demonstrate that the DCDA and the DRA are useful techniques to measure stresses at a depth as great as ~ 3.3 km. Furthermore, they can contribute to the mitigation of the risks of rock bursting in deep mines.

In addition to DCDA and DRA, criteria for borehole breakout and core disking and the coseismic slip direction were taken into account to constrain the principal stress state in each section. The maximum stress directions in the host rock and the dike-hanging wall were subvertical, being almost identical to that in an area where the effect of mining was minimal. These principal directions agree well with the focal mechanism solution of the Mw2.2 earthquake. The average vertical stress among the three sections was consistent with that expected at the depth of studied site from a standard model for the mining district.

It was found that the vertical stresses in the footwall was reduced and that it was enhanced in the hanging wall of the fault of the Mw2.2 earthquake. The former seems attributable to the stress redistribution due to a coseismic slip on a nonplanar fault, which was delineated by the precisely determined aftershock distribution. The latter cannot be reproduced by a uniform slip on the nonplanar fault, but requires a nonuniform slip suggested by the numerically evaluated shear stress distribution, in addition to the non-planarity of the fault.